Первый слайд презентации: Математическая статистика. Числовые характеристики распределений. Нормальное распределение
Автор: доцент кафедры информатики и математики Грязнов Сергей Александрович ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА
Слайд 2: Основные понятия
Для экспериментальных данных, полученных по выборке, можно вычислить ряд числовых характеристик (мер)
Слайд 3: Мода
Числовой характеристикой выборки, как правило, не требующей вычислений, является так называемая мода. Мода — это такое числовое значение, которое встречается в выборке наиболее часто. Мода обозначается иногда как X.
Слайд 4: Мода. Пример
В ряду значений (2, 6, 6, 8, 9, 9, 9, 10) модой является 9, потому что 9 встречается чаще любого другого числа. Мода представляет собой наиболее часто встречающееся значение (в данном примере это 9), а не частоту встречаемости этого значения (в данном примере равную 3).
Слайд 5: Мода. Правила нахождения
1) В том случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды. Например: 5, 5, 6, 6, 7, 7 — в этой выборке моды нет.
Слайд 6: Мода. Правила нахождения
2) Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений.
Слайд 7: Мода. Правила нахождения
Например, в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1). Следовательно, модой этого ряда будет величина
Слайд 8: Мода. Правила нахождения
3)Если два несмежных (не соседних) значения в выборке имеют равные частоты, которые больше частот любого другого значения, то выделяют две моды. В ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной.
Слайд 9: Мода. Правила нахождения
Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод). Например: 1, 2, 2, 2, 5, 7, 8, 8, 8, 12, 15, 15, 15 или 35, 35, 40, 43, 43, 52, 64, 64, 70, 71, 86, 86
Слайд 10: Мода. Правила нахождения
4)Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной группой.
Слайд 11: Медиана. Определение
Медиана — обозначается ( X с волной или Md ) и определяется как величина, по отношению к которой, по крайней мере, 50% выборочных значений меньше неё и, по крайней мере, 50% — больше.
Слайд 12: Медиана. Определение
Можно дать второе определение, сказав, что медиана — это значение, которое делит упорядоченное множество данных пополам.
Слайд 14: Медиана. Решение
Сначала упорядочим выборку по величинам входящих в нее значений. Получим: 3, 4, 5, 8, 9, 11, 13. Поскольку в выборке семь элементов, четвертый по порядку элемент будет иметь значение большее, чем первые три, и меньшее, чем последние три. Медианой будет четвертый элемент — 8.
Слайд 16: Медиана. Решение
Упорядочим выборку: 1, 4, 9, 11, 13, 20. Поскольку здесь имеется четное число элементов, то существует две «середины» — 9 и 13. В этом случае медиана определяется как среднее арифметическое этих значений.
Слайд 17: Среднее арифметическое
Среднее арифметическое ряда из n числовых значений обозначается X и подсчитывается как: Здесь величины 1, 2... n являются так называемыми индексами.
Слайд 18: Среднее арифметическое
В том случае, если отдельные значения выборки повторяются, среднюю арифметическую вычисляют по формуле: в таком случае называют взвешенной средней, где — частоты повторяющихся значений.
Слайд 19: Среднее арифметическое
Знак является символом операции суммирования. Он означает, что все значения должны быть просуммированы. Числа, стоящие над и под знаком называются пределами суммирования и указывают наибольшее и наименьшее значения индекса суммирования, между которыми расположены его промежуточные значения.
Слайд 20: Среднее арифметическое
Например, в формуле вычисления среднего арифметического суммирование начинается с первого элемента выборки, поэтому и пишется так: i = 1, и заканчивается последним, поэтому наверху символа суммирования стоит величина n.
Слайд 21: Среднее арифметическое
Если же мы запишем так: то, поскольку нижний индекс суммирования i равен 4, а верхний равен 6, то будут просуммированы следующие элементы ряда Х 4, Х 5 и Х 6, и в результате будет получено: Х 4 + Х 5 + Х 6.
Слайд 22: Среднее арифметическое
Если же будет записано: то, поскольку нижний индекс суммирования i равен 1, а верхний равен 3, то будут просуммированы следующие элементы ряда Х 1, Х 2 и Х 3, и в результате будет получено: Х 1 + Х 2 + Х 3.
Слайд 23: Среднее арифметическое
В дальнейшем мы будем пользоваться сокращением, которое состоит в том, что если производится суммирование всех элементов выборки от первого до последнего, то верхний и нижний пределы суммирования указываться не будут, а пишется просто: или
Слайд 24: Среднее арифметическое
При вычислении величины средней по таблице чисел в дальнейшем будет использоваться следующая формула: где x IJ — значения всех переменных, полученных в эксперименте, или все элементы таблицы; при этом индекс j меняется от 1 до p, где р число столбцов в таблице, а индекс i меняется от 1 до n, где n — число испытуемых или число строк в таблице.
Слайд 25: Среднее арифметическое
Тогда — общая средняя всей анализируемой совокупности данных; N – общее число всех элементов в таблице (анализируемой совокупности эксперимен - тальных данных) и в общем случае N =p*n.
Слайд 26: Среднее арифметическое
Символ (двойная сумма) означает, что вначале осуществляется суммирование всех элементов таблицы по индексу i — т.е. по строкам, затем полученные суммы по строчкам складываются по столбцам, или, иначе говоря, по индексу j.
Слайд 27: Среднее арифметическое
Следует подчеркнуть, что средние величины характеризуют выборку одним (средним) числом. Информативная значимость, средних величин заключается в их способности аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяя отличить одну выборку от другой, а на этой основе, например, одно измеренное свойство от другого.
Слайд 28: Среднее арифметическое
Среднее арифметическое оказывается достаточно чувствительным к очень маленьким или очень большим величинам, отличающимся от основных значений измеренных характеристик.
Слайд 29: Среднее арифметическое
Пусть 9 человек имеют доход от 4500 до 5200 тыс. рублей в месяц. Величина их среднего дохода равняется 4900 рублей. Если же к этой группе добавить человека, имеющего доход в 20000 тыс. рублей в месяц, то средняя всей группы сместится и окажется равной 6410 рублей, хотя никто из всей выборки (кроме одного человека) реально не получает такой суммы.
Слайд 30: Среднее арифметическое
Важно подчеркнуть, что подобные крайние величины, т.е. те, которые существенно искажают величину средней, оказываются в то же время и наименее характерными для изучаемой генеральной совокупности. Именно поэтому в статистике, кроме средней величины, используются и другие характеристики «типичных значений» выборки, такие, как мода, медиана и ряд других характеристик.
Слайд 31: Разброс выборки
Разброс (иногда эту величину называют размахом) выборки обозначается буквой R. Это самый простой показатель, который можно получить для выборки — разность между максимальной и минимальной величинами данного конкретного вариа- ционного ряда, т.е.
Слайд 32: Разброс выборки
Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный.
Слайд 33: Разброс выборки
Например, даны две выборки При равенстве средних и разбросов для этих двух выборочных рядов характер их варьи- рования различен. Для того чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям.
Слайд 34: Дисперсия
Рассмотрим еще одну очень важную числовую характеристику выборки, называемую дисперсией. Дисперсия представляет собой наиболее часто использующуюся меру рассеяния случайной величины (переменной).
Слайд 35: Дисперсия
Дисперсия это среднее арифметическое квадратов отклонений значений переменной от её среднего значения. где n — объем выборки i - индекс суммирования - среднее.
Слайд 36: Дисперсия
Вычислим дисперсию следующего ряда 2 4 6 8 10 Прежде всего найдем среднее ряда. Оно равно = 6.
Слайд 37: Дисперсия
Рассмотрим величины: для каждого элемента ряда. Иными словами, из каждого элемента ряда вычтем величину среднего этого ряда. Полученные величи- ны характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду.
Слайд 38: Дисперсия
Обозначим полученную совокупность разностей как множество Т. Тогда Т есть: Т = (2 - 6 = -4; 4 - 6 = -2; 6 - 6 = 0; 8 - 6 = 2; 10 - 6 = 4).
Слайд 39: Дисперсия
Так образуется новый ряд чисел. Его особенность в том, что при сложении этих чисел обязательно получится ноль. Проверим: (-4) + (-2) + 0 + 2 + 4 = 0.
Слайд 40: Дисперсия
Отметим, что сумма такого ряда всегда будет равна нулю. Для того чтобы избавиться от нуля, каждое значение разности возводят в квадрат, все их суммируют и затем делят на число элементов, т.е. применяют фор - мулу вычисления дисперсии.
Слайд 42: Дисперсия. Алгоритм вычисления
Общий алгоритм вычисления дисперсии для одной выборки следующий: 1. Вычисляется среднее по выборке. 2. Для каждого элемента выборки вычис- ляется его отклонение от средней, т.е. получается множество Т.
Слайд 43: Дисперсия. Алгоритм вычисления
3. Каждый элемент множества T возводят в квадрат. 4. Находится сумма этих квадратов.
Слайд 44: Дисперсия. Алгоритм вычисления
5. Эта сумма, как и в случае вычисления среднего, делится на общее количество членов ряда — n. В ряде случаев, особенно когда величина выборки мала, деление осуществляется не на величину n, а на величину n — 1.
Слайд 45: Дисперсия
Расчет дисперсии для таблицы чисел осуществляется по формуле: где x,j — значения всех переменных, полученных в эксперименте, или все элементы таблицы; индекс j меняется от 1 до p где p число столбцов в таблице, а индекс i меняется от 1 до n, где n — число испытуемых или число строк в таблице. — общая средняя всех элементов таблицы; N — общее число всех элементов в таблице ( N = р *n).
Слайд 46: Дисперсия
Дисперсию для генеральной совокупности принято обозначать как, а дисперсию выборки как, причем индекс х обозначает, что дисперсия характеризует варьирование числовых значений признака вокруг их средней арифметической.
Слайд 47: Дисперсия
Однако сама дисперсия, как характерис - тика отклонения от среднего, часто неудоб - на для интерпретации. Предположим, что в эксперименте измерялся рост в сантиметрах, тогда размерность дисперсии будет являться характеристикой площади, а не линейного размера (поскольку при подсчете диспер- сии сантиметр возводится в квадрат).
Слайд 48: Дисперсия
Для того чтобы приблизить размерность дисперсии к размерности измеряемого признака применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называют стандартным отклонением.
Слайд 49: Дисперсия
Стандартное отклонение выборки S х представ- ляет собой корень квадратный, извлеченный из дисперсии выборки В нашем примере
Слайд 50: Дисперсия
Генеральной дисперсией D Г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения х Г.
Слайд 51: Дисперсия
Если все значения х 1, х 2,..., x n признака генеральной совокупности объема N различны, то
Слайд 52: Дисперсия
Если же значения признака х 1, х 2,..., х n имеют соответственно частоты N 1, N 2,..., N k, причем N 1 +N 2 + N k = N, то
Слайд 53: Дисперсия
Генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
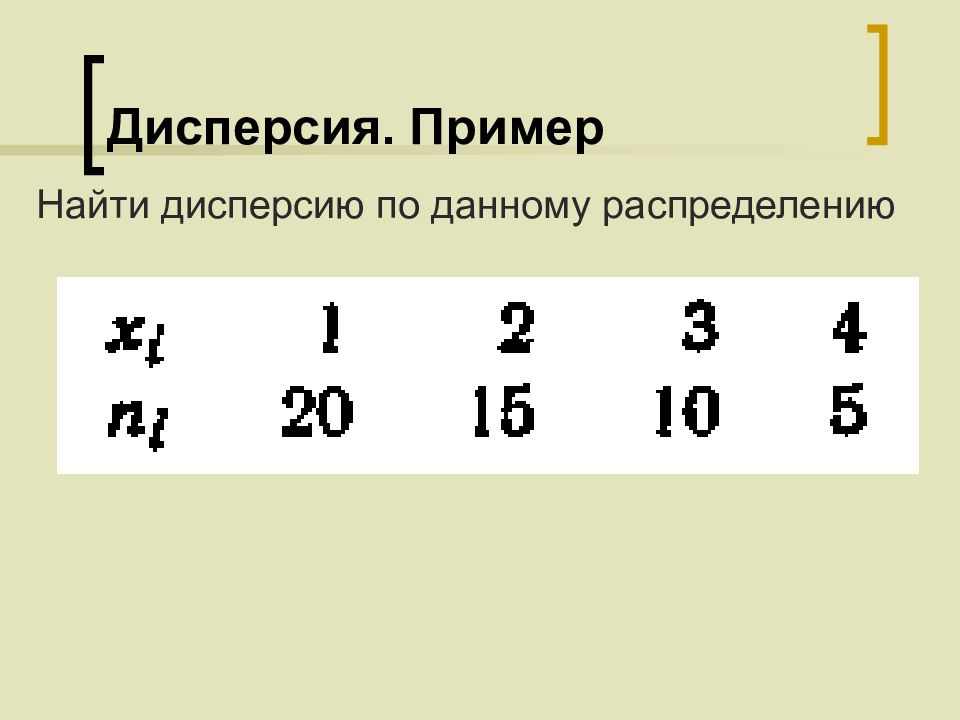
Слайд 54: Дисперсия. Пример
Генеральная совокупность задана таблицей распределения Найти генеральную дисперсию.
Слайд 57: Дисперсия
Выборочной дисперсией D B называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения х В.
Слайд 58: Дисперсия
Вычисление дисперсии, безразлично – выборочной или генеральной, можно упростить, используя следующую теорему. Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:
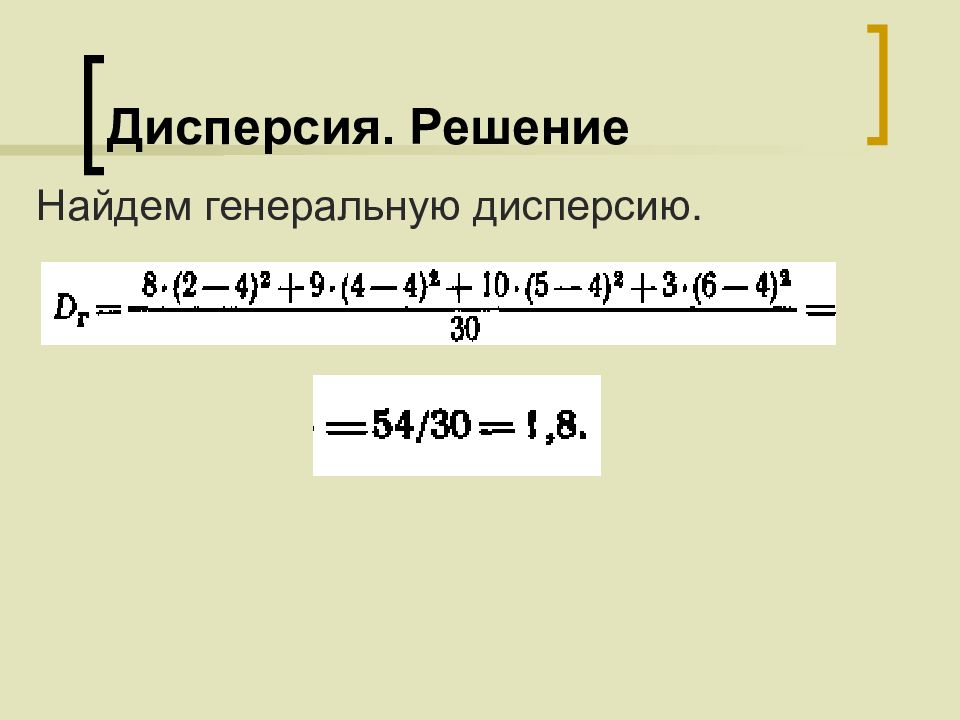
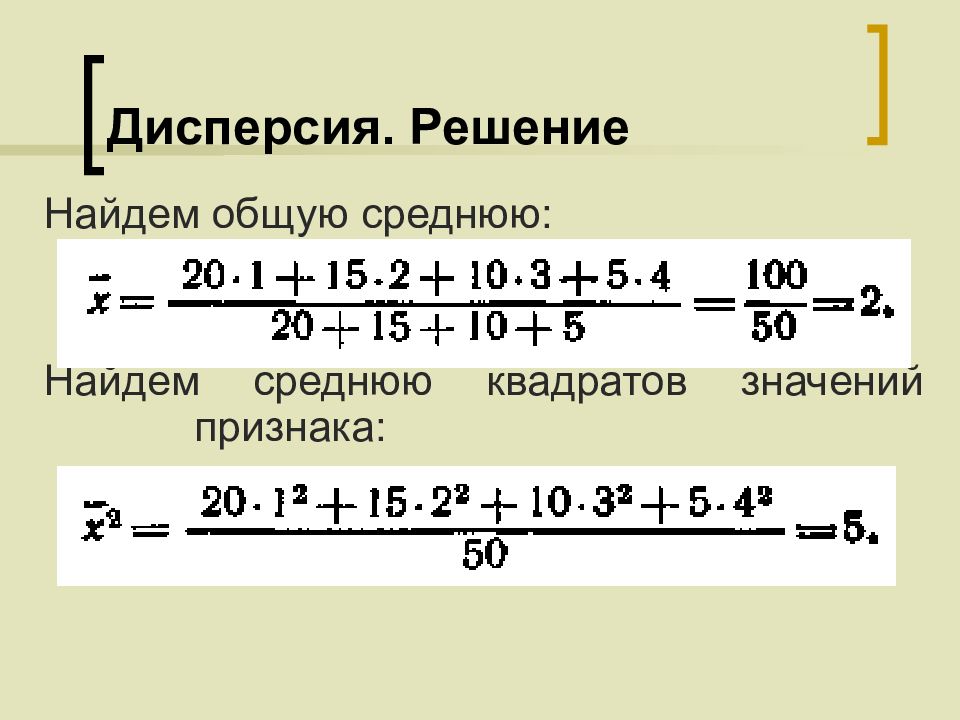
Слайд 60: Дисперсия. Решение
Найдем общую среднюю: Найдем среднюю квадратов значений признака:
Слайд 62: Групповая, внутригрупповая, межгрупповая и общая дисперсии
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
Слайд 63: Групповая, внутригрупповая, межгрупповая и общая дисперсии. Пример
Найти групповые дисперсии совокупности, состоящей из следующих двух групп:
Слайд 64: Групповая, внутригрупповая, межгрупповая и общая дисперсии. Пример
Найдем групповые средние
Слайд 65: Групповая, внутригрупповая, межгрупповая и общая дисперсии. Пример
Найдем искомые групповые дисперсии:
Слайд 66: Групповая, внутригрупповая, межгрупповая и общая дисперсии
Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп: где N j – объем группы j ; - объем всей совокупности
Слайд 67: Групповая, внутригрупповая, межгрупповая и общая дисперсии. Пример
Найти внутригрупповую дисперсию (по данным вышеописанного примера) Искомая внутригрупповая дисперсия равна
Слайд 68: Групповая, внутригрупповая, межгрупповая и общая дисперсии
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
Слайд 69: Групповая, внутригрупповая, межгрупповая и общая дисперсии. Пример
Найти межгрупповую дисперсию (по данным вышеописанного примера) Найдем общую среднюю:
Слайд 70: Групповая, внутригрупповая, межгрупповая и общая дисперсии. Пример
Используя вычисленные выше величины ,, найдем искомую межгрупповую дисперсию:
Слайд 71: Групповая, внутригрупповая, межгрупповая и общая дисперсии
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
Слайд 72: Групповая, внутригрупповая, межгрупповая и общая дисперсии. Пример
Найти общую дисперсию (по данным вышеописанного примера) Найдем искомую общую дисперсию, учитывая, что общая средняя равна 14/3:
Слайд 73: Групповая, внутригрупповая, межгрупповая и общая дисперсии
Найденная общая дисперсия равна сумме внутригрупповой и межгрупповсй дисперсий:
Слайд 75: Степень свободы
Число степеней свободы – это число свободно варьирующих единиц в составе выборки.
Слайд 76: Степень свободы
Если вся выборка состоит из n элементов и характеризуется средней , то любой элемент этой совокуп- ности может быть получен как раз- ность между величиной и суммой всех остальных элементов, кроме самого этого элемента.
Слайд 77: Степень свободы. Пример
Рассмотрим ряд: 2 4 6 8 10. Мы помним, что средняя этого ряда равна 6. В этом ряду 5 чисел, следовательно N = 5. Предположим, что мы хотим получить последний элемент ряда — 10, зная все предыдущие элементы и среднее этого ряда.
Слайд 79: Степень свободы. Пример
Предположим, что мы хотим получить пер- вый элемент ряда — 2, зная все после- дующие элементы и среднее этого ряда. Тогда: 5*6-4-6-8-10 = 2 и т.д.
Слайд 80: Степень свободы
Следовательно, один элемент выборки не имеет свободы вариации и всегда может быть выражен через другие элементы и среднее.
Слайд 81: Степень свободы
Это означает, что число степеней свободы у выборочного ряда обозначаемое в таких случаях символом к будет определяться как k = n - 1, где n — общее число элементов ряда (выборки).
Слайд 82: Степень свободы
При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы, обозначаемое как (греческая буква ню) будет равно = n - k, где k соответствует числу ограничений свободы вариации.
Последний слайд презентации: Математическая статистика. Числовые характеристики распределений. Нормальное: Математическая статистика. Числовые характеристики распределений. Нормальное распределение
Автор: доцент кафедры информатики и математики Грязнов Сергей Александрович ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА