ОСНОВНЫЕ ПОНЯТИЯ Дифференциальные уравнения Определение дифференциального уравнения (ДУ). Общее и частное решение ДУ. Задача Коши.
Определение Уравнение, связывающее независимую переменную x с неизвестной функцией y(x) и ее производными до некоторого порядка n включительно, называется дифференциальным уравнением n -ого порядка. Примеры дифференциальное уравнение 1-ого порядка 2-ого порядка 3-его порядка
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНОВЕННОЕ В ЧАСТНЫХ ПРОИЗВОДНЫХ искомая функция зависит от одной переменной искомая функция зависит от нескольких переменных Будем рассматривать обыкновенные дифференциальные уравнения
ОБЩИЙ ВИД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ n -ОГО ПОРЯДКА F – некоторая функция от n+2 переменных, x – независимая переменная, y(x) – искомая функция, - ее производные Определение Дифференциальное уравнение n- ого порядка называется разрешенным относительно старшей производной, если оно имеет вид : (1)
Определение Решением дифференциального уравнения (1) называется функция y(x), имеющая производные до n -ого порядка включительно, и такая, что ее подстановка в уравнение (1) обращает его в тождество Пример Решением уравнения является функция
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИМЕЕТ БЕСКОНЕЧНОЕ МНОЖЕСТВО РЕШЕНИЙ Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения Частное решение дифференциального уравнения получается из общего путем придания конкретных значений произвольным постоянным
Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения График решения дифференциального уравнения называется интегральной кривой Определение Общим решением дифференциального уравнения (1) n -ого порядка называется такое его решение которое является функцией переменной x и n произвольных независимых постоянных
Из статистических данных известно, что для некоторого региона число новорожденных и число умерших за единицу времени пропорциональны численности населения с коэффициентами пропорциональности и соответственно. Найти закон изменения численности населения с течением времени (то есть описать протекание демографического процесса)
Пусть y=y(t) – число жителей региона в момент времени t. Число родившихся в момент времени t равно k1y, а число умерших равно k 2 y Тогда прирост населения за время равен разности между числом родившихся и умерших за это время : Обозначим или
Переходя к пределу при, получим уравнение Решим это уравнение : C – постоянная, определяемая начальным условием (численностью населения в начальный момент времени)
Определение Отыскание частного решения дифференциального уравнения (1) n -ого порядка, удовлетворяющего n начальным условиям вида : называется задачей Коши По n начальным условиям определяются значения всех n произвольных постоянных, входящих в общее решение диффер. уравнения n – ого порядка
ОБЩИЙ ВИД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 1-ОГО ПОРЯДКА ( 2 ) ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 1-ОГО ПОРЯДКА, РАЗРЕШЕННОЕ ОТНОСИТЕЛЬНО СТАРШЕЙ ПРОИЗВОДНОЙ ( 3 ) f – некоторая функция двух переменных
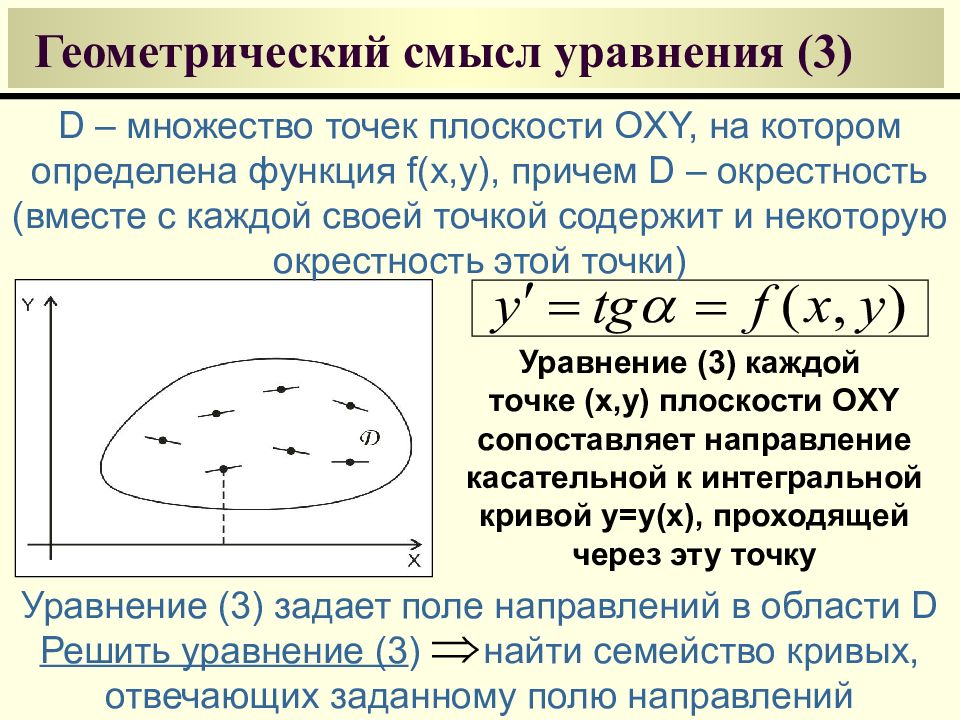
D – множество точек плоскости OXY, на котором определена функция f(x,y), причем D – окрестность (вместе с каждой своей точкой содержит и некоторую окрестность этой точки) Уравнение (3) каждой точке ( x,y) плоскости OXY сопоставляет направление касательной к интегральной кривой y=y(x), проходящей через эту точку Уравнение (3) задает поле направлений в области D Решить уравнение (3 ) найти семейство кривых, отвечающих заданному полю направлений
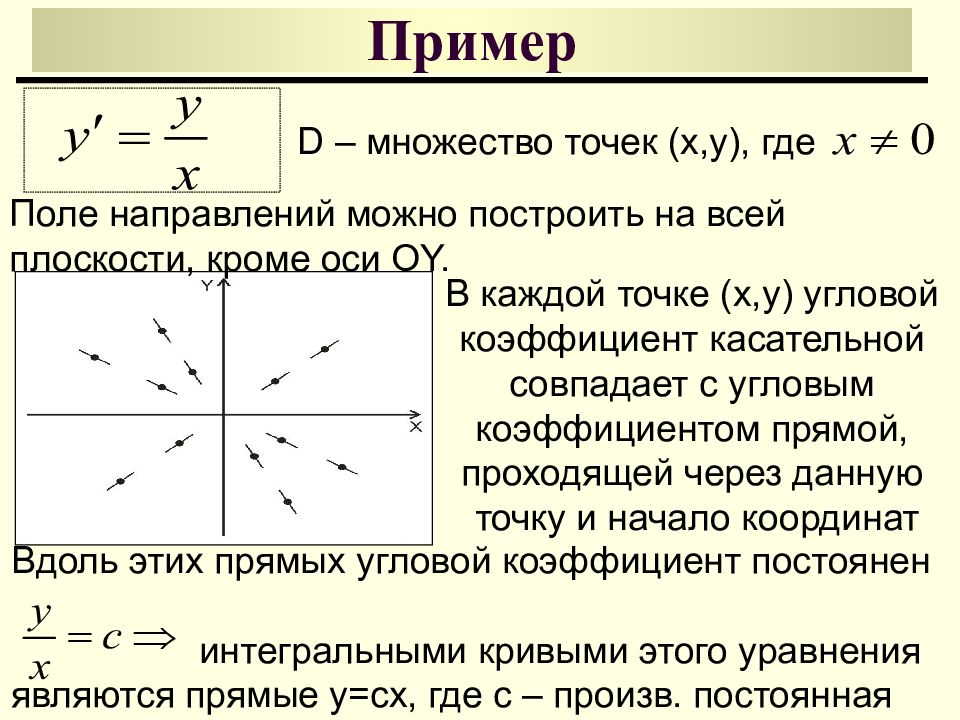
D – множество точек (x,y), где В каждой точке (x,y) угловой коэффициент касательной совпадает с угловым коэффициентом прямой, проходящей через данную точку и начало координат Вдоль этих прямых угловой коэффициент постоянен интегральными кривыми этого уравнения являются прямые y=cx, где с – произв. постоянная Поле направлений можно построить на всей плоскости, кроме оси О Y.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИМЕЕТ БЕСКОНЕЧНОЕ МНОЖЕСТВО РЕШЕНИЙ Задача о нахождении решений дифференциального уравнения (3), удовлетворяющих начальному условию (4), называется задачей Коши ДЛЯ ВЫДЕЛЕНИЯ КОНКРЕТНОГО РЕШЕНИЯ, МОЖНО ЗАДАТЬ НАЧАЛЬНОЕ УСЛОВИЕ ( 4 )
Теорема Если в уравнении функция f(x,y) и ее частная производная непрерывны в некоторой области D, содержащей точку, то существует единственное решение этого уравнения, удовлетворяющее начальному условию (о существовании и единственности решения задачи Коши) Геометрическая интерпритация теоремы При выполнении условий теоремы существует единственная интегральная кривая дифференциального уравнения, проходящая через точку
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С РАЗДЕЛЕННЫМИ ПЕРЕМЕННЫМИ ( 5 ) - ОБЩИЙ ИНТЕГРАЛ Пример уравнение с разделенными переменными общий интеграл
