Двугранный угол
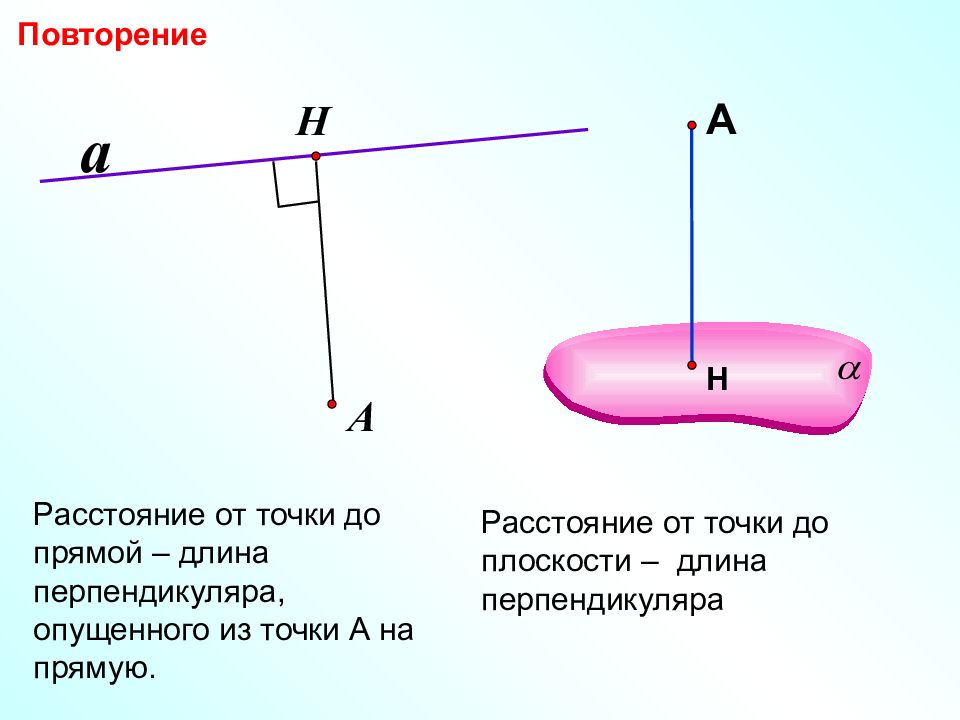
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки А на прямую. a Н А Расстояние от точки до плоскости – длина перпендикуляра Повторение Н А
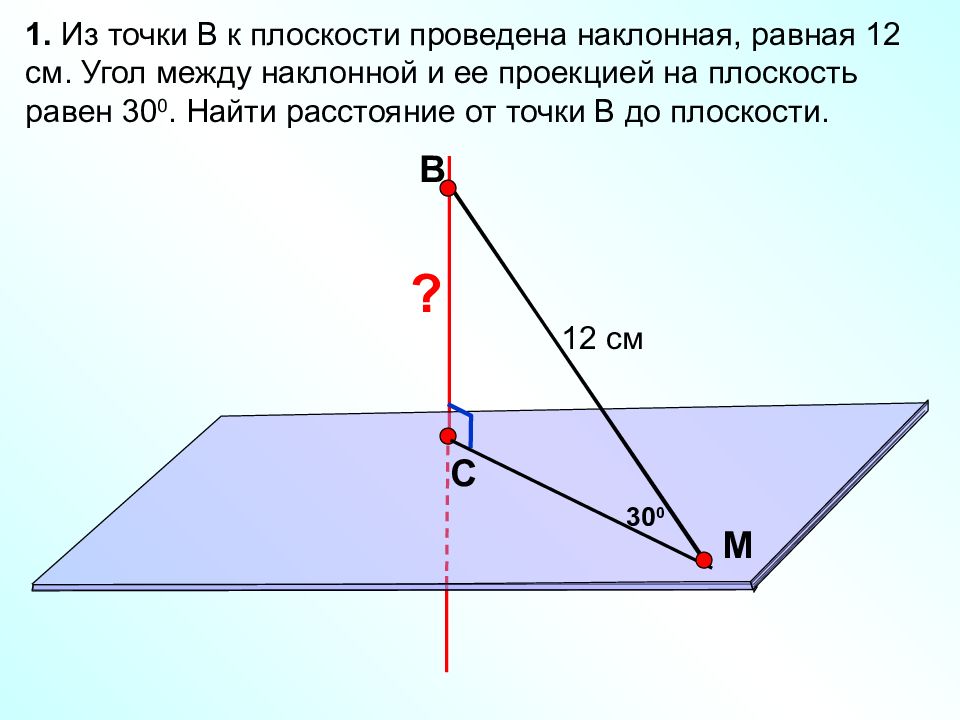
В С M 1. Из точки В к плоскости проведена наклонная, равная 12 см. Угол между наклонной и ее проекцией на плоскость равен 30 0. Найти расстояние от точки В до плоскости. 12 см 30 0 ?
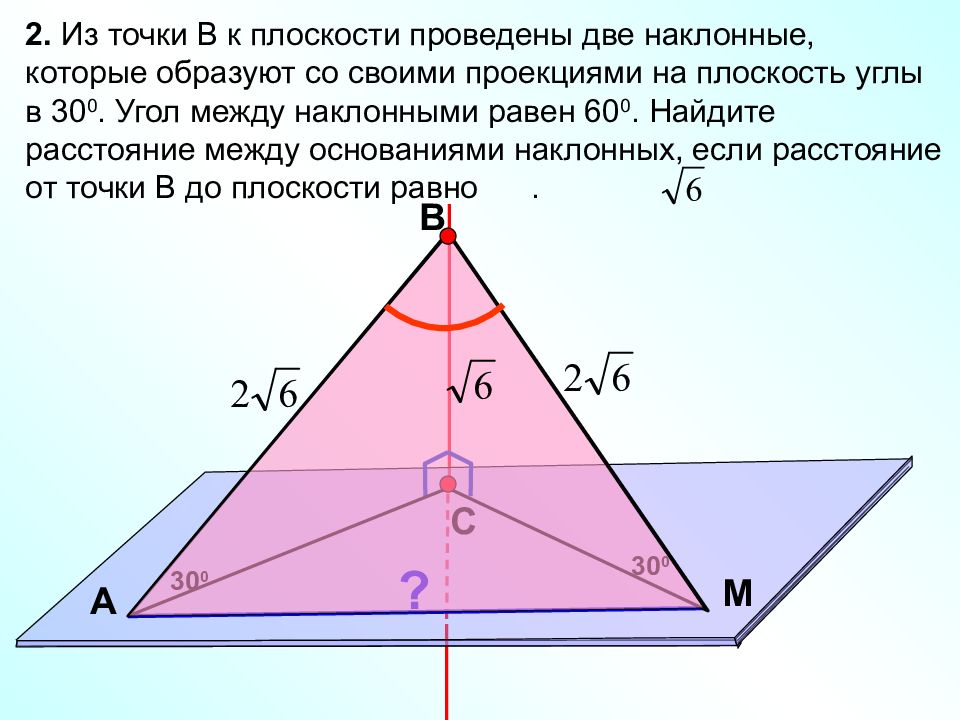
В С M А 2. Из точки В к плоскости проведены две наклонные, которые образуют со своими проекциями на плоскость углы в 30 0. Угол между наклонными равен 60 0. Найдите расстояние между основаниями наклонных, если расстояние от точки В до плоскости равно. 30 0 30 0 ?
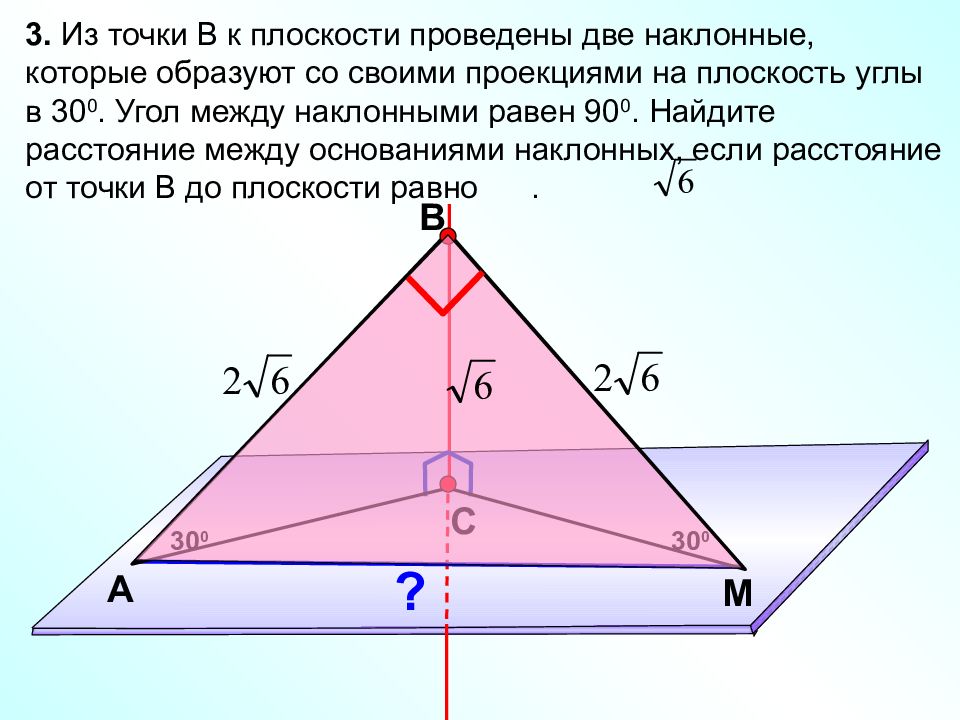
В С M А 3. Из точки В к плоскости проведены две наклонные, которые образуют со своими проекциями на плоскость углы в 30 0. Угол между наклонными равен 90 0. Найдите расстояние между основаниями наклонных, если расстояние от точки В до плоскости равно. 30 0 30 0 ?
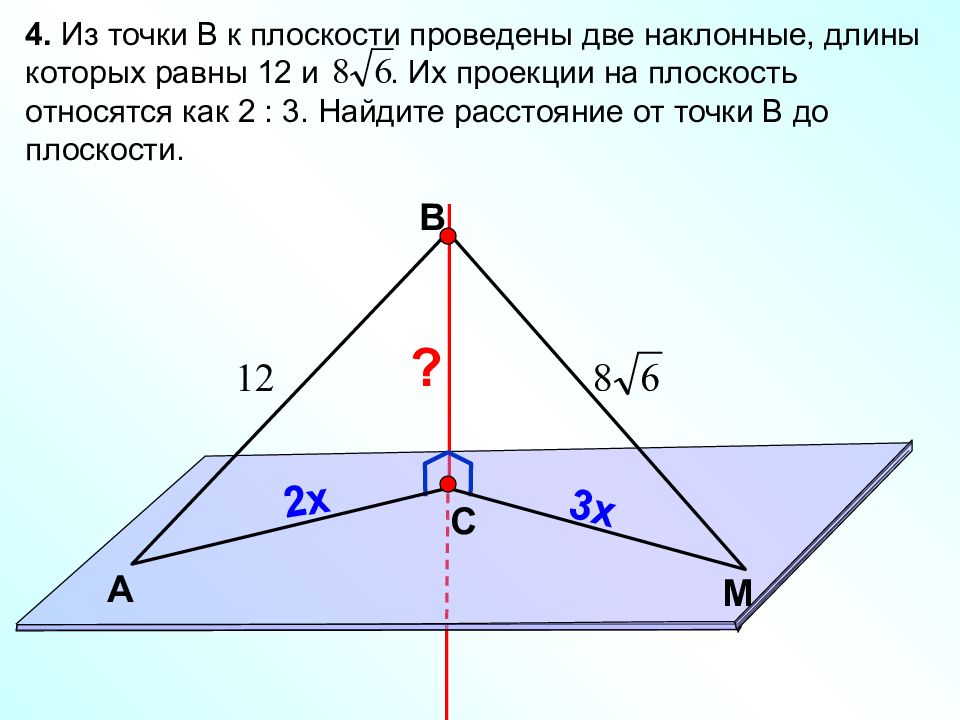
В С M А 4. Из точки В к плоскости проведены две наклонные, длины которых равны 12 и. Их проекции на плоскость относятся как 2 : 3. Найдите расстояние от точки В до плоскости. ? 2х 3х
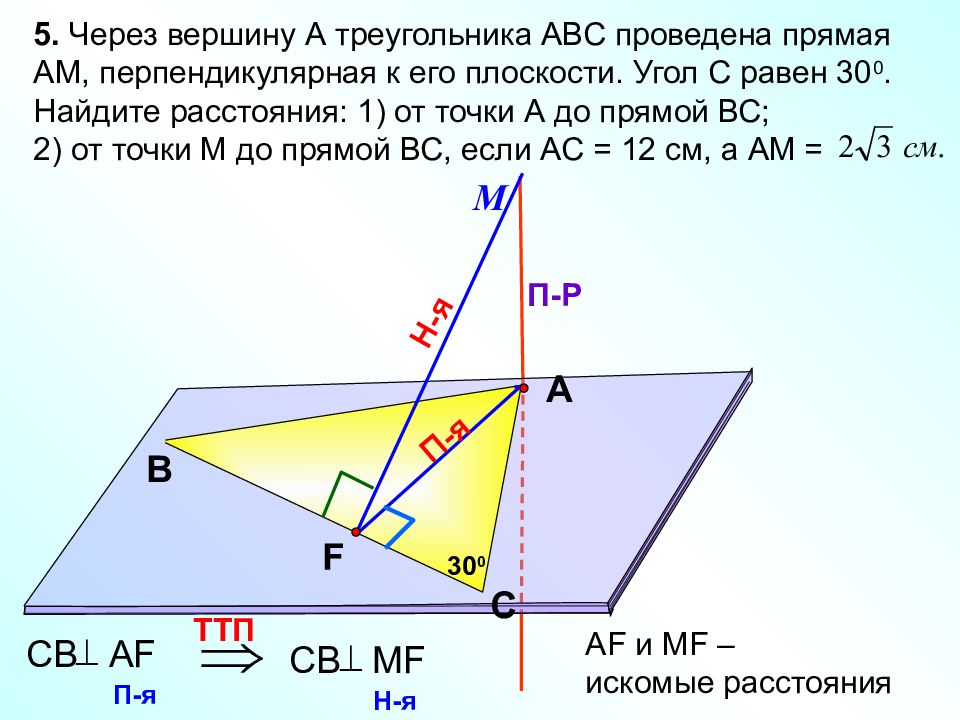
М П-я 5. Через вершину А треугольника АВС проведена прямая АМ, перпендикулярная к его плоскости. Угол С равен 30 0. Найдите расстояния: 1) от точки А до прямой ВС; 2) от точки М до прямой ВС, если АС = 12 см, а АМ = А В С П-Р Н-я TT П СВ А F П-я СВ MF Н-я А F и М F – искомые расстояния F 30 0
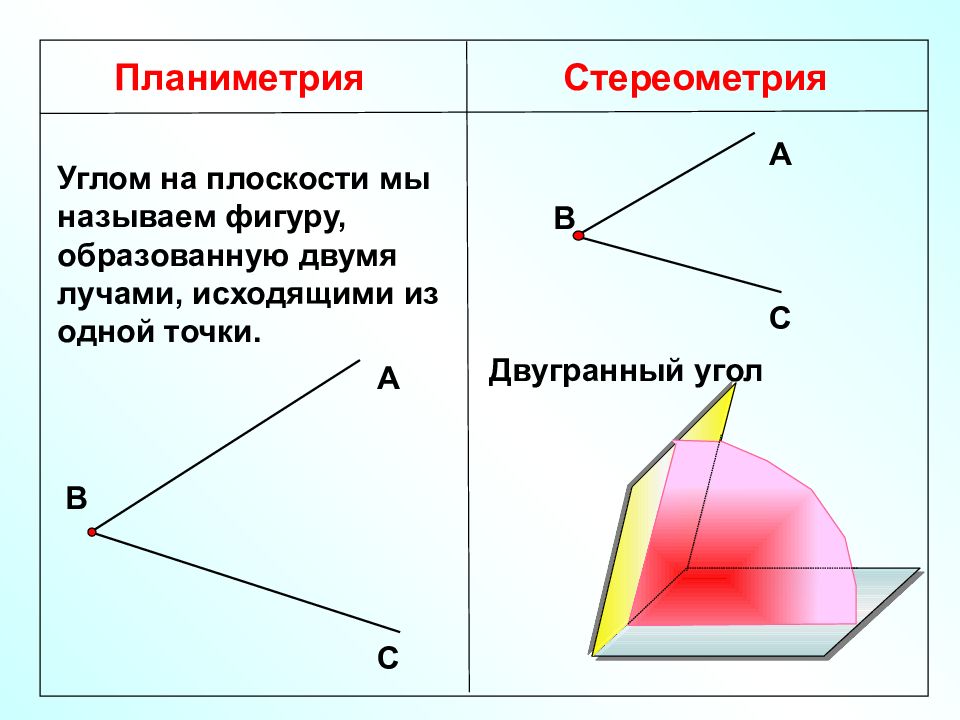
Планиметрия Стереометрия Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки. Двугранный угол А В С А В С
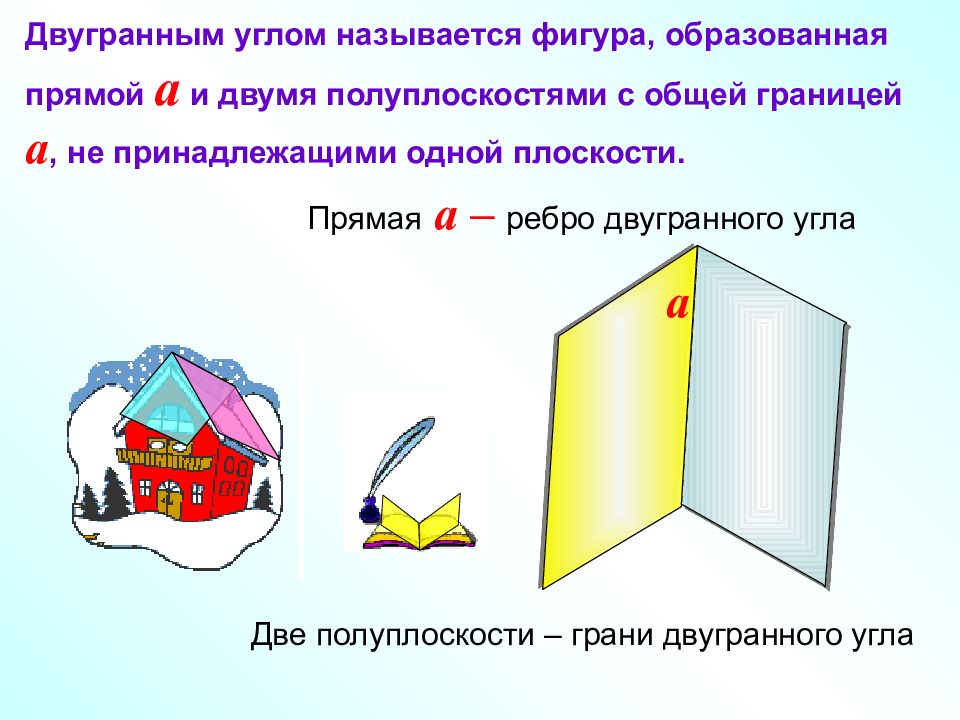
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Две полуплоскости – грани двугранного угла Прямая a – ребро двугранного угла a
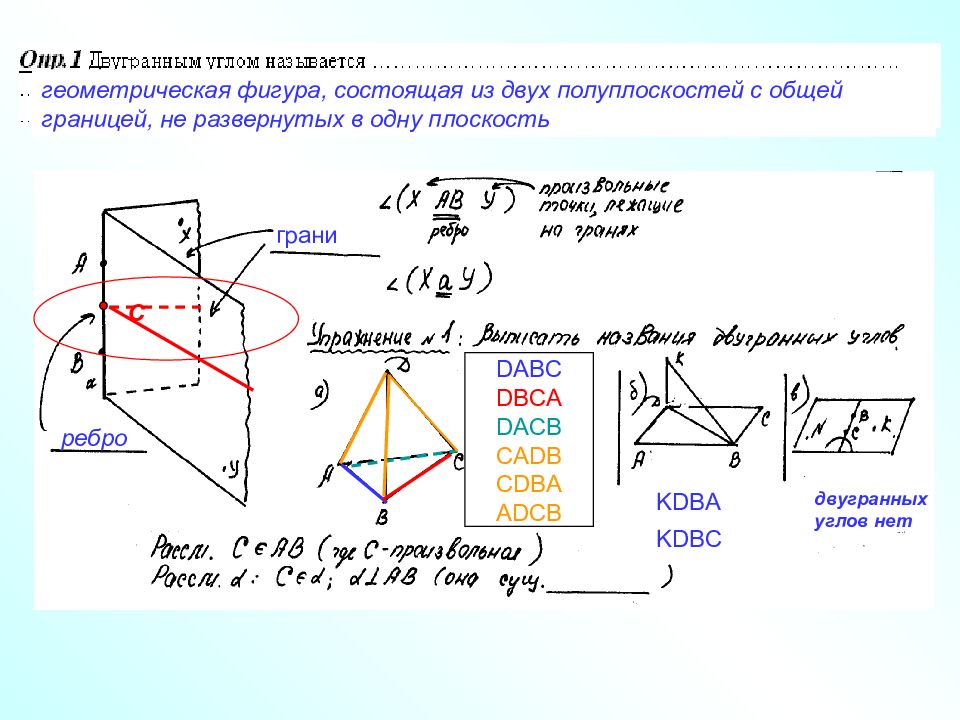
геометрическая фигура, состоящая из двух полуплоскостей с общей границей, не развернутых в одну плоскость DABC DBCA DACB CADB CDBA ADCB ребро грани KDBA KDBC двугранных углов нет С
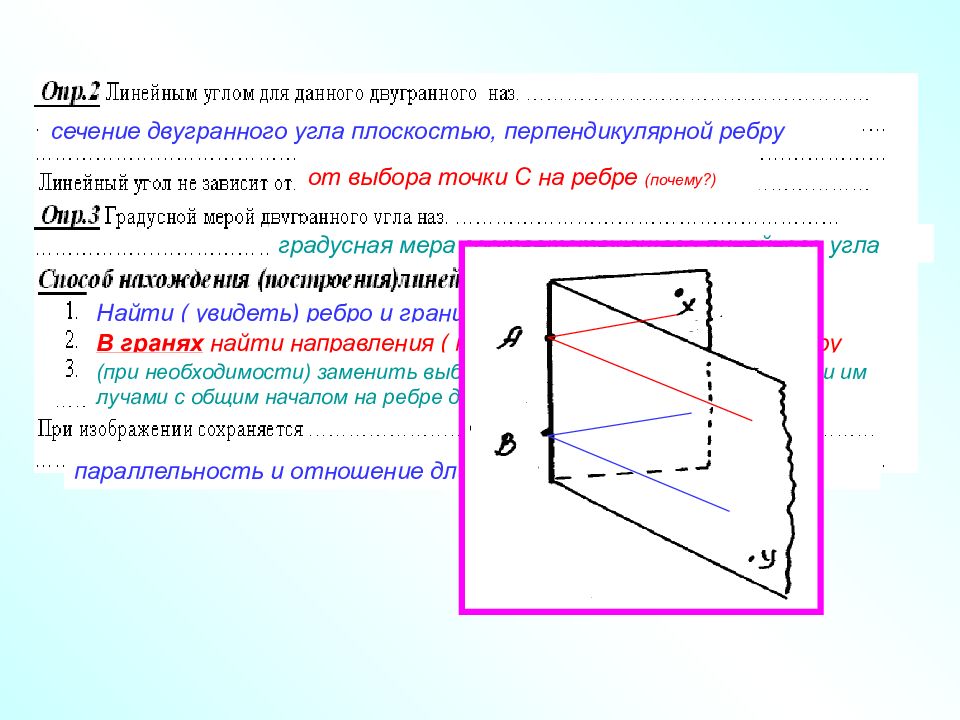
сечение двугранного угла плоскостью, перпендикулярной ребру от выбора точки С на ребре (почему?) градусная мера соответствующего линейного угла Найти ( увидеть) ребро и грани двугранного угла В гранях найти направления ( прямые) перпендикулярные ребру (при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла параллельность и отношение длин параллельных отрезков
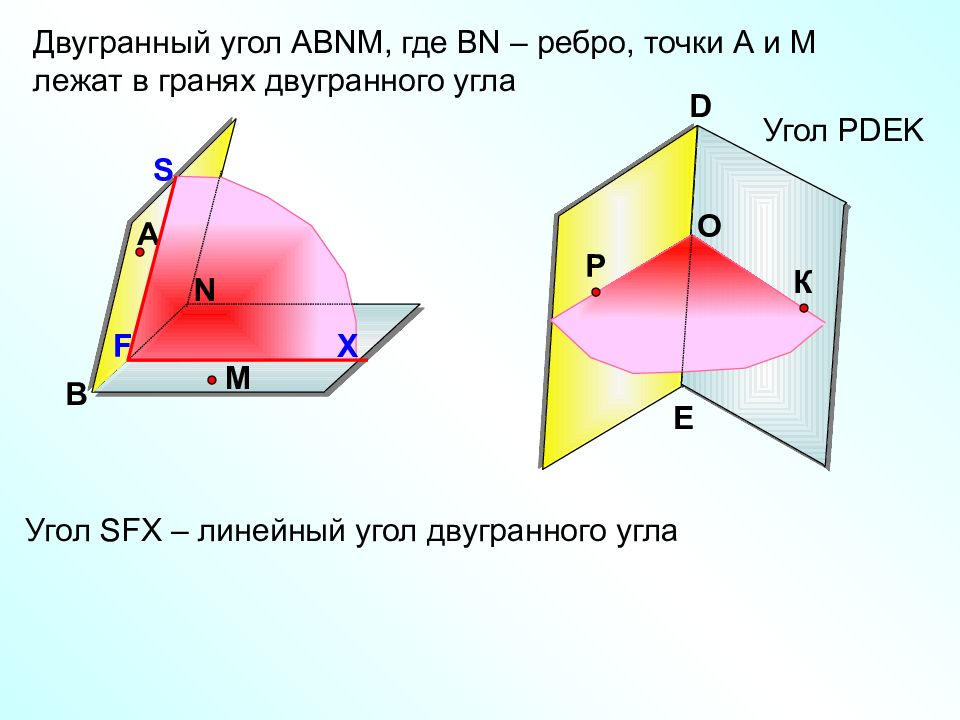
O Угол Р DEK Двугранный угол АВ N М, где В N – ребро, точки А и М лежат в гранях двугранного угла А В N Р M К D E Угол SFX – линейный угол двугранного угла S X F
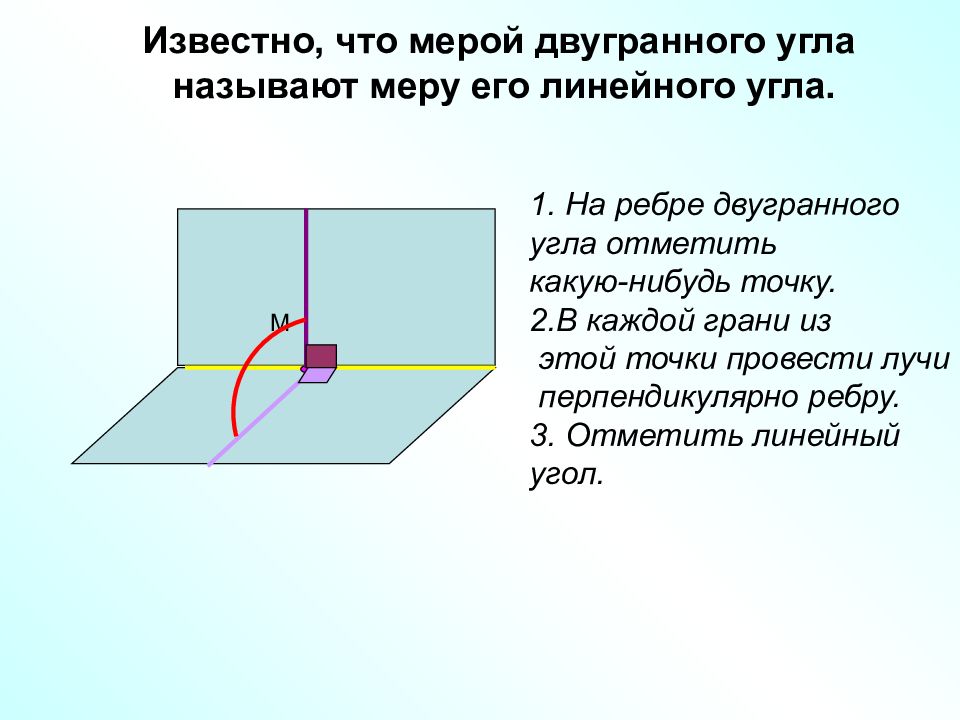
Известно, что мерой двугранного угла называют меру его линейного угла. 1. На ребре двугранного угла отметить какую-нибудь точку. 2.В каждой грани из этой точки провести лучи перпендикулярно ребру. 3. Отметить линейный угол. М
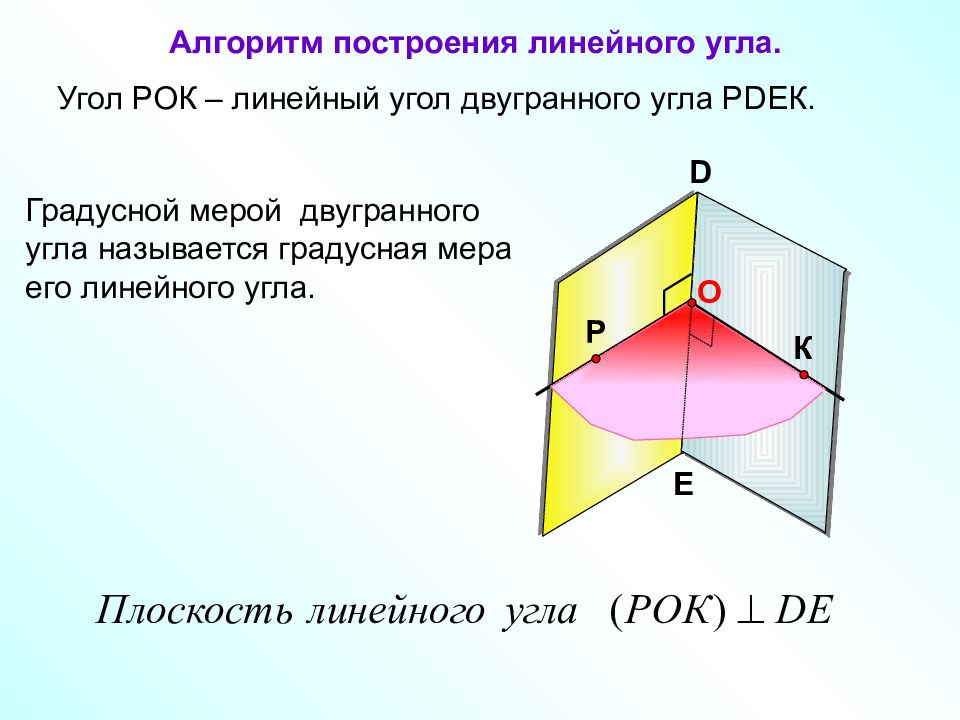
Угол РОК – линейный угол двугранного угла Р DE К. D E Р К O Градусной мерой двугранного угла называется градусная мера его линейного угла. Алгоритм построения линейного угла.
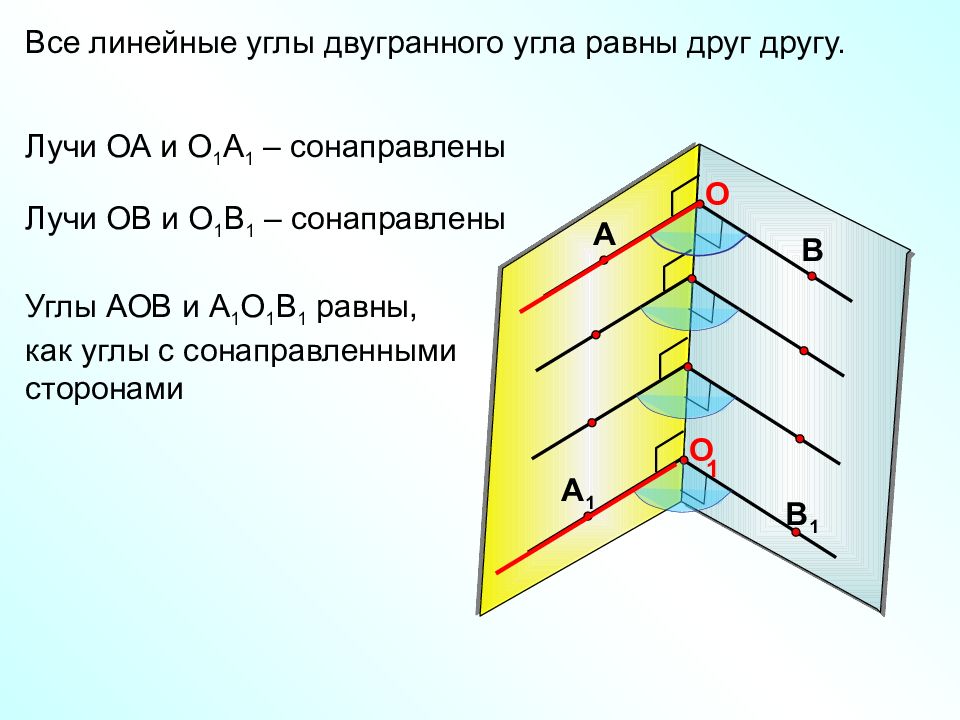
Все линейные углы двугранного угла равны друг другу. А В O А 1 В 1 O 1 Лучи ОА и О 1 А 1 – сонаправлены Лучи ОВ и О 1 В 1 – сонаправлены Углы АОВ и А 1 О 1 В 1 равны, как углы с сонаправленными сторонами
Двугранный угол может быть прямым, острым, тупым
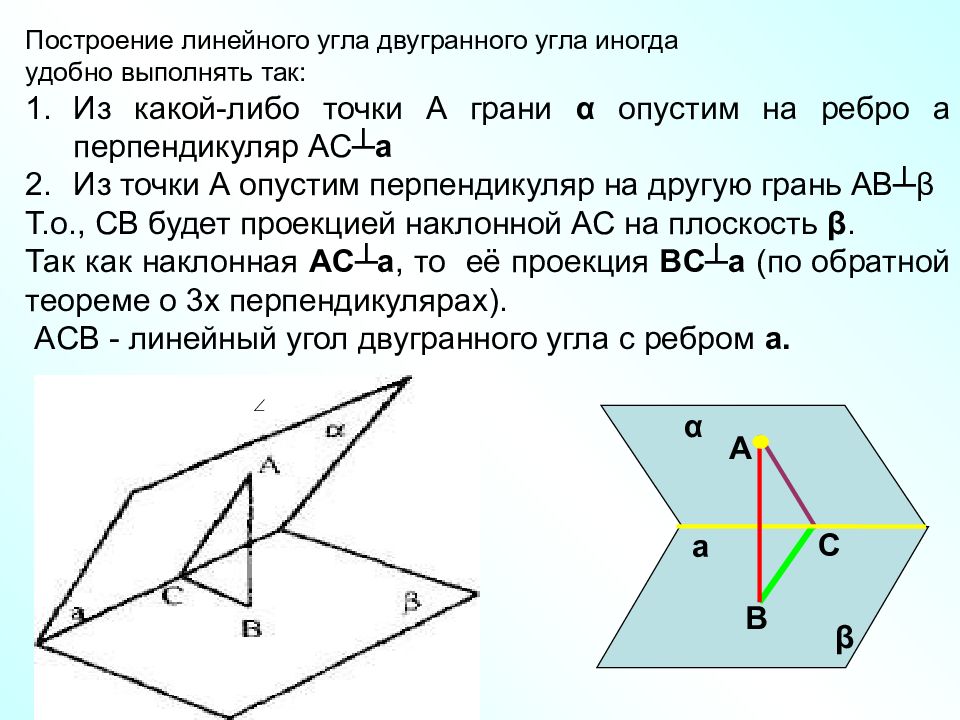
Построение линейного угла двугранного угла иногда удобно выполнять так: Из какой-либо точки А грани α опустим на ребро а перпендикуляр AC┴ а Из точки А опустим перпендикуляр на другую грань AB┴ β Т.о., СВ будет проекцией наклонной АС на плоскость β. Так как наклонная AC ┴ а, то её проекция BC┴ а (по обратной теореме о 3х перпендикулярах). ACB - линейный угол двугранного угла с ребром а. А В С а α β
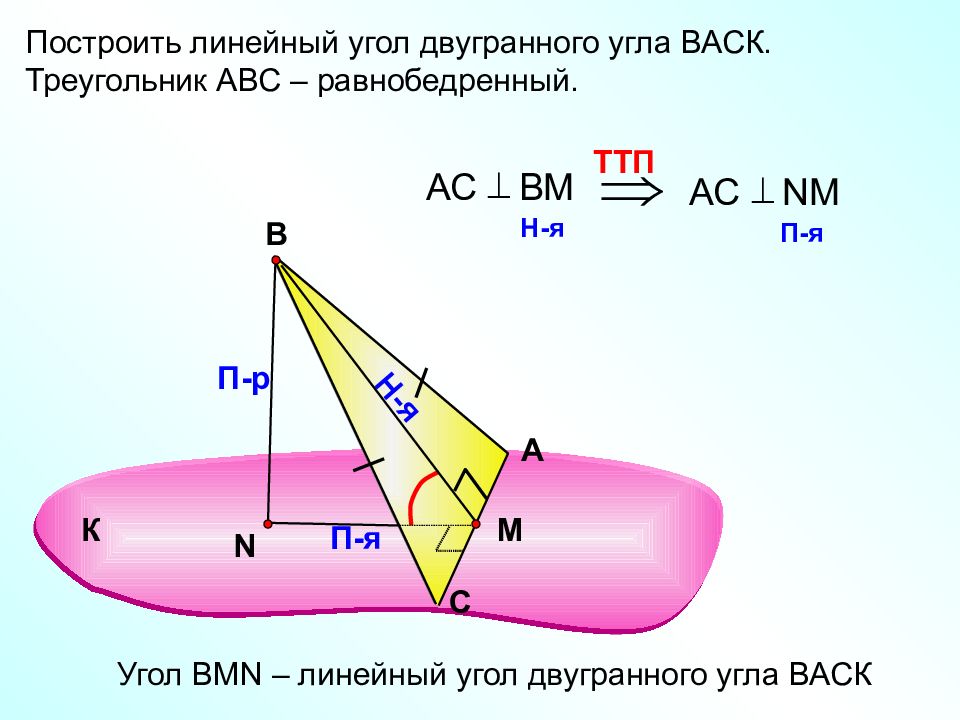
Построить линейный угол двугранного угла ВАСК. Треугольник АВС – равнобедренный. А С В N П-р Н-я П-я TT П АС ВМ H -я АС N М П-я Угол В MN – линейный угол двугранного угла ВАСК К M
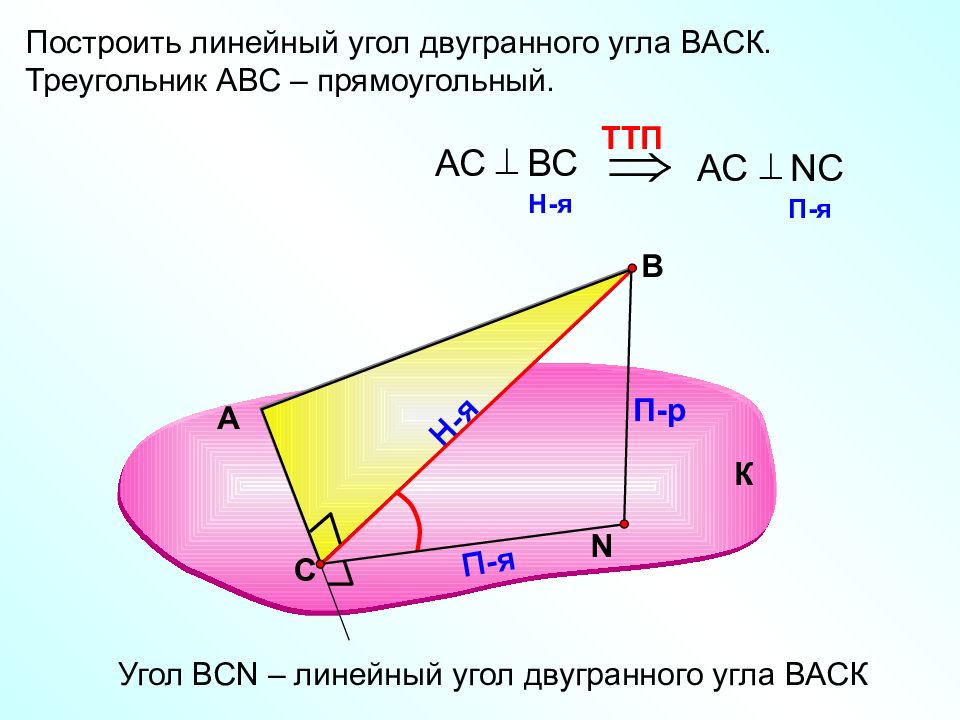
Построить линейный угол двугранного угла ВАСК. Треугольник АВС – прямоугольный. А В N П-р Н-я П-я TT П АС ВС H -я АС N С П-я Угол ВС N – линейный угол двугранного угла ВАСК К С
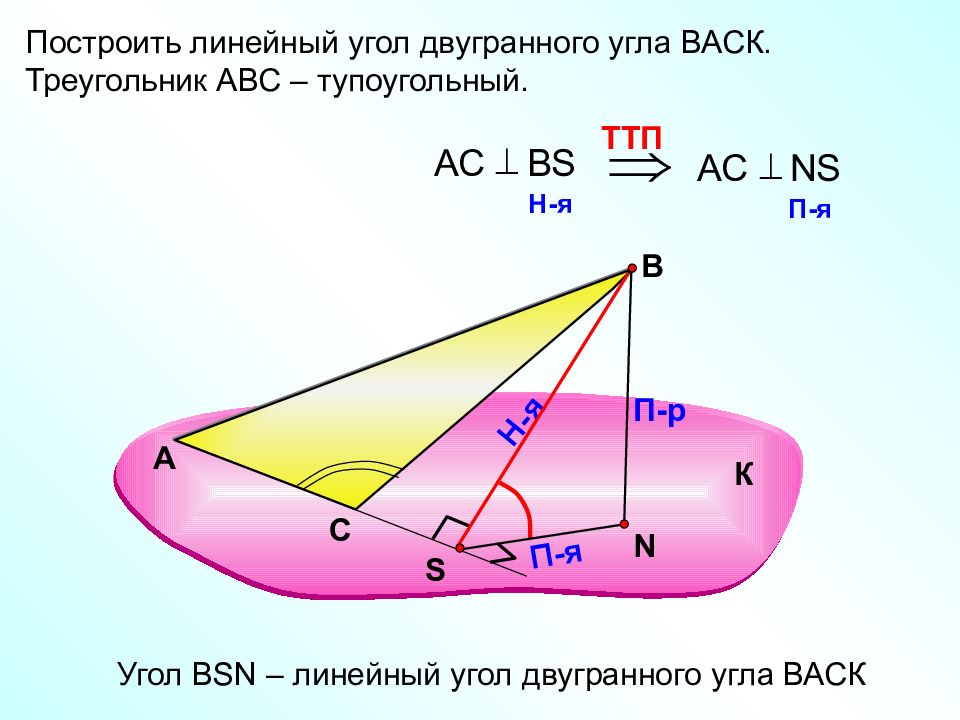
Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. А В N П-р Н-я П-я TT П АС В S H -я АС NS П-я Угол В SN – линейный угол двугранного угла ВАСК К С S
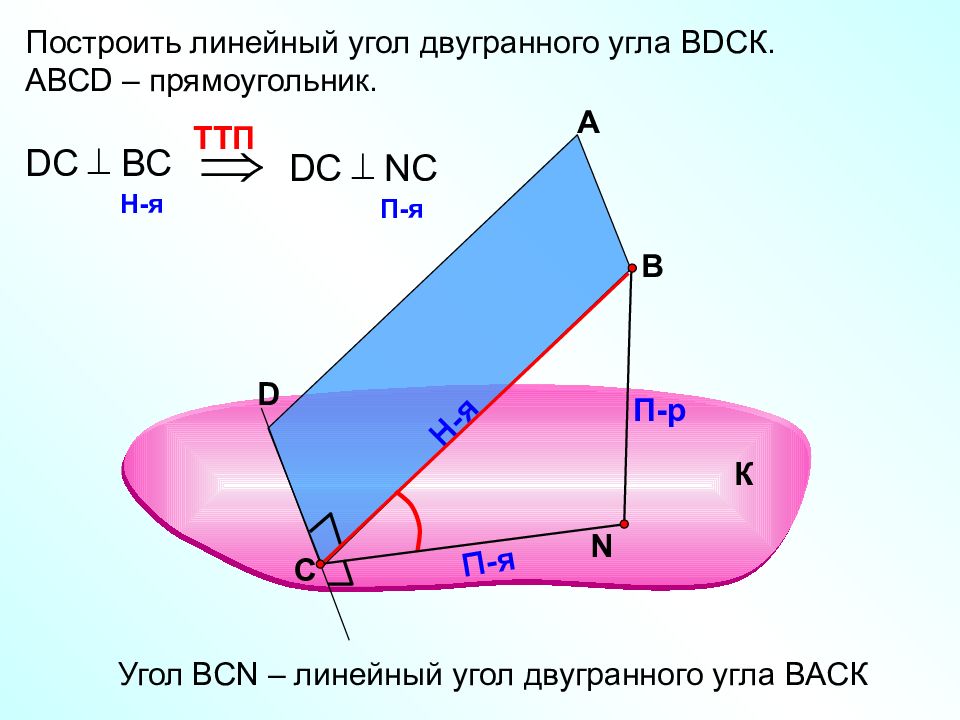
Построить линейный угол двугранного угла В D СК. АВС D – прямоугольник. А В N П-р Н-я П-я TT П D С B С H -я D С N С П-я Угол ВС N – линейный угол двугранного угла ВАСК К С D
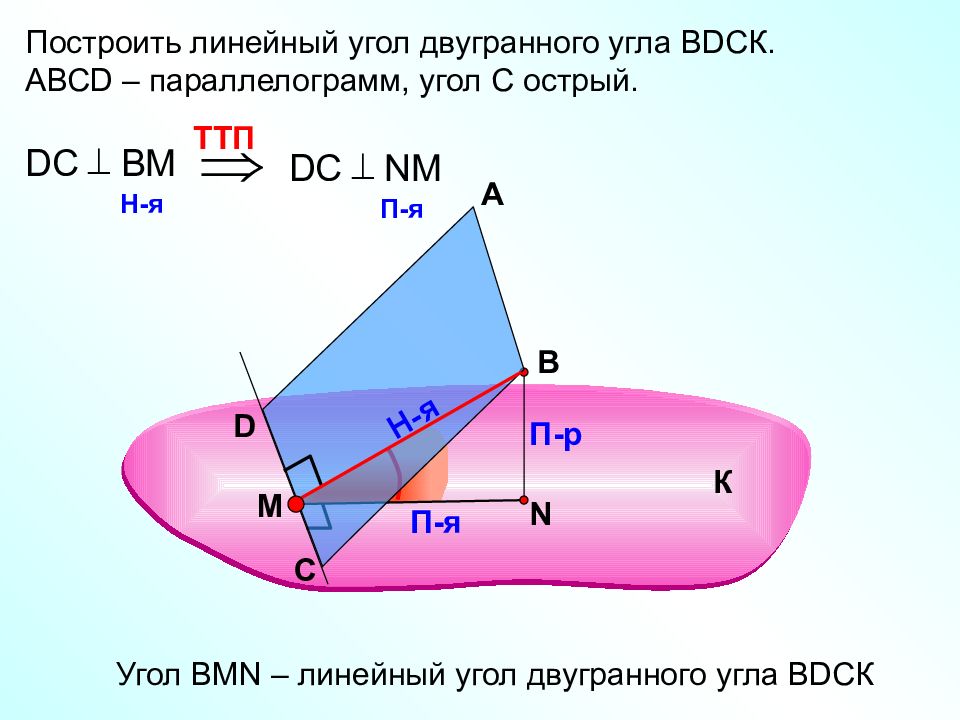
Построить линейный угол двугранного угла В D СК. АВС D – параллелограмм, угол С острый. А В П-р П-я TT П D С В M H -я D С NM П-я Угол В MN – линейный угол двугранного угла В D СК К С D N Н-я M
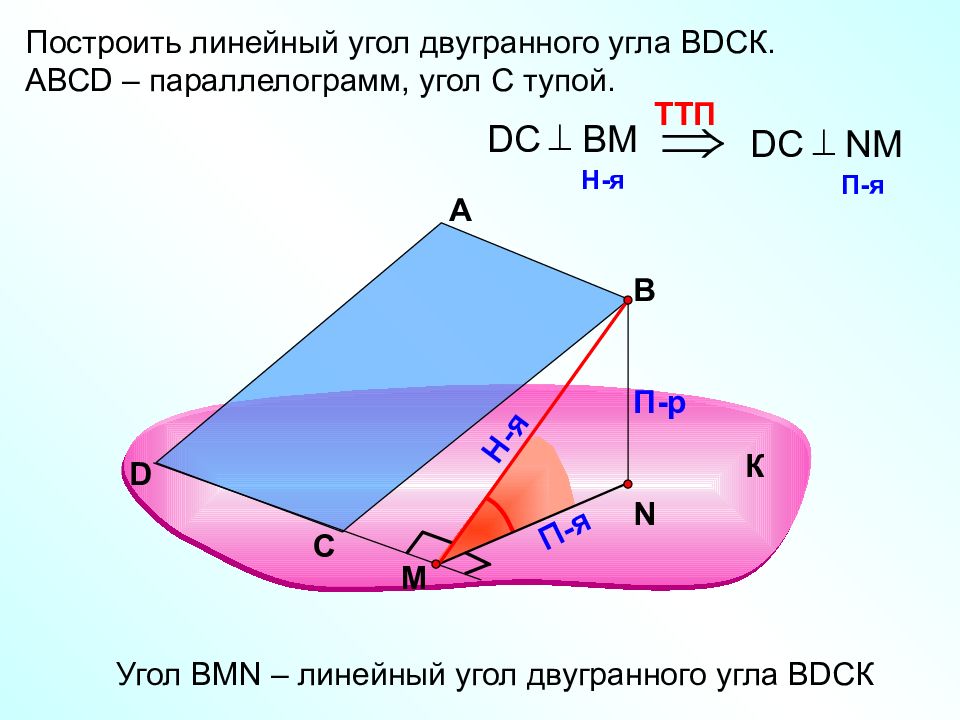
Построить линейный угол двугранного угла В D СК. АВС D – параллелограмм, угол С тупой. А В П-р П-я TT П D С В M H -я D С NM П-я Угол В MN – линейный угол двугранного угла В D СК К С D Н-я M N
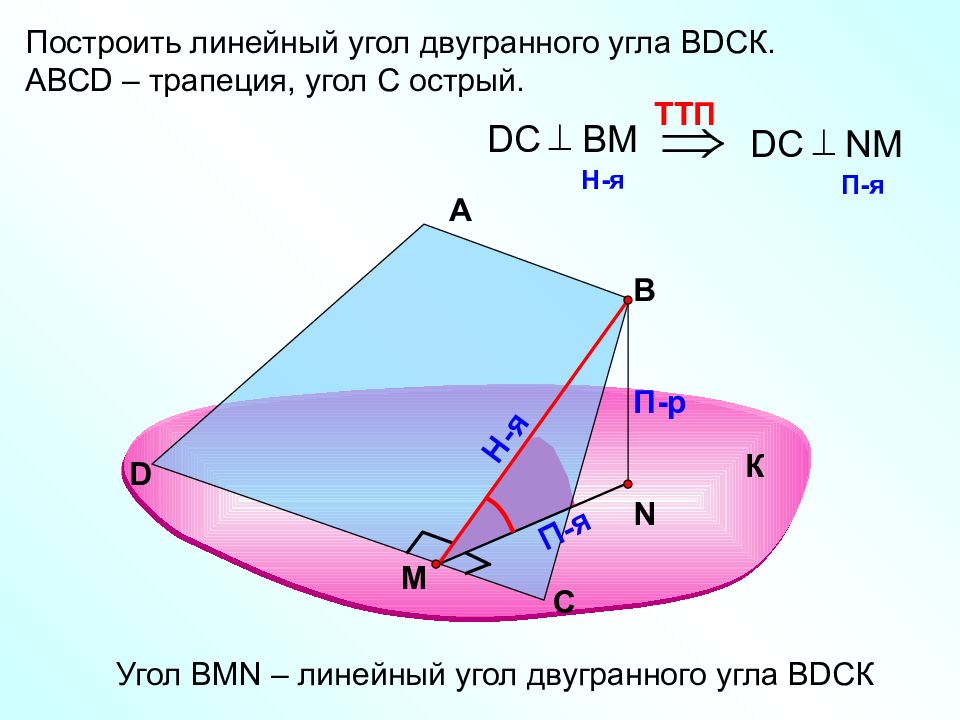
Построить линейный угол двугранного угла В D СК. АВС D – трапеция, угол С острый. А В П-р П-я TT П D С В M H -я D С NM П-я Угол В MN – линейный угол двугранного угла В D СК К С D Н-я M N
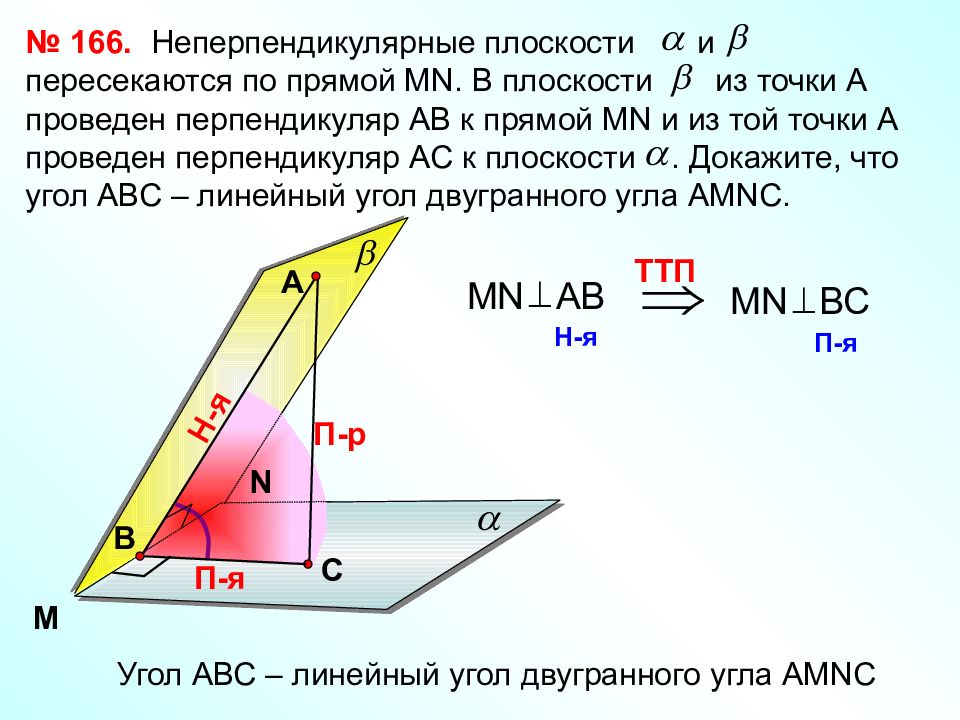
Неперпендикулярные плоскости и пересекаются по прямой М N. В плоскости из точки А проведен перпендикуляр АВ к прямой М N и из той точки А проведен перпендикуляр АС к плоскости. Докажите, что угол АВС – линейный угол двугранного угла АМ NC. № 166. M N А С В П-р Н-я П-я TT П М N А B H -я MN ВС П-я Угол АВС – линейный угол двугранного угла АМ NC
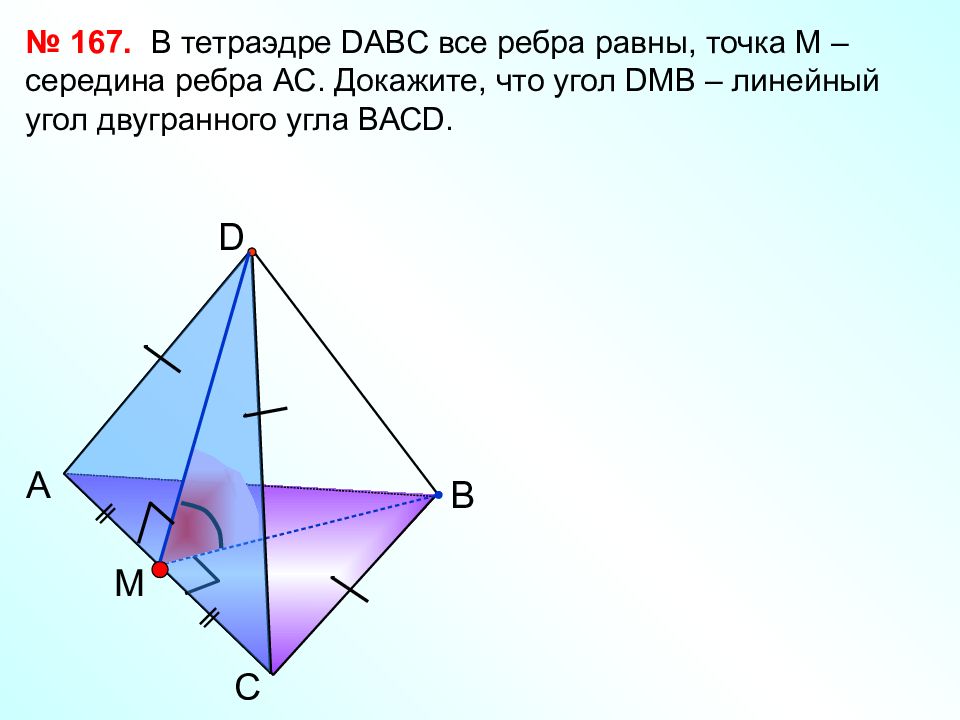
С А В D M В тетраэдре D АВС все ребра равны, точка М – середина ребра АС. Докажите, что угол D МВ – линейный угол двугранного угла ВАС D. № 167.
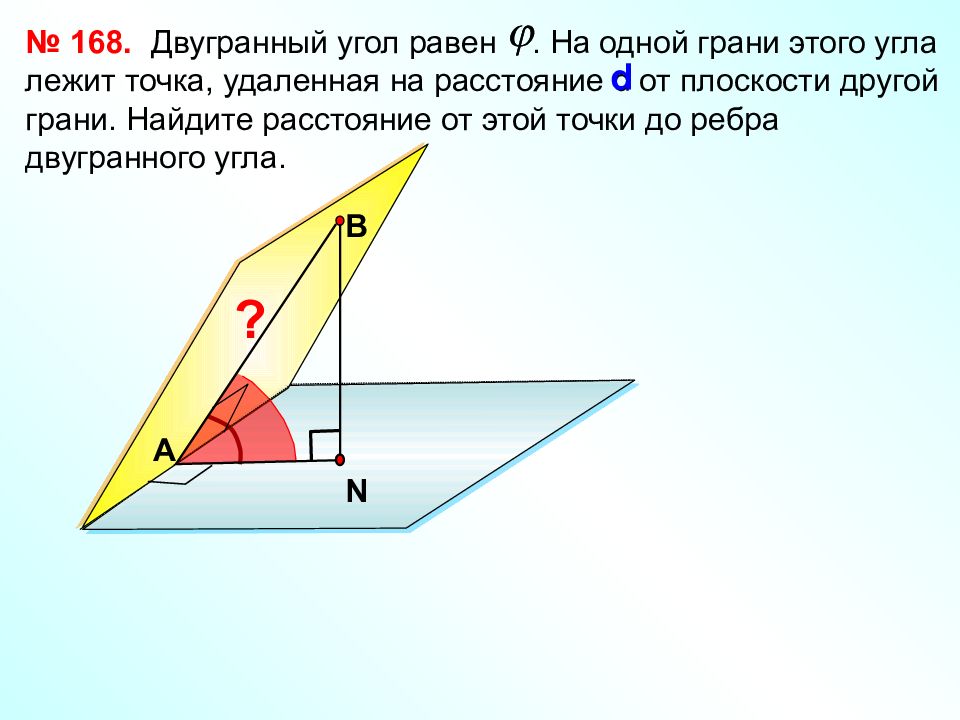
Двугранный угол равен. На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла. № 168. В d N А ?
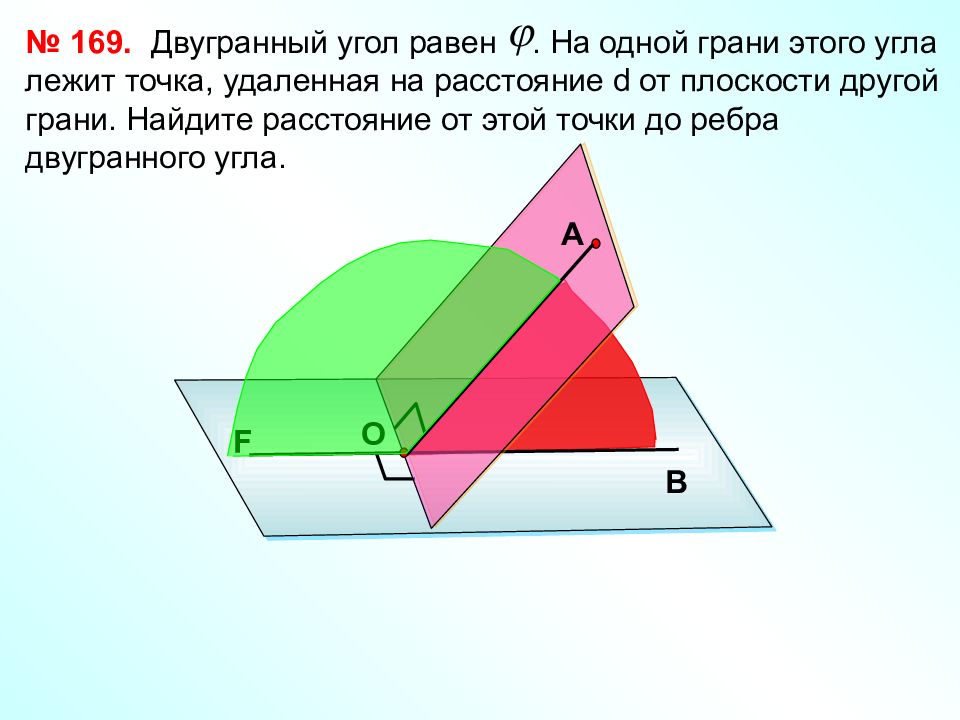
Двугранный угол равен. На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла. № 169. F В А О
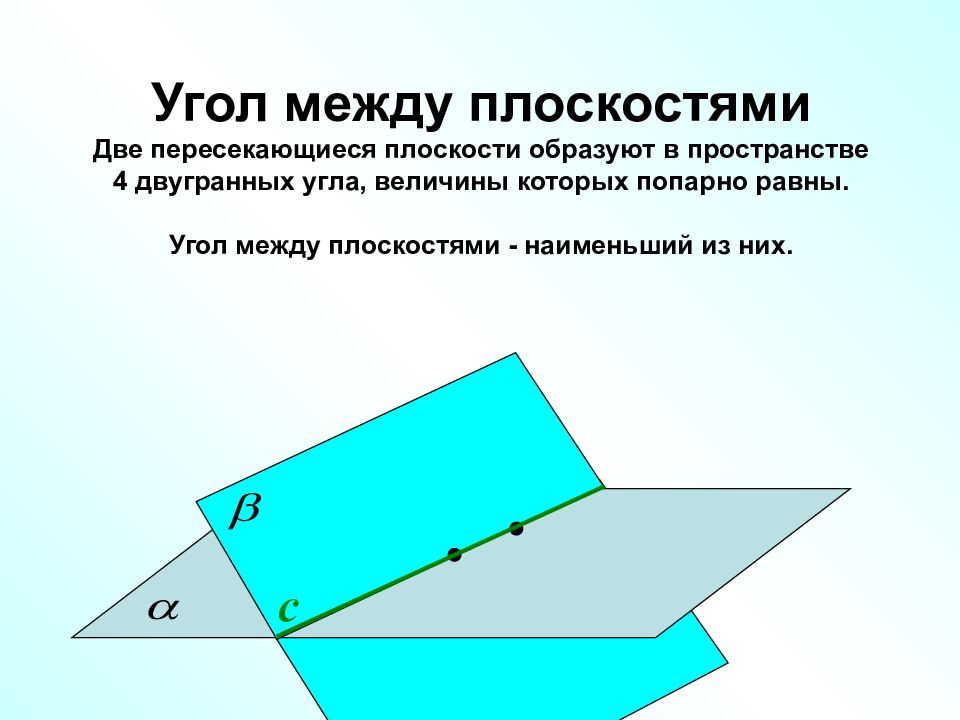
с Угол между плоскостями Две пересекающиеся плоскости образуют в пространстве 4 двугранных угла, величины которых попарно равны. Угол между плоскостями - наименьший из них.
Конспект (или §3, п.22) № 170, №173.
