Целые и рациональные числа Урок №1 в 10 классе
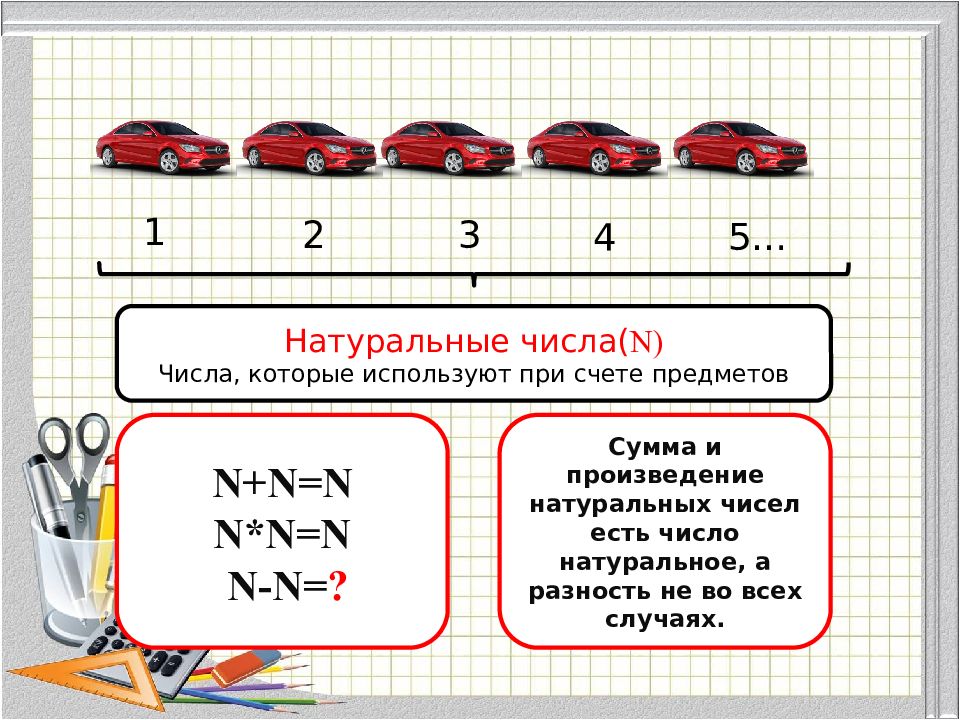
1 2 3 4 5… Натуральные числа( N) Числа, которые используют при счете предметов N+N=N N*N=N N-N= ? Сумма и произведение натуральных чисел есть число натуральное, а разность не во всех случаях.
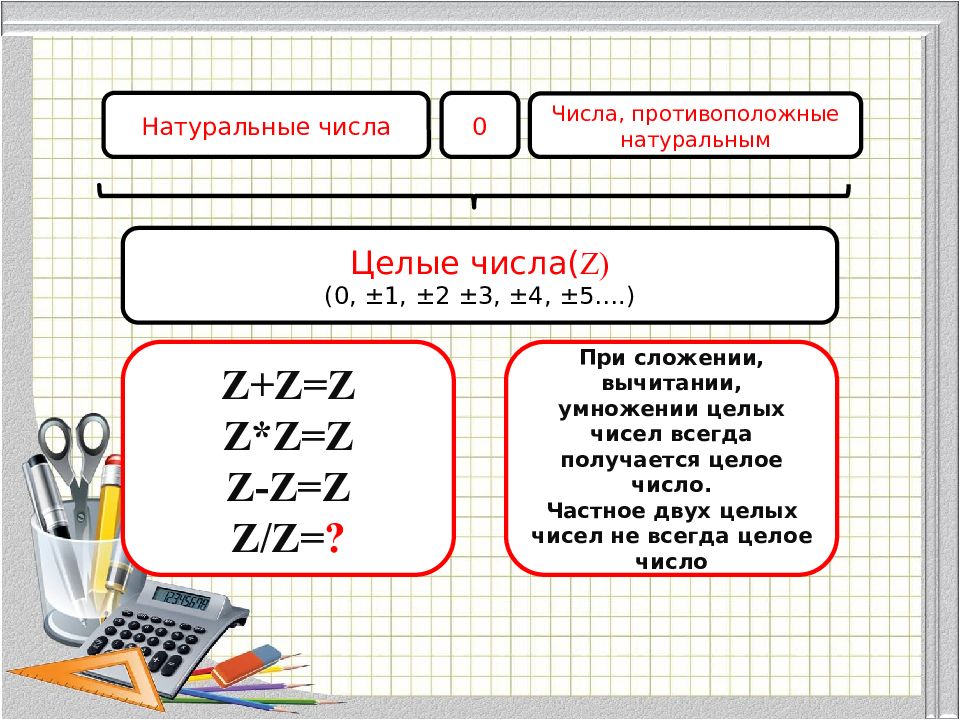
Натуральные числа Числа, противоположные натуральным 0 Целые числа( Z) (0, ±1, ±2 ±3, ±4, ±5….) Z+Z=Z Z*Z=Z Z-Z=Z Z/Z= ? При сложении, вычитании, умножении целых чисел всегда получается целое число. Частное двух целых чисел не всегда целое число
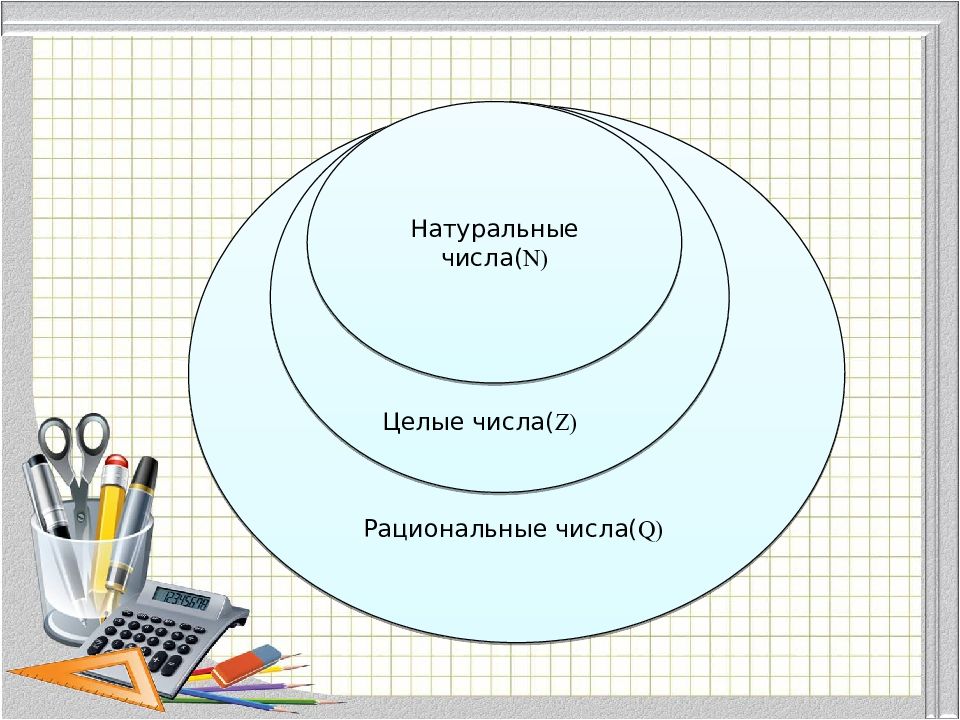
Рациональные числа( Q) - – это числа, которые можно представить в виде дроби m/n, где m – целое число, а n – натуральное число. Например, 2; 3,02; ; 4,2(3)… Обыкновенные дроби Конечные десятичные дроби Бесконечные периодические дроби ; ; … 2,5; 5,67; 3,4…
Натуральные числа( N) Целые числа( Z) Рациональные числа( Q)
Бесконечная периодическая дробь – Это бесконечные десятичные дроби, у которых одна цифра или группа цифр повторяются(период дроби). 23,14565656…=23,14(56) 0,33333…=0,(3) 67,8909090…=67,8(9) Читается «23 целых 14 сотых и 56 в периоде» Пример 1. Записать число в виде бесконечной десятичной дроби
Каждое рациональное число можно представить в виде бесконечной периодической дроби Каждая бесконечная периодическая дробь является рациональным числом. Пример 2. Представить бесконечную периодическую дробь 0,2(18) в виде рационального числа. Пусть х=0,2181818… х=0,2181818 … ×10 10 х=2.1818… ×100 1000х=218,18.. 1000х=218,18.. 10 х=2.1818… 990х=216 Так как в записи числа до периода 1 десятичный знак Так в периоде два знака
З Задания для классной работы №1, №3(чет) З З адания для домашней работы №1, №3(нечет),№4(1)
