7 ноября Классная работа
Множество натуральных чисел бесконечно. Множество натуральных чисел имеет наименьший элемент — число 1. Множество натуральных чисел не имеет наибольшего элемента. Во множестве N всегда выполнимы операции сложения и умножения. Множество N не является плотным, так как не всегда между двумя его любыми элементами можно найти хотя бы один элемент этого множества.
Множество целых чисел бесконечно. Множество целых чисел не имеет наименьшего элемента. Множество целых чисел не имеет наибольшего элемента. Во множестве Z выполняются операции сложения, вычитания и умножения. Множество Z не обладает свойством плотности, так как не всегда между любыми двумя его элементами можно найти хотя бы один элемент этого множества.
Множество рациональных чисел бесконечно. Множество рациональных чисел не имеет наименьшего элемента. Множество рациональных чисел не имеет наибольшего элемента. Во множестве Q выполняются операции сложения, вычитания, умножения и деления на число, не равное нулю. Множество Q обладает свойством плотности, между любыми двумя его элементами можно найти хотя бы один элемент этого множества (вообще между любыми двумя рациональными числами находится бесконечно много рациональных чисел).
Ещё 2500 лет назад греческими математиками было обнаружено, что нужды геометрии не обеспечиваются рациональными числами. Они были удивлены и обескуражены, заметив, что длина диагонали квадрата, стороны которого имеют длину единица, не может быть выражена никаким рациональным числом. Если к положительным бесконечным десятичным дробям присоединить противоположные им числа и число нуль, то получим множество чисел, которые называют действительными числами. Обозначают R – от лат. realis – реальный, существующий в действительности.
Действи́тельное число — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений. Если натуральные числа возникли в процессе счёта, рациональные — из потребности оперировать частями целого, то действительные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству действительных чисел, которое помимо чисел рациональных включает также иррациональные числа (« ир » - отрицание ).
Бесконечные десятичные дроби могут быть периодическими и непериодическими. Бесконечные десятичные периодические дроби – рациональные числ а ( m/n ): 1/3; 1,(56); – 4; 67; 8,12; 0,(3); 8/37 … Бесконечные десятичные непериодические – иррациональные числа: 5,10100100010000…; 4,101100111000… (пи) – отношение длины окружности к диаметру, = 3,141592654… Иррациональные числа нельзя представить в виде отношения , где m — целое число, а n — натуральное. При выполнении действий над действительными числами в практических задачах их заменяют приближенными значениями (производят округление до десятых, сотых и т.д.)
Множество действительных чисел бесконечно. Множество действительных чисел не имеет наименьшего элемента. Множество действительных чисел не имеет наибольшего элемента. Во множестве R выполняются операции сложения, вычитания, умножения и деления на число, не равное нулю, а также выполняются операции извлечения корня, вычисления логарифмов. Множество R обладает свойством плотности, между любыми двумя его элементами можно найти хотя бы один элемент этого множества (вообще между любыми двумя действительными числами находится бесконечно много действительных чисел).
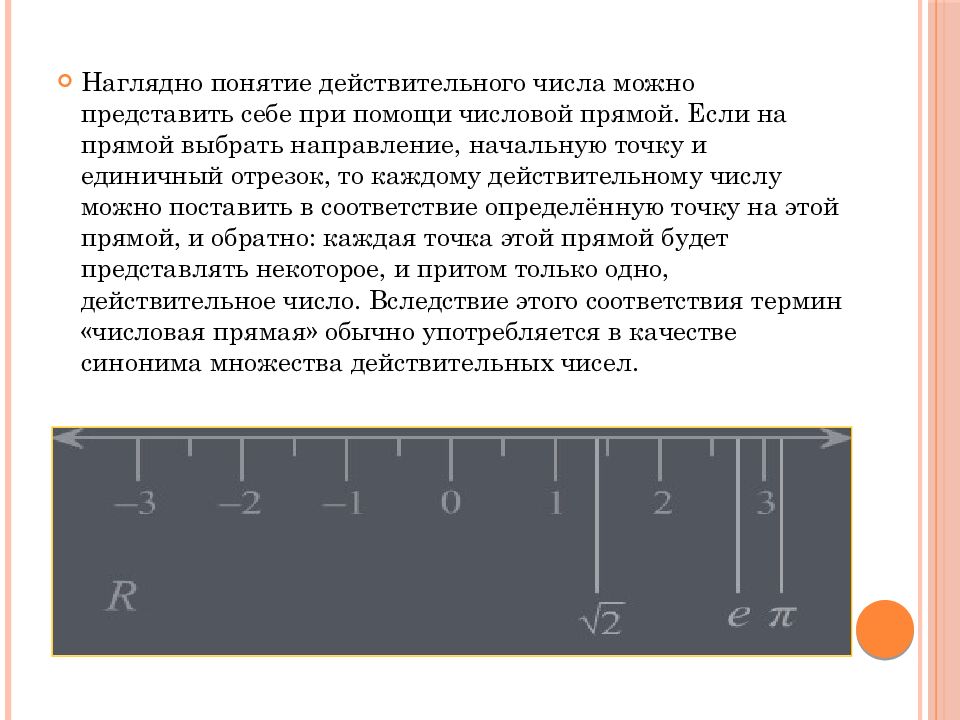
Наглядно понятие действительного числа можно представить себе при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единичный отрезок, то каждому действительному числу можно поставить в соответствие определённую точку на этой прямой, и обратно: каждая точка этой прямой будет представлять некоторое, и притом только одно, действительное число. Вследствие этого соответствия термин «числовая прямая» обычно употребляется в качестве синонима множества действительных чисел.
Между множеством действительных чисел и множеством точек координатной прямой существует взаимно однозначное соответствие: Если имеются два множества А и В и по некоторому правилу каждому элементу множества А поставлен в соответствие единственный элемент множества В, при этом любой элемент множества В является соответствующим для некоторого единственного элемента множества А, то говорят, что между множествами А и В установлено взаимно однозначное соответствие.
немецкий математик, известный работами по абстрактной алгебре и основаниям действительных чисел, член Берлинской академии наук (1880). Учился у К. Гаусса и Л. Дирихле в Гёттингенском университете. Создал ряд общих концепций, лежащих в основе современной алгебры. В сочинении «Непрерывность и иррациональные числа» (1872) дал одну из первых систем строгого обоснования теории действительных чисел.
285. Расположите в порядке возрастания числа 4,62; 3,(3); –2,75...; –2,63.... 286. Расположите в порядке убывания числа 1,371...; 2,065; 2,056...; 1,(37); –0,078.... 287. Какие целые числа расположены между числами: а) −3,168... и 2,734...; б) −5,106... и −1,484...; в) −4,06 и −1,601; г) −1,29 и 0,11? 289. Найдите приближённое значение выражения a − b, где a = 59,678... и b = 43,123..., округлив предварительно а и b : а) до десятых; б) до сотых. Домашнее задание: выучить определение рационального и иррационального чисел, сравнить числа Сравните числа:
