Число является одним из основных понятий математики. Существует большое количество определений понятия «число». Евклид «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». «Начала» 355 г. до н.э.
Русский математик, педагог, помощником учителя математики в школе математических и навигацких наук Магницкий Леонтий Филиппович в своей «Арифметике» в 1703 г. писал: «Арифметика - есть наука числительная. « Число есть бесконечно, Умом нам недотечно Никто не знает конца, Кроме всех, Бога творца».
Еще раньше Евклида Аристотель дал такое определение: « Число есть множество, которое измеряется с помощью единиц». Аристотель
Фалес Милетский – родоначальник греческой стихийно-материалистической философии – учил, что « Чи сло - есть система единиц».
Исаак Ньютон – великий английский физик, механик, астроном и математик в своей «Общей арифметике» (1707 г.) пишет: «Под числом мы подразумеваем не столько множество единиц, сколько абстрактное отношение какой-нибудь величины к другой величине такого же рода, взятой за единицу. Число бывает трех видов: целое, дробное и иррациональное. Целое число есть то, что измеряется единицей; дробное – кратной частью единицы; иррациональное – число, не соизмеримое с единицей».
Папирус из «Начал» Евклида Глиняные таблички Материалом, служащим для записи чисел стали:
Числа 1, 2, 3 … - натуральные числа Натуральные числа – числа, возникающие естественным образом при счёте. Существуют два подхода к определению натуральных чисел — числа, используемые при: перечислении (нумеровании) предметов ( первый, второй, третий, …); обозначении количества предметов ( нет предметов, один предмет, два предмета, …). N 9
Множество целых чисел = натуральные числа + противоположные им числа и нуль -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 Z 10
Множество рациональных чисел Множество рациональных чисел обозначается и может быть записано в виде: Нужно понимать, что численно равные дроби такие как, например, и, входят в это множество как одно число. Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
Для всех рациональных чисел можно использовать один и тот же способ записи. Рассмотрим 1. Целое число 5 5,000 2. Обыкновенную дробь 0, 3(18) 3. Десятичную дробь 8,377 8,3(7)
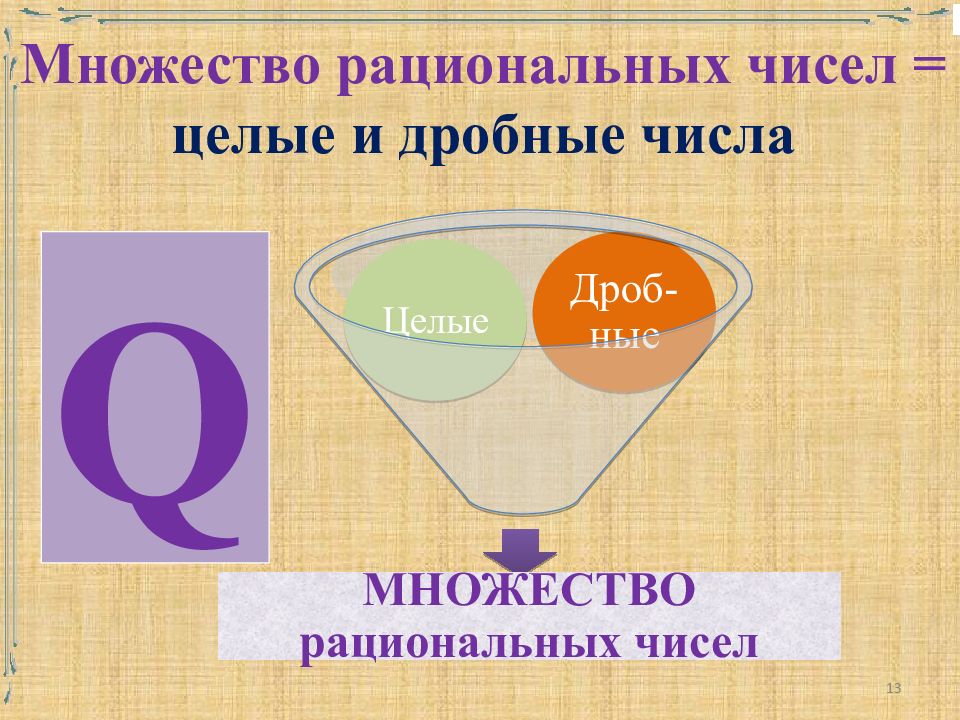
Множество рациональных чисел = целые и дробные числа Q МНОЖЕСТВО рациональных чисел Дроб-ные Целые 13
Леонард Эйлер - Все числа, о которых мы сегодня говорили, изобра-жаются на схеме, которая называется Круги Эйлера. Q Z N
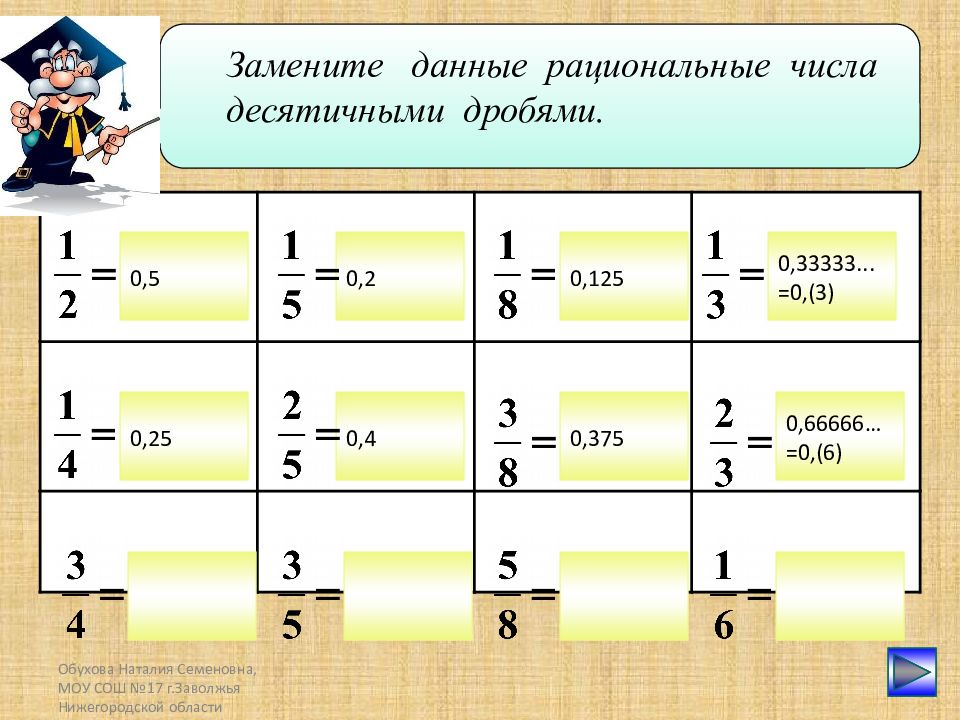
Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области 0,375 0,66666…=0,(6) 0,4 0,25 0,33333...=0,(3) 0,125 0,2 0,5 Замените данные рациональные числа десятичными дробями.
16
17
1. Записать в виде десятичных дробей: а) б) 2. Представьте в виде обычных дробей: а) 15,(3) б ) 1,6(1) Домашнее задание
