Слайд 2: Интерференция механических волн
Сложение волн Что происходит со звуковыми волнами при беседе нескольких человек, когда играет оркестр, поет хор и т.д.? Что мы наблюдаем, когда в воду одновременно падают два камня или капли?
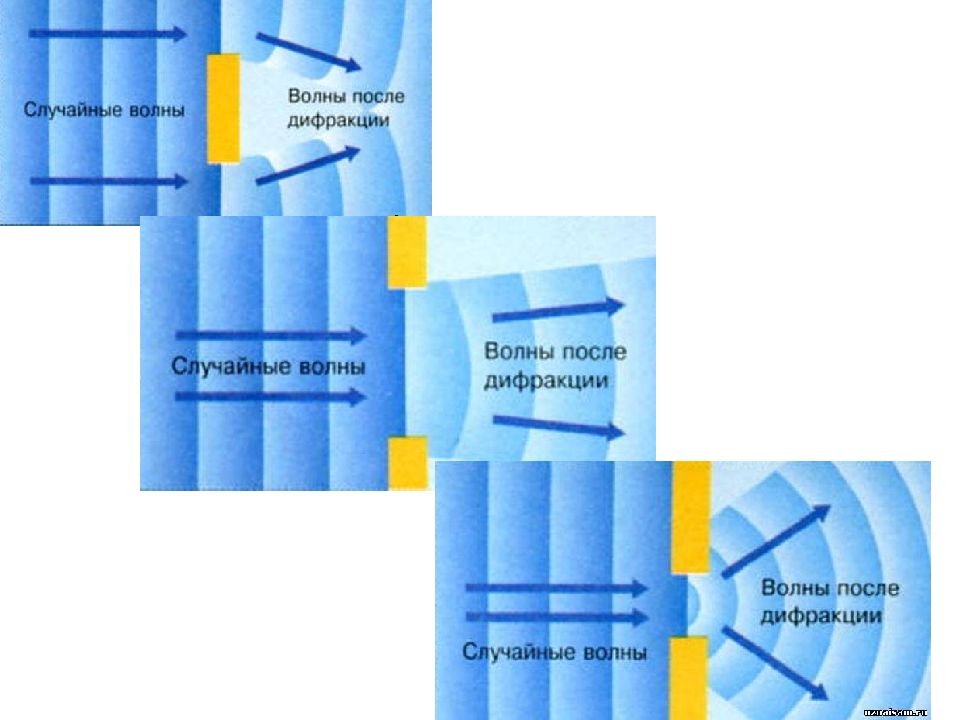
Слайд 3: Проследим это на механической модели
Мы наблюдаем чередование светлых и темных полос. Это означает, в что любой точке поверхности колебания складываются.
Слайд 4
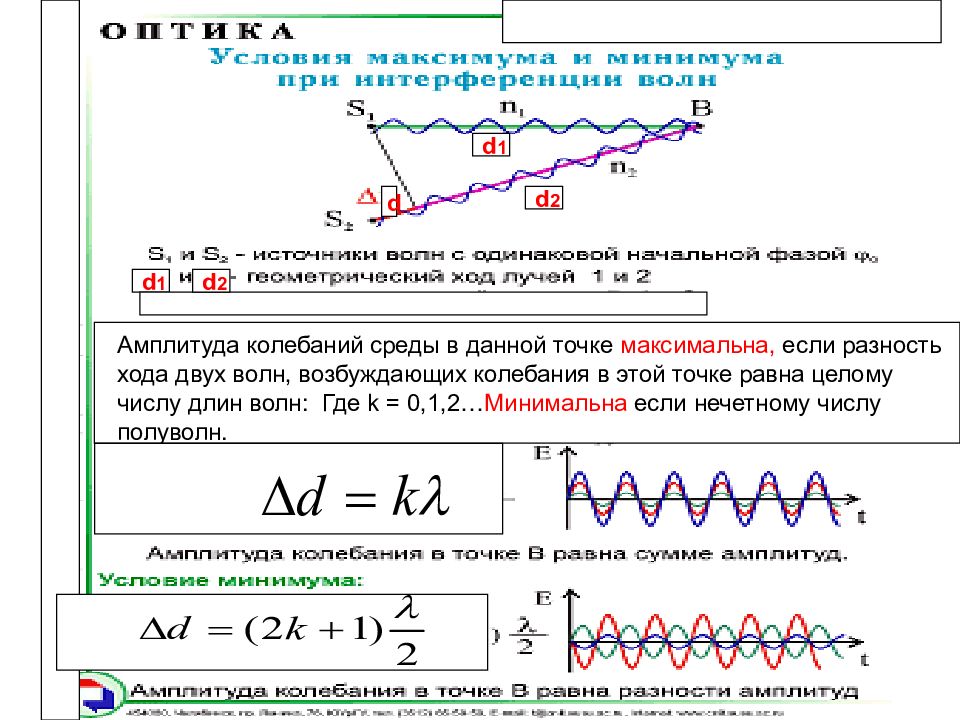
d d 2 d 1 Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке равна целому числу длин волн: Где k = 0,1,2… Минимальна если нечетному числу полуволн. d 1 d 2
Слайд 5: Интерференция
Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний, называется интерференцией.
Слайд 6: Когерентные волны
Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной. Источники, удовлетворяющие этим условиям, называются когерентными.
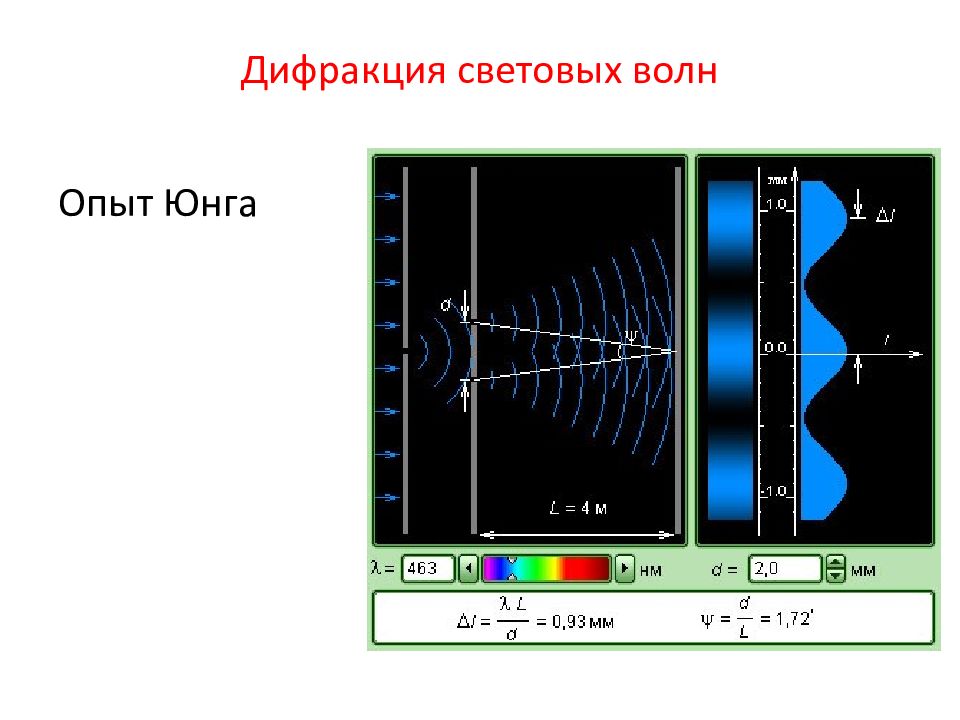
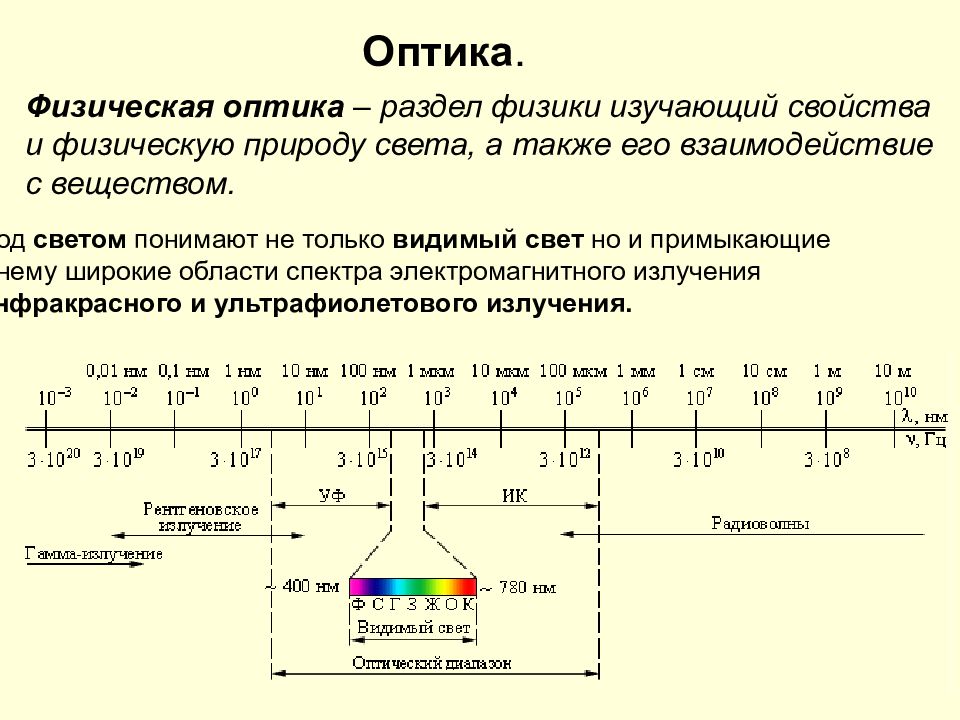
Слайд 8: Интерференция света
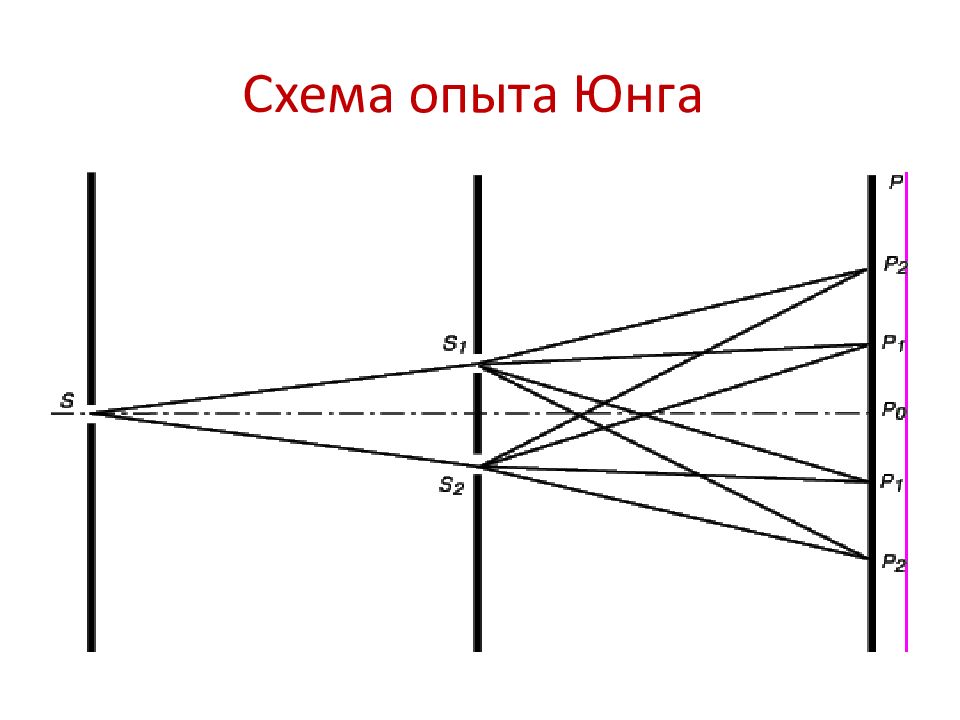
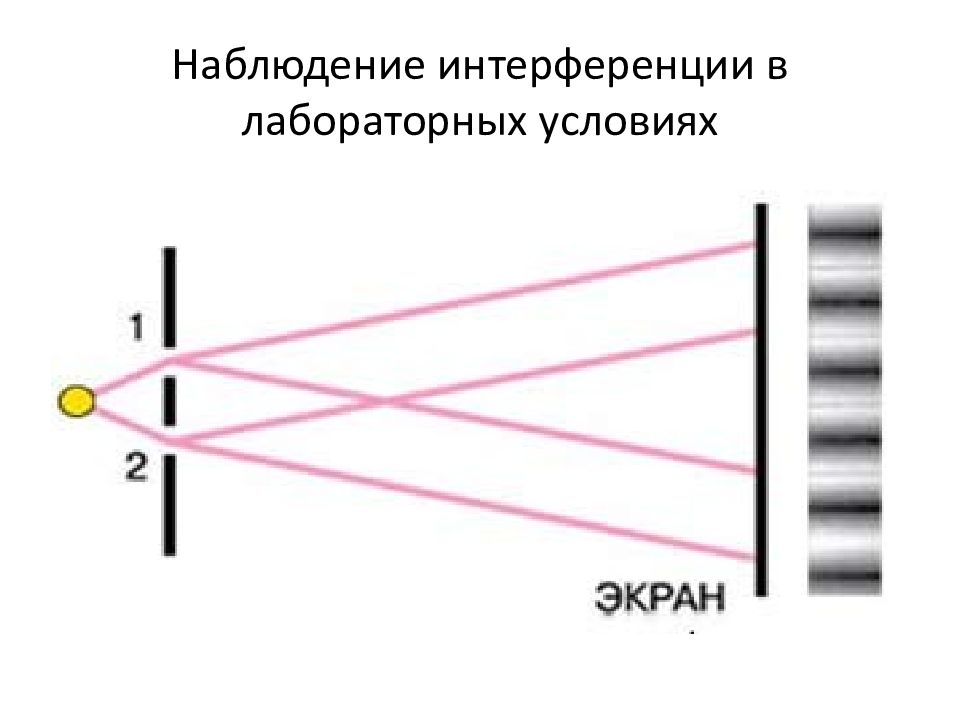
Для получения устойчивой интерференционной картины нужны согласованные волны. Они должны иметь одинаковую длину волны и постоянную разность фаз в любой точке пространства.
Слайд 9: Интерференция в тонких пленках
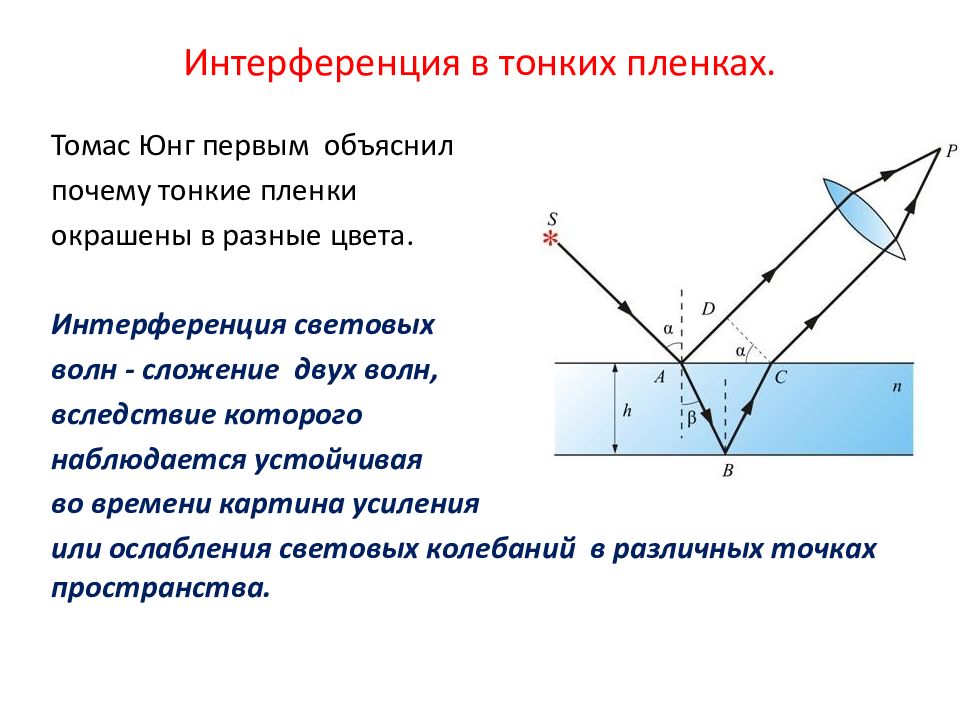
Томас Юнг первым объяснил почему тонкие пленки окрашены в разные цвета. Интерференция световых волн - сложение двух волн, вследствие которого наблюдается устойчивая во времени картина усиления или ослабления световых колебаний в различных точках пространства.
Слайд 12: Интерференционные максимумы и минимумы
Интерференционные максимумы наблюдаются в точках, для которых разность хода волн ∆ d равна четному числу полуволн, или, что то же самое, целому числу волн: Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, равна нечётному числу полуволн:
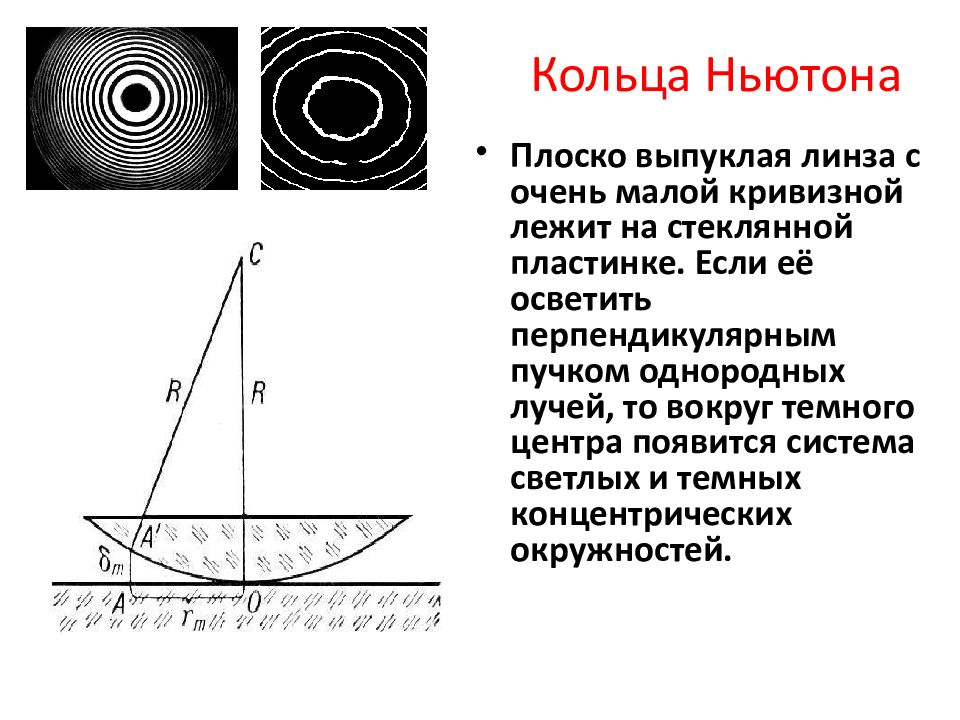
Слайд 14: Кольца Ньютона
Плоско выпуклая линза с очень малой кривизной лежит на стеклянной пластинке. Если её осветить перпендикулярным пучком однородных лучей, то вокруг темного центра появится система светлых и темных концентрических окружностей.
Слайд 16
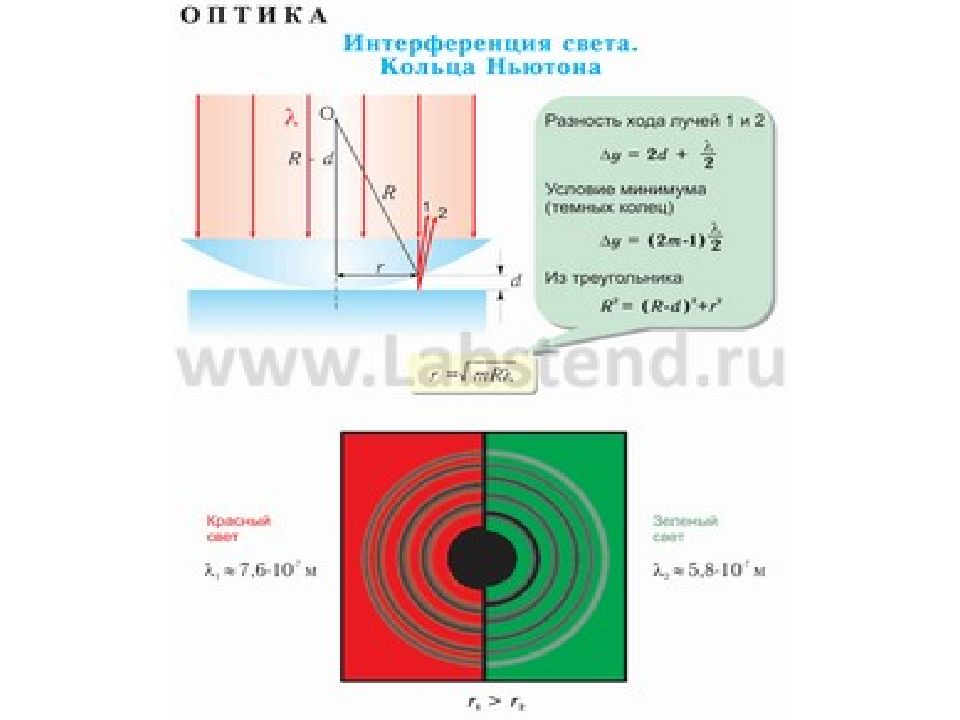
Расстояние между окрашенными кольцами зависит от цвета; кольца красного цвета отстоят друг от друга дальше, чем кольца голубые. Кольца Ньютона можно также наблюдать в проходящем свете. Цвета в проходящем свете являются дополнительными к цветам в отраженном свете.
Слайд 17
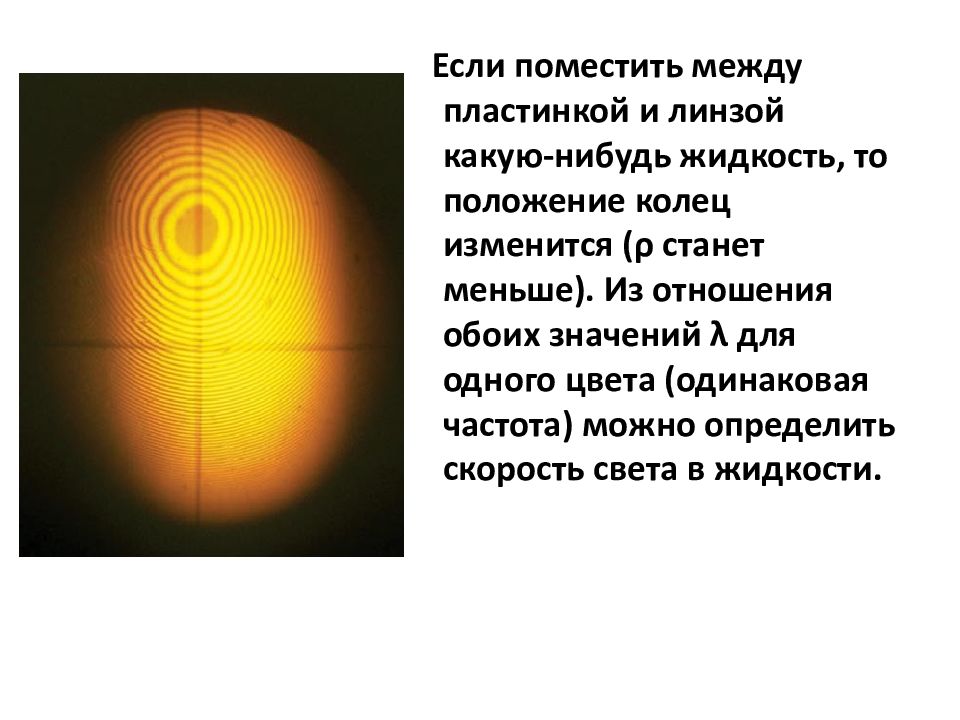
Если поместить между пластинкой и линзой какую-нибудь жидкость, то положение колец изменится (ρ станет меньше). Из отношения обоих значений λ для одного цвета (одинаковая частота) можно определить скорость света в жидкости.
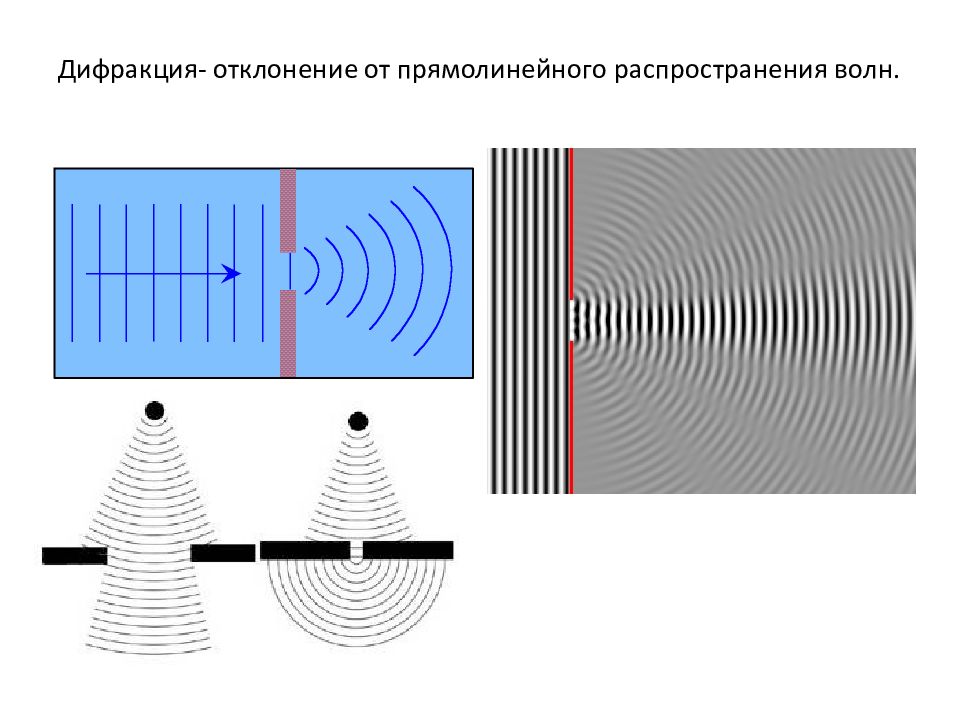
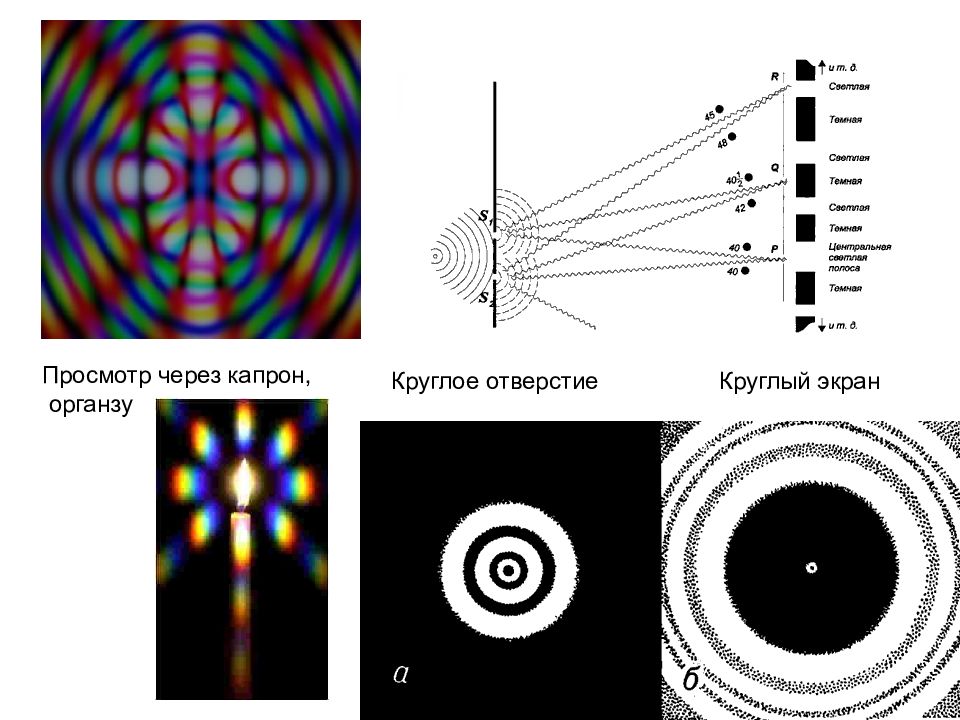
Слайд 22: Теория Френеля
Волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.
Слайд 24
Дифракционная решётка. Дифракционная решётка- оптический прибор, представляющий собой совокупность большого числа параллельных, равноотстоящих друг от друга штрихов одинаковой формы, нанесённых на плоскую или вогнутую оптическую поверхность.
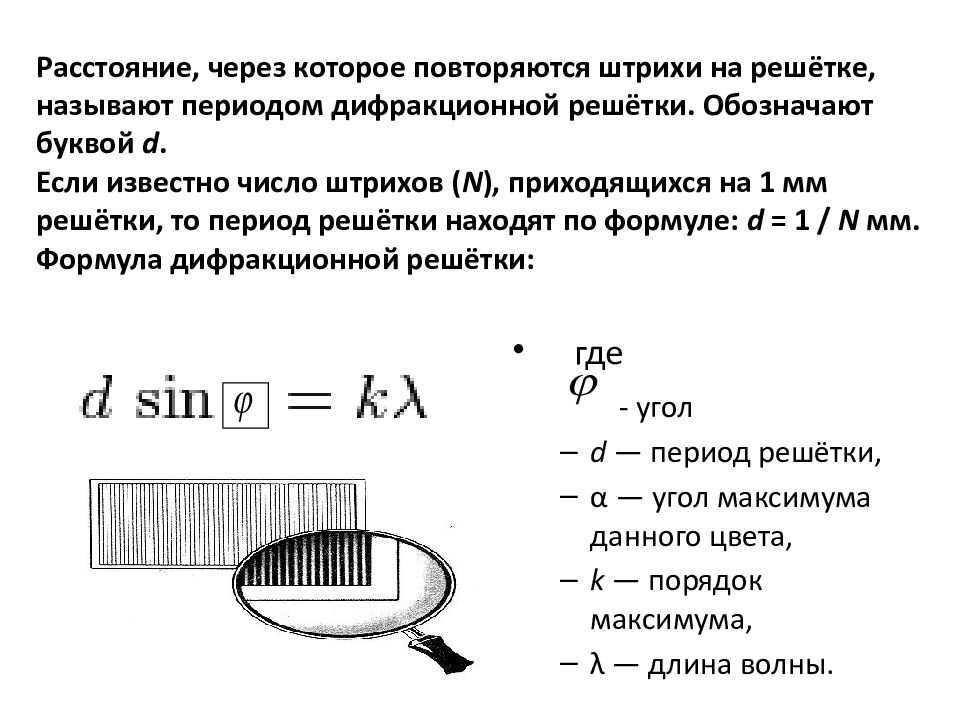
Слайд 25: Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d. Если известно число штрихов ( N ), приходящихся на 1 мм решётки, то период решётки находят по формуле: d = 1 / N мм. Формула дифракционной решётки:
где - угол d — период решётки, α — угол максимума данного цвета, k — порядок максимума, λ — длина волны.
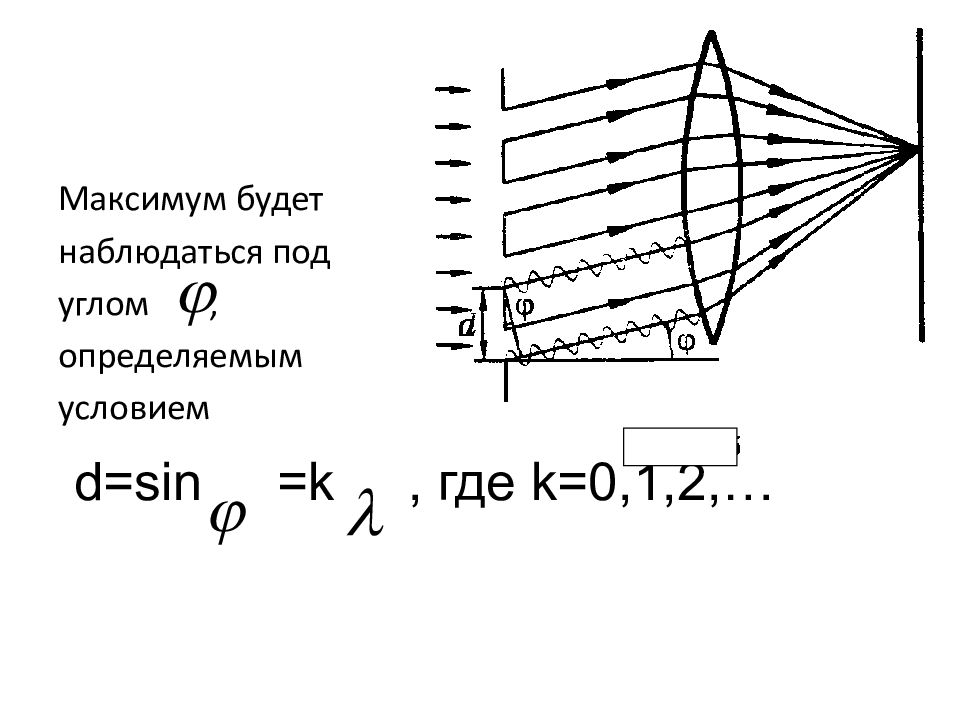
Слайд 26
Максимум будет наблюдаться под углом, определяемым условием d=sin = k, где k =0,1,2,…