Первый слайд презентации: Раздел 5 Физика колебаний и волн. Оптика
Курс лекций по общей физики Доцент Петренко Л.Г. Кафедра общей и экспериментальной физики НТУ «ХПИ» Харьков - 2013 год
Слайд 2
5.5.1. Интерференция монохроматических волн. Квазимонохроматические волны. Время и длина когерентности. Временное и спектральное рассмотрение интерференционных явлений. 5.5. ИНТЕРФЕРОМЕТРИЯ Интерференция света является частным случаем интерференции волн. Видимый свет можно представлять как электромагнитные волны длиной = 0,4 0,8 мкм. Необходимым условием интерференции является когерентность - согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны. Однако, реальные источники света излучают не бесконечные монохроматические, а в лучшем случае квазимонохроматические волны, представляющие собой сменяющие друг друга волновые цуги (переходя из возбуждённого состояния в нормальное, атомы излучают свет в виде отдельных коротких импульсов). Средняя продолжительность одного цуга называется временем когерентности и составляет примерно ког 10 -8 с.
Слайд 3
Расстояние, при прохождении которого две или несколько волн утрачивают когерентность, называется длиной когерентности : l ког = с. ког, где с =3. 10 8 м/с – скорость света в вакууме. Наблюдение интерференции света от двух источников света возможно лишь при оптических разностях хода волн, меньших длины когерентности. Когерентность колебаний, которые совершаются в одной и той же точке пространства, зависит от степени монохроматичности волн ( ) и называется временной когерентностью. Когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках плоскости, перпендикулярной направлению распространения волны, называется пространственной когерентностью. Два источника света, размеры и взаимное расположение которых позволяют наблюдать интерференцию, называются пространственно когерентными. Максимальное расстояние, поперечное направлению распространения волны, на котором возможно проявление интерференции, называется радиусом когерентности : где - длина световой волны; - угловые размеры источника света. r ког / ,
Слайд 4
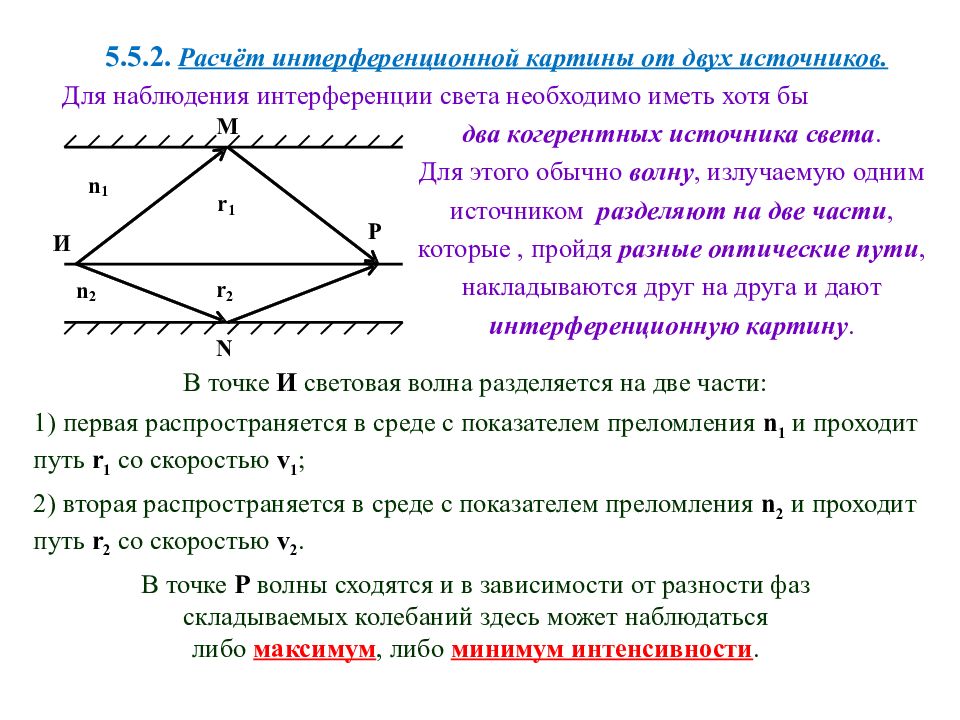
5.5.2. Расчёт интерференционной картины от двух источников. Для наблюдения интерференции света необходимо иметь хотя бы два когерентных источника света. Для этого обычно волну, излучаемую одним источником разделяют на две части, которые, пройдя разные оптические пути, накладываются друг на друга и дают интерференционную картину. В точке И световая волна разделяется на две части: 1) первая распространяется в среде с показателем преломления n 1 и проходит путь r 1 со скоростью v 1 ; 2) вторая распространяется в среде с показателем преломления n 2 и проходит путь r 2 со скоростью v 2. В точке Р волны сходятся и в зависимости от разности фаз складываемых колебаний здесь может наблюдаться либо максимум, либо минимум интенсивности.
Слайд 5
Уравнения колебаний, создаваемых этими волнами в точке Р, имеют вид: Разность фаз складываемых колебаний: где 0 – длина световой волны в вакууме. Величина L = r. n называется оптической длиной пути. Величина = r 2 n 2 - r 1 n 1 называется оптической разностью хода волн. Таким образом, Максимуму интерференции соответствует: Минимуму интерференции соответствует: где m = 0,1,2,3,... - порядок интерференционного максимума или минимума.
Слайд 6
Существует несколько методов наблюдения интерференции света, например: 1) метод Юнга, 2) метод зеркал Френеля, 3) метод бипризмы Френеля. Можно показать, что оптическая разность хода лучей, исходящих из щелей И 1 и И 2 и сходящихся в точке наблюдения Р равна: Р где n – показатель преломления среды. Координаты точек максимумов интенсивности: Координаты точек минимумов интенсивности: Все эти методы принципиально можно свести к одному - методу Юнга, в котором источником света являются две узкие щели, расположенные на небольшом расстоянии друг от друга.
Слайд 7
Расстояние между двумя соседними максимумами или соседними минимумами называется шириной интерференционной полосы и равно: Это расстояние при заданных L и d постоянно. Таким образом, интерференционная картина от двух щелевых источников представляет собой чередование тёмных и светлых полос, параллельных друг другу и находящихся на одинаковом расстоянии друг от друга. Если источник немонохроматичный, например, белый, то интерференционная картина представляет собой радужные полосы, расположенные фиолетовой стороной ближе к центру интерференционной картины. И только центральная полоса оказывается белой.
Слайд 8
5.5.3. Интерференция в тонких плёнках. Линии равной толщины и равного наклона. Кольца Ньютона. Просветление оптики. Интерференцию можно наблюдать визуально в естественных условиях в тонких плёнках – на мыльных пузырях, масляных пятнах на поверхности воды, окисных плёнках на поверхности металла, тонких покрытиях на линзах, стёклах очков, автомобильных фарах и т.п. В этих случаях интерферируют волны, отражённые от двух поверхностей плёнок. Результат интерференции (увеличение или уменьшение интенсивности света) зависит от разности фаз или оптической разности хода складываемых в олн.
Слайд 9
Рассмотрим интерференцию света в тонкой плёнке с показателем преломления n, помещённой в некоторую среду с показателями преломления: над плёнкой n 1, а под плёнкой n 2. После многократных отражений и преломлений на верхней и нижней поверхностях плёнки образуются пары когерентных волн – а)в отражённом свете - 1 и 2 и б) в проходящем свете - 1* и 2*. Эти пары волн, собранные линзой на экране (или хрусталиком глаза на сетчатке), образуют интерференционную картину в отражённом ( 1 и 2 ) и проходящем ( 1* и 2* ) свете. Можно показать, что оптическая разность хода равна: При отражении световой волны от границы раздела с оптически более плотной средой происходит сдвиг фазы волны на , что эквивалентно увеличению оптической длины пути на 0 /2. При отражении световой волны от границы раздела с оптически менее плотной средой и при преломлении такого сдвига фазы и удлинения оптического пути не происходит. Поэтому условия интерференции в отражённом и проходящем свете существенным образом зависят от соотношения между показателями преломления плёнки и окружающей среды.
Слайд 10
Условия интерференционного усиления и ослабления интенсивности света при отражении и преломлении его в тонких плёнках Соотношения между показателями преломления Отражённый свет Проходящий свет max min max min n >n 1, n >n 2 или n <n 1, n <n 2 2d. n. cos =(2m-1) 0 /2 2d. n. cos =2 m 0 /2 2d. n. cos =2 m 0 /2 2d. n. cos =(2m-1) 0 /2 n >n 1, n <n 2 или n <n 1, n >n 2 2d. n. cos =2 m 0 /2 2d. n. cos =(2m-1) 0 /2 2d. n. cos =(2m-1) 0 /2 2d. n. cos =2 m 0 /2 m = 0, 1, 2,… ; - угол преломления; - угол падения света;
Слайд 11
Возможность ослабления отражённого света вследствие интерференции в тонких плёнках используется в современных оптических приборах (линзы микроскопов, фотоаппаратов, биноклей и т.п.). На переднюю стенку линзы наносят покрытие с показателем преломления меньшим, чем у материала линзы. Толщина плёнки подбирается так, чтобы минимум отражения наблюдался для света с длиной волны =5,5. 10 -7 м, соответствующей наибольшей чувствительности сетчатки глаза ( зелёный свет ). В отражённом свете линзы кажутся фиолетовыми, так как хорошо отражают красные и сине-фиолетовые лучи.
Слайд 12
Как показывают формулы, выражающие условия интерференционных максимумов и минимумов, эти условия зависят от длины световой волны, от толщины плёнки и от угла падения и преломления света. Для точечного источника расходящегося пучка света линии равного наклона представляют собой концентрические окружности. При освещении плёнки белым светом линии равного наклона имеют радужную окраску, причём ближе к центру располагаются фиолетовые части колец, а дальше от центра - красные. Если на плоскопараллельную плёнку падает расходящийся или сходящийся пучок света - углы падения (преломления ) для разных лучей в пучке разные. Интерференционная картина в этом случае представляет собой чередующиеся светлые и тёмные линии. Каждой линии соответствует определённое значение угла . Эти линии называются линиями равного наклона.
Слайд 13
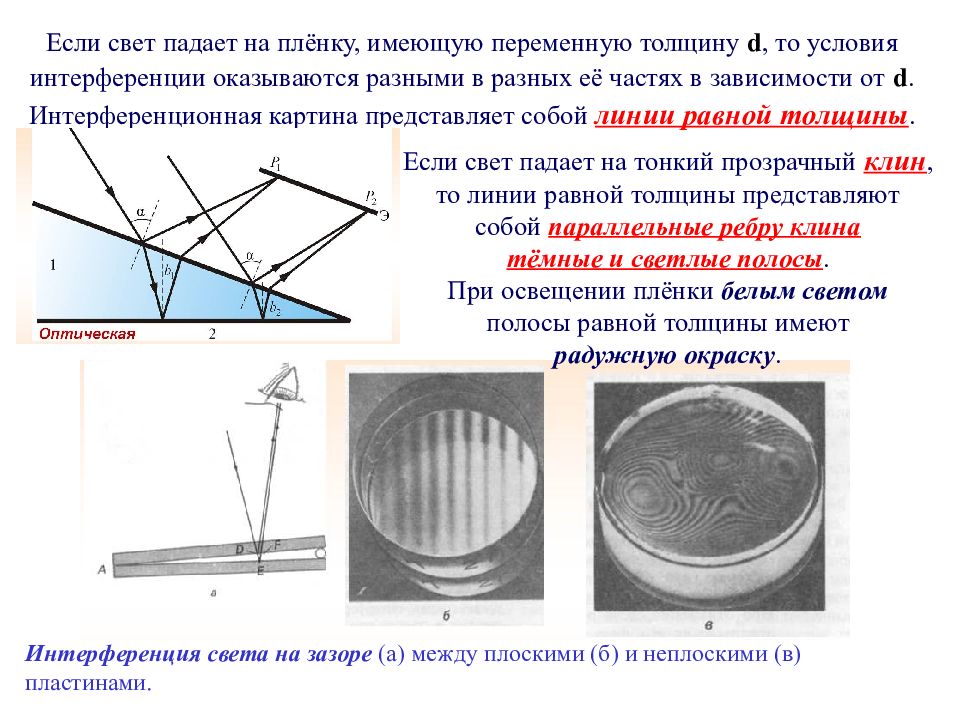
Если свет падает на плёнку, имеющую переменную толщину d, то условия интерференции оказываются разными в разных её частях в зависимости от d. Интерференционная картина представляет собой линии равной толщины. Если свет падает на тонкий прозрачный клин, то линии равной толщины представляют собой параллельные ребру клина тёмные и светлые полосы. При освещении плёнки белым светом полосы равной толщины имеют радужную окраску. Интерференция света на зазоре (а) между плоскими (б) и неплоскими (в) пластинами.
Слайд 14
Частным случаем линий равной толщины являются кольца Ньютона. Плоско выпуклая линза с большим радиусом кривизны R выпуклой поверхностью соприкасается в точке О с плоскопараллельной пластинкой. Параллельный пучок света падает перпендикулярно плоской поверхности линзы. Роль тонкой плёнки играет зазор между выпуклой поверхностью линзы и верхней поверхностью пластинки. Толщина плёнки-зазора увеличивается от точки О к периферии. Интерференционная картина представляет собой концентрические кольца равной толщины. В отражённом свете в центре наблюдается тёмное пятно, в проходящем свете – светлое. Цвет светлых колец определяется длиной волны падающего света. Если используется источник белого света, то кольца имеют радужную окраску, причём ближе к центру располагаются фиолетовые части колец, а дальше от центра - красные.
Слайд 15
Радиусы светлых (интерференционные максимумы) и тёмных (интерференционные минимумы) колец Ньютона можно рассчитать следующим образом. Из треугольника О АВ (см. рисунок) следует: r m 2 =R 2 -(R-d m ) 2 =2Rd m -d m 2 ; 2Rd m >>d m 2 ; (R>>d m ) ; При перпендикулярном падении света =0 и cos =1. Тогда условие интерференционного максимума имеет вид: 2 d m n = (2 m - 1) 0 / 2. А радиус m -го светлого кольца Ньютона в отражённом свете равен: А радиус m -го тёмного кольца Ньютона в отражённом свете равен: Отсюда следует, что толщина зазора в месте наблюдения m -го светлого кольца равна: d m = (2 m - 1) 0 / 4 n. Условие интерференционного минимума имеет вид: 2 d m. n = m 0. Отсюда следует, что толщина зазора в месте наблюдения m -го тёмного кольца равна: d m = m 0 / 2 n.
Слайд 16
Ширина колец Ньютона быстро убывает по мере роста номера кольца m : Наблюдение колец Ньютона позволяет: 1) измерять радиусы кривизны линз ; 2) выявлять и оценивать величину малейших дефектов на выпуклой поверхности линз, то есть производить их отбраковку.
Слайд 17
5.5.4. Интерферометры Майкельсона, Линника, Жамена и их практическое применение. Явление интерференции широко используется в таких точных приборах, как интерферометры. Работа всех интерферометров основана на едином принципе и отличаются они лишь конструктивно. Интерферометр Майкельсона. Световой луч от источника света И падает под углом 45 0 на плоско параллельную пластинку П 1, посеребрённую со стороны, противоположной от источника света И. Преломившись в пластине, луч в точке О разделяется на две части: Принципиальная схема интерферометра Майкельсона. 1) луч 1 отражается от посеребрённого покрытия и направляется на вертикально расположенное зеркало З 1, отражается от него и, пройдя через пластинку П 1, возвращается в точку О, а затем, преломившись, направляется на экран Э (луч 1* ); 2) луч 2 проходит к зеркалу З 2, отражается от него и возвращается в точку О, дважды пройдя че- рез пластинку-компенсатор П 2 (пластинка П 2 такая же, как и П 1, только не покрытая серебром); в точке О луч отражается от пластинки П 1 и направляется на экран Э (луч 2* ). Зеркала З 1 и З 2 располагают друг по отношению к другу под углом, отличающимся от 90 0 на небольшую величину . Тогда на экране наблюдается интерференционная картина в виде чере-дующихся светлых и тёмных полос равной толщины, аналогичная интерференционной картине, получаемой на тонком воздушном клине с углом в его вершине (клин в этом случае образуют зеркало З 1 и мнимое изображением зеркала З 2 на посеребрённом покрытии пластины П 1 ).
Слайд 18
Интерферометры Майкельсона используются для точного ( порядка 10 -7 м) измерения длины тел, длины световой волны, изменения длины тел при изменении температуры (интерференционные дилатометры). Блок зеркал интерферометра Современный интерферометр Майкельсона Таким образом, при малых перемещениях зеркал на расстояние ∆ ℓ происходит сдвиг интерференционных полос на величину ∆ m Разность хода лучей 1* и 2* изменяется при малейшем сдвиге одного из зеркал. Перемещение его на 0 /4 изменяет разность хода на 0 /2, а результат интерференции при этом изменяется на противоположный.
Слайд 19
Интерферометры Майкельсона используются также как рефрактометры для определения незначительного изменения показателя преломления прозрачных тел в зависимости от давления, температуры, примесей и т.д. Интерференционные рефрактометры позволяют измерять показатели преломления с точностью до 10 -6. На пути интерферирующих лучей располагаются две одинаковые кюветы длиною ℓ, одна из которых заполнена веществом с известным n, а другая – с неизвестным n x показателями преломления. При этом между интерферирующими лучами возникает дополнительная разность хода ∆=2ℓ( n х - n ), что приведёт к сдвигу интерференционных полос на величину ∆ m. Ручной рефрактометр Неизвестный показатель преломления вещества определяется по формуле:
Слайд 20
Интерферометр Линника. Советский физик В.П.Линник использовал принцип действия интерферометра Майкельсона для создания микроинтерферометра ( комбинации интерферометра и микроскопа ), служащего для контроля чистоты обработки поверхностей. На фотографии представлена интерференционная картина – полосы равной толщины, позволяющая оценивать степень шероховатости поверхности исследуемого образца.
Слайд 21
Интерферометр Жамена. 2 1 Л К 1 К 2 Э В А И В результате отражения света от обеих поверхностей пластины образуются две когерентных волны 1 и 2. Пройдя сквозь две совершенно одинаковые закрытые кюветы К 1 и К 2, имеющие длину ℓ, эти волны после отражения от пластины В собираются линзой Л и интерферируют, образуя на экране Э полосы равного наклона. Если кювету К 1 заполнить газом с известным показателем преломления n, а кювету К 2 – газом с неизвестным показателем преломления n x, то между интерферирующими волнами возникает дополнительная оптическая разность хода, равная ( n x - n )ℓ. Это приводит к смещению интерференционной картины на ∆ m полос. При этом выполняется равенство: ( n x - n )ℓ=∆ m 0. Интерферометр Жамена применяется для точных измерений показателей преломления газов и их зависимостей от температуры, давления и влажности. Таким образом, неизвестный показатель преломления вещества может быть определён по формуле Две одинаковые плоскопараллельные стеклянные пластины А и В установлены параллельно друг другу. Монохроматический свет (с длиной волны 0 ) от источника И падает на пластину А под различными углами близкими к 45 0.
Слайд 22
5.6. ДИФРАКЦИЯ ВОЛН Дифракция в переводе с латинского означает «преломление». Дифракция - огибание волнами препятствий, встречающихся на их пути. В более широком смысле слова: дифракция - это любое отклонение от законов геометрической оптики при распространении волн в оптически неоднородной среде. Дифракцию звуковых и радиоволн наблюдать легко. Для наблюдения дифракции света размер препятствий d должен быть сопоставимым с длиной световой волны . В результате дифракции свет попадает в область геометрической тени. 5.6.1. Принцип Гюйгенса-Френеля. Общая формулировка дифракционной задачи. Дифракция Френеля и Фраунгофера. Приближение Френеля (метод зон Френеля). Различают два вида дифракции световых волн : 1) в параллельных лучах - дифракция Фраунгофера (дифракция плоских волн ); при этом выполняется условие: L >> d 2 / , где L - расстояние от источника до экрана; 2) в сходящихся лучах - дифракция Френеля (дифракция сферических волн ); при этом выполняется условие: L d 2 / . При выполнении условия L << d 2 / действуют законы геометрической оптики.
Слайд 23
Явление дифракции объясняется с помощью принципа Гюйгенса – каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени. Для объяснения этого противоречия О.Ж. Френель дополнил принцип Гюйгенса идеей об интерференции когерентных вторичных волн при их наложении. Объединённый принцип, основанный на этой идее Френеля, получил название принципа Гюйгенса-Френеля. Таким образом, волна может огибать края отверстий. Однако принцип Гюйгенса не объясняет : 1) возможность прямолинейного распространения света, 2) перераспределение интенсивности дифрагированного светового потока. На нём основан приближённый метод решения дифракционной задачи - световая волна, возбуждаемая каким-либо источником, может быть представлена как суперпозиция вторичных когерентных волн, излучаемых фиктивными источниками на волновой поверхности и интерферирующих друг с другом.
Слайд 24
Принцип Гюйгенса-Френеля в рамках волновой теории позволяет решить основную задачу - одновременно объяснить и явление дифракции, то есть огибание волнами препятствий, и в определённых условиях явление прямолинейного распространения света. Френель решил эту задачу, применив приём, получивший название метода зон Френеля. Метод заключается в следующем. Световые волны распространяются в оптически однородной среде от точечного источника света S. Волновые поверхности являются сферами, одна из которых имеет радиус a. На этой поверхности, согласно принципу Гюйгенса-Френеля, располагается бесконечное множество фиктивных источников когерентных вторичных волн. Световая волна, регистрируемая в некоторой точке Р на экране, расположенном на расстоянии b от рассматриваемой волновой поверхности и на расстоянии а+ b от источника света S, является результатом интерференции этих вторичных волн. Френель предложил волновую поверхность разбить на кольцевые зоны такого размера, чтобы расстояния от краёв зон до точки Р отличались на величину /2. Построенные таким образом зоны называются зонами Френеля.
Слайд 25
Можно показать (геометрически), что при небольшом номере зоны радиус внешней границы m - ой зоны Френеля равен: а площади зон одинаковы и равны: Поскольку площади зон Френеля одинаковы, то на них располагается одинаковое количество фиктивных источников вторичных волн. Каждому источнику световой волны в m -ой зоне соответствует источник в соседней ( m +1 )-ой зоне, излучающий волну в противофазе относительно первой. Эти две волны ослабляют друг друга. Амплитуды колебаний с ростом m очень медленно убывают: А 1 >А 2 >А 3 >А 4 >... Поэтому амплитуда А результирующих световых волн в точке Р будет равна: То есть, амплитуда световой волны, создаваемой всей волновой поверхностью в точке Р, равна половине амплитуды волны, создаваемой одной центральной зоной Френеля, а действие всей волновой поверхности сводится к действию малого участка, меньшего центральной зоны.
Слайд 26
Например, если а = b = 1 м и = 0,5мкм, то r 1 = 0,5мм. Отсюда следует вывод, что распространение света от S к Р происходит вдоль узкого канала по линии SP, то есть прямолинейно. Таким образом, метод зон Френеля позволяет объяснить и дифракцию света, и прямолинейность его распространения. Правомерность деления светового фронта на зоны Френеля подтверждается экспериментально с помощью так называемых зонных пластинок, которые перекрывают все чётные зоны и оставляют свободными нечётные. В результате амплитуда световой волны в точке Р оказывается равной : А=А 1 +А 3 +А 5 +..., Интенсивность света в точке Р многократно возрастает, а зонная пластинка действует как собирающая линза. то есть значительно большей, чем при полностью открытом волновом фронте. Р
Слайд 27
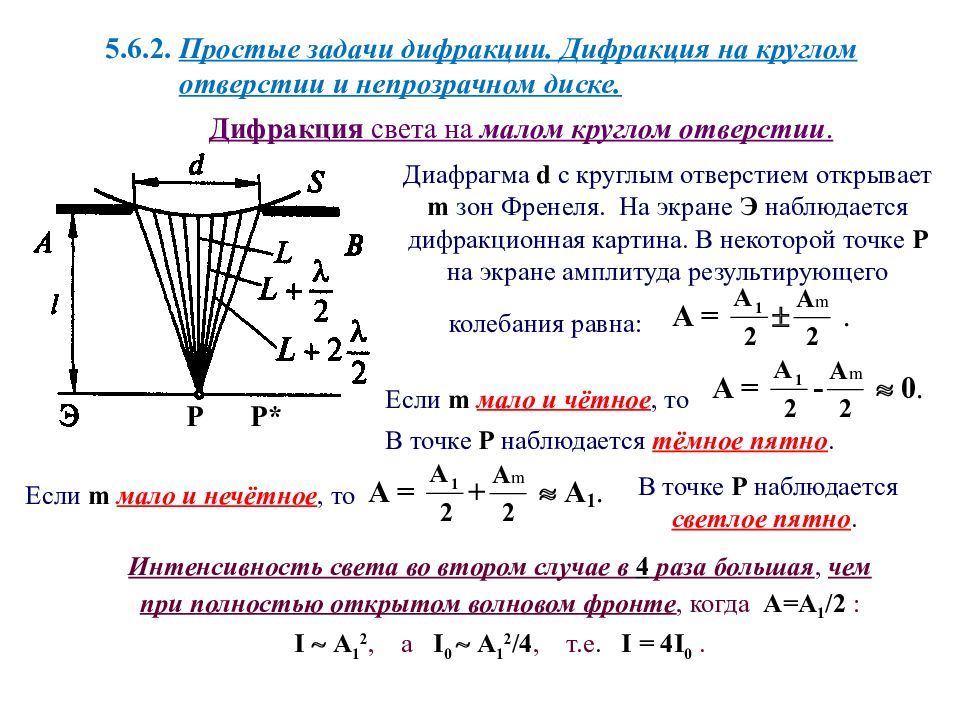
5.6.2. Простые задачи дифракции. Дифракция на круглом отверстии и непрозрачном диске. Диафрагма d с круглым отверстием открывает m зон Френеля. На экране Э наблюдается дифракционная картина. В некоторой точке Р на экране амплитуда результирующего колебания равна: Дифракция света на малом круглом отверстии. Р Если m мало и чётное, то В точке Р наблюдается тёмное пятно. В точке Р наблюдается светлое пятно. Р * Если m мало и нечётное, то Интенсивность света во втором случае в 4 раза большая, чем при полностью открытом волновом фронте, когда А= A 1 / 2 : I A 1 2, а I 0 A 1 2 /4, т.е. I = 4 I 0.
Слайд 28
Расчёт интерференционной картины на внеосевых точках (например, в точке Р * ) более сложен, так как отверстие в диафрагме открывает в этом случае зоны Френеля, располагающиеся несимметрично относительно отверстия. Полная дифракционная картина на экране представляет собой чередующиеся тёмные и светлые кольца. Если диаметр отверстия велик, то А m << A 1 и результирующая амплитуда А=А 1 /2, то есть такая же, как при полностью открытом волновом фронте. Дифракционная картина не возникает. Свет распространяется прямолинейно. В центре дифракционной картины наблюдается светлое пятно, если отверстие открывает нечётное число зон Френеля, и в центре - тёмное пятно, если отверстие открывает чётное число зон.
Слайд 29
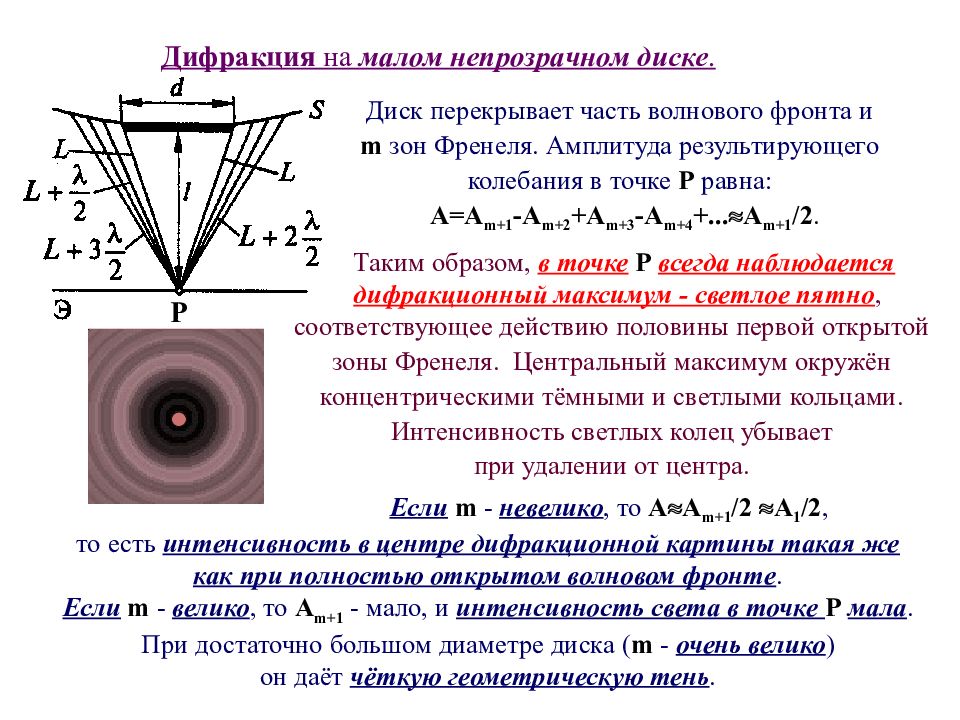
Дифракция на малом непрозрачном диске. Р Диск перекрывает часть волнового фронта и m зон Френеля. Амплитуда результирующего колебания в точке Р равна: А=А m +1 -А m +2 +А m +3 -А m +4 +... А m +1 /2. Таким образом, в точке Р всегда наблюдается дифракционный максимум - светлое пятно, Если m - невелико, то А А m +1 /2 А 1 /2, то есть интенсивность в центре дифракционной картины такая же как при полностью открытом волновом фронте. Если m - велико, то А m +1 - мало, и интенсивность света в точке Р мала. При достаточно большом диаметре диска ( m - очень велико ) он даёт чёткую геометрическую тень. соответствующее действию половины первой открытой зоны Френеля. Центральный максимум окружён концентрическими тёмными и светлыми кольцами. Интенсивность светлых колец убывает при удалении от центра.
Слайд 30
Аналогично происходит дифракция плоских волн на малом шаре – волны огибают шар, вторичные волны при наложении интерферируют и дают дифракционную картину в виде концентрических тёмных и светлых колец, причём в центре наблюдается дифракционный максимум - светлое пятно. Модель процесса дифракции плоских волн на малом шаре – образование вторичных волн и их интерференция при наложении.
Слайд 31
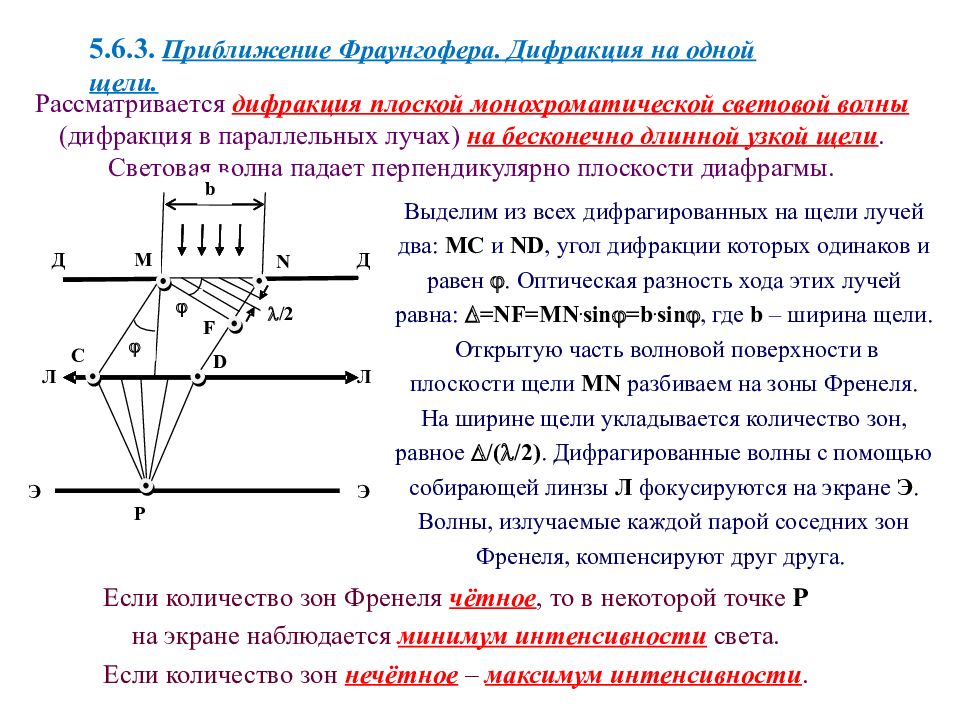
5.6.3. Приближение Фраунгофера. Дифракция на одной щели. Рассматривается дифракция плоской монохроматической световой волны (дифракция в параллельных лучах) на бесконечно длинной узкой щели. Световая волна падает перпендикулярно плоскости диафрагмы. Выделим из всех дифрагированных на щели лучей два: MC и ND, угол дифракции которых одинаков и равен . Оптическая разность хода этих лучей равна: = NF = MN. sin = b. sin , где b – ширина щели. Открытую часть волновой поверхности в плоскости щели MN разбиваем на зоны Френеля. На ширине щели укладывается количество зон, равное /( /2). Дифрагированные волны с помощью собирающей линзы Л фокусируются на экране Э. Волны, излучаемые каждой парой соседних зон Френеля, компенсируют друг друга. Если количество зон Френеля чётное, то в некоторой точке Р на экране наблюдается минимум интенсивности света. Если количество зон нечётное – максимум интенсивности.
Слайд 32
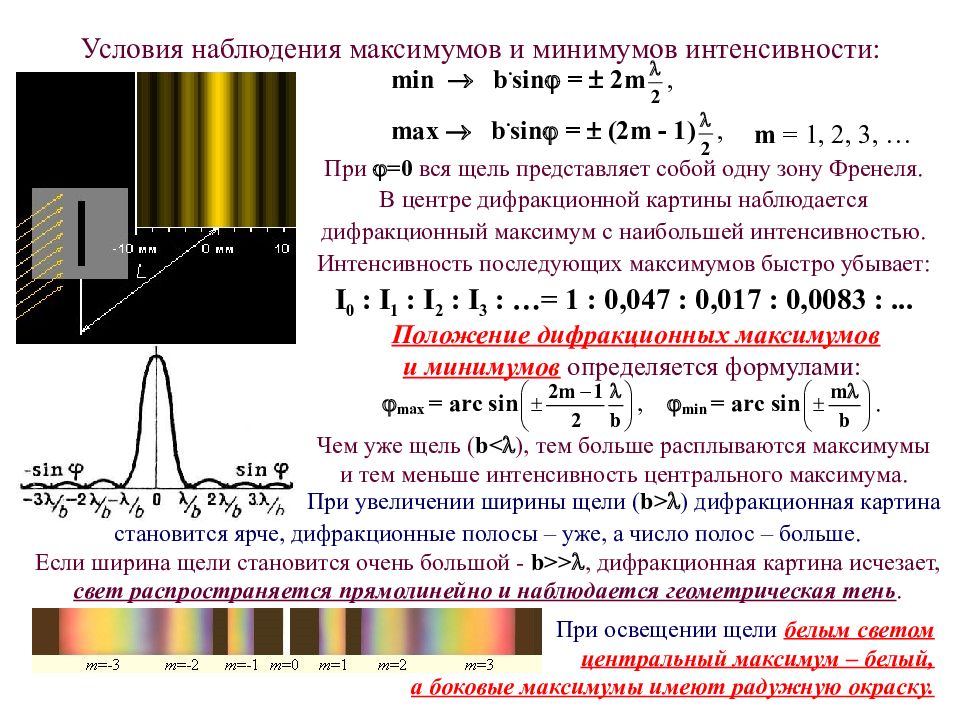
Условия наблюдения максимумов и минимумов интенсивности: m = 1, 2, 3, … При =0 вся щель представляет собой одну зону Френеля. В центре дифракционной картины наблюдается дифракционный максимум с наибольшей интенсивностью. Интенсивность последующих максимумов быстро убывает: I 0 : I 1 : I 2 : I 3 : …= 1 : 0,047 : 0,017 : 0,0083 :... Положение дифракционных максимумов и минимумов определяется формулами: Чем уже щель ( b < ), тем больше расплываются максимумы и тем меньше интенсивность центрального максимума. При увеличении ширины щели ( b > ) дифракционная картина становится ярче, дифракционные полосы – уже, а число полос – больше. Если ширина щели становится очень большой - b >> , дифракционная картина исчезает, свет распространяется прямолинейно и наблюдается геометрическая тень. При освещении щели белым светом центральный максимум – белый, а боковые максимумы имеют радужную окраску.
Слайд 33
5.6.4. Дифракционная решётка. Дифракция Фраунгофера и спектральное разложение. Разрешающая способность. При дифракции Фраунгофера на одной щели картина не изменяется при перемещении щели параллельно самой себе (положение дифракционных максимумов зависит только от угла дифракции ). Поэтому, если параллельно данной щели разместить сколь угодно большое количество щелей, то дифрагированные на каждой из них волны складываются и дают единую интерференционную картину. Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решётку – систему параллельных щелей равной ширины а, лежащих в одной плоскости и разделённых равными по ширине b непрозрачными промежутками. Величина d = a + b называется постоянной или периодом дифракционной решётки. Оптическая разность хода лучей, дифрагированных под углом и идущих от двух соседних щелей, будет одинаковой в пределах всей решётки и равной: = d. sin .
Слайд 34
Если какие-то значения одновременно удовлетворяют условиям максимумов для всех щелей решётки, то в этом направлении наблюдаются главные максимумы для всей решётки. Значения , удовлетворяющие условию минимума для одной щели, соответствуют главным минимумам и для всей решётки в целом. Вследствие взаимной интерференции световых лучей, идущих от разных щелей, в некоторых направлениях они будут гасить друг друга, то есть возникнут где N – количество щелей в решётке; m '=1,2,3,… N -1, N +1,…2 N -1,2 N +1,… Таким образом, дифракционная картина, создаваемая дифракционной решёткой, представляет собою систему ярких главных дифракционных максимумов, между которыми наблюдается N -1 дополнительных минимумов, разделённых дополнительными максимумами, создающими очень слабый фон.
Слайд 35
Количество главных максимумов ограничено, поскольку sin 1, то m d / , а m max ={ d / } (фигурные скобки означают целую часть отношения). Положение главных дифракционных максимумов зависит от . При пропускании через решётку белого света все максимумы, кроме центрального (нулевого), разлагаются в спектр, причём наибольшее отклонение испытывают красные лучи ( ~0,65мкм ), а наименьшее – фиолетовые ( ~0,38мкм ). Основные характеристики дифракционной решётки. Дисперсия – угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на 1. Это свойство позволяет использовать дифракционную решётку как спектральный прибор. Линейная дисперсия : Угловая дисперсия :
Слайд 36
Существует так называемый критерий Рэлея, согласно которому две спектральные линии с равными интенсивностями и одинаково симметричными контурами разрешены (разделены для восприятия), если главный максимум одной линии совпадает с первым минимумом другой линии (интенсивность «провала» между максимумами двух линий составляет 80% интенсивности самого максимума). Простой расчёт позволяет определить, что То есть разрешающая способность дифракционной решётки пропорциональна порядку m спектра и полному числу N щелей в решётке. При заданном N разрешающая способность выше для более высоких порядков спектра. В заданном порядке m спектра разрешение тем больше, чем больше щелей содержит решётка. Современные дифракционные решётки имеют R ~10 5. Разрешающая способность : - безразмерная величина, равная отношению длины волны к к минимальной разности длин волн двух соседних спектральных линий (вблизи данной ), при которой эти линии регистрируются раздельно. 1 2 l
Слайд 38
4.7. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ 4.7.1. Распространение света в веществе. Явление дисперсии света. Спектральный анализ, его научное и практическое значение. Все среды за исключением вакуума, обладают дисперсией. Дисперсией света называются явления, обусловленные зависимостью показателя преломления n вещества или фазовой скорости света v от длины световой волны (или от её частоты ). n = f ( ), n = f *( ) или v = ( ), v = *( ). Количественной мерой дисперсии является величина:, называемая дисперсией вещества. Сейчас известно, что цвет света связан с длиной световой волны, то есть эксперименты Ньютона показали, что показатель преломления n убывает с увеличением длины волны – dn/d <0. Такая дисперсия называется нормальной. В результате дисперсии пучок белого света при прохождении через стеклянную призму разлагается в спектр. Ещё в 1666 году Ньютон установил, что при этом фиолетовые лучи отклоняются сильнее, чем красные.
Слайд 39
Отклонение от этой закономерности впервые наблюдал французский физик Пьер Леру в 1862 году - в призме, наполненной парами йода, синие лучи преломляются меньше красных. Лучи других цветов сильно поглощаются и практически не наблюдаются. Таким образом, показатель преломления паров йода возрастает при увеличении длины волны, то есть dn/d > 0. Поскольку до 1862 года такое явление не наблюдалось, оно было названо аномальной дисперсией. Систематические экспериментальные исследования были выполнены немецким физиком Августом Кундтом в 1871 году с помощью метода скрещенных призм, разработанного ещё Ньютоном. Этот метод позволяет наблюдать дисперсионные кривые непосредственно на экране. Кундт установил важный экспериментальный факт - аномальная дисперсия наблюдается в области спектра, близкой к полосе поглощения.
Слайд 40
Таким образом, аномальная дисперсия - вполне нормальное явление, наблюдающееся у всех веществ в области спектра, соответствующей максимальному поглощению. У прозрачных веществ это обычно инфракрасная или ультрафиолетовая области. Этот метод особенно эффективен в области поглощения света. С его помощью были проведены систематические исследования аномальной дисперсии. Это способствовало развитию теории строения атомов и систематизации атомных спектров. Российский физик академик Д.С.Рождественский в 1909 году применил ещё более усовершенствованный метод, получивший название «метода крюков», в котором скрещены интерферометр и спектрограф, главным элементом которого является стеклянная призма или дифракционная решётка.
Слайд 41
Призматический и дифракционный спектры существенно отличаются. 2) Для дифракционной решётки зависимость ( ) чётко задана формулой dsin = m , а для призмы эту зависимость нужно определять, используя градуировочную кривую ( ) конкретного спектрографа. 1) Дифракционная решётка отклоняет красные лучи сильнее, чем фиолетовые в соответствии с формулой dsin = m ( кр > ф ), призма при нормальной дисперсии сильнее отклоняет фиолетовые лучи ( n - 1), где - преломляющий угол призмы ( n ф > n кр ). Несмотря на это, призменные спектрографы широко используются в научных исследованиях и для технических целей, поскольку их основной элемент – призму легче и дешевле изготовить, чем дифракционную решётку.
Слайд 42
4.7.2. Поглощение света. Закон Бугера-Ламберта. Связь дисперсии с поглощением. Понятие о механизме дисперсии света. Поглощением ( абсорбцией ) света называется явление потери энергии световой волной, проходящей через вещество. Эта энергия преобразуется в другие виды энергии - внутреннюю, энергию вторичного излучения. В результате поглощения света при прохождении через вещество его интенсивность уменьшается. Закон изменения интенсивности света I при поглощении был установлен в 1729 году французским физиком П.Бугером и в 1760 году немецким физиком Й.Ламбертом и получил название закона Бугера-Ламберта – где I 0 и I - интенсивности света на входе и выходе из слоя среды толщиной h, - коэффициент поглощения вещества, зависящий от химической природы, состояния поглощающей среды и от частоты световой волны (длины волны ). интенсивность плоской монохроматической световой волны уменьшается по мере прохождения через поглощающую среду по экспоненциальному закону :
Слайд 43
Экспериментально установлено, что уменьшение интенсивности света dI при прохождении его через слой вещества толщиной dh пропорционально интенсивности I света, падающего на этот слой, и самой толщине dh. Таким образом, dI = - I dh. Интегрирование этого уравнения позволяет получить закон Бугера-Ламберта : Экспериментально обнаружена дисперсия не только показателя преломления света n = n ( ), но и дисперсия коэффициента поглощения = ( ). На рисунке представлены зависимости показателя преломления n и коэффициента поглощения от частоты волн . В области полосы поглощения наблюдается аномальная дисперсия. Зависимостью коэффициента поглощения от частоты (длины волны ) объясняется окрашенность веществ, многообразие цветов и красок в окружающем мире. Это явление используется при изготовлении светофильтров. Коэффициент поглощения у диэлектриков невелик ~10 -3 10 -1 м -1, у металлов - довольно большой ~10 1 10 3 м -1. Поэтому диэлектрики - прозрачными, а металлы - непрозрачны.
Слайд 44
Теория дисперсии создана на основе электронной теории Лоренца и классической электромагнитной теории Максвелла. Согласно этой теории, дисперсия является результатом взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле световой волны. В первом приближении считается, что колебания совершают только внешние, наименее связанные с ядром электроны - так называемые оптические электроны. где N 0 - концентрация атомов в веществе, 0 - электрическая постоянная, e i, m i - заряд и масса i -ой колеблющейся частицы, 0 i - собственная частота i -ой частицы, - частота вынуждающей силы, то есть частота электромагнитной волны. Лоренц решил дифференциальное уравнение вынужденных колебаний электрона для простейшего случая – без учёта силы трения, обуславливающей поглощение, и получил значение показателя преломления :
Слайд 45
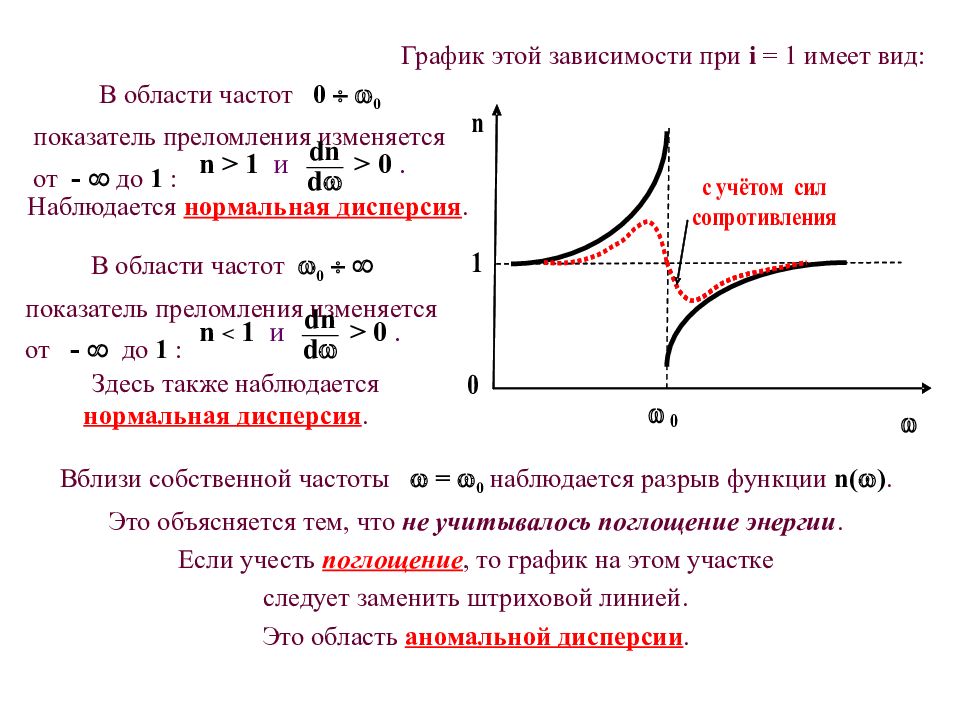
В области частот 0 0 показатель преломления изменяется от - до 1 : График этой зависимости при i = 1 имеет вид: Наблюдается нормальная дисперсия. Вблизи собственной частоты = 0 наблюдается разрыв функции n ( ). Это объясняется тем, что не учитывалось поглощение энергии. Если учесть поглощение, то график на этом участке следует заменить штриховой линией. Это область аномальной дисперсии. В области частот 0 показатель преломления изменяется от - до 1 : Здесь также наблюдается нормальная дисперсия.
Слайд 46
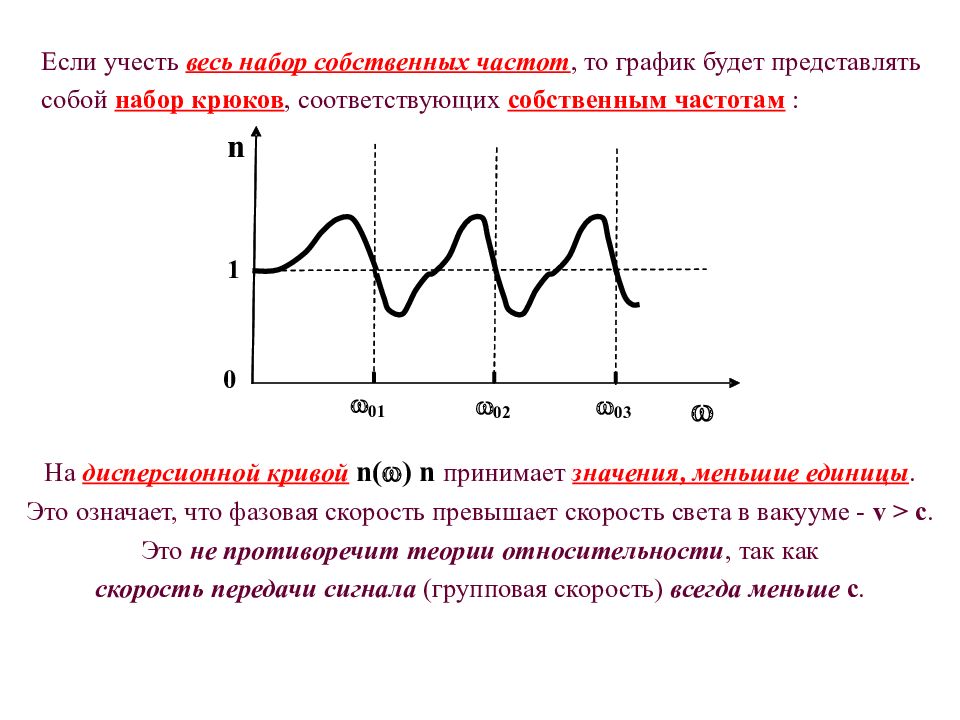
Если учесть весь набор собственных частот, то график будет представлять собой набор крюков, соответствующих собственным частотам : На дисперсионной кривой n ( ) n принимает значения, меньшие единицы. Это означает, что фазовая скорость превышает скорость света в вакууме - v > c. Это не противоречит теории относительности, так как скорость передачи сигнала (групповая скорость) всегда меньше с.
Слайд 47
4.7.3. Поляризация волн. Поляризация волн при отражении и преломлении. Законы Брюстера и Малюса. Согласно теории Максвелла свет представляет собой поперечные электромагнитные волны, в которых векторы напряжённости электрического и магнитного полей образуют с вектором скорости волны или волновым вектором правую тройку векторов. Световые электромагнитные волны излучаются множеством атомов, а атомы излучают свет независимо друг от друга. Поэтому свет, излучаемый нагретым телом, представляет собой наложение множества отдельных световых цугов, в каждом из которых ориентировка светового вектора может быть произвольной в плоскости, перпендикулярной вектору скорости. Такой свет называется естественным. Вектор принято называть световым вектором. Свет, в котором направления колебаний светового вектора каким-либо образом упорядочены, называется поляризованным.
Слайд 48
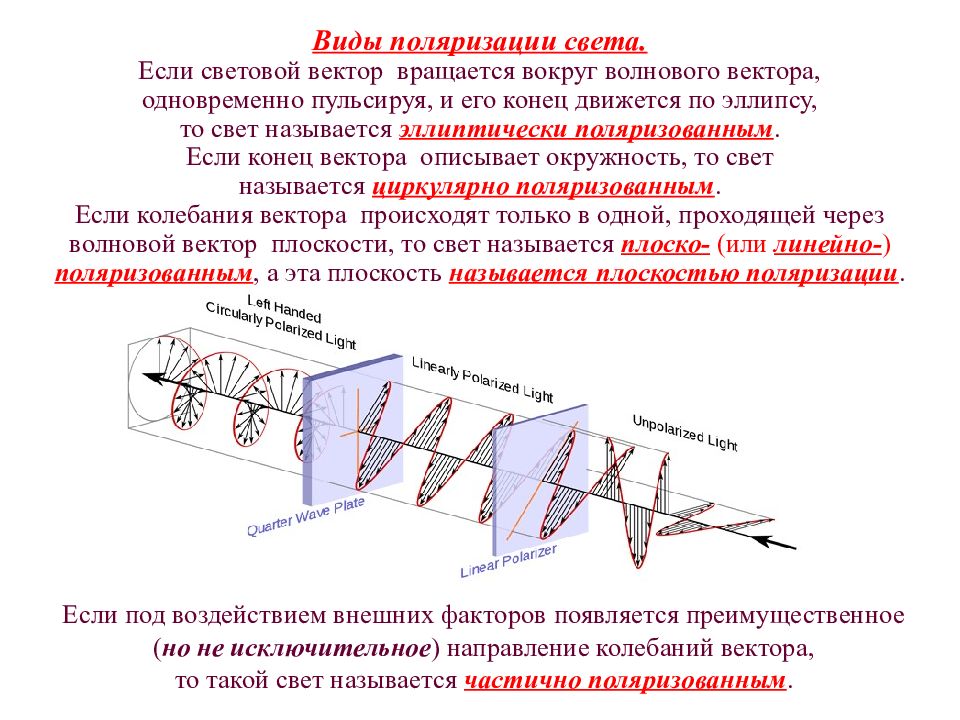
Виды поляризации света. Если световой вектор вращается вокруг волнового вектора, одновременно пульсируя, и его конец движется по эллипсу, то свет называется эллиптически поляризованным. Если конец вектора описывает окружность, то свет называется циркулярно поляризованным. Если колебания вектора происходят только в одной, проходящей через волновой вектор плоскости, то свет называется плоско- (или линейно- ) поляризованным, а эта плоскость называется плоскостью поляризации. Если под воздействием внешних факторов появляется преимущественное ( но не исключительное ) направление колебаний вектора, то такой свет называется частично поляризованным.
Слайд 49
Существуют различные способы получения поляризованного света, в которых используется свойство электромагнитных световых волн поляризоваться при отражении и преломлении на границе раздела прозрачных сред. Приборы или устройства, способные поляризовать естественный свет, называются поляризаторами. Если частично поляризованный свет пропустить через поляризатор (в этом случае его называют анализатором ), то при его вращении вокруг светового луча, интенсивность прошедшего света будет изменяться в пределах от I min до I max. Таким образом, можно измерять степень поляризации первичного частично поляризованного света : После прохождения естественного света через поляризатор его интенсивность уменьшается вдвое: I П = 0,5 I 0. Действительно, Для естественного света I max = I min и Р = 0. Для полностью поляризованного света I min = 0 и Р = 1.
Слайд 50
Если на пути плоско поляризованного света поставить анализатор, то интенсивность прошедшего через него света I А будет зависеть от взаимного расположения оптических осей поляризатора и анализатора : Этот закон был установлен в 1808 году французским физиком Э.Л.Малюсом и впоследствии назван законом Малюса. Интенсивность света, прошедшего через два поляризатора (поляризатор и анализатор) равна: Таким образом, Если оптические оси обоих поляризаторов параллельны, то Если оси взаимно перпендикулярны (поляризаторы скрещены), то I А = 0.
Слайд 51
Если естественный свет падает на границу раздела двух диэлектриков, то часть его отражается, а часть преломляется. Шотландский физик Д.Брюстер в 1815 году экспериментально установил закон, впоследствии названный законом Брюстера, согласно которому, если угол падения Б удовлетворяет условию: ( n 21 – относительный показатель преломления второй среды относительно первой), то отражённый свет полностью поляризован в плоскости, перпендикулярной плоскости падения светового луча, а преломлённый свет максимально (но частично) поляризован в плоскости, параллельной направлению светового луча. Угол Б называется углом Брюстера.
Слайд 52
Если свет падает на границу раздела сред под углом Брюстера, то отражённый и преломлённый лучи взаимно перпендикулярны. Действительно: Степень поляризации преломлённого луча можно повысить, если использовать 8-10 стеклянных пластинок, наложенных друг на друга таким образом, что на каждую границу раздела свет падает под углом Брюстера. Такая пачка пластин называется стопой Столетова. Стопа может служить для анализа поляризованного света, как при его отражении, так и при преломлении.
Слайд 53
5.7.4. Элементы кристаллоптики. Двойное лучепреломление в одноосных кристаллах и его объяснение. Газы, жидкости и аморфные (стеклообразные) твёрдые тела в обычных условиях являются изотропными, то есть их физические свойства не зависят от выбора пространственной системы координат. Расчёт интерференции вторичных волн в анизотропном кристалле на основе Максвелловской теории электромагнитного поля основывается на предположении, что оптическая анизотропия кристалла является следствием анизотропии диэлектрической проницаемости, а следовательно, и показателя преломления. В кристаллах происходит интерференция первичной световой волны и вторичных волн, излучаемых молекулами и атомами, поляризованными под воздействием электрического поля световой волны. Поэтому оптические свойства кристаллов зависят от взаимного расположения в них атомов. В отличие же от них твёрдые кристаллические тела (кроме имеющих кубически симметричную элементарную ячейку) обладают оптической анизотропией.
Слайд 54
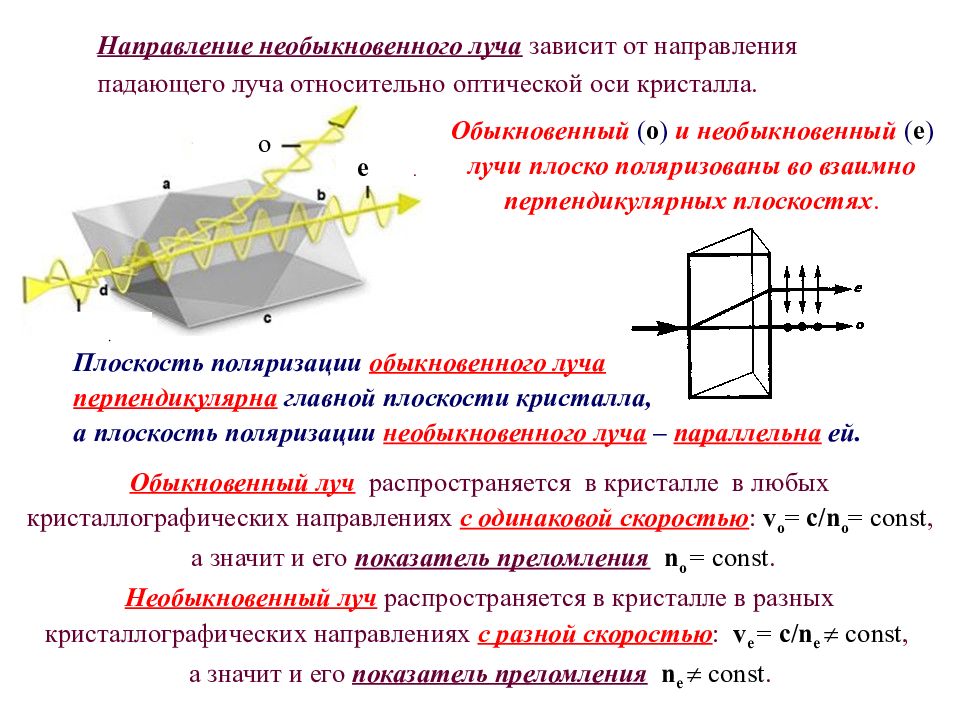
В оптически анизотропных кристаллах наблюдается явление двойного лучепреломления – луч света, падающий на поверхность кристалла раздваивается в нём на два преломлённых луча. Один из преломлённых лучей подчиняется закону преломления света и называется обыкновенным лучом ( о ), а другой – не подчиняется этому закону и называется необыкновенным лучом ( е ). Это явление впервые было обнаружено датским физиком Э.Бартолином в 1669 году в кристаллах исландского шпата (разновидность кальцита - СаСО 3 ). В кристаллах существуют только одно или два кристаллографических направления, называемых оптическими осями кристалла, вдоль которых преломлённый луч не разделяется. В соответствии с этим кристаллы бывают одноосными или двуосными. Плоскость, в которой расположены оптическая ось кристалла и падающий луч, называется главной плоскостью или главным сечением кристалла.
Слайд 55
Направление необыкновенного луча зависит от направления падающего луча относительно оптической оси кристалла. Обыкновенный луч распространяется в кристалле в любых кристаллографических направлениях с одинаковой скоростью : v o = c / n o = const, а значит и его показатель преломления n o = const. Необыкновенный луч распространяется в кристалле в разных кристаллографических направлениях с разной скоростью : v е = c / n е const, а значит и его показатель преломления n е const. о Обыкновенный ( о ) и необыкновенный ( е ) лучи плоско поляризованы во взаимно перпендикулярных плоскостях. е. . Плоскость поляризации обыкновенного луча перпендикулярна главной плоскости кристалла, а плоскость поляризации необыкновенного луча – параллельна ей.
Слайд 56
5.7.5. Поляризационные устройства. Поляризационные устройства служат для получения поляризованного света. В них используется явление двойного лучепреломления. 1. В поляризационных призмах используется явление полного внутреннего отражения одного из лучей (например, обыкновенного) на границе раздела двух кристаллов, из которых состоит призма, в то время как другой луч (необыкновенный), преломляясь на этой границе, выходит поляризованным из призмы. Поскольку оба преломлённых луча плоско поляризованы, то для получения на выходе поляризованного света необходимо один из лучей (например, обыкновенный) каким-либо образом изолировать. Наиболее распространены два типа поляризационных устройств – призматические и поляроидные.
Слайд 57
В поляризаторе Николя две призмы из исландского шпата склеены специальным клеем - канадским бальзамом, имеющим показатель преломления n = 1,55 меньший, чем у обыкновенного луча n 0 = 1,66, но больший - чем у необыкновенного n е = 1,51. полное внутреннее отражение на границе раздела призм, а затем поглощается зачернённой поверхностью призмы. Необыкновенный луч выходит из кристалла параллельно первоначальному лучу, чуть сместившись относительно него. Первый призматический поляризатор изобрёл в 1828 году и усовершенствовал его в 1839 году шотландский физик Уильям Николь. При соответствующем подборе угла падения обыкновенный луч испытывает
Слайд 58
2. В поляроидах используется свойство дихроизма - зависимости показателя поглощения света от ориентации электрического вектора световой волны. Благодаря этому обыкновенный луч поглощается плёнкой, а из неё выходит плоско поляризованный необыкновенный луч. Поляроиды представляют собою аморфные плёнки с вкраплёнными кристалликами вещества с сильно выраженным дихроизмом. Примеры: 1)кристаллы турмалина поглощают почти полностью обыкновенные лучи на глубине ~1мм, 2)целлулоидная плёнка с вкраплёнными в неё кристалликами герапатита (сернокислого йод-хинина ) поглощает обыкновенные лучи при толщине 0,1мм. Поляроиды в сравнении с призмами имеют преимущества. С одной стороны – миниатюрность, а с другой – при необходимости можно изготовить плёнки площадью несколько квадратных метров.
Слайд 59
Среди недостатков поляроидов следует отметить большую зависимость степени поляризации от длины световой волны, а также их меньшую, чем у призм, прозрачность и небольшую термостойкость. Поляроидные плёнки применяются в поляризационных микроскопах при проведении минералогического анализа; в качестве покрытий, предохраняющих глаза от ослепляющего действия солнечных лучей и от света автомобильных фар встречного транспорта; в медицине (например, при лечении косоглазия). Поляризационные светофильтры используют в фотографии : для устранения нежелательных эффектов (бликов, отражений), для достижения художественных целей (регулирования яркости и контрастности, повышения насыщенности цвета).
Слайд 60
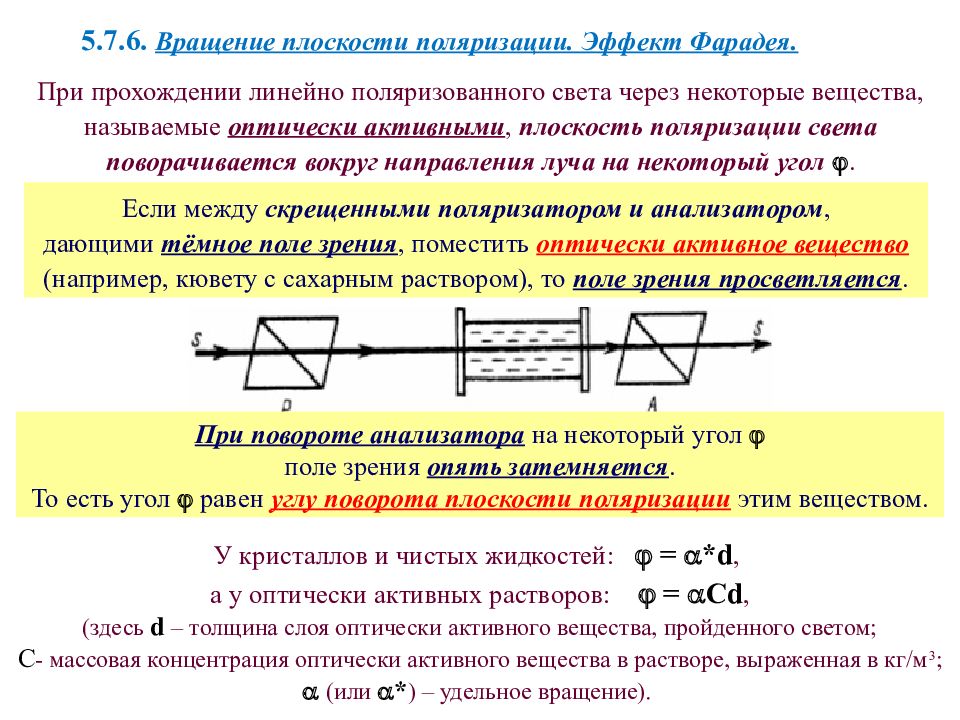
5.7.6. Вращение плоскости поляризации. Эффект Фарадея. При прохождении линейно поляризованного света через некоторые вещества, называемые оптически активными, плоскость поляризации света поворачивается вокруг направления луча на некоторый угол . Если между скрещенными поляризатором и анализатором, дающими тёмное поле зрения, поместить оптически активное вещество (например, кювету с сахарным раствором), то поле зрения просветляется. У кристаллов и чистых жидкостей: = * d, а у оптически активных растворов: = С d, (здесь d – толщина слоя оптически активного вещества, пройденного светом; С - массовая концентрация оптически активного вещества в растворе, выраженная в кг/м 3 ; (или * ) – удельное вращение). При повороте анализатора на некоторый угол поле зрения опять затемняется. То есть угол равен углу поворота плоскости поляризации этим веществом.
Слайд 61
Удельное вращение – это величина, равная углу поворота плоскости поляризации света слоем оптически активного вещества единичной концентрации или единичной толщины. зависит от природы вещества и от длины световой волны 0. Эффект поворота плоскости поляризации оптически активными веществами используется в поляризационном приборе сахариметре для определения концентрации сахара в растворах. Вращение плоскости поляризации впервые было объяснено О.Френелем в 1817 году. В основе его теории лежит предположение о том, что плоско поляризованную световую волну можно представить в виде комбинации двух одновременно распространяющихся циркулярно поляризованных в противоположных направлениях плоских монохроматических волн той же частоты. В оптически активных средах скорости распространения этих волн различны. Из-за этого возникает сдвиг фаз , пропорциональный d (и С ). В результате наложения этих волн образуется плоская монохроматическая волна, плоскость поляризации которой повёрнута относительно падающей на угол /2.
Слайд 62
М.Фарадей в 1845 году экспериментально установил, что оптически неактивная среда приобретает под действием внешнего магнитного поля способность вращать плоскость поляризации света, распространяющегося вдоль направления поля. Это явление называется эффектом Фарадея. где H - напряжённость магнитного поля; d - толщина слоя вещества; V - постоянная Верде, зависящая от природы вещества и от длины световой волны. Направление магнитного вращения плоскости поляризации одинаково при распространении света как в направлении поля, так и против поля. Угол поворота плоскости поляризации определяется формулой:
Слайд 63
5.7.7. Искусственная оптическая анизотропия при механической деформации изотропных тел и её практические применения. Электрооптические и магнитооптические явления (эффекты Керра, Коттона-Мутона). Оптически изотропные вещества становятся анизотропными при механической деформации, под действием электрических и магнитных полей. Кристаллы с кубической решёткой, аморфные вещества под действием одностороннего сжатия или растяжения становятся анизотропными. В них возникает явление двойного лучепреломления. 1. Явление фотоупругости. Впервые это явление было обнаружено в 1813 году Т.Зеебеком, а затем – в 1816 году Д.Брюстером. П А Экран Пресс Образец
Слайд 64
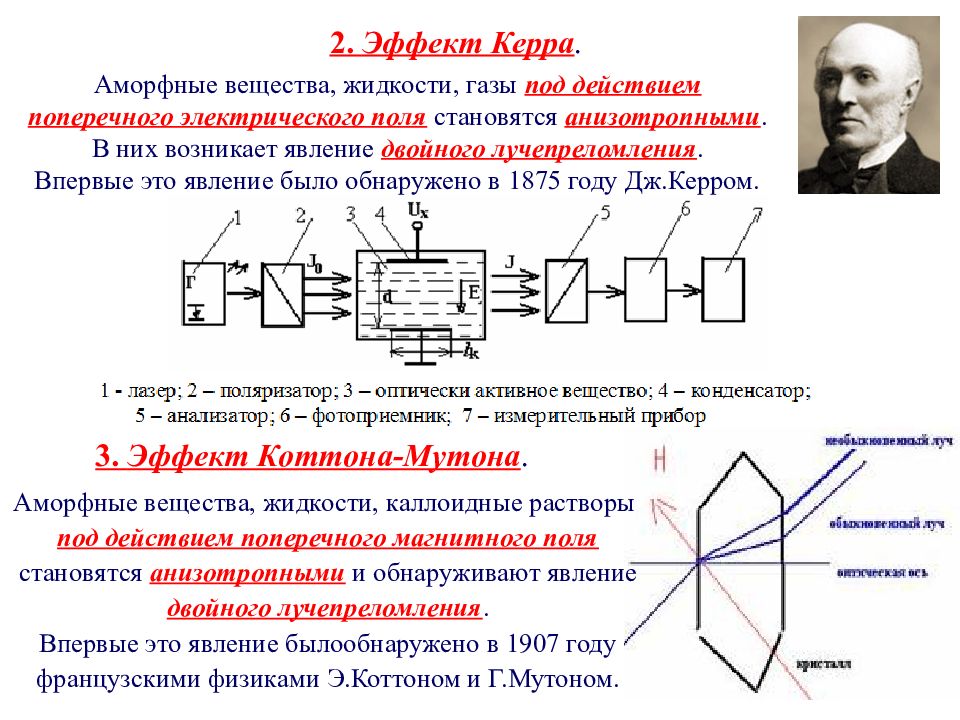
Аморфные вещества, жидкости, газы под действием поперечного электрического поля становятся анизотропными. В них возникает явление двойного лучепреломления. Впервые это явление было обнаружено в 1875 году Дж.Керром. 2. Эффект Керра. 3. Эффект Коттона-Мутона. Аморфные вещества, жидкости, каллоидные растворы под действием поперечного магнитного поля становятся анизотропными и обнаруживают явление двойного лучепреломления. Впервые это явление былообнаружено в 1907 году французскими физиками Э.Коттоном и Г.Мутоном.
Слайд 65
Во всех перечисленных явлениях вещество приобретает свойства одноосного кристалла, ось которого совпадает с направлением деформации, электрического или магнитного поля соответственно. Мерой возникающей анизотропии служит разность показателей преломления обыкновенного и необыкновенного лучей в направлении, перпендикулярном оптической оси: n e - n o = k 1 ( фотоупругость ); n e - n o = k 2 E 2 ( эффект Керра ); n e - n o = k 3 Н 2 ( эффект Коттона-Мутона ), где - нормальное механическое напряжение = F n / S, Е и Н –напряжённости электрического и магнитного полей соответственно. Практические применения. 1. Явление фотоупругости используется при исследовании характера и распределения напряжений в механических конструкциях под действием различных нагрузок. 2. Электрооптический эффект Керра используется в оптоволоконных технологиях для электрической модуляции пропускаемости оптических сигналов. 3. Исследования эффекта Коттона-Мутона позволяют получить информацию о структуре молекул, образовании межмолекулярных агрегатов и подвижности молекул.
Последний слайд презентации: Раздел 5 Физика колебаний и волн. Оптика
Радиусы светлых (интерференционные максимумы) и тёмных (интерференционные минимумы) колец Ньютона можно рассчитать следующим образом. Из треугольника О АВ (см. рисунок) следует: r m 2 =R 2 -(R-d m ) 2 =2Rd m -d m 2 ; 2Rd m >>d m 2 ; (R>>d m ) ; При перпендикулярном падении света =0 и cos =1. Тогда условие интерференционного максимума имеет вид: 2 d m n = (2 m - 1) 0 / 2. А радиус m -го светлого кольца Ньютона в отражённом свете равен: А радиус m -го тёмного кольца Ньютона в отражённом свете равен: Отсюда следует, что толщина зазора в месте наблюдения m -го светлого кольца равна: d m = (2 m - 1) 0 / 4 n. Условие интерференционного минимума имеет вид: 2 d m. n = m 0. Отсюда следует, что толщина зазора в месте наблюдения m -го тёмного кольца равна: d m = m 0 / 2 n.