Применение второго закона Ньютона
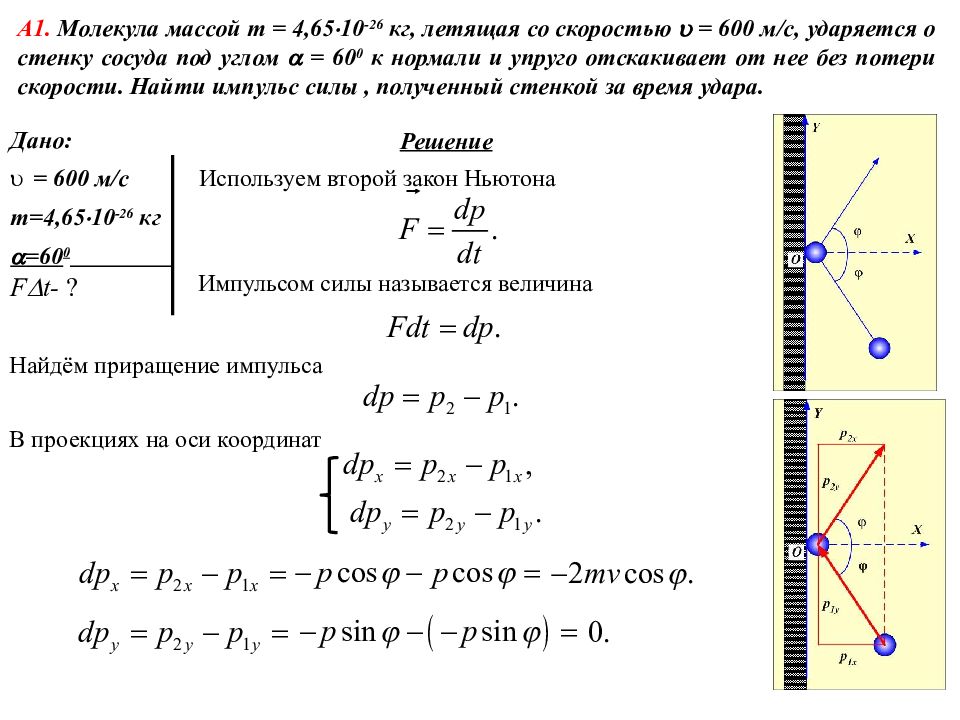
Дано: = 600 м/ c m=4,65 10 -26 кг =60 0 F D t - ? Решение А1. Молекула массой m = 4,65 10 -26 кг, летящая со скоростью = 600 м/c, ударяется о стенку сосуда под углом = 60 0 к нормали и упруго отскакивает от нее без потери скорости. Найти импульс силы, полученный стенкой за время удара. Используем второй закон Ньютона Импульсом силы называется величина Найдём приращение импульса В проекциях на оси координат
Решение (продолжение) А1. Молекула массой m = 4,65 10 -26 кг, летящая со скоростью = 600 м/c, ударяется о стенку сосуда под углом = 60 0 к нормали и упруго отскакивает от нее без потери скорости. Найти импульс силы, полученный стенкой за время удара. Знак «-» у проекции на ось OX и равенство нулю проекции на ось OY означает, что приращение импульса и сила, действующая на молекулу, направлена «от стенки» (см. рис.). В то же время, сила, действующая на стенку со стороны молекулы, направлена в противоположную сторону. Ответ:
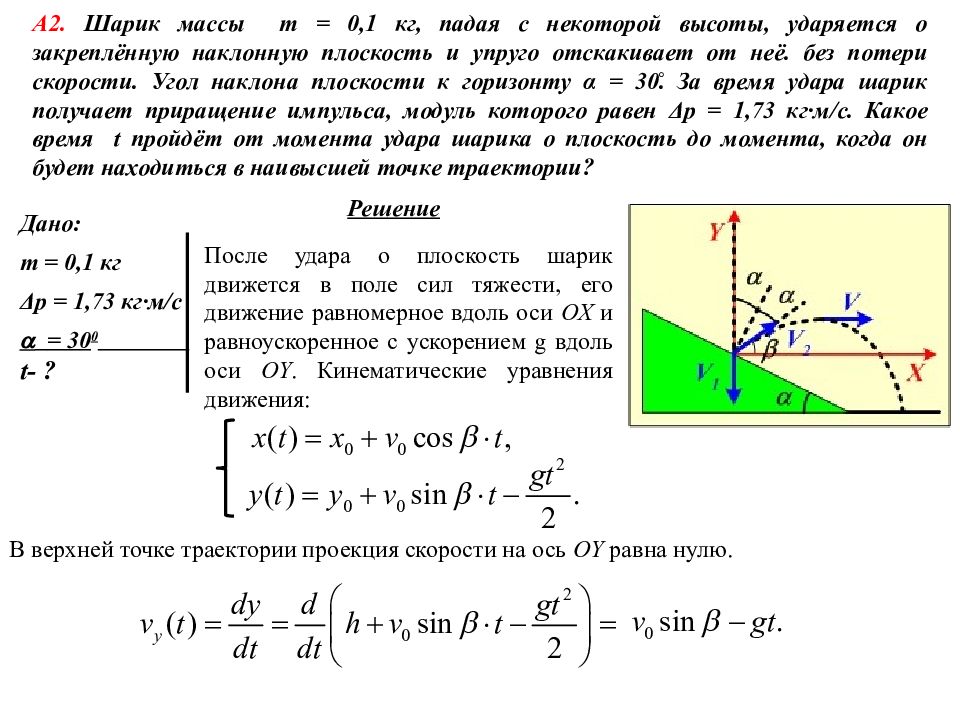
Дано: m = 0,1 кг Δ p = 1,73 кг·м/с = 30 0 t - ? Решение А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 30̊. За время удара шарик получает приращение импульса, модуль которого равен Δ p = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? После удара о плоскость шарик движется в поле сил тяжести, его движение равномерное вдоль оси OX и равноускоренное с ускорением g вдоль оси OY. Кинематические уравнения движения: В верхней точке траектории проекция скорости на ось OY равна нулю.
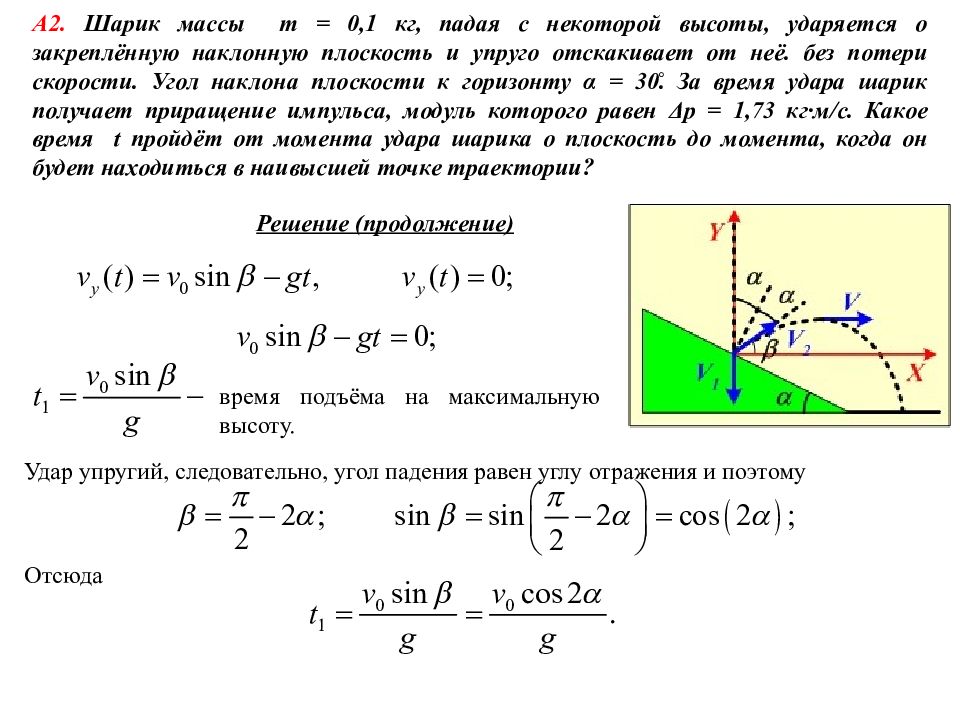
Решение (продолжение) А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 30̊. За время удара шарик получает приращение импульса, модуль которого равен Δ p = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? время подъёма на максимальную высоту. Удар упругий, следовательно, угол падения равен углу отражения и поэтому Отсюда
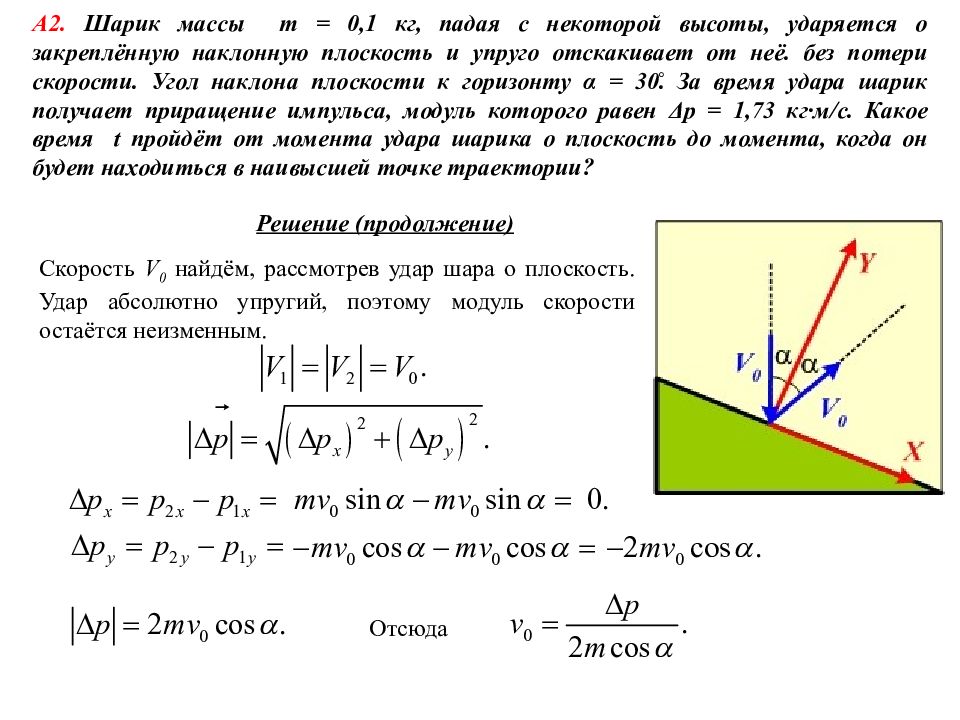
Решение (продолжение) А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 30̊. За время удара шарик получает приращение импульса, модуль которого равен Δ p = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? Скорость V 0 найдём, рассмотрев удар шара о плоскость. Удар абсолютно упругий, поэтому модуль скорости остаётся неизменным. Отсюда
Решение (продолжение) А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 30̊. За время удара шарик получает приращение импульса, модуль которого равен Δ p = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? Подставим полученное выражение для скорости в формулу для времени подъёма на максимальную высоту. Ответ : 0,5 с.
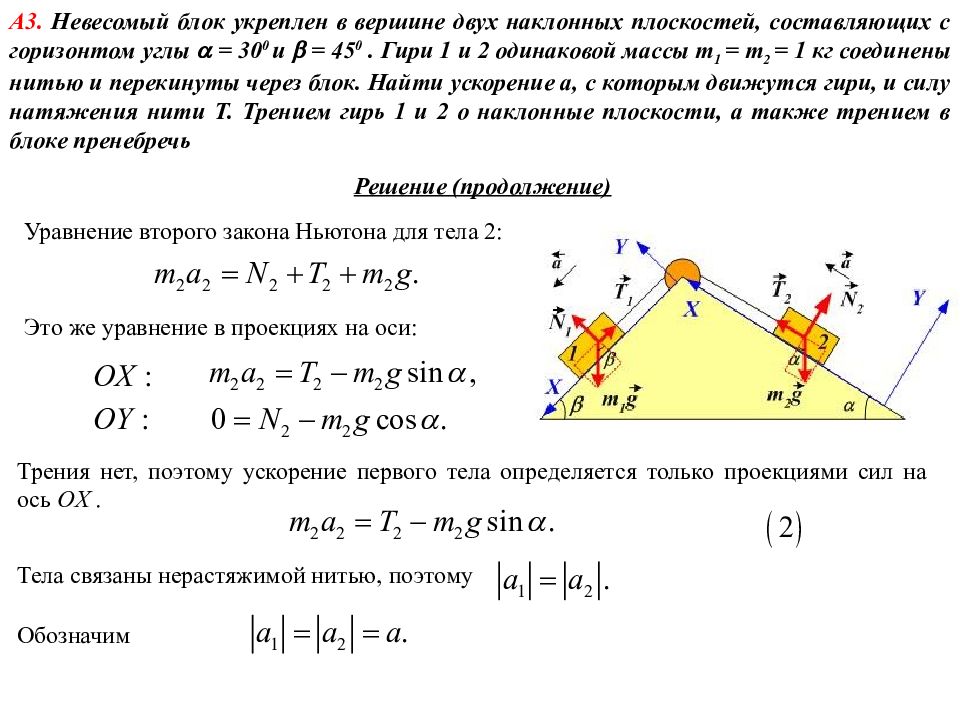
Дано: = 30 ◦ = 45 ◦ m 1 = m 2 = 1 кг T - ? Решение А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0. Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Если массой блока можно пренебречь, то ускорение можно найти из второго закона Ньютона. Для тела 1: Предположим, что система движется справа налево на рисунке. Перепишем это уравнение в проекциях на оси (см. рис.) : Трения нет, поэтому ускорение первого тела определяется только проекциями сил на ось OX.
Решение (продолжение) А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0. Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Уравнение второго закона Ньютона для тела 2: Тела связаны нерастяжимой нитью, поэтому Это же уравнение в проекциях на оси: Трения нет, поэтому ускорение первого тела определяется только проекциями сил на ось OX. Обозначим
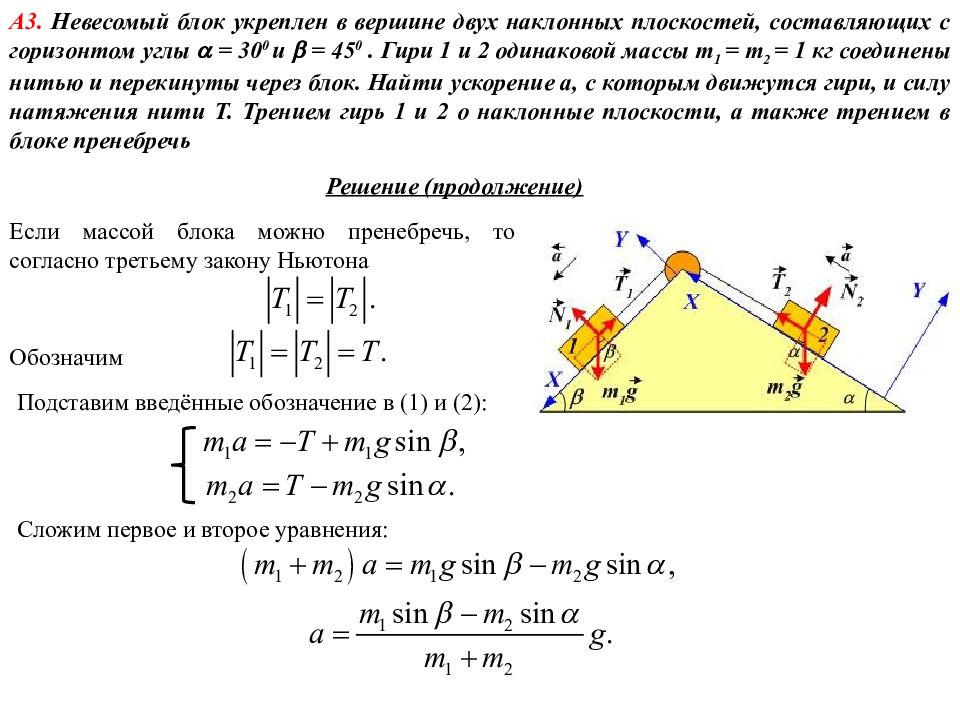
Решение (продолжение) А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0. Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Если массой блока можно пренебречь, то согласно третьему закону Ньютона Подставим введённые обозначение в (1) и (2): Обозначим Сложим первое и второе уравнения:
А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0. Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Подставим полученное выражение для ускорения в первое уравнение системы: Решение (продолжение)
Решение (продолжение) Выполним вычисления: А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0. Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь
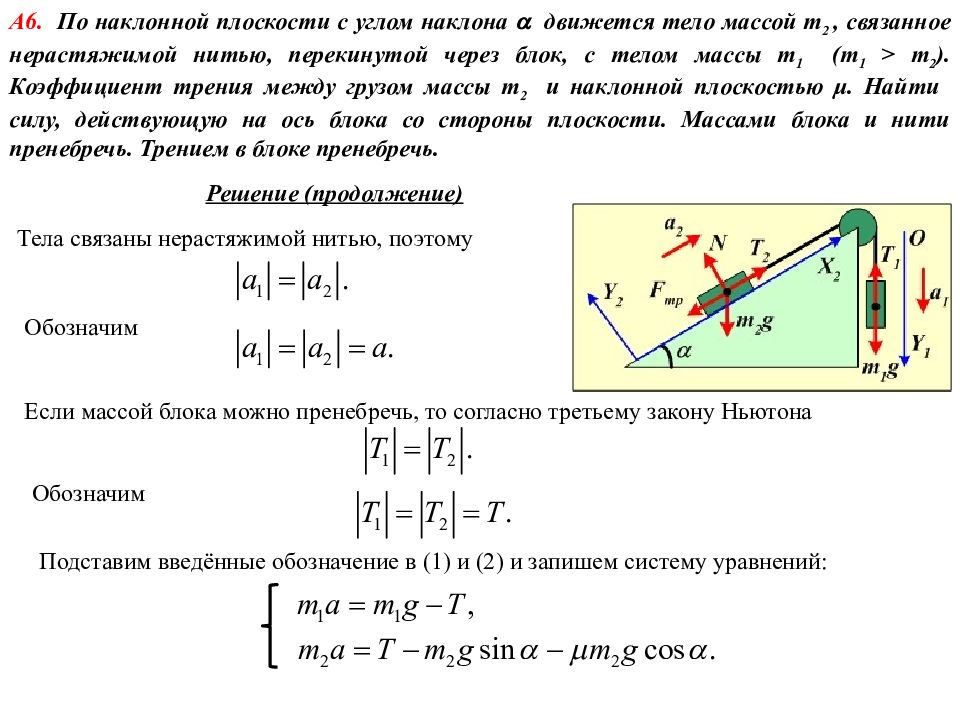
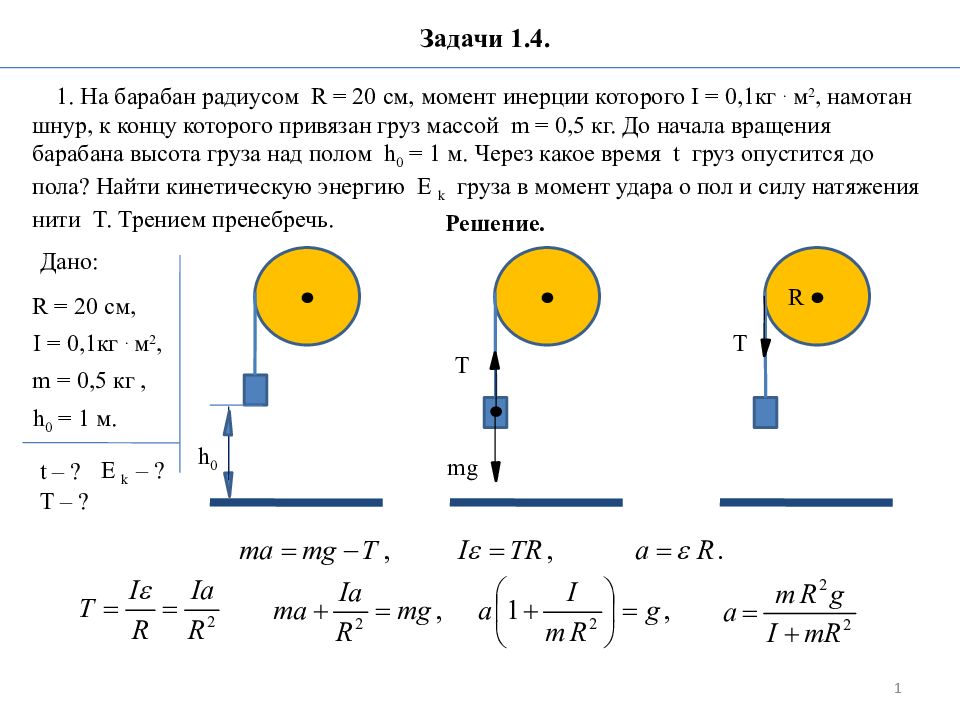
Дано: m 1 m 2 μ F - ? Решение А6. По наклонной плоскости с углом наклона движется тело массой m 2, связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Если массой блока можно пренебречь, то ускорение и силу натяжения можно найти, рассматривая лишь поступательное движение грузов. Из второго закона Ньютона для тела 1: Это же уравнение в проекции на ось OY 1 : Второй закон Ньютона для тела 2: В проекциях на оси OX 2, OY 2 :
Решение ( продолжение) А6. По наклонной плоскости с углом наклона движется тело массой m 2, связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Величина силы трения скольжения равна Из второго уравнения системы: Тогда первое уравнение системы принимает вид:
А6. По наклонной плоскости с углом наклона движется тело массой m 2, связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( продолжение) Тела связаны нерастяжимой нитью, поэтому Обозначим Если массой блока можно пренебречь, то согласно третьему закону Ньютона Подставим введённые обозначение в (1) и (2) и запишем систему уравнений: Обозначим
А6. По наклонной плоскости с углом наклона движется тело массой m 2, связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( продолжение) Из этой системы уравнений найдём силу натяжения. Разделим первое уравнение на второе:
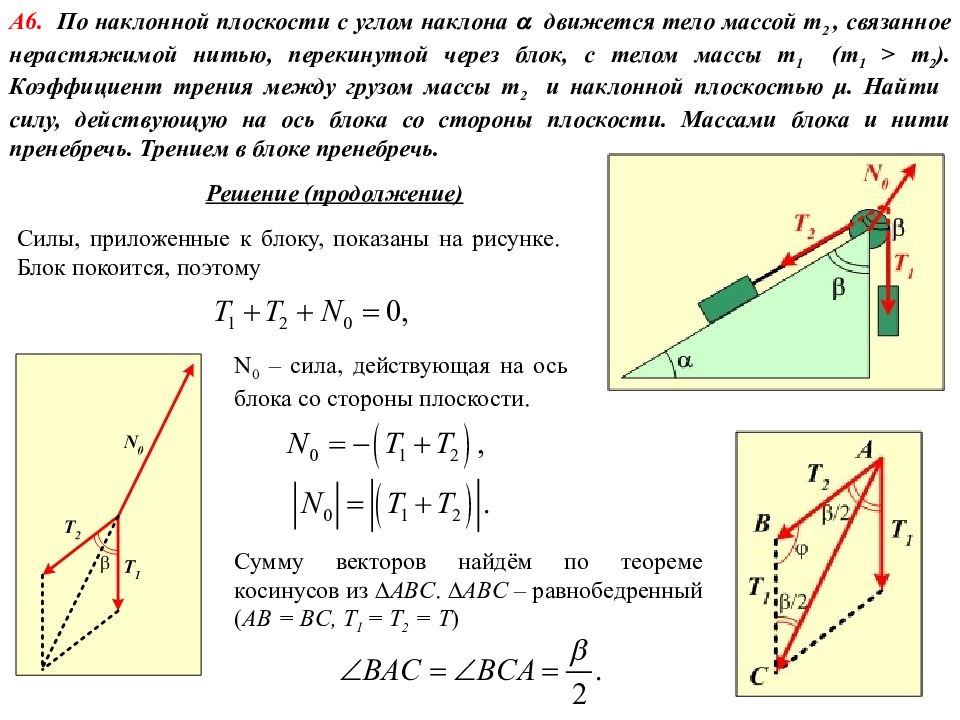
А6. По наклонной плоскости с углом наклона движется тело массой m 2, связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( продолжение) Силы, приложенные к блоку, показаны на рисунке. Блок покоится, поэтому N 0 – сила, действующая на ось блока со стороны плоскости. Сумму векторов найдём по теореме косинусов из D ABC. D ABC – равнобедренный ( AB = BC, T 1 = T 2 = T )
А6. По наклонной плоскости с углом наклона движется тело массой m 2, связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( продолжение) Ответ:
Дано: m 1 =10 т m 2 =5 т m 3 =100 кг 0 =500 м/с u 1 - ? Решение А5а. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа стояла неподвижно. Согласно закону сохранения импульса, записанному в лабораторной системе отсчёта - скорость платформы после выстрела, - скорость снаряда после выстрела в лабораторной системе отсчёта. В лабораторной системе отсчёта скорость снаряда В лабораторной системе отсчёта в проекциях на ось OX
Решение (продолжение) А5а. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа стояла неподвижно. Откуда проекция скорости платформы после выстрела Скорость платформы после выстрела направлена против оси OX ( влево на рисунке ). Ответ:
Решение А 5 б. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении ее движения. Дано: m 1 =10 т m 2 =5 т m 3 =100 кг =18 км/ч 0 =500 м/с u 1 - ? Согласно закону сохранения импульса, записанному в лабораторной системе отсчёта - скорость платформы после выстрела, - скорость снаряда после выстрела в лабораторной системе отсчёта. В лабораторной системе отсчёта скорость снаряда В лабораторной системе отсчёта в проекциях на ось OX
Решение (продолжение) А 5 б. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении ее движения. Откуда проекция скорости платформы после выстрела Проекции скоростей на ось OX : Ответ:
Решение А 5 в. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении, противоположном направлению ее движения. Дано: m 1 =10 т m 2 =5 т m 3 =100 кг =18 км/ч 0 =500 м/с u 1 - ? Согласно закону сохранения импульса, записанному в лабораторной системе отсчёта - скорость платформы после выстрела, - скорость снаряда после выстрела в лабораторной системе отсчёта. В лабораторной системе отсчёта скорость снаряда В лабораторной системе отсчёта в проекциях на ось OX
Решение (продолжение) А 5 в. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении, противоположном направлению ее движения. Откуда проекция скорости платформы после выстрела Проекции скоростей на ось OX : Ответ: Скорость платформы после выстрела направлена против оси OX ( влево на рисунке ).
А6. Граната, летевшая со скоростью v = 10 м/с, разорвалась на два осколка. Большой осколок, масса которого составила 0,6 массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью u 1 = 25 м/с. Найти скорость u 2 малого осколка гранаты. Дано: m 1 = 0,6 т m 2 =0,4 т v = 10 м/с u 1 = 2 5 м/с u 2 - ? Решение Выберем ось OX направленной вдоль первоначального направления движения гранаты. В проекциях на оси координат закон сохранения импульса имеет вид: Согласно закону сохранения импульса В выбранной нами системе отсчёта по условию задачи Из последнего уравнения следует, что Это означает, что оба осколка после взрыва движутся вдоль оси OX, хотя, возможно, и в разных направлениях. Из уравнения для проекций импульсов на ось OX
А6. Граната, летевшая со скоростью v = 10 м/с, разорвалась на два осколка. Большой осколок, масса которого составила 0,6 массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью u 1 = 25 м/с. Найти скорость u 2 малого осколка гранаты. Решение ( продолжение) В выбранной нами системе отсчёта Это означает, что меньший осколок полетит в направлении, противоположном первоначальному направлению движения гранаты. Ответ:
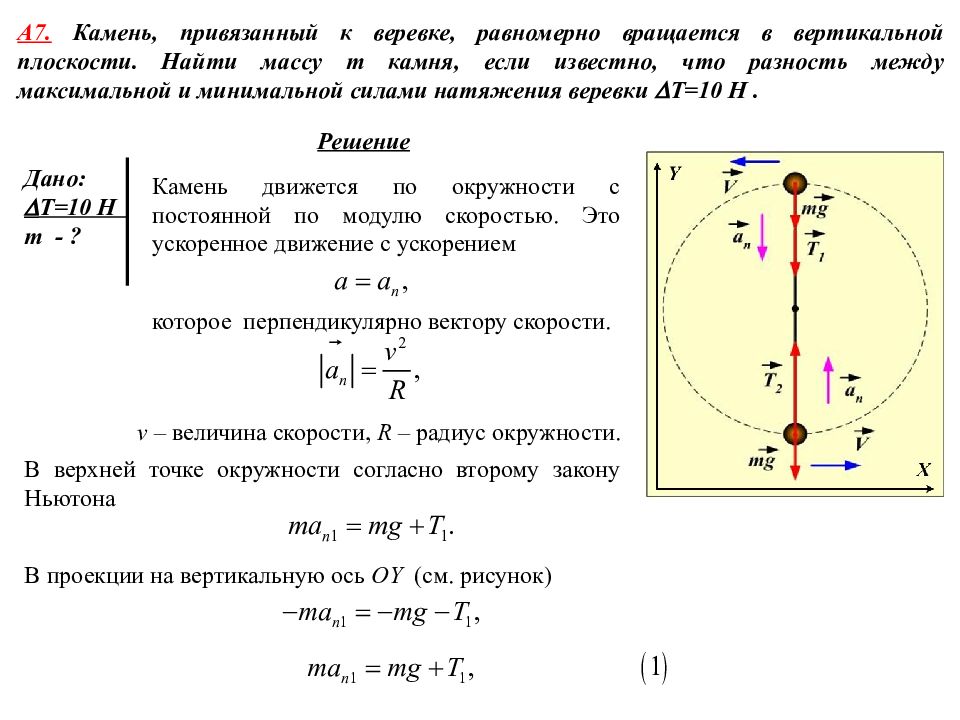
А 7. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки T=10 Н. Дано: T=10 Н m - ? Решение Камень движется по окружности с постоянной по модулю скоростью. Это ускоренное движение с ускорением которое перпендикулярно вектору скорости. v – величина скорости, R – радиус окружности. В верхней точке окружности согласно второму закону Ньютона В проекции на вертикальную ось OY ( см. рисунок)
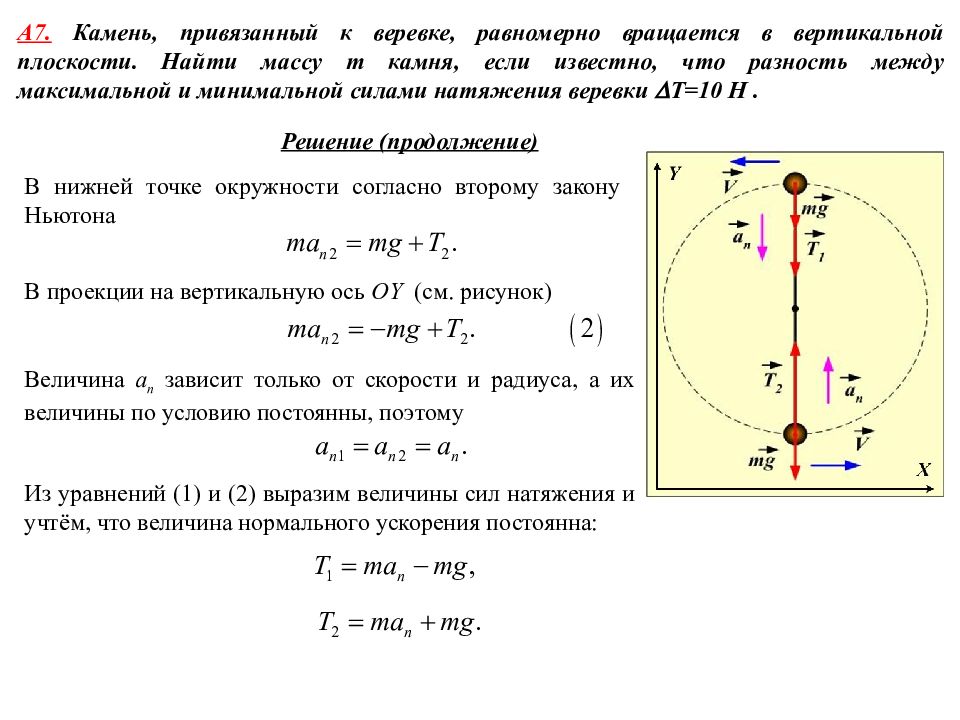
А 7. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки T=10 Н. Решение (продолжение) В нижней точке окружности согласно второму закону Ньютона В проекции на вертикальную ось OY ( см. рисунок) Величина a n зависит только от скорости и радиуса, а их величины по условию постоянны, поэтому Из уравнений (1) и (2) выразим величины сил натяжения и учтём, что величина нормального ускорения постоянна:
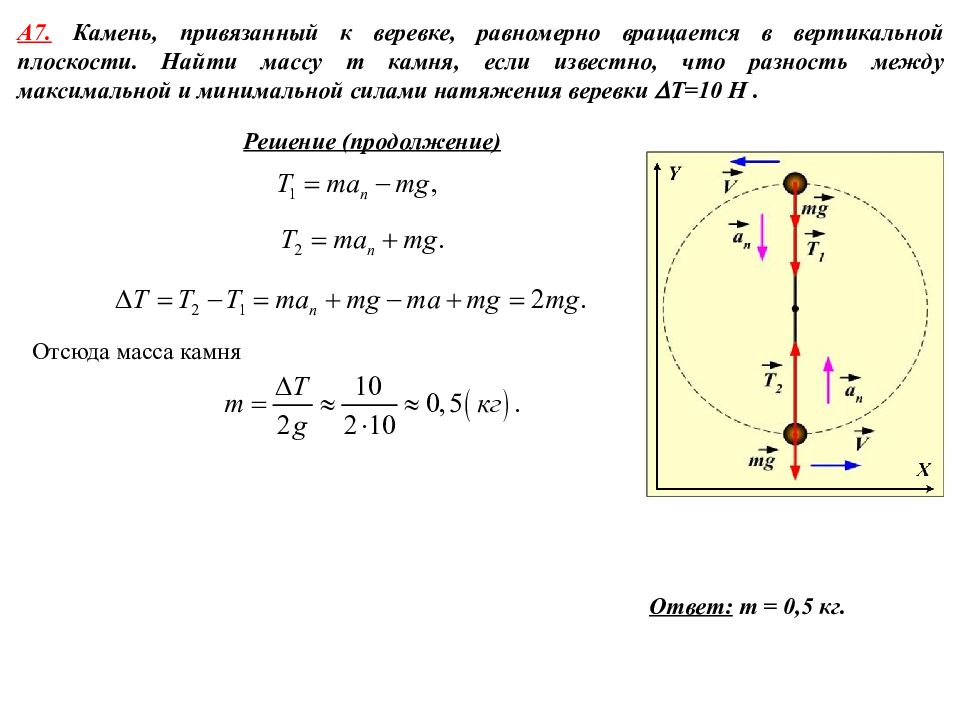
А 7. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки T=10 Н. Решение (продолжение) Отсюда масса камня Ответ: m = 0,5 кг.
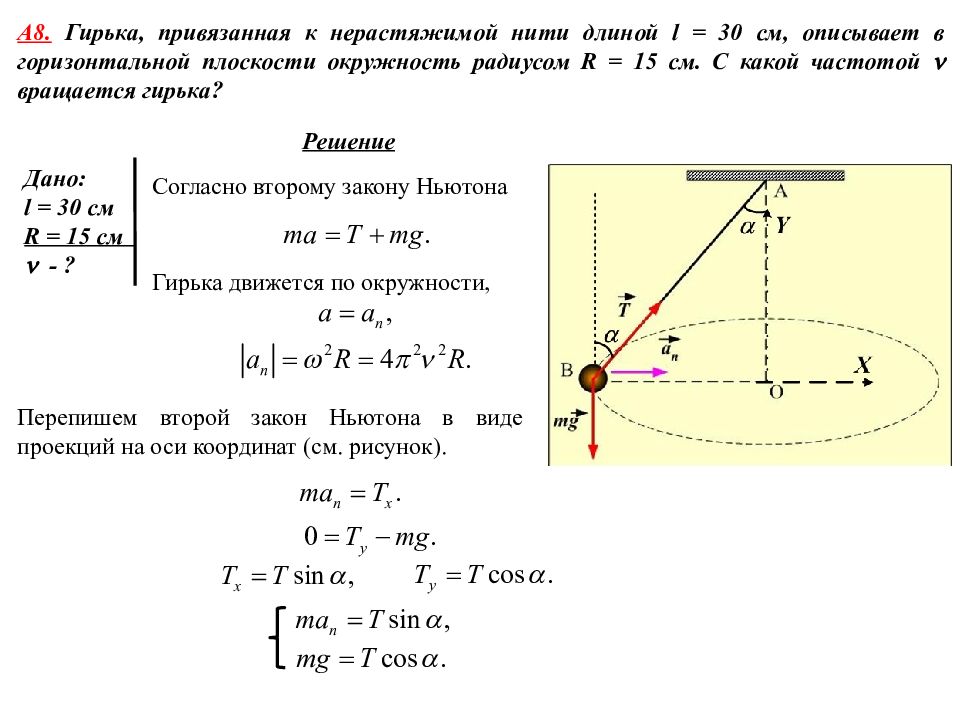
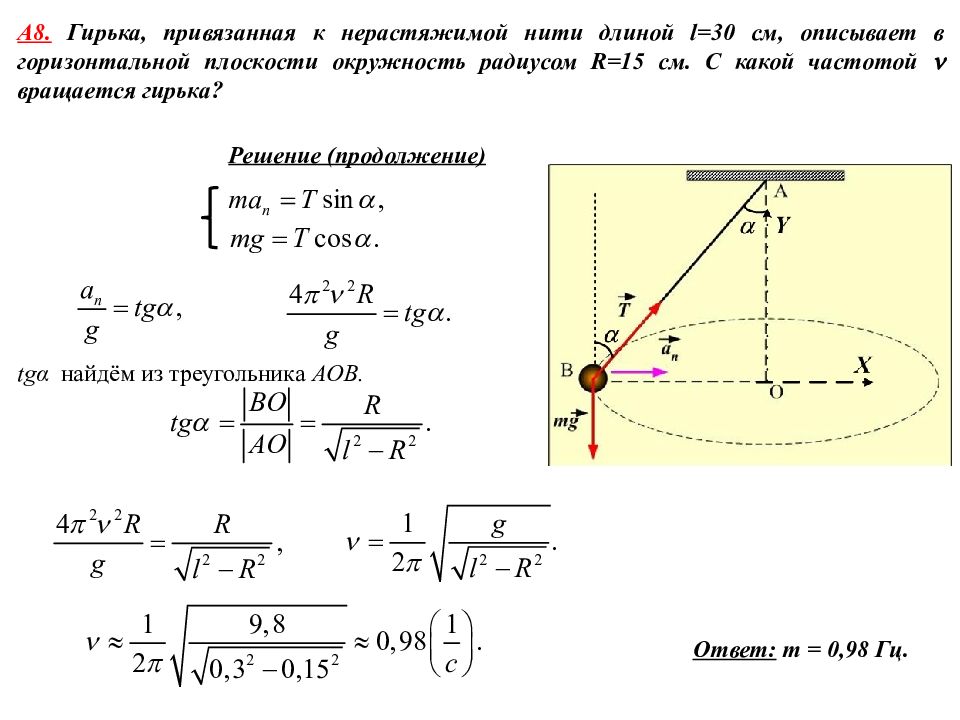
А 8. Гирька, привязанная к нерастяжимой нити длиной l = 30 см, описывает в горизонтальной плоскости окружность радиусом R = 15 см. С какой частотой вращается гирька? Дано: l = 30 см R = 15 см n - ? Решение Согласно второму закону Ньютона Гирька движется по окружности, Перепишем второй закон Ньютона в виде проекций на оси координат (см. рисунок).
А 8. Гирька, привязанная к нерастяжимой нити длиной l=30 см, описывает в горизонтальной плоскости окружность радиусом R=15 см. С какой частотой вращается гирька? Решение (продолжение) tg α найдём из треугольника AOB. Ответ: m = 0, 98 Гц.
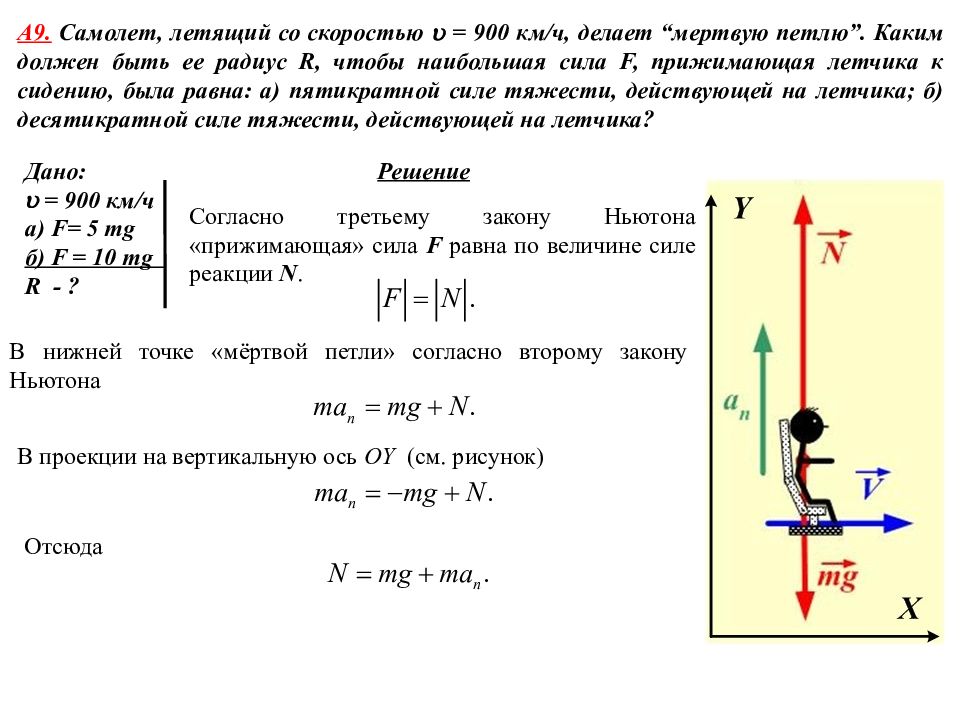
А 9. Самолет, летящий со скоростью = 900 км/ч, делает “мертвую петлю”. Каким должен быть ее радиус R, чтобы наибольшая сила F, прижимающая летчика к сидению, была равна: а) пятикратной силе тяжести, действующей на летчика; б) десятикратной силе тяжести, действующей на летчика? Дано: = 900 км/ч а) F= 5 mg б) F = 10 mg R - ? Решение Согласно третьему закону Ньютона «прижимающая» сила F равна по величине силе реакции N. В нижней точке «мёртвой петли» согласно второму закону Ньютона В проекции на вертикальную ось OY ( см. рисунок) Отсюда
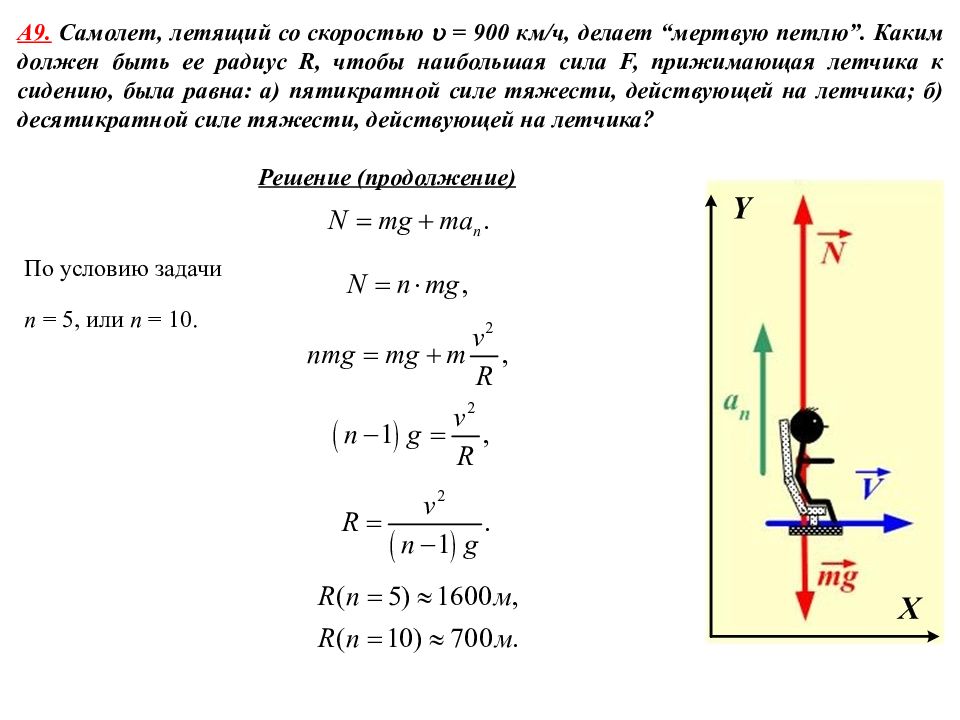
А 9. Самолет, летящий со скоростью = 900 км/ч, делает “мертвую петлю”. Каким должен быть ее радиус R, чтобы наибольшая сила F, прижимающая летчика к сидению, была равна: а) пятикратной силе тяжести, действующей на летчика; б) десятикратной силе тяжести, действующей на летчика? Решение (продолжение) По условию задачи n = 5, или n = 10.
A10. Искусственный спутник Земли движется по круговой орбите в плоскости экватора с запада на восток. На какой высоте h от поверхности Земли должен находиться этот спутник, чтобы он был неподвижен по отношению к наблюдателю, находящемуся на поверхности Земли у экватора? Дано: m = 6·10 24 кг R = 6380 км Решение T = 24 ч h - ? На спутник действует сила тяжести, которая второму закону Ньютона создаёт нормальное (центростремительное) ускорение. Если ось OY направить по направлению ускорения (см. рисунок), то где m – масса спутника, M – масса Земли, r – радиус орбиты. где R – радиус Земли, r – радиус орбиты, h – высота.
A10. Искусственный спутник Земли движется по круговой орбите в плоскости экватора с запада на восток. На какой высоте h от поверхности Земли должен находиться этот спутник, чтобы он был неподвижен по отношению к наблюдателю, находящемуся на поверхности Земли у экватора? Решение (продолжение)
