Задачи на нахождение расстояния от точки до плоскости ( типовые задачи С2) Подготовила: учитель математики МОУ «Гимназия №1» г. Железногорска Курской области Агашкова Н.А.
Нахождение расстояния от точки до плоскости по определению. Построение перпендикуляра к плоскости на основании признака перпендикулярности прямой и плоскости. Нахождение расстояния от точки до плоскости по определению. Построение перпендикуляра к плоскости на основании признака перпендикулярности прямой и плоскости. Нахождение расстояния от точки до плоскости. Построение перпендикуляра к плоскости на основании свойства перпендикулярных плоскостей. Нахождение расстояния от точки до плоскости. Построение перпендикуляра к плоскости на основании свойства параллельности прямой и плоскости. Нахождение расстояния от точки до плоскости методом объемов. Нахождение расстояния от точки до плоскости методом координат. План проведения занятий.
Метод координат – это один из самых универсальных методов геометрии. В принципе почти любую геометрическую задачу можно решить методом координат. Однако, попытки решать каждую задачу только координатным методом (имеются в виду, конечно, те задачи, в условии которых не говорится о координатах) часто приводят к тому, что даже простая геометрическая задача становится очень сложной алгебраической. Главное при решении геометрических задач координатным методом – удачный выбор системы координат, т.е. выбор начала координат и направления осей. Обычно в качестве осей координат выбирают прямые, фигурирующие в условии задачи, или оси симметрии (если они есть) фигур, рассматриваемых в задаче. Желательно, чтобы выбранная система координат естественным образом определялась условием задачи. Следует отметить, что при решении задачи координатным методом выпускник должен получить правильный ответ, и только тогда его решение будет оценено в 2 балла. В противном случае его решение не соответствует приведенным критериям и будет оценено в 0 баллов.
Метод координат Метод координат можно использовать, вычисляя: расстояние между двумя точками; расстояние от точки до прямой; расстояние от точки до плоскости; угол между прямой и плоскостью; угол между плоскостями; расстояние между скрещивающимися прямыми.
Расположение относительно прямоугольной системы координат некоторых видов многогранников, наиболее часто используемых в задачах.
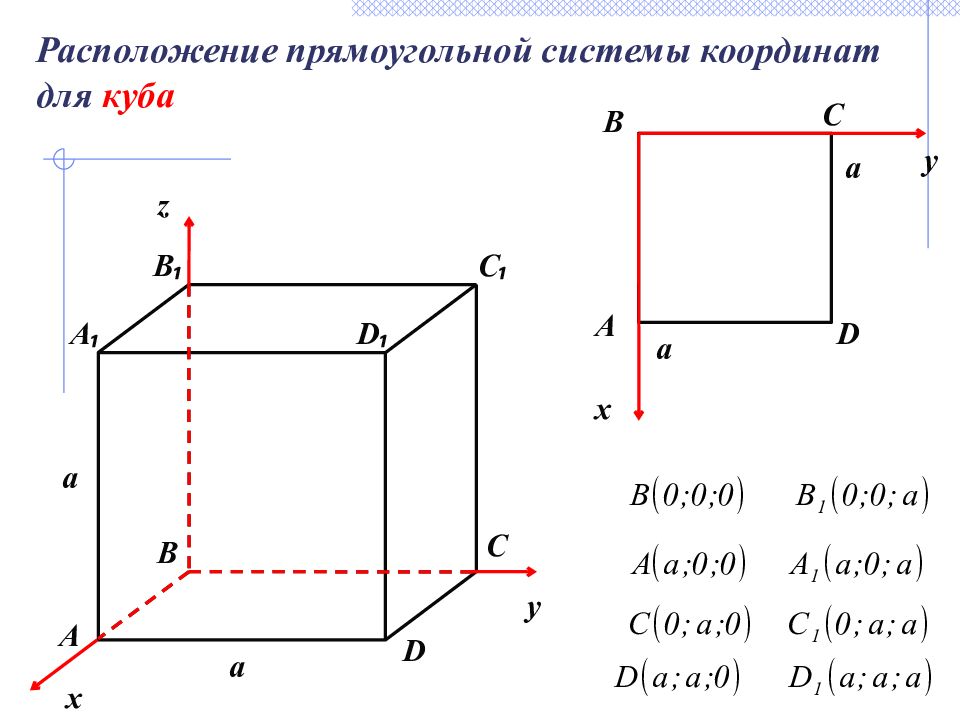
Расположение прямоугольной системы координат для куба А ₁ А B ₁ C ₁ C B a a D ₁ D a x y А D B C x a y z
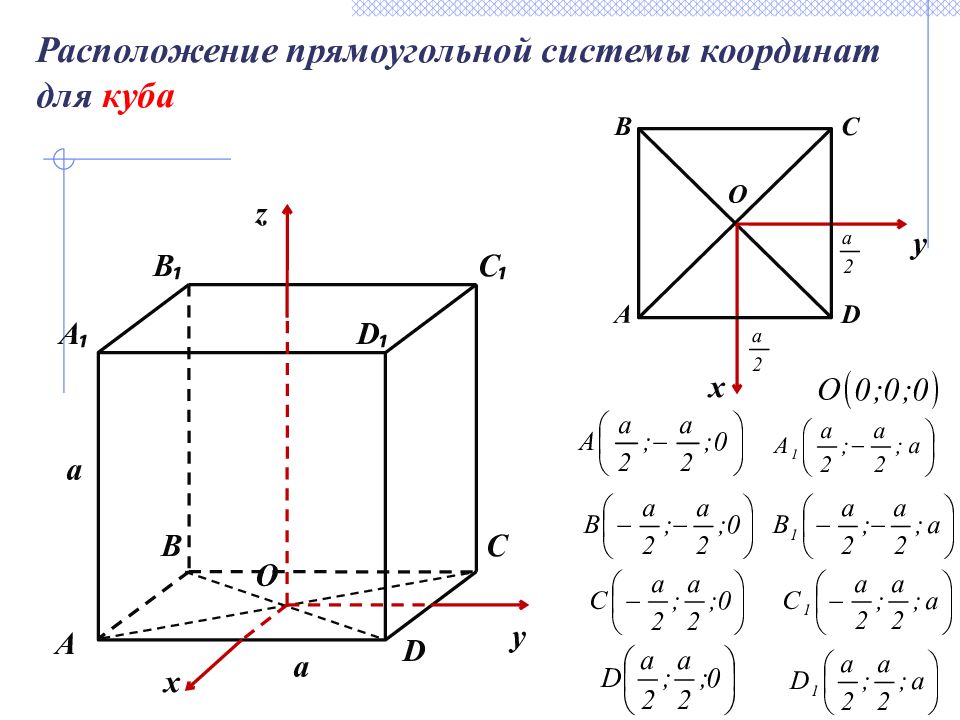
Расположение прямоугольной системы координат для куба А ₁ А B ₁ C ₁ C B D ₁ D A B C D O O z y y x x a a
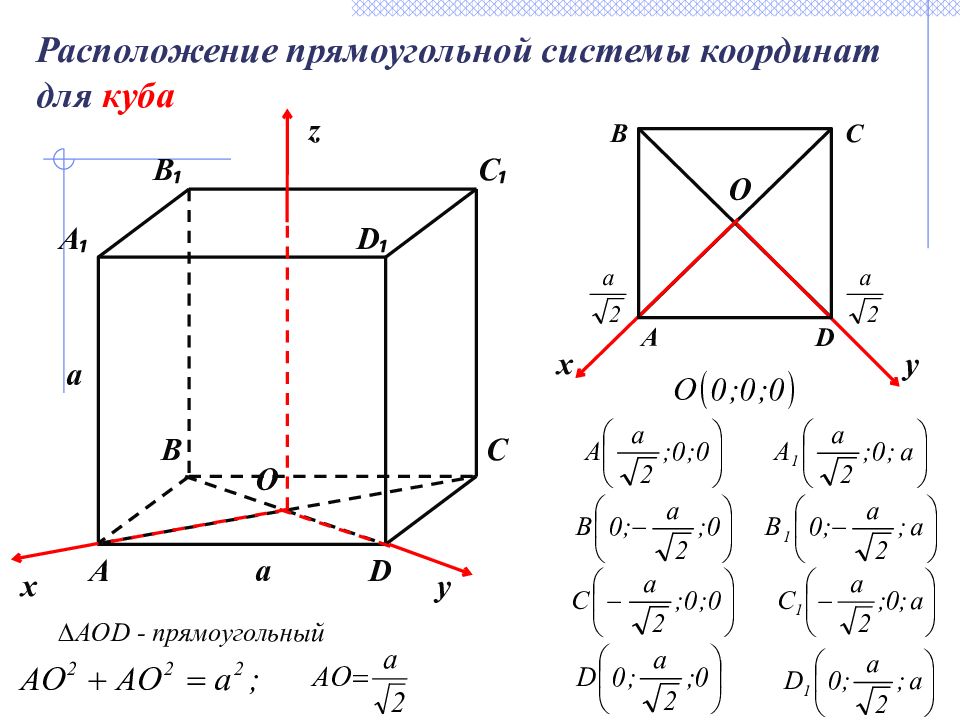
Расположение прямоугольной системы координат для куба O y x А ₁ А B ₁ C ₁ C B D ₁ D O z y x a a A B C D ∆ AOD - прямоугольный
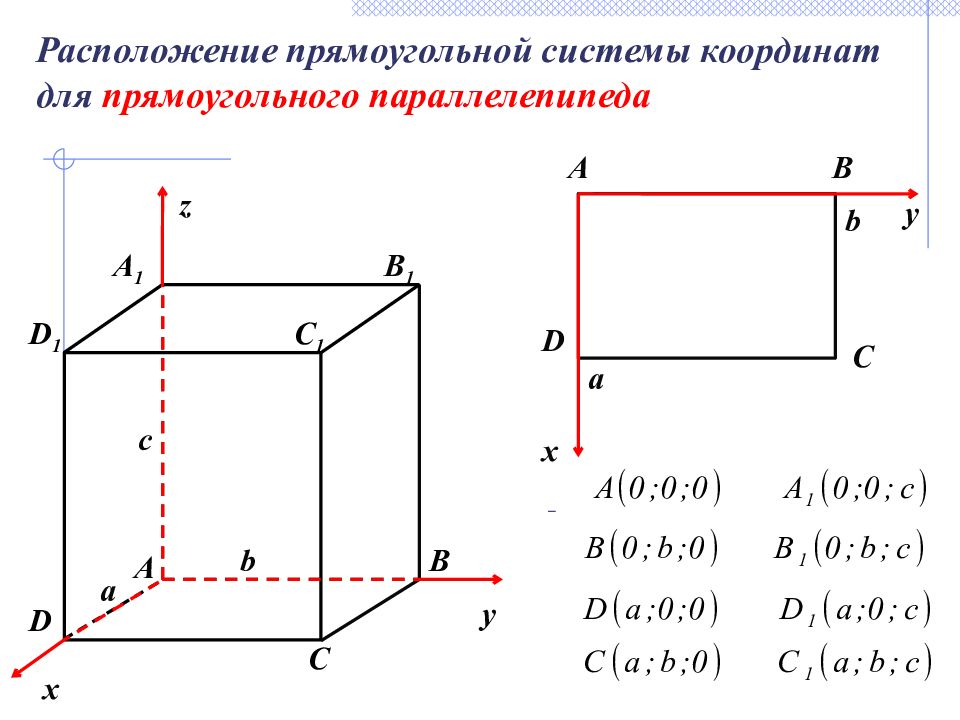
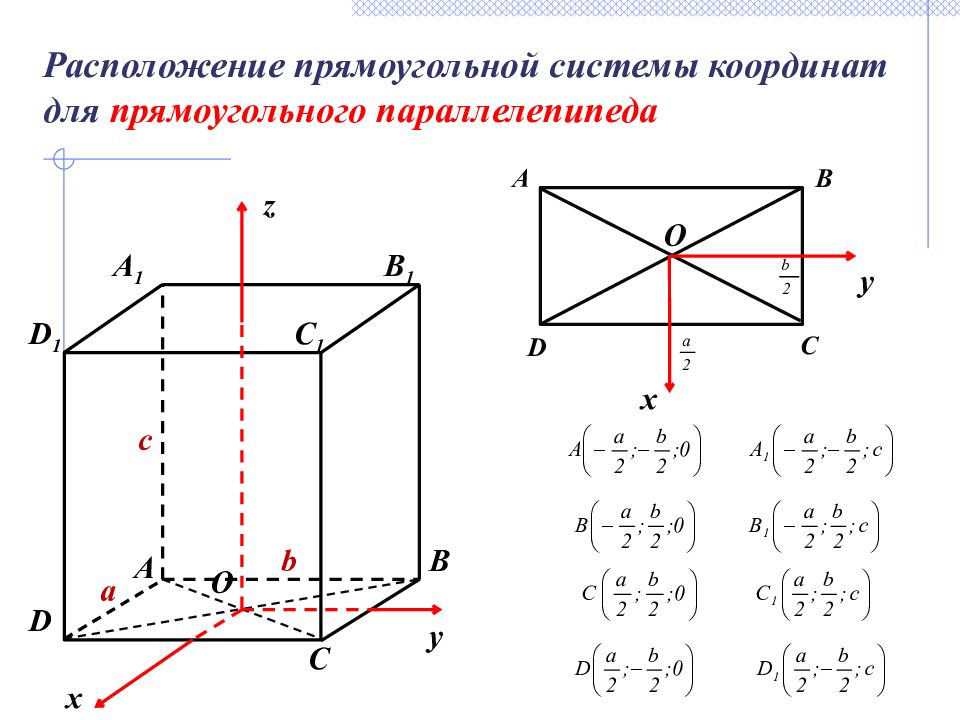
A 1 C 1 D 1 C B A D B 1 x y c a b D A B C a b z y x Расположение прямоугольной системы координат для прямоугольного параллелепипеда
A 1 C 1 D 1 C B A D B 1 O x y z Расположение прямоугольной системы координат для прямоугольного параллелепипеда A D B O x y C c a b
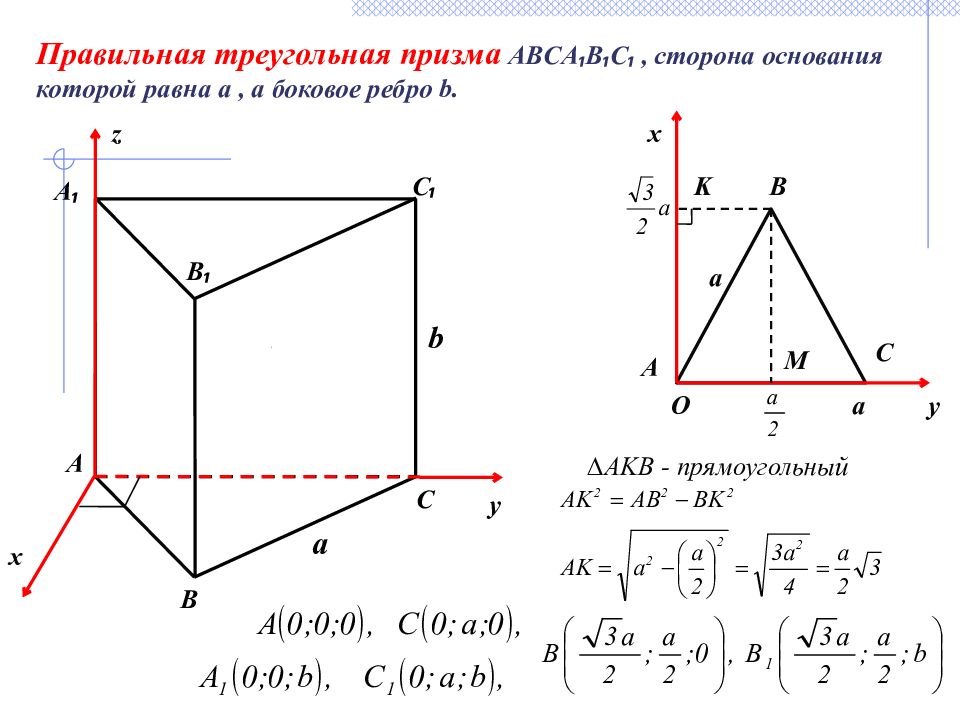
B A b a C C ₁ A ₁ B ₁ Правильная треугольная призма ABCA ₁ B ₁ C ₁, сторона основания которой равна a, а боковое ребро b. A B C a O x y x y z a ∆ AKB - прямоугольный K M
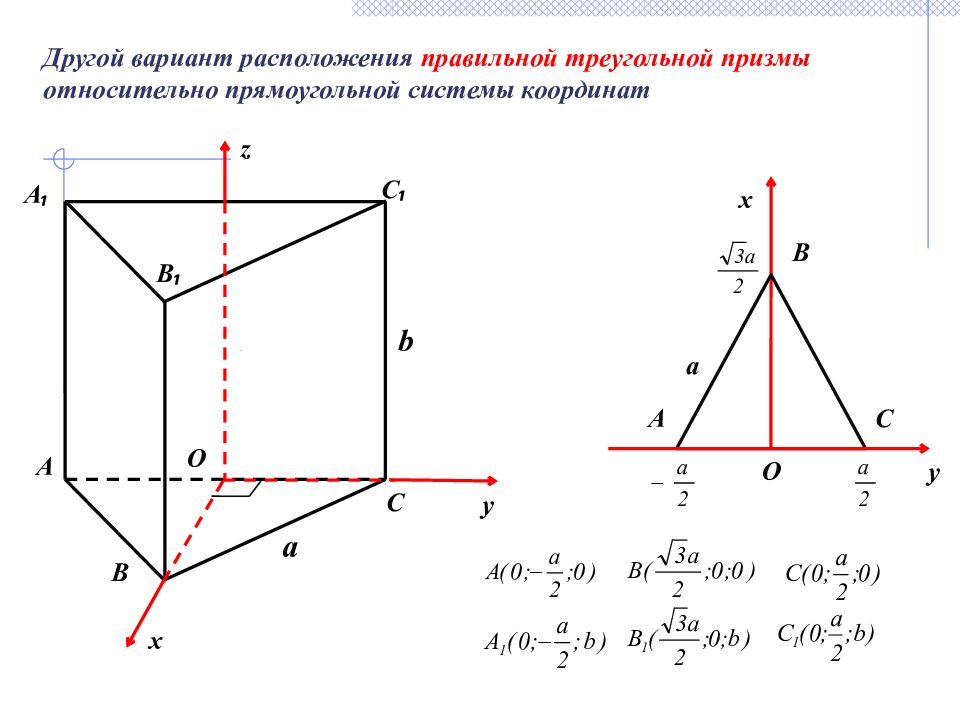
B A b a C C ₁ A ₁ B ₁ Другой вариант расположения правильной треугольной призмы относительно прямоугольной системы координат O z y x O x y A B C a
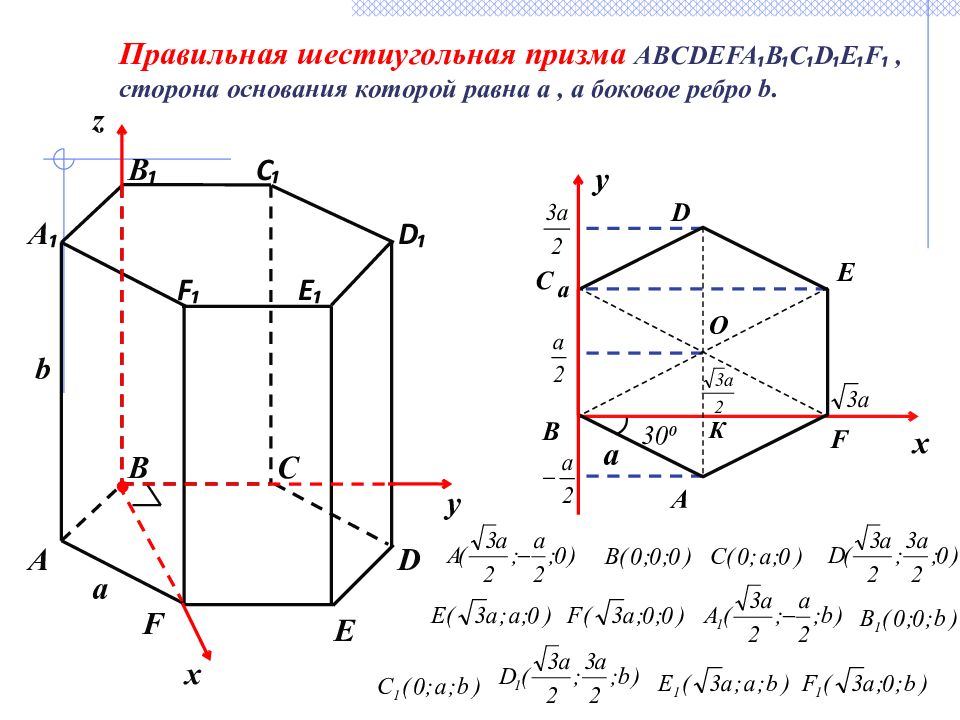
B E B ₁ C ₁ F ₁ C D ₁ А a b F E ₁ D А ₁ x z y Правильная шестиугольная призма ABCDEFA ₁ B ₁ C ₁ D ₁ E ₁ F ₁, сторона основания которой равна a, а боковое ребро b. y x К F E D C B A O а 30⁰ а
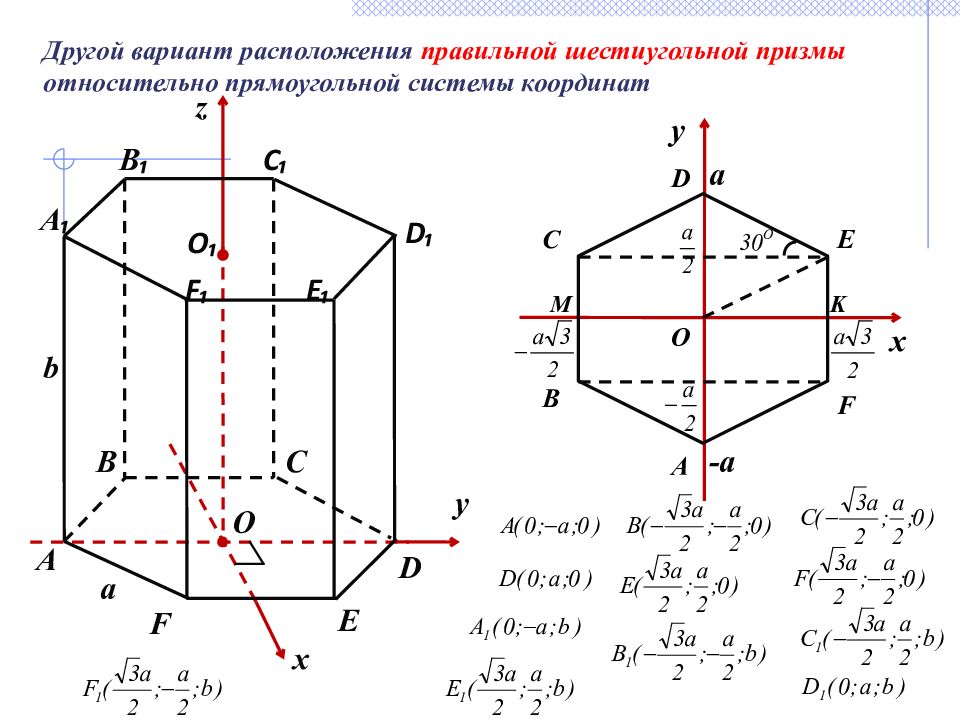
x z y О О₁ B E B ₁ C ₁ F ₁ C D ₁ А a b F E ₁ D А ₁ Другой вариант расположения правильной шестиугольной призмы относительно прямоугольной системы координат х F E D C B A K M a -a O у
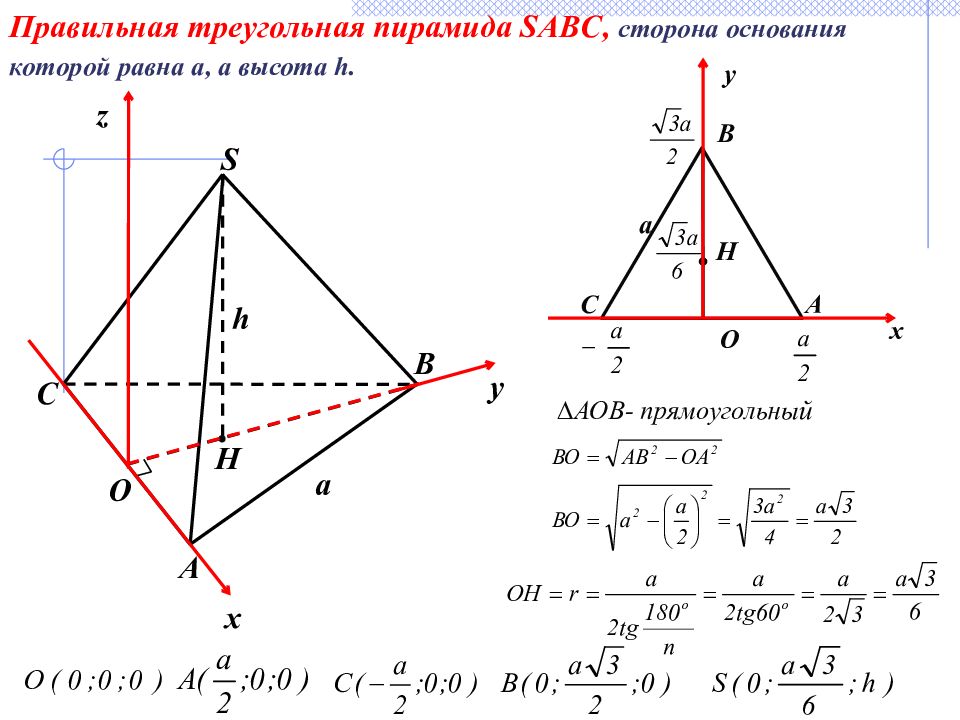
O A B C Н a A S H O C B a h z y x Правильная треугольная пирамида SABC, сторона основания которой равна а, а высота h. y x ∆ АОВ- прямоугольный
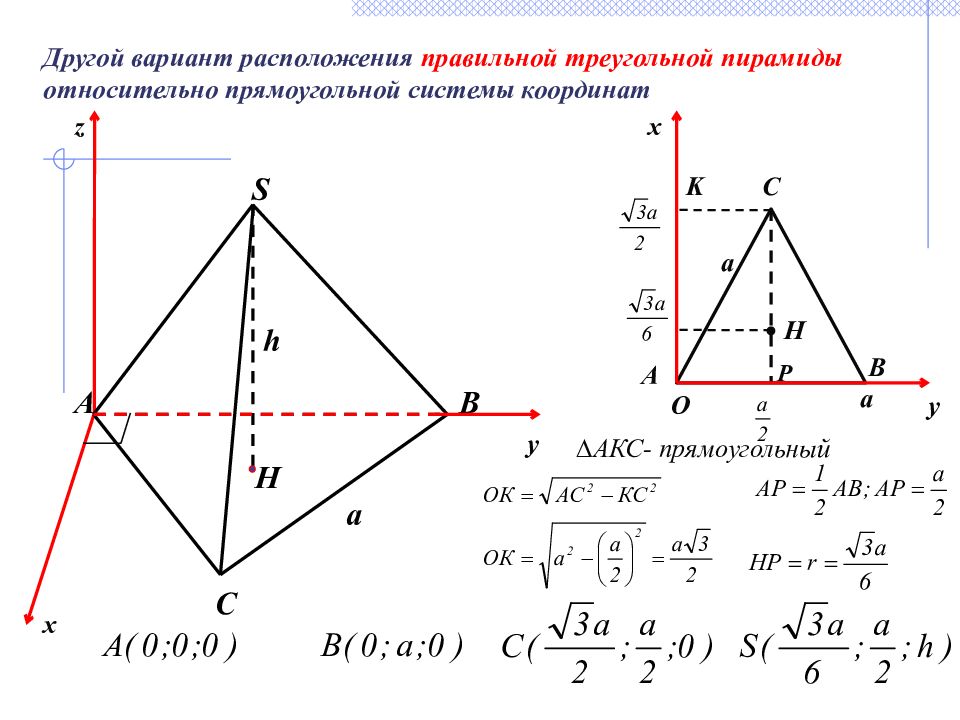
Другой вариант расположения правильной треугольной пирамиды относительно прямоугольной системы координат O x y C S H A B a h y x z a A C B a H K P ∆ АКС- прямоугольный
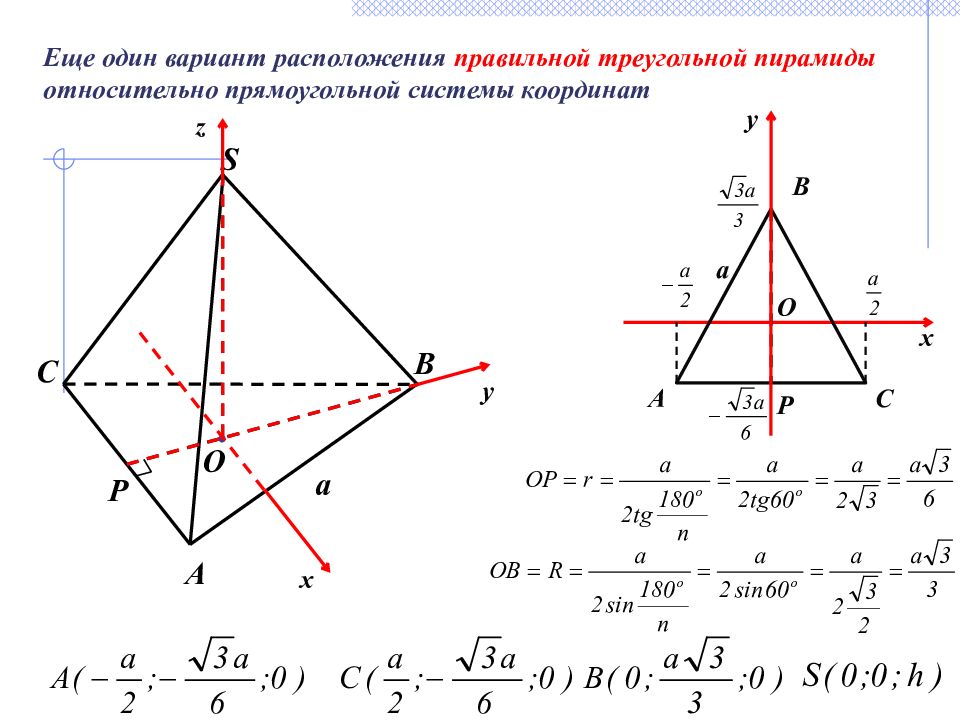
Еще один вариант расположения правильной треугольной пирамиды относительно прямоугольной системы координат x y A S O P C B a O a A B C Р x y z
Правильная четырехугольная пирамида SABCD, сторона основания которой равна а, а высота h. D S B A C Н h a x y O H D C B A a a x y z
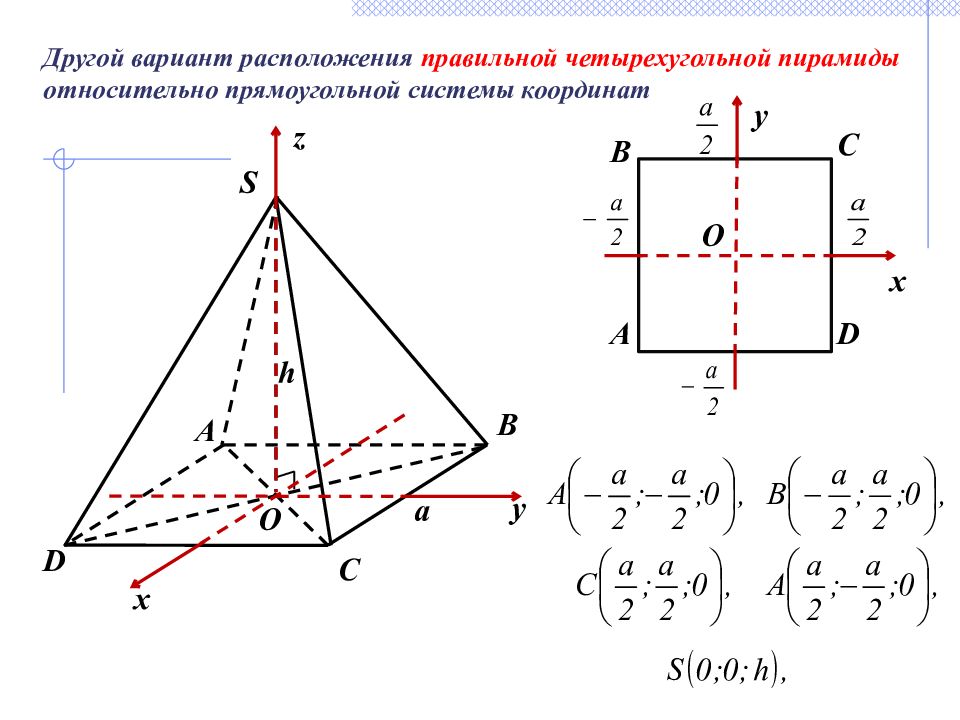
D S B A C O h a Другой вариант расположения правильной четырехугольной пирамиды относительно прямоугольной системы координат z y x O D C B A y x
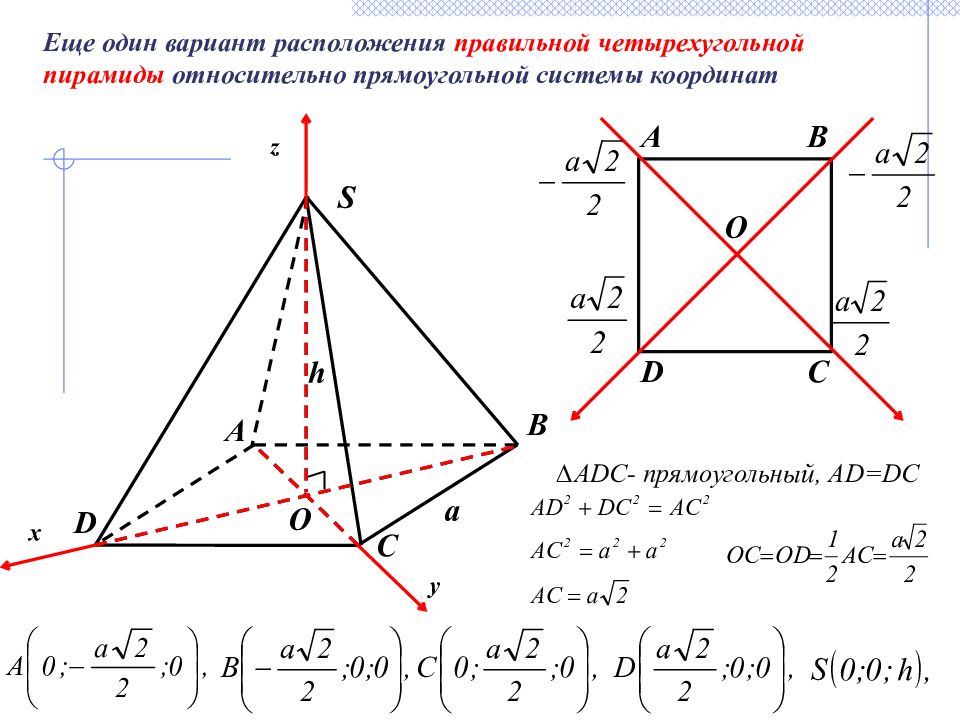
D S B A C O h a Еще один вариант расположения правильной четырехугольной пирамиды относительно прямоугольной системы координат ∆ ADC - прямоугольный, AD=DC O D C B A y z x
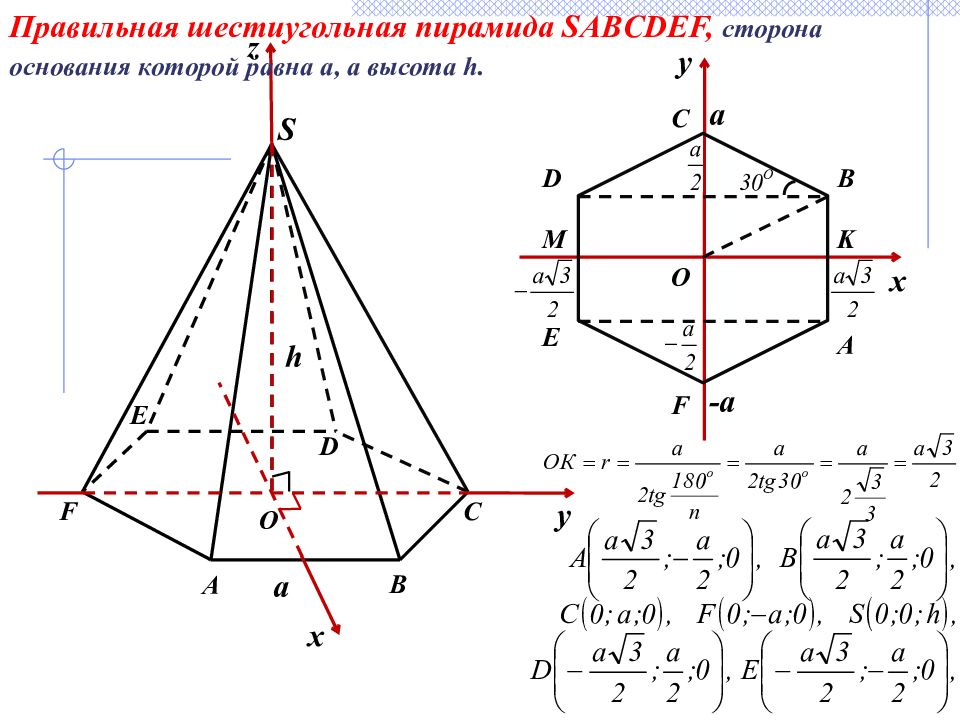
F C A a O D E B S у z х у х A B C D E F K M a -a O Правильная шестиугольная пирамида SABCDEF, сторона основания которой равна а, а высота h. h
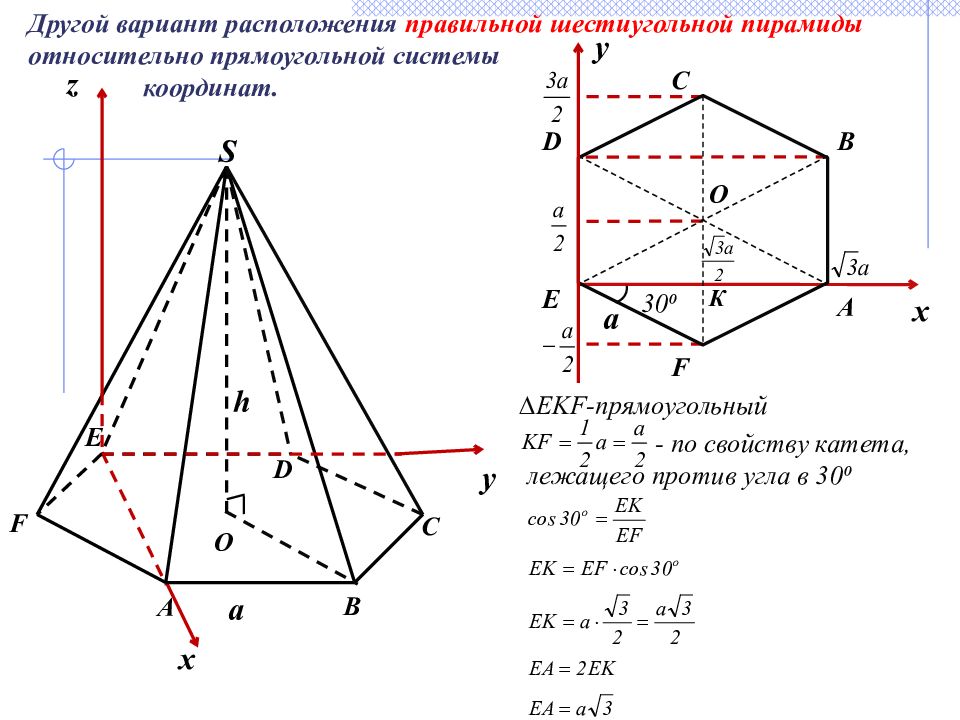
F C A a O D E B S z y x A B C D E F O ∆ EKF -прямоугольный - по свойству катета, лежащего против угла в 30⁰ y x К а 30⁰ Другой вариант расположения правильной шестиугольной пирамиды относительно прямоугольной системы координат. h
Например:
Уравнение плоскости имеет вид Числа a, b, c находим из системы уравнений
Например: Написать уравнение плоскости, проходящей через точки - уравнение плоскости, проходящей через три данные точки.
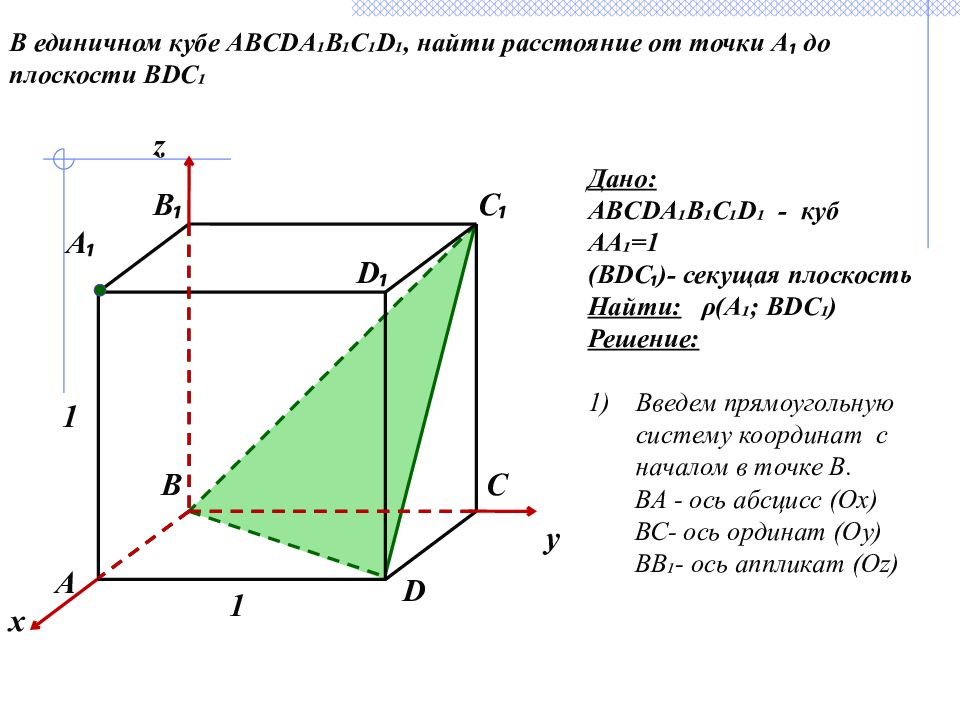
x C ₁ 1 А ₁ А B ₁ C B 1 D ₁ D y z В единичном кубе ABCDA₁B₁C₁D₁, найти расстояние от точки А ₁ до плоскости BDC₁ Дано: ABCDA₁B₁C₁D₁ - куб АА₁=1 ( BDC ₁ ) - секущая плоскость Найти: ρ (А₁; BDC₁ ) Решение: Введем прямоугольную систему координат с началом в точке В. BA - ось абсцисс (Ox) ВС- ось ординат (Oy) ВВ₁- ось аппликат (Oz)
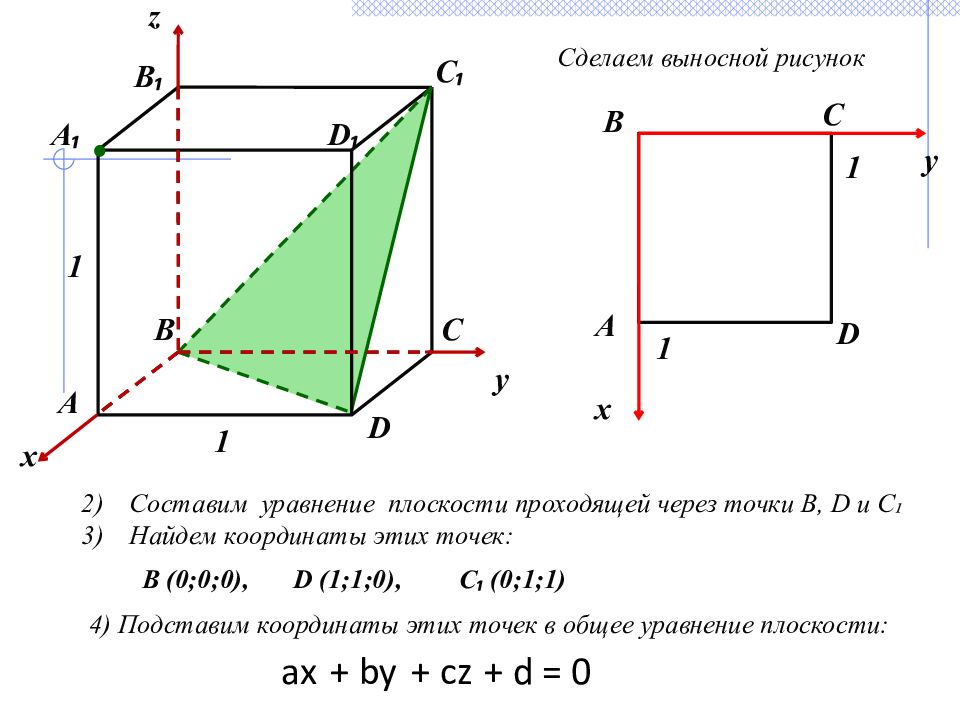
1 x y А D B C 1 А ₁ А B ₁ C ₁ x C B 1 1 D ₁ D y z Составим уравнение плоскости проходящей через точки В, D и С₁ Найдем координаты этих точек: В (0;0;0), D (1;1;0), С ₁ (0;1;1) Сделаем выносной рисунок 4) Подставим координаты этих точек в общее уравнение плоскости:
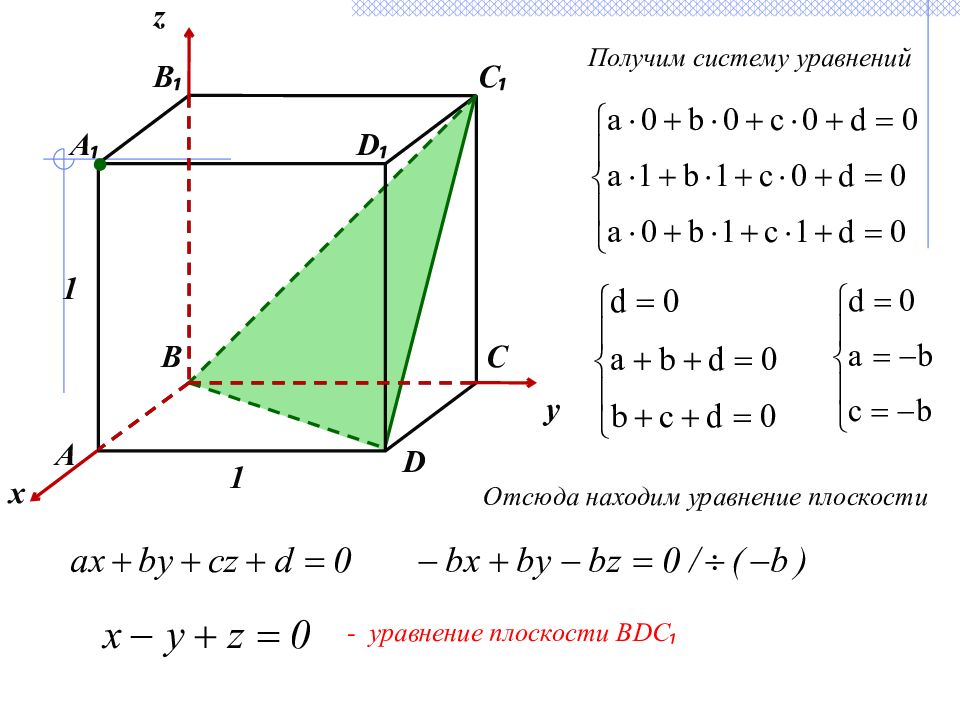
Получим систему уравнений А ₁ А B ₁ C ₁ x C B 1 1 D ₁ D y z Отсюда находим уравнение плоскости - уравнение плоскости BDC ₁
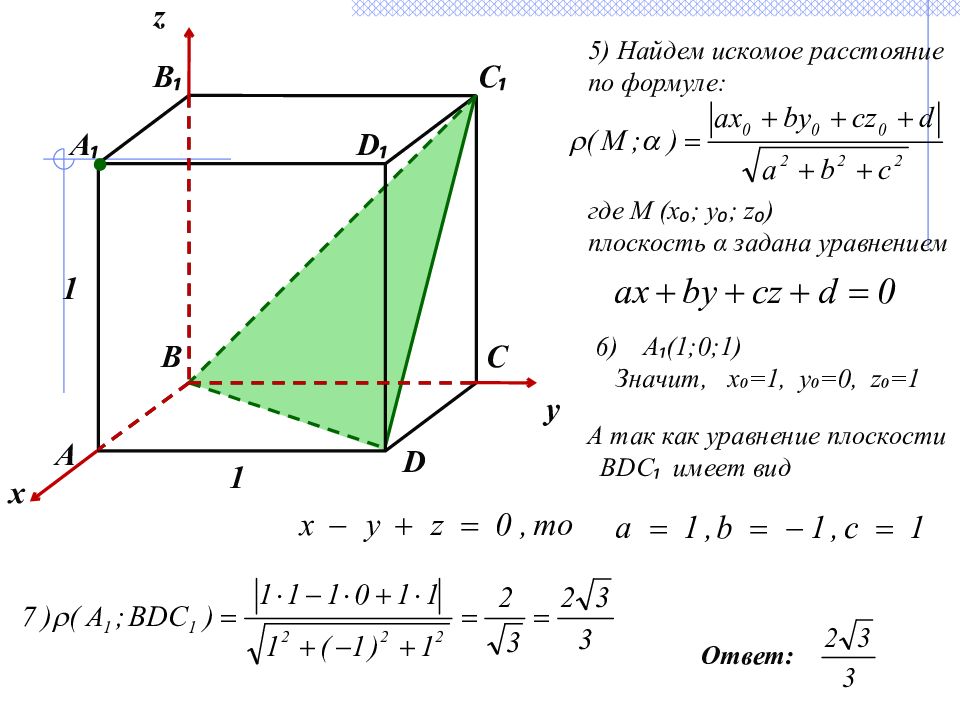
А ₁ А B ₁ C ₁ x C B 1 1 D ₁ D y z 5) Найдем искомое расстояние по формуле: где М (х ₀ ; у ₀ ; z ₀ ) плоскость α задана уравнением А ₁ (1;0;1) Значит, x₀=1, y₀=0, z₀=1 Ответ: А так как уравнение плоскости BDC ₁ имеет вид
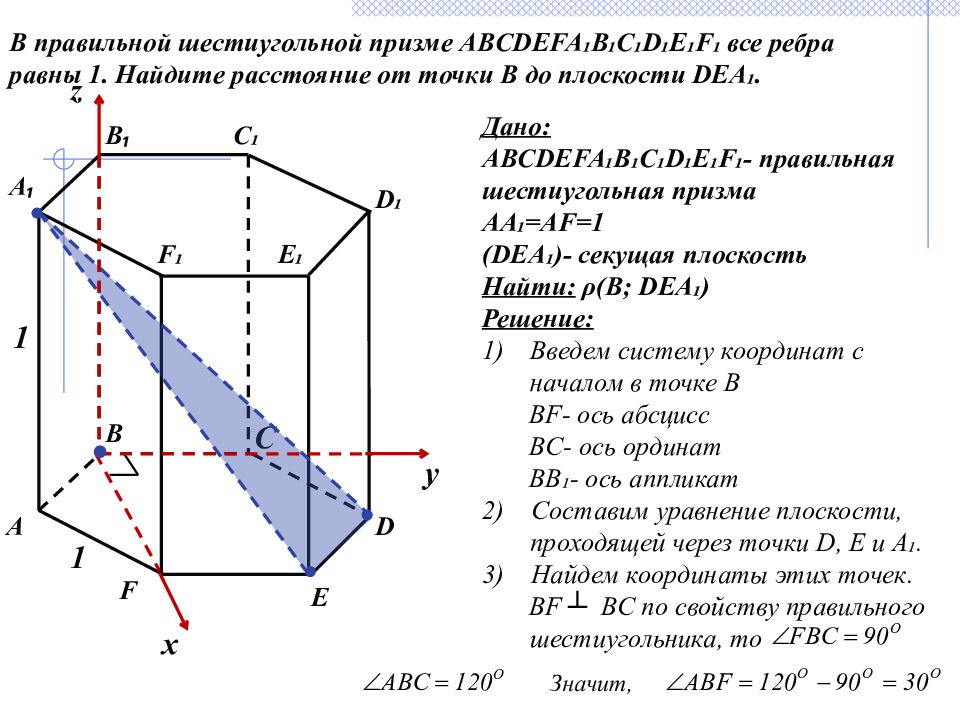
B E B ₁ C ₁ F ₁ C D ₁ А 1 1 F E ₁ D А ₁ В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние от точки B до плоскости DEA₁. Дано: ABCDEFA₁B₁C₁D₁E₁F₁ - правильная шестиугольная призма AA₁=AF=1 ( DEA₁)- секущая плоскость Найти: ρ ( B; DEA₁) Решение: Введем систему координат с началом в точке В BF- ось абсцисс BC- ось ординат BB₁- ось аппликат 2) Составим уравнение плоскости, проходящей через точки D, E и A₁. 3) Найдем координаты этих точек. BF ┴ BC по свойству правильного шестиугольника, то x z y Значит,
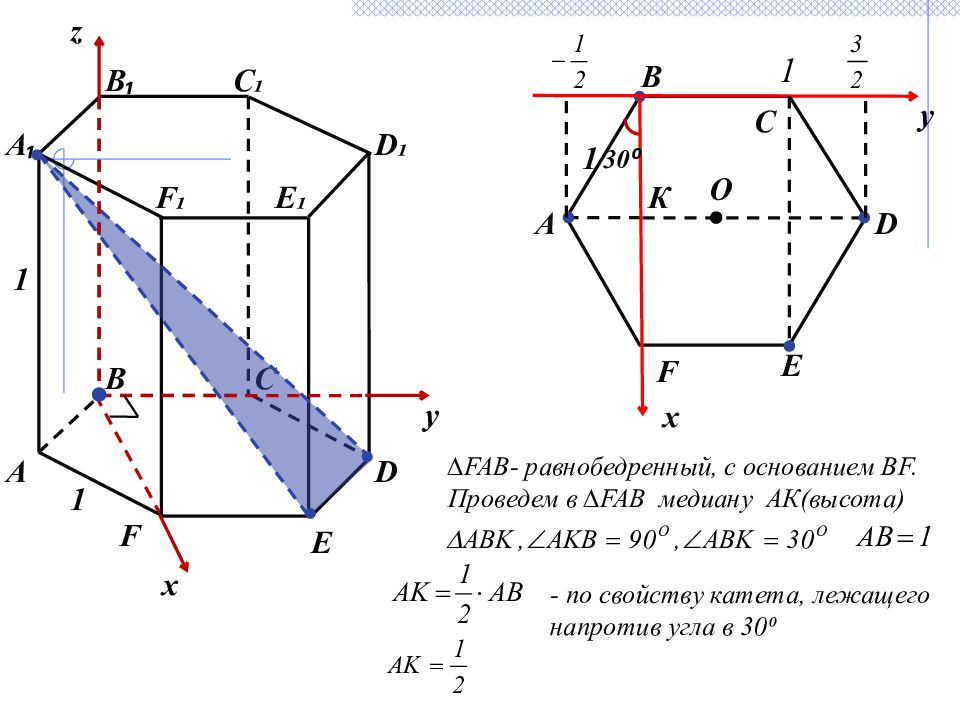
B E B ₁ C ₁ F ₁ C D ₁ А 1 1 F E ₁ D А ₁ D Е F В С А О x z y 1 К 30 ⁰ y x ∆ FAB - равнобедренный, с основанием BF. Проведем в ∆ FAB медиану АК(высота) - по свойству катета, лежащего напротив угла в 30⁰
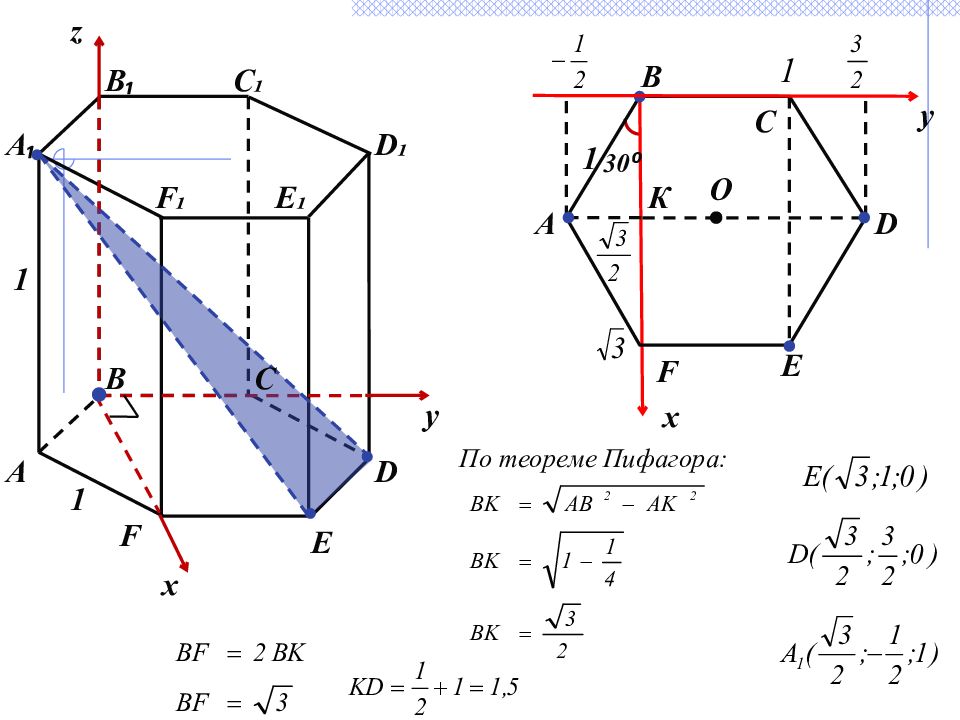
B E B ₁ C ₁ F ₁ C D ₁ А 1 1 F E ₁ D А ₁ x z y 1 К 30 ⁰ D Е F В С А О y x По теореме Пифагора:
4) Подставим координаты точек E, D и А₁ в общее уравнение плоскости (для точки Е) (для точки D ) (для точки A₁ ) Получим систему уравнений « + »
- уравнение плоскости DEA ₁ Отсюда находим уравнение плоскости
6) B(0;0;0), значит х₀=0, y ₀=0, z ₀=0 5)Найдем искомое расстояние по формуле где М( x₀;y₀;z₀ ), плоскость α задана уравнением Ответ:
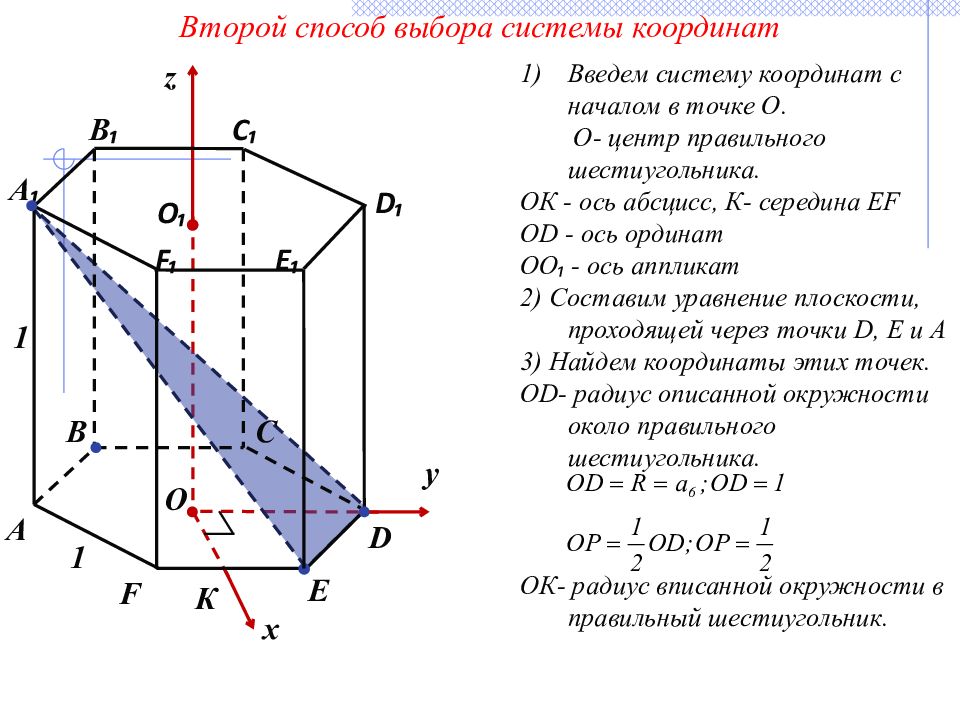
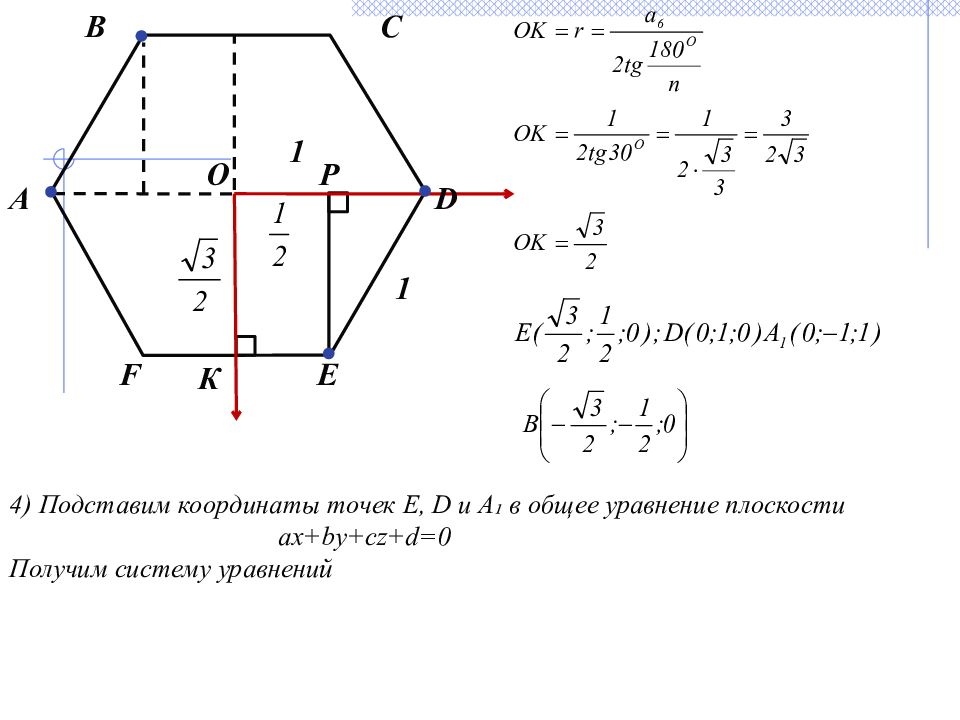
Второй способ выбора системы координат Введем систему координат с началом в точке О. О- центр правильного шестиугольника. ОК - ось абсцисс, К- середина Е F OD - ось ординат OO ₁ - ось аппликат 2) Составим уравнение плоскости, проходящей через точки D, E и A 3) Найдем координаты этих точек. О D - радиус описанной окружности около правильного шестиугольника. ОК- радиус вписанной окружности в правильный шестиугольник. x z y О О₁ B E B ₁ C ₁ F ₁ C D ₁ А 1 1 F E ₁ D А ₁ К
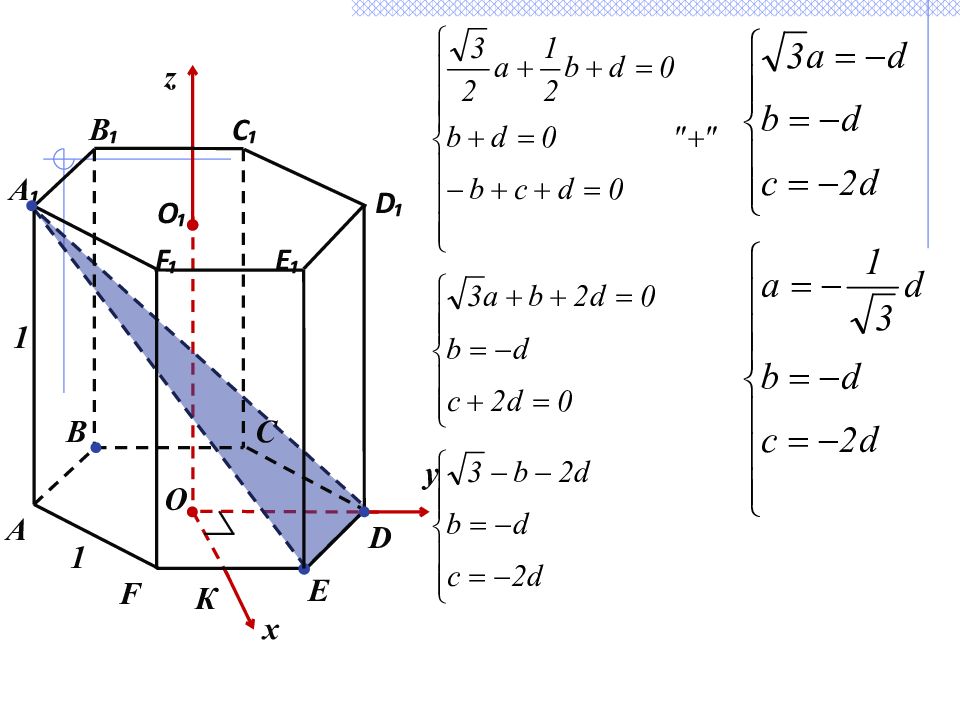
1 D Е F В С А К О 1 Р 4) Подставим координаты точек Е, D и А₁ в общее уравнение плоскости ax+by+cz+d=0 Получим систему уравнений
x z y О О₁ B E B ₁ C ₁ F ₁ C D ₁ А 1 1 F E ₁ D А ₁ К
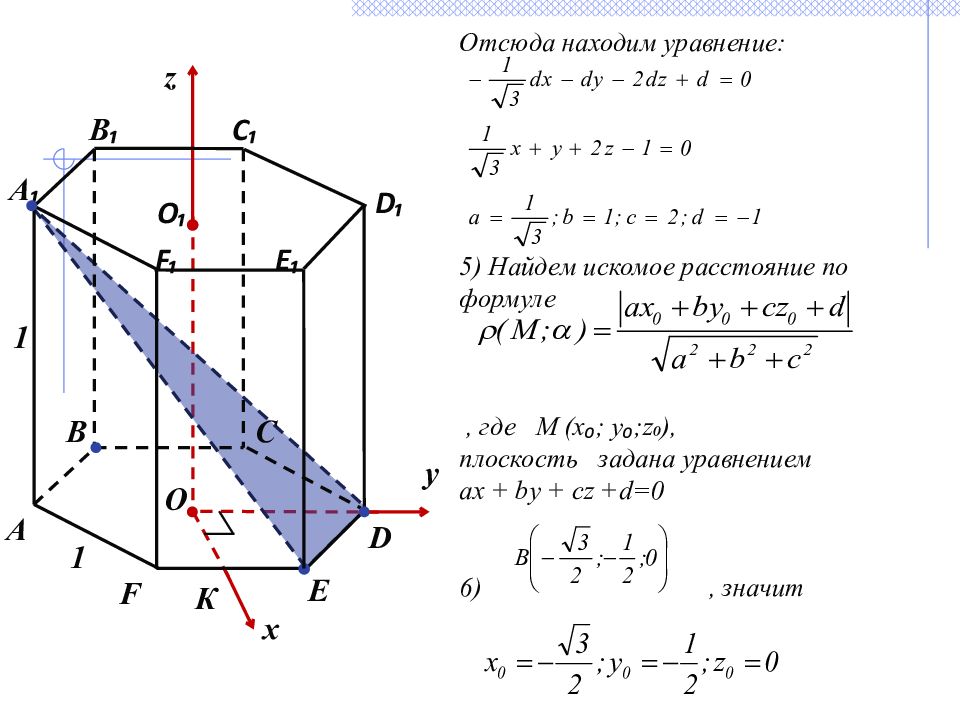
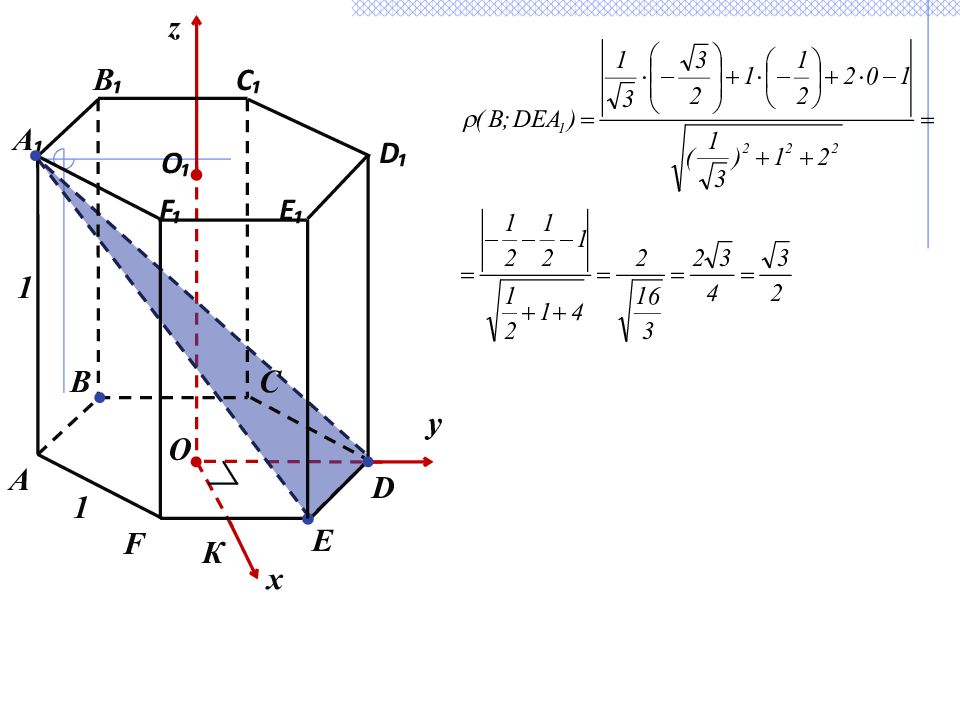
Отсюда находим уравнение: 5) Найдем искомое расстояние по формуле , где М ( х ₀ ; у ₀ ; z ₀ ), плоскость задана уравнением ах + by + cz +d=0 , значит x z y О О₁ B E B ₁ C ₁ F ₁ C D ₁ А 1 1 F E ₁ D А ₁ К
x z y О О₁ B E B ₁ C ₁ F ₁ C D ₁ А 1 1 F E ₁ D А ₁ К
