Динамика твердого тела Уравнения движения твердого тела Твердое тело – это тело, расстояния между точками которого не меняется. Твердое тело – механическая система с 6 степенями свободы для описания его движения требуется 6 скалярных уравнений или 2 векторных уравнения: – теорема о движении центра масс – уравнение моментов L, M – а) относительно неподвижного начала или центра масс; б) относительно подвижного начала с v = v C.
Динамика твердого тела Равновесие твердого тела Условия равновесия: M (e) = 0 относительно любого начала Равновесие балки 1 2 x 1 x 2 O центр масс
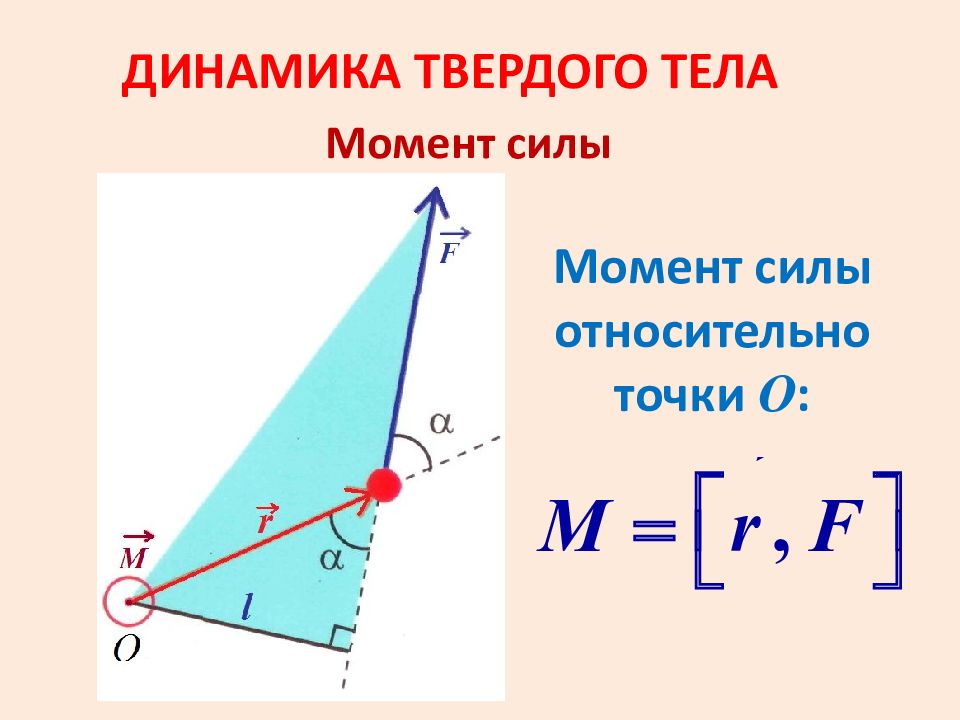
Динамика твердого тела Уравнение моментов относительно неподвижной оси O z – неподвижная ось (ось моментов) Уравнение моментов При проецировании на ось z – уравнение моментов относительно неподвижной оси В цилиндрической системе координат
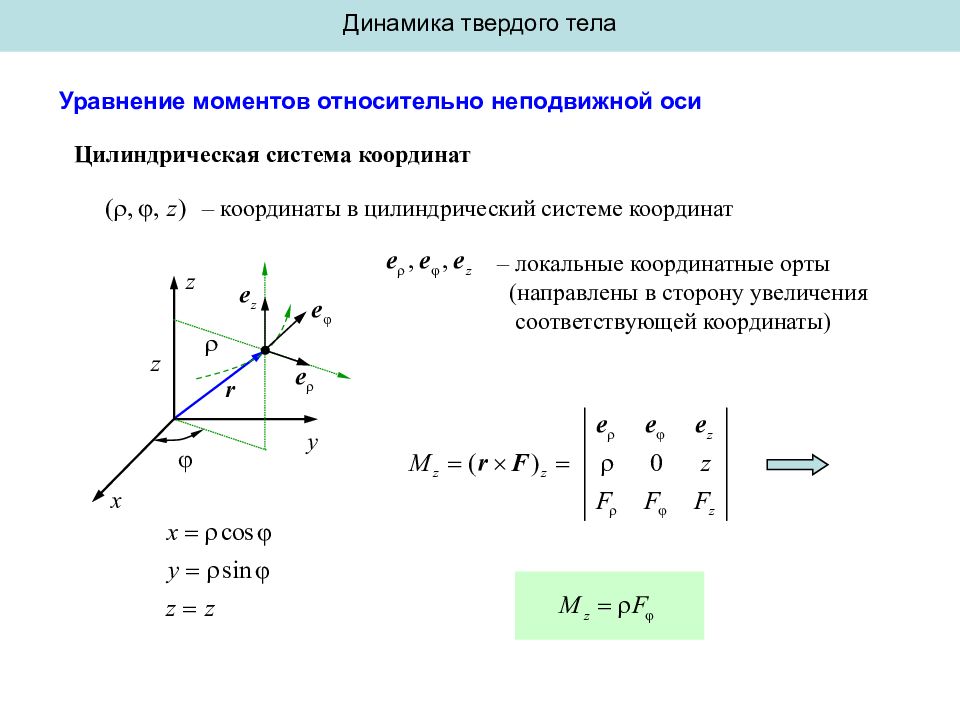
Динамика твердого тела Уравнение моментов относительно неподвижной оси Цилиндрическая система координат x y z – координаты в цилиндрический системе координат – локальные координатные орты (направлены в сторону увеличения соответствующей координаты)
Динамика твердого тела Уравнение динамики вращательного движения O – ось моментов – момент инерции ( характеризует инерционные свойства тела относительно данной оси вращения ) из уравнения моментов относительно неподвижной оси – уравнение динамики вращательного движения вокруг неподвижной оси M z – момент внешних сил относительно оси вращения
Динамика твердого тела Уравнение динамики вращательного движения Работа, совершаемая моментом силы Кинетическая энергия твердого тела при вращательном движении Кинетическая энергия твердого тела v C – скорость центра масс, I C – момент инерции относительно оси вращения, проходящей через центр масс
Динамика твердого тела Теорема Гюйгенса –Штейнера O A a, , ' – аксиальные вектора ось O || оси A Если O проходит через центр масс, то и – теорема Гюйгенса-Штейнера
Динамика твердого тела Вычисление моментов инерции Общая формула 1) Кольцо 2) Диск (цилиндр) Диск = система колец
Динамика твердого тела Вычисление моментов инерции 3) Сфера Сфера = система колец
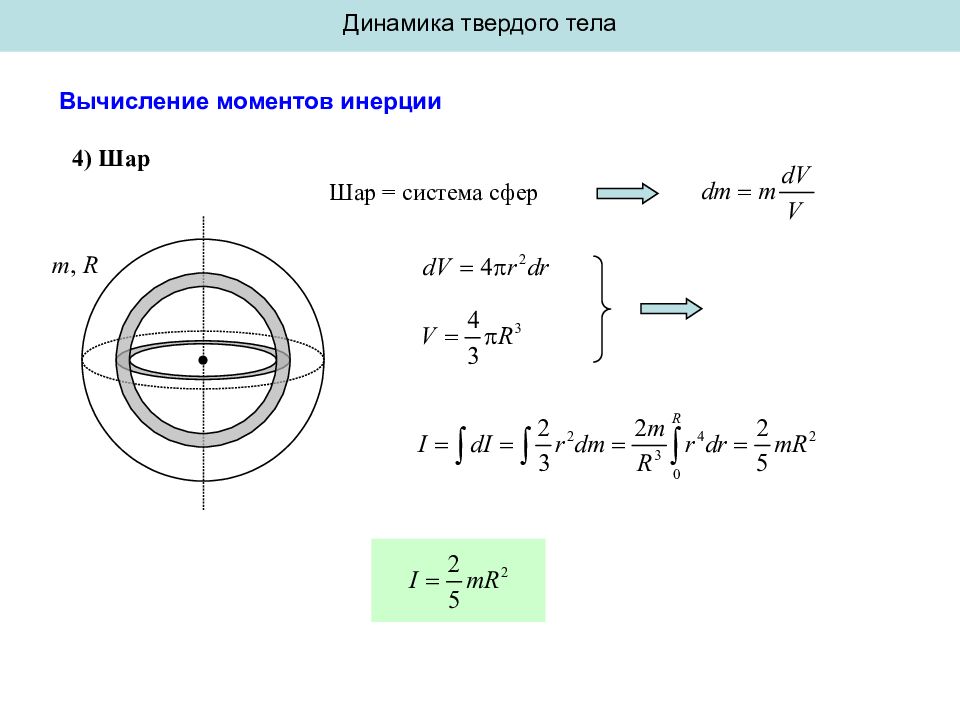
Динамика твердого тела Вычисление моментов инерции 4) Шар Шар = система сфер
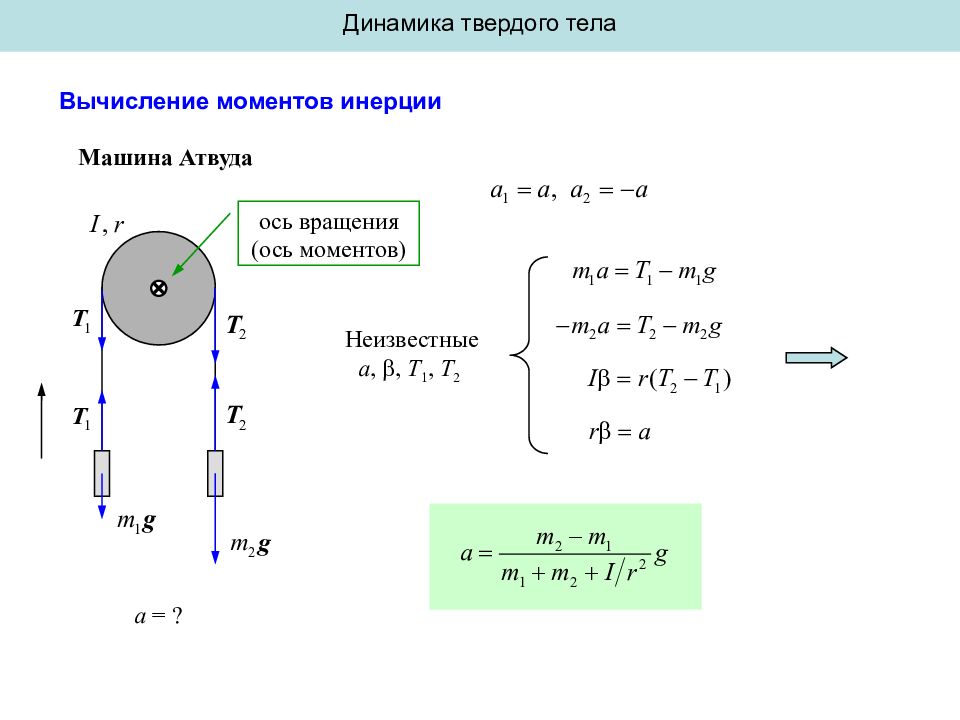
Динамика твердого тела Вычисление моментов инерции Машина Атвуда ось вращения (ось моментов) a = ? Неизвестные a, , T 1, T 2
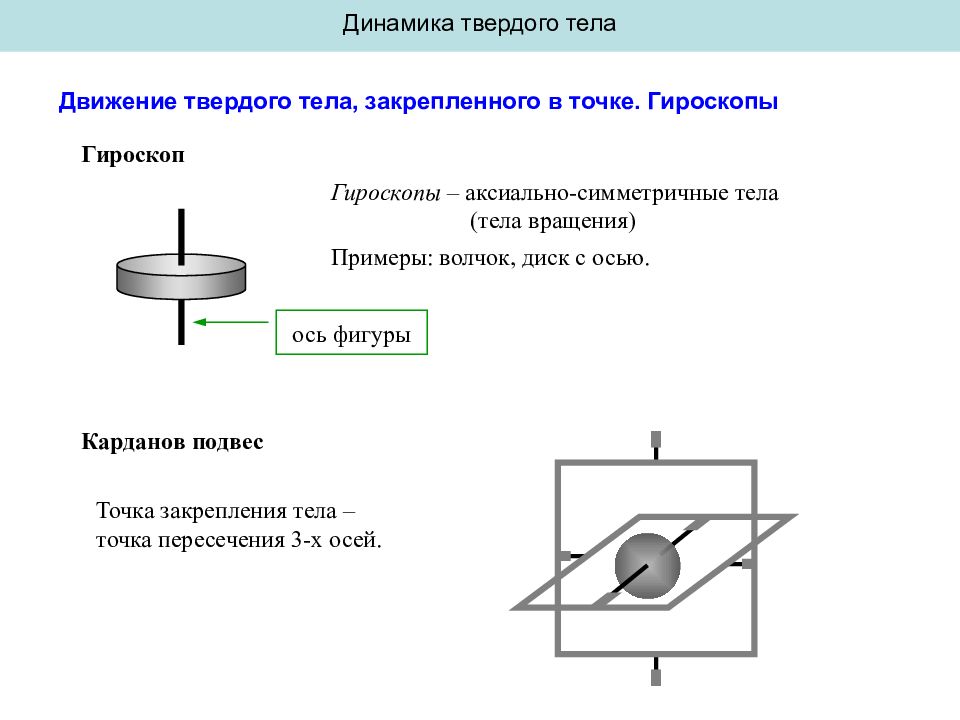
Динамика твердого тела Движение твердого тела, закрепленного в точке. Гироскопы Гироскоп Гироскопы – аксиально-симметричные тела (тела вращения) Примеры: волчок, диск с осью. ось фигуры Карданов подвес Точка закрепления тела – точка пересечения 3-х осей.
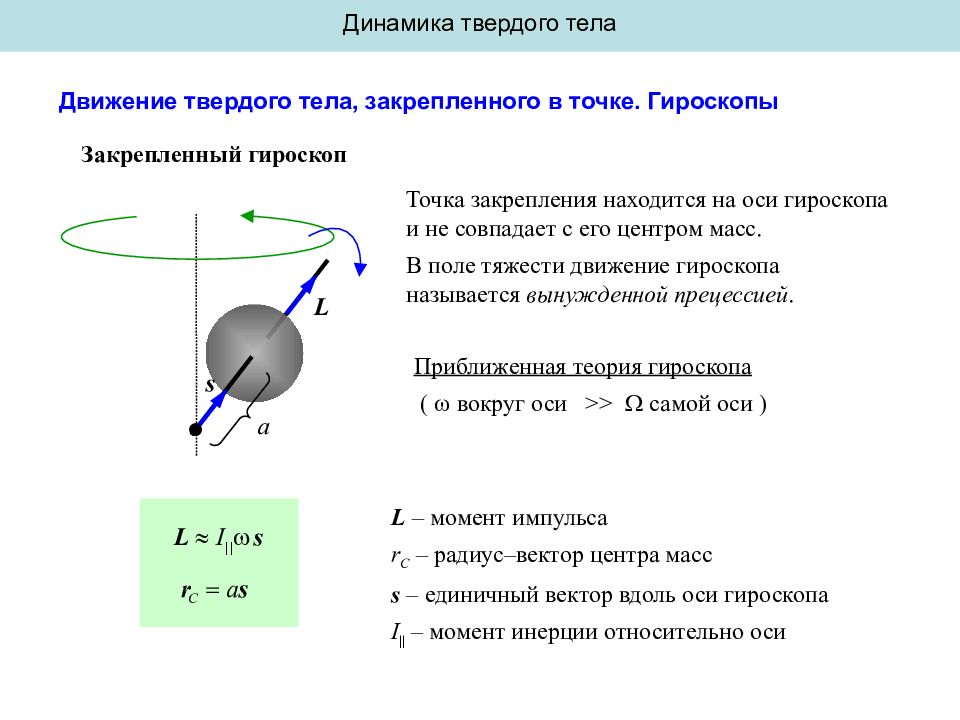
Динамика твердого тела Движение твердого тела, закрепленного в точке. Гироскопы Закрепленный гироскоп Точка закрепления находится на оси гироскопа и не совпадает с его центром масс. В поле тяжести движение гироскопа называется вынужденной прецессией. Приближенная теория гироскопа ( вокруг оси >> самой оси ) L – момент импульса r C – радиус–вектор центра масс s – единичный вектор вдоль оси гироскопа I || – момент инерции относительно оси
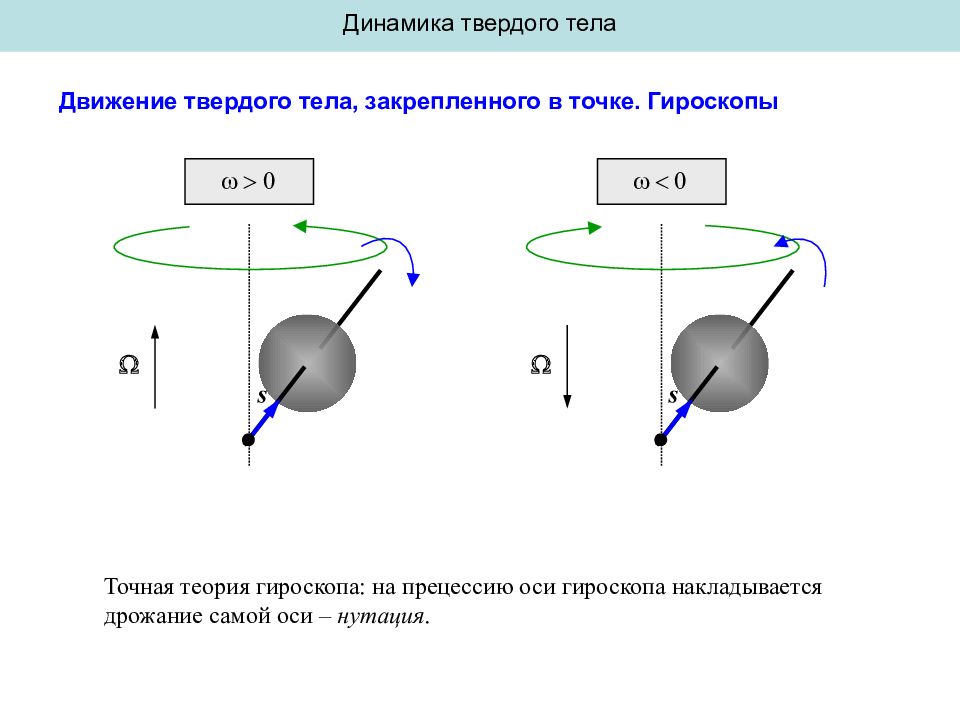
Динамика твердого тела Движение твердого тела, закрепленного в точке. Гироскопы = L Уравнение моментов для гироскопа Из аналогии – вращательного движения мат. точки Вектор L ( s ) вращается вокруг вертикальной оси с – момент сил, действующий на гироскоп
Динамика твердого тела Движение твердого тела, закрепленного в точке. Гироскопы Точная теория гироскопа: на прецессию оси гироскопа накладывается дрожание самой оси – нутация.
