Первый слайд презентации
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции относительно неподвижной оси Момент инерции материальной точки относительно оси, перпендикулярной плоскости её обращения МТ движется по окружности с угловой скоростью в плоскости, перпендикулярной оси ( z ), проходящей через центр окружности. Момент импульса МТ относительно точки О : Проекция момента импульса на ось z - момент инерции материальной точки относительно оси z. Момент инерции материальной точки относительно оси – это величина, равная произведению массы материальной точки на квадрат расстояния до оси вращения.
Слайд 2
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции относительно неподвижной оси Момент инерции материальной точки относительно оси перпендикулярной плоскости её обращения Можно момент импульса относительно оси представить в векторной форме: - орт, направленный по z. и сонаправлены (коллинеарны)
Слайд 3
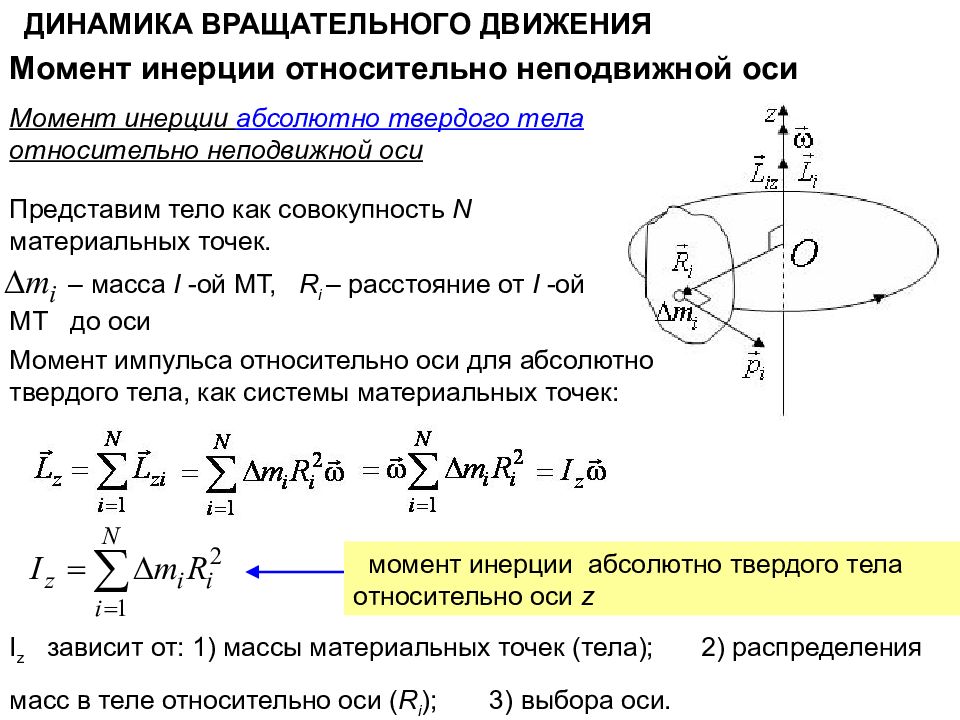
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции относительно неподвижной оси Момент инерции абсолютно твердого тела относительно неподвижной оси Представим тело как совокупность N материальных точек. – масса I -ой МТ, R i – расстояние от I -ой МТ до оси Момент импульса относительно оси для абсолютно твердого тела, как системы материальных точек: момент инерции абсолютно твердого тела относительно оси z I z зависит от: 1) массы материальных точек ( тела); 2) распределения масс в теле относительно оси ( R i ); 3) выбора оси.
Слайд 4
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции относительно неподвижной оси Момент инерции абсолютно твердого тела относительно неподвижной оси Выражение для момента инерции абсолютно твердого тела относительно неподвижной оси в интегральном виде. dm R i r - плотность. Для однородного по объему тела. Момент инерции твёрдого тела вычисляется интегрированием по объёму.
Слайд 5
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции относительно неподвижной оси Момент инерции зависит от формы тела и может изменяться. Если L z = const, то при изменении момента инерции, угловая скорость будет меняться Примеры: фигурное катание и т. п.
Слайд 6
Основное уравнение динамики вращательного движения ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Рассмотрим абсолютно твердое тело, вращающееся относительно неподвижной оси. Момент импульса тела относительно оси Возьмем производную по времени от обеих частей уравнения Под действием внешних сил и будут меняться. основное уравнение динамики вращательного движения момент инерции тела -мера инертности при вращательном движении (аналог массы).
Слайд 7
Примеры расчета момента инерции абсолютно твердого тела ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ 1. Тонкое кольцо, полый тонкостенный цилиндр. Найдём момент инерции относительно оси симметрии 2. Однородный диск, сплошной цилиндр. Найдём момент инерции относительно оси симметрии, проходящей через центр масс.
Слайд 8
Теорема Штейнера ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции тела относительно произвольной оси Z равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс этого тела, и произведения массы тела на квадрат расстояния между осями I z – искомый момент инерции тела относительно оси Z; I C - момент инерции тела относительно оси, параллельной оси Z и проходящей через центр масс тела – точку С ; d – расстояние между осями; m – масса тела.
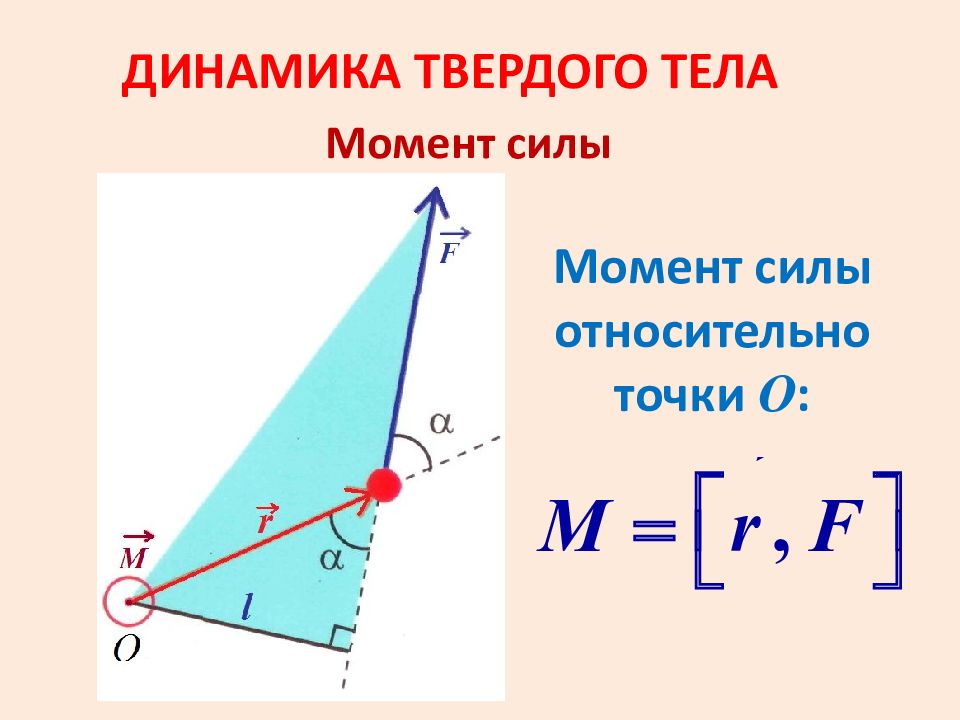
Последний слайд презентации: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции относительно неподвижной
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Момент инерции однородного стержня. 1. Момент инерции стержня относительно оси Z C, перпендикулярной стержню и проходящей через его центр ( центр масс). P азобьем стержень на элементарные участки длиной dr. 2. Момент инерции относительно оси Z, проходящей через конец стержня параллельной оси Z C. Согласно теореме Штейнера