Слайд 2: 6.2. Динамика твёрдого тела
6.2.1. Динамика поступательного движения. Внешние и внутренние силы. Для определения влияния взаимодействия тел на характер движения т.т. разделим, прежде всего, все силы, действующие на т.т. на два вида. Внутренние силы – это силы, действующие между частицами самого т.т.; и внешние силы – это силы, действующие на частицы твёрдого тела со стороны тел, не принадлежащих т.т.
Слайд 3: Второй закон Ньютона для т.т
Тогда для каждой частицы твёрдого тела можно написать второй закон Ньютона с учётом разделения сил на внутренние и внешние. . Верхний индекс здесь означает внешние силы, действующие на частицу твёрдого тела с номером, верхний индекс означает внутренние силы.
Слайд 4: Общее уравнение движения т.т
Просуммируем все такие уравнения по . Согласно третьему закону Ньютона сумма всех внутренних сил равна нулю. Сумму всех внешних сил обозначим просто. В первой сумме массу частицы поднесём под знак производной, а знак производной вынесем за знак суммы .
Слайд 5: Полный импульс т.т
Под знаком суммы стоит сумма импульсов всех частиц тела. Назовём эту сумму полным импульсом всего т.т. и обозначим, т.е. Тогда .
Слайд 6: Закон изменения полного импульса т.т
Это утверждение носит название закона изменения полного импульса т.т. Оно гласит. Скорость изменения полного импульса т.т. равна равнодействующей всех внешних сил, действующих на твёрдое тело. Внутренние силы не принимают участи в изменении полного импульса т.т.
Слайд 7: Р адиус-вектор центра масс
Т.к., то полный импульс т.т. можно представить как . Определение. Вектор, задаваемый формулой, называется радиусом-вектором центра масс, а сама точка с таким радиусом-вектором называется центром масс т.т.
Слайд 8: Полный импульс через радиус-вектор ц.м
С его помощью полный импульс системы можно записать так . Производная от радиус-вектора центра масс по времени, очевидно, есть скорость движения центра масс ,
Слайд 9: Полный импульс и скорость движения ц.м.т.т
поэтому полный импульс т.т. ещё можно представить так , а изменение полного импульса т.т. можно представить через скорость движения ц.м.
Слайд 10: Теорема о движении центра масс
Подставим это в закон изменения полного импульса. в этом виде он называется теоремой о движении центра масс т.т. и гласит: центр масс т.т. движется так же, как двигалась бы материальная точка, масса которой равна массе всего т.т. под действием силы, равной равнодействующей всех внешних сил, действующих на т.т.
Слайд 11: 6.2.2. Динамика вращательного движения
Для описания динамики вращательного движения нужно ввести понятие момента импульса т.т. Для этого выпишем снова уравнения Ньютона для всех частиц т.т. с использованием понятия импульса частиц и умножим их слева векторно на радиус-вектор соответствующей частицы:
Слайд 12: Суммирование законов Ньютона
Теперь просуммируем все эти уравнения почленно: *) В этом выражении первая сумма справа вновь равна нулю, согласно третьему закону Ньютона.
Слайд 13: Момент сил
Определение. Моментом силы называется векторное произведение радиуса вектора её точки приложения на саму силу. Значит, вторая сумма справа представляет собой суммарный момент всех внешних сил, действующих на т.т. Обозначается момент сил.
Слайд 14: Момент сил
Из определения момента сил следует: 1. Момент силы – векторная величина, её направление определяется правилом буравчика. 2. Размерность:
Слайд 15: Преобразование левой части равенства
В выражении слева от равенства воспользуемся формулой . Но последнее слагаемое справа равно нулю в силу коллинеарности перемножаемых векторов. Поэтому (*) приобретает вид .
Слайд 16: Момент импульса
Определение. Моментом импульса материальной точки называется величина, равная векторному произведению радиуса-вектора материальной точки на её импульс. Обозначается.
Слайд 17: Замечание
Момент импульса учитывает с одной стороны скорость вращения т.т., а с другой его массу и её распределение относительно оси вращения.
Слайд 18: Следствия из определения момента импульса
Момент импульса, как видно из определения, есть векторная величина. Его направление определяется снова векторным произведением и значит правилом правого винта. Т.е. если буравчик вращать через меньший угол от радиус-вектора точки к её импульсу, вкручивание буравчика покажет направление момента импульса.
Слайд 19: Полный момент импульса т.т
А вся сумма моментов импульса частиц т.т. называется полным моментом импульса т.т. и обозначается. Это тоже векторная величина, но её направление определяется геометрической суммой векторов её составляющих.
Слайд 20: Теорема о полном моменте импульса
Тогда . Это утверждение называется теоремой о полном моменте импульса твёрдого тела или теоремой о кинетическом моменте т.т. Оно гласит: Скорость изменения полного момента импульса т.т. равна полному моменту всех внешних сил, действующих на т.т.
Слайд 21: Вращение т.т
Предположим, что т.т. может вращаться около неподвижной оси. Найдём момент импульса такого т.т. .
Слайд 22: Формула двойного векторного произведения
В последнем выражении воспользовались формулой скоростей т.т., выбрав точку О на оси вращения. Тогда её скорость равна нулю. Теперь воспользуемся формулой двойного векторного произведения .
Слайд 23: Момент импульса т.т
Тогда момент импульса т.т. может быть представлен так: Выберем ось направленной вдоль оси вращения и спроецируем на эту ось момент импульса т.т. При этом нужно иметь ввиду, что
Слайд 24: Проекция момента импульса т.т
- расстояние от данной точки т.т. до оси вращения по перпендикуляру. Т.к. в последнем равенстве угловая скорость одинакова для всех точек т.т., то её можно вынести за знак суммы .
Слайд 25: Момент инерции точки
Определение. Моментом инерции м.т. Называется величина, численно равная произведению массы материальной точки на квадрат расстояния до оси вращения. Эта величина является аналогом понятия массы для поступательного движения. Она показывает насколько трудно раскрутить данную точку относительно оси вращения.
Слайд 26: Размерность момента инерции
Эта величина зависит не только от массы точки, но и от расстояния её до оси вращения. Измеряется момент инерции в единицах массы, умноженных на квадрат расстояния до оси вращения. Обозначается момент инерции точки. Т.о..
Слайд 27: Момент инерции т.т
Вся сумма при этом называется моментом инерции т.т. и обозначается. . Эта величина показывает, насколько трудно раскрутить т.т. вокруг данной оси. Определяется не только полной массой т.т., но и распределением её относительно оси вращения.
Слайд 28: Закон изменения момента импульса т.т
С помощью понятия момента инерции проекцию момента импульса на ось вращения можно записать так . Если т.т. вращается вокруг оси, формулу теоремы о моменте импульса можно записать в проекции на эту ось . Здесь - проекция результирующего момента внешних сил на ось вращения.
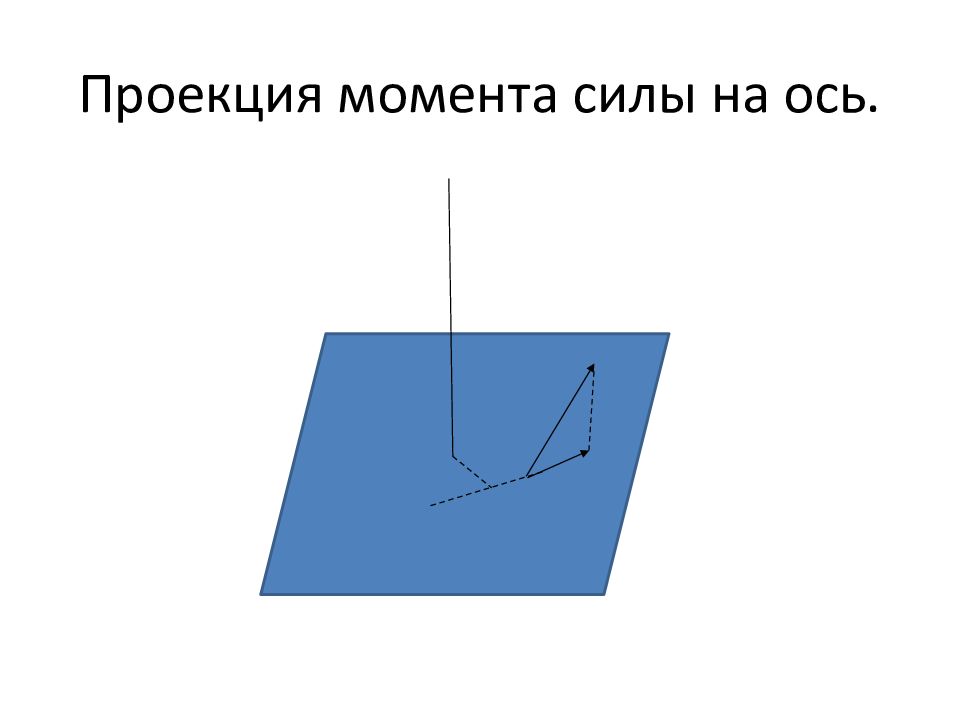
Слайд 29: Плечо силы
Для отыскания проекции момента некоторой силы на некоторую ось нужно спроецировать силу на плоскость, перпендикулярную оси, и умножить величину этой проекции на расстояние от оси до линии-проекции силы на плоскость, перпендикулярную оси. Это расстояние называется плечом силы. Т.о. проекция момента силы на ось равна произведению проекции этой силы на плоскость, перпендикулярную оси, на её плечо.
Слайд 31: Основное уравнение динамики вращательного движения т.т
С помощью понятия момента инерции закон изменения момента импульса можно записать так: . Согласно определению - угловое ускорение т.т., поэтому .
Слайд 32: Аналог второго закона Ньютона
Это равенство носит название основного уравнения динамики вращательного движения и выполняет роль второго закона Ньютона для вращения. Позволяет найти угловое ускорение, а через него и остальные кинематические характеристики вращения, если известны моменты сил, действующих на тело.
Слайд 33: Формулировка основного уравнения динамики вращательного движения т.т
Произведение момента инерции т.т. На проекцию углового ускорения на ось вращения, равно проекции момента всех внешних сил на ось вращения. Или. Угловое ускорение прямо пропорционально моменту внешних сил и обратно пропорционально моменту инерции тела.
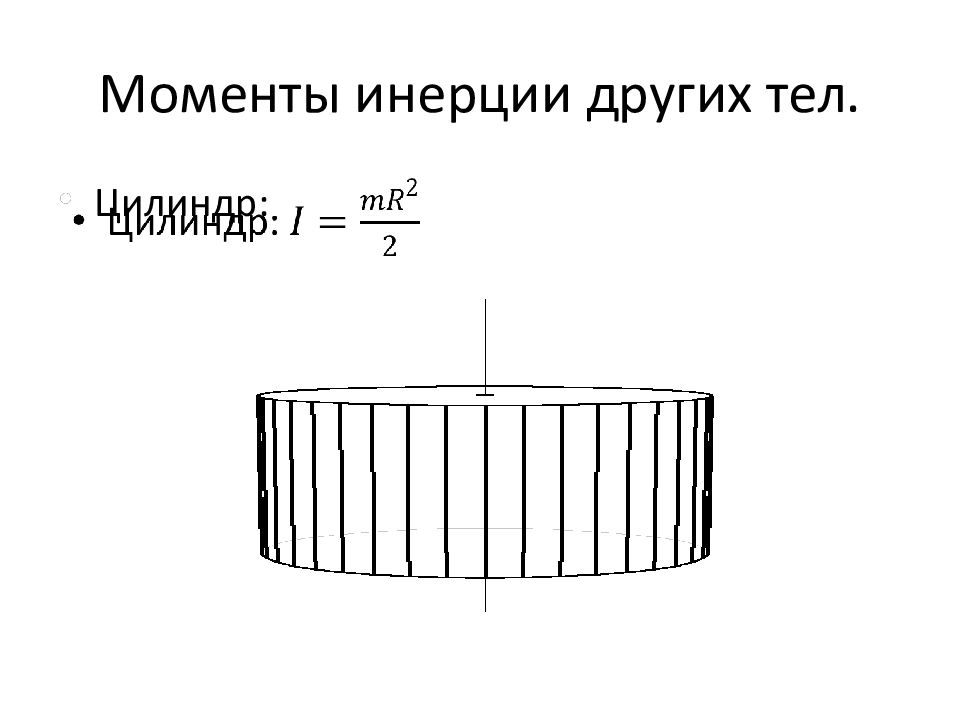
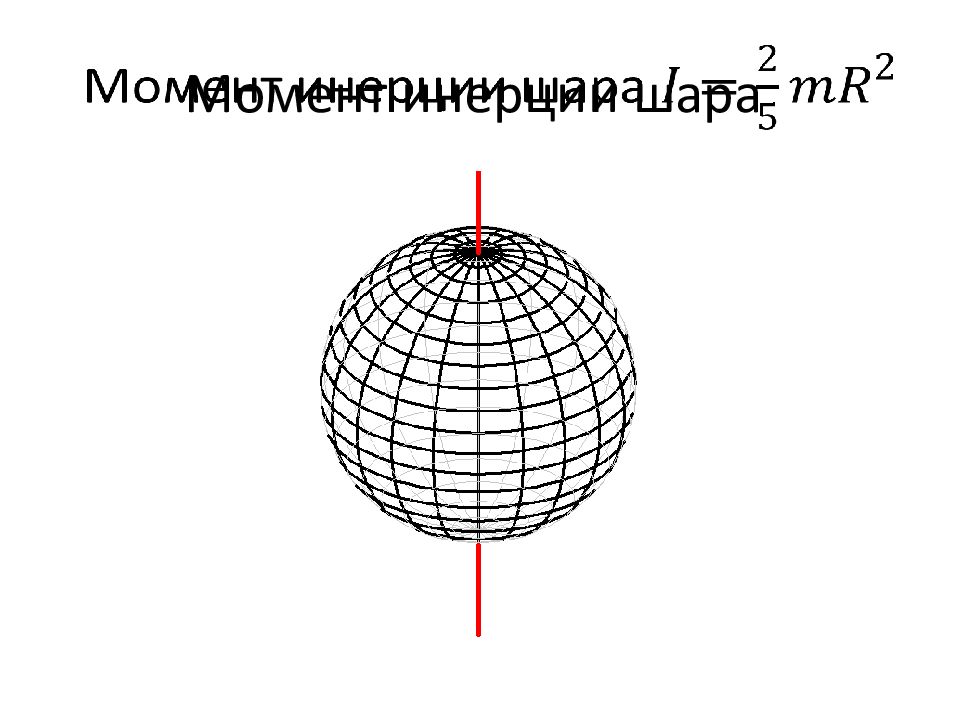
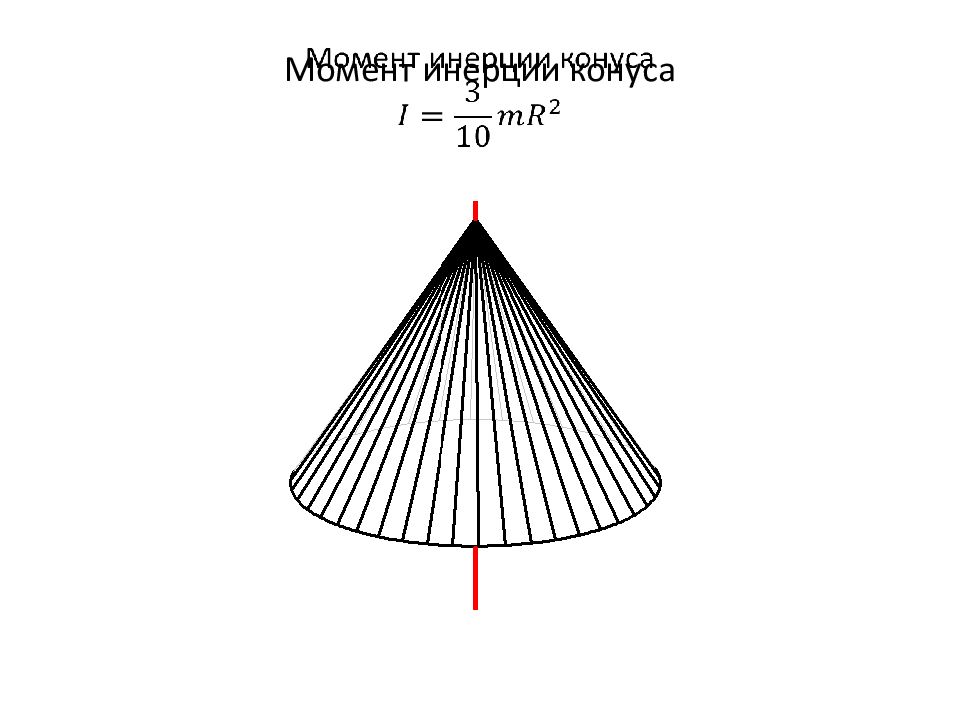
Слайд 35: 6.2.3. Моменты инерции различных тел
Для использования основного уравнения динамики вращательного движения необходимо знать моменты инерции различных тел. Для вычисления моментов инерции тел нужно использовать суммирование по всем частицам т.т. Но поскольку для реальных т.т. частицы, их составляющие, намного меньше самих тел, суммирование можно заменить интегрированием, считая, что масса частицы – это элемент массы т.т. . При этом интегрирование выполняется по всему объёму тела.
Слайд 36: Расчёт момента инерции с помощью плотности т.т
Если ввести понятие плотности т.т. ,то момент инерции можно вычислять по формуле . (3.2.26) Плотность т.т. есть величина скалярная и измеряется в единицах массы, делённых на единицу объёма.
Слайд 37: Момент инерции т.т. плоской формы
В том случае, когда тело имеет плоскую форму (один из размеров на много меньше остальных) и вращается вокруг оси, перпендикулярной этой плоскости, интеграл упрощается. В этом случае вместо тройного интеграла нужно искать двойной. Но в этом случае нужно использовать т.н. поверхностную плотность – массу единицы площади тела ,которая измеряется в единицах массы, делённых на единицу площади. Тогда и .
Слайд 38: Момент инерции т.т. линейной формы
Если же т.т. имеет линейную форму (два размера много меньше третьего), то при нахождении момента инерции нужно находить лишь одинарный интеграл, но при этом использовать понятие линейной плотности, как массы единицы длины т.т. ,измеряется линейная плотность в единицах массы, делённых на единицу длины. Тогда элемент массы можно выразить через элемент длины, а момент инерции через интеграл .
Слайд 39: Момент инерции кольца
Найдём таким образом момент инерции тонкого кольца относительно оси, проходящей через его центр, перпендикулярно плоскости. Пусть масса кольца, его радиус. Тогда линейная плотность кольца ,а момент инерции .
Слайд 40: Момент инерции стержня
Найдём теперь момент инерции стержня относительно оси, проходящей через его середину, перпендикулярно его длине. Масса стержня, его длина, поэтому линейная плотность равна,а момент инерции . В этом интеграле это расстояние от оси вращения до элемента массы т.т.
Слайд 42: Теорема Штейнера
Найдём разницу между этим результатом и предыдущим. Получим, что эта разница равна. Но величина есть расстояние между осями, относительно которых находились моменты инерции одного и того же тела. Этот результат имеет общий характер и выражает т.н. теорему Штейнера, которая гласит: «Момент инерции тела относительно произвольной оси равен моменту инерции тела относительно оси, проходящей через его центр масс, параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями», т.е. .
Слайд 43: Обозначения в теореме Штейнера
Здесь - момент инерции тела относительно произвольной оси, - момент инерции тела относительно оси, проходящей через центр масс тела, параллельно данной оси и - расстояние между осями.