Лектор: Юлия Абдулловна Ахкамова, доцент кафедры математики и методики обучения математике ЮУрГГПУ akhkamovayua@cspu.ru
Он- лайн 1 лекции 5 баллов ( max 1*5= 5 ) ; 3 лаб. занятия по 5 баллов( max 3*5=1 5 ); Контрольная работа №1 задачи 1,3а,б.в,8 ( max 60); Защита-обсуждение занятий или кр (электронного варианта) max 10 баллов); Зачетная работа до 20 баллов. 60 баллов и выше «Зачтено»,
3.Учебный вопрос. Метод Гаусса систем линейных алгебраических уравнений.
Карл Фридрих Гаусс (30.04.1777-23.02.1855) Немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков». Иностранный член Шведской и Российской Академий наук, английского Королевского общества.
Рассмотрим систему m линейных алгебраических уравнений с n неизвестными. Расширенной матрицей системы называется основная матрица с приписанным справа столбцом свободных членов:
Напомним, элементарными преобра-зованиями строк матрицы называются: 1) перемена местами двух строк матрицы; 2) умножение строки на любое ненулевое число; 3) прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на некоторое число; 4) вычеркивание нулевой строки.
Напомним, р ангом матрицы размерности m×n называется количество ненулевых строк в эквивалентной ей ступенчатой матрице. Ступенчатая матрица получена из исходной с помощью элементарных преобразований строк.
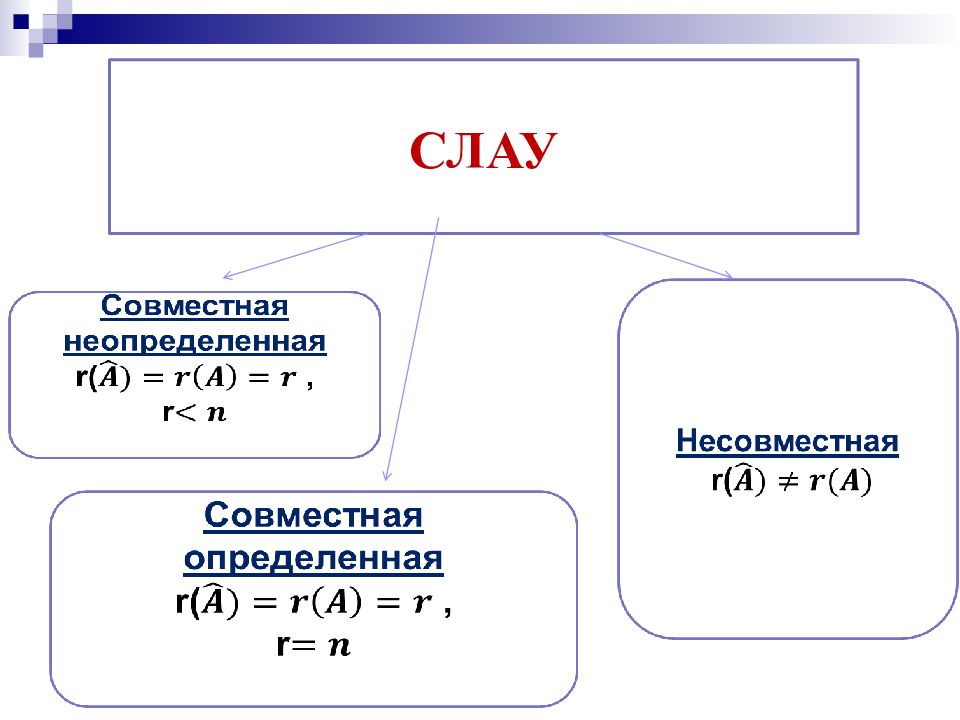
Определение. Две системы линейных алгебраических уравнений называются эквивалентными или равносильными, если они имеют одно и то же множество решений.
Метод Гаусса. В отличие от матричного метода и метода Крамера метод Гаусса может быть применен к СЛАУ с произвольным числом уравнений и неизвестных. Суть метода Гаусса заключается в последовательном исключении неизвестных.
Алгоритм решения систем линейных уравнений методом Гаусса.
1)Расширенную матрицу системы с помощью элементарных преобразований приводим к ступенчатому виду. 2)Отбрасываем нулевые строки. 3) Применяем следующую теорему: Теорема Кронеккера-Капелли: При совпадении рангов расширенной и основной матриц СЛАУ совместна; при равенстве ранга с числом неизвестных СЛАУ определена.
СЛАУ
Если система имеет единственное решение, то, двигаясь по системе снизу вверх, последовательно находим значения неизвестных. Если система имеет бесконечное множество решений, то сначала выделяем базисные неизвестные.
4) Неизвестная, соответствующая столбцу, в котором стоит первый ненулевой элемент данной строки, является базисной. Остальные неизвестные – свободные. 5) Двигаясь по системе снизу вверх, последовательно выражаем базисные неизвестные через свободные.
Пример. Решить систему методом Гаусса. Решение. –2 –1 –2 3 + +
+ 1 / 5
однородная неоднородная СЛАУ
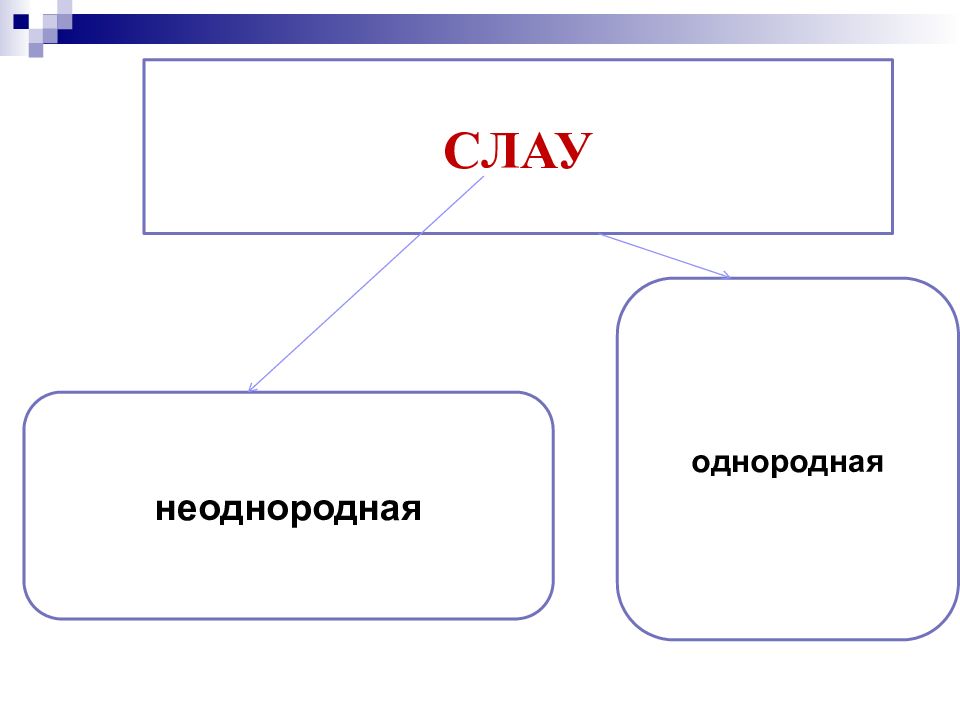
Система линейных алгебраических уравнений называется однородной СЛАУ, если свободный член в каждом уравнении равен нулю. Пример. однородной системы линейных уравнений Однородная система всегда совместна.
Очевидно, что x 1 = x 2 =…= x n =0 – нулевое или тривиальное решение однородной системы. Кроме тривиального, система может иметь и другие решения (нетривиальные).
Данко П.Е., др. Высшая математика в упражнениях и задачах, часть I, с.39-43, 70-79. Контрольная работа №1 задания 1;(3а,3б);3в;8.
