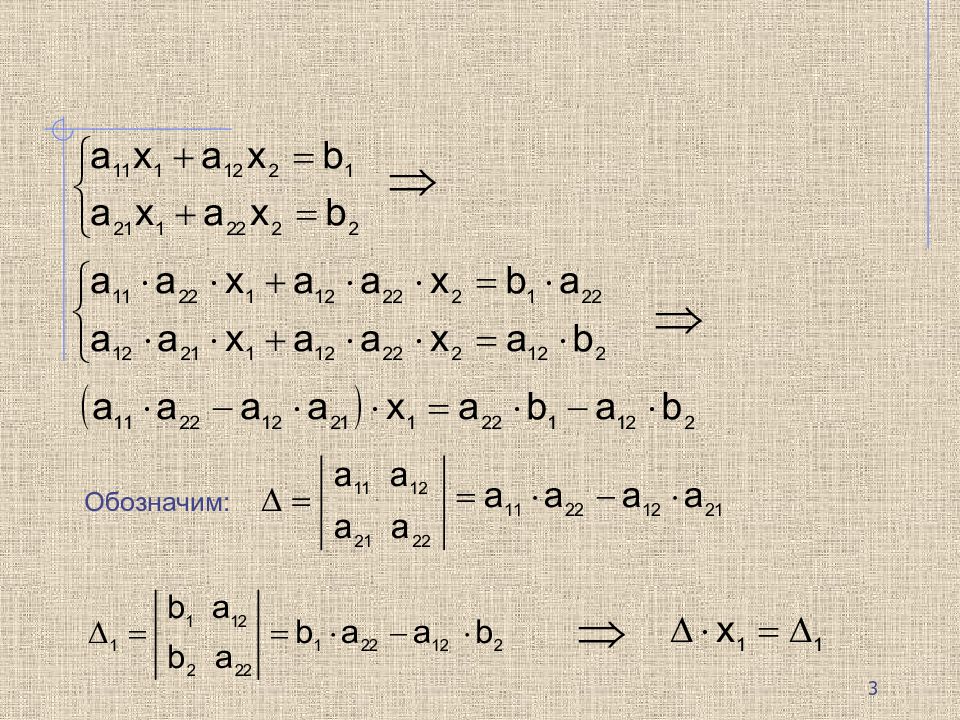Первый слайд презентации: Тема 3. Системы линейных уравнений
Системы из двух линейных уравнений с двумя неизвестными Системы из n линейных уравнений с n неизвестными. Метод Крамера Метод обратной матрицы решения систем линейных уравнений Метод Гаусса решения систем линейных уравнений 1
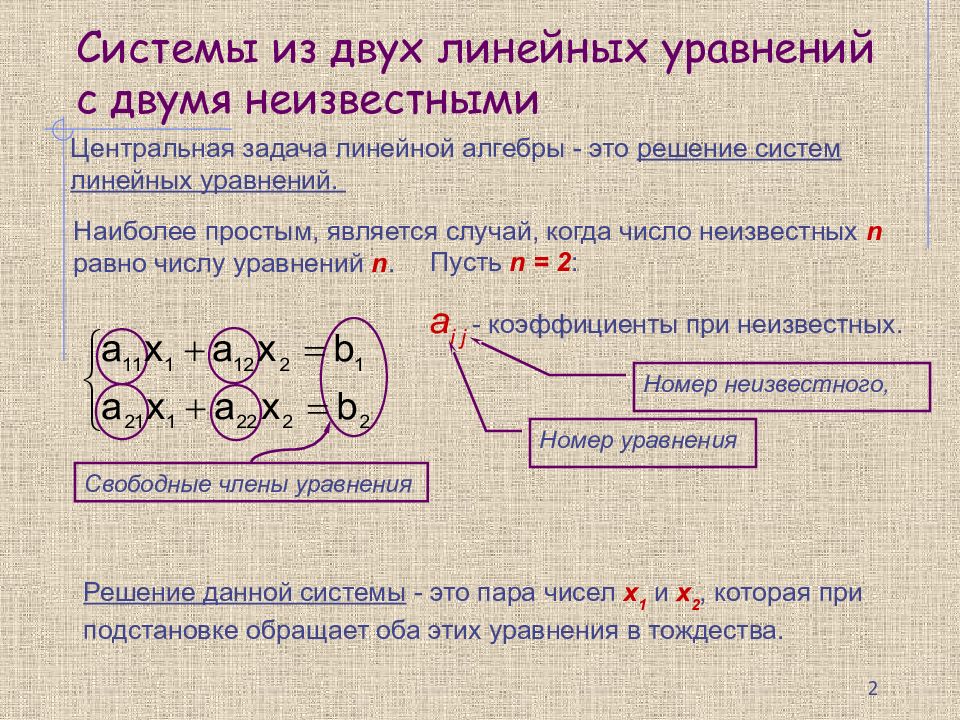
Центральная задача линейной алгебры - это решение систем линейных уравнений. Решение данной системы - это пара чисел х 1 и х 2, которая при подстановке обращает оба этих уравнения в тождества. Свободные члены уравнения Н аиболее простым, является случай, когда число неизвестных n равно числу уравнений n. Пусть n = 2 : a i j - коэффициент ы при неизвестных. Номер уравнения Номер неизвестного, 2
Слайд 4
Аналогично получим: обозначив: Система уравнений будет иметь вид: Если, то решение системы находится по формулам: Формулы Крамера Главный определитель системы Вспомогательные определители системы 4
Слайд 5
Решить систему методом Крамера: Вычислим главный и вспомогательные определители системы: Найдем решение системы по формулам Крамера: 5
Слайд 6: Системы из n линейных уравнений с n неизвестными
Рассмотрим общую квадратную систему линейных уравнений: Система линейных уравнений называется совместной, если она имеет решение и несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесконечное множество решений. Система называется однородной, если Однородная система совместна, так как всегда имеет нулевое решение. 6
Слайд 7: Метод Крамера
Для сокращения выкладок запишем систему из трех уравнений с тремя неизвестными: Вспомогательные определители получаются из главного определителя, если заменить соответствующий столбец столбцом свободных членов: 7
Слайд 8
По величине главного и вспомогательных определителей можно судить о характере системы: Если то система совместна и определенна. Если то система совместна и неопределенна. Если, но или или то система несовместна. В общем случае будем иметь n +1 определителей n – ого порядка и, если, то решение системы находится по формулам Крамера: 8
Слайд 9: Метод обратной матрицы решения систем линейных уравнений
Тогда систему можно записать так: Найдем решение системы в матричном виде. Предположим, что det A отличен от нуля и, следовательно, существует обратная матрица А -1. Умножим слева матричную запись системы на обратную матрицу: Метод обратной матрицы применим для решения квадратных систем с невырожденной основной матрицей. 9
Рассмотрим задачу решения системы линейных уравнений размерностью (m x n). Запишем систему в матричном виде : Е сли закрепить раз и навсегда нумерацию неизвестных, то можно опустить неизвестные в записи системы и записать ее в виде матрицы, отделяя столбец свободных членов вертикальной чертой. Расширенная матрица системы 11
Слайд 12
12 Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные. Переход системы к равносильной ей системе называется прямым ходом метода Гаусса, а нахождение переменных из системы – обратным ходом.
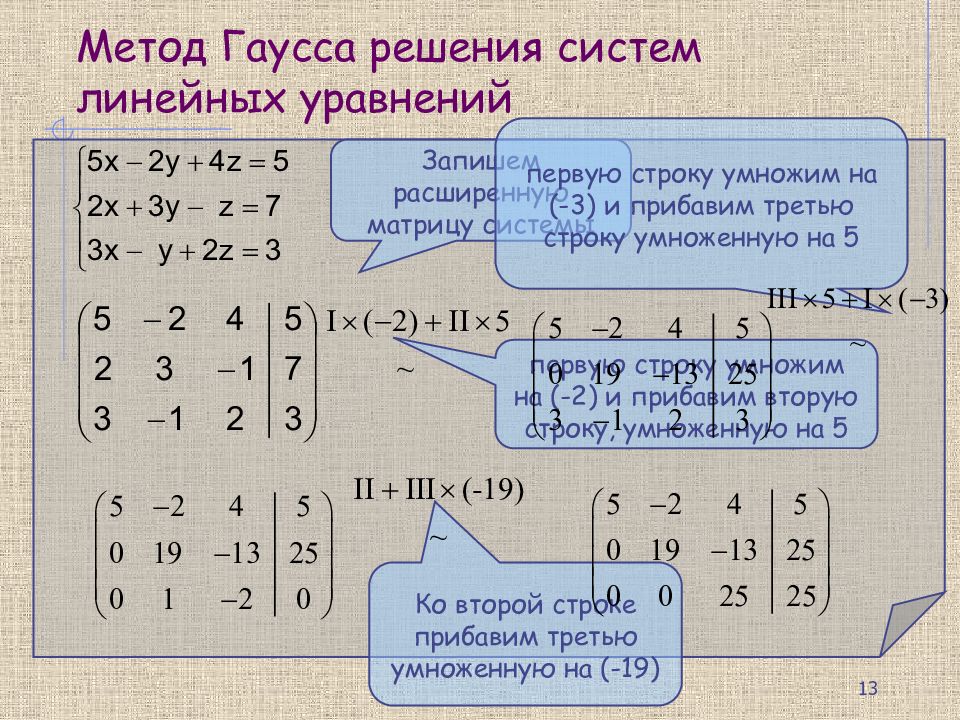
Слайд 13: Метод Гаусса решения систем линейных уравнений
Запишем расширенную матрицу системы первую строку умножим на (-2) и прибавим вторую строку, умноженную на 5 первую строку умножим на (-3) и прибавим третью строку умноженную на 5 Ко второй строке прибавим третью умноженную на (-19) 13