Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля
В теории многочленов часто двучлены называют биномами. Вычислите: ( a+b ) 0 ( a+b ) 1 ( a+b ) 2 ( a+b ) 3 ( a+b ) 4
( a+b ) 0 =1 ( a+b ) 1 = a+b ( a+b ) 2 =a 2 +2ab+b 2 ( a+b ) 3 =a 3 +3a 2 b+3ab 2 +b 3 ( a+b ) 4 =a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4 Коэффициенты при a и b запишем в виде треугольника.
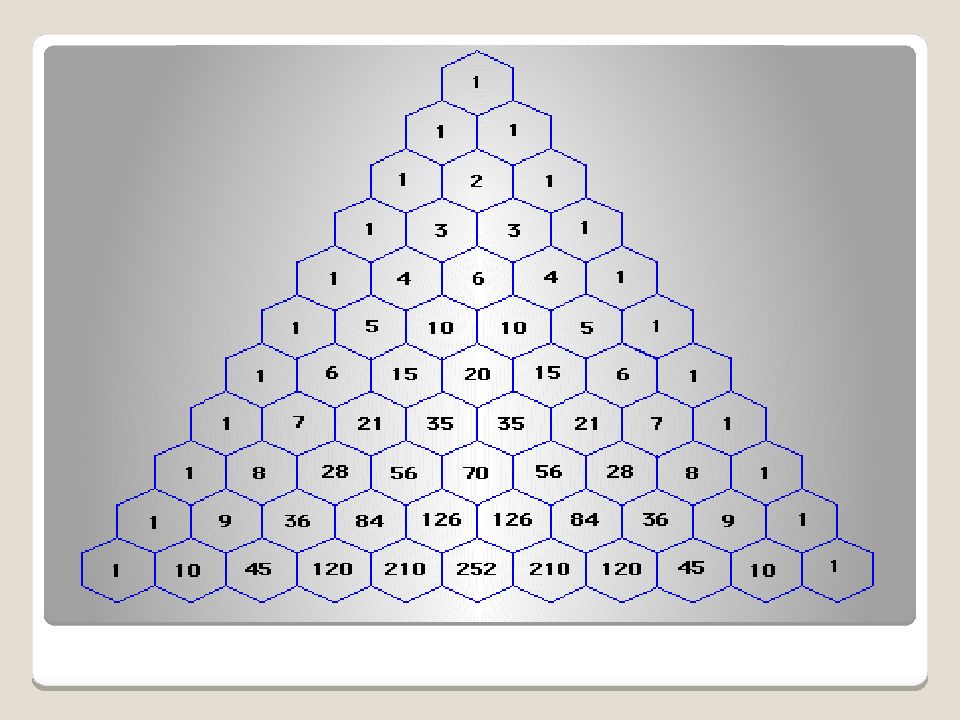
Треугольник Паскаля – Это бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается как сумма двух предшествующих чисел.
Постройте треугольник Паскаля для:
Формула бинома Ньютона – для всех действительных чисел a, b и для всех натуральных чисел n : называют биномиальными коэффициентами, а так же числом сочетаний n элементов по k.
Свойства биномиальных коэффициентов. Биномиальный коэффициент – коэффициент при смежных Z в разложении бинома Ньютона. ( a + b ) n, где Z = a k b n - k. 1 свойство : свойство симметрии: 2 свойство: свойство сложения: 3 свойство: 4 свойство: 5 свойство: – это равенство формулы бинома Ньютона.
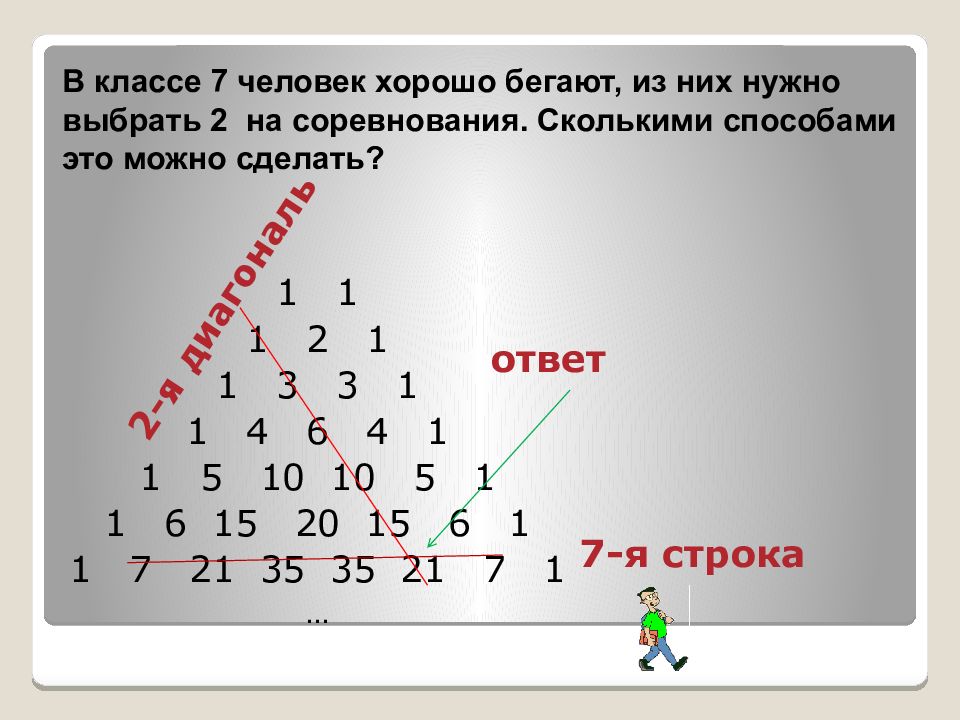
1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 … В классе 7 человек хорошо бегают, из них нужно выбрать 2 на соревнования. Сколькими способами это можно сделать? 7-я строка 2-я диагональ ответ
Запишите разложение бинома (х-2) 6
Запишите разложение бинома (х-2) 6
