Функция. Функцияның графигі
Сабақтың мақсаты 7.5.1.1функция және функцияның графигі ұғымдарын біледі; 7.5.1.2 функцияның берілу тәсілдерін біледі; 7.5.1.4 функционалды және функционалды емес тәуелділіктерді танып біледі; 7.5.1.3 функцияның анықталу облысы және мәндер жиынын анықтайды.
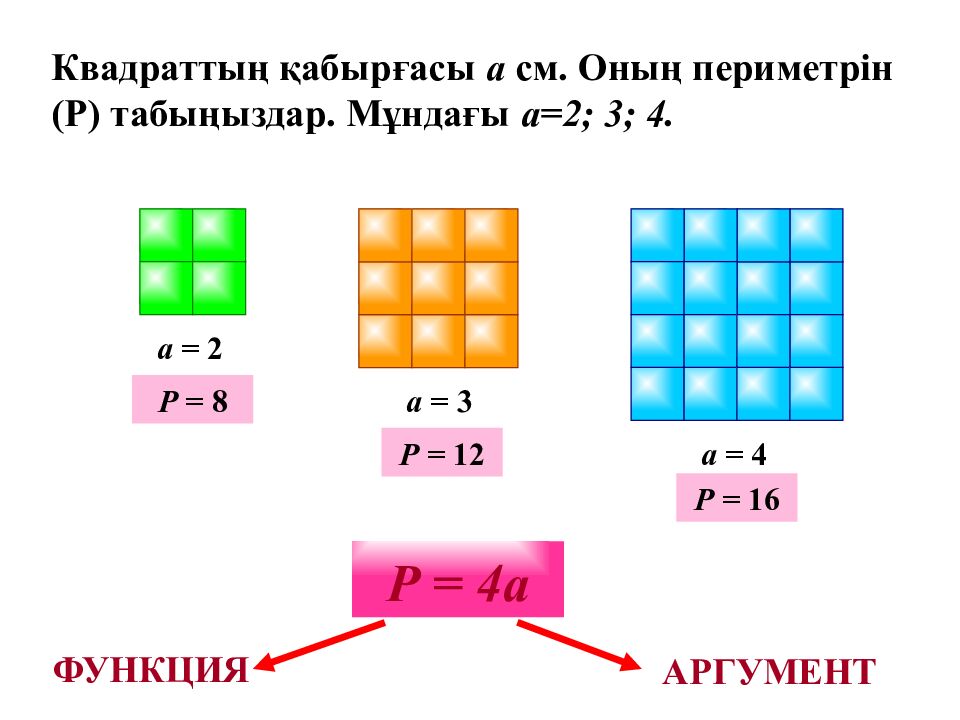
Квадраттың қабырғасы a см. Оның периметрін (Р) табыңыздар. Мұндағы а =2 ; 3; 4. a = 2 a = 3 a = 4 Р = 4 a Р = 8 Р = 12 Р = 16 ФУНКЦИЯ АРГУМЕНТ
Машина 70 км/сағ жылдамдықпен қозғалып келеді. Машинаның t сағатта қанша жол жүретінін табыңыздар. Мұндағы t = 1 ; 1,5; 3. Машина t сағатта S = 70 · t км жол жүреді. Кез-келген уақыттағы жүрілген жолды оңай анықтауға болады: Егер t = 1, онда Егер t = 1,5, онда Егер t = 3, онда S = 70 · 1 = 70 S = 70 · 1,5 = 105 S = 70 · 3 = 210 S = 70 · t Тәуелсіз айнымалы АРГУМЕНТ Тәуелді айнымалы ФУНКЦИЯ
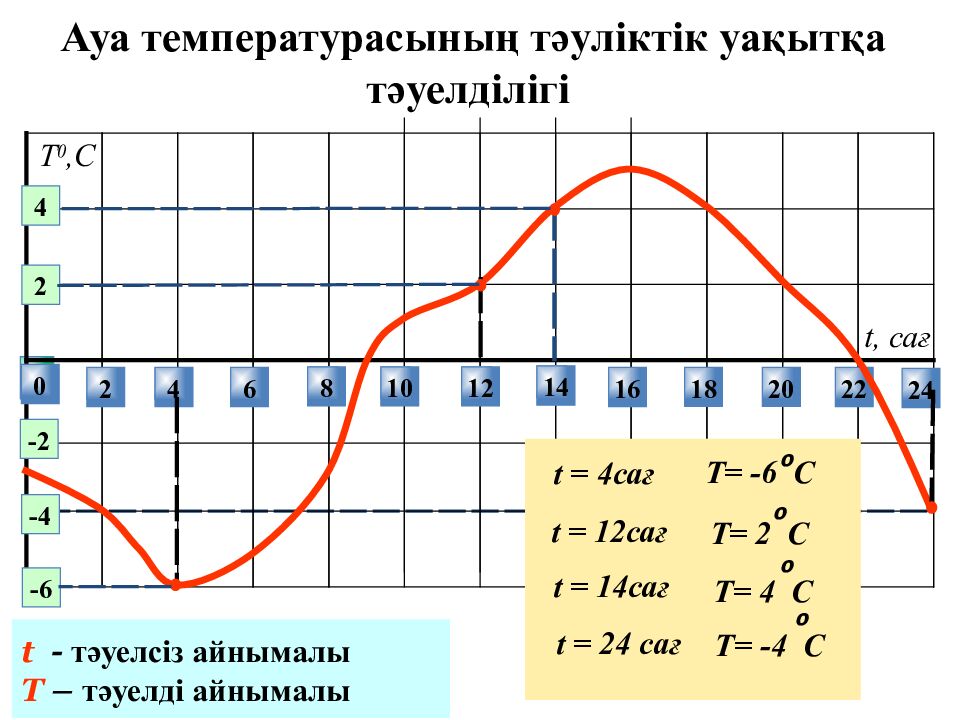
Ауа температурасының тәуліктік уақытқа тәуелділігі 0 2 4 6 8 10 12 14 22 24 16 18 20 t, сағ 2 4 -2 -6 -4 Т 0,С t = 4сағ Т= -6 С о t = 12сағ Т= 2 С о t = 14сағ Т= 4 С о t = 24 сағ Т= -4 С о t - тәуелсіз айнымалы T – тәуелді айнымалы
Натурал сандар квадратының кестесі: х 6 7 8 9 10 у = х 2 х 1 2 3 4 5 у = х 2 1 4 9 16 25 36 49 64 81 100 Әрбір х мәніне тек бір ғ ана у мәні сәйкес келеді. у = х 2 АРГУМЕНТ ФУНКЦИЯ
Қарастырылған тапсырмаларда тәуелсіз айнымалының әрбір мәніне тәуелді айнымалының тек бір мәні сәйкес келетінін байқауға болады. Тәуелсіз айнымалының әрбір мәніне тәуелі айнымалының тек бір ғана мәні сәйкес келетін тәуелділікті функционалдық тәуелділік немесе функция деп атайды. Функциияның анықтамасы
Функцияның анықталу және мәндерінің аймағы. Машина 70 км/сағ жылдамдықпен қозғалып келеді. Машина t сағат уақытта S = 70 · t км жол жүреді. t қандай мәндер қабылдауы мүмкін? S қандай мәндер қабылдауы мүмкін? t ≥ 0 S ≥ 0 Тәуелсіз айнымалының қабылдайтын мәндерінің жиыны функцияның анықталу аймағы деп аталады. Белгіленуі: D ( f ) Функцияның мәндерінің жиыны функцияның мәндерінің аймағы деп аталады. Белгіленуі: Е ( f )
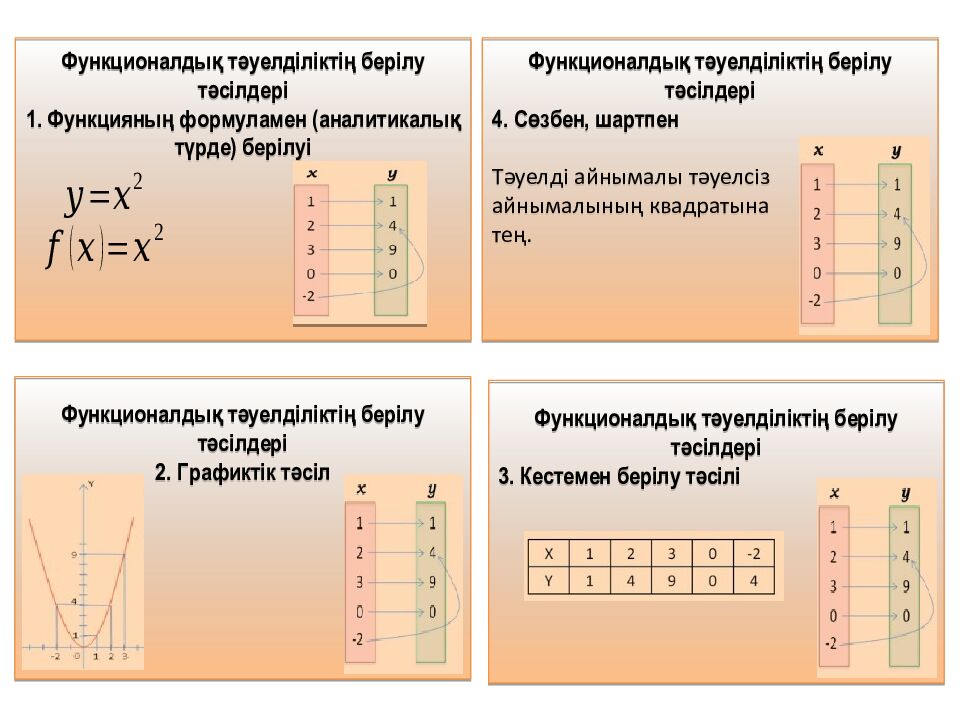
Функционалдық тәуелділіктің берілу тәсілдері 1. Функцияның формуламен (аналитикалық түрде) берілуі Функционалдық тәуелділіктің берілу тәсілдері 2. Графиктік тәсіл Функционалдық тәуелділіктің берілу тәсілдері 3. Кестемен берілу тәсілі Функционалдық тәуелділіктің берілу тәсілдері 4. Сөзбен, шартпен Тәуелді айнымалы тәуелсіз айнымалының квадратына тең.
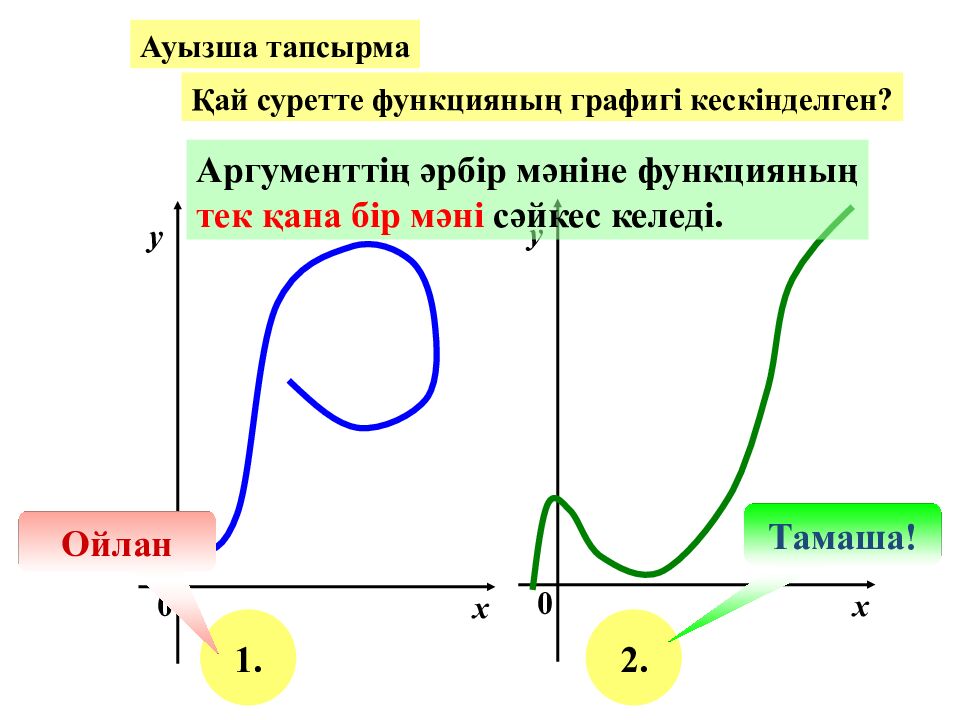
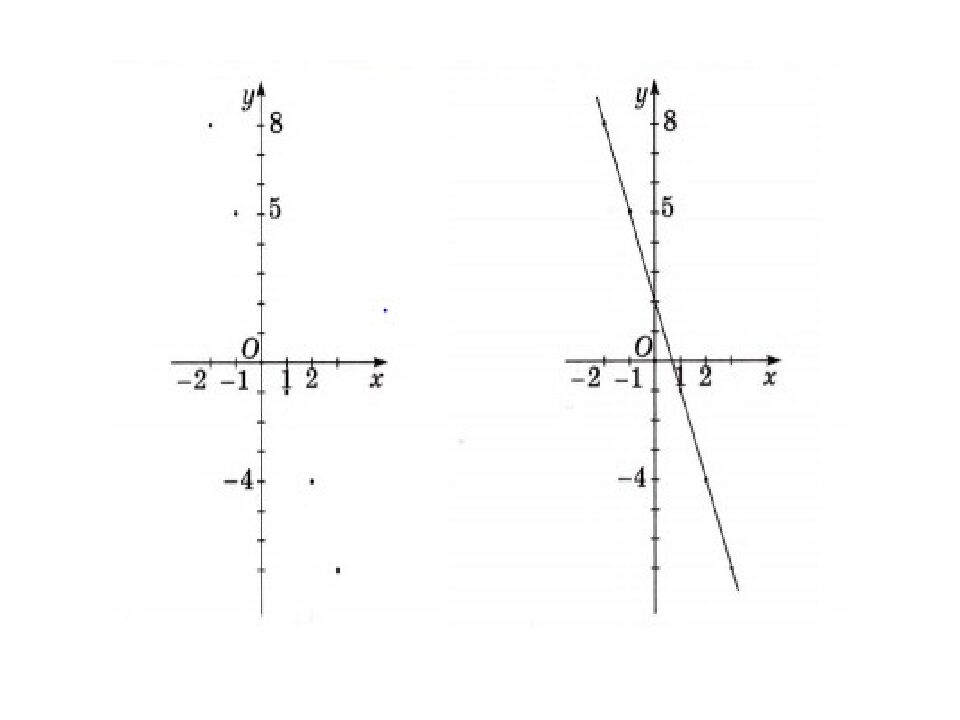
Ауызша тапсырма Қай суретте функцияның графигі кескінделген? х у 0 х у 0 1. 2. Ойлан Тамаша! Аргументтің әрбір мәніне функцияның тек қана бір мәні сәйкес келеді.
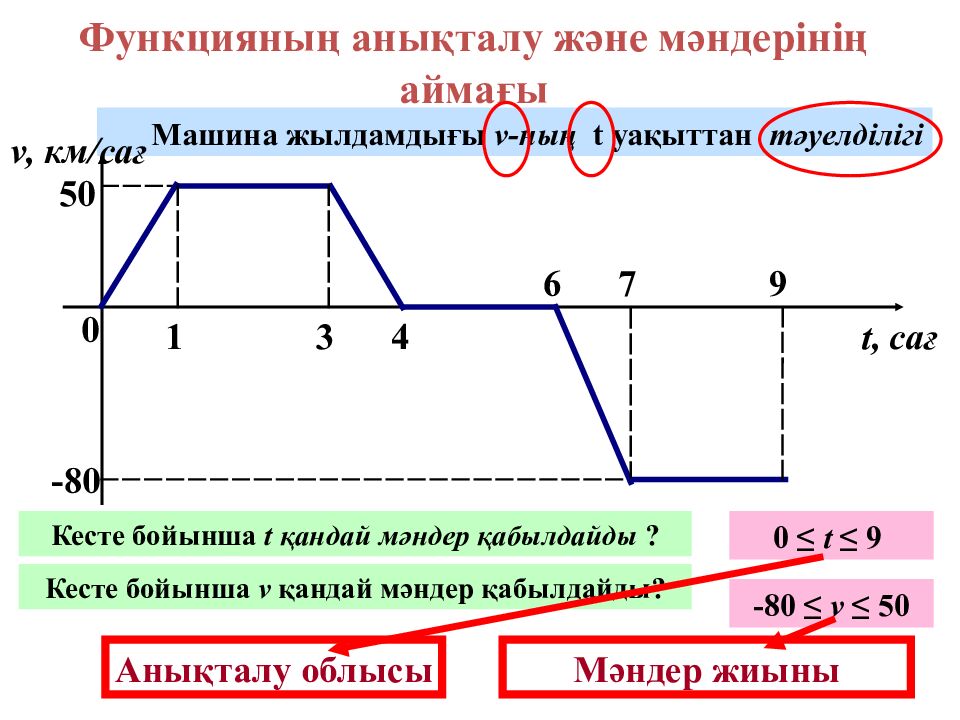
Функцияның анықталу және мәндерінің аймағы 0 1 3 4 6 7 9 t, сағ 5 0 -8 0 Машина жылдамдығы v- ның t уақыттан тәуелділігі Кесте бойынша t қандай мәндер қабылдайды ? 0 ≤ t ≤ 9 Кесте бойынша v қандай мәндер қабылдайды? -80 ≤ v ≤ 50 Анықталу облысы Мәндер жиыны v, км/сағ
D ( f ) = (- ; 3) (3;+ ) 2) Функцияның анықталу облысын табуға мысалдар 1) f ( х ) = 3+1,5х D ( f ) = R немесе D ( f ) = (- ; + ) 3) D ( f ) = R немесе D ( f ) = (- ; + ) 3
Тапсырма Кубтың көлемі оның қырының ұзындығына тәуелді. а см – куб қырының ұзындығы, V см 3 – оның көлемі болсын. V –ның а-ға тәуелділігін формуламен көрсетіңіз. V функцияның а = 5; 7,1 болғандағы мәндерін анықтаңдар. Тексеру (3) а а а V = а 3 Егер а = 5, онда V = 5 3 = 125 Егер а = 7,1, онда V = 357,911
Функцияның формуламен берілуі. Формула аргументтің кез келген мәніне оған сәйкес функцияның мәнін есептеу нәтижесінде анықтауға мүмкіндік береді. 1 мысал. y(x) = x 3 + x функцияның мәнін анықтаңыздар мұндағы х = - 2; х = 5; х = а; х = 3а. 1. у (-2) = (-2) 3 + (-2) = -8 – 2 = -10 2. у (5) = 5 3 + 5 = 125 + 5 = 130 3. у ( а ) = а 3 + а 4. у (3 а ) = (3 а ) 3 + 3 а = 27 а 3 + 3 а
2 мысал. Функция келесі формуламен берілген, мұндағы 2 ≤ х ≤ 9 1. Функцияның анықталу аймағы 2 ≤ х ≤ 9 аралығындағы кез-келген х Функция келесі формуламен берілген 2. Бұл жағдайда анықталу облысы көрсетілмеген. Функция үшін берілген формула мағынасы бар болатындай аргументті анықтаймыз. Шешімі
Тапсырма. Функцияның анықталу облысын анықтаңыздар: 1. 2. 3.
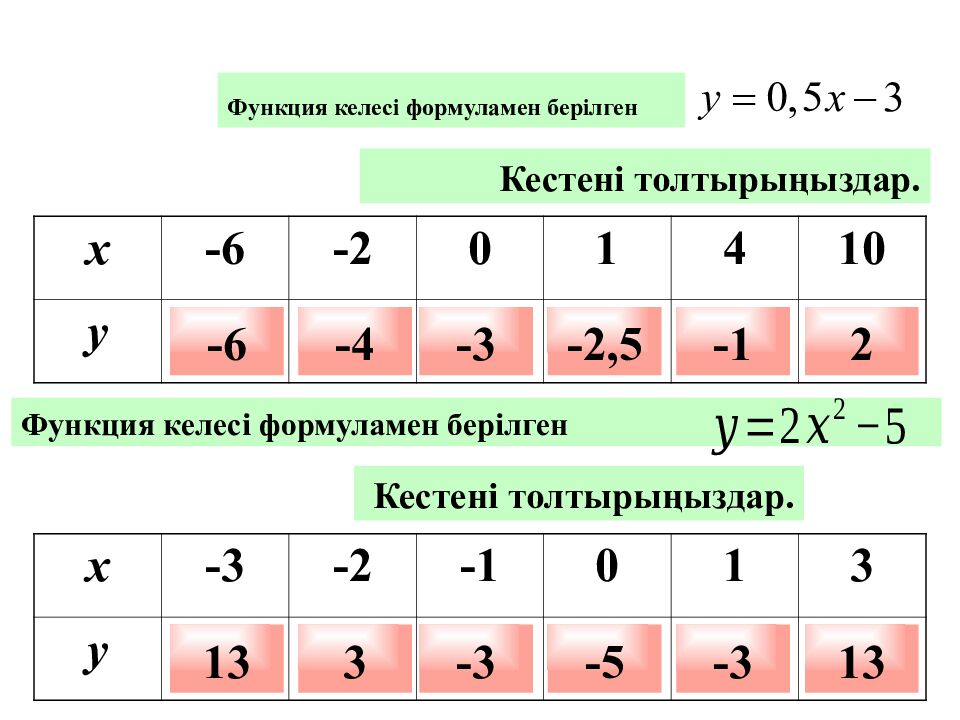
Функция келесі формуламен берілген Кестені толтырыңыздар. x -6 -2 0 1 4 10 y -6 -4 -3 -2,5 -1 2 Кестені толтырыңыздар. x -3 -2 -1 0 1 3 y 13 3 -3 -5 -3 13 Функция келесі формуламен берілген
Әр түрлі екі шаманың арасындағы тәуелділік координаталық жазықтықта сызықпен кескінделсе, оларды график деп атайды.
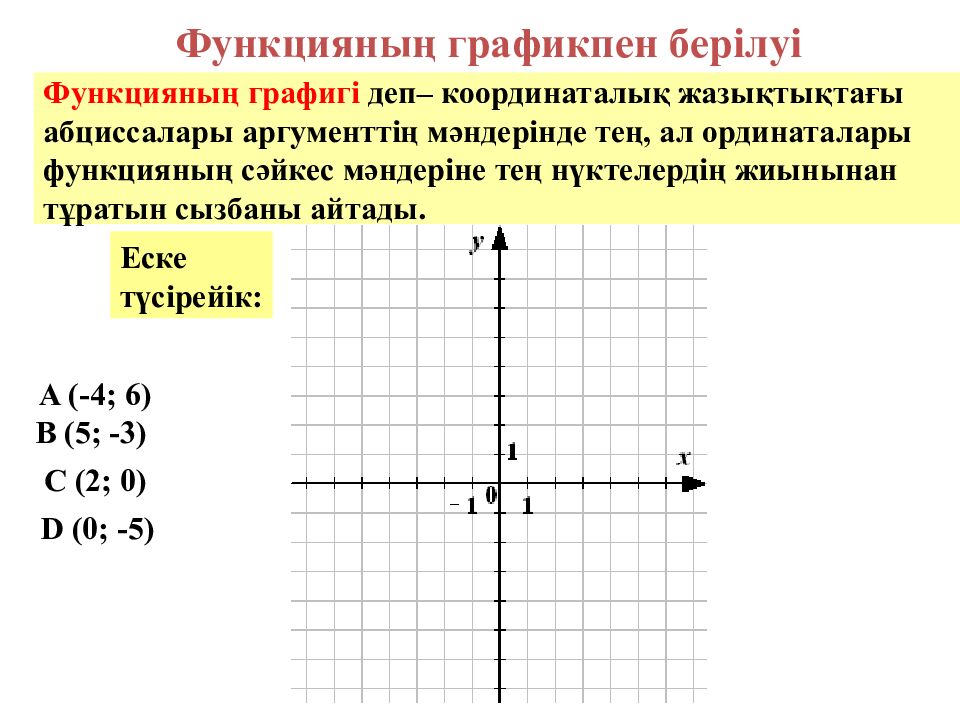
Функцияның графикпен берілуі Функцияның графигі деп– координаталық жазықтықтағы абциссалары аргументтің мәндерінде тең, ал ординаталары функцияның сәйкес мәндеріне тең нүктелердің жиынынан тұратын сызбаны айтады. Еске түсірейік: A (-4; 6) B (5; -3) C (2; 0) D (0; -5)
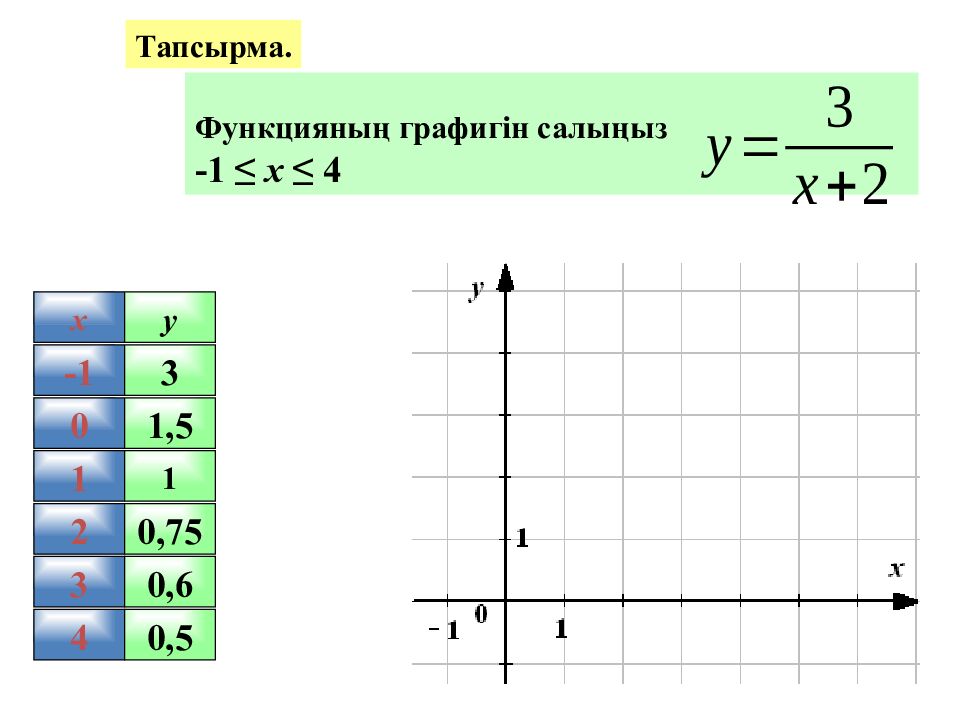
Тапсырма. Функцияның графигін салыңыз -1 ≤ х ≤ 4 -1 0 1 2 3 4 x y 1 0,75 0,6 0,5 3 1,5
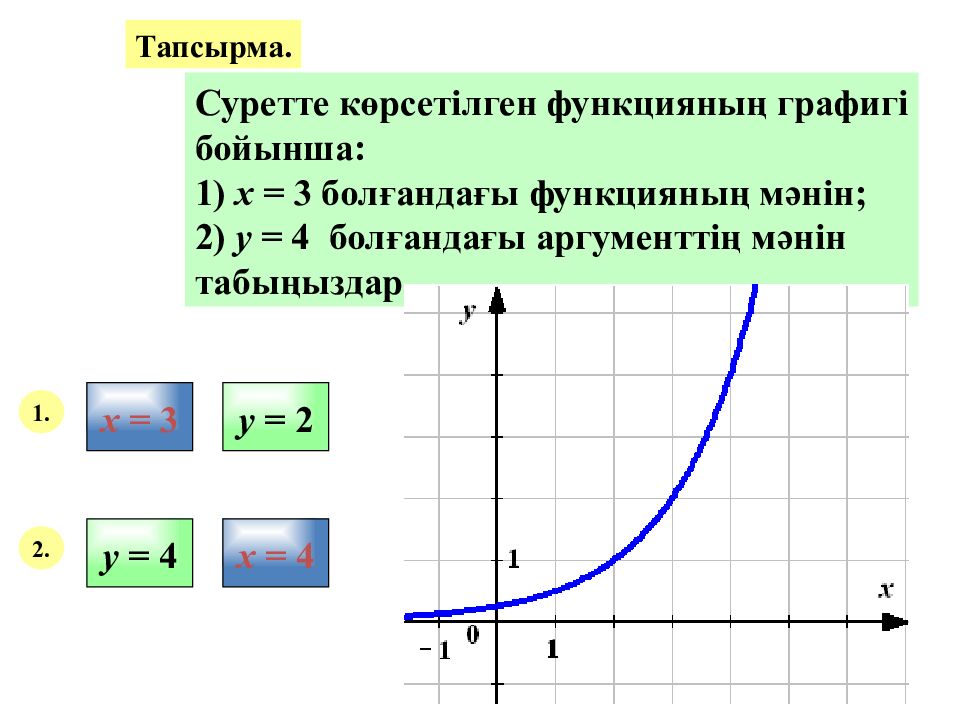
Тапсырма. Суретте көрсетілген функцияның графигі бойынша: 1) х = 3 болғандағы функцияның мәнін; 2) у = 4 болғандағы аргументтің мәнін табыңыздар. 1. х = 3 у = 2 3 2 2. у = 4 4 4 х = 4
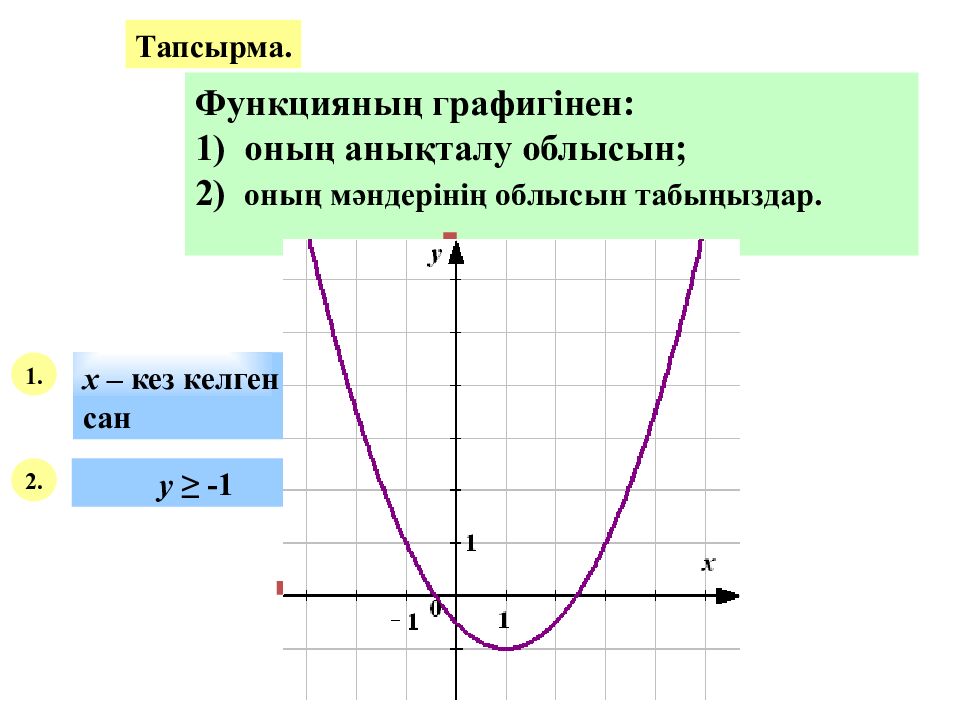
Тапсырма. Функцияның графигінен: 1) оның анықталу облысын; 2) оның мәндерінің облысын табыңыздар. 1. х – кез келген сан 2. у ≥ -1
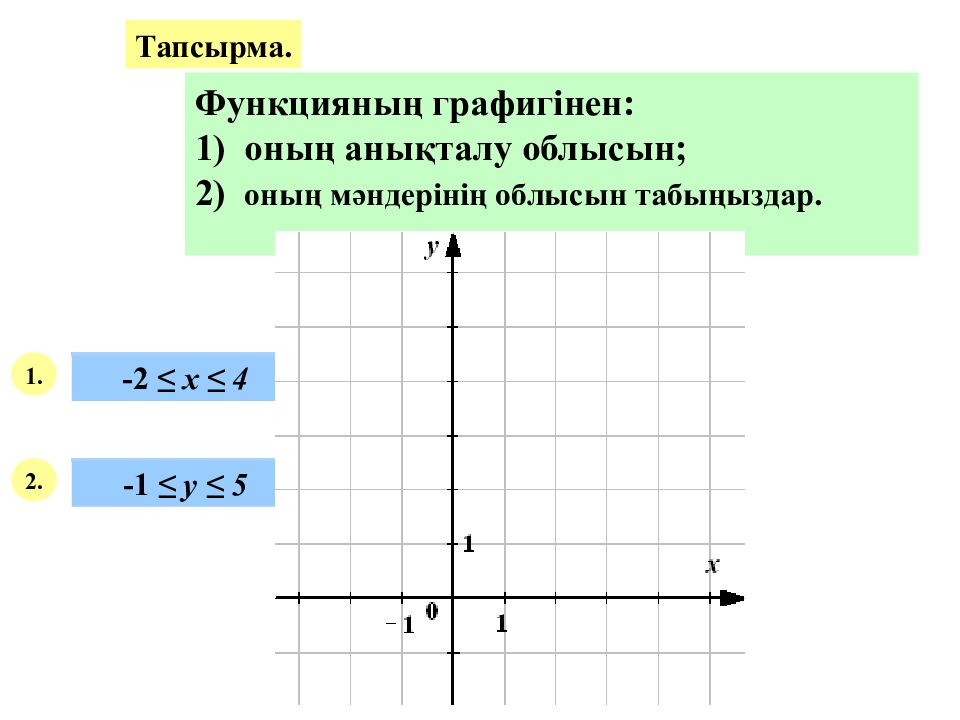
Тапсырма. Функцияның графигінен: 1) оның анықталу облысын; 2) оның мәндерінің облысын табыңыздар. 1. 2. -2 ≤ х ≤ 4 -1 ≤ у ≤ 5
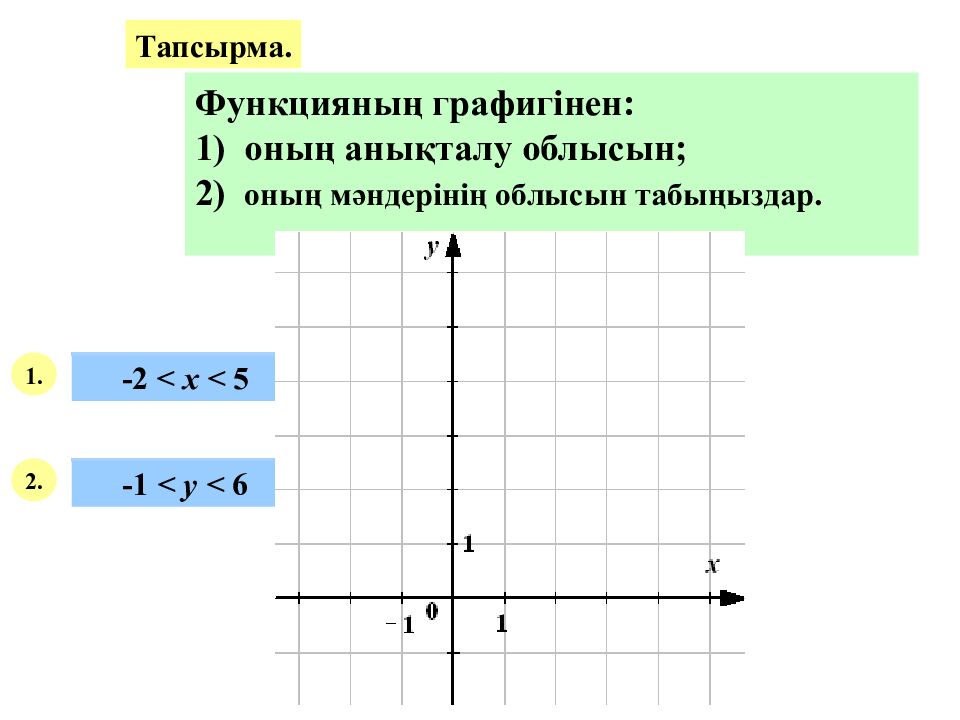
Тапсырма. Функцияның графигінен: 1) оның анықталу облысын; 2) оның мәндерінің облысын табыңыздар. 1. 2. -2 < х < 5 -1 < у < 6
Функция келесі форуламен берілген Функция үшін берілген формула мағынасы бар болатындай аргументті анықтаймыз. Формула бөлшек түрінде берілгендіктен, онда оның бөлімі 0-ге тең болмауы керек, яғни, мұндағы және Сонымен берілген функцияның анықталу облысы– -3 және 1 ден өзге кез-келген сан.
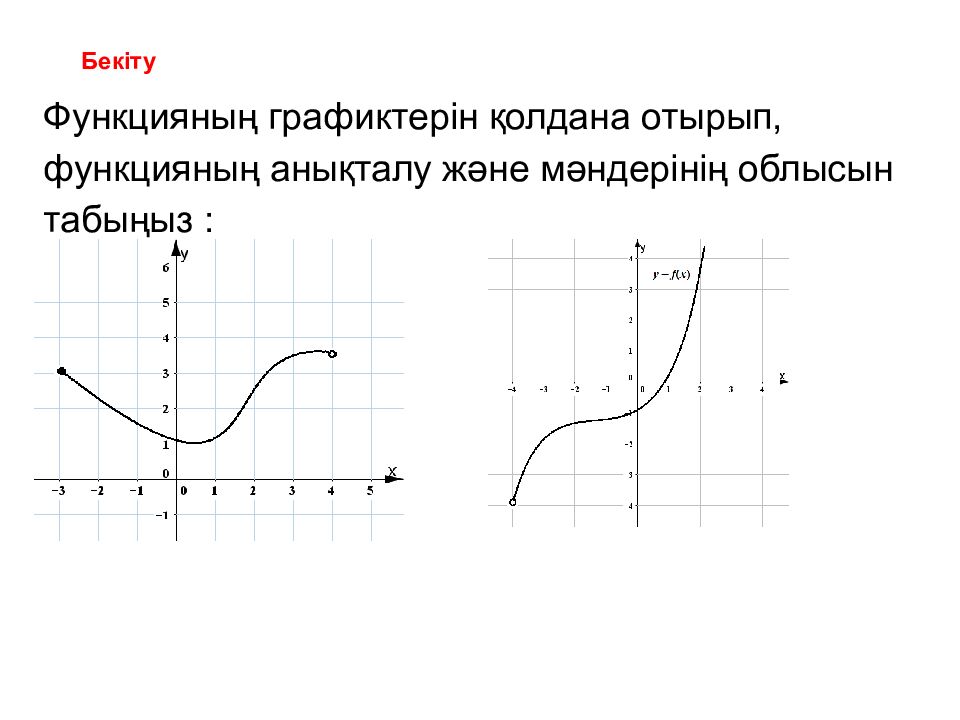
Функцияның графиктерін қолдана отырып, функцияның анықталу және мәндерінің облысын табыңыз :
Сызықтық функция
l=3,
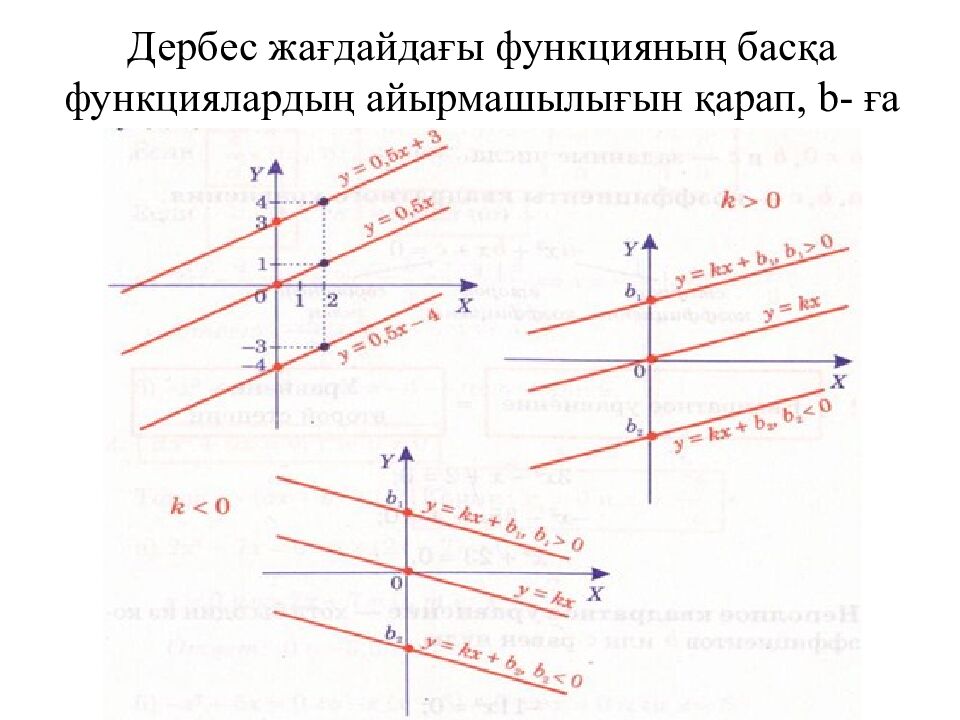
Дербес жағдайдағы функцияның басқа функциялардың айырмашылығын қарап, b- ға қатысты қорытынды шығар:
Жұптық жұмысы
Сыныппен есептер шығару.
Қолданылған әдебиеттер Алдамұратова Алгебра: Жалпы білім беретін 6–сыныбына арналған оқулық. 4–басылымы. –Алматы: Атамұра, 2012. Мордкович А.Г., Николаев Н.П. Алгебра. 7 класс. В 2 ч. Ч. 1. Задачник для учащихся общеобразоват. учреждений – М.:Мнемозина, 2009. Мордкович А.Г., Николаев Н.П. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразоват. учреждений – М.:Мнемозина, 2009. http://bilimland.kz/kk/content/lesson/11526-funkcziya_grafigin_salu http://nsportal.ru/shkola/algebra/library/2012/11/05/prezentatsiya-k-uroku-algebry-7-klass-po-teme-ponyatie-funktsii
