Голубева А., гр. 19ФХ1 Геометрическое распределение. Гипергеометрическое распределение. Равномерный закон распределения
Дискретная случайная величина X = m имеет геометрическое распределение с параметром p, если она принимает значения 1,2,.., m … (бесконечное, но счетное множество значений) с вероятностями где 0 < p < 1, q = 1 – p Ряд геометрического распределения случайной величины имеет вид
Нетрудно видеть, что вероятности р i образуют геометрическую прогрессию с первым членом р и знаменателем q (отсюда название «геометрическое распределение»). Определение геометрического распределения корректно, так как сумма ряда
Случайная величина Х = т, имеющая геометрическое распределение, представляет собой число m испытаний, проведенных по схеме Бернулли, с вероятностью р наступления события в каждом испытании до первого положительного исхода.
Математическое ожидание случайной величины Х, имеющей геометрическое распределение с параметром р и ее дисперсия где q = 1- p
Дискретная с лучайная величина X имеет гипергеометрическое распределение с параметрами n, M, N, если она принимает значения 0, 1, 2, m, …, min(n, M) с вероятностями: где M N, n N ; n, M, N – натуральные числа.
Математическое ожидание случайной величины X, имеющей гипергеометрическое распределение с параметрами n, M, N, есть а ее дисперсия:
Случайную величину X = m, распределенную по биномиальному закону, можно интерпретировать как число m объектов, случайно извлеченных из некоторой воображаемой бесконечной совокупности, доля p объектов которой обладает этим свойством. Поэтому гипергеометрическое распределение можно рассматривать как модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов, M из которых обладают этим свойством. При N →, M → при условии, что M/ N → p, функция вероятностей гипергеометрического распределения стремится к соответствующей функции биноминального закона.
Формула принимает вид: После деления делимого и делителя на получим: Переходя к пределу N → M →, M/ N → p получаем:
Гипергеометрическое распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочных обследований, и в других областях.
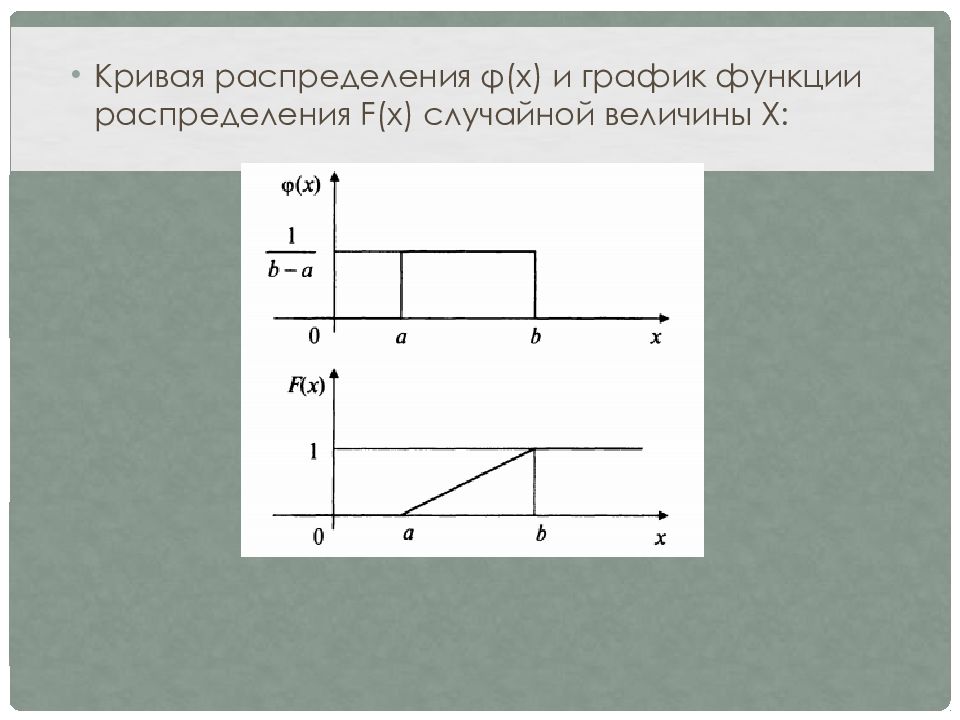
Непрерывная случайная величина X имеет равномерный (прямоугольный) закон распределения на отрезке [a, b], если ее плотность φ ( x) постоянна на этом отрезке и равна нулю вне его, т.е.
Кривая распределения φ ( x ) и график функции распределения F(x) случайной величины X :
Функция распределения случайной величины X, распределенной по равномерному закону, есть а ее математическое ожидание а дисперсия
При x a функция распределения F(x)=0. При x b Также: И:
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
