Первый слайд презентации: Геометрия 9 класс Вводное повторение
Учитель математики Семёнова Е.Ю. МБОУ СОШ №5 «Школа здоровья и развития» г. Радужный
Слайд 2
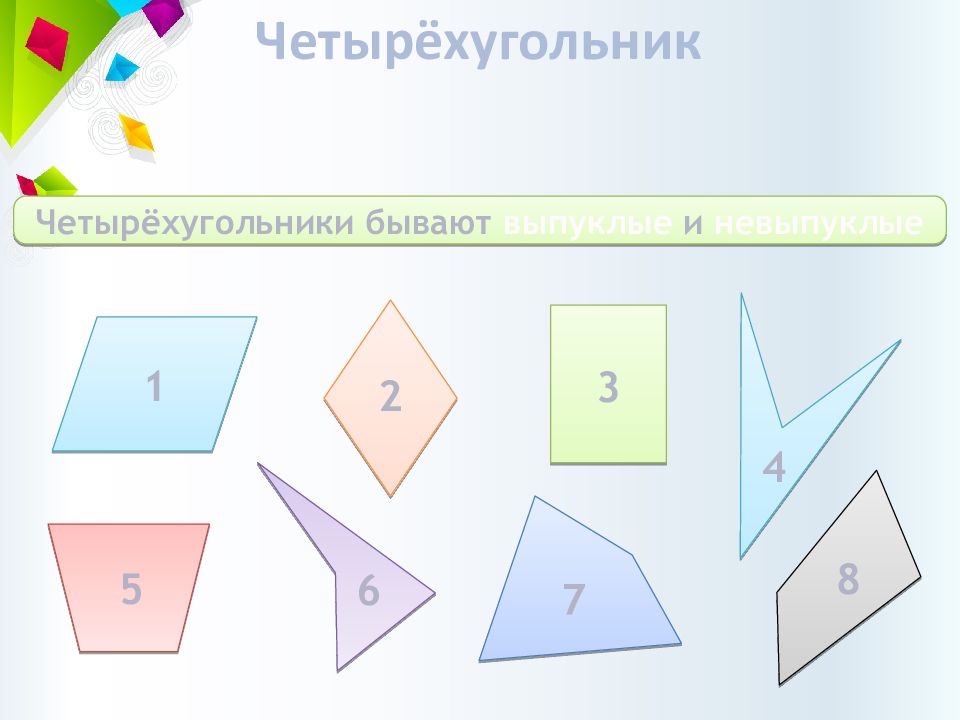
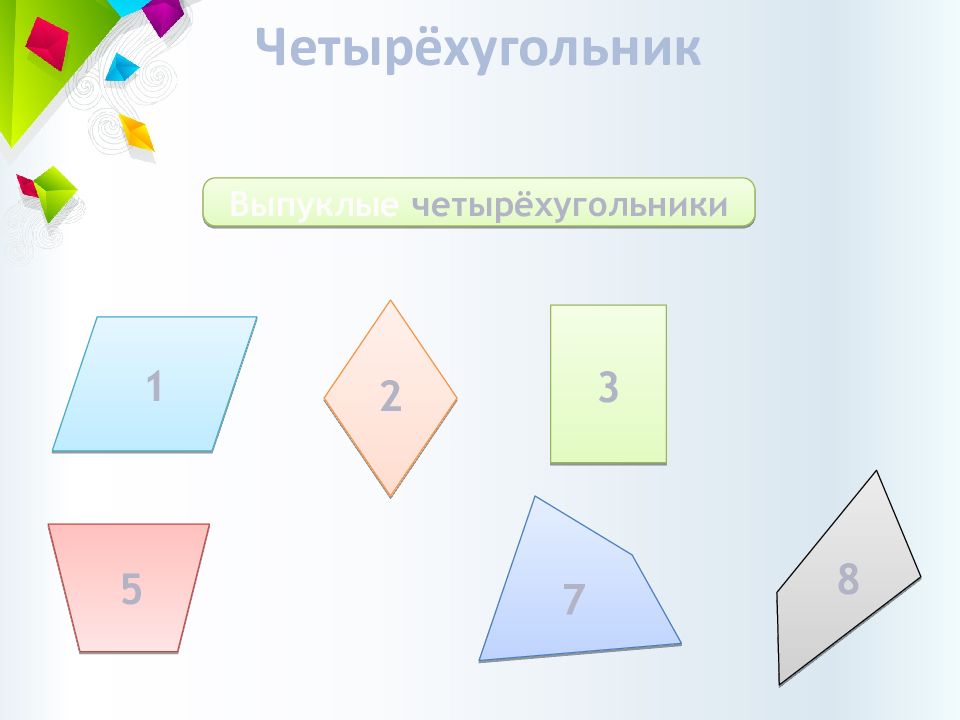
Четырёхугольник Четырёхугольники бывают выпуклые и невыпуклые 1 2 3 4 5 6 7 8
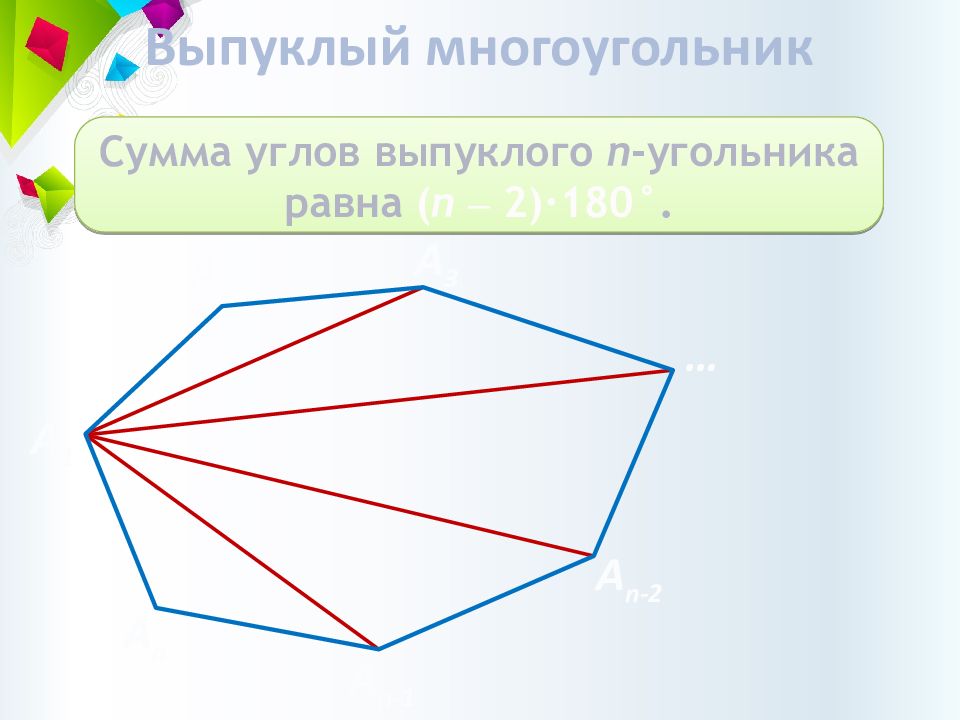
Слайд 4: Выпуклый многоугольник
Сумма углов выпуклого n - угольника равна ( n ‒ 2 )· 180°. А 1 А 2 А 3 … А n-1 А n-2 А n
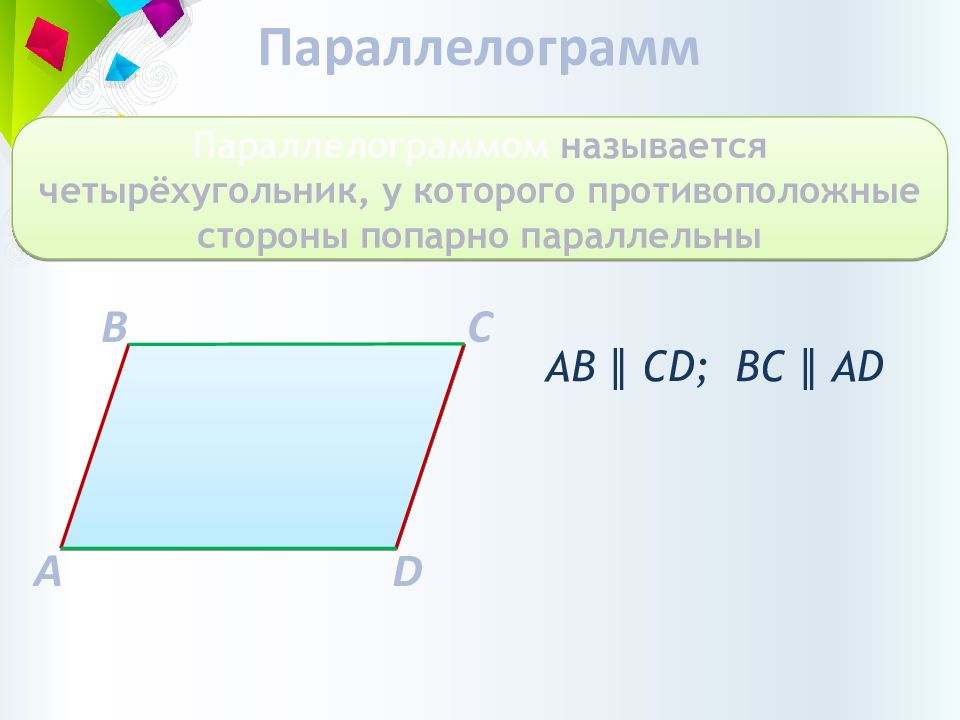
Слайд 5: Параллелограмм
Параллелограммом называется четыр ё хугольник, у которого противоположные стороны попарно параллельны A C B D АВ ∥ CD; BC ∥ AD
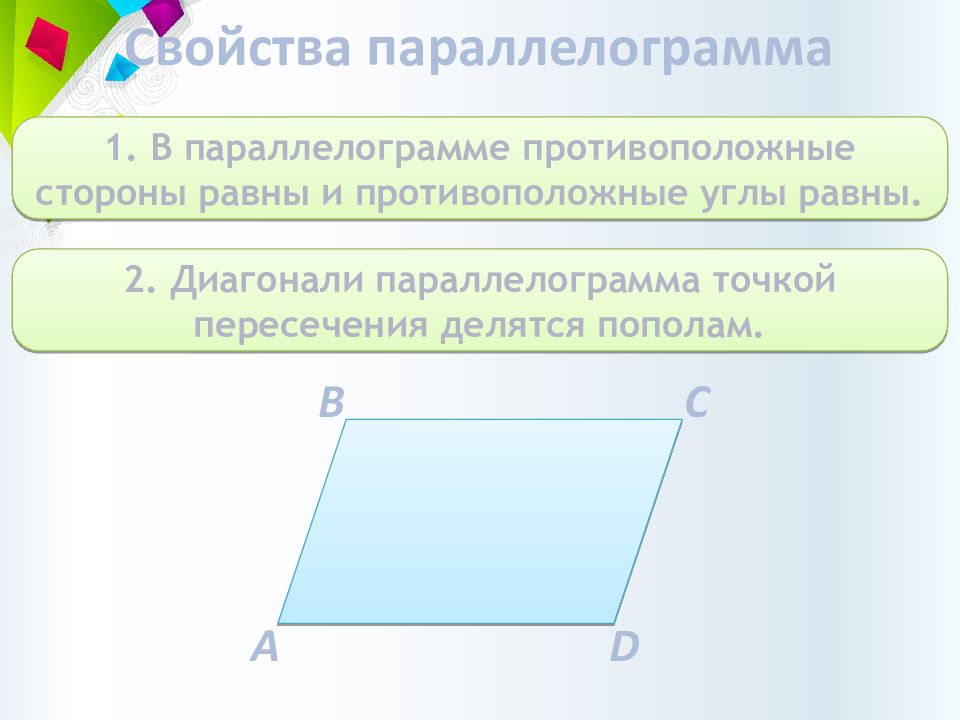
Слайд 6: Свойства параллелограмма
1. В параллелограмме противоположные стороны равны и противоположные углы равны. 2. Диагонали параллелограмма точкой пересечения делятся пополам. A C B D
Слайд 7: Признаки параллелограмма
1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник ‒ параллелограмм. 2) Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник ‒ параллелограмм. 3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник ‒ параллелограмм.
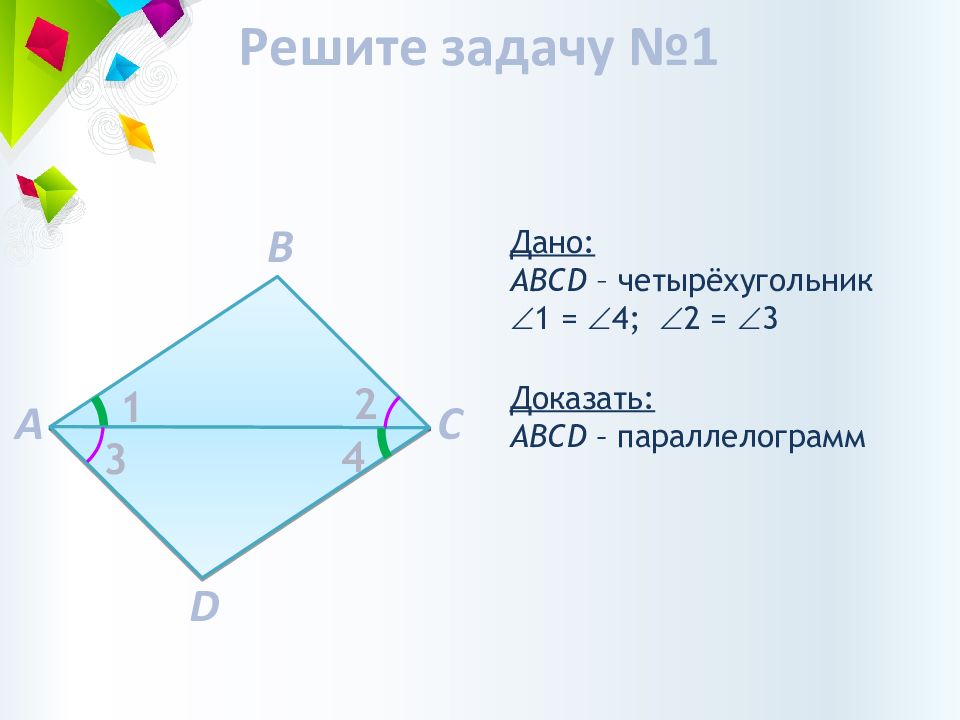
Слайд 8: Решите задачу №1
Доказать: АВ CD – параллелограмм A B D C 3 2 1 4 Дано: АВ CD – четырёхугольник 1 = 4; 2 = 3 Решите задачу №1
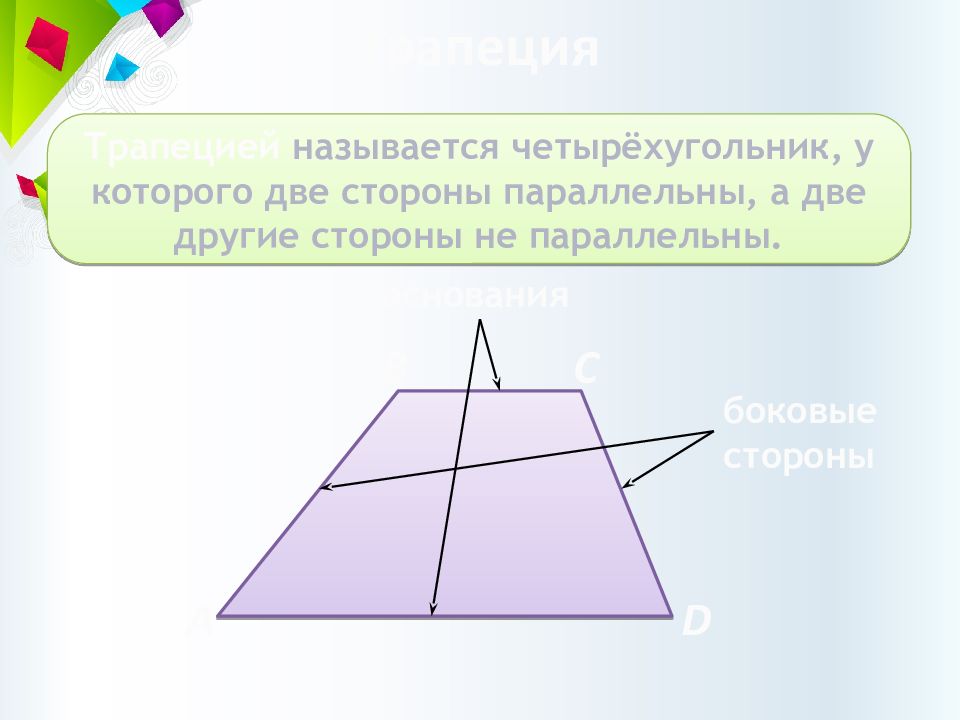
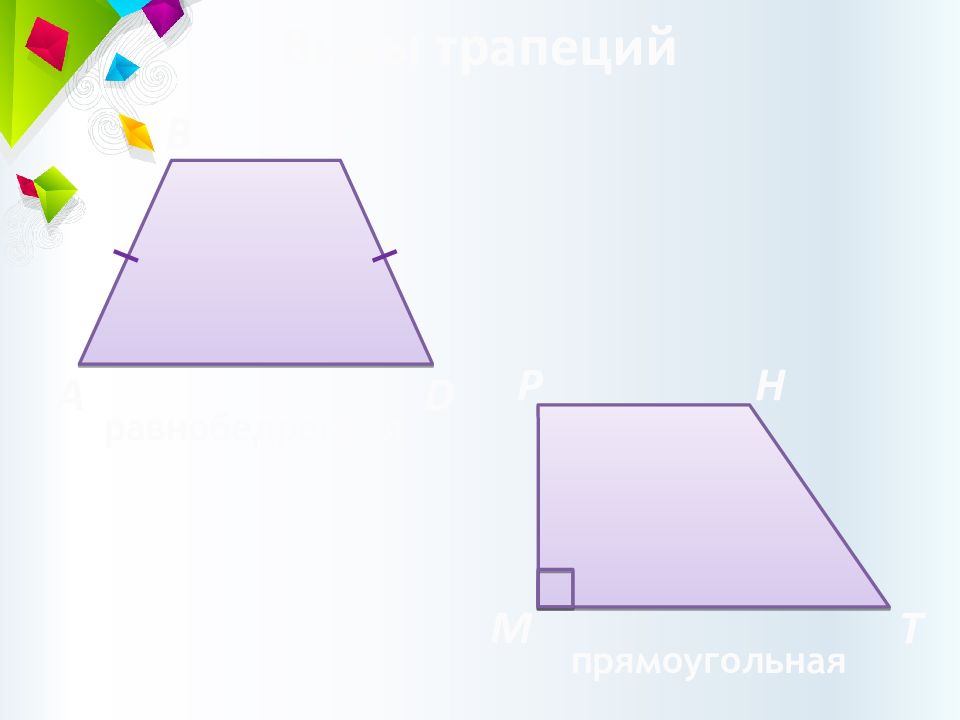
Слайд 9: Трапеция
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. C B A D основания боковые стороны
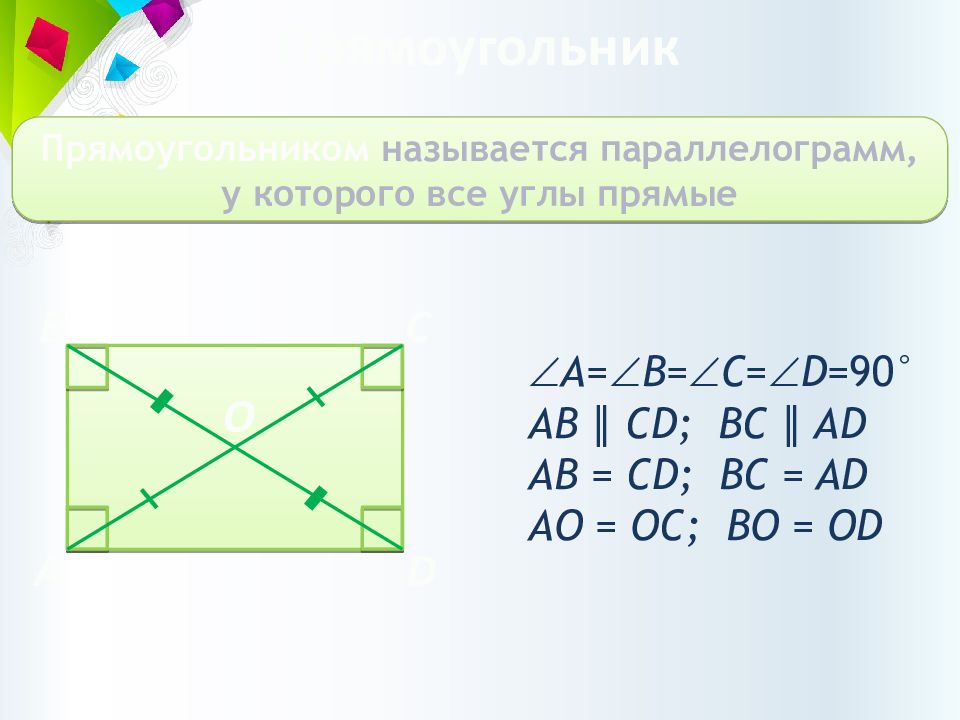
Слайд 12: Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые A C B D А= В= С= D =90° АВ ∥ CD; BC ∥ AD АВ = CD; BC = AD АО = О C; B О = О D О
Слайд 13: Свойства прямоугольника
Диагонали прямоугольника равны A C B D Признак прямоугольника Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
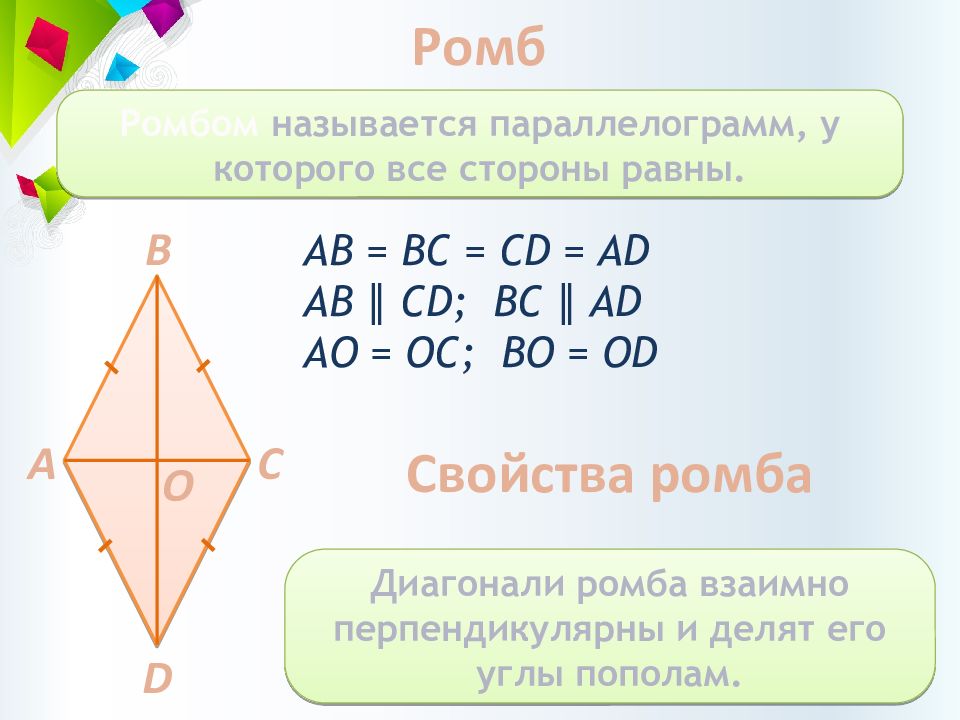
Слайд 14: Ромб
Ромбом называется параллелограмм, у которого все стороны равны. АВ = BC = CD = AD АВ ∥ CD; BC ∥ AD АО = О C; B О = О D A C B D О Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Свойства ромба
Слайд 15: Квадрат
Квадратом называется прямоугольник, у которого все стороны равны. АВ = BC = CD = AD АВ ∥ CD; BC ∥ AD A C B D Свойства квадрата 1) Все углы квадрата прямые. 2) Диагонали квадрата равны. 3) Диагонали взаимно перпендикулярны.
Слайд 16
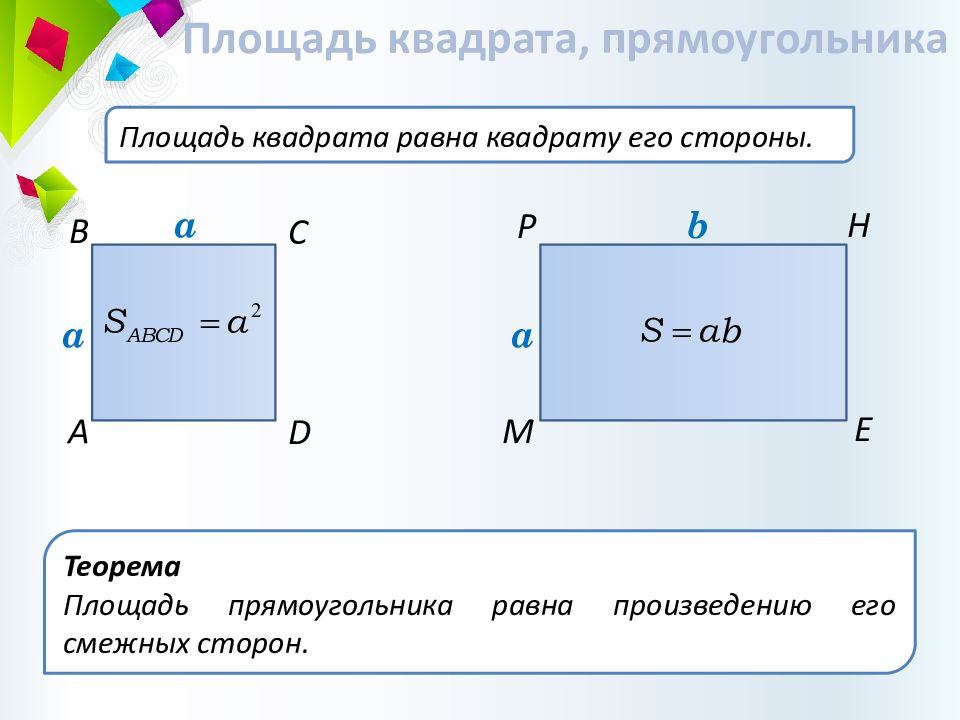
Площадь квадрата равна квадрату его стороны. Площадь квадрата, прямоугольника C B D A a Теорема Площадь прямоугольника равна произведению его смежных сторон. Н Р Е М a b a
Слайд 17
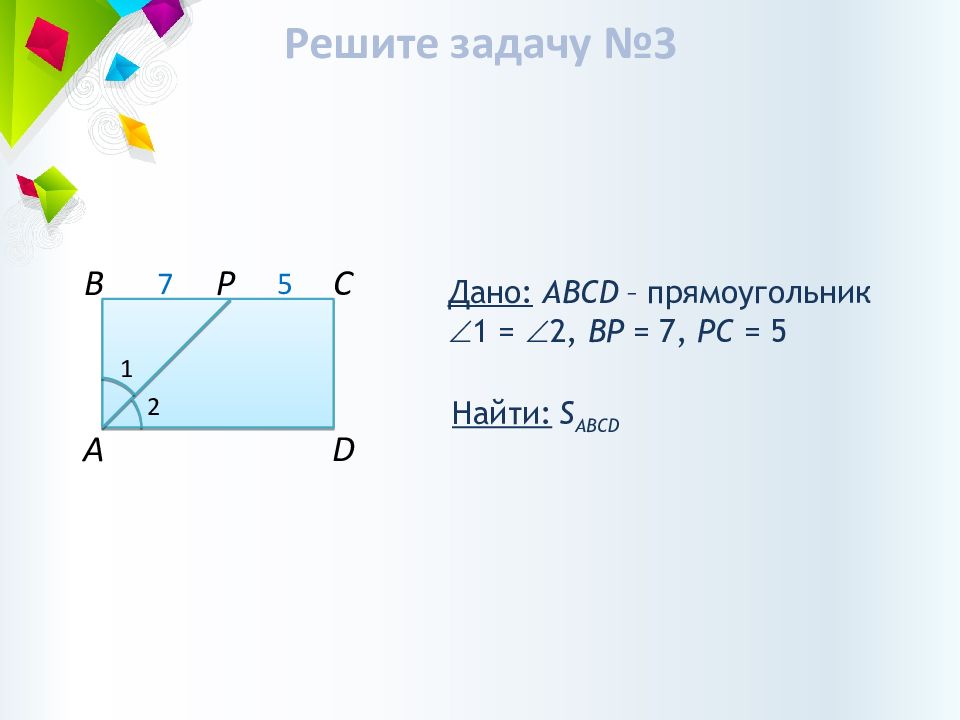
7 C B D A 5 2 Дано: ABCD – прямоугольник 1 = 2, BP = 7, Р C = 5 Найти: S ABCD P 1 Решите задачу №3
Слайд 18
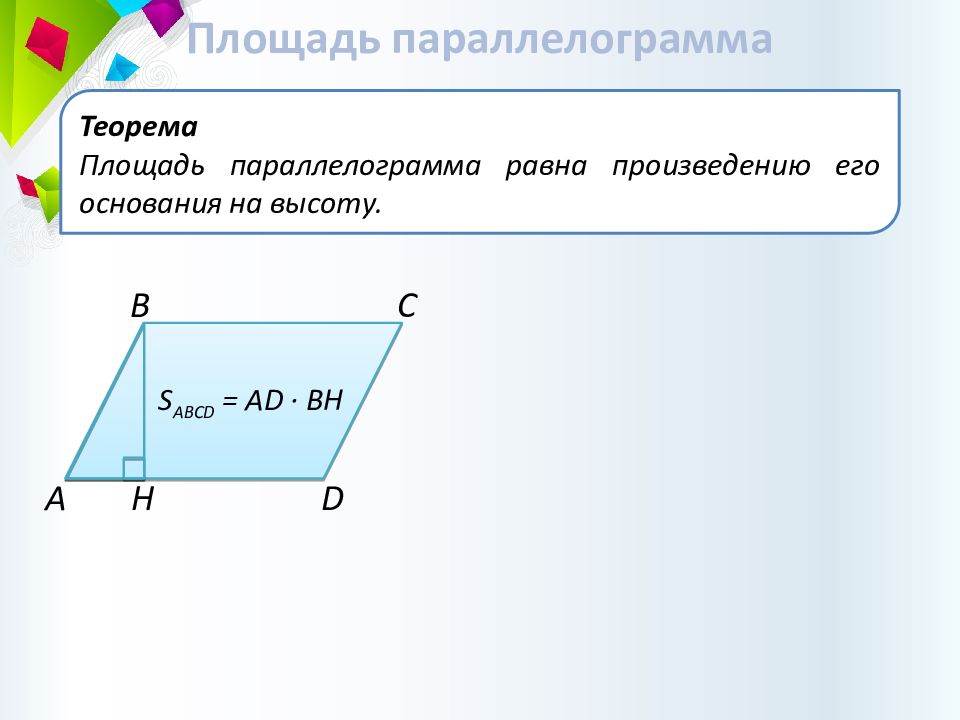
Теорема Площадь параллелограмма равна произведению его основания на высоту. Площадь параллелограмма C B D A Н S ABCD = AD · BH
Слайд 19
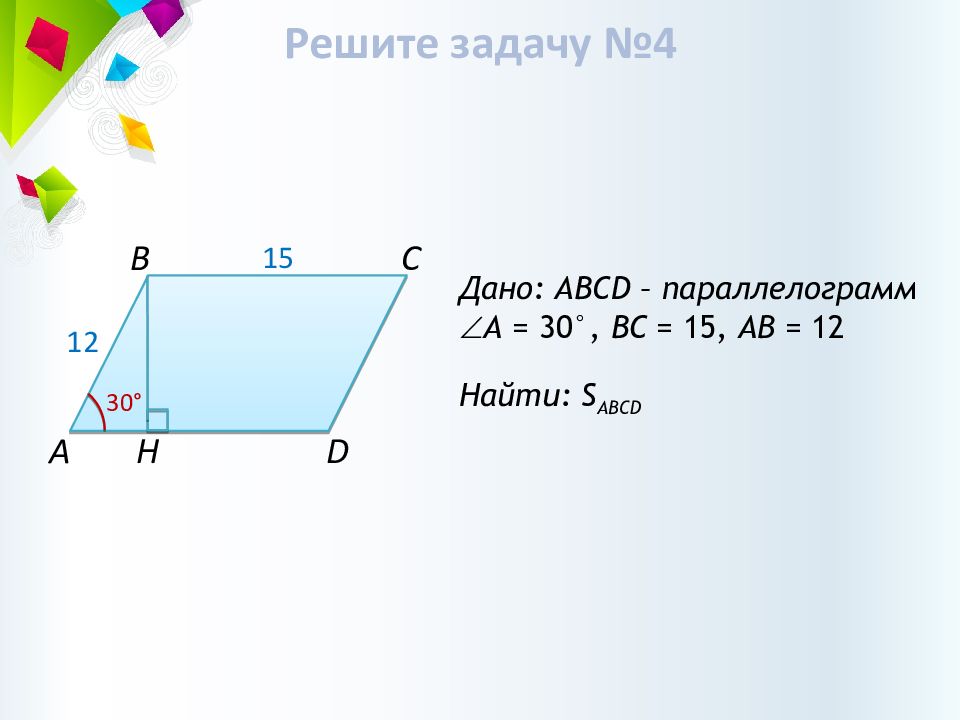
Н C B D A 30° 12 15 Дано: ABCD – параллелограмм А = 30°, B С = 15, АВ = 12 Найти: S ABCD Решите задачу №4
Слайд 20
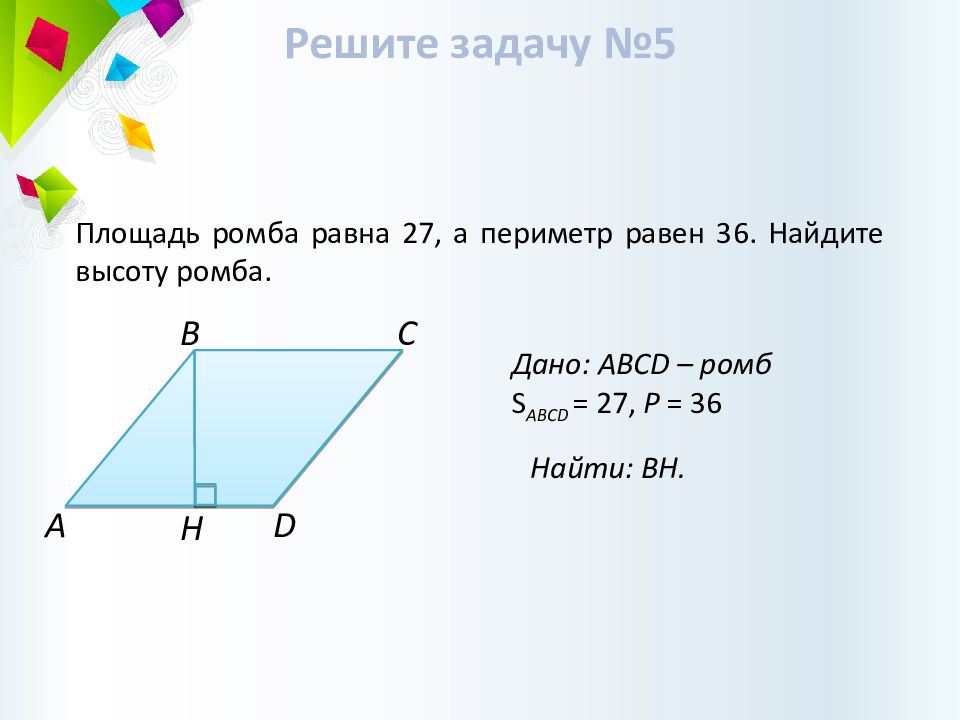
Н C B D A Дано: ABCD – ромб S А BCD = 27, P = 36 Найти: BH. Решите задачу №5 Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Слайд 21
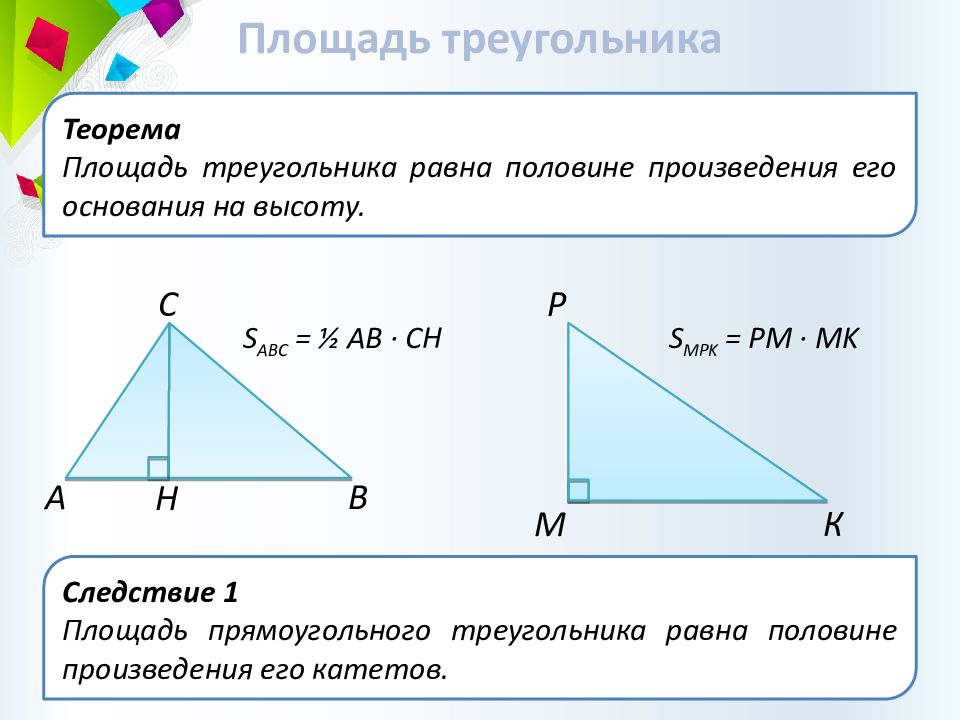
Теорема Площадь треугольника равна половине произведения его основания на высоту. Площадь треугольника C B A Н Следствие 1 Площадь прямоугольного треугольника равна половине произведения его катетов. М К Р S ABC = ½ AB · CH S MPK = PM · MK
Слайд 22
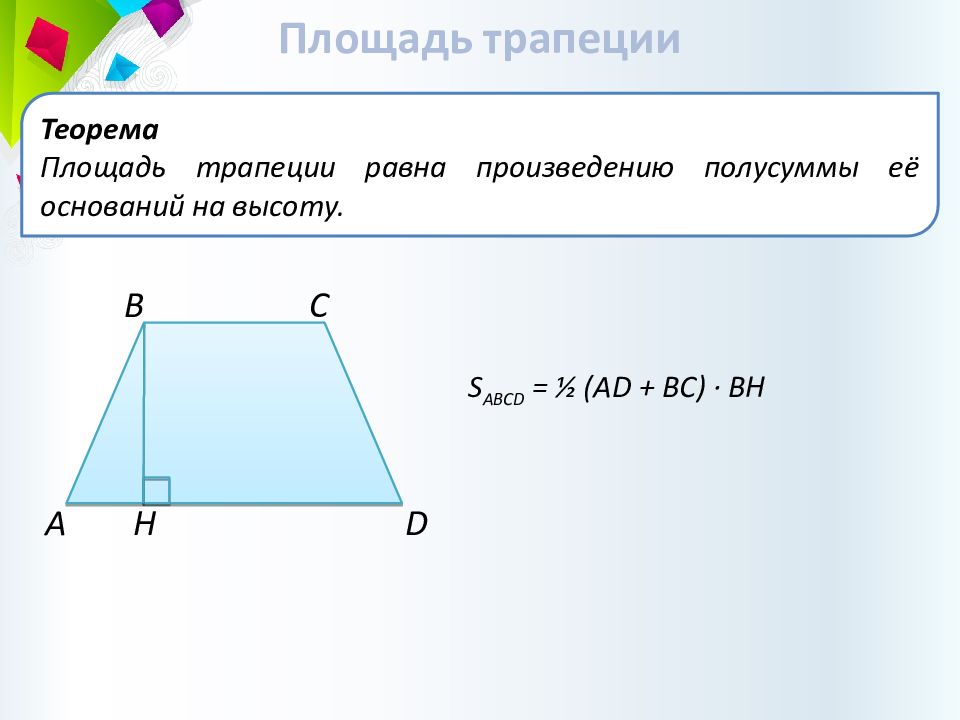
Площадь трапеции Теорема Площадь трапеции равна произведению полусуммы её оснований на высоту. В С A Н D S ABCD = ½ (AD + BC) · BH
Слайд 23
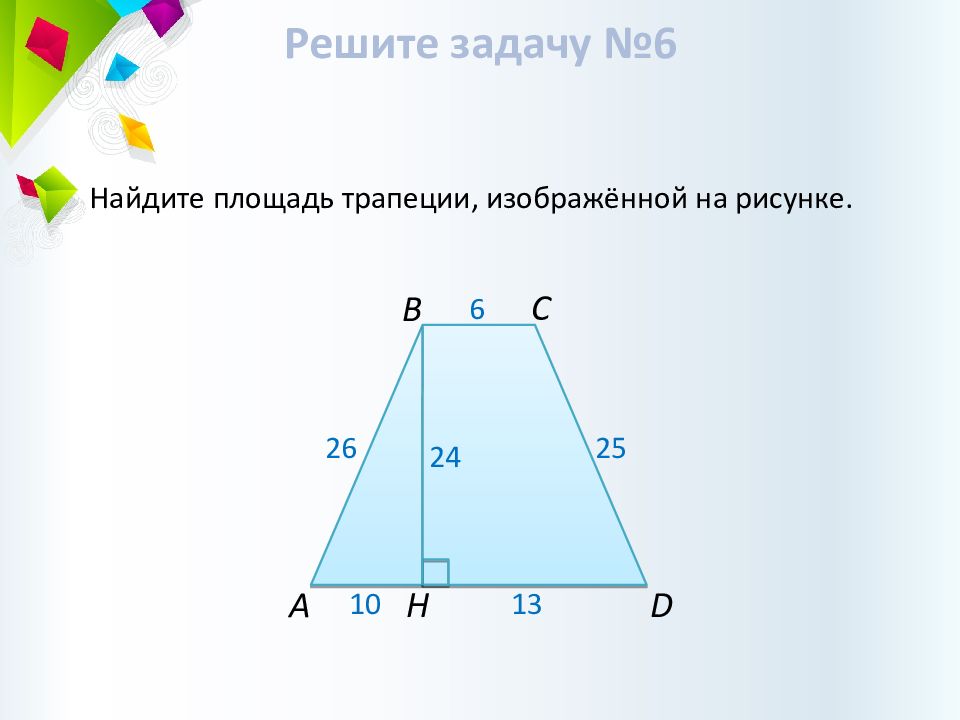
Решите задачу №6 Найдите площадь трапеции, изображённой на рисунке. В С A Н D 2 6 2 5 2 4 10 13 6
Слайд 24
Теорема Пифагора c 2 = a 2 + b 2 c b В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. a
Слайд 25
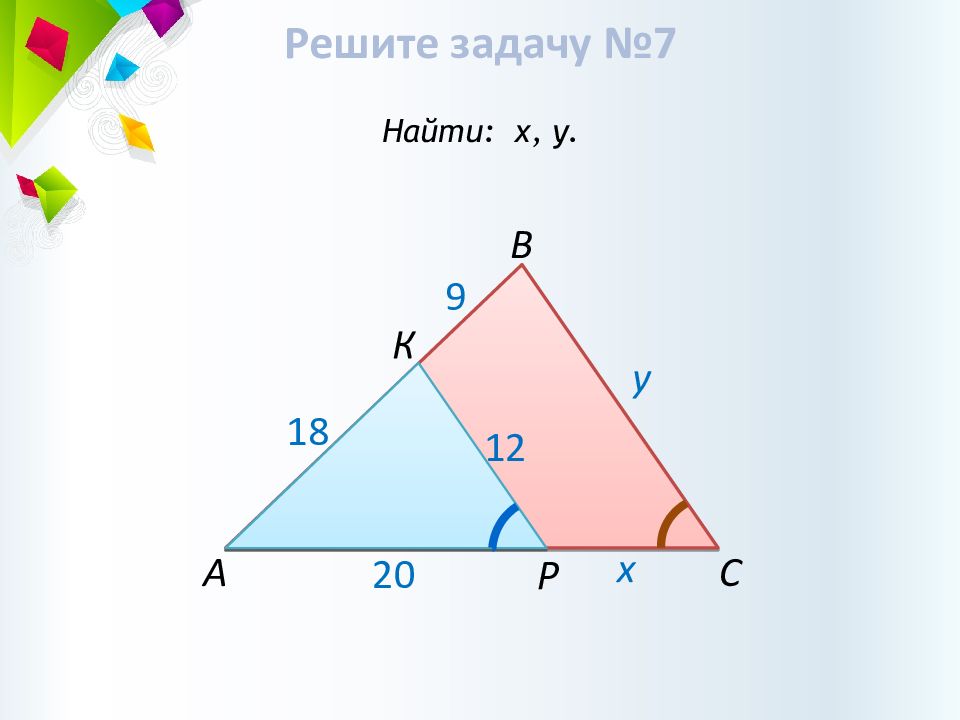
Первый признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Второй признак подобия треугольников Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Третий признак подобия треугольников Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Слайд 27
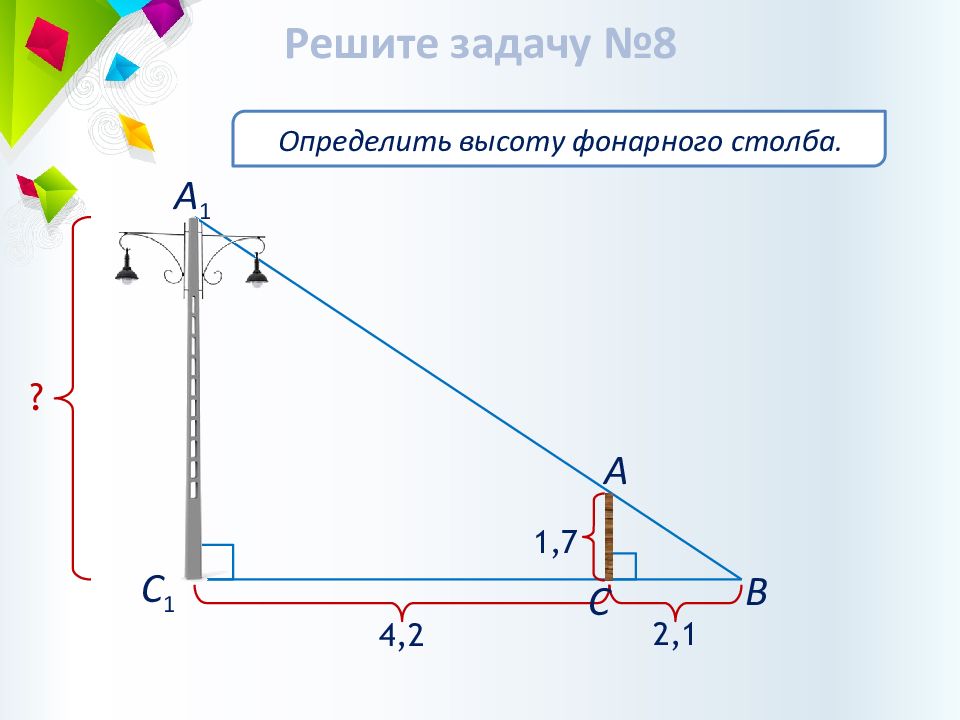
Определить высоту фонарного столба. 2,1 4,2 1,7 ? А В С А 1 С 1 Решите задачу №8
Слайд 28
Синус острого угла прямоугольного треугольника Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. c b a α А В С (1)
Слайд 29
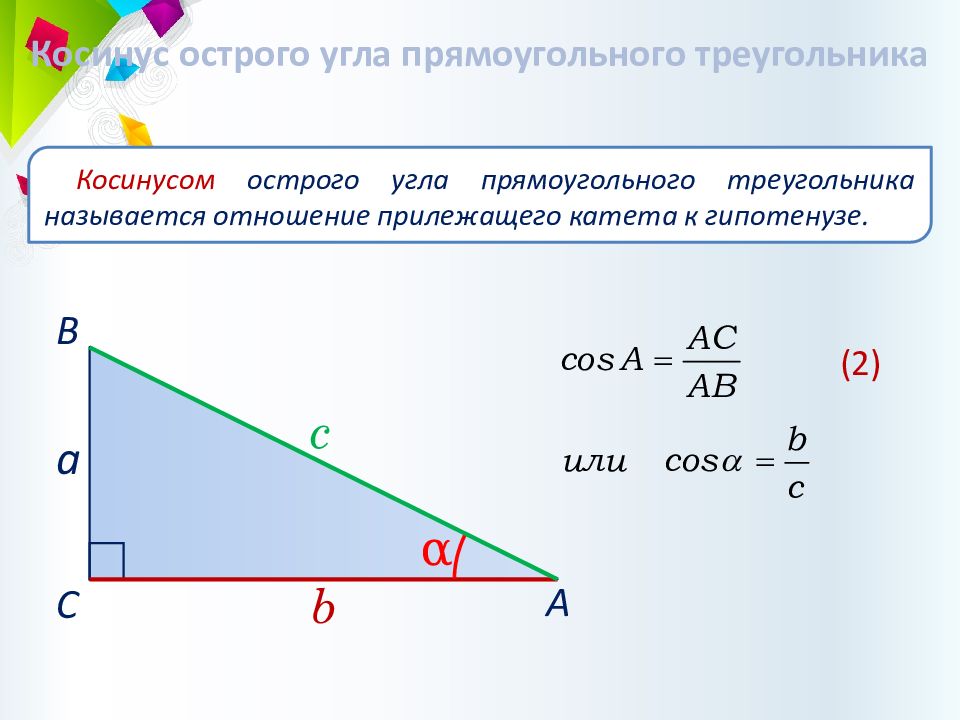
Косинус острого угла прямоугольного треугольника К осинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. c b a α А В С (2)
Слайд 30
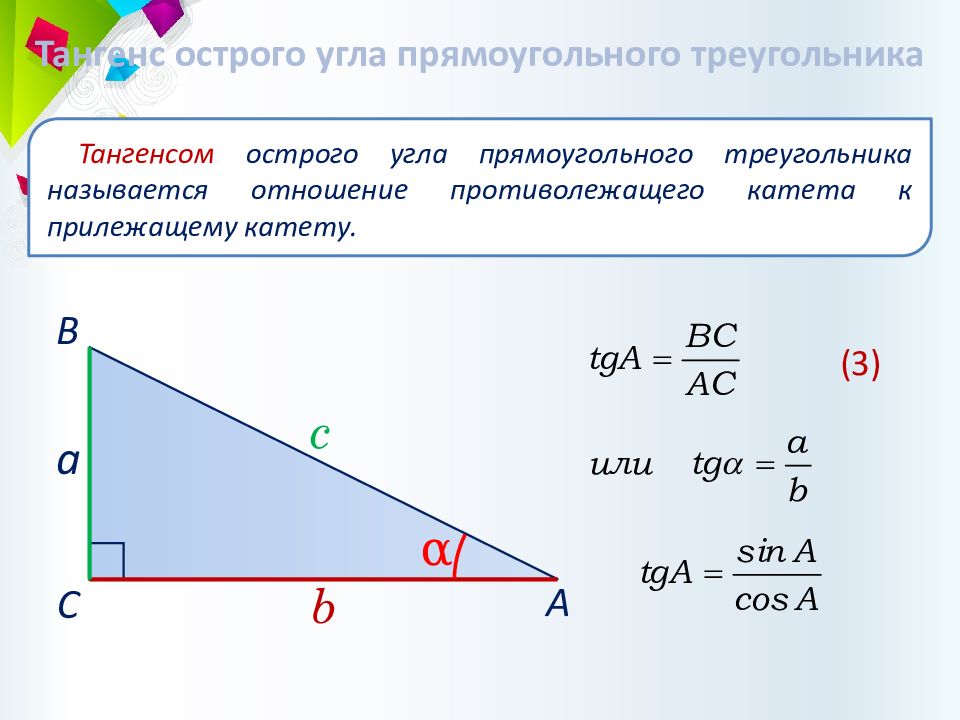
Тангенс острого угла прямоугольного треугольника Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. c b a α А В С (3)
Слайд 31
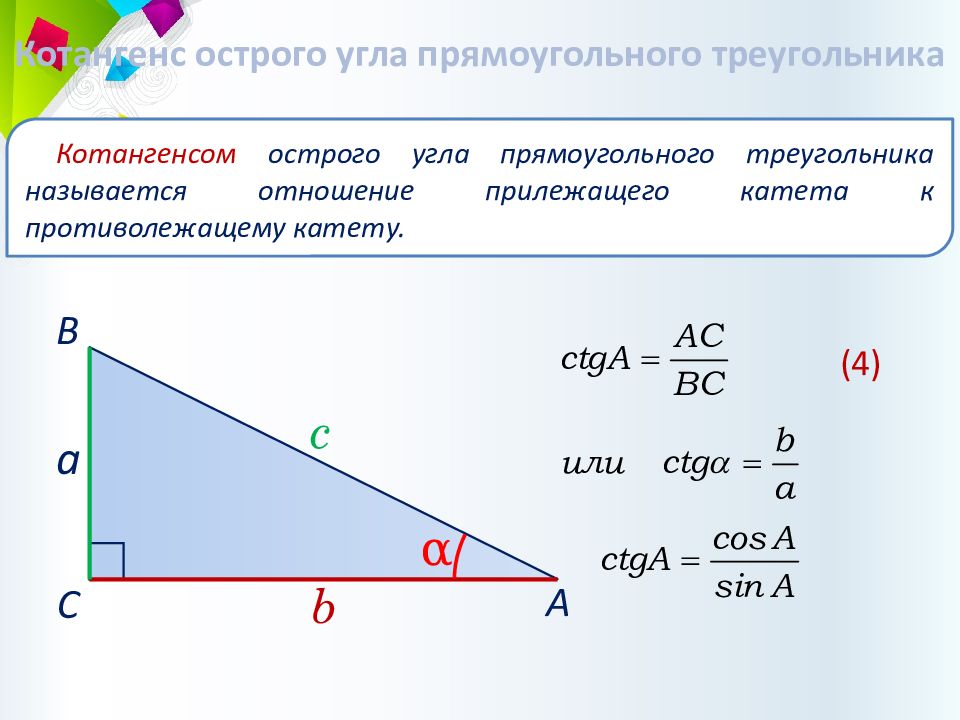
Котангенс острого угла прямоугольного треугольника Котангенсом острого угла прямоугольного треугольника называется отношение п р илежащего катета к противолежащему катету. c b a α А В С (4)
Слайд 33
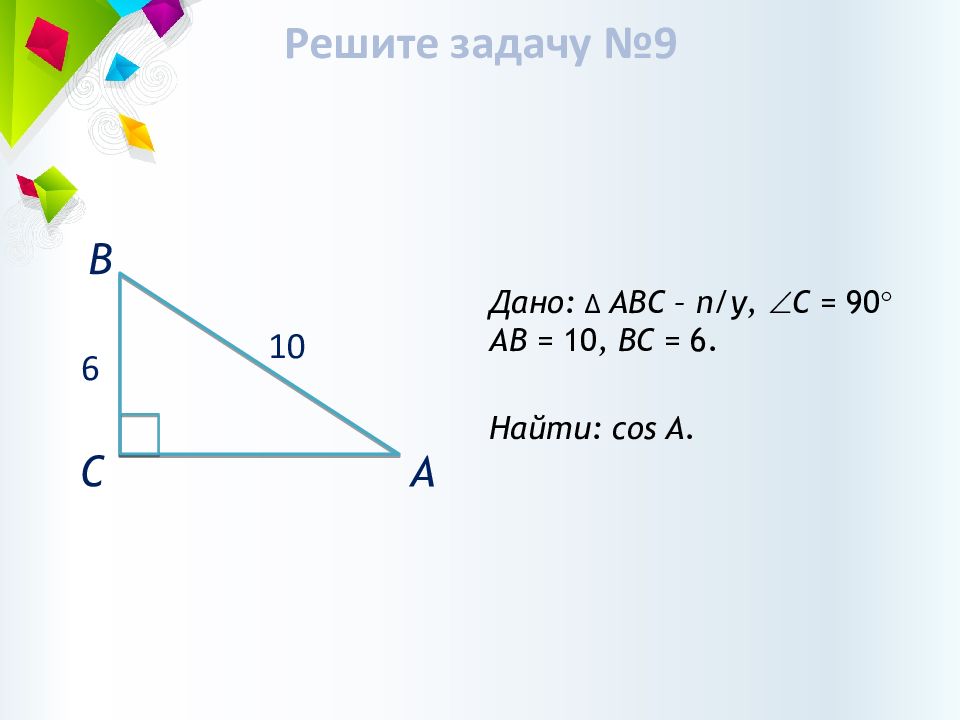
Дано: ∆ АВС – п/у, С = 90 АВ = 10, ВС = 6. А В С 6 10 Найти: cos A. Решите задачу №9
Слайд 34
Дано: ∆ АВС – п/у, С = 90 АВ = 1 3, АС = 12. А В С 12 1 3 Найти: tg A. Решите задачу №10
Слайд 35
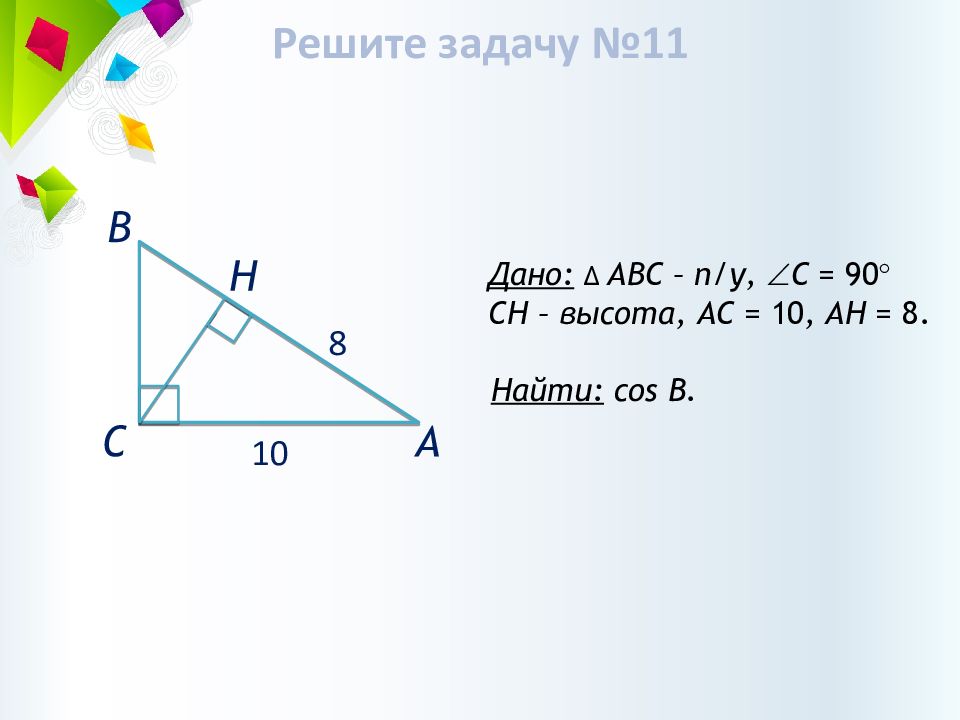
Дано: ∆ АВС – п/у, С = 90 CH – высота, АС = 10, АН = 8. Найти: cos B. А В С H 1 0 8 Решите задачу №11
Слайд 36
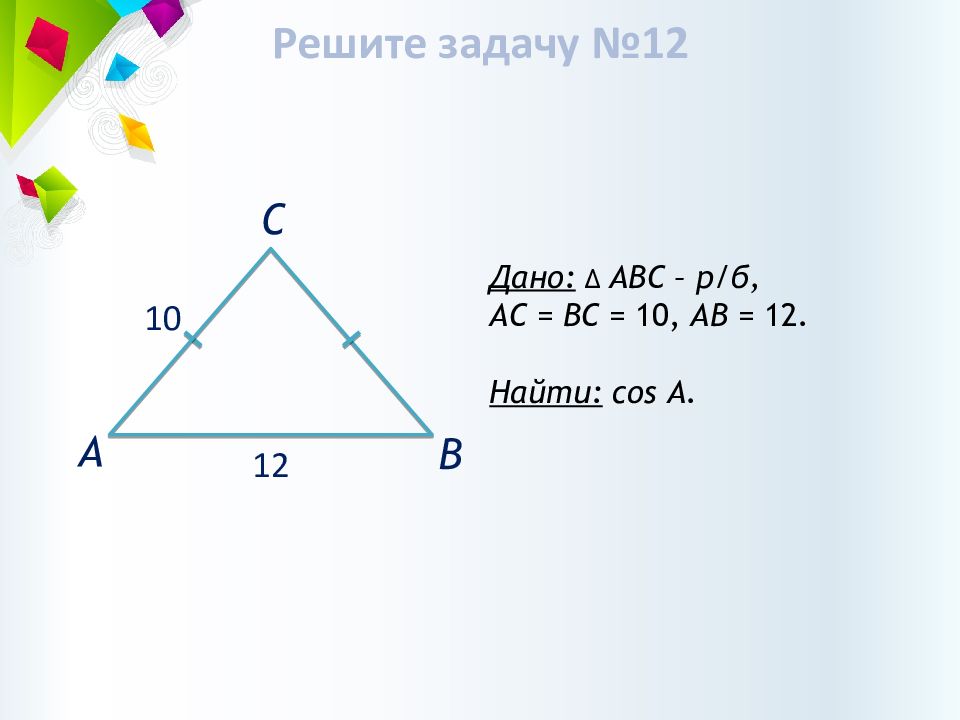
Дано: ∆ АВС – р/б, АС = ВС = 10, АВ = 12. Найти: cos А. А В С 1 0 12 Решите задачу №12
Слайд 37
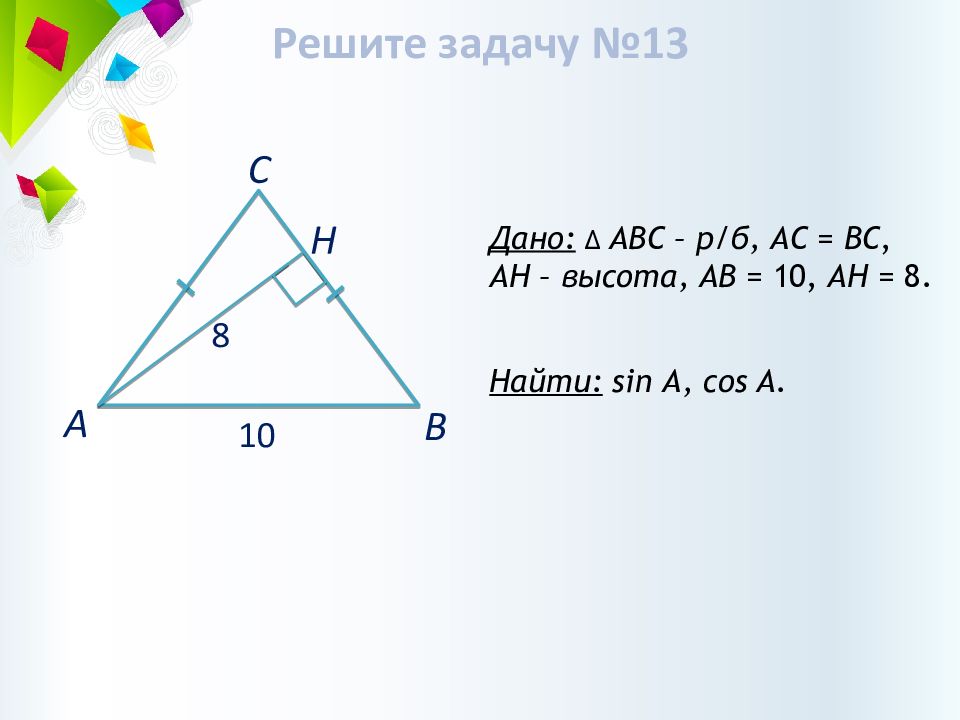
Дано: ∆ АВС – р/б, АС = ВС, AH – высота, АВ = 1 0, AH = 8. Найти: sin А, cos A. А В С 8 1 0 Н Решите задачу №13
Слайд 38
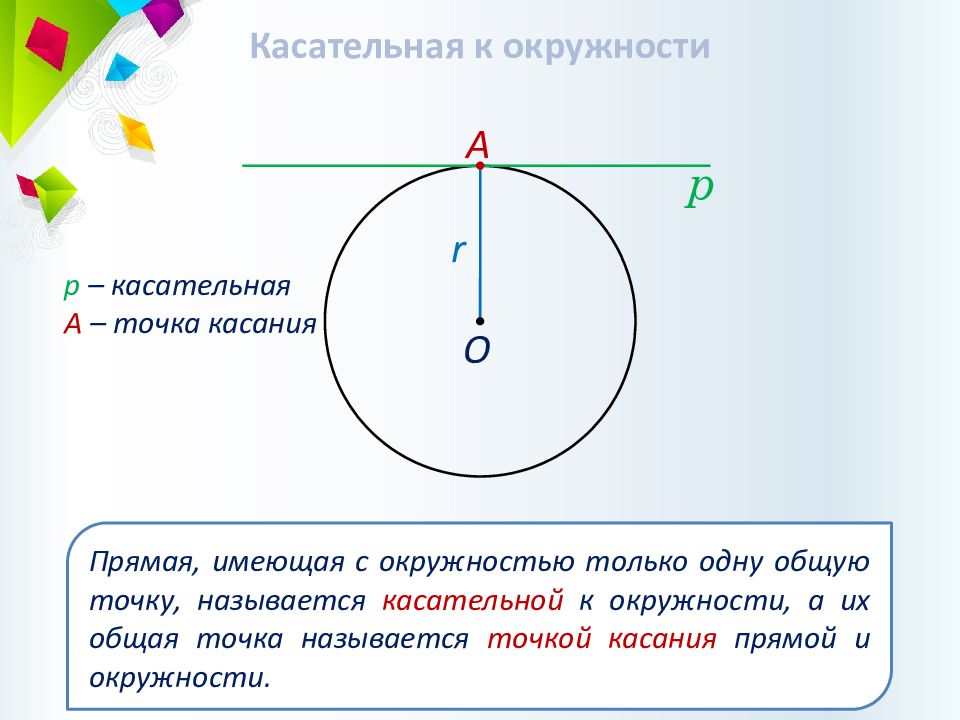
Касательная к окружности р р – касательная А – точка касания А О Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. r
Слайд 39
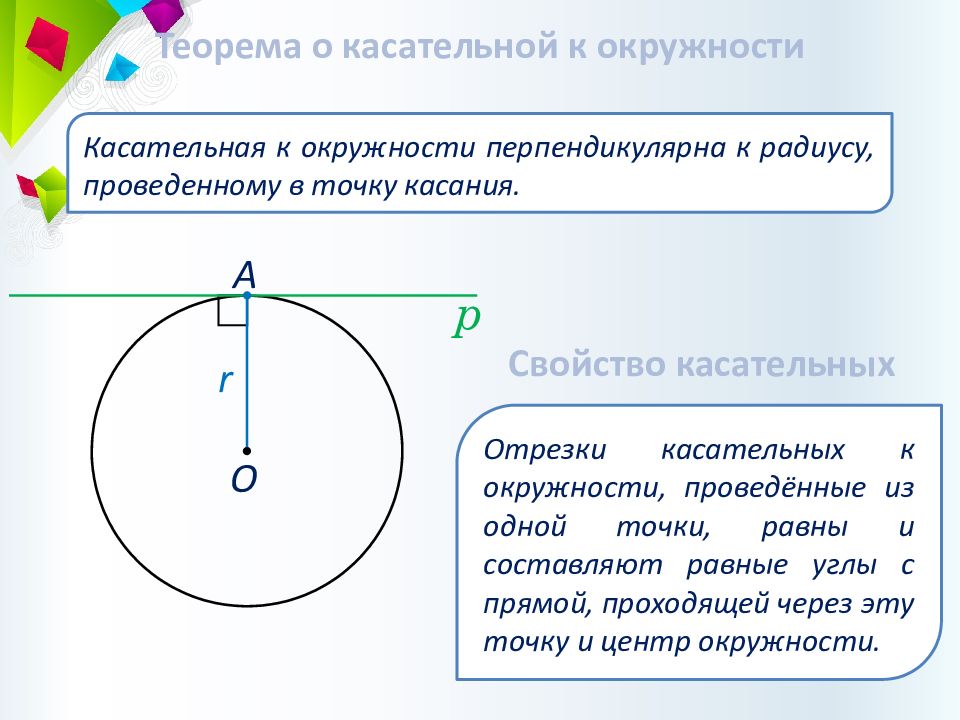
Теорема о касательной к окружности Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. р А О r Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Свойство касательных
Слайд 40
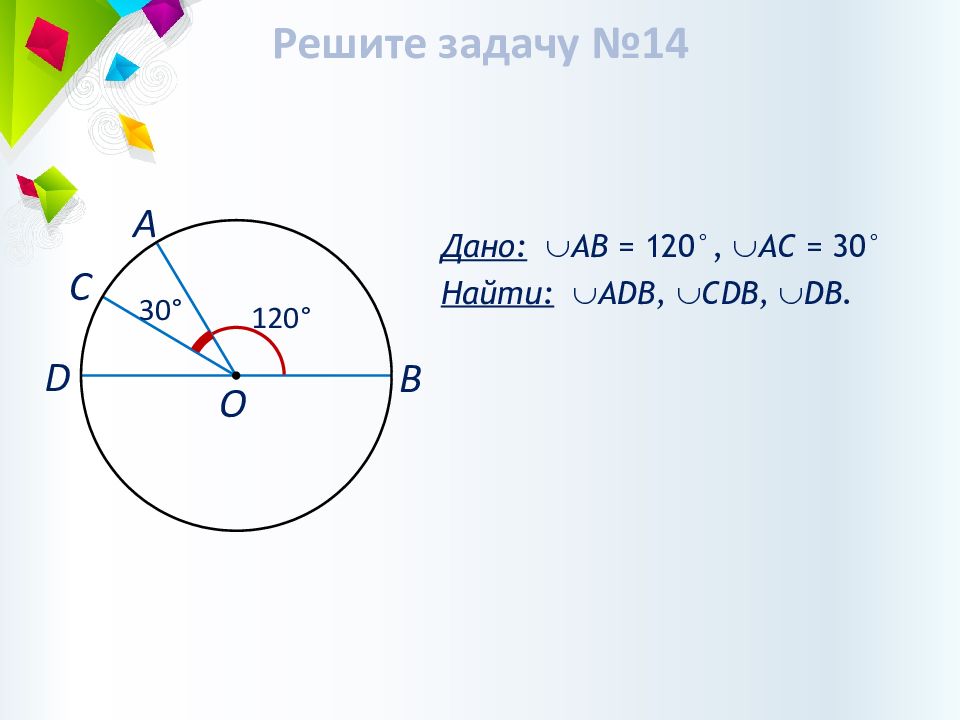
А О В С D 120° 30° Дано: АВ = 12 0°, AC = 30° Найти: А D В, CDB, DB. Решите задачу №14
Слайд 41
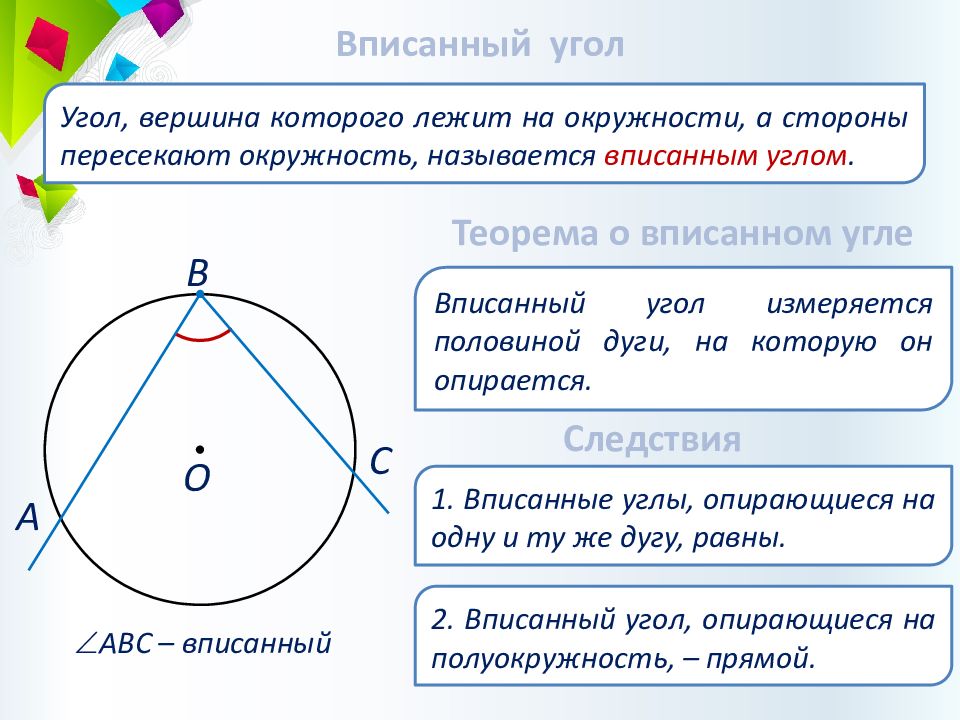
Вписанный угол Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. АВС – вписанный В О А С Теорема о вписанном угле Вписанный угол измеряется половиной дуги, на которую он опирается. 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны. Следствия 2. Вписанный угол, опирающиеся на полуокружность, – прямой.
Слайд 42
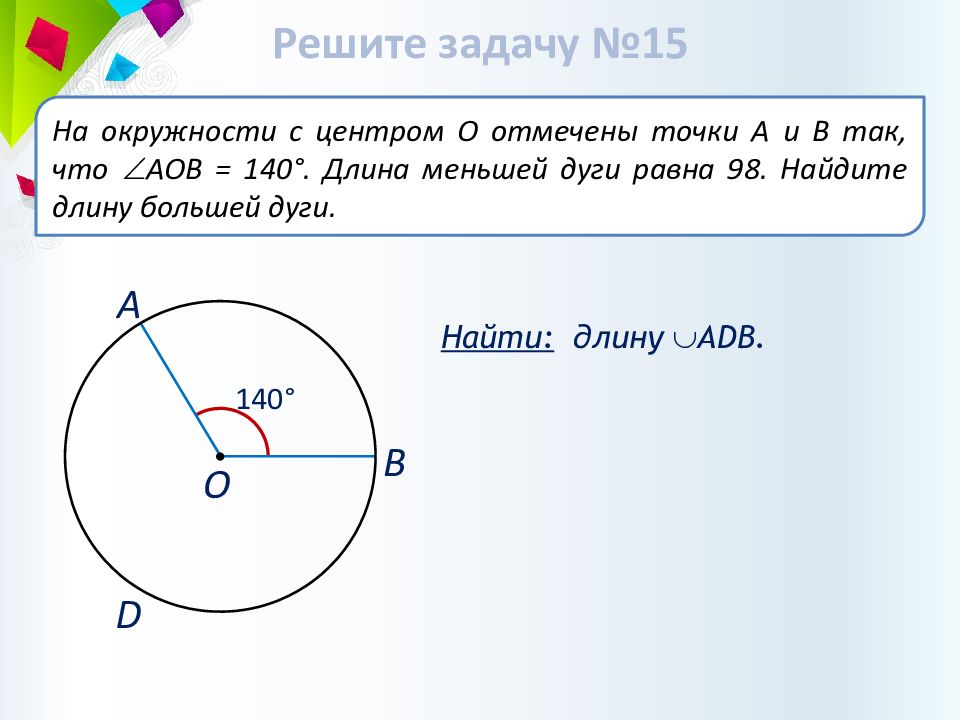
Найти: длину А D В. На окружности с центром О отмечены точки А и В так, что АОВ = 140°. Длина меньшей дуги равна 98. Найдите длину большей дуги. А О В 1 4 0° D Решите задачу №15
Слайд 43
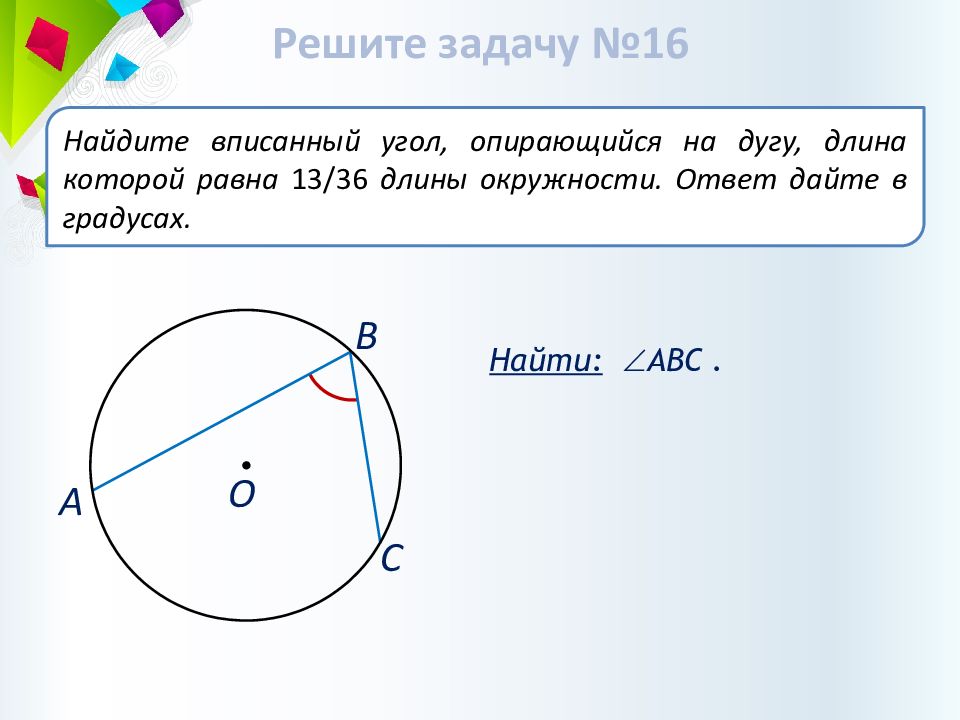
Найти: АВС. Найдите вписанный угол, опирающийся на дугу, длина которой равна 13/36 длины окружности. Ответ дайте в градусах. А О В С Решите задачу №16
Последний слайд презентации: Геометрия 9 класс Вводное повторение
Использованы ресурсы Геометрия, 7 – 9 классы: учеб. для общеобразоват. организаций / [ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ] – 6- е изд. – М.: Просвещение, 2016. Изучение геометрии в 7 – 9 классах: Пособие для учителей / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. – 7-е изд. – М.: Просвещение, 2009. http://mathege.ru/or/ege/Main.html - материалы открытого банка заданий ЕГЭ по математике.