Площадь параллелограмма Геометрия 8 класс
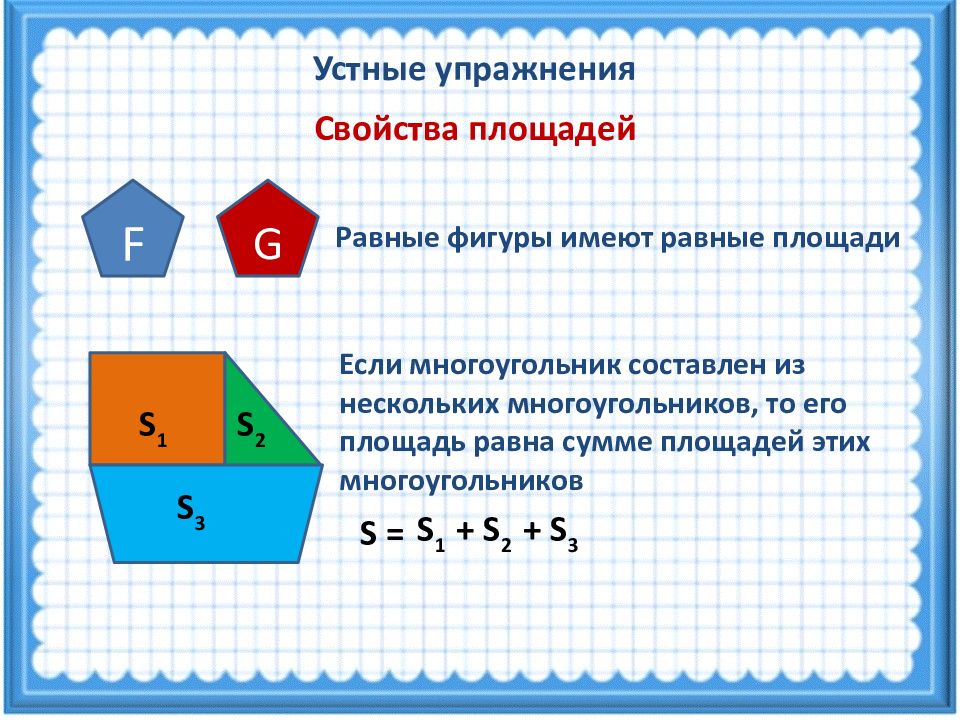
Устные упражнения Свойства площадей F G Равные фигуры имеют равные площади S 1 S 2 S 3 Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников S 1 + S 2 + S 3 S =
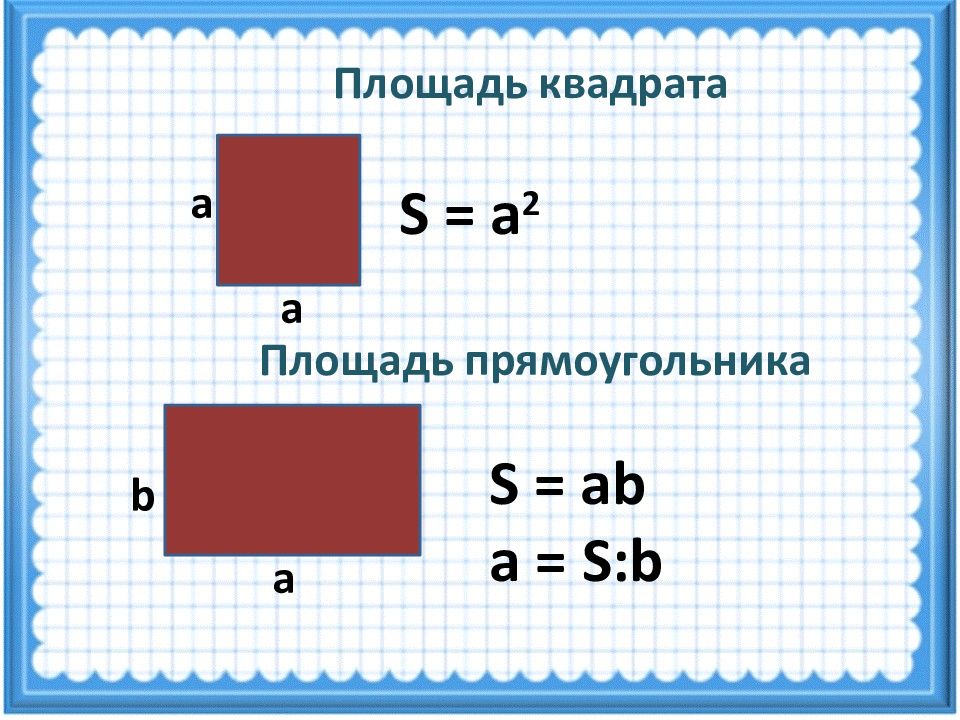
S = 8 2 =64см 2 1.Найдите площадь квадрата, если его сторона равна 8см 1) 16 2) 64 3) 32 Тест на повторение
а = 4см Р = 4·4 =16см 2.Найдите периметр квадрата, если площадь равна 16 см 2 1) 64 3) 16 2) 32 Тест на повторение
S = 10 2 :2=50см 2 3.Найдите площадь треугольника, если его катеты равны по 10см 3) 20 1) 50 2) 25 Тест на повторение
S = 10·8 = 80см 2 4.Найдите площадь прямоугольника, если его смежные стороны равны 10см и 8см 1) 36 3) 80 2) 40 Тест на повторение
S = (4·8):2= 16см 2 2) 32 3) 16 1) 24 Тест на повторение 4 8 5.Найдите площадь треугольника, если его катеты равны 4см и 8см
Площадь квадрата S = a 2 a a b a S = ab а = S:b Площадь прямоугольника
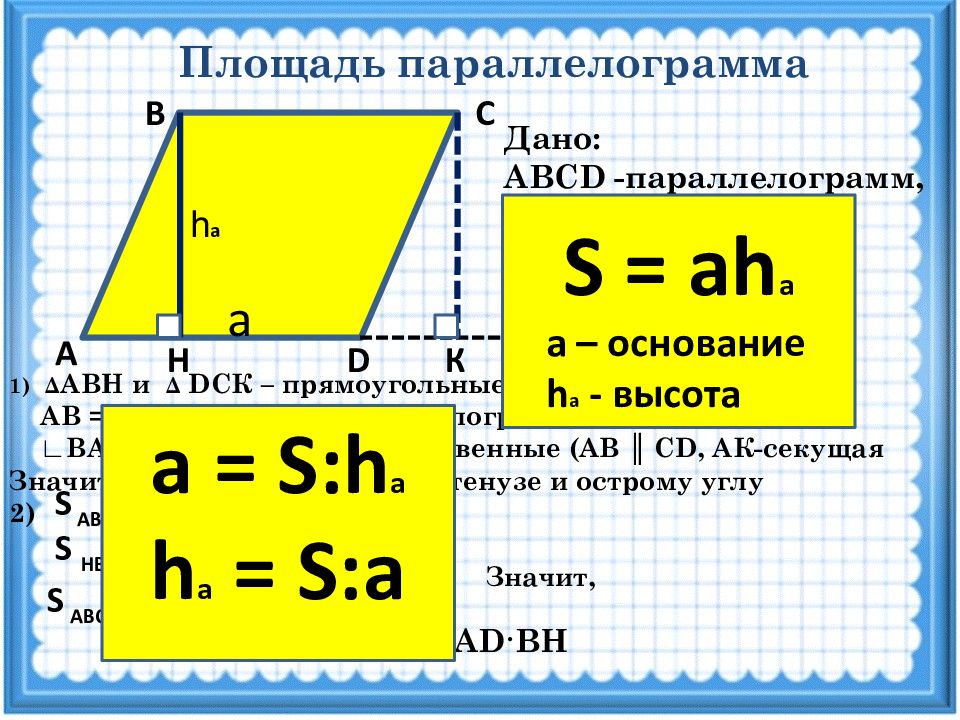
Площадь параллелограмма А D Н К С В Дано: ABCD -параллелограмм, ВН - высота AD - основание Доказать: S = AD·BH Решение Δ АВН и Δ DC К – прямоугольные, т.к. ВН ┴ AD, C К ┴ AD AB = CD, т.к. ABCD –параллелограмм ∟ВАН = ∟ CD К как соответственные ( AB ║ CD, A К-секущая Значит, Δ АВН = Δ DC К по гипотенузе и острому углу 2) Значит, = S AB Н S ABCD + S B Н DC S Н BC К = S DC К + S B Н DC S ABCD = S HBCK = ВС·ВН = AD ·ВН S = ah а а – основание h а - высота h а a а = S : h а h а = S :а
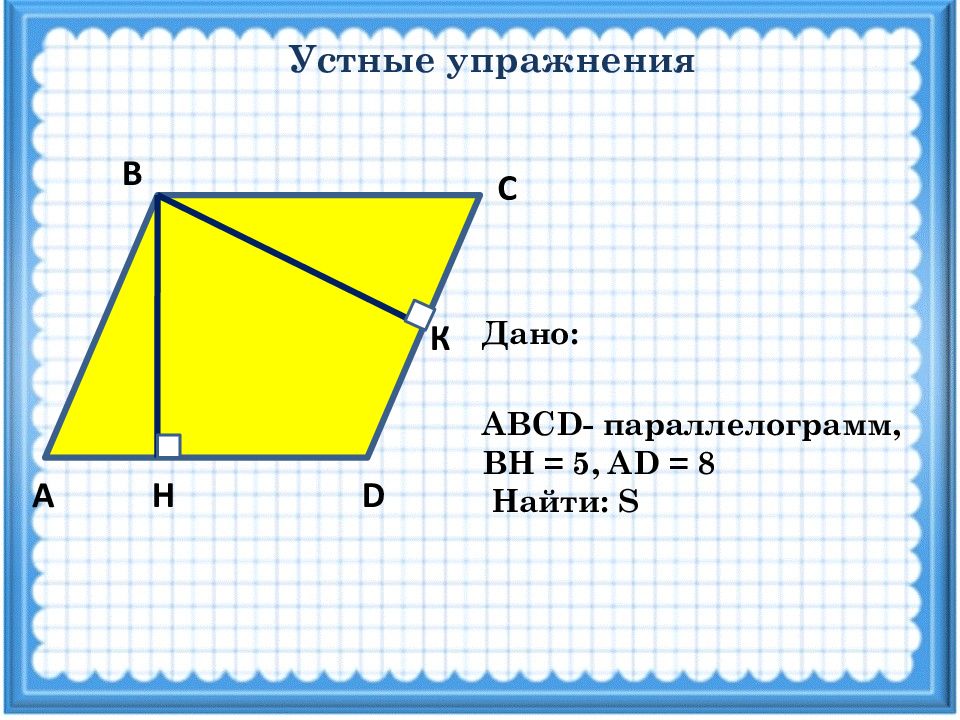
Устные упражнения А D Н С В К ABCD - параллелограмм, ВН = 5, А D = 8 Найти: S Дано:
Закрепление изученного материала №4 59 А) а = 15 см Решение: h = 12 c м S = a ·h = 15·12 = 180 c м 2 S - ? 15 х 12 30 15 18 0
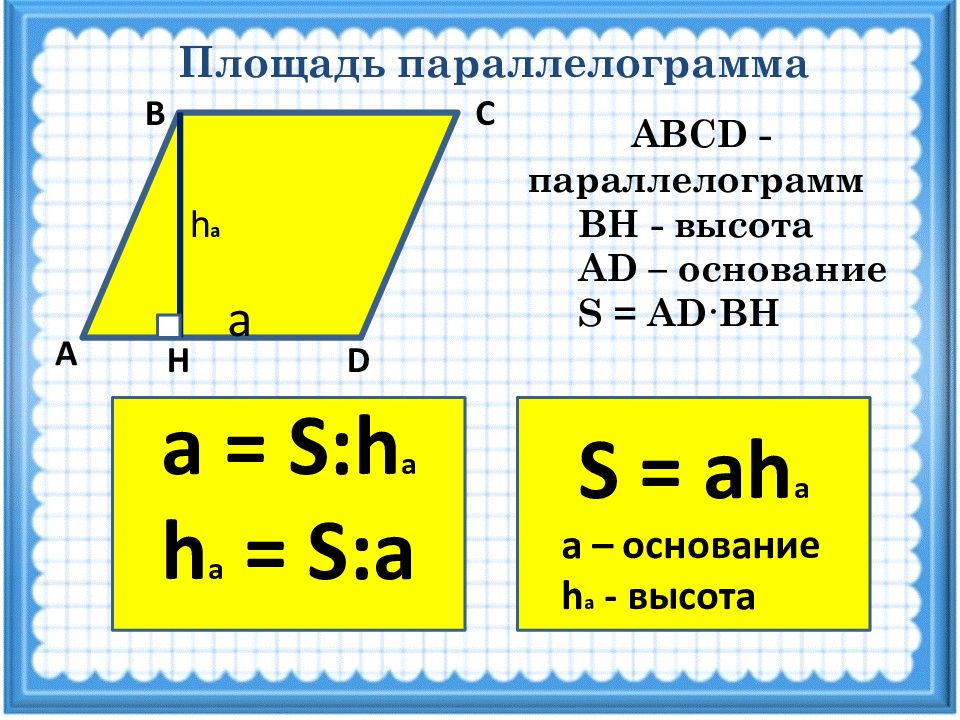
Площадь параллелограмма А D Н С В ABCD -параллелограмм ВН - высота AD – основание S = AD·BH S = ah а а – основание h а - высота h а a а = S : h а h а = S :а
Домашнее задание п. 5 1, с. 133 вопрос 4, №460, №462.
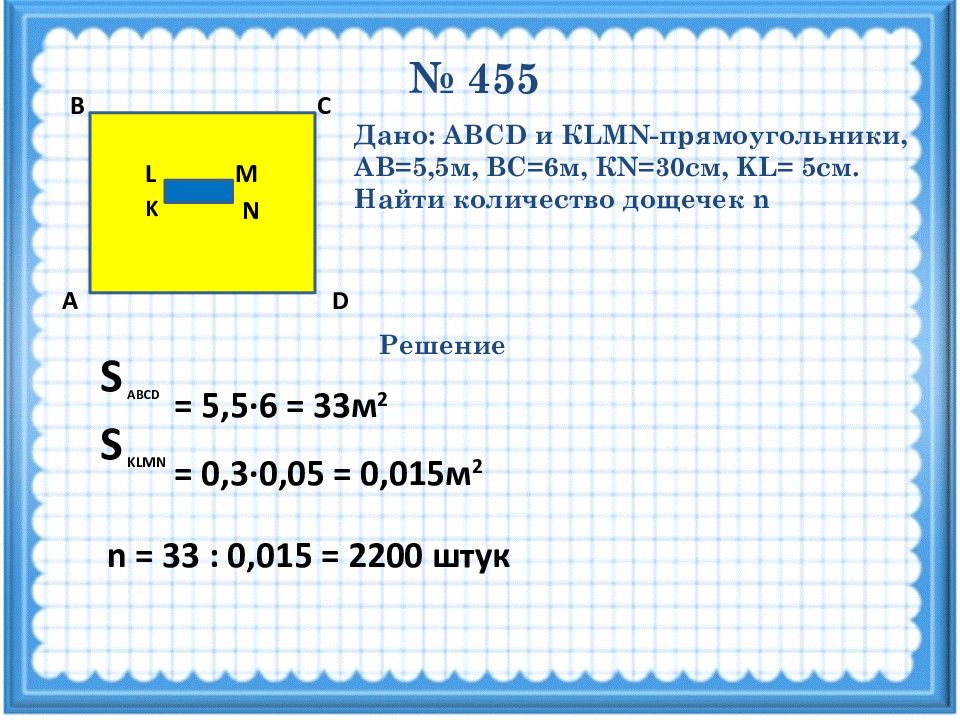
№ 455 M N K L D С В А Дано: ABCD и К LMN -прямоугольники, АВ=5,5м, ВС=6м, К N=30 см, KL = 5см. Найти количество дощечек n Решение S ABCD = 5, 5· 6 = 33м 2 = 0, 3·0, 0 5 = 0,015м 2 S KLMN n = 33 : 0, 0 15 = 2200 штук
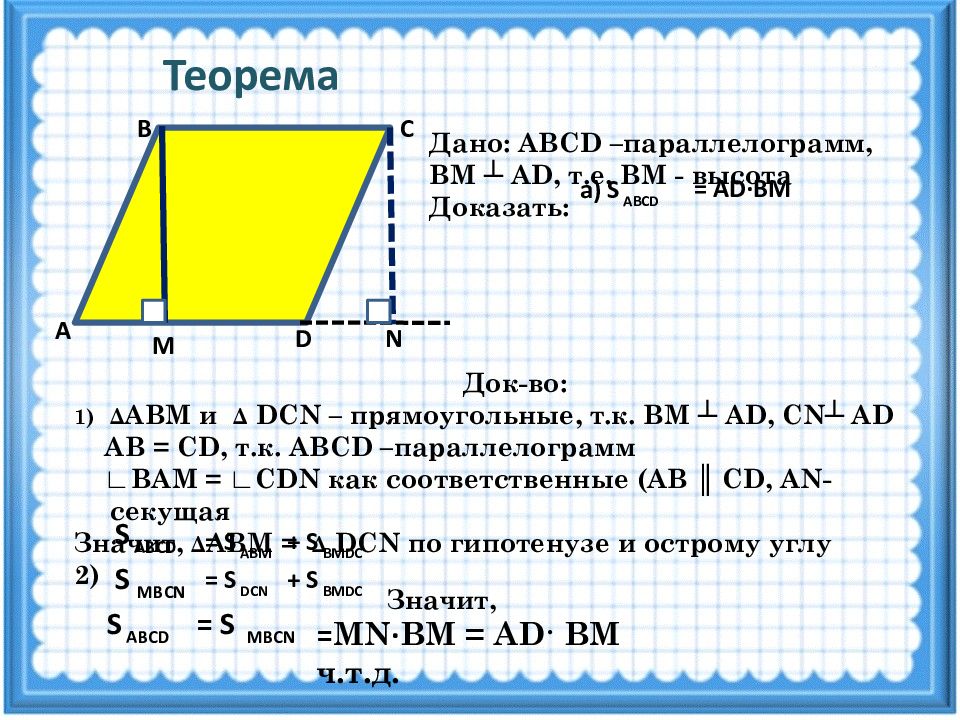
Теорема А D M N С В Дано: ABCD –параллелограмм, ВМ ┴ AD, т.е. ВМ - высота Доказать: а ) S ABCD = AD·BM Док-во : Δ АВМ и Δ DCN – прямоугольные, т.к. ВМ ┴ AD, CN┴ AD AB = CD, т.к. ABCD –параллелограмм ∟ВАМ = ∟ CDN как соответственные ( AB ║ CD, AN -секущая Значит, Δ АВМ = Δ DCN по гипотенузе и острому углу 2) = S AB М S ABCD + S B М DC S MBCN = S DCN + S B М DC S ABCD = S MBCN = MN · ВМ = AD · BM ч.т.д. Значит,
