Первый слайд презентации: Геометрия 8 класс Тема: Удвоение медианы. Центральная симметрия
Автор презентации: Попов дмитрий сергеевич
Слайд 2
Сегодня мы познакомимся с методом удвоения медианы, узнаем определение центральной симметрии.
Слайд 3: ВСПОМНИ!
Что называют трапецией? Четырёхугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией. Что называют основанием трапеции, а какие стороны называют боковыми? Параллельные стороны называются основаниями трапеции, непараллельные стороны – боковыми сторонами. Какую трапецию называют прямоугольной? Если один из углов трапеции прямой, то она называется прямоугольной. Какую трапецию называют равнобокой? Если боковые стороны трапеции равны, то она называется равнобедренной трапецией (равнобокой).
Слайд 6
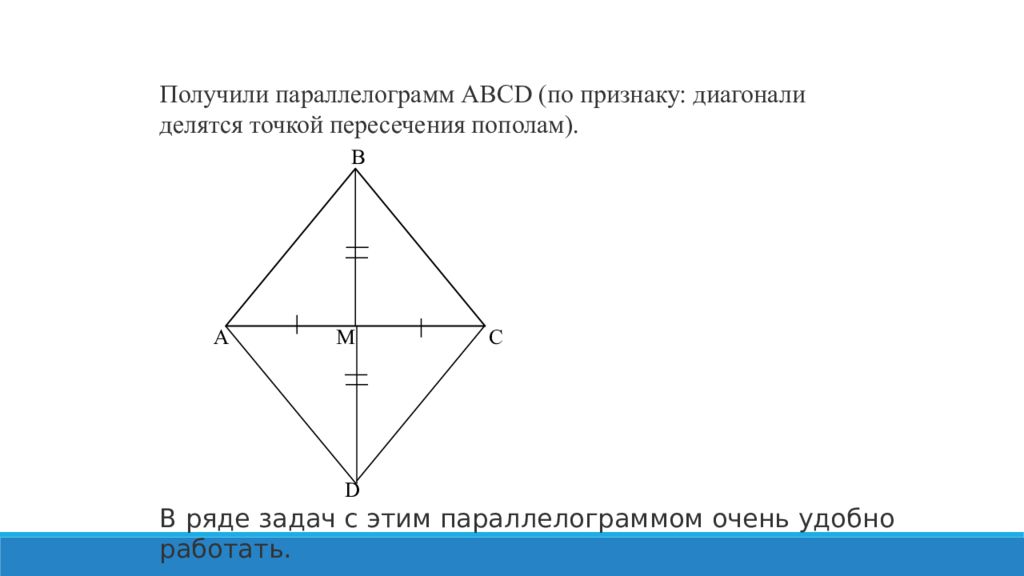
Получили параллелограмм ABCD (по признаку: диагонали делятся точкой пересечения пополам). В А М С D В ряде задач с этим параллелограммом очень удобно работать.
Слайд 7
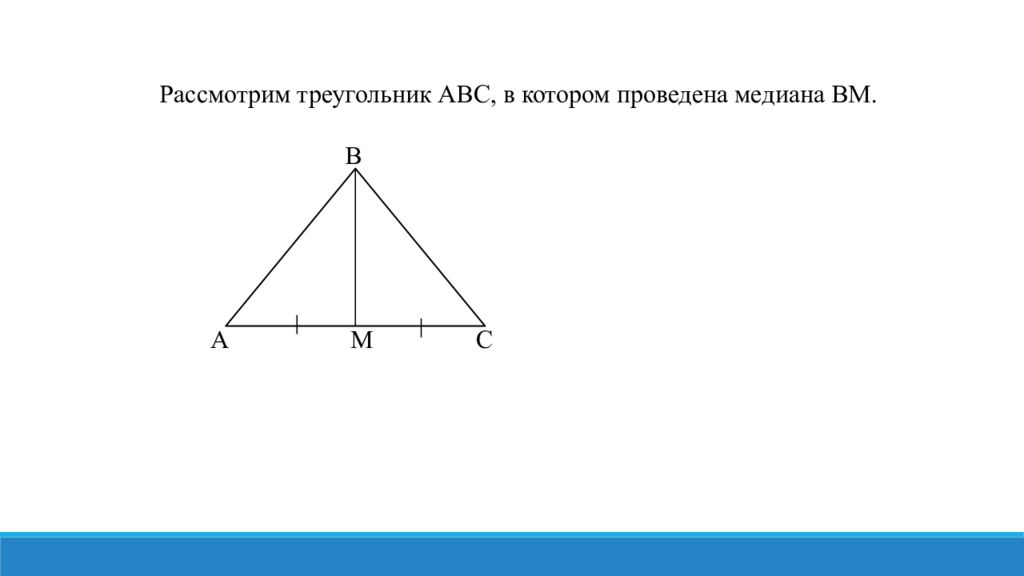
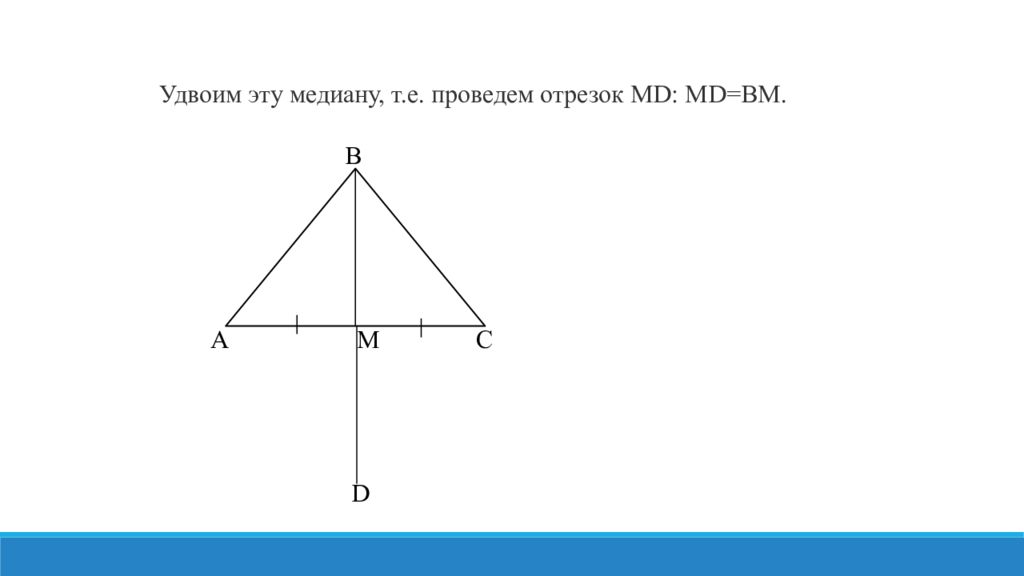
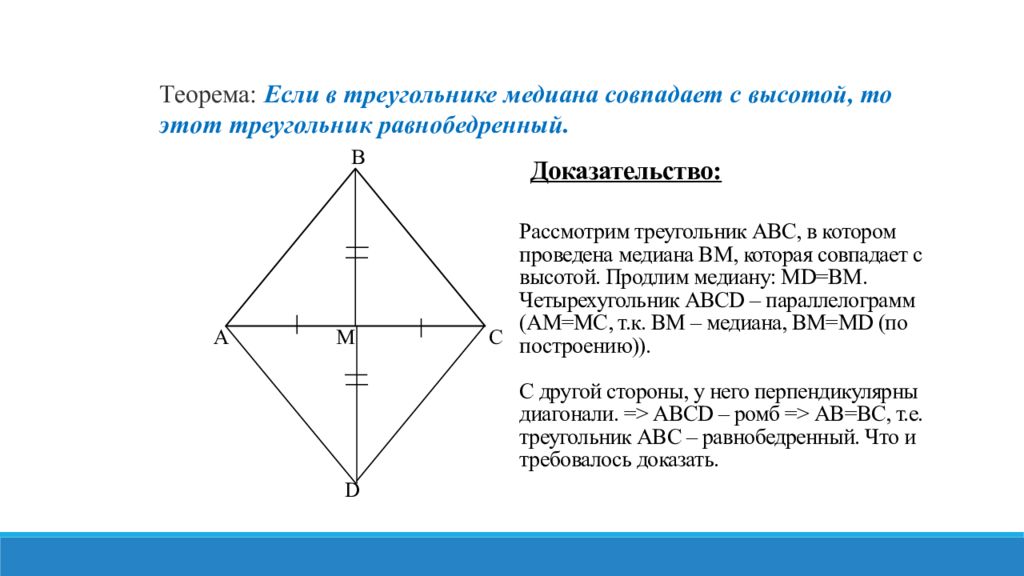
Теорема: Если в треугольнике медиана совпадает с высотой, то этот треугольник равнобедренный. В А М С D Доказательство: Рассмотрим треугольник ABC, в котором проведена медиана BM, которая совпадает с высотой. Продлим медиану: MD=BM. Четырехугольник ABCD – параллелограмм (AM=MC, т.к. BM – медиана, BM=MD (по построению)). С другой стороны, у него перпендикулярны диагонали. => ABCD – ромб => AB=BC, т.е. треугольник ABC – равнобедренный. Что и требовалось доказать.
Слайд 8
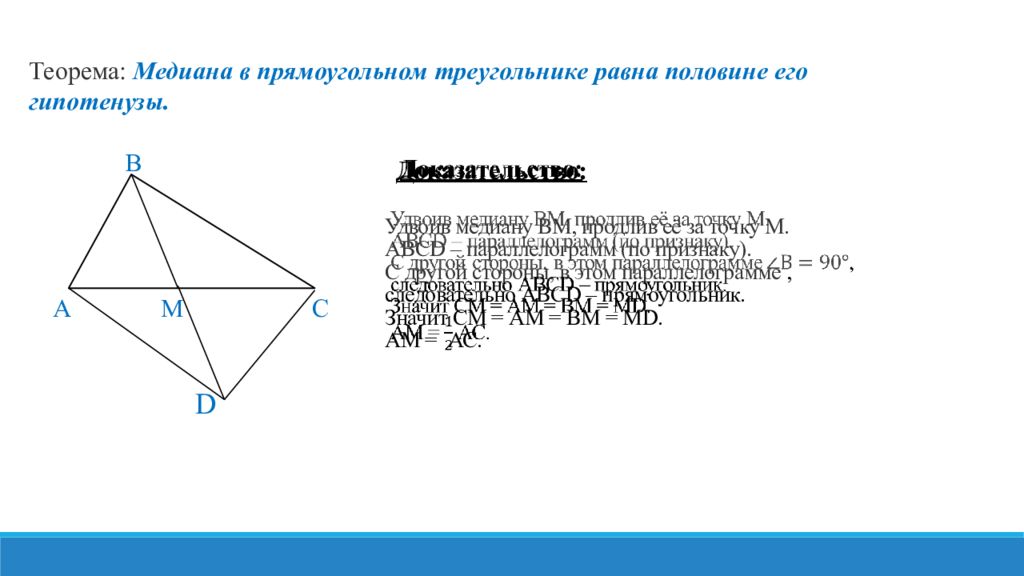
Теорема: Медиана в прямоугольном треугольнике равна половине его гипотенузы. В А M С D Доказательство: Удвоив медиану ВМ, продлив её за точку М. АВС D – параллелограмм (по признаку). C другой стороны, в этом параллелограмме, следовательно АВС D – прямоугольник. Значит СМ = АМ = ВМ = М D. АМ = АС.
Слайд 9
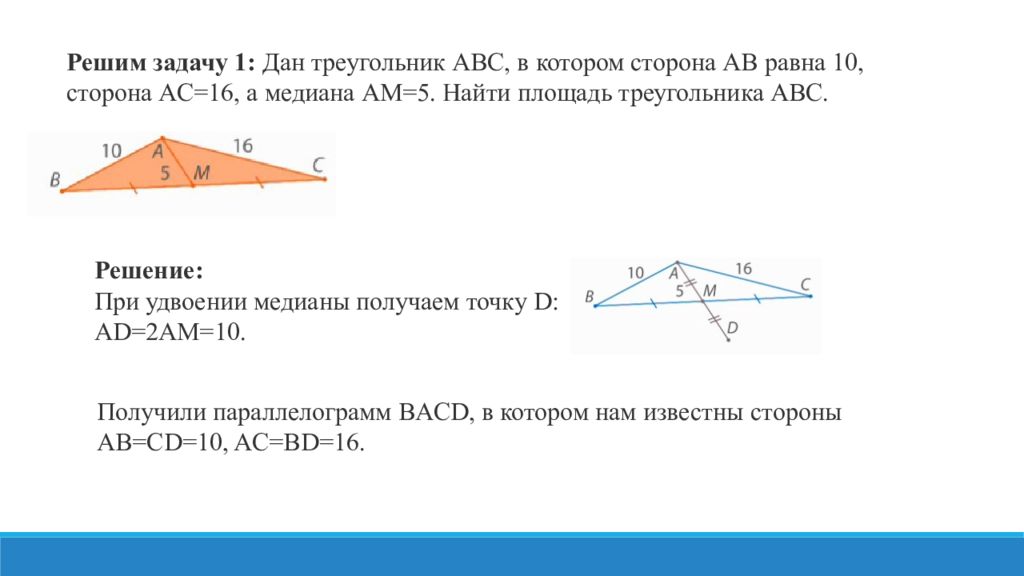
Решим задачу 1: Дан треугольник ABC, в котором сторона AB равна 10, сторона AC=16, а медиана AM=5. Найти площадь треугольника ABC. Решение: При удвоении медианы получаем точку D : AD=2AM=10. Получили параллелограмм BACD, в котором нам известны стороны AB=CD=10, AC=BD=16.
Слайд 10
Продолжение решения задачи 1 Рассмотрим треугольник BAD. В этом треугольнике мы знаем все 3 стороны: 10, 10, 16. Получился равнобедренный треугольник. Проведём высоту АН. По теореме Пифагора АН = 36. S BAD = · BD · AH = · 16 · 6 = 48. S ABCD = · S ABD = · S ABC S ABC = S ABD = 48.
Слайд 11: C делаем вывод:
Если в задаче дана медиана, то очень часто полезно ее удвоить, чтобы свести задачу к параллелограмму, ромбу или прямоугольнику, с помощью чего можно решать ряд задач.
Слайд 12: Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение: Центральной симметрие й называется симметрия относительно точки. На картинках центральная симметрия: точка O здесь — центр симметрии. Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Слайд 13
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
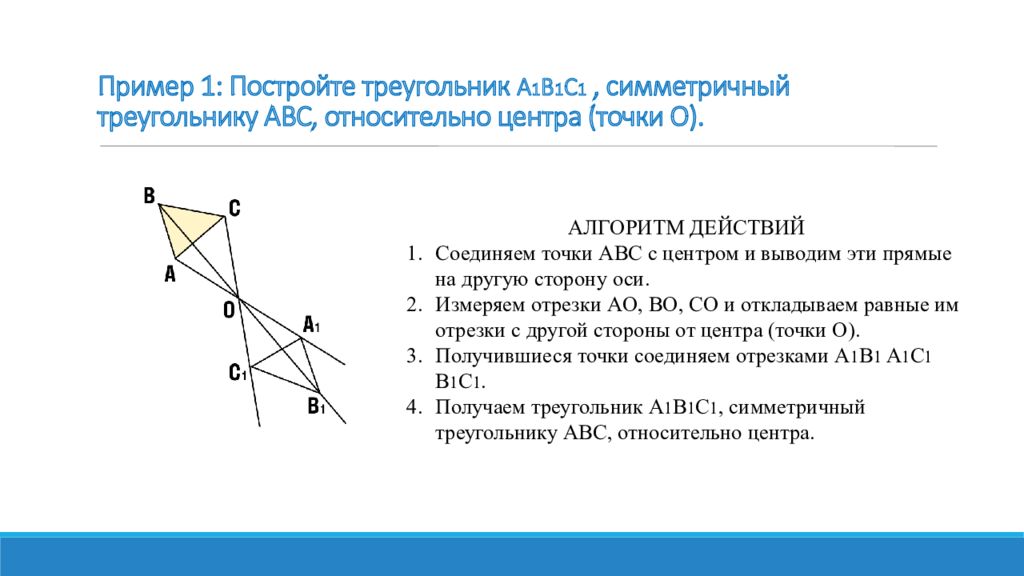
АЛГОРИТМ ДЕЙСТВИЙ Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О). Получившиеся точки соединяем отрезками A 1 B 1 A 1 C 1 B 1 C 1. Получаем треугольник A 1 B 1 C 1, симметричный треугольнику ABC, относительно центра.
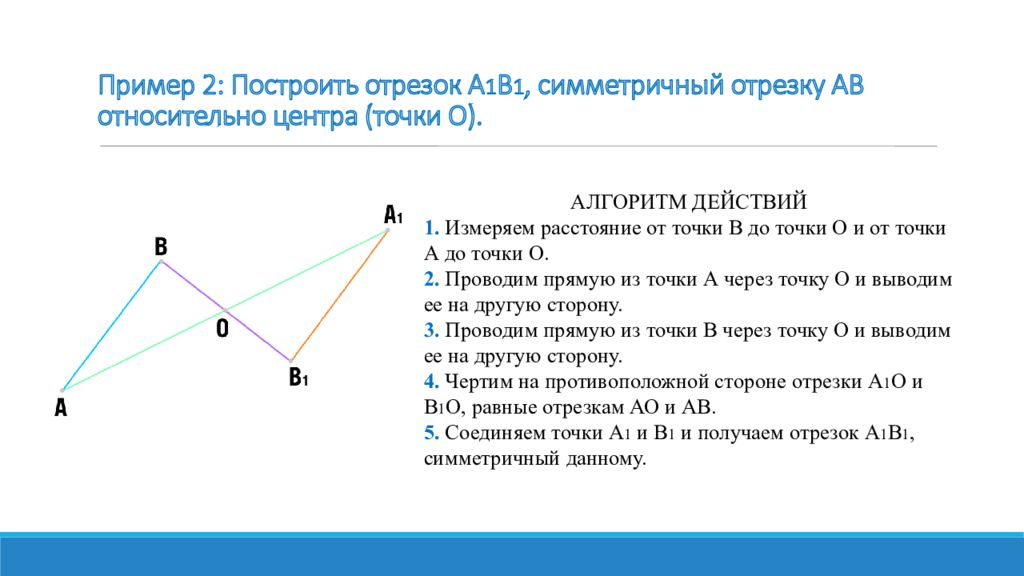
Слайд 15: Пример 2: Построить отрезок A 1 B 1, симметричный отрезку AB относительно центра (точки О)
АЛГОРИТМ ДЕЙСТВИЙ 1. Измеряем расстояние от точки B до точки О и от точки А до точки О. 2. Проводим прямую из точки А через точку О и выводим ее на другую сторону. 3. Проводим прямую из точки B через точку О и выводим ее на другую сторону. 4. Чертим на противоположной стороне отрезки А 1 О и B 1 О, равные отрезкам АО и АB. 5. Соединяем точки A 1 и B 1 и получаем отрезок A 1 B 1, симметричный данному.
Слайд 16: Задачи для классной работы:
1. Две стороны треугольника равны 10 и 12, а медиана, проведенная к третьей стороне, равна 5. Найдите площадь треугольника. 2. Медиана треугольника образует с его сторонами, выходящими из той же вершины, углы 40° и 70°. Докажите, что эта медиана равна половине одной из них. 3. В треугольнике ABC проведена медиана BM. Найдите BC, если BAC = 30°, а BMC =45°. В выпуклом четырёхугольнике ABCD стороны AB, BC и CD равны, M — середина стороны AD.
Слайд 18: Домашнее задание
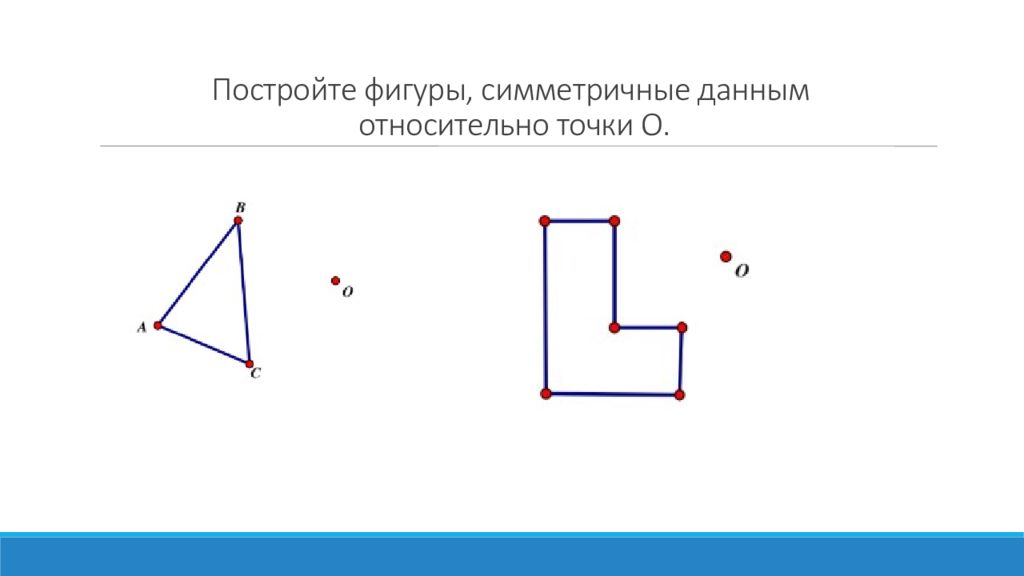
Найдите гипотенузу прямоугольного треугольника, если высота, проведённая к ней, равна 1 см, а один из углов треугольника равен 15 º. Известно, что BMC = 90◦. Найдите угол между диагоналями четырёхугольника ABCD. Постройте фигуры, симметричные данным относительно точки О.
Последний слайд презентации: Геометрия 8 класс Тема: Удвоение медианы. Центральная симметрия: Использованные источники:
https://multiurok.ru/files/praktichieskaia-rabota-po-tiemie-tsientral-naia-i-.html https://yandex.ru/video/preview/10270951172070887587 https://interneturok.ru/lesson/geometry/9-klass/itogovoe-povtorenie-kursa-geometrii-za-79-klassy/udvoenie-mediany https://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya https://drive.google.com/drive/folders/1xIzzlOUxFTs7161-IwoKiUdl5R9fsECT