03.11.20 г. Числовая окружность на координатной плоскости
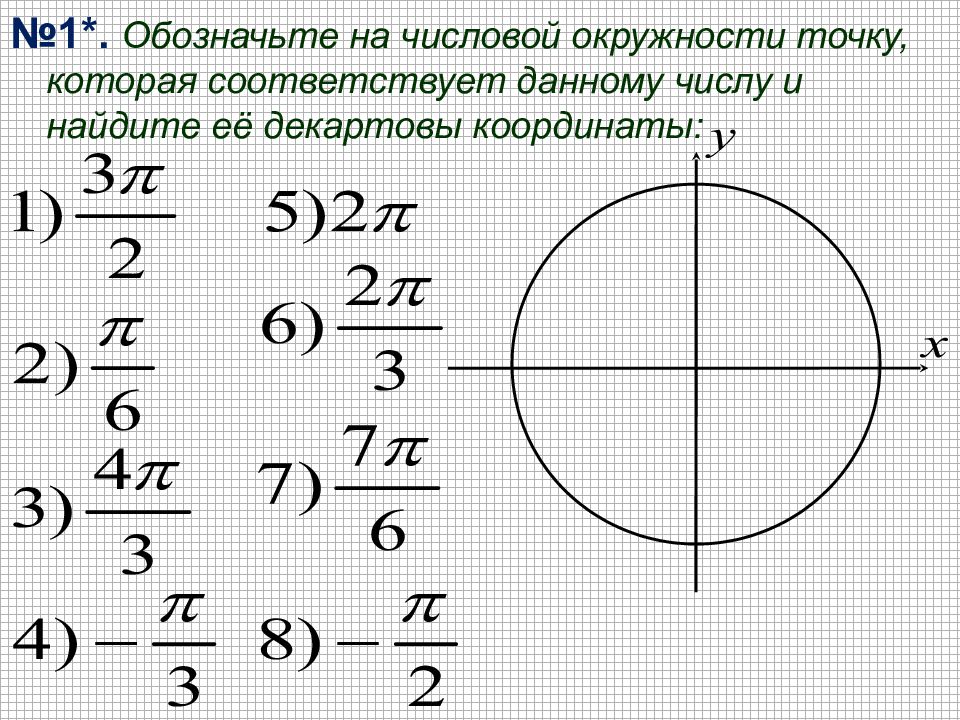
№1*. Обозначьте на числовой окружности точку, которая соответствует данному числу и найдите её декартовы координаты:
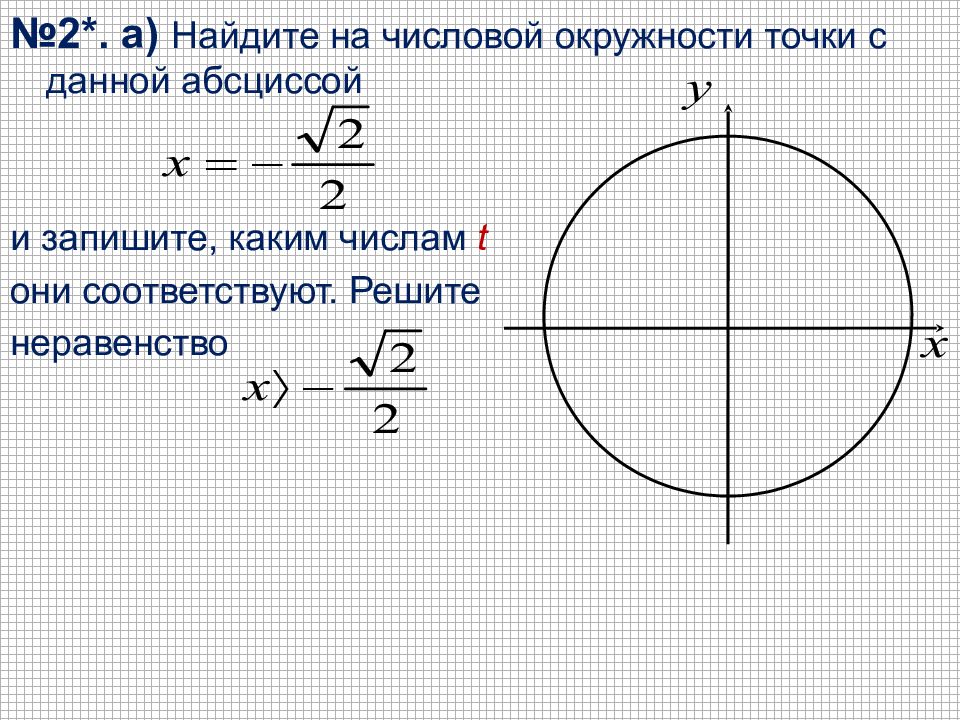
№2*. а) Найдите на числовой окружности точки с данной абсциссой и запишите, каким числам t они соответствуют. Решите неравенство
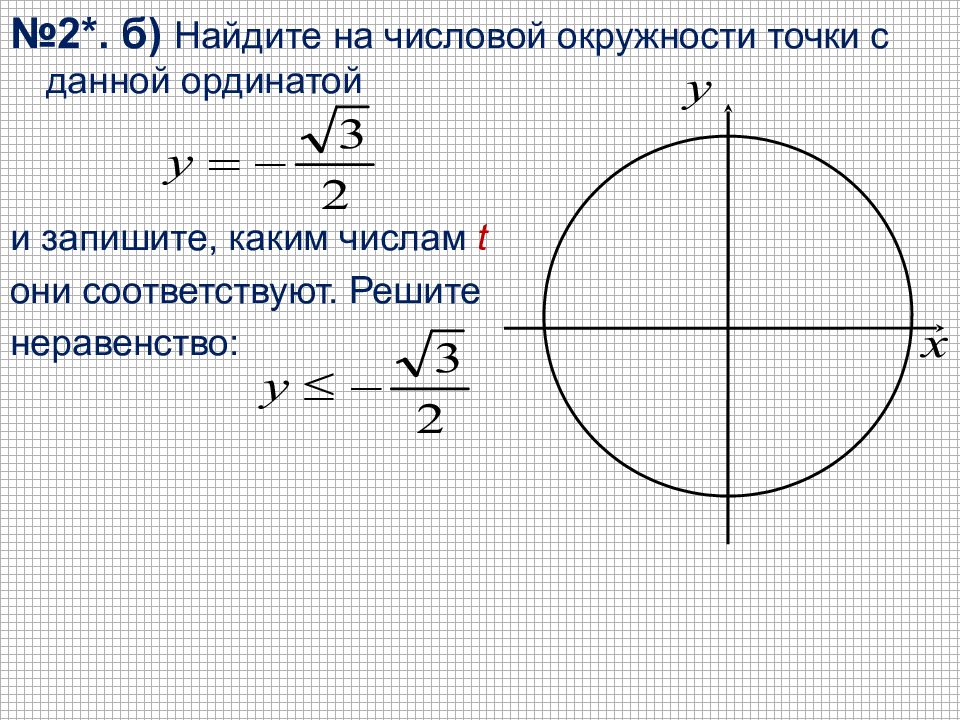
№2*. б) Найдите на числовой окружности точки с данной ординатой и запишите, каким числам t они соответствуют. Решите неравенство:
03.11.20 г. Синус и косинус. Тангенс и котангенс.
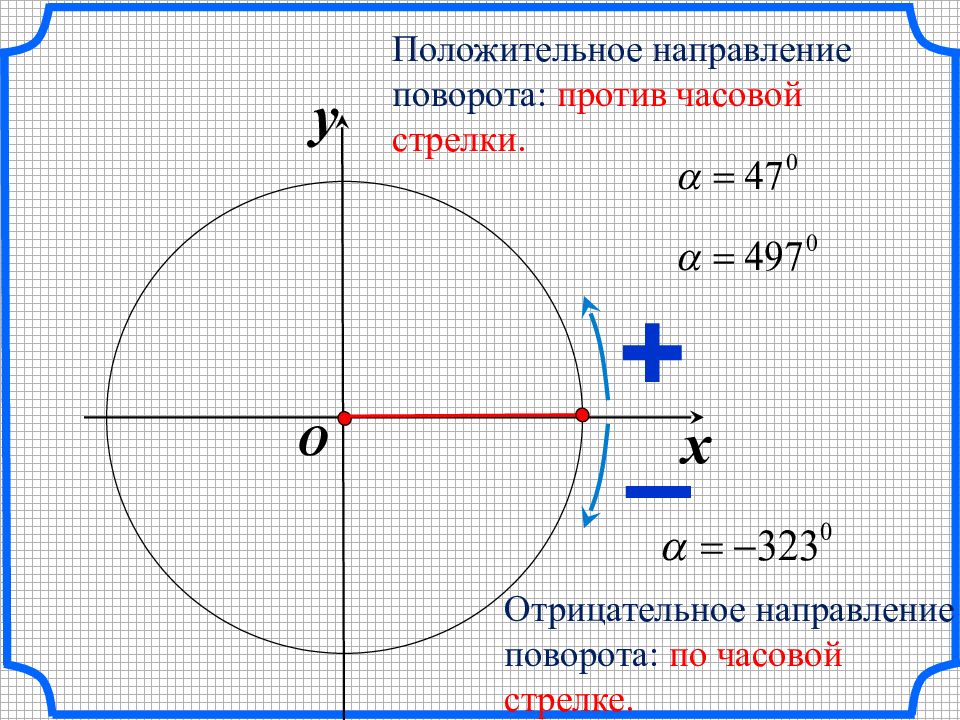
x y O Положительное направление поворота: против часовой стрелки. Отрицательное направление поворота: по часовой стрелке. + –
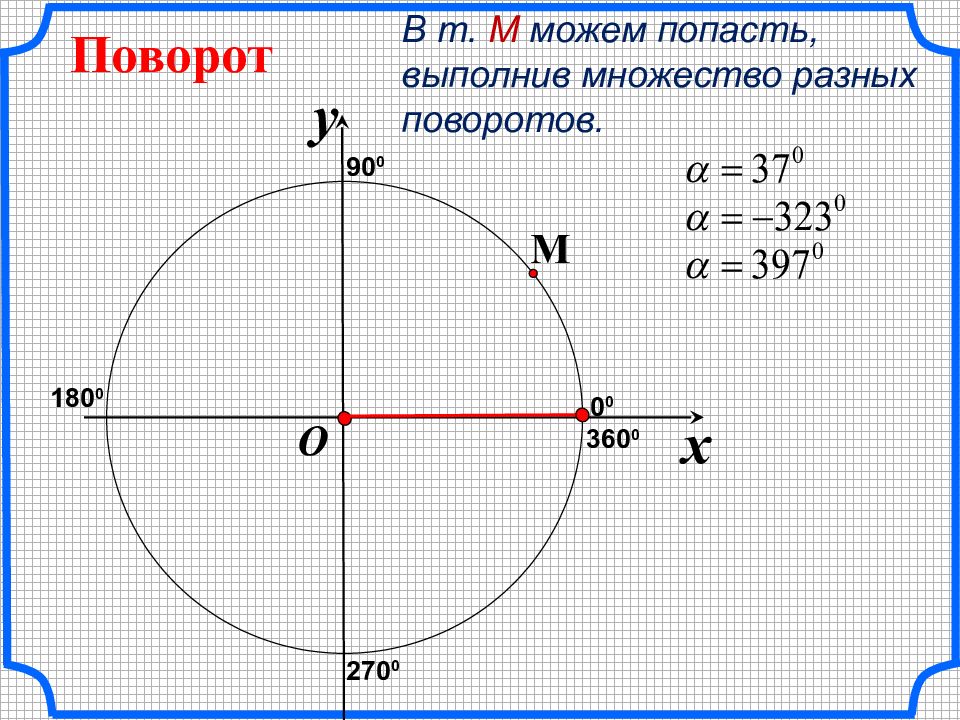
x y O Поворот M В т. М можем попасть, выполнив множество разных поворотов. 90 0 180 0 270 0 360 0 0 0
x Единичная окружность r = 1 y O x y D * * M ( x;y )
x Единичная окружность r = 1 y O x y D * * M ( x;y )
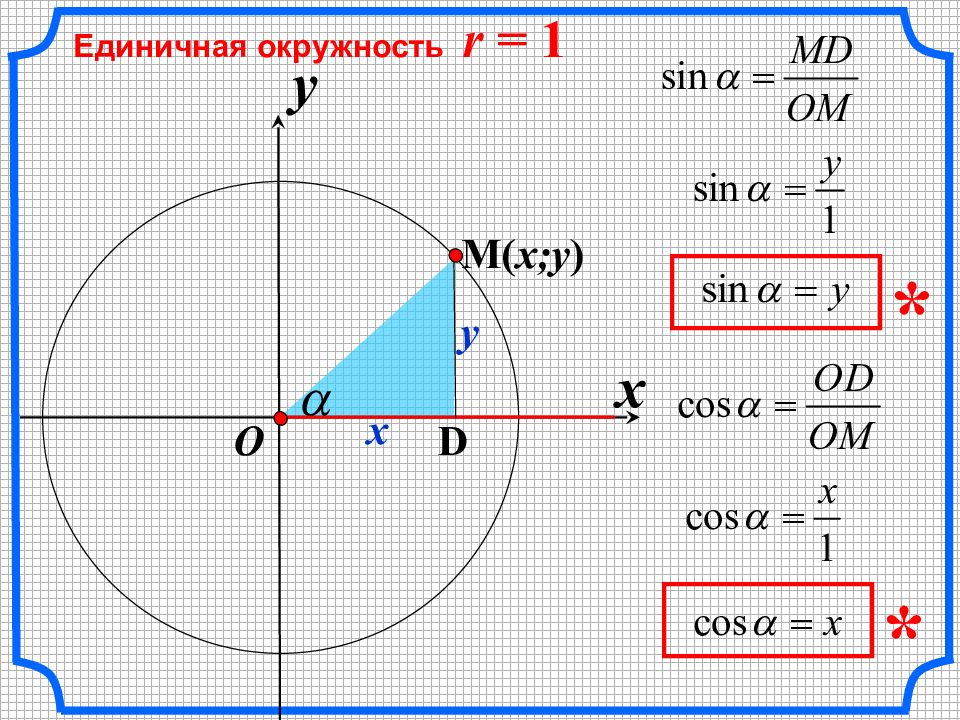
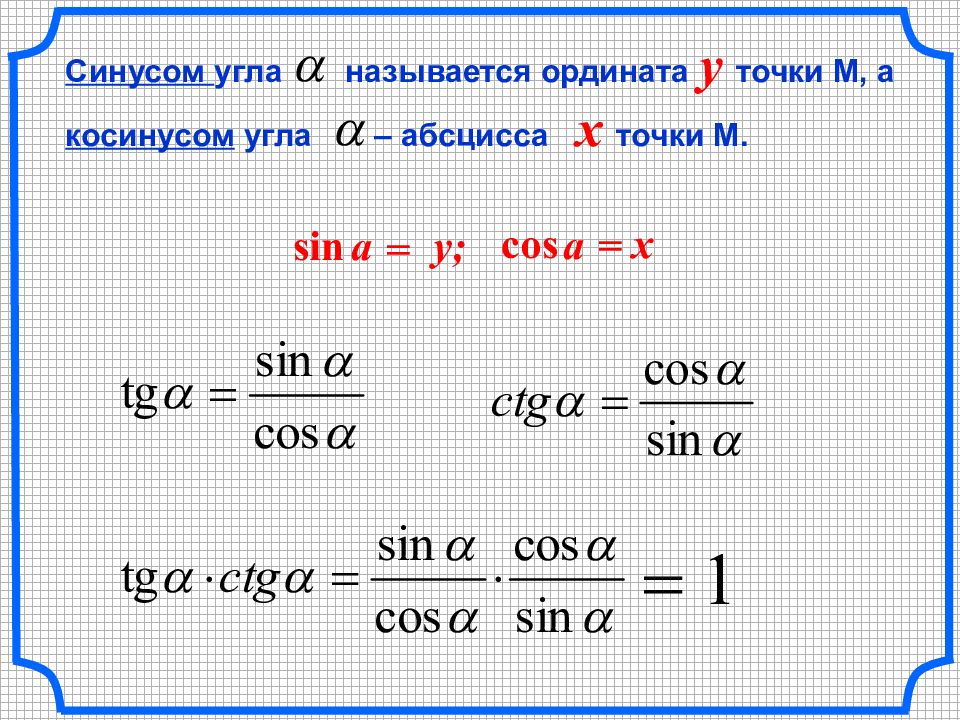
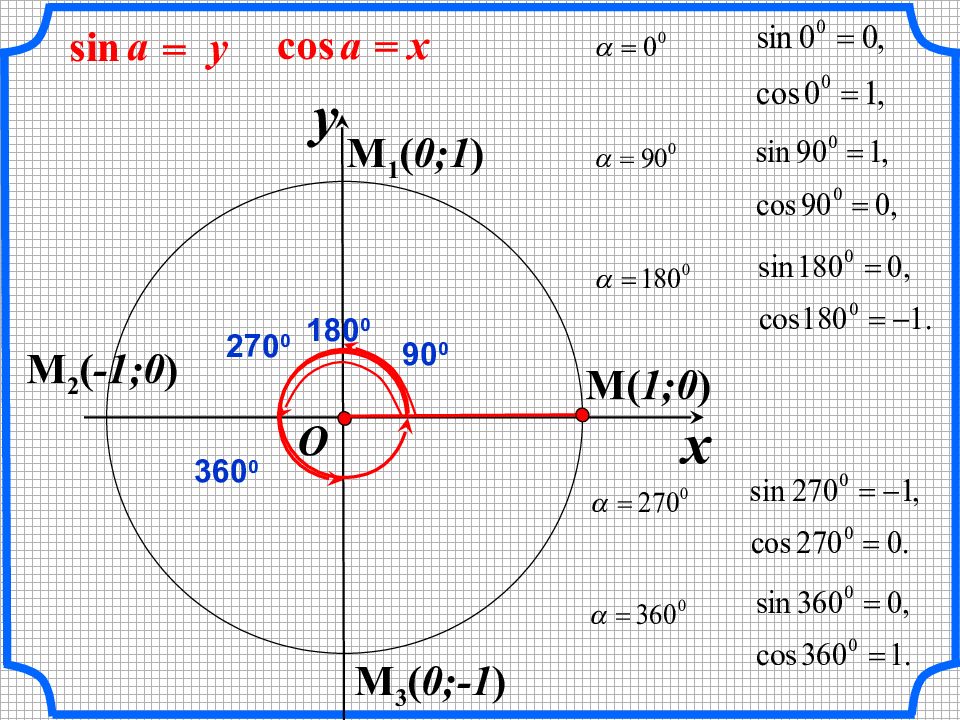
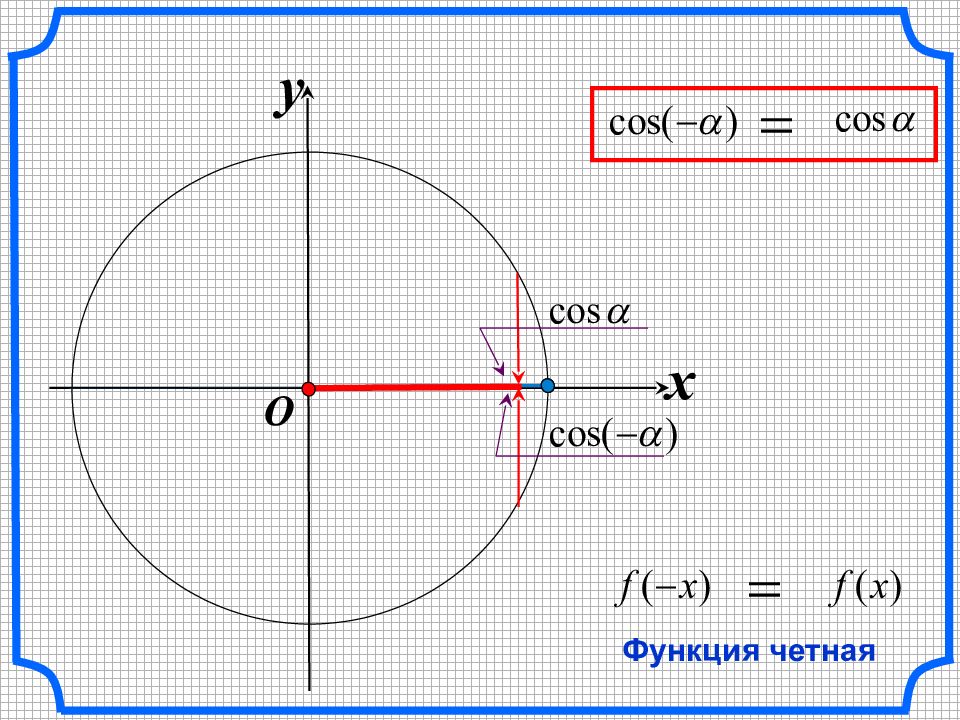
C инусом угла называется ордината y точки М, а косинусом угла – абсцисса x точки М. x = a cos y ; = a sin
M ( 1;0 ) x y O x = a cos y = a sin M 1 ( 0;1 ) 90 0 180 0 M 2 ( -1;0 ) M 3 ( 0;-1 ) 270 0 360 0
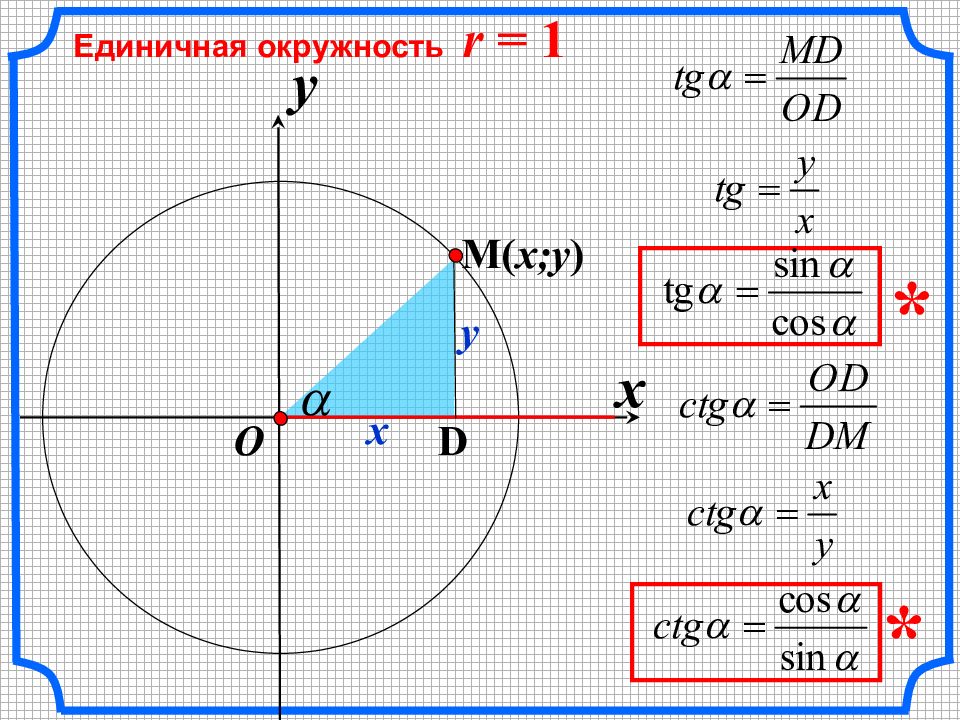
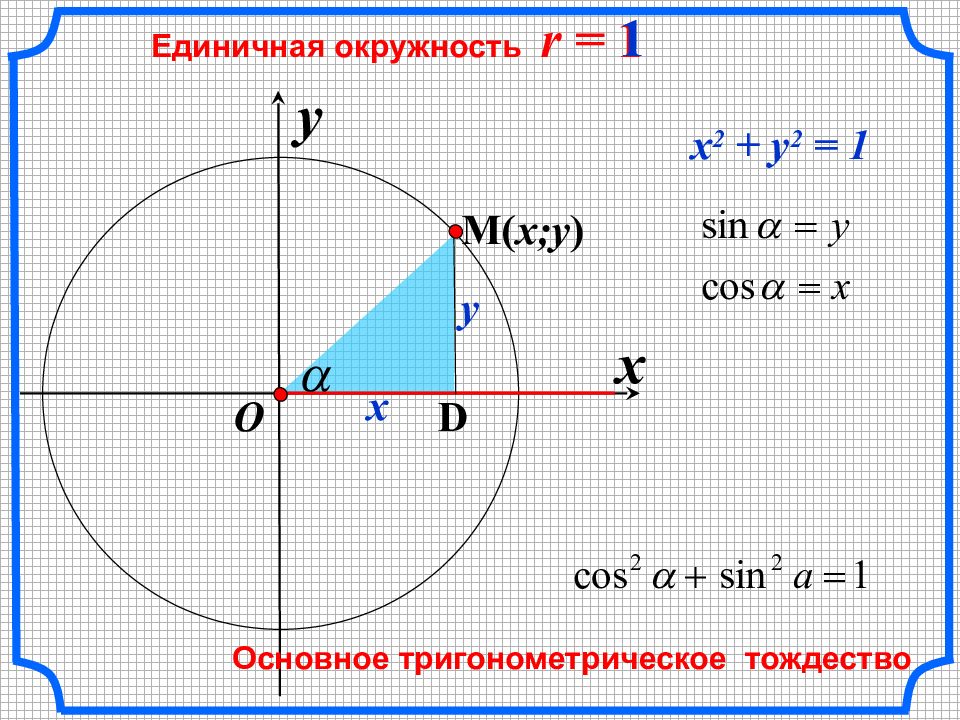
x Единичная окружность r = 1 y O x y D M ( x;y ) x 2 + y 2 = 1 1 Основное тригонометрическое тождество
x y O Если угол острый, то и I
x y O Если угол тупой, то и II
x y O III Если угол, то и
x y O IV Если угол, то и
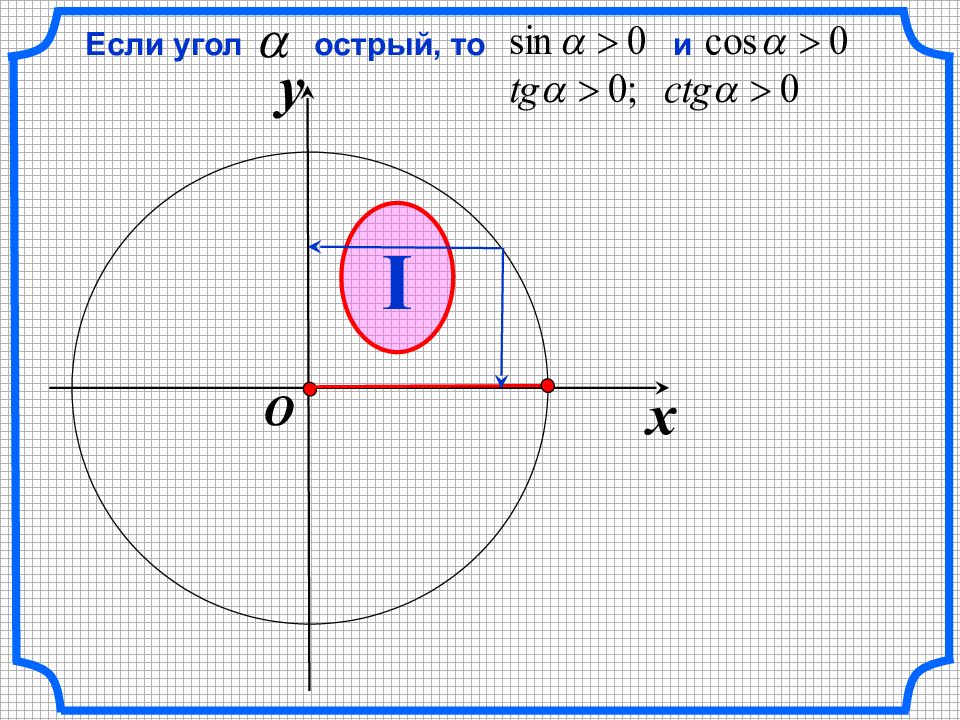
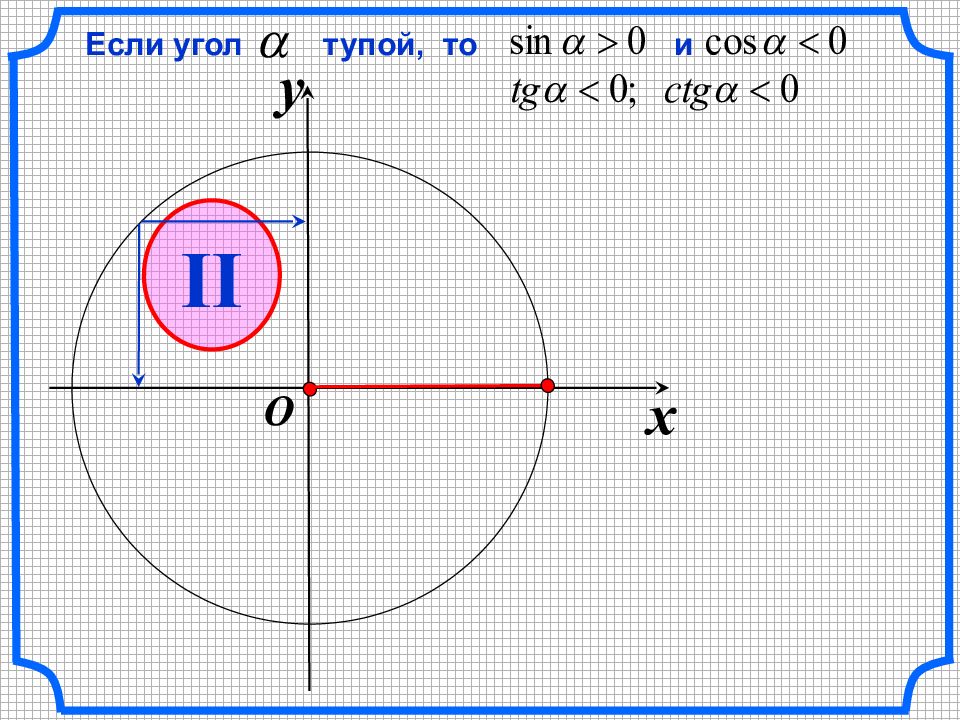
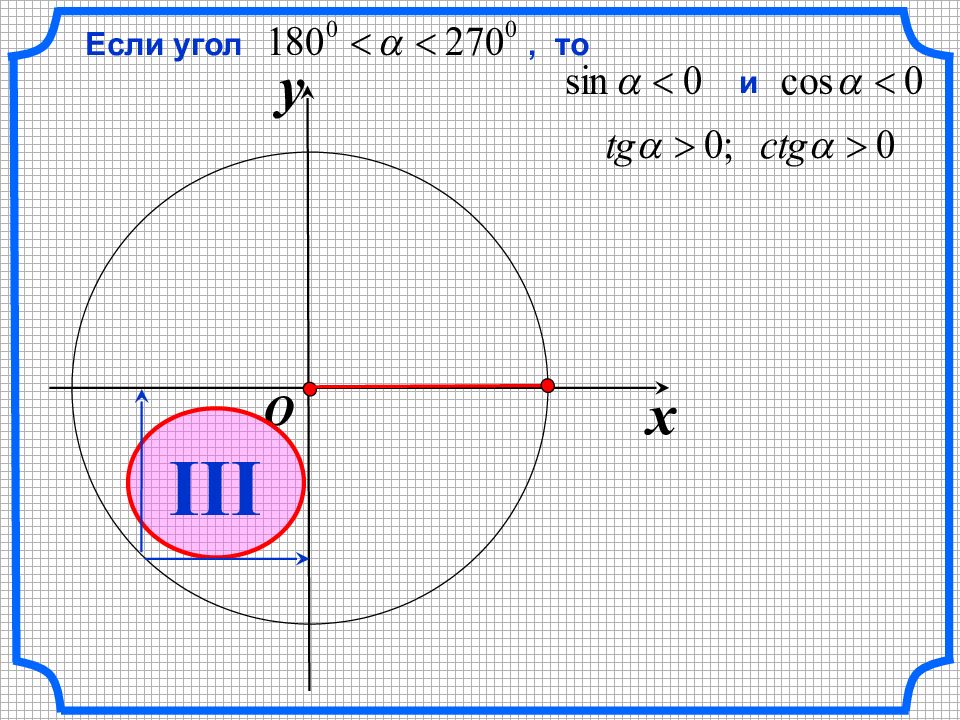
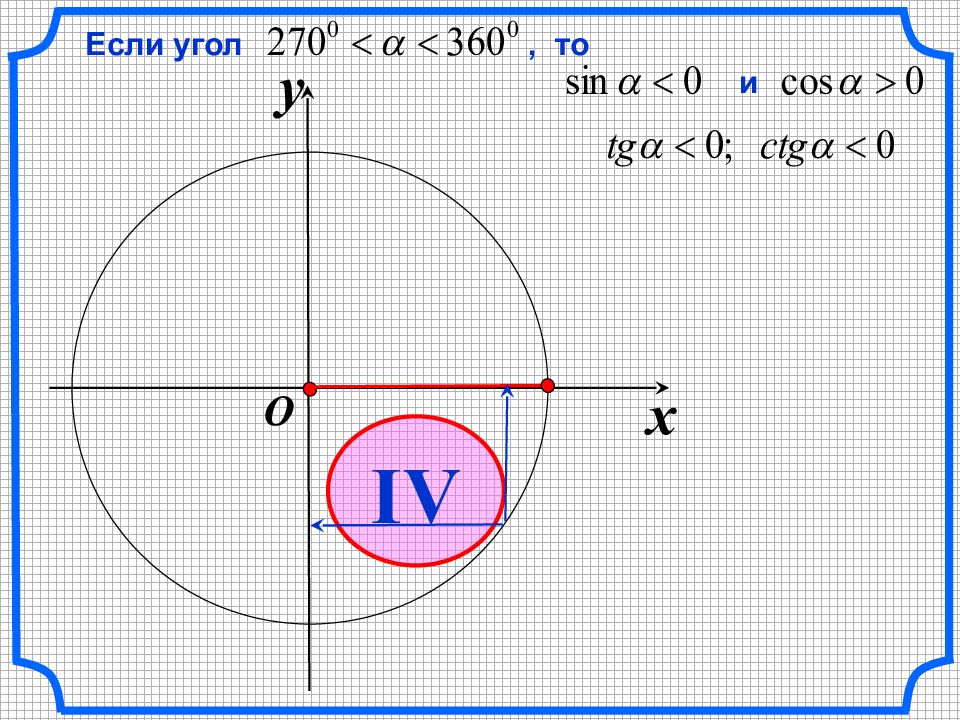
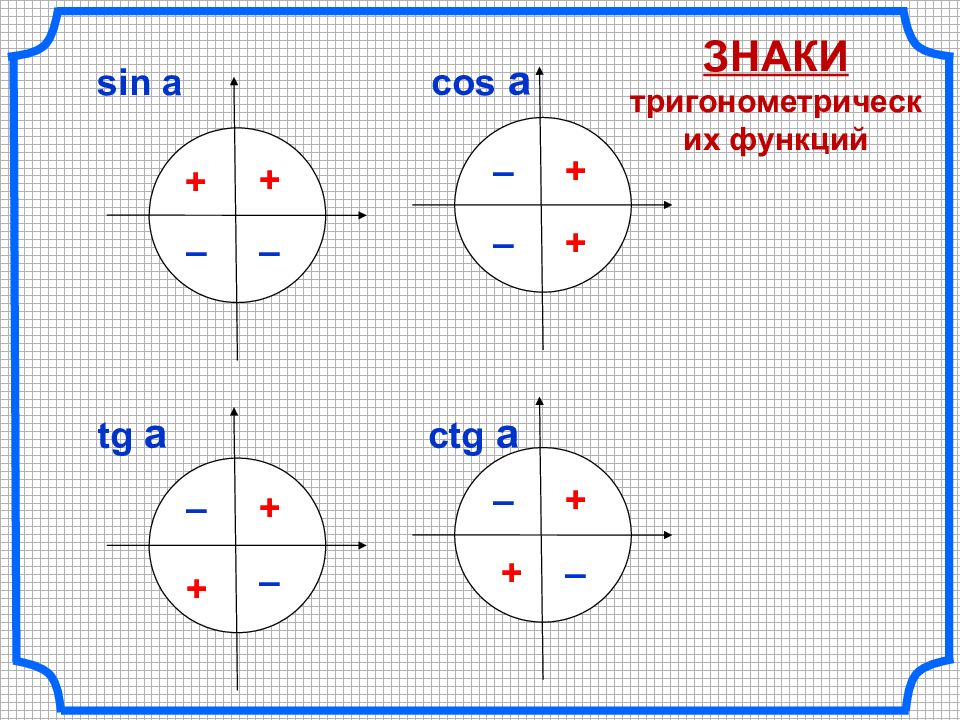
sin a cos a tg a ctg a – + + + + + + + + – – – – – – – ЗНАКИ тригонометрических функций
x y O Функция нечетная
x y O Функция четная
Функция нечетная Докажи самостоятельно
Функция четная Функция нечетная
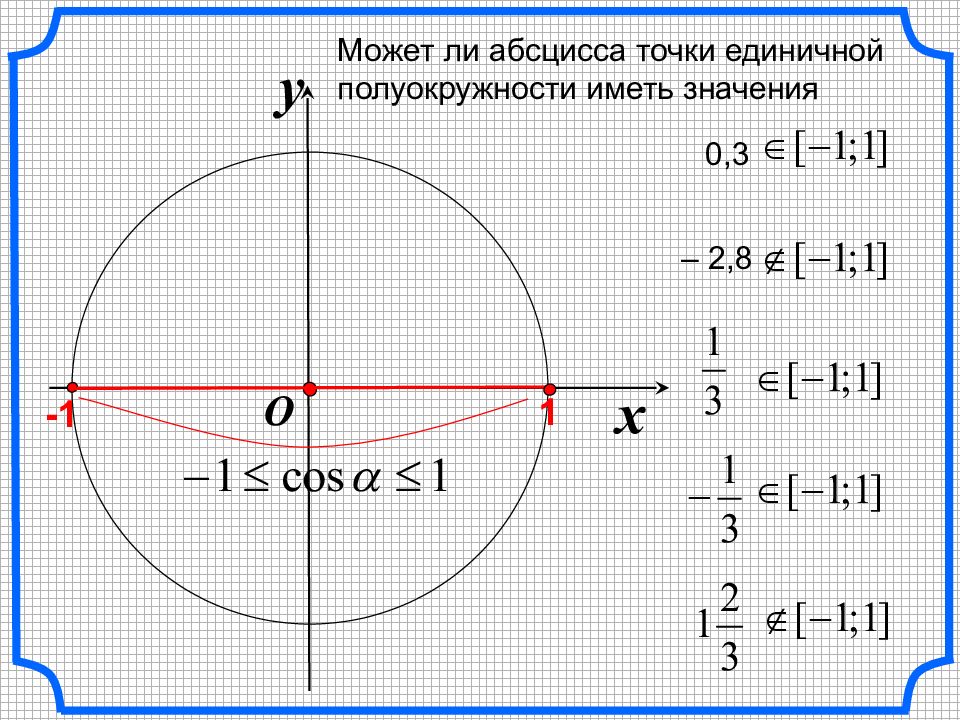
x y O Может ли абсцисса точки единичной полуокружности иметь значения -1 1 0,3 – 2,8
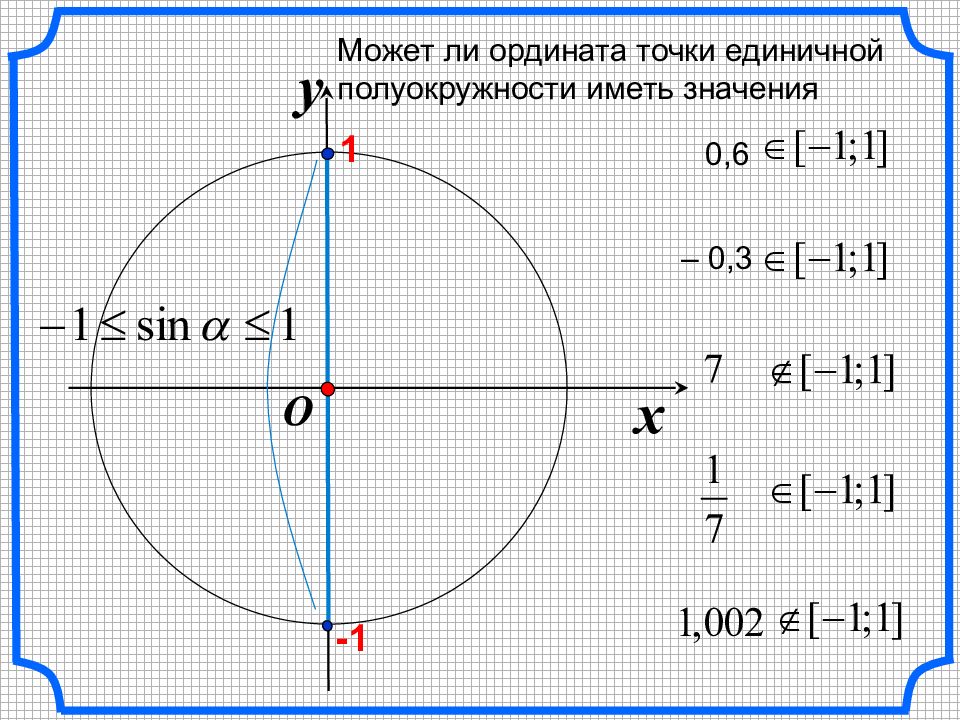
x y O Может ли ордината точки единичной полуокружности иметь значения 0,6 – 0,3 -1 1
На уроке: 1*, 2* Новая тема 3) § 13: №2, 3, 4…
