Первый слайд презентации: Кодирование
Слайд 2: Кодирование
Кодирование – преобразование дискретного сообщения в дискретный сигнал, осуществляемое по определенному правилу. Декодирование – восстановление дискретного сообщения по сигналу на выходе дискретного канала, осуществляемое с учетом правила кодирования. Код – совокупность условных сигналов, обозначающих дискретные сообщения.
Слайд 3: Десятичные и двоичные коды
Десятичные коды: 0, 1, …, 10, 11, …, 99 Двоичные коды: 0, 1, 10, 11, 100, 101, …, 1100011 U ( t) t 2 4 0 6 8 83 U ( t) t 0 1 1010011
Слайд 4: Равномерные и неравномерные коды
Равномерные коды – коды, при использовании которых, длина всех кодовых комбинаций (кодовых слов) одинакова. 001, 010, 011, 100 – равномерные коды. 1, 10, 11, 100 – неравномерные коды.
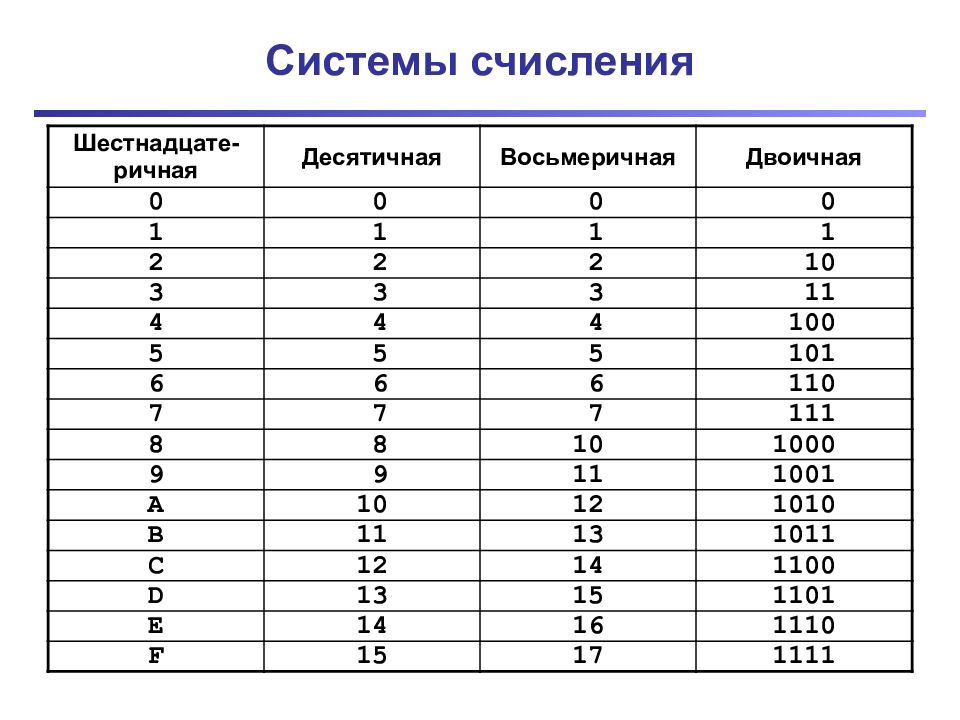
Слайд 5: Системы счисления
Шестнадцате-ричная Десятичная Восьмеричная Двоичная 0 0 0 0 1 1 1 1 2 2 2 10 3 3 3 11 4 4 4 100 5 5 5 101 6 6 6 110 7 7 7 111 8 8 10 1000 9 9 11 1001 A 10 12 1010 B 11 13 1011 C 12 14 1100 D 13 15 1101 E 14 16 1110 F 15 17 1111
Слайд 6: Непомехозащищенные коды
Непомехозащищенные коды – коды, содержащие кодовые комбинации, отличающиеся друг от друга в одном разряде. 0010 и 0011 отличаются в первом разряде; 1110 и 0110 – в четвертом разряде; 1110 и 0100 – во втором и четвертом разрядах.
Слайд 7: Двоичный код на все комбинации
Кодовые комбинации соответствуют записи натурального ряда чисел в двоичной системе счисления. Пример: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111. Количество кодовых комбинаций:
Слайд 8: Единично-десятичный код
Каждый разряд десятичного числа записывается в виде соответствующего числа единиц; разряды при передаче по каналу связи разделяются интервалами. Неравномерный единично-десятичный код 352: 111 11111 11 149: 1 1111 111111111 Равномерный единично-десятичный код 352: 000000111 000011111 000000011 149: 000000001 000001111 111111111
Слайд 9: Двоично-десятичный код
Каждый разряд десятичного числа записывается в виде комбинации двоичного кода. Пример 352: 0011 0101 0011 149: 0001 0100 1001
Слайд 10: Код Морзе
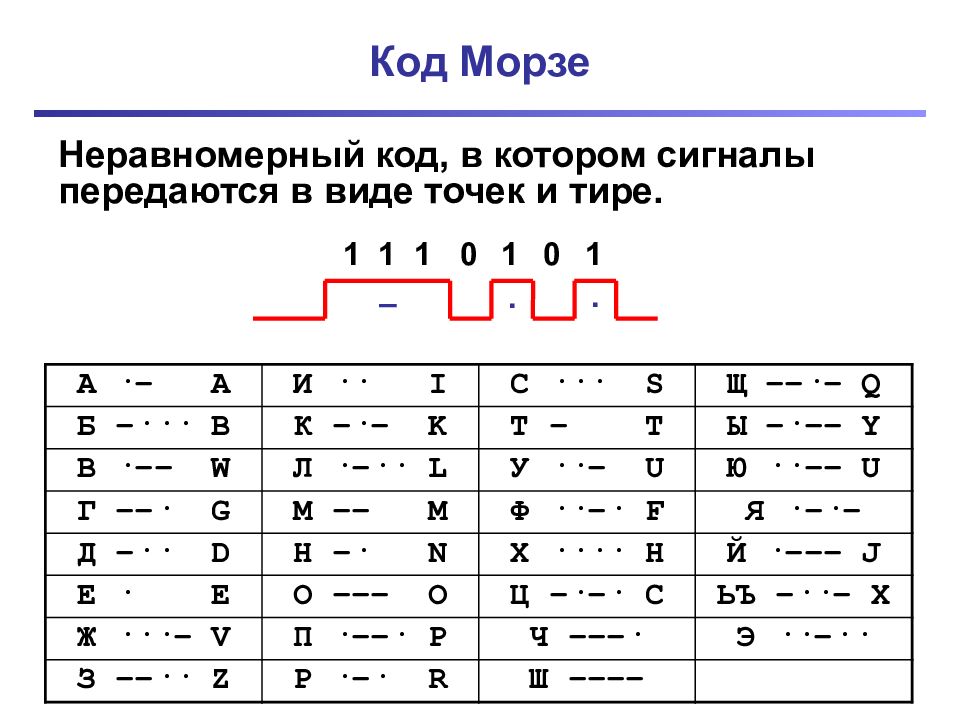
Неравномерный код, в котором сигналы передаются в виде точек и тире. 1 1 1 1 0 1 0 – . . А · – A И ·· I С ··· S Щ –– · – Q Б – ··· B К – · – K Т – T Ы – · –– Y В · –– W Л · – ·· L У ·· – U Ю ·· –– U Г –– · G М –– M Ф ·· – · F Я · – · – Д – ·· D Н – · N Х ···· H Й · ––– J Е · E О ––– O Ц – · – · C ЬЪ – ·· – X Ж ··· – V П · –– · P Ч ––– · Э ·· – ·· З –– ·· Z Р · – · R Ш ––––
Слайд 11: Помехозащищенные коды
Помехозащищенные коды (корректирующие коды) – коды, позволяющие обнаружить ошибки в кодовых комбинациях. Помехозащищенные коды разделяются на две группы: коды с обнаружением ошибок; коды с обнаружением и исправлением ошибок.
Слайд 12: Кодовое расстояние
Кодовое расстояние – минимальное число элементов, в которых могут отличаться друг от друга две кодовые комбинации в используемом коде. 0 1 0 1 1 n = 1 : 0 0 0 1 0 1 n = 2: 0 0 0 1 11 10 0 0 10 1 0 0 0 11 1 1 0 1 11 1 0 0 1 10 1 1 10 11 01 d = 1 d = 1 d = 1 d = 2 d = 1 d = 2 d = 1
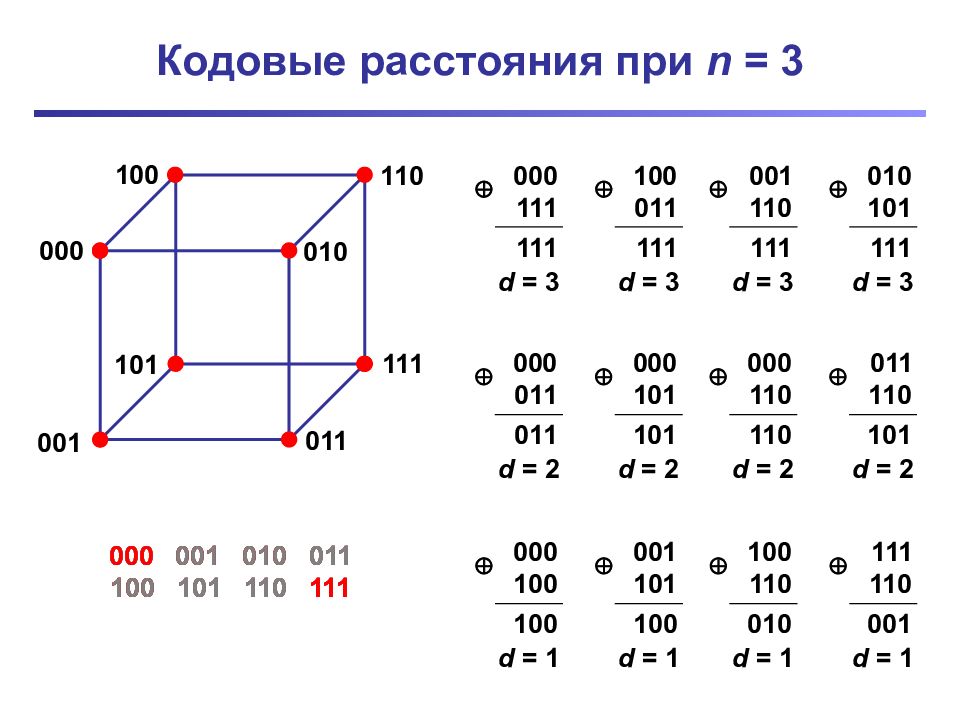
Слайд 13: Кодовые расстояния при n = 3
00 0 001 011 01 0 10 0 101 111 110 0 0 011 1 11 1 d = 3 1 0 001 1 11 1 d = 3 0 0 1110 11 1 d = 3 010101 11 1 d = 3 0 0 001 1 01 1 d = 2 0 0 010 1 10 1 d = 2 0 0 0110 110 d = 2 011110 10 1 d = 2 0 0 0100 100 d = 1 001 10 1 100 d = 1 1 0 0110 010 d = 1 111110 00 1 d = 1 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111 000 001 010 011 100 101 110 111
Слайд 14: Корректирующая способность кода
d min – минимальное кодовое расстояние; r – количество обнаруживаемых ошибок; s – количество исправляемых ошибок;
Слайд 15: Коды с обнаружением ошибок
коды, построенные путем уменьшения количества используемых кодовых комбинаций; коды, в которых используются все возможные кодовые комбинации, но к каждой комбинации добавляются контрольные символы.
Слайд 16: Код с постоянным числом единиц и нулей в комбинациях
l – число единиц в слове длиной n. Общее число кодовых комбинаций: N = 10 11000 01010 01100 00101 00110 10010 00011 01001 10001 10100 N = 35 1010100 0101010 1110000 0000111 1001001 0010101 1101000 1011000 0110100 0101100 …
Слайд 17: Распределительный код
Код с постоянным весом, равным единице 00001 00010 00100 01000 10000
Слайд 18: Код с проверкой на четность
k – количество информационных символов (разрядов) в кодовой комбинации. Информационные символы Контрольные символы Кодовая комбинация 1 1 0 1 1 0 1 1 0 1 1 0 1 0 1 0 1 1 1 0 1 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
Слайд 19: Код с числом единиц, кратным трем
k – количество информационных символов (разрядов) в кодовой комбинации. Информационные символы Контрольные символы Кодовая комбинация 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 1 0 0 1 0 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 1 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0 0 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1
Слайд 20: Код с удвоением элементов (корреляционный код)
Каждый элемент двоичного кода на все сочетания передается двумя символами: 1 преобразуется в 10, а 0 – в 01. Двоичный код на все сочетания Корреляционный код 1 1 0 1 1 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 1 1 1 0 0 0 1 0 1 0 0 1 0 1 0 1 1 1 1 1 0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0
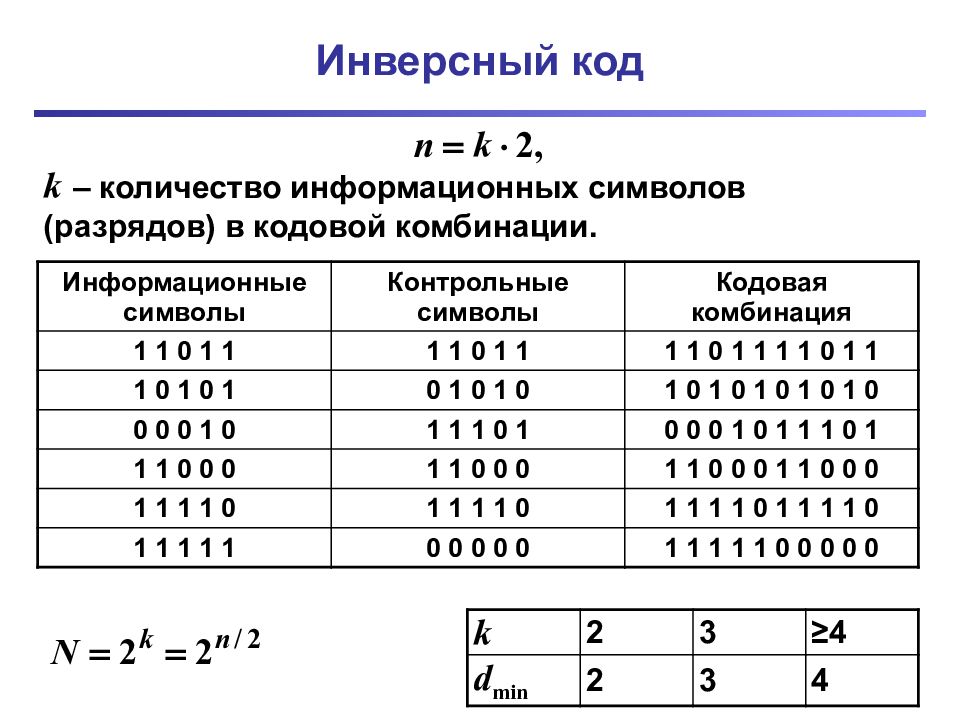
Слайд 21: Инверсный код
k – количество информационных символов (разрядов) в кодовой комбинации. Информационные символы Контрольные символы Кодовая комбинация 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0 1 0 1 1 1 0 1 0 0 0 1 0 1 1 1 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 k 2 3 ≥4 d min 2 3 4
Слайд 22: Коды с обнаружением и исправлением ошибок
Образуются путем добавления к кодовой комбинации контрольных символов коды Хэмминга; циклические коды; итеративные коды.
Слайд 23: Коды Хэмминга
В качестве исходного используется k - разрядный двоичный код на все сочетания. К нему добавляются m контрольных символов. При передаче кодовой комбинации может быть искажен любой из n символов, т.е. число вариантов искажения равно n +1 ( включая передачу без искажений). k 1 2,3,4 5…11 12…26 m 2 3 4 5
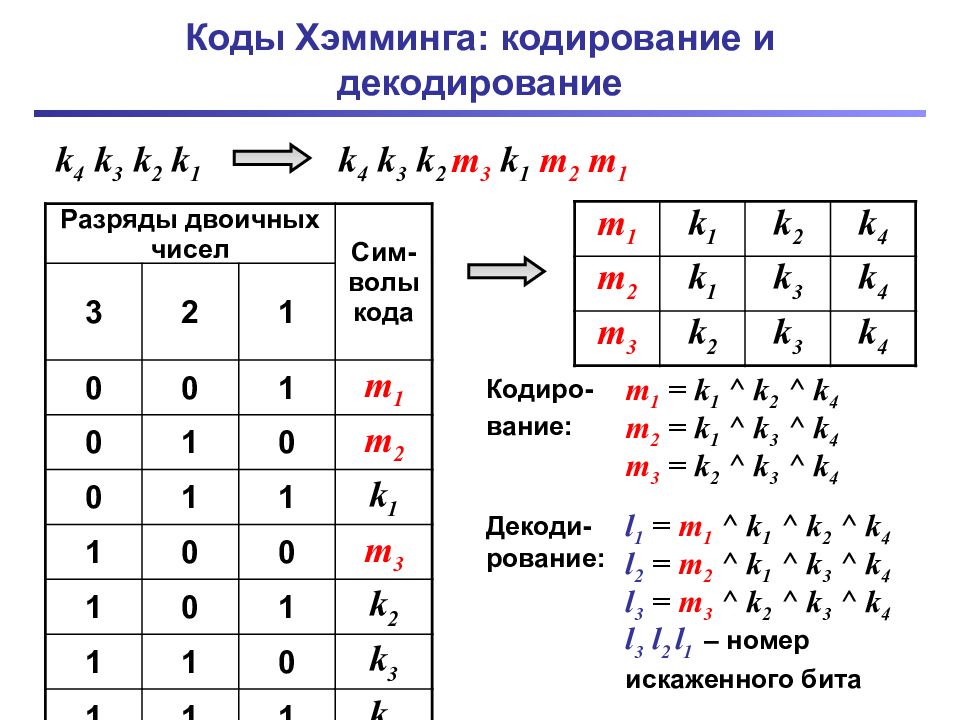
Слайд 24: Коды Хэмминга: кодирование и декодирование
Разряды двоичных чисел Сим - волы кода 3 2 1 0 0 1 m 1 0 1 0 m 2 0 1 1 k 1 1 0 0 m 3 1 0 1 k 2 1 1 0 k 3 1 1 1 k 4 k 4 k 3 k 2 k 1 k 4 k 3 k 2 m 3 k 1 m 2 m 1 m 1 k 1 k 2 k 4 m 2 k 1 k 3 k 4 m 3 k 2 k 3 k 4 m 1 = k 1 ^ k 2 ^ k 4 m 2 = k 1 ^ k 3 ^ k 4 m 3 = k 2 ^ k 3 ^ k 4 Кодиро- вание: l 1 = m 1 ^ k 1 ^ k 2 ^ k 4 l 2 = m 2 ^ k 1 ^ k 3 ^ k 4 l 3 = m 3 ^ k 2 ^ k 3 ^ k 4 l 3 l 2 l 1 – номер искаженного бита Декоди-рование:
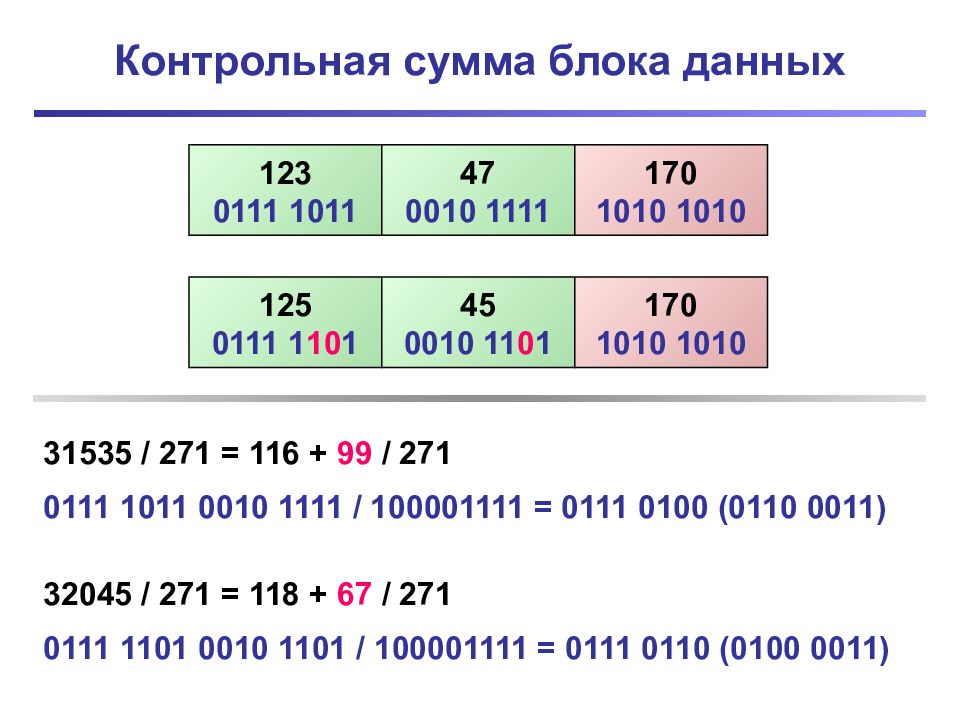
Слайд 25: Контрольная сумма блока данных
123 0111 1011 47 0010 1111 170 1010 1010 125 0111 1 10 1 45 0010 11 0 1 170 1010 1010 31535 / 271 = 116 + 99 / 271 0111 1011 0010 1111 / 100001111 = 0111 0100 (0110 0011) 32045 / 271 = 118 + 67 / 271 0111 1 10 1 0010 11 0 1 / 100001111 = 0111 0110 (0100 0011)
Слайд 26: Циклические коды
101101 = X 5 + X 3 + X 2 + 1, X=2 Приводимый полином – полином, который можно представить в виде произведения многочленов низших степеней Неприводимый полином – полином, который нельзя представить в виде произведения многочленов низших степеней P ( X 1 ) X + 1 11 3 P ( X 2 ) X 2 + X + 1 111 7 P ( X 3 ) X 3 + X + 1 1011 11 P ( X 3 ) X 3 + X 2 + 1 1101 13 P ( X 4 ) X 4 + X + 1 10011 19
Слайд 27: Сложение полиномов
При операциях с полиномами применяется сложение двоичных чисел по модулю 2, эквивалентное операции «исключающее ИЛИ» с каждым разрядом. 0^0=0 0^1=1 1^0= 1 1^1=0 1010 0110 0100 1111 ^ 1110 1001 1 · X 7 + 0 · X 6 + 1 · X 5 + 0 · X 4 + 0 · X 3 + 1 · X 2 + 1 · X 1 + 0 · X 0 0 · X 7 + 1 · X 6 + 0 · X 5 + 0 · X 4 + 1 · X 3 + 1 · X 2 + 1 · X 1 + 1 · X 0 ^ 1 · X 7 + 1 · X 6 + 1 · X 5 + 0 · X 4 + 1 · X 3 + 0 · X 2 + 0 · X 1 + 1 · X 0
Слайд 28: Деление полиномов
1 1 100110 1010 1 1010 1000 1010 01011 1010 0010 1 0 1 0 Деление двоичных полиномов аналогично делению целых чисел. При этом операция вычитания эквивалентна операции «исключающее ИЛИ».
Слайд 29: Метод построения циклического кода
G ( X ) – исходная кодовая комбинация P ( X ) – образующий полином X m – одночлен той же степени, что и P ( X ) Q ( X ) – частное от деления R ( X ) – остаток от деления F ( X ) – закодированное сообщение
Слайд 30: Пример построения циклического кода
P ( X ) = X + 1 → 1 1 G ( X ) = X 2 + X → 0110 01100 11 0100 11 0 0 00 G ( X ) · X 1 → 01100 F ( X ) → 0110 0 G ( X ) = X 3 + X + 1 → 1011 10110 11 1101 11 11 11 010 11 1 G ( X ) · X 1 → 10110 F ( X ) → 1011 1
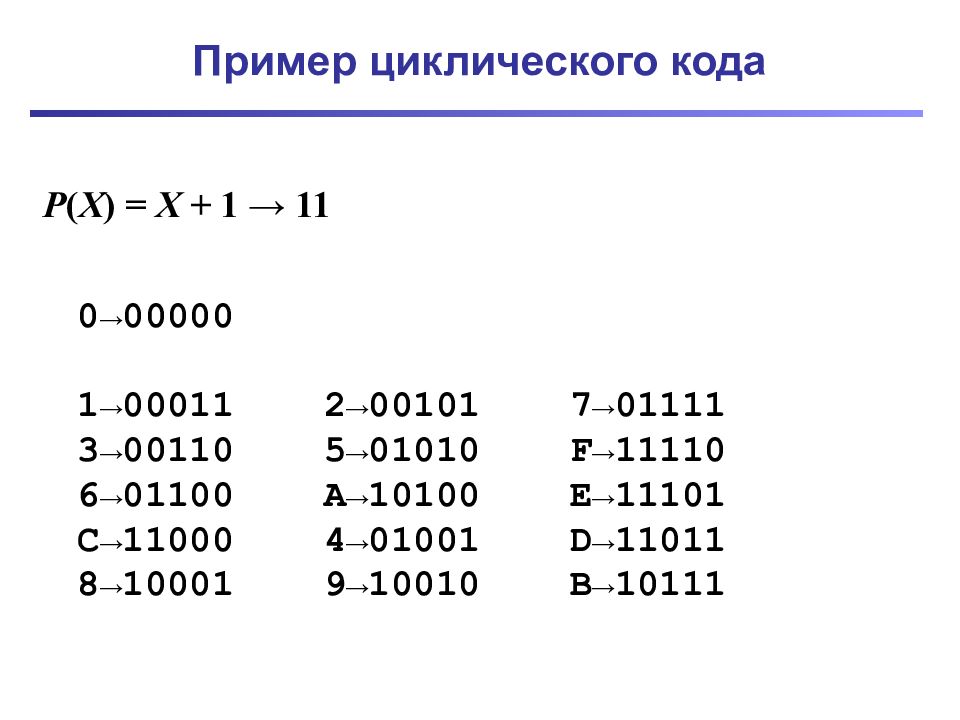
Слайд 31: Пример циклического кода
P ( X ) = X + 1 → 1 1 0→00000 1→00011 2 →00101 7 →01111 3→00110 5 →01010 F →11110 6→01100 A →10100 E →11101 C →11000 4 →01001 D →11011 8 →10001 9 →10010 B →10111
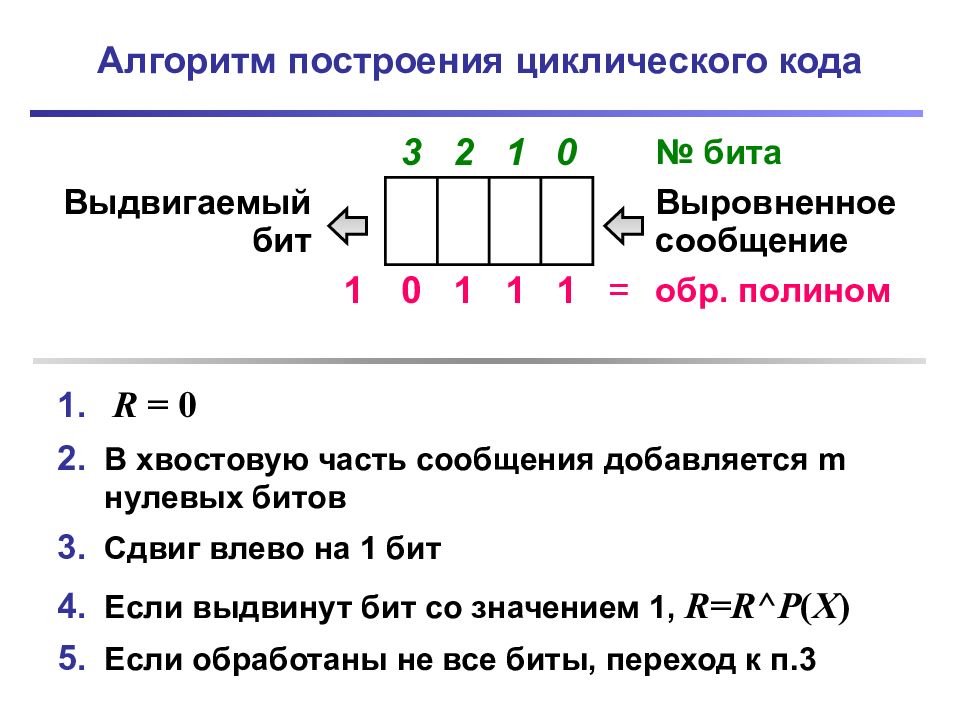
Слайд 32: Алгоритм построения циклического кода
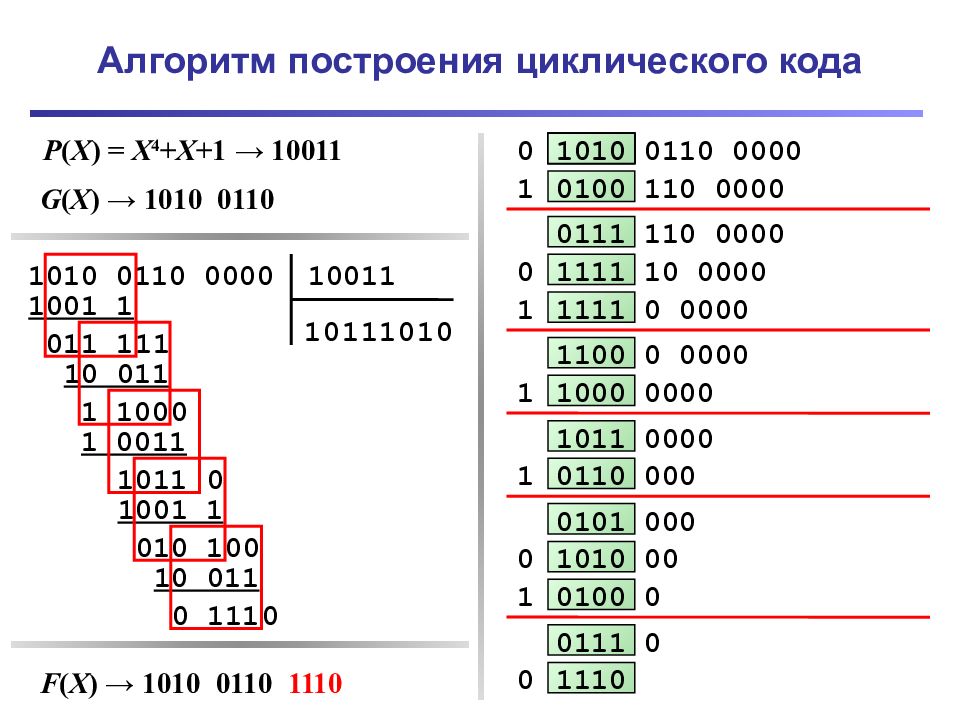
3 2 1 0 № бита Выдвигаемый бит Выровненное сообщение 1 0 1 1 1 = обр. полином R = 0 В хвостовую часть сообщения добавляется m нулевых битов Сдвиг влево на 1 бит Если выдвинут бит со значением 1, R = R ^ P ( X ) Если обработаны не все биты, переход к п.3
Слайд 33: Алгоритм построения циклического кода
1010 0110 0000 10011 1 1 0 01 1 011 1 0 1 1 1 0 1 0 1 1 1 0 01 1 1 100 0 1 0 01 1 1011 0 1001 1 010 1 0 0 10 011 0 111 0 0000 1010 0110 0000 0001 010 0110 0000 0 0100 110 0000 1 0111 110 0000 1111 10 0000 0 1111 0 0000 1 1100 0 0000 1000 0000 1 1011 0000 0110 000 1 0101 000 0010 10 0110 0000 0 0101 0 0110 0000 0 1010 0110 0000 0 1010 00 0 0100 0 1 0111 0 1110 0 P ( X ) = X 4 + X +1 → 10011 G ( X ) → 1010 0110 F ( X ) → 1010 0110 ???? F ( X ) → 1010 0110 1110
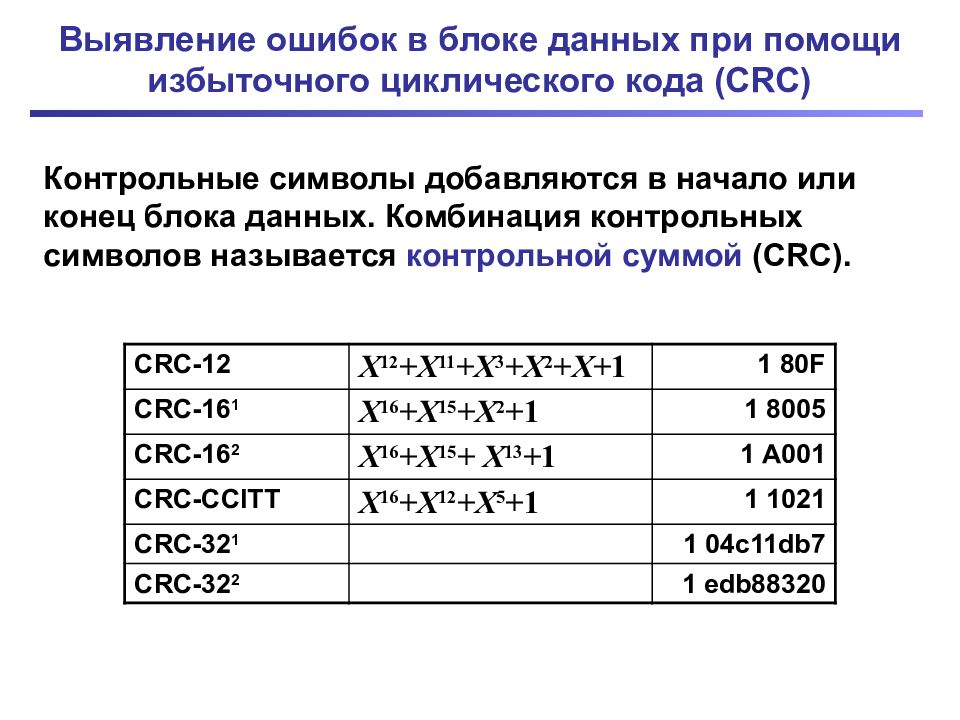
Слайд 34: Выявление ошибок в блоке данных при помощи избыточного циклического кода ( CRC)
Контрольные символы добавляются в начало или конец блока данных. Комбинация контрольных символов называется контрольной суммой ( CRC). CRC -12 X 12 +X 11 + X 3 + X 2 + X + 1 1 80F CRC -1 6 1 X 16 +X 1 5 + X 2 + 1 1 8005 CRC-16 2 X 16 +X 1 5 + X 1 3 + 1 1 A001 CRC-CCITT X 16 +X 1 2 + X 5 + 1 1 1021 CRC-32 1 1 04c11db7 CRC-32 2 1 edb88320
Слайд 35: Алгоритм вычисления 16-битного избыточного циклического кода
CRC = FFFF С использованием значения X очередного байта выполняется операция CRC=CRC^ X Сохраняется значение младшего бита CRC: L=CRC&1 CRC сдвигается вправо на 1 бит Если L=1, выполняется операция CRC=CRC^A001 Если выполнено меньше 8 сдвигов CRC, происходит переход к п.3 Если обработаны не все байты блока данных, происходит переход к п.2
Последний слайд презентации: Кодирование: Вычисление 16-битного избыточного циклического кода на языке С++
unsigned CalcCRC ( unsigned char * Buf, unsigned Len ) { unsigned CRC = 0xFFFF ; for( unsigned i = 0 ; i < Len ; ++ i, ++ Buf ) { CRC ^= * Buf ; for( unsigned j = 0 ; j < 8 ; ++ j ) { bool LSB = CRC & 0x0001 ; CRC >>= 1 ; if( LSB ) CRC ^= 0xA001 ; } } return CRC ; }