Работу выполнил: Кудряев Кирилл
Шестнадцатеричная система счисления — это позиционная система счисления с основанием 16. Для записи чисел в шестнадцатеричной системе используется 10 цифр от нуля до девяти (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и латинские буквы A, B, C, D, E, F, обозначающие числа от 10 до 15. Таким образом, все символы шестнадцатеричной системы : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Шестнадцатеричная система счисления внедрена американской корпорацией IBM. Широко используется в программировании для IBM-совместимых компьютеров. Минимальной адресуемой (пересылаемой между компонентами компьютера) единицей информации является байт, состоящий, как правило, из 8 бит (англ. bit — binary digit — двоичная цифра, цифра двоичной системы), а два байта, то есть 16 бит, составляют машинное слово (команду). Таким образом, для записи команд удобно использовать систему с основанием 16.
Шестнадцатеричная система используется в цифровой электронике и компьютерной технике, в частности в низкоуровневом программировании на языке ассемблера для различных ЭВМ.
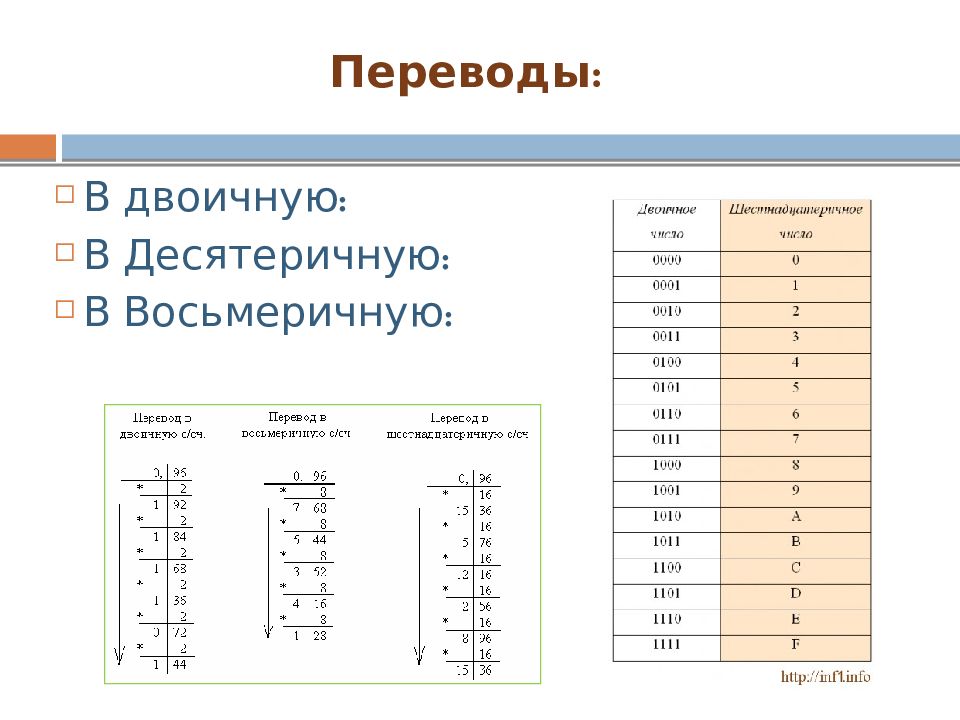
Для шестнадцатеричной системы, как и для восьмеричной, характерен легкий перевод в двоичную систему счисления и обратно с помощью простой таблицы, в которой все цифры шестнадцатеричной системы от 0 до F(15) представлены в виде двоичных тетрод (четверок): 0 16 0000 2 1 16 0001 2 2 16 0010 2 3 16 0011 2 4 16 0100 2 5 16 0101 2 6 16 0110 2 7 16 0111 2 8 16 1000 2 9 16 1001 2 A 16 1010 2 B 16 1011 2 C 16 1100 2 D 16 1101 2 E 16 1110 2 F 16 1111 2. Виды переводов:
Обратный перевод из шестнадцатеричной системы счисления в двоичную также прост. Для этого в двоичной записи числа нужно выделить тетроды (четверки) и заменить каждую тетроду соответствующей шестнадцатеричной цифрой. Отсчитывать тетроды нужно справа налево. В случае необходимости неполные тетроды дополняются нулями. Например: 1110111101 2 = 0011 1011 1101 2 = 3BD 16
Сейчас шестнадцатеричная система используется для обозначения цвета в языке гипертекстовой разметки HTML, графических программах. Чтобы задать определенный цвет применяются комбинации RGB-значения цвета (Red Green Blue — красный, зеленый, синий), записанные в шестнадцатеричном виде. Перед обозначением цвета ставят символ решетки (префикс). Например: # 7B917B — Первое число — 7B — отвечает за красную составляющую, второе — 91 — за зеленую и третье — 7B — за синюю.
В различных системах и языках программирования используется разный синтаксис для обозначения шестнадцатеричных чисел. В ассемблерах используют букву h (от англ. hexadecimal ) в конце числа, например: 5A3h 16 = 1443 10, при этом, если число начинается не с цифры, а с буквы, впереди ставится 0, например: 0FFh 16 = 255 10, для того, чтобы отличать число от других идентификаторов. В Паскале (Pascal) и Бейсике (Basic) используют префикс $, например: «$5A3», в некоторых версиях Бейсика используется также сочетание «&h».
В двоичную: В Десятеричную: В Восьмеричную:
Для перевода чисел из шестнадцатеричной системы счисления в десятичную сосчитаем количество разрядов шестнадцатеричного числа N и запишем степени шестнадцати от нулевой до N - 1 справа налево (помним, что каждая последующая степень получается умножением предыдущей на 16). Запишем под ними шестнадцатеричное число в прямом порядке. Умножим записанные числа на соответствующие им степени. Найдем сумму всех произведений. Результатом будет десятичное число, представленное в виде суммы различных степеней числа 16, умноженных на соответствующие коэффициенты.
Перевести число 21 16 в десятичную систему. Считаем число разрядов — 2, значит, нужно записать справа налево степени шестнадцати от нулевой до первой: 16 1 16 0 16 1 Запишем под степенями наше шестнадцатеричное число (слева направо, как есть): 16 1 2 1 Умножим числа на соответствующие степени шестнадцати и сложим их: 2 * 16 + 1 * 1 = 32 + 1 = 33, это и есть результат перевода: 21 16 = 33 10 Таким образом, шестнадцатеричное число 21 1 представлено в виде суммы ряда степеней числа 16 (основание шестнадцатеричной системы):
С помощью специальной программы — шестнадцатеричного редактора чисел, можно просмотреть любой файл в виде набора байтов, представленных в шестнадцатеричном коде и внести определенные изменения. Это широко используется как для отладки, так и для взлома программ.
Спасибо за внимание
