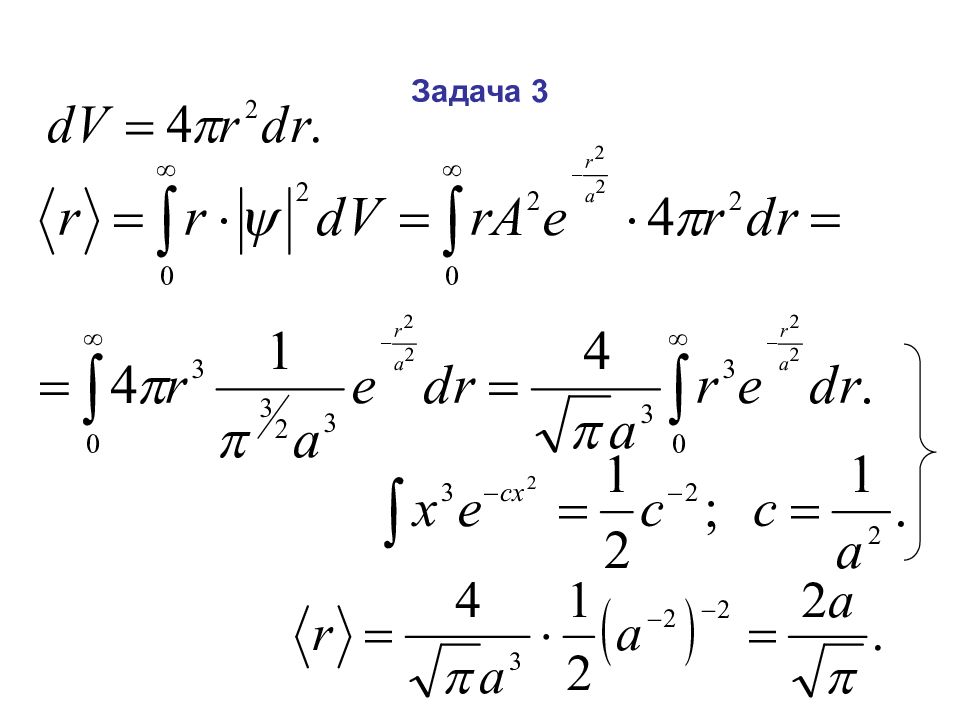Первый слайд презентации: Уравнение Шредингера
Волновая функция и её статистический смысл
Квантовая механика описывает законы движения и взаимодействия микрочастиц с учётом их волновых свойств.
Слайд 3: Сравнение дифракции световых волн и микрочастиц
• Для света : дифракционная картина – ослабление или усиление света в различных точках пространства. Интенсивность ~ A 2 световой волны.
Слайд 4: Сравнение дифракции световых волн и микрочастиц
• Для частиц : дифракционная картина объясняется неодинаковым распределением потоков микрочастиц в различных направлениях после рассеяния (отражения), т.е. проявляются вероятностные (статистические) закономерности распространения волн де Бройля. Но по волновому закону меняется не вероятность обнаружить частицу в точке пространства, а амплитуда вероятности, т.к. вероятность не может меняться по гармоническому закону, поскольку она не может быть отрицательной.
Слайд 5
В квантовой механике положение частицы в пространстве в данный момент времени определяется волновой функцией (пси-функцией) амплитуда вероятности. Вероятность dW того, что частица находится в элементарном объёме dV, пропорциональна
Слайд 6
ψ может быть комплексной. Квадрат модуля волновой функции: ψ * - функция комплексно сопряженная с ψ.
Слайд 7
Описание состояния микрообъекта с помощью волновой функции имеет статистический (вероятностный) характер. плотность вероятности, т.е. определяет вероятность нахождения частицы в момент времени t в единичном объёме dV в окрестности точки с координатой ( x, y, z ).
Слайд 8
Физический смысл имеет не ψ– функция, а интенсивность волн де Бройля. Вероятность найти частицу в момент t в конечном объёме V : При интегрировании по бесконечному V вероятность обнаружить частицу равна 1. Из этого следует условие нормировки :
Слайд 9: Ограничения на ψ– функцию :
1. конечная (т.к. вероятность не может быть > 1), 2. однозначна (вероятность не может быть неоднозначной величиной), 3. непрерывна (вероятность не может изменяться скачком). Следовательно, ψ– регулярная.
если система может находиться в различных состояниях, описываемых волновыми функциями ψ 1, ψ 2 … ψ n, то она может находиться в состоянии ψ, описываемом линейной комбинацией этих функций.
Слайд 11
ψ– функция – основная характеристика состояния микрообъекта, позволяет вычислять средние значения физических величин, характеризующих данный микрообъект: L – физическая величина, например, энергия или координата.
Слайд 12: Временное и стационарное уравнение Шредингера
Т.к. микрообъекты (в соответствии с предположением де Бройля) обладают волновыми свойствами, то уравнение, описывающее их движение в различных силовых полях должно быть волновым уравнением подобно уравнению электромагнитной волны.
Слайд 13
В 1926 г. Шредингер постулировал временное уравнение Шредингера для частицы массой m, движущейся в поле с потенциальной энергией U ( x, y, z, t ) со скоростью v << c : общее уравнение Шредингера оператор Лапласа, – мнимая единица.
Слайд 14: Условия, накладываемые на ψ– функцию:
1. ψ– функция регулярная, т.е. конечная, непрерывная, однозначная, 2. непрерывные, 3. удовлетворяет условию нормировки.
Слайд 15
● Во многих случаях силовое поле, в котором движется частица, – стационарное, т.е. потенциальная энергия U ( x, y, z ) не зависит от t. Для этого случая записывается стационарное уравнение Шредингера (уравнение Шредингера для стационарных состояний).
Слайд 16
Решение стационарного уравнения Шредингера можно представить в виде произведения двух функций: E = const – полная энергия частицы для стационарного поля.
Слайд 18: стационарное уравнение Шредингера
Решение этого уравнения имеет бесконечное множество решений, но с учётом условий, накладываемых на ψ– функцию (регулярная, непрерывны первые производные, т.е. на ψ– функцию накладываются граничные условия), отбираются только решения, имеющие физический смысл – собственные функции. Собственные функции существуют лишь при определённых значениях полной энергии Е, называемых собственными значениями энергии. Совокупность собственных значений Е образуют энергетический спектр частицы.
Слайд 19
Если потенциальная энергия U – монотонная функция и U → 0 на бесконечности, то в области Е < 0 собственные значения энергии образуют дискретный спектр. Отыскание собственных значений энергии Е и собственных ψ– функций составляет основную задачу квантовой механики.
Слайд 20: Движение свободной частицы
Частица движется в отсутствие внешних полей, т.е. U = 0, E = E к (полная энергия частицы равна кинетической энергии). Уравнение Шредингера для одномерного случая движения вдоль оси x : дифференциальное уравнение плоской волны.
Слайд 21: Движение свободной частицы
Решением (методом подстановки) является функция: Формула Эйлера: уравнение плоской волны.
Слайд 22: Движение свободной частицы
плоская волна де Бройля. В последнем уравнении экспонента с минусом, но это не играет роль, т.к. физический смысл имеет.
Слайд 23: Движение свободной частицы
Из уравнений (4), (6) следует, что свободная частица описывается плоской монохроматической волной де Бройля. Все положения свободной частицы в пространстве равновероятны, т.к. вероятность обнаружить частицу в любой точке пространства
Слайд 24: Движение свободной частицы
коэффициент в уравнении (3). собственные значения энергии, как для обычной нерелятивистской частицы, т.е. энергетический спектр свободной частицы – непрерывный.
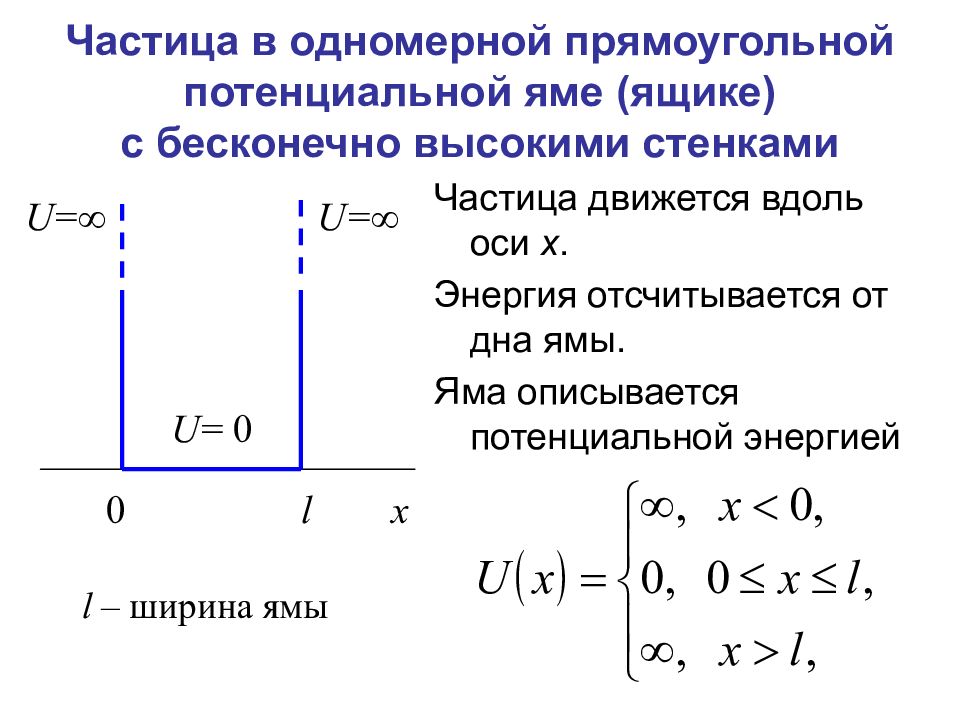
Слайд 25: Частица в одномерной прямоугольной потенциальной яме (ящике) с бесконечно высокими стенками
Частица движется вдоль оси x. Энергия отсчитывается от дна ямы. Яма описывается потенциальной энергией l – ширина ямы
Уравнение Шредингера для стационарного состояния в одномерном случае: Из граничных условий следует: бесконечно высокие стенки → частица не проникает за пределы ямы → 2. на границе ямы ( x = 0, x = l ) непрерывная функция ψ обращается в нуль: 3. в яме U = 0
Слайд 27: Частица в одномерной прямоугольной потенциальной яме
в яме U = 0 Дифференциальное уравнение гармонического осциллятора: Общее решение диф. уравнения: условие на границе:
Слайд 28: Частица в одномерной прямоугольной потенциальной яме
условие на границе:
Слайд 29
т.е. уравнение Шредингера удовлетворяется только при собственных значениях E n = E n ( n ). Т.о. E n принимает дискретные значения – квантуется. Квантованные значения E n называются уровнями энергии. n – главное квантовое число определяет энергию уровня.
Слайд 30: Частица в одномерной прямоугольной потенциальной яме
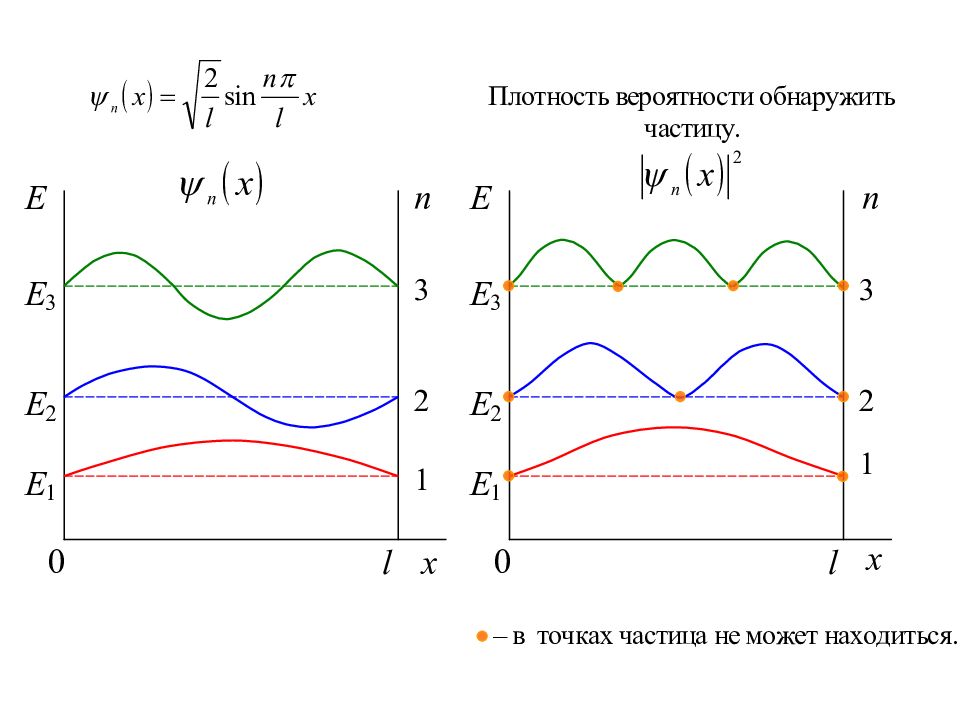
Условие нормировки: В одномерном случае:
Слайд 32: Частица в одномерной прямоугольной потенциальной яме
Собственным функциям соответствуют уровни энергии Следовательно, энергетический интервал между двумя соседними уровнями:
Слайд 34: Частица в одномерной прямоугольной потенциальной яме
• Критерий l. Свободный электрон в металле, размер ямы т.е. энергетические уровни расположены так тесно, что спектр можно считать непрерывным для зоны проводимости. Размер ямы соизмерим с атомом т.е. дискретные значения энергии, спектр – линейчатый.
Слайд 35: Частица в одномерной прямоугольной потенциальной яме
• Критерий n. соседние уровни расположены очень тесно, можно говорить о непрерывных уровнях, т.е. о энергетической зоне (квазинепрерывные уровни). частица в потенциальной яме и не может иметь энергию меньше E min. Все остальные уровни n >1 имеют Е > E min.
Слайд 36: Задачи
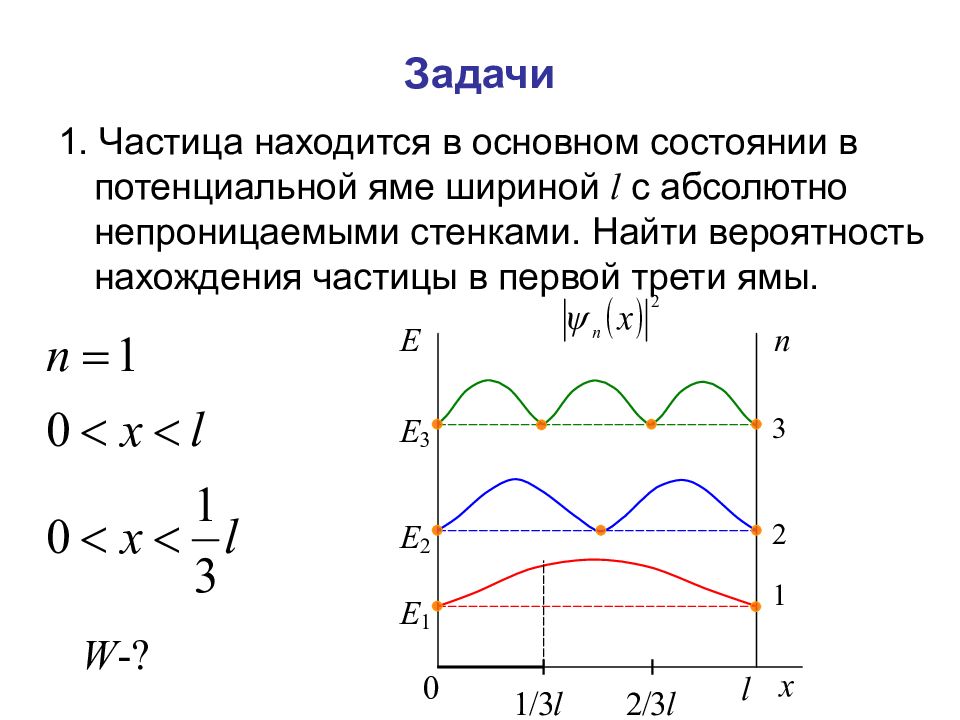
1. Частица находится в основном состоянии в потенциальной яме шириной l с абсолютно непроницаемыми стенками. Найти вероятность нахождения частицы в первой трети ямы. W -?
Слайд 37: Задача 1
Вероятность нахождения частицы в интервале dx связана с плотностью вероятности соотношением: ψ( x ) – волновая функция, которая для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме:
Слайд 39: Задача 2
ψ – функция некоторой частицы имеет вид где r – расстояние этой частицы до силового центра, a – некоторая константа. Используя условие нормировки вероятности, определить нормировочный коэффициент A. А- ?
Слайд 41: Задача 3
Волновая функция, описывающая некоторую частицу, имеет вид где r – расстояние этой частицы до силового центра, a – некоторая константа. Определить среднее расстояние частицы до силового центра. Из условия нормировки ищется нормировочный коэффициент А :
Слайд 43: Задача 4
Волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид где r – расстояние электрона от ядра, a – первый Боровский радиус. Определить наиболее вероятное расстояние электрона до ядра. r вер - ?
Слайд 44: Задача 4
Вероятность обнаружить частицу на dr : Наиболее вероятное расстояние: