1
1.Фермионы подчиняются принципу Паули: в любом квантовом состоянии может находиться не более одной частицы. 2.Бозоны не подчиняются принципу Паули: в любом квантовом состоянии может находиться неограниченное число частиц. 2
§ 13.1. Фермионы. Электроны в металле. Распределение Ферми-Дирака 3
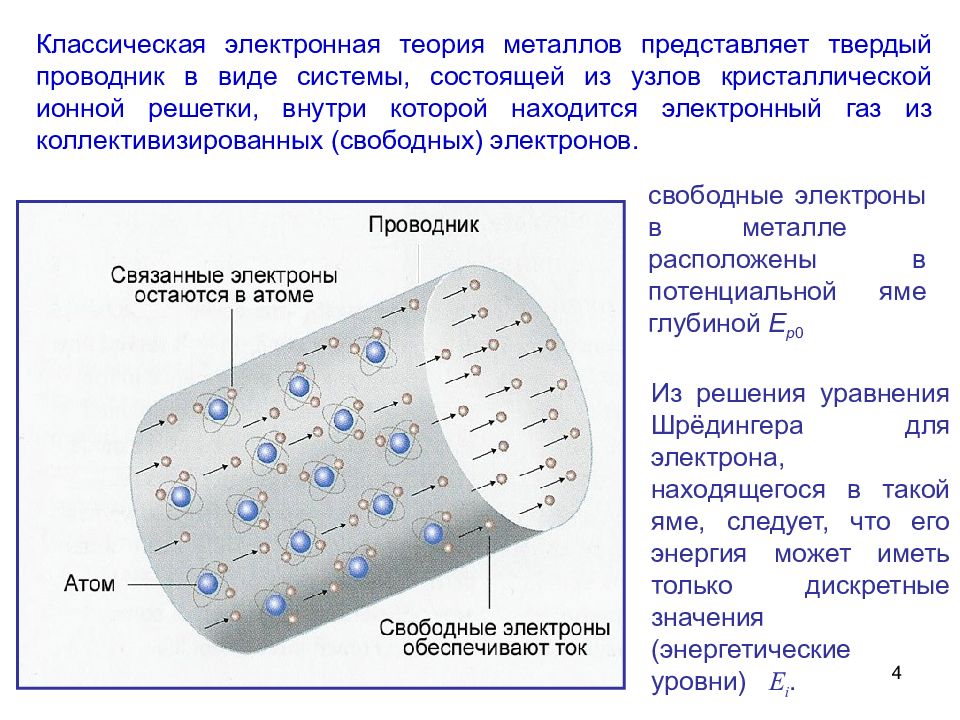
Классическая электронная теория металлов представляет твердый проводник в виде системы, состоящей из узлов кристаллической ионной решетки, внутри которой находится электронный газ из коллективизированных (свободных) электронов. свободные электроны в металле расположены в потенциальной яме глубиной Е р 0 Из решения уравнения Шрёдингера для электрона, находящегося в такой яме, следует, что его энергия может иметь только дискретные значения (энергетические уровни) E i. 4
- Электроны являются фермионами и подчиняются принципу Паули, согласно которому каждый энергетический уровень заселяется не более чем двумя электронами с противоположными спинами; Паули Вольфганг Эрнст (1890–1958) Австрийско-швейцарский физик-теоретик Распределение Ферми-Дирака определяет среднее число фермионов в состоянии с энергией E i - энергетический спектр квазинепрерывный; 5
При температурах Т→0 заполнены все состояния с энергией Е < ε F f(E i ) 2 0 ε F E Рассмотрим поведение электронного газа при Т=0 К 6
энергетический уровень, отделяющий заполненные уровни от пустых при Т = 0 К, называется энергией Ферми n – концентрация свободных электронов m e - масса электрона 7
Классическому идеальному газу с Е= ε F =3/2 k Т соответствует Т ~ 10 4 К 8
9
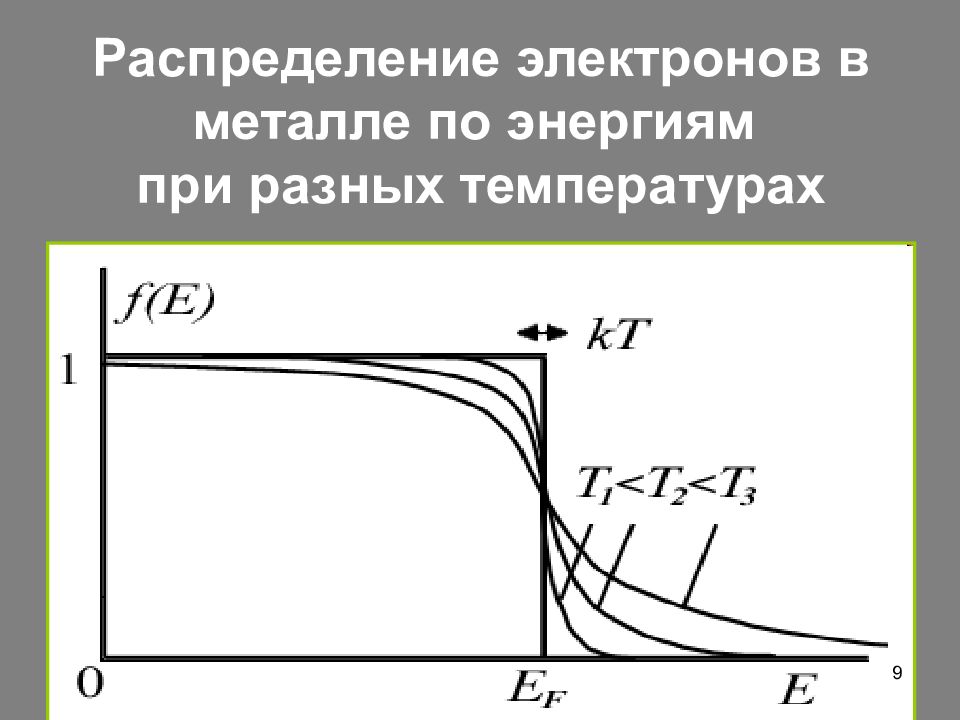
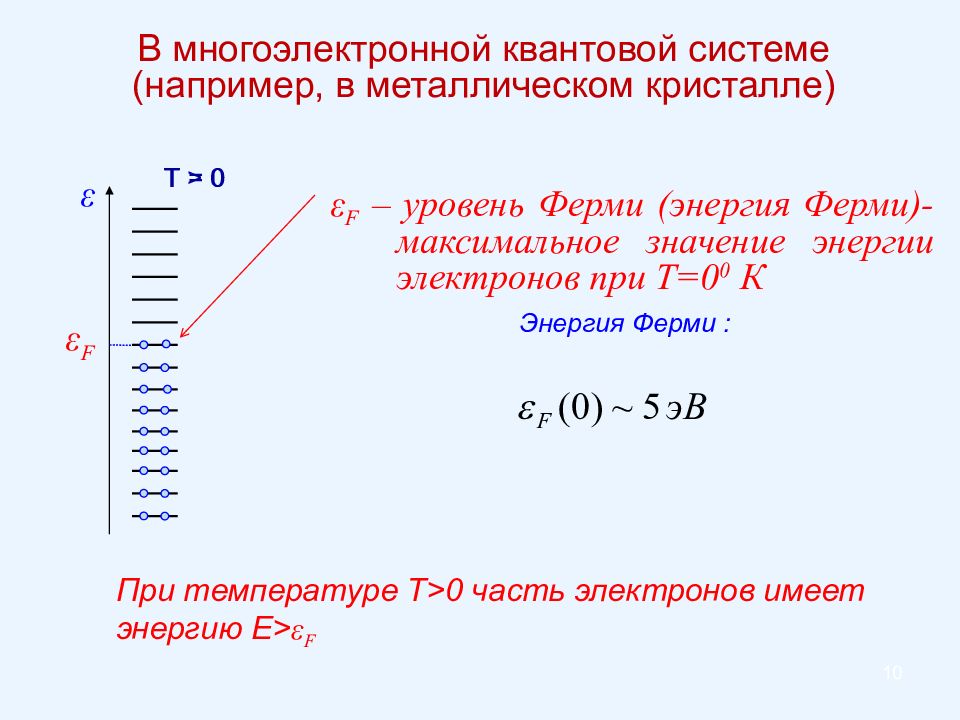
ε ε F T = 0 ε F – уровень Ферми (энергия Ферми)- максимальное значение энергии электронов при Т=0 0 К В многоэлектронной квантовой системе (например, в металлическом кристалле) Энергия Ферми : При температуре Т >0 часть электронов имеет энергию Е > ε F T > 0 10
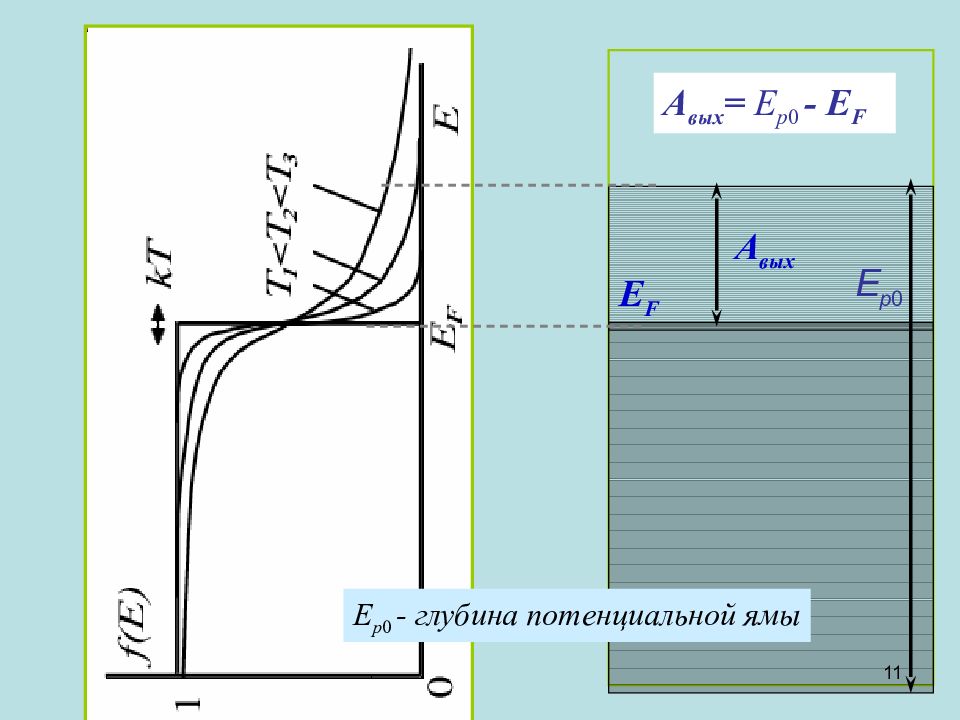
E F Е р 0 A вых А вых = Е р 0 - E F Е р 0 - глубина потенциальной ямы 11
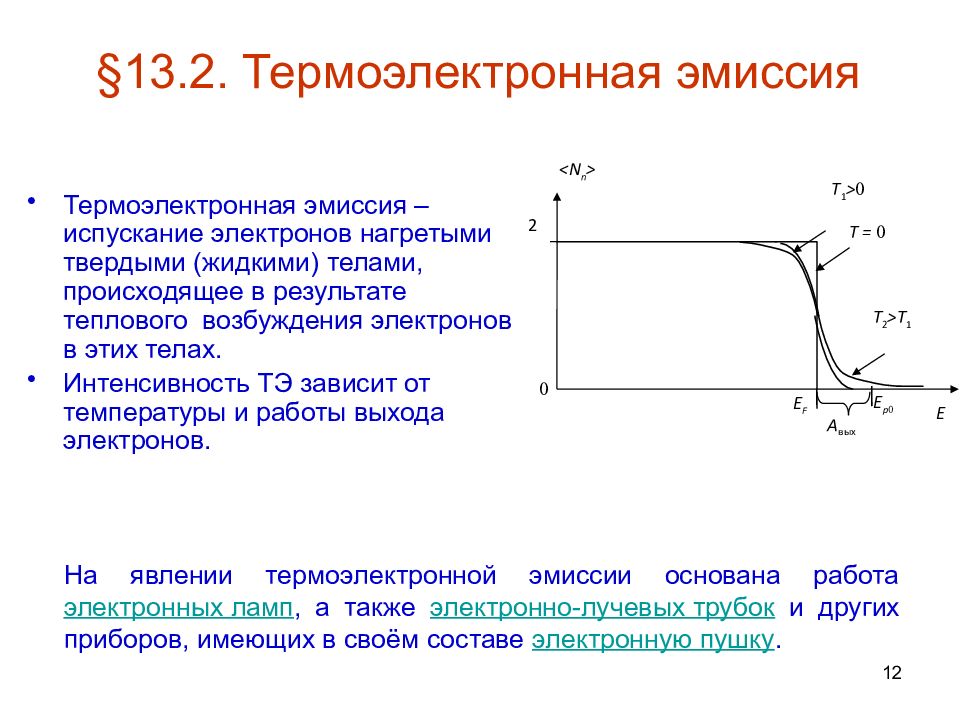
Термоэлектронная эмиссия – испускание электронов нагретыми твердыми (жидкими) телами, происходящее в результате теплового возбуждения электронов в этих телах. Интенсивность ТЭ зависит от температуры и работы выхода электронов. На явлении термоэлектронной эмиссии основана работа электронных ламп, а также электронно-лучевых трубок и других приборов, имеющих в своём составе электронную пушку. 2 E 0 <N n > E F T = 0 T 1 > 0 T 2 > Т 1 А вых Е р 0 12
13
Плотность тока насыщения определяется формулой Ричардсона — Дешмана: 14
Концентрация основных носителей тока в проводниках практически не зависит от температуры: n осн ~ 10 22 – 10 23 1/ м 3 Рассеяние электронов на атомах примеси и на узлах кристаллической решетки приводит к возникновению электросопротивления металлов. ρ = ρ колеб + ρ прим ( ρ колеб сопротивление, обусловленное тепловыми колебаниями решетки) ρ ~ ρ 0 (1+ α Т) § 13.3. Зависимость сопротивления проводников от температуры. Сверхпроводимость 15
Каммерлинг Оннес (Нидерланды) в 1911 г. обнаружил, что электросопротивление ртути при Т=4,15 К скачкообразно обращается в нуль ρ Т, К Т кр T<T кр 16
1. Эффект Мейсснера : Свойства сверхпроводников Магнитное поле не проникает в толщу сверхпроводника вывод о существовании незатухающих токов внутри сверхпроводника, которые создают внутреннее магнитное поле, противоположно направленное внешнему, приложенному магнитному полю и компенсирующее его. 17
2. Температура, при которой происходит скачкообразный переход в сверхпроводящее состояние, называется критической. (Т ~ 4 0 К достигаются с помощью жидкого гелия, Т ~ 100 0 К – с помощью жидкого азота) 3. Сильное внешнее магнитное поле разрушает сверхпроводящее состояние: В=В кр В кр Т, К Т кр 18
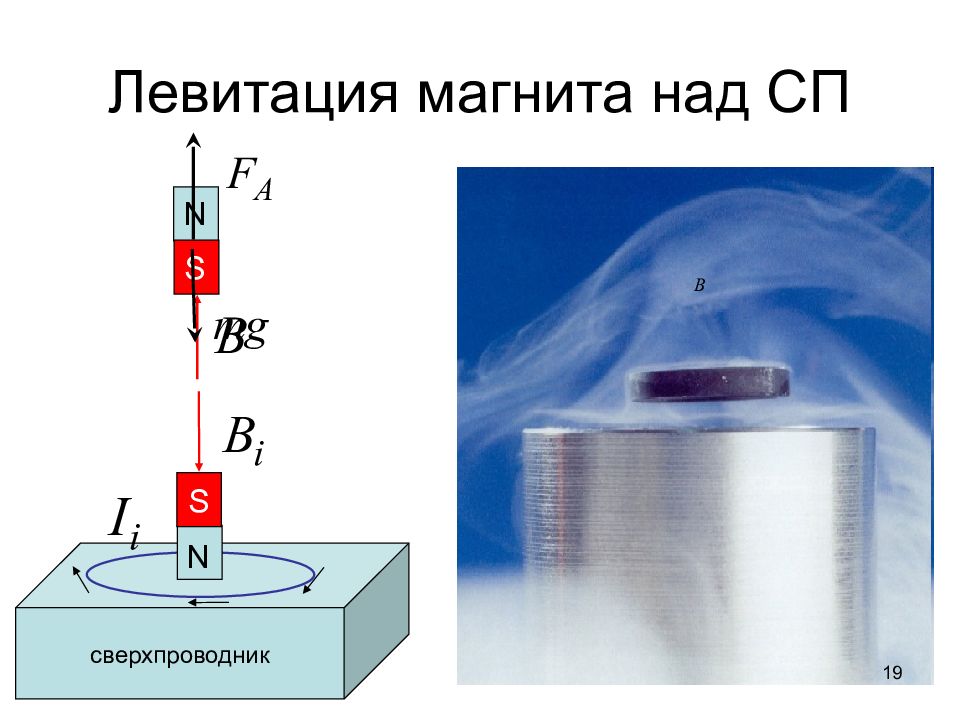
сверхпроводник Левитация магнита над СП S N S N 19
Отсутствие электрического сопротивления позволяет использовать сверхпроводники для эффективной передачи электроэнергии. Ограничивающим фактором является необходимость поддержания проводника при низкой температуре, что само по себе требует энергозатрат Создание мощных электромагнитов (на транспорте, в медицине и пр.) 20
Магнитоплан – поезд на магнитном подвесе Применение сверхпроводников : настоящее и будущее 21
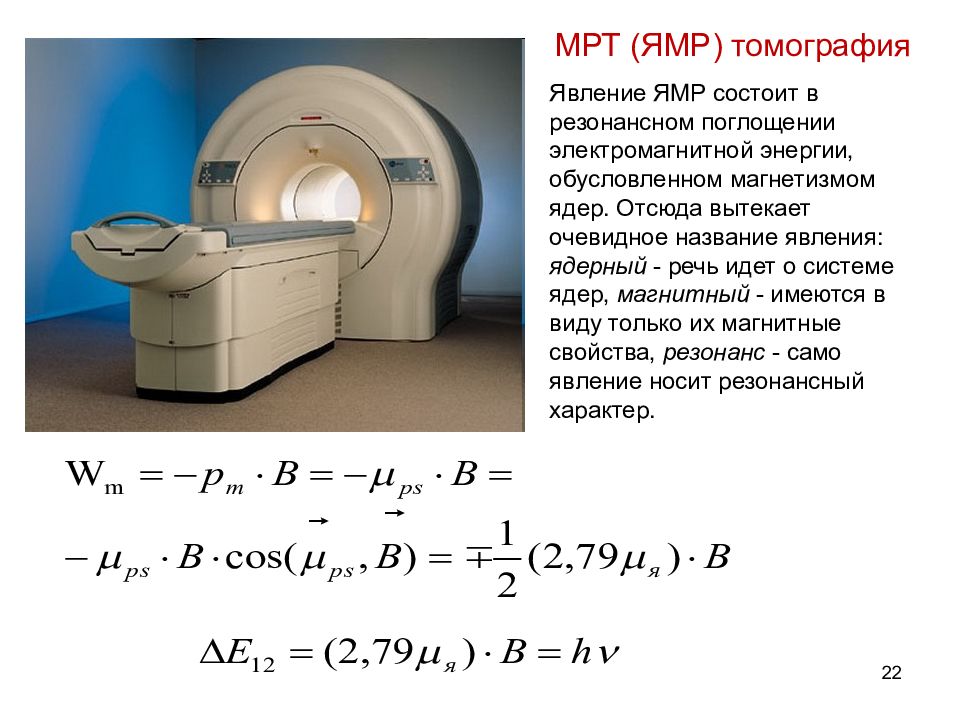
Явление ЯМР состоит в резонансном поглощении электромагнитной энергии, обусловленном магнетизмом ядер. Отсюда вытекает очевидное название явления: ядерный - речь идет о системе ядер, магнитный - имеются в виду только их магнитные свойства, резонанс - само явление носит резонансный характер. МРТ (ЯМР) томография 22
§ 13.4. Энергетические уровни в атоме и энергетические зоны в кристалле 23
ε II 2N ур N ур Образование энергетических зон в кристалле «Расстояние» между уровнями внутри зон ~ 10 – 23 эВ в кристалле ( N атомов) 1 атом 2 атома I В кристаллах энергетические спектр электронов распадается на N (число атомов в кристалле) близких уровней 24
ε Разрешенные и запрещенные зоны Разрешенные зоны Запрещенные зоны 25
§ 13.5. Распределение электронов по квантовым состояниям в кристалле. Проводники и диэлектрики 26
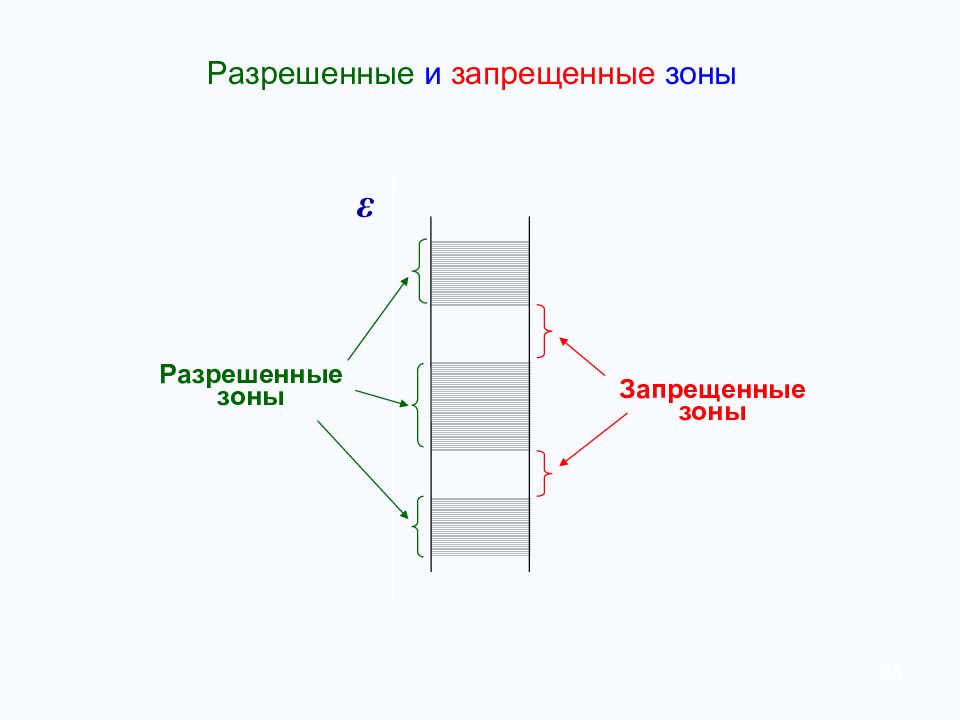
В зависимости от степени заполнения валентной зоны электронами и ширины запрещенной зоны кристаллы подразделяют на проводники (металлы), полупроводники и диэлектрики. 27
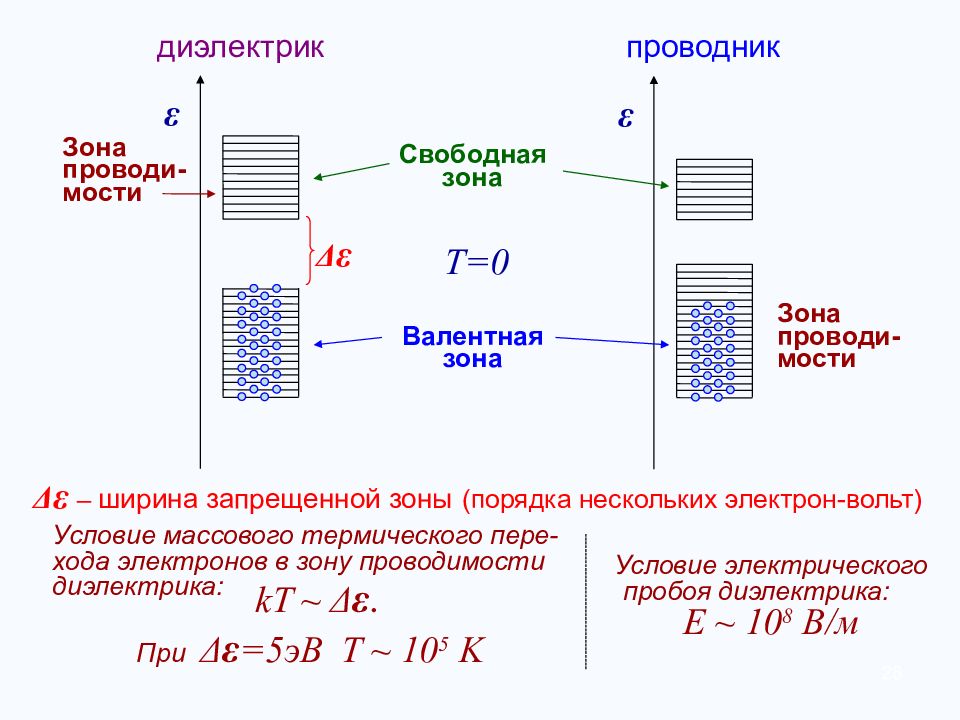
ε ε диэлектрик проводник Δ ε Δ ε – ширина запрещенной зоны (порядка нескольких электрон-вольт) Валентная зона Свободная зона Т=0 Зона проводи-мости Условие массового термического пере-хода электронов в зону проводимости диэлектрика: При Δ ε =5эВ Т ~ 10 5 K Зона проводи-мости Условие электрического пробоя диэлектрика: E ~ 10 8 В/м kT ~ Δ ε. 28
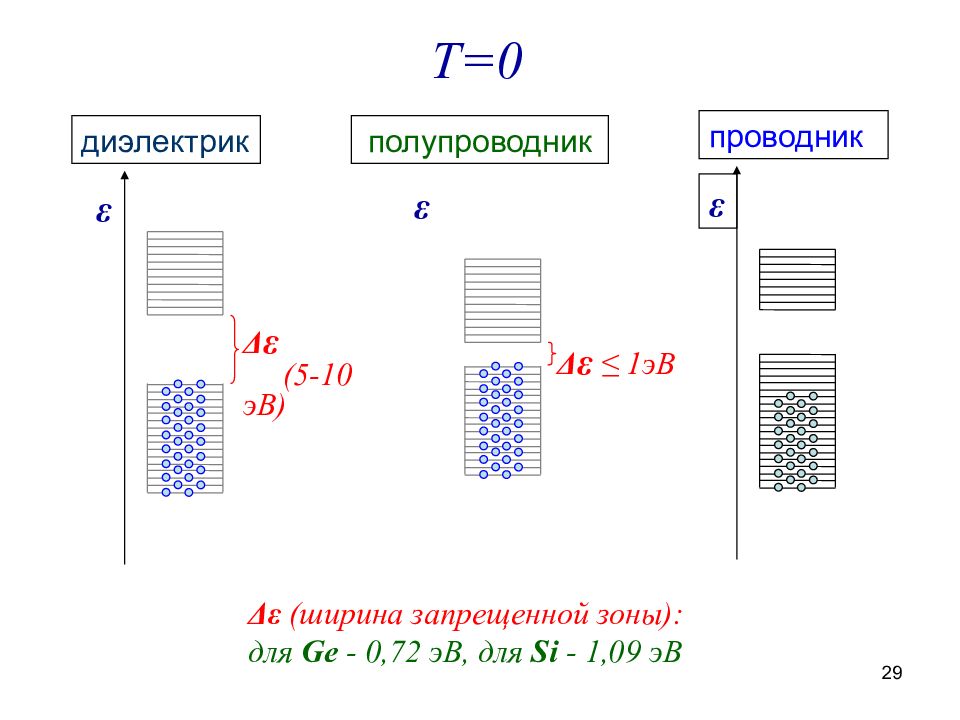
ε диэлектрик полупроводник Δ ε ( 5-10 эВ) Δ ε ≤ 1эВ Δε (ширина запрещенной зоны): для Ge - 0,72 эВ, для Si - 1,09 эВ ε проводник ε Т=0 29
§ 13.6. Полупроводники. Электроны и дырки в полупроводниках 30
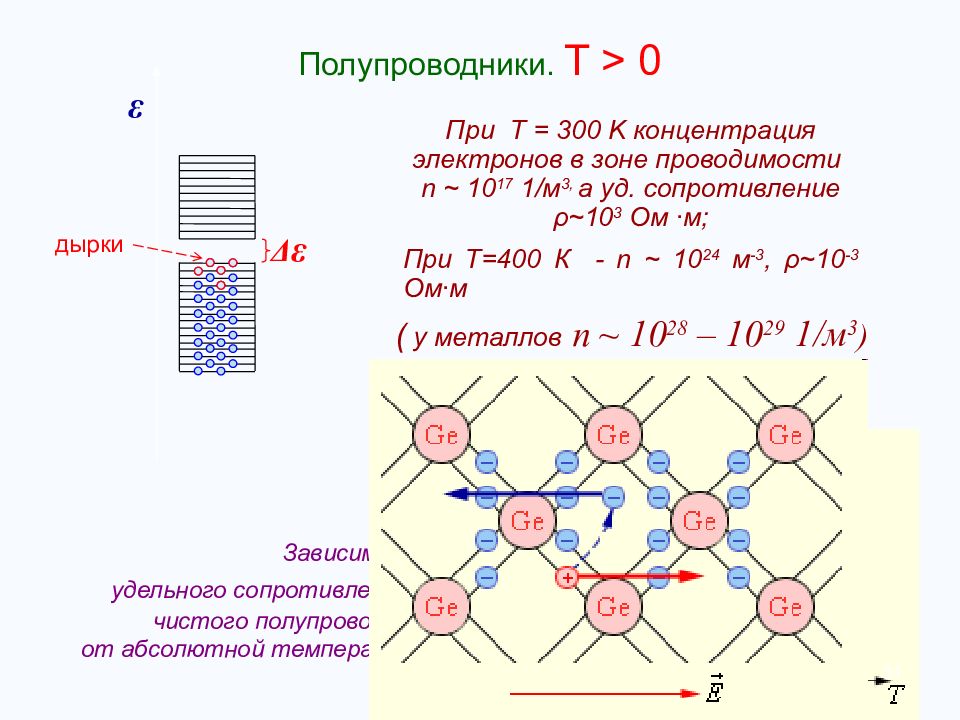
ε Полупроводники. T > 0 Δ ε При Т = 30 0 K концентрация электронов в зоне проводимости n ~ 10 1 7 1/ м 3, а уд. сопротивление ρ ~ 10 3 Ом ∙м; При Т=400 К - n ~ 10 24 м -3, ρ ~ 10 -3 Ом∙м ( у металлов n ~ 10 28 – 10 2 9 1/ м 3 ) дырки Зависимость удельного сопротивления ρ чистого полупроводника от абсолютной температуры 31
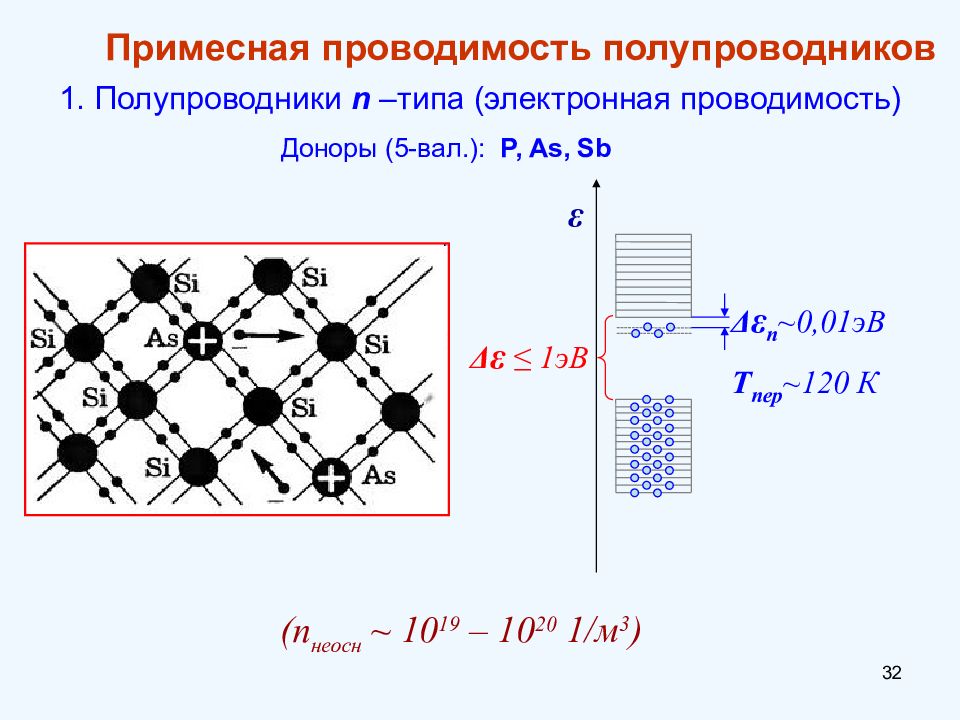
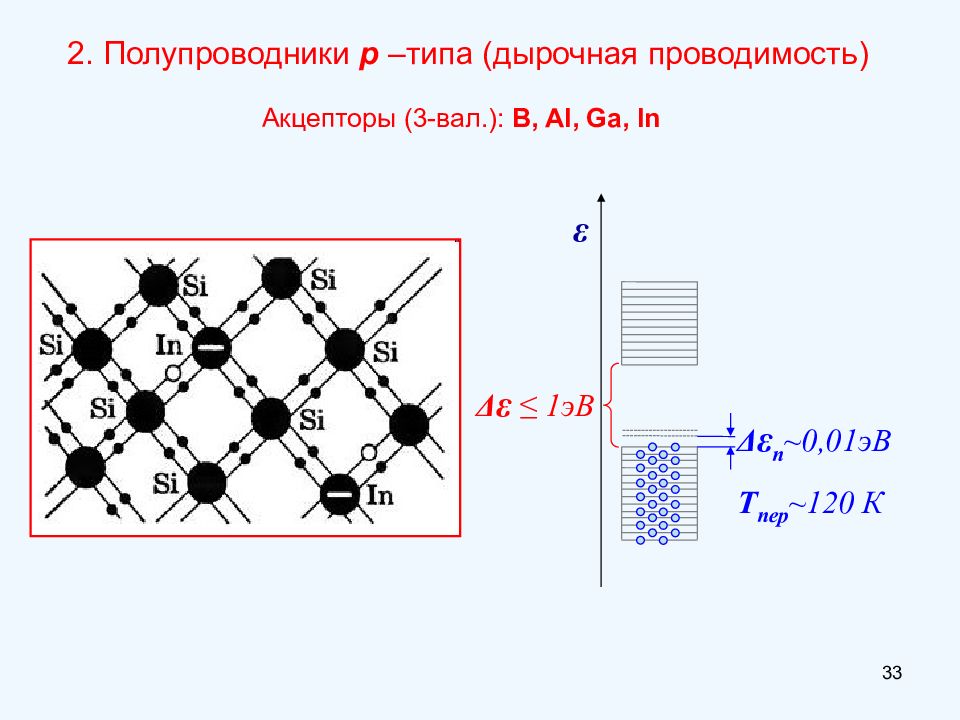
Δ ε ≤ 1эВ ε Доноры (5-вал.): P, As, Sb Δ ε п ~0,0 1эВ Т пер ~ 120 К 1. Полупроводники n –типа (электронная проводимость) ( n неосн ~ 10 19 – 10 20 1/ м 3 ) Примесная проводимость полупроводников 32
Акцепторы (3-вал.): B, Al, Ga, In 2. Полупроводники р –типа (дырочная проводимость) Δ ε ≤ 1эВ ε Δ ε п ~0,0 1эВ Т пер ~ 120 К 33
