Слайд 2
Р ост качества материалов, строительных конструкций, деталей машин и механизмов, изменение эстетических видов сооружений ведет повышению требований к надежности и долговечности, а также к экономичности материалов. Создание современных гражданских и промышленных сооружений, машин и механизмов невозможно без знания теоретических расчетов их деталей и конструкций. Таким образом, при решении задач создания высокотехнологических конструкций в строительстве и в машиностроении основная роль остается за механикой деформируемых тел частью, которой является «Сопротивление материалов», как науки о методах расчета, экономичных в изготовлении и надежных в работе и эксплуатации, сооружений, машин и механизмов.
Слайд 3
Действительное строение твердых тел, физико - механические свойство материалов и поведение в работе реального сооружения настолько сложны и многообразны и при изучении их в курсе сопротивления материалов не возможно учитывать все разнобразия. Поэтому необходимо ввести различные исходные предпосылки, использующие кинематические и статические гипотезы, в достаточной степени, оправдываемые на практике. При изучении сложных процессов деформирования конструкций перед инженером возникает задача выявления главного в сложном физическом явлении, абстрагируясь от менее существенного. Это приводит к рассмотрению различных моделей, так называемых расчетных схем, учитывающих только те особенности реального объекта, которые в каждом конкретном случае являются определяющими.
Слайд 4
Невозможность учета всех особенностей строения реальных тел приводит к различным гипотезам и допущениям, таким как линейной зависимостью между напряжениями и деформациями в элементах конструкций, идеальной упругости материалов элементов, тело элемента является идеально однородным, сплошным и изотропным, т.е. любой бесконечно малый объем элемента конструкции не имеет пустот, обладает одинаковыми физико-механическими характеристиками и одними и теми же свойствами по всем направлениям. При этом первоначальное состояние предполагает отсутствие каких-либо начальных внутренних усилий. Одним из основных допущений является гипотеза Бернулли или гипотеза плоских сечений.
Слайд 5
Необходимо постоянно помнить о пределах применимости тех или иных гипотез. Указанные допущения, справедливость которых проверена огромным количеством опытных наблюдений, дают возможность весьма просто оценивать поведение некоторых классов материалов элементов конструкций в определенных условиях. Прежде всего это металлы и их сплавы, имеющие наибольшее распространение в инженерных конструкциях. Таким образом, сопротивление материалов является наукой, опирающейся на результаты опыта и наблюдений и использующей математический аппарат при анализе этих результатов.
Слайд 6
ОСНОВНЫЕ ПОНЯТИЯ Сопротивление материалов – это наука о прочности, жесткости и устойчивости элементов конструкций, сооружений, деталей машин и механизмов. Сопротивление материалов относится к фундаментальным дисциплинам общетехнической подготовки специалистов с высшим техническим образованием.
Слайд 7
При проектировании строительных конструкций, машин и механизмов инженер должен обеспечить необходимые величины, характеризующие их прочность, жесткость и устойчивость.
Слайд 8
Под прочностью понимают способность материала элемента конструкции сопротивляться разрушению. Жесткость конструкции характеризует ее способность сопротивляться деформированию. Устойчивость конструкции – способность сохранять первоначальную форму равновесия.
Слайд 9
Объектом исследования в сопротивлении материалов являются наиболее распространенные элементы многих конструкций: Брус (стержень) – тело, длина которого существенно превышает линейные размеры поперечного сечения. Ось бруса – геометрическое место точек, являющихся центрами тяжести поперечных сечений стержня. Поперечное сечение б руса – сечение, перпендикулярное к его оси.
Слайд 10
Пластина – тело, у которого толщина существенно меньше двух других размеров. Срединная поверхность пластины – поверхность, равностоящая от крайних образующих поверхностей. Плита – пластина, у которой срединная поверхность представляет плоскость. Оболочка – пластина, у которой срединная поверхность представляет криволинейную поверхность.
Слайд 11
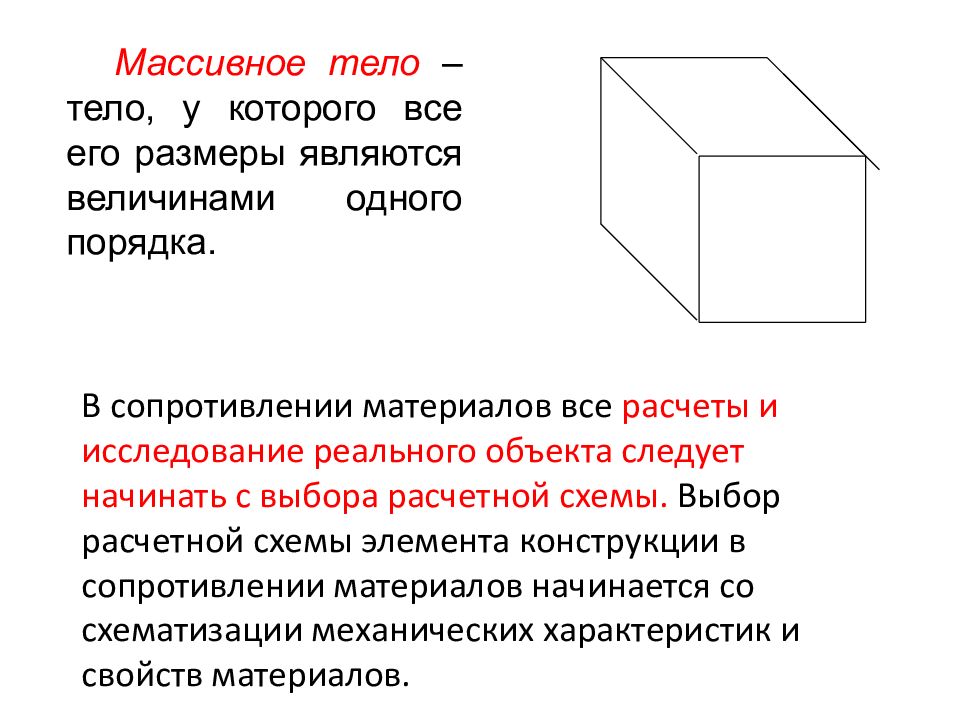
Массивное тело – тело, у которого все его размеры являются величинами одного порядка. В сопротивлении материалов все расчеты и исследование реального объекта следует начинать с выбора расчетной схемы. Выбор расчетной схемы элемента конструкции в сопротивлении материалов начинается со схематизации механических характеристик и свойств материалов.
Слайд 12
Все материалы рассматриваются как однородная сплошная среда, непрерывно заполненная веществами, имеющими одинаковые физико-механические характеристики по всем направлениям независимо от особенностей их микроструктуры. Однородная с плошная среда элемента конструкции при выборе расчетной схемы наделяется свойствами, отвечающими основным свойствам реального материала.
Слайд 13
В механике деформируемого твердого тела вводят различные гипотезы и допущения, касающиеся характера процесса деформирования тела элементов конструкций и свойств его материала:
Слайд 14
1 Гипотезы п о свойствам материала : гипотеза однородности. Материал элемента однороден, т.е. тело элемента состоит из материала с одними и теми же физико-механическими характеристиками; гипотеза сплошности. Материал элемента абсолютно сплошной, т.е. весь объем тела элемента полностью заполнен материалом без каких-либо пустот, трещин и ослаблений ;
Слайд 15
г ипотеза изотропности – материал элемента обладает свойством изотропности, т.е. материал имеет по всем направлениям одинаковые физико-механические характеристики; м атериал элемента идеально упругий - - до определенного предела нагружения элемента его материал обладает идеальной упругостью т. е. деформация элемента вызванные внешними нагрузками полностью исчезает и востанавливается первоначальные размер и форма. ;
Слайд 16
2. Гипотезы п о характеру деформаций элементов конструкции : перемещения точек или отдельных элементов конструкции, обусловленные общей деформацией, весьма малы по сравнению с ее размерами; деформации элементов конструкции прямо пропорциональны действующим силам; плоские поперечные сечения элементов остаются плоскими и после деформации;
Слайд 17
3 Гипотеза п ринципа независимости действия сил – совокупный результат действия системы (группы) сил равен сумме результатов действия каждой силы этой системы в отдельности (данная гипотеза справедлива в пределах малых (упругих) деформаций);
Слайд 18
4 Принцип Сен-Венана (принцип локальности эффекта самоуравновешенных внешних нагрузок).-- Если в какой-либо части тела приложена уравновешенная система сил, то она вызывает в теле местные напряжения и деформации, очень быстро убывающие по мере удаления от этой части. В точках, достаточно удаленных от мест приложения внешних нагрузок, напряжения и деформации весьма мало зависят от способа приложения этих нагрузок и подчиняются общим законам распространения деформаций и внутренних сил по рассматриваемому элементу.
Слайд 19
Внешние и внутренние силы. В процессе работы или эксплуатации конструкций сооружения и машин их элементы испытывают воздействие различных сил. Силы являются мерой механического взаимодействия отдельных тел межу собой. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на конструкцию заменяется силами, которые называются внешними.
Слайд 20
Внешние силы, действующие на элементы конструкции, это давление на контактную часть элемента конструкции от окружающей ее среды или от соседних частей конструкции. Внешние силы подразделяются на объемные и поверхностные:
Слайд 21
Объемные силы распределены по всему объему и приложены к каждой его частице (собственный вес, инерционные силы, действия магнитного поля и т.п.), (единица измерения Н/м 3 ).
Слайд 22
1 Поверхностные силы приложены к участкам поверхности, характеризуют непосредственное контактное взаимодействие рассматриваемого объекта с окружающими телами и представляют: 2 Сосредоточенные силы – это давления, передающиеся на элемент конструкции через площадку, размеры которой очень малы ( H) ; 3 Распределенные нагрузки – это давления, передающиеся на элементы конструкции непрерывно через некоторую площадку или длину (Н/м 2, Н/м); 4 Момент силы – это действие пары сил, равное произведению силы на плечо ( Н м ). q P M
Слайд 23
Внешние силы различают: по времени действия: постоянные нагрузки – нагрузки, действующие в течение всего или длительного периода времени эксплуатации конструкции (собственный вес сооружения, оборудования и т.п.); временные нагрузки – нагрузки, действующие лишь в течение некоторого промежутка времени;
Слайд 24
по характеру действия: нагрузки статического действия нагружают конструкцию постепенно, будучи приложены к сооружению, они не меняются или меняются незначительно. При приложении статических нагрузок на конструкции ускорения массы элементов от деформации практически отсутствуют или настолько малы, что ими можно пренебречь;
Слайд 25
2. Нагрузки динамического действия вызывают значительные ускорения масс элементов конструкции или изменение их скорости при деформации за короткий промежуток времени; а. инерционные нагрузки – динамические нагрузки, вызванные при движении тела массой т с некоторым ускорением; в. ударные нагрузки – динамические нагрузки, возникающие при быстром изменении скорости соприкасающихся элементов конструкции (ударяющего тела); г. повторно-переменные нагрузки – динамические нагрузки, действующие на элемент конструкции, повторяясь значительное количество раз. д. импульсные нагрузки – динамические нагрузки, возникающие при кратковременном действии нагрузок т. е. характерна быстрым развитием и исчезновением (мгновенное действие нагрузки); е. подвижная нагрузка – характерна изменением своего положения на сооружение; ж. сейсмическая нагрузка -- это беспорядочное движение основания сооружения (толчки, удары, колебания при землетрясении).
Слайд 26
Внутренние силы Взаимодействие между отдельными частями рассматриваемого элемента внутри очерченной области объекта характеризуется внутренними силами. Внутренние силы в элементах конструкции – это дополнительные силы взаимодействия между отдельными частицами элемента, которые вызываются стремлением внешних сил разрушить элемент, изменить его форму и размеры, отделить одну часть от другой.
Слайд 27
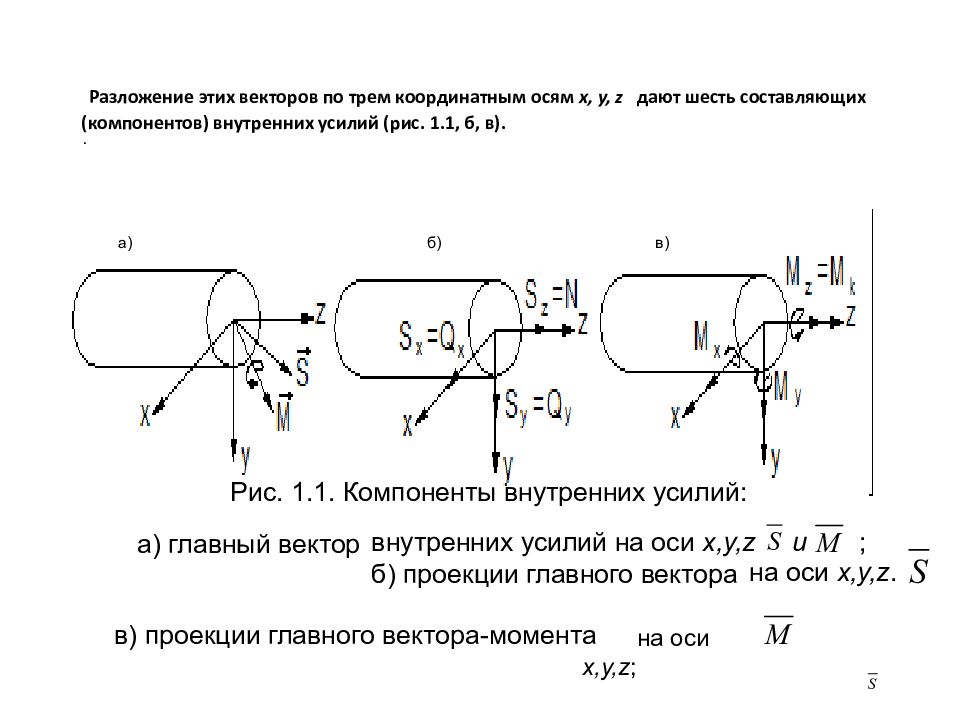
Определение внутренних усилий в элементах конструкций. Для определения внутренних усилий, возникающих в элементе конструкции, применяют метод сечений. Элемент мысленно разрезается сечением и разделяется на две части. Взаимодействие отдельных частей заменяется их усилиями, действующими по всему сечению, которые представляются через главный вектор приложенных к центру тяжести сечения. и главный вектор-момент
Рис. 1.1. Компоненты внутренних усилий: . а) главный вектор внутренних усилий на оси x, y, z и ; б) проекции главного вектора в) проекции главного вектора-момента на оси x, y, z. на оси x, y, z ; а) б) в)
Слайд 29
S z = N – продольная сила, единица измерения ( Н ); S y = Q y – поперечная сила по оси y, единица измерения ( Н ); S x = Q x – поперечная сила по оси x, единица измерения ( Н ); M z = M k – крутящий момент, единица измерения ( Н м ); M y – изгибающий момент относительно оси y, единица измерения ( Н м ); M x – изгибающий момент относительно оси x, единица измерения ( Н м ).
Слайд 30
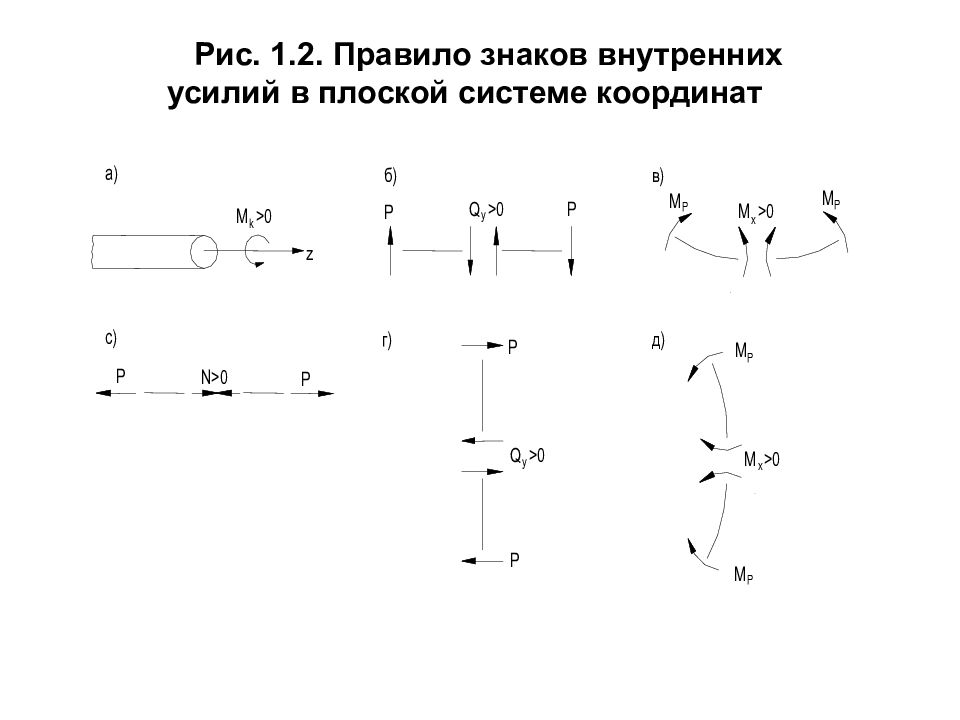
Знаки внутренних сил впространственной системе координат Когда нормальная сила направлена от сечения, имеем растягивающие внутренние силы, и нормальная сила N имеет положительный знак (рис. 1.2, с). Когда сила N направлена к сечению, имеем сжимающие внутренние силы с отрицательным знаком. Поперечные силы Q x и Q y считаются положительными, если они стараются повернуть отсеченную часть по ходу часовой стрелки (рис. 1.1, б, 1.2, б, г). Крутящие и изгибающие моменты считаются положительными, если они поворачивают против хода часовой стрелки, если смотреть от конца осей z, x и y (правило правого буравчика (рис. 1.1, а, в, рис. 1.2, а)).
Слайд 32
В сопротивлении материалов расчет элементов конструкций всегда начинается с определения внутренних усилий и построения их эпюр. При использовании метода сечений для определения внутренних усилий элемент конструкции мысленно разрезается сечением в том месте, где необходимо определить внутренние силы и разделяется на две части. При этом любая из этих частей находится в состоянии равновесия под действием всех внутренних и внешних сил, действующих на эту часть, если вся система находится в состоянии равновесия.
Слайд 34
Составляем уравнения равновесия для рассматриваемой части: – в общем случае из которых определяем шесть компонентов внутренних усилий N, Q x, Q y, M x, M y и M k ; – при плоской системе координат из которых определяем N, Q y, M x.
Слайд 35
Напряжение – внутренняя сила, приходящаяся на единицу площади, в окрестности какой-либо точки рассматриваемого сечения. – полное напряжение, где S – элементарное внутреннее усилие, приходящееся на элементарную площадь А в окрестности рассматриваемой точки. Единица измерения полного напряжения – Паскаль ( Па=Н /м 2 ).
Слайд 36
На практике применяются составляющие полного напряжения на нормальные и касательные оси (рис. 1.3). Нормальной называется ось, направленная перпендикулярно к рассматриваемому сечению. Касательной называется ось, направленная по рассматриваемому сечению. – нормальное напряжение, составляющая полного напряжения, равная проекции р на ось n, перпендикулярную к данному сечению ( Па, МПа ). – касательное напряжение, составляющая полного напряжения, равная проекции р на ось, касательную к данному сечению ( Па, МПа ).
Слайд 37
Деформация – это изменение формы и размеров элементов конструкции под действием внешних сил: Упругие деформации – это такие изменения формы и размеров элементов конструкции, которые исчезают после снятия вызвавших их сил, тело полностью восстанавливает свои первоначальные форму и размеры; 2. Остаточные деформации – это изменения формы и размеров элементов конструкции от действия внешних нагрузок, которые остаются в элементах после снятия этих нагрузок ; 3. Линейные деформации – это изменение линейных размеров элемента; 4. l – абсолютное удлинение или укорочение линейных размеров элемента; 5. – относительное удлинение или укорочение линейных размеров элемента; 6. Угловые деформации ( , , ) – это изменение углов между отдельными гранями элемента за счет изменения первоначальной формы.
Слайд 38
Перемещение ( f, ) – изменение положения элемента или точки элемента конструкции в рассматриваемом пространстве. f x = u – проекция перемещения f на ось X ; f y = v – проекция перемещения f на ось Y ; f z = w – проекция перемещения f на ось Z ; – угол поворота в пространстве; – угол поворота поперечного сечения элемента. Для обеспечения надежной работы элементов конструкции составляются условия прочности, жесткости, устойчивости и проверяются их выполнения. Надежностью называется способность объекта сохранять в процессе эксплуатации качество, заложенное при проектировании.
Слайд 39
Условие прочности. При расчете конструкций на действие внешних нагрузок действительные значения напряжений, возникающие в элементах конструкции, не должны превышать допускаемые напряжения, установленные для материала этих элементов: Где: – это максимальные значение напряжений, которых не должны превышать действительные значения напряжений, возникающие в элементах конструкции под действием внешних нагрузок и называются допускаемыми напряжениями.
Слайд 40
Допускаемые напряжения для определенных материалов устанавливаются по результатам лабораторных испытаний и эксплуатационных наблюдений: для хрупких и для высокопрочных материалов с небольшими остаточными деформациями: ; для упруго-пластичных материалов со значительными остаточными деформациями и с нехарактерными площадками текучести:
Слайд 41
Где: в – предел прочности или временное сопротивление материала; т – физический предел текучести материала; 0.2 – условный предел текучести материала; К – коэффициент запаса прочности элементов (по материалу) – число, показывающее во сколько раз допускаемые напряжения в элементах конструкции меньше предела прочности или предела текучести материала.
Слайд 42
Для обеспечения жесткости элементов конструкции должны быть выполнены условия жесткости: f f . Условия жесткости требуют, чтобы действительные значения перемещений (линейные и углы поворота) элементов конструкций, вызванные общей деформацией конструкции, не должны превышать установленные их предельные величины. f – предельные величины линейных угловых перемещений, которые устанавливаются по технологическим и эксплуатационным требованиям к конструкциям и их элементам и называются, соответственно, допускаемыми линейными и угловыми перемещениями.
Слайд 43
Простейшие виды деформации В общем случае элементы конструкции могут быть подвержены сложному деформированию, которые можно разбить на четыре простейших вида: растяжение (сжатие), сдвиг, кручение, изгиб. Растяжение и сжатие наблюдаются, когда в элементе возникает деформация удлинения или укорочения под действием продольных сил. Сдвиг возникает, когда в элементе соседние сечения перемещаются параллельно друг другу под действием поперечных сил. Кручение возникает, когда соседние поперечные сечения элемента поворачиваются относительно друг друга под действием крутящих моментов, относительно рассматриваемой оси. Изгиб возникает, когда ось бруса или срединная поверхность пластины меняет свою кривизну под действием изгибающих моментов.
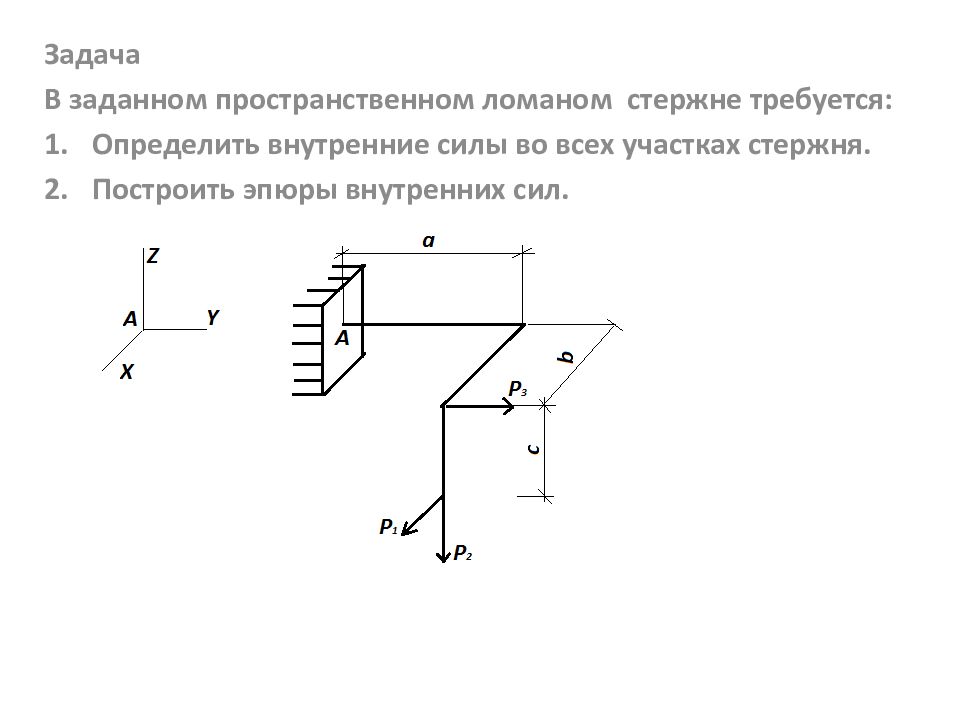
Слайд 44
Задача В заданном пространственном ломаном стержне требуется: Определить внутренние силы во всех участках стержня. Построить эпюры внутренних сил.
Слайд 45
Из условия равновесия всей системы определяем составляющих опорных реакций:
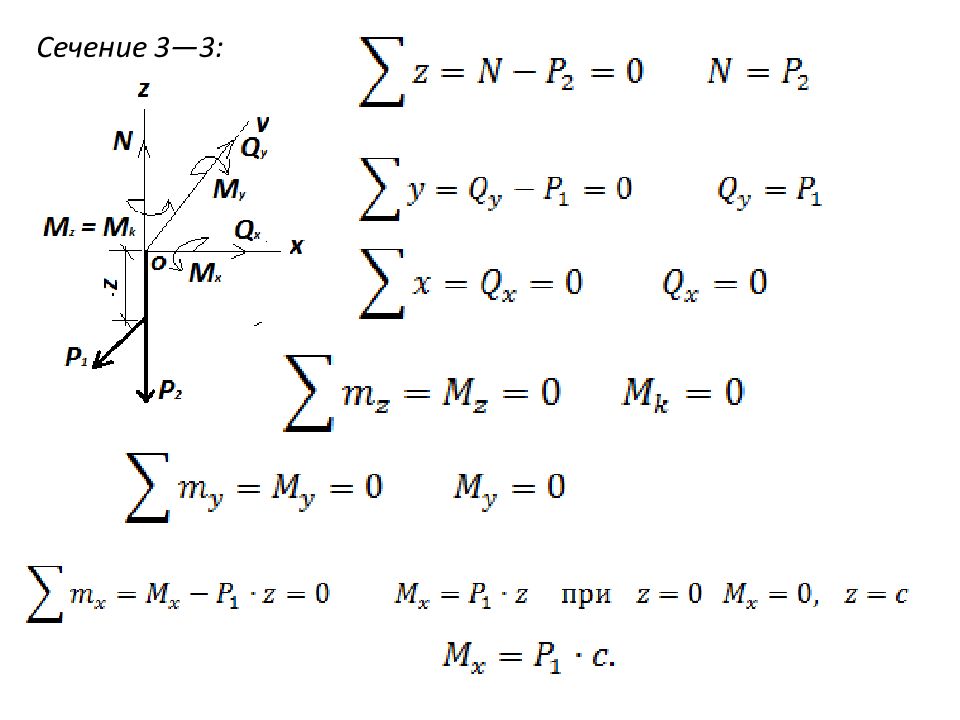
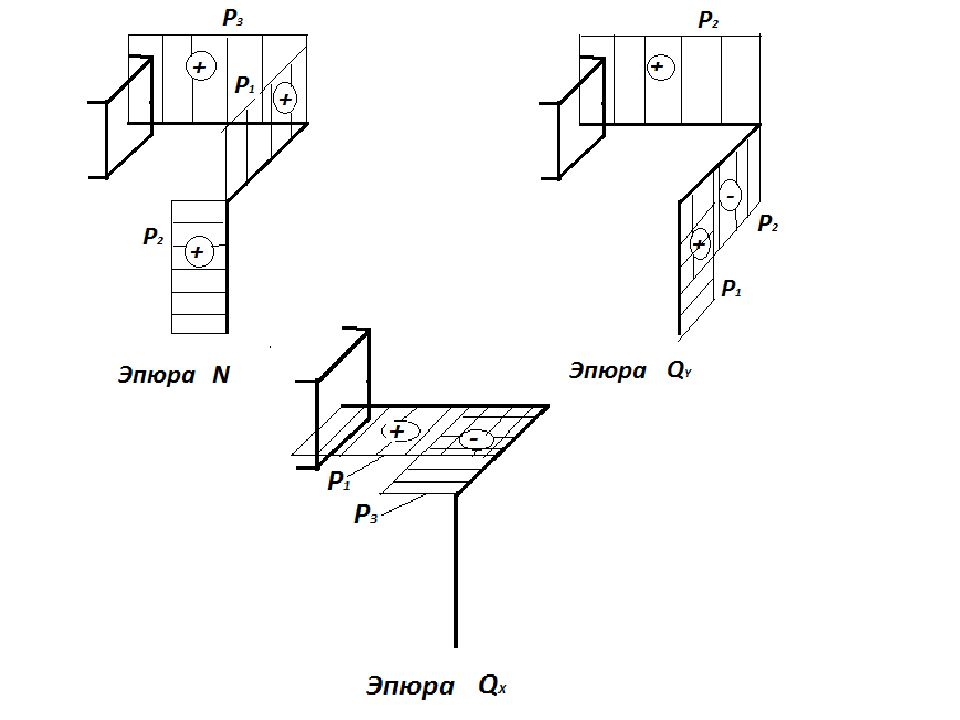
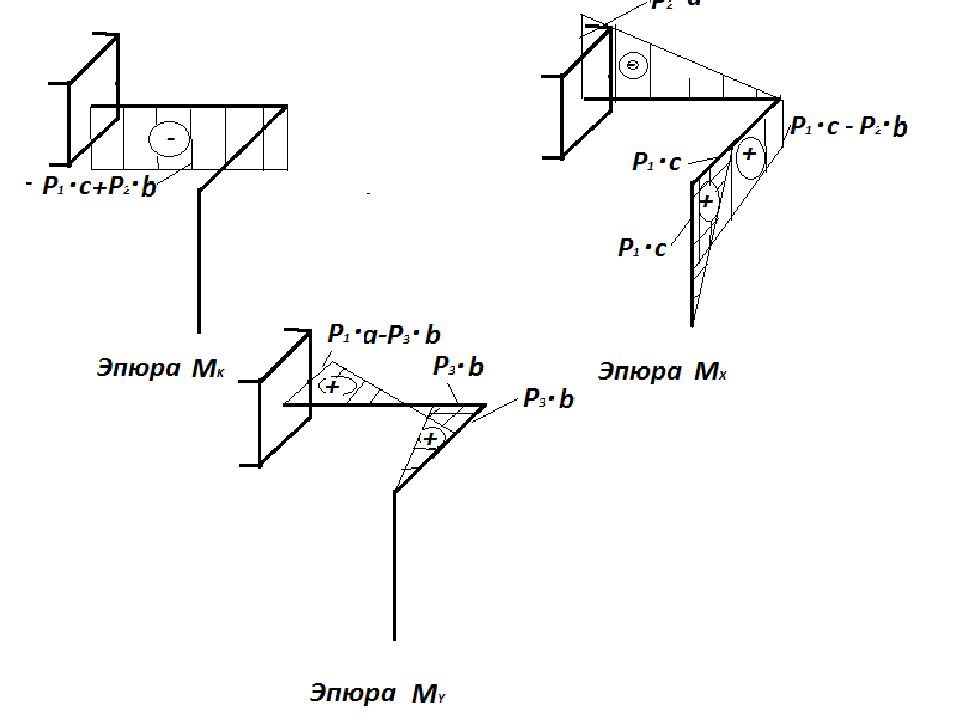
Слайд 46
Рассматривая равновесия отсеченных частей системы определяем значения внутренних усилий на каждом участке. Сечение 1—1: При z=0
Слайд 52
РАСТЯЖЕНИЕ И СЖАТИЕ Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях бруса (стержня) возникают только продольные силы N, а все другие внутренние силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Слайд 53
Определение продольной силы в поперечном сечении производится методом сечения. Рис. 2.1 Если Р i = 0 (рис. 2.1, а), то из Z I = 0, или Z II = 0, N = P 3 + P 4 (рис. 2.1, б); если – P 1 + q l + P 2 = 0 (рис. 2.1, в), то из Z I = 0, (рис.2.1, г). Если продольная сила положительная ( N 0 ), то стержень растягивается, а если отрицательная ( N 0 ), то стержень сжимается.
Слайд 54
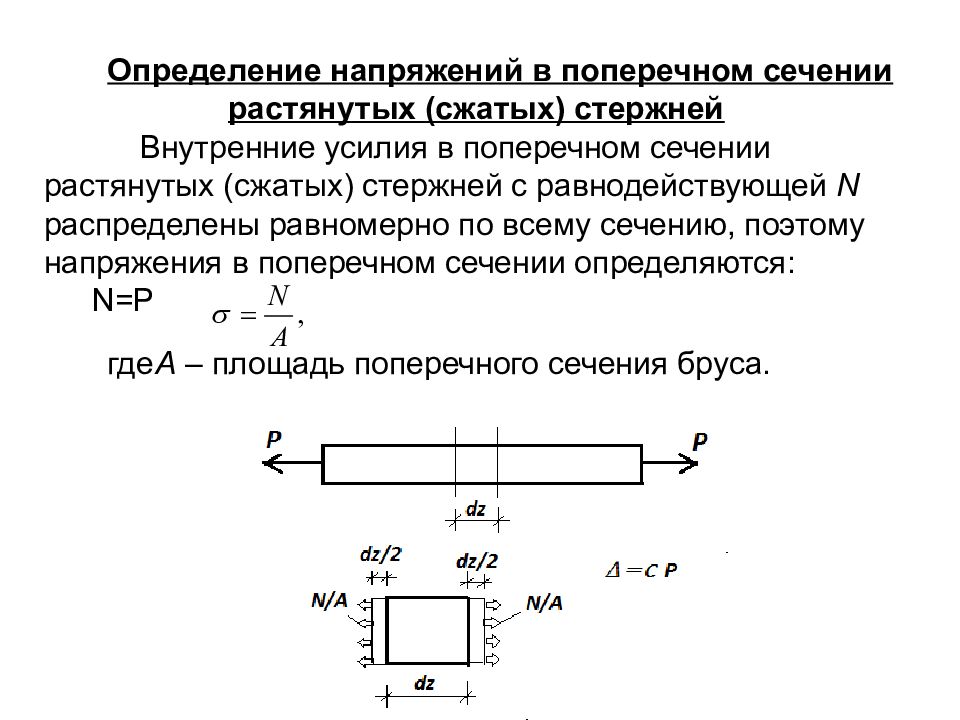
Определение напряжений в поперечном сечении растянутых (сжатых) стержней Внутренние усилия в поперечном сечении растянутых (сжатых) стержней с равнодействующей N распределены равномерно по всему сечению, поэтому напряжения в поперечном сечении определяются: N=P где А – площадь поперечного сечения бруса.
Слайд 55
Условие прочности при растяжении (сжатии) стержня: . Подбор сечения растянутых (сжатых) стержней. Если известны действующие силы и материал стержня, то требуемая площадь сечения: . Определение допускаемой нагрузки. Если известны геометрические размеры и материал стержня, то допускаемая нагрузка на стержень определяется:
Слайд 56
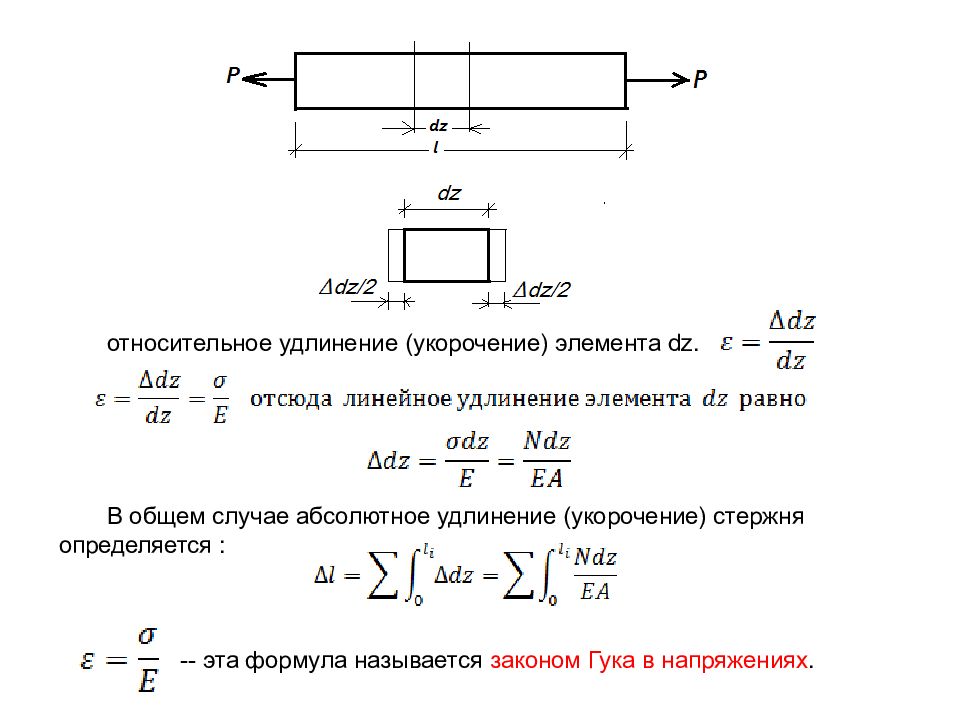
Деформация растянутых (сжатых) элементов Деформация растяжения или сжатия элемента – это линейное удлинение или укорочение стержней вдоль оси. Относительное удлинение стержня равно: Где: -- длина стержня после деформации; -- первоначальная длина стержня; l – абсолютное удлинение (укорочение) стержня (м);
Слайд 57
Если стержень растягивается (сжимается) одной силой Р, то общее удлинение стержня определяется по формуле : Эта формула называется законом Гука при растяжении (сжатии) стержня. ЕА —это произведение модуля упругости стержня на площадь её поперечного сечения называется жесткостью растянутого (сжатого) стержня. Е—модуль упругости материала стержня, это её механическая характеристика; А– площадь поперечного сечения рассматриваемого стержня.
Слайд 58
относительное удлинение (укорочение) элемента dz. В общем случае абсолютное удлинение (укорочение) стержня определяется : -- эта формула называется законом Гука в напряжениях.
Слайд 59
Продольные силы и напряжения в поперечном сечении стержня определяются по формулам: Удлинение (укорочение) стержня с учетом собственного веса с объемным весом ( Н/м 3 )
Слайд 60
Продольные силы и напряжения в поперечном сечении стержня с равномерно распределенной нагрузкой q, действующей по оси стержня определяются по формулам: Удлинение (укорочение) стержня при действии равномерно распределенной нагрузки q определяются по формулам: .
Слайд 61
Условие жесткости при растяжении или сжатии – наибольшее удлинение или укорочение не должно превышать установленной допускаемой величины по технологическим и эксплуатационным требованиям: или , . Подбор сечения бруса из условия жесткости: . Определение допускаемой нагрузки из условия жесткости:
Слайд 62
Потенциальная энергия упругой деформации при растяжении (сжатии) стержня. Потенциальная энергия упругой деформации стержня – это накопленная в стержне энергия, которая будет восстанавливать размеры и формы стержня после удаления внешней нагрузки (Дж): , . Если стержень растягивается (сжимается) одной силой Р Удельная потенциальная энергия – это потенциальная энергия, приходящаяся на единицу объема элемента :
Слайд 63
– относительная линейная деформация; – закон Гука в напряжениях; E A – жесткость стержня при растяжении (сжатии). -- нормальное напряжение в поперечном сечении бруса -- Условие прочности при растяжении (сжатии) стержня -- Подбор сечения растянутых (сжатых) стержней -- Определение допускаемой нагрузки --Определение деформаций растянутых (сжатых) стержней, закон Гука --Если стержень растягивается (сжимается) одной силой Р, закон Гука.
Слайд 64
--Продольная сила в растянуты (сжатых) стержнях с учетом собственного веса. – Напряжения в поперечном сечении бруса. -- Удлинение (укорочение) стержня с учетом собственного веса с объемным весом ,( Н/м 3 ) --Продольная сила при действии равномерно распределенной нагрузки q. --Напряжения в поперечном сечении бруса. -- Удлинение (укорочение) стержня при действии равномерно распределенной нагрузки q
Слайд 65
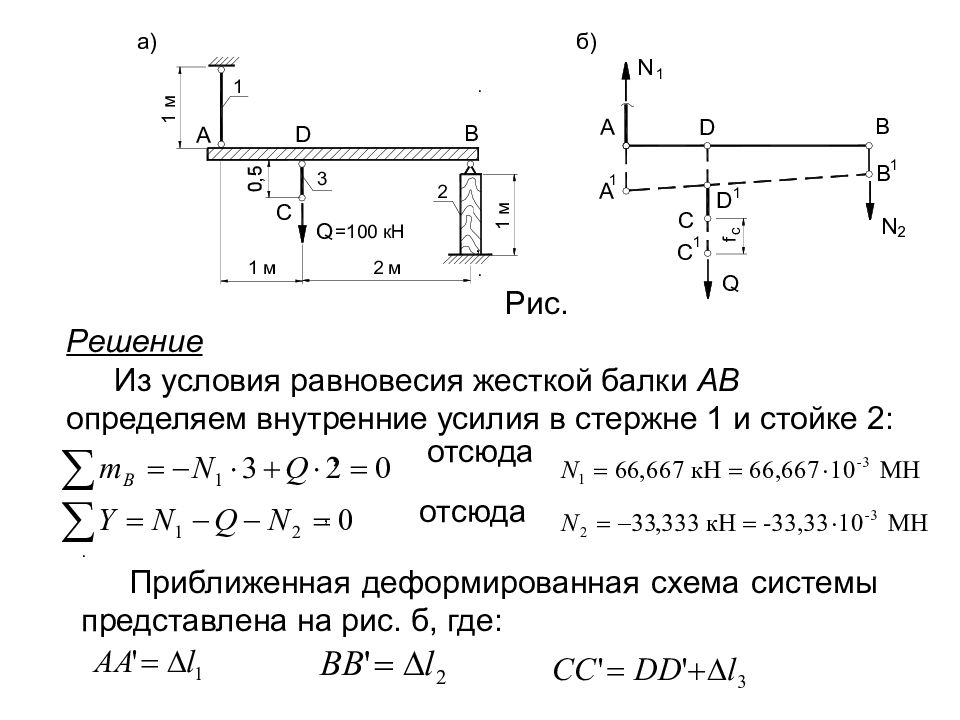
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ НА РАСТЯЖЕНИЕ И СЖАТИЕ Задача 1 Жесткая балка, деформацией которой пренебрегаем, закреплена и нагружена силой Q =100 кН, как показано рисунке. Стержень 1 – стальной, сечением 10 см 2, стойка 2 – деревянная, сечением 100 см 2, стержень 3 – медный, сечением 30 см 2. Определить вертикальное перемещение точки С, если линейные модули упругости материалов стержней равны Е ст =2,1 10 5 МПа, Е м =1 10 5 МПа, Е д =1 10 4 МПа.
Слайд 66
Рис. Решение Из условия равновесия жесткой балки АВ определяем внутренние усилия в стержне 1 и стойке 2: , отсюда . , отсюда . Приближенная деформированная схема системы представлена на рис. б, где: , .
Слайд 67
Из закона Гука определяем удлинение стержней 1 и 3 и укорочение стойки 2: , , Из рис. б определяем: Вертикальное перемещение точки С будет:
Слайд 68
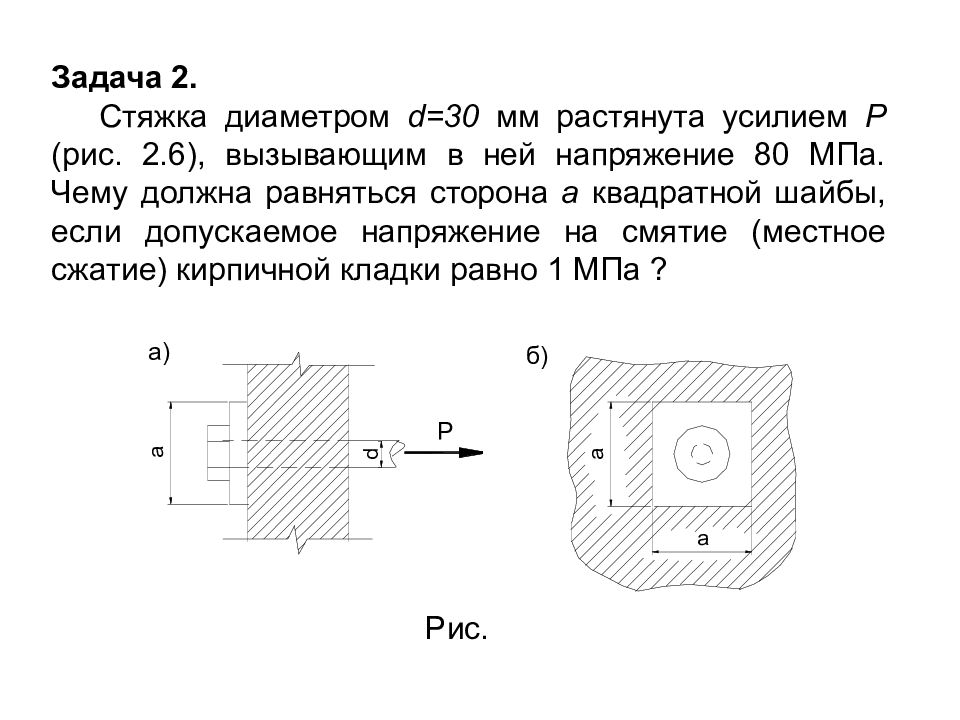
Задача 2. Стяжка диаметром d =30 мм растянута усилием Р (рис. 2.6), вызывающим в ней напряжение 80 МПа. Чему должна равняться сторона а квадратной шайбы, если допускаемое напряжение на смятие (местное сжатие) кирпичной кладки равно 1 МПа ? Рис.
Слайд 69
Решение Определяем растягивающее усилие Р в стяжке: Из условия прочности на смятие кирпичной стенки Определяем размеры шайбы: Принимаем а =24 см.
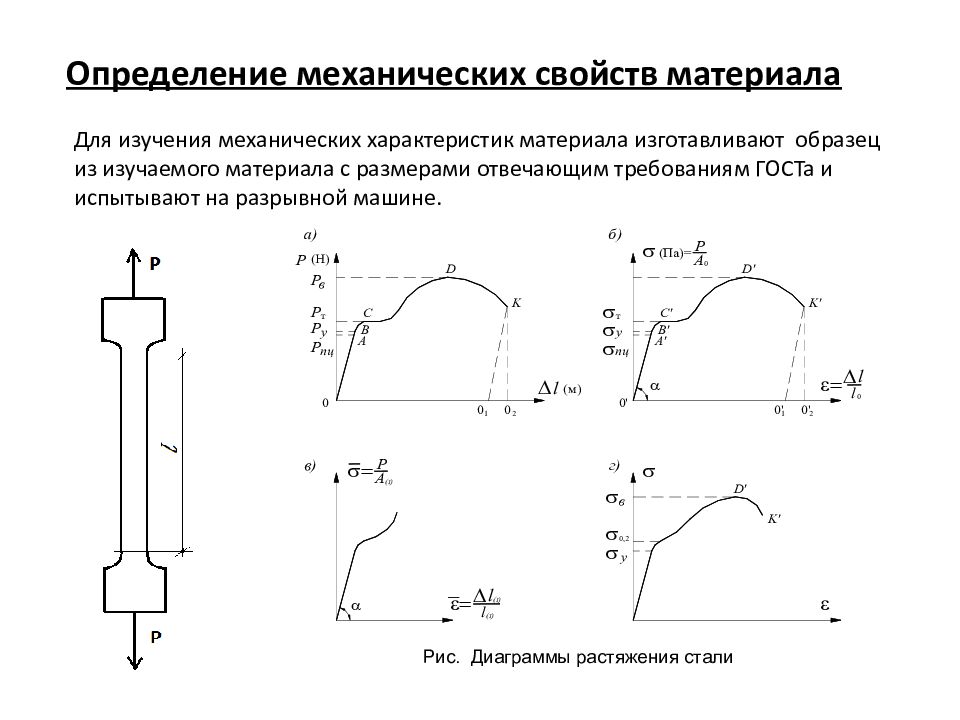
Слайд 70
Определение механических свойств материала Для изучения механических характеристик материала изготавливают образец из изучаемого материала с размерами отвечающим требованиям ГОСТа и испытывают на разрывной машине. Рис. Диаграммы растяжения стали
Слайд 71
Из условной диаграммы получаем механические характеристики материалов: – предел пропорциональности ( па или Мпа ); наименьшее напряжение, при котором в образце нарушается линейный закон зависимости между нагрузкой и деформацией; – предел упругости ( па или Мпа ) наименьшее напряжение, при котором в образце появляется 0,05% остаточного удлинения. На практике принимают );
Слайд 72
– физический предел текучести (па или Мпа ); наименьшее напряжение, при котором образец деформируется без заметного увеличения нагрузки; – условный предел текучести (па или Мпа ); напряжение, при котором остаточное удлинение достигает 0,2% длины рабочей части образца; – временное сопротивление (па или Мпа ) напряжение, соответствующее н аибольшей нагрузке, предшествующей разрыву образца;
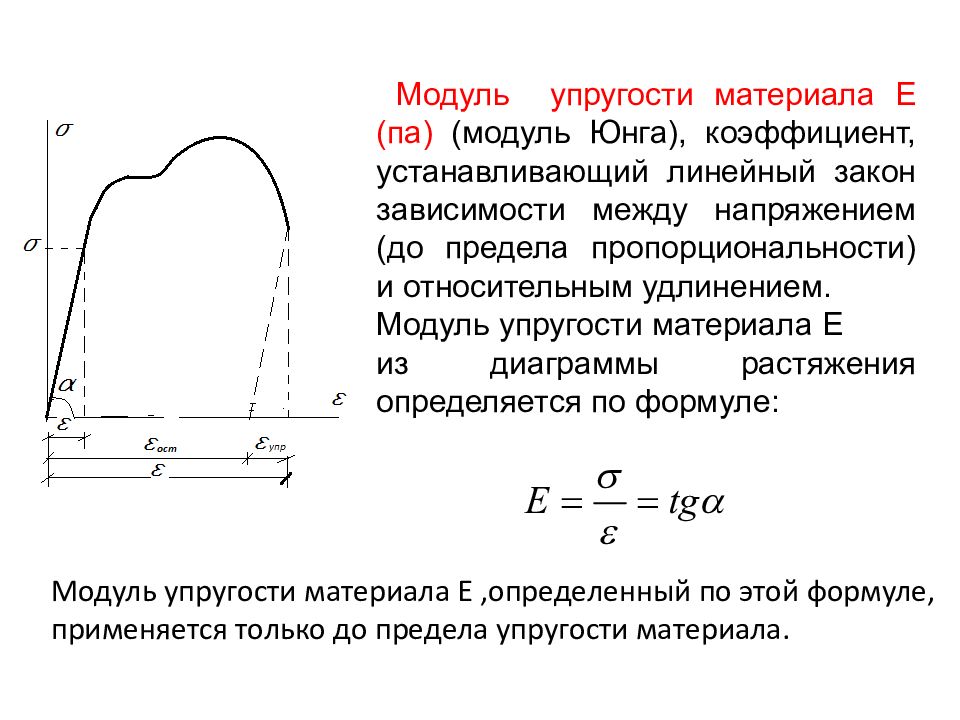
Слайд 73
М одуль упругости материала Е (па) (модуль Юнга), коэффициент, устанавливающий линейный закон зависимости между напряжением (до предела пропорциональности) и относительным удлинением. Модуль упругости материала Е из диаграммы растяжения определяется по формуле: Модуль упругости материала Е,определенный по этой формуле, применяется только до предела упругости материала.
Слайд 74
По результатам испытания определяют основные свойства материала. Упругость – свойство материала восстанавливать свои первоначальные форму и размеры после снятия внешних сил. Пластичность – свойство материала получать значительные остаточные деформации до разрушения. Хрупкость – свойство материала разрушаться при небольших деформациях. Твердость – свойство материала сопротивляться продавливанию в него других тел под действием внешних сил.
Слайд 75
Пластичность материала оценивается: остаточным равномерным относительным удлинением: остаточным относительным удлинением: остаточным равномерным сужением: остаточным относительным сужением шейки:
Слайд 76
где А 0 – начальная площадь поперечного сечения образца; А ш – площадь поперечного сечения образца в месте разрыва (шейка); А кр – площадь поперечного сечения образца в местах с равномерным сужением; l кр – длина участков образца после разрыва с равномерными остаточными удлинениями; l ор – начальная длина участков образца с равномерными остаточными удлинениями; l 0 – начальная длина образца; l к – длина образца после разрыва.
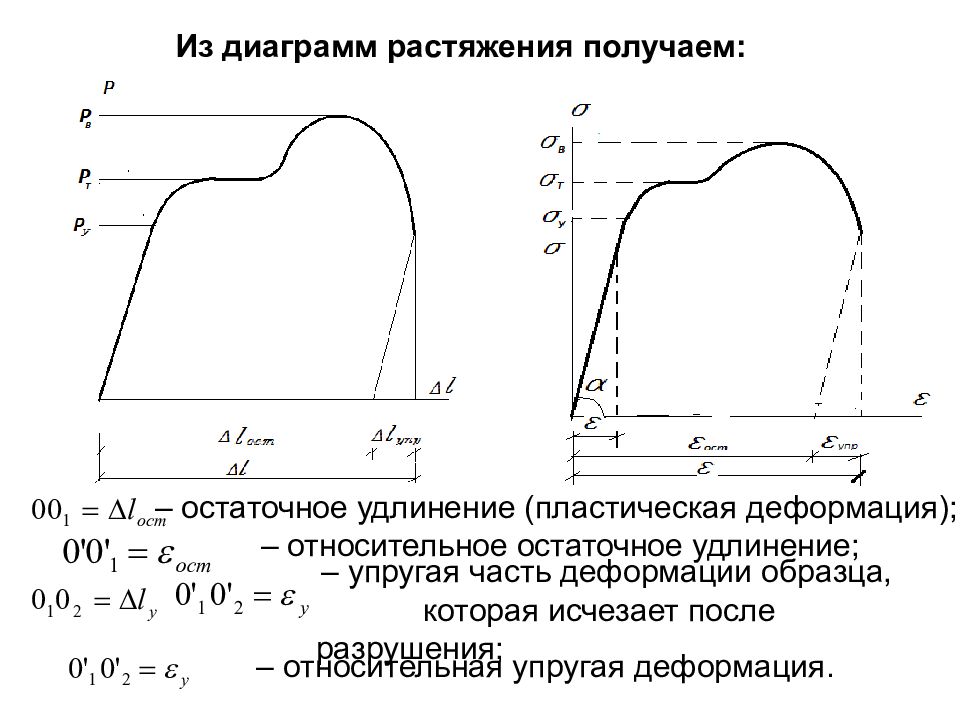
Слайд 77
Из диаграмм растяжения получаем: – остаточное удлинение (пластическая деформация); – относительное остаточное удлинение; – упругая часть деформации образца, которая исчезает после разрушения; – относительная упругая деформация.
Слайд 78
Из графика Р – l строится истинная диаграмма растяжения при этом по горизонтальной оси откладывается величина относительной деформации, полученная как отношение абсолютного удлинения к действительной длине образца, т.е. с учетом деформации по вертикальной оси – действительное напряжение, полученное как отношение действующей силы к действительной площади сечения, т.е. с учетом сужения где А ( t ) – площадь поперечного сечения образца с учетом деформации в момент измерения; l ( t ) – удлинение длины образца в момент измерения l ( t ) = l ( t ) – l 0.
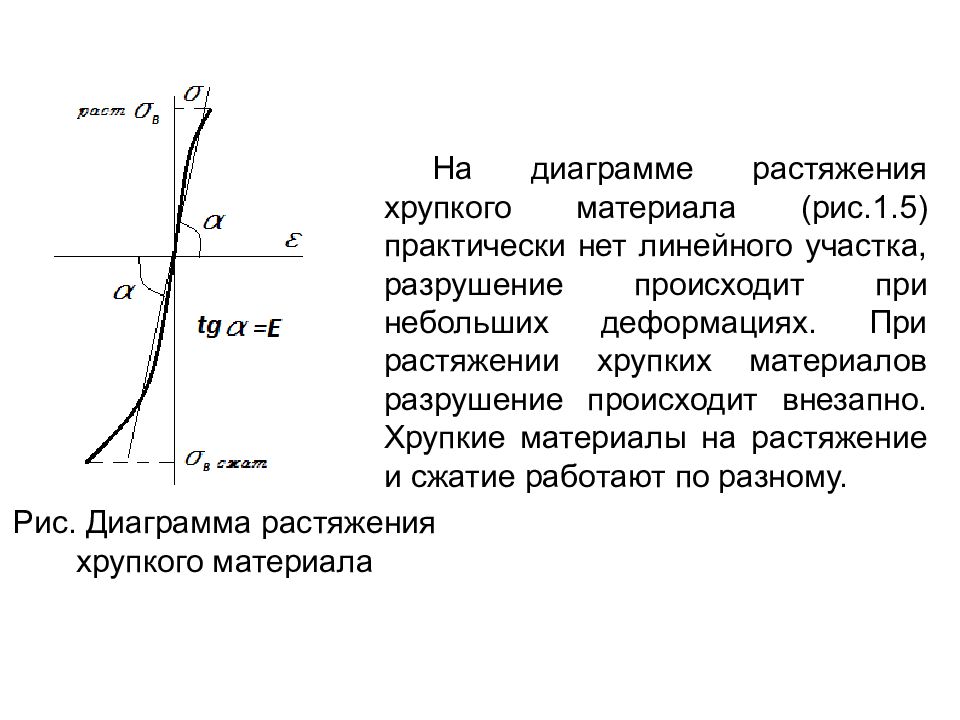
Слайд 79
На диаграмме растяжения хрупкого материала (рис.1.5) практически нет линейного участка, разрушение происходит при небольших деформациях. При растяжении хрупких материалов разрушение происходит внезапно. Хрупкие материалы на растяжение и сжатие работают по разному. Рис. Диаграмма растяжения хрупкого материала
Слайд 80
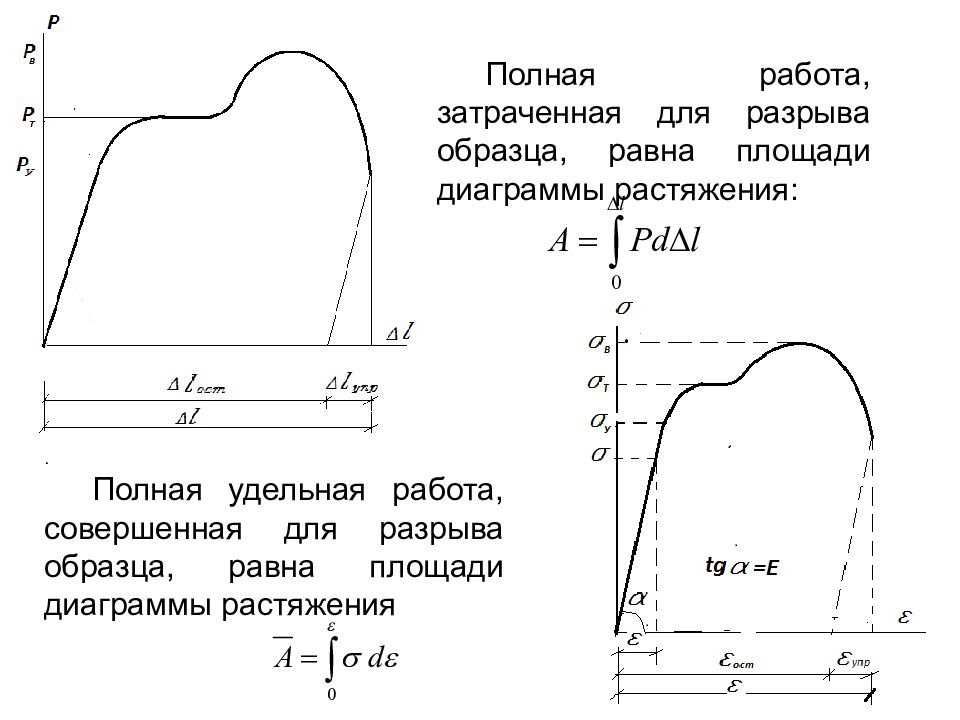
Полная работа, затраченная для разрыва образца, равна площади диаграммы растяжения: . Полная удельная работа, совершенная для разрыва образца, равна площади диаграммы растяжения
Слайд 81
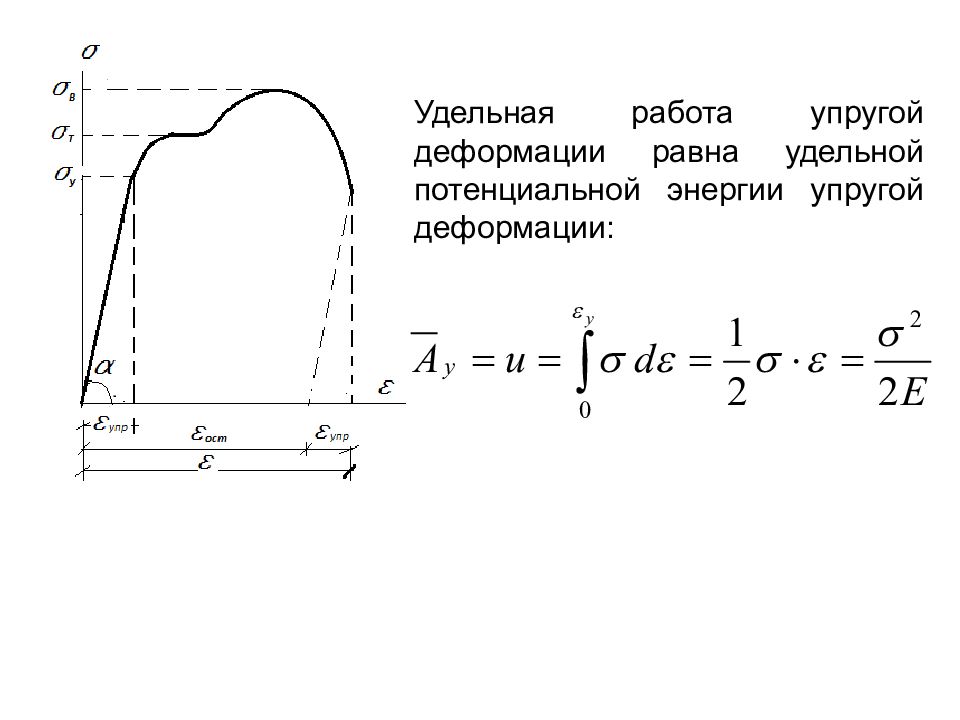
Удельная работа упругой деформации равна удельной потенциальной энергии упругой деформации:
Слайд 82
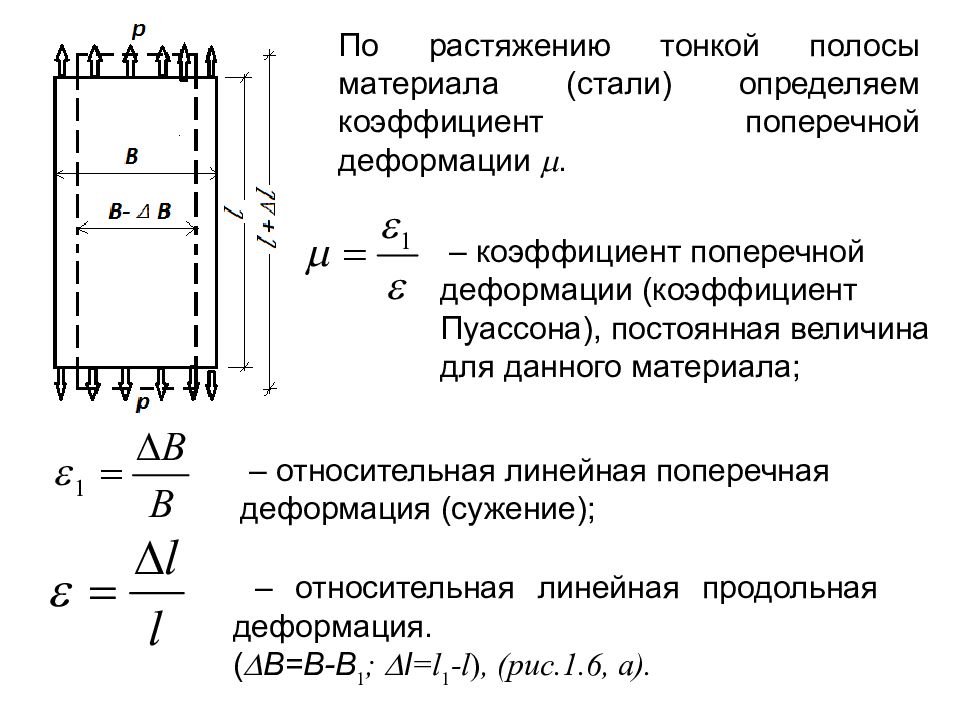
По растяжению тонкой полосы материала (стали) определяем коэффициент поперечной деформации . – коэффициент поперечной деформации (коэффициент Пуассона), постоянная величина для данного материала; – относительная линейная поперечная деформация (сужение); – относительная линейная продольная деформация. ( В=В-В 1 ; l = l 1 - l ), (рис.1.6, а).
Слайд 83
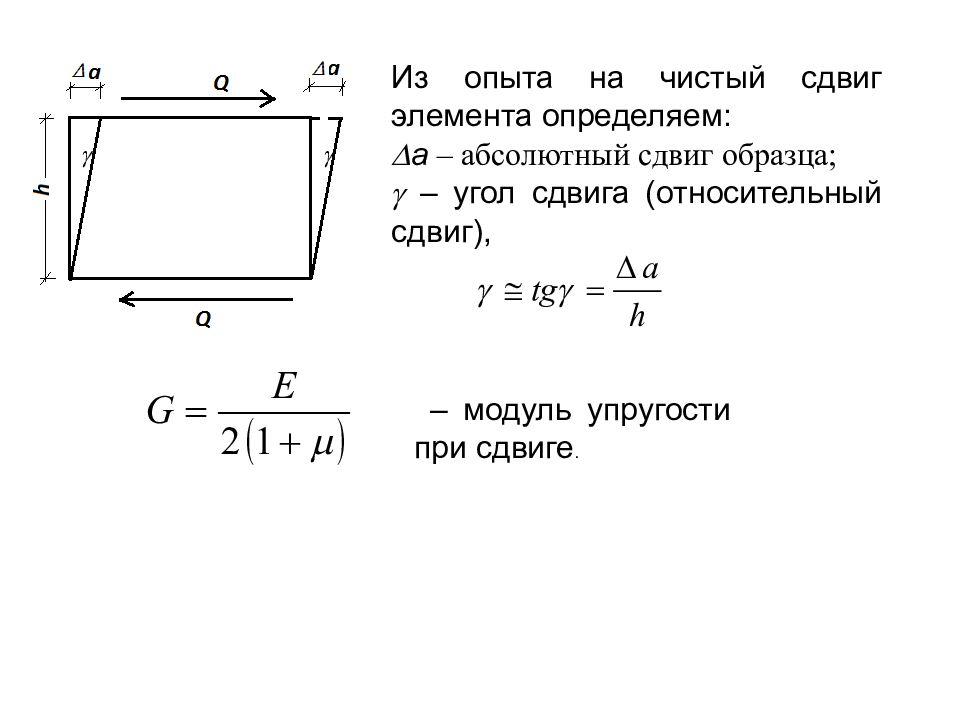
Из опыта на чистый сдвиг элемента определяем: а – абсолютный сдвиг образца; – угол сдвига (относительный сдвиг), – модуль упругости при сдвиге.
Слайд 84
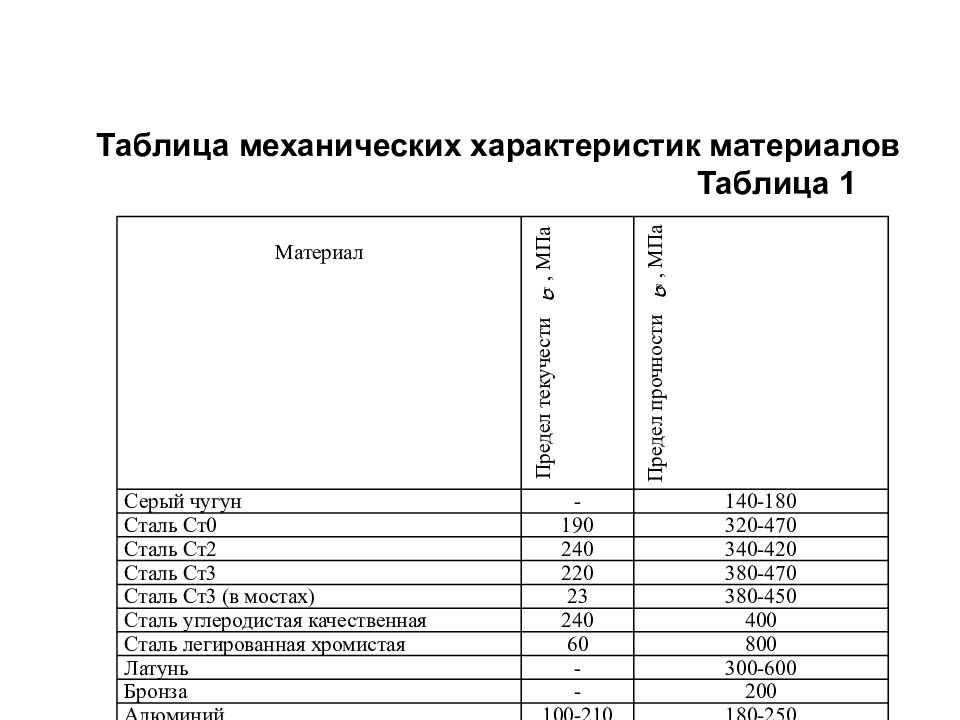
Материал Предел текучести т, МПа Предел прочности в, МПа Серый чугун - 140-180 Сталь Ст0 190 320-470 Сталь Ст2 240 340-420 Сталь Ст3 220 380-470 Сталь Ст3 (в мостах) 23 380-450 Сталь углеродистая качественная 240 400 Сталь легированная хромистая 60 800 Латунь - 300-600 Бронза - 200 Алюминий 100-210 180-250 Алюминиевая бронза - 600 Дюралюминий 50-250 180-420 Таблица механических характеристик материалов Таблица 1
Слайд 85
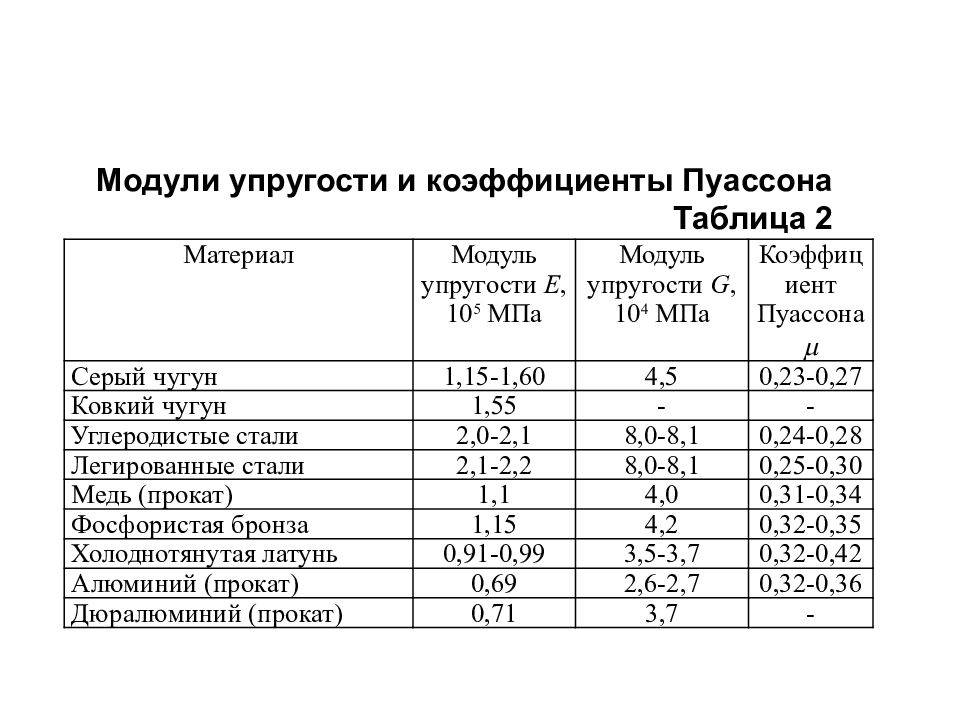
Материал Модуль упругости Е, 10 5 МПа Модуль упругости G, 10 4 МПа Коэффициент Пуассона Серый чугун 1,15-1,60 4,5 0,23-0,27 Ковкий чугун 1,55 - - Углеродистые стали 2,0-2,1 8,0-8,1 0,24-0,28 Легированные стали 2,1-2,2 8,0-8,1 0,25-0,30 Медь (прокат) 1,1 4,0 0,31-0,34 Фосфористая бронза 1,15 4,2 0,32-0,35 Холоднотянутая латунь 0,91-0,99 3,5-3,7 0,32-0,42 Алюминий (прокат) 0,69 2,6-2,7 0,32-0,36 Дюралюминий (прокат) 0,71 3,7 - Модули упругости и коэффициенты Пуассона Таблица 2
Слайд 86
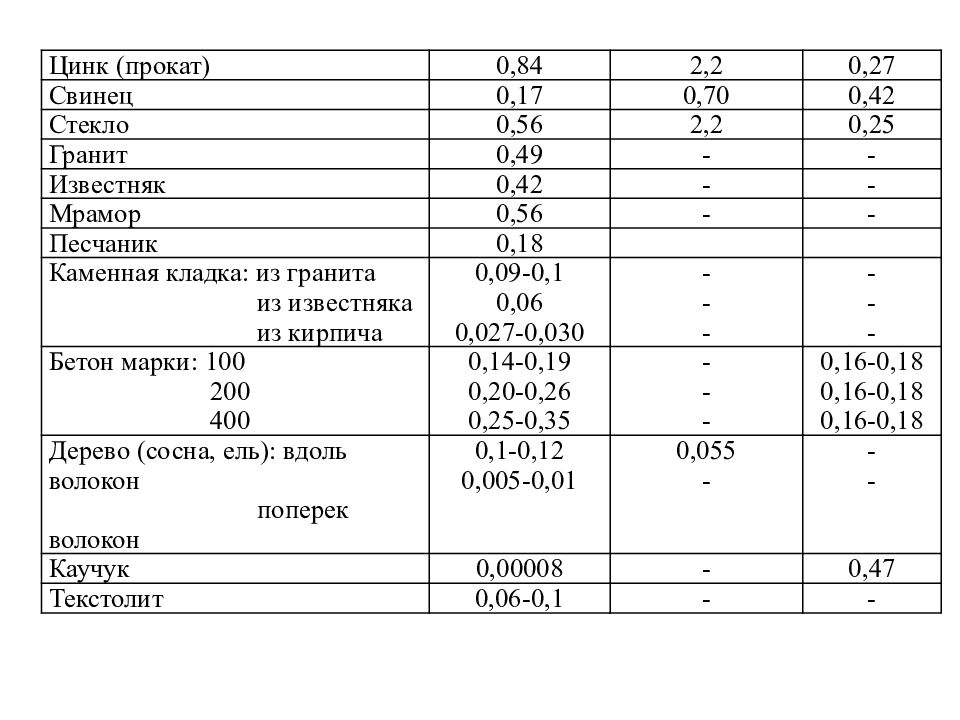
Цинк (прокат) 0,84 2,2 0,27 Свинец 0,17 0,70 0,42 Стекло 0,56 2,2 0,25 Гранит 0,49 - - Известняк 0,42 - - Мрамор 0,56 - - Песчаник 0,18 Каменная кладка: из гранита из известняка из кирпича 0,09-0,1 0,06 0,027-0,030 - - - - - - Бетон марки: 100 200 400 0,14-0,19 0,20-0,26 0,25-0,35 - - - 0,16-0,18 0,16-0,18 0,16-0,18 Дерево (сосна, ель): вдоль волокон поперек волокон 0,1-0,12 0,005-0,01 0,055 - - - Каучук 0,00008 - 0,47 Текстолит 0,06-0,1 - -
Слайд 87
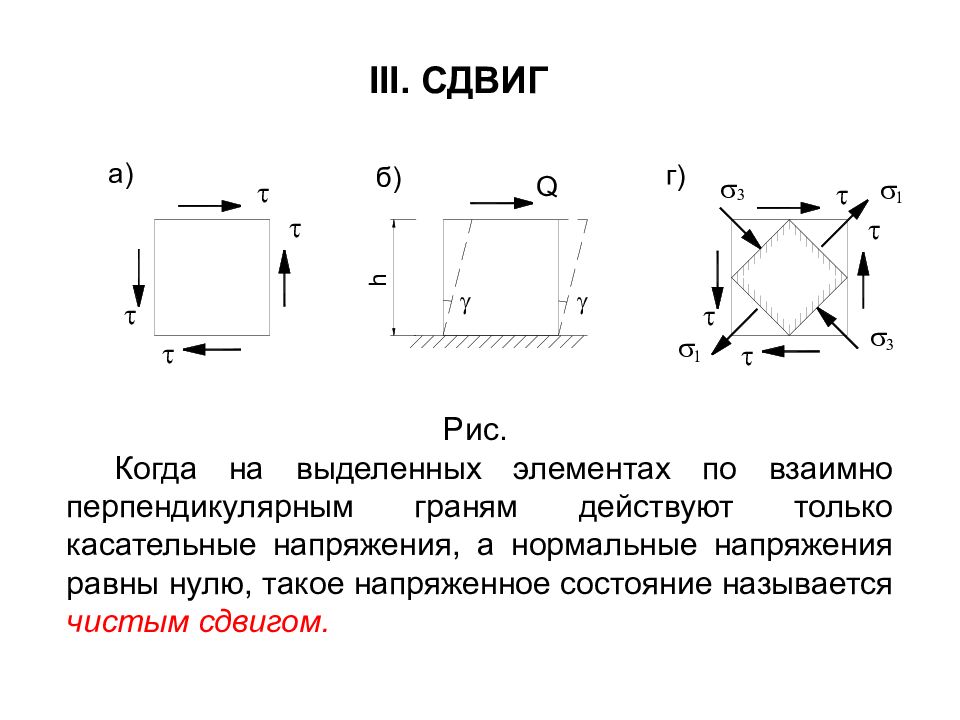
III. СДВИГ Рис. Когда на выделенных элементах по взаимно перпендикулярным граням действуют только касательные напряжения, а нормальные напряжения равны нулю, такое напряженное состояние называется чистым сдвигом.
Слайд 88
Касательные н апряжения при чистом сдвиге определяются: , где Q – сдвигающая сила; А сд – площадь сдвига. --Условие прочности при сдвиге: -- Закон Гука при сдвиге в напряжениях: где GA сд – жесткость элемента при сдвиге. Поставляя значение , получим
Слайд 89
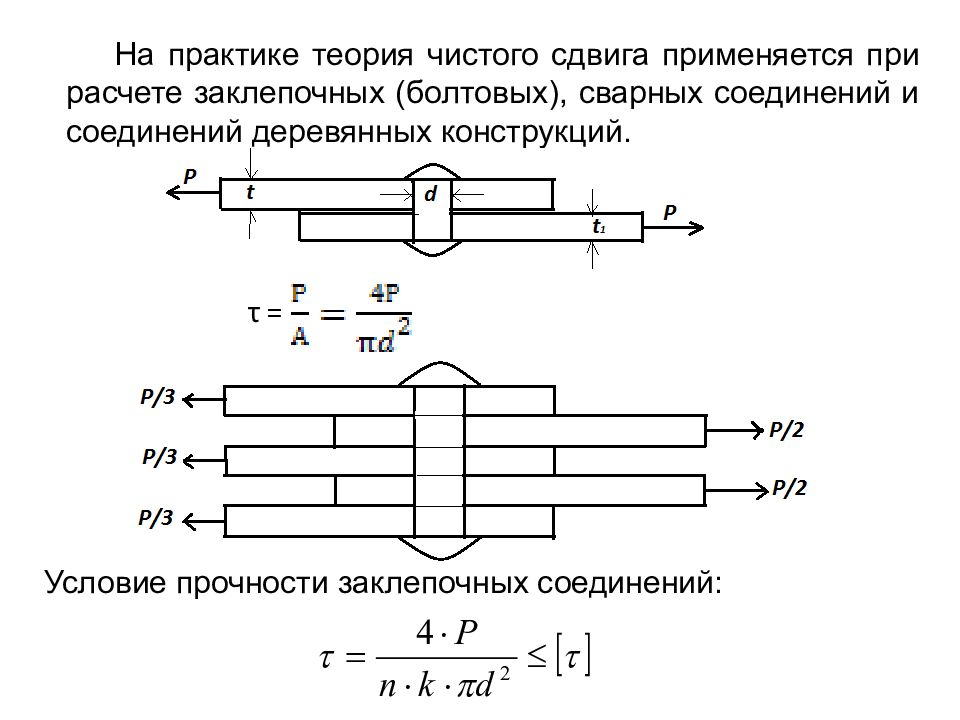
На практике теория чистого сдвига применяется при расчете заклепочных (болтовых), сварных соединений и соединений деревянных конструкций. τ = Условие прочности заклепочных соединений:
Слайд 90
Когда известны диаметры заклепок и материал, требуемое их количество заклепок или болтов определяется: . Когда известно количество заклепок n и материал, требуемый их диаметр определяется: . Когда известны размеры, количество и материал заклепок допускаемая нагрузка на соединение определяется: где k – количество площадок среза заклепки. n – количество заклепок.
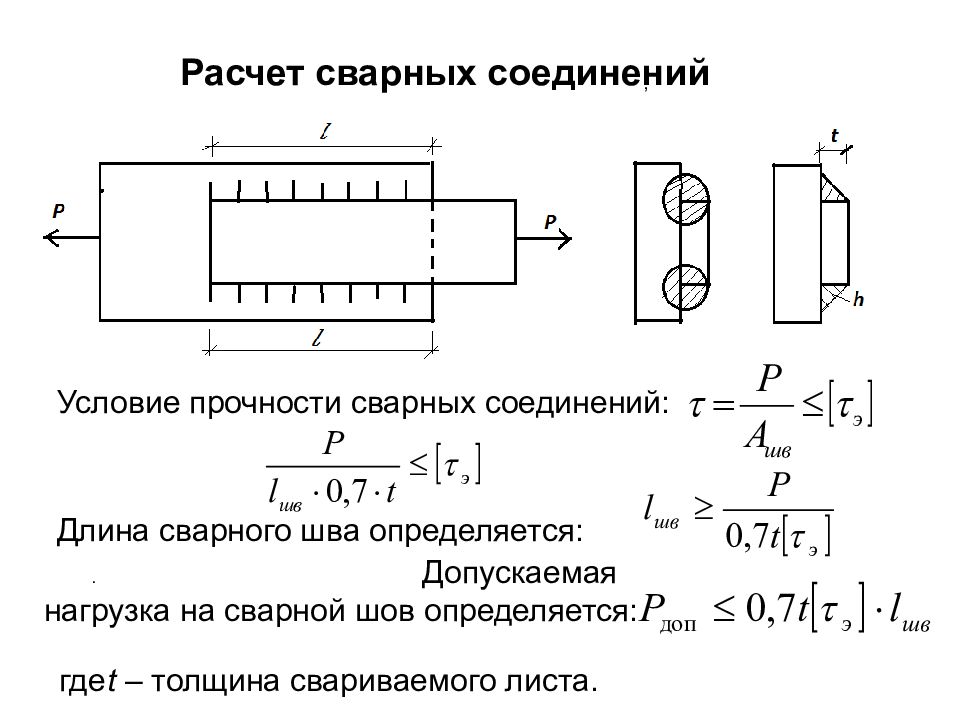
Слайд 91
Условие прочности сварных соединений: , Длина сварного шва определяется: . Допускаемая нагрузка на сварной шов определяется: где t – толщина свариваемого листа. Расчет сварных соединений
Слайд 92
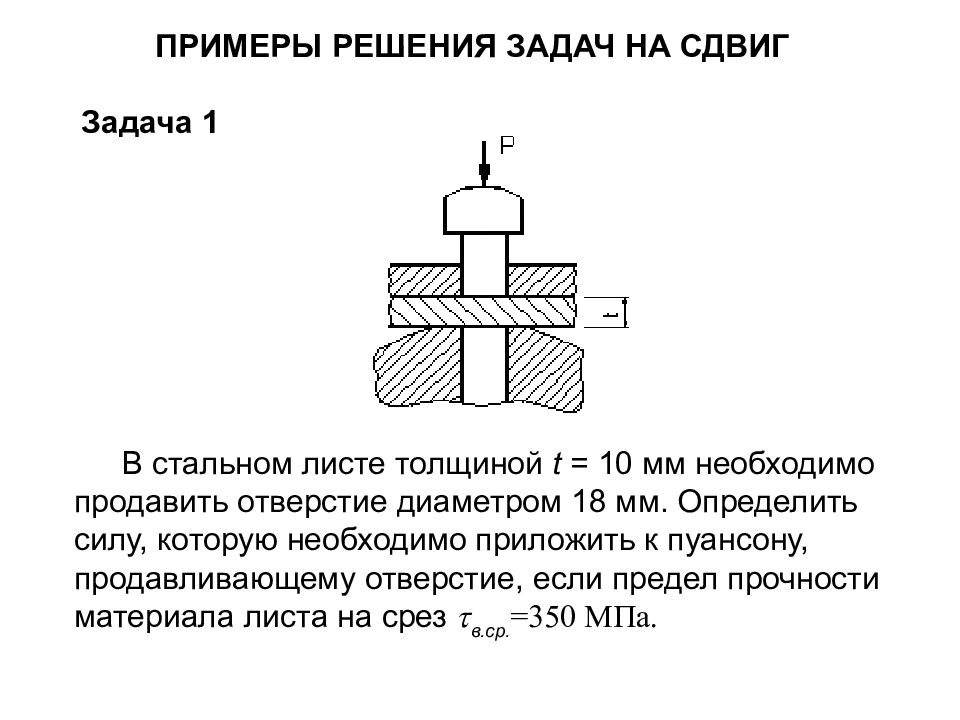
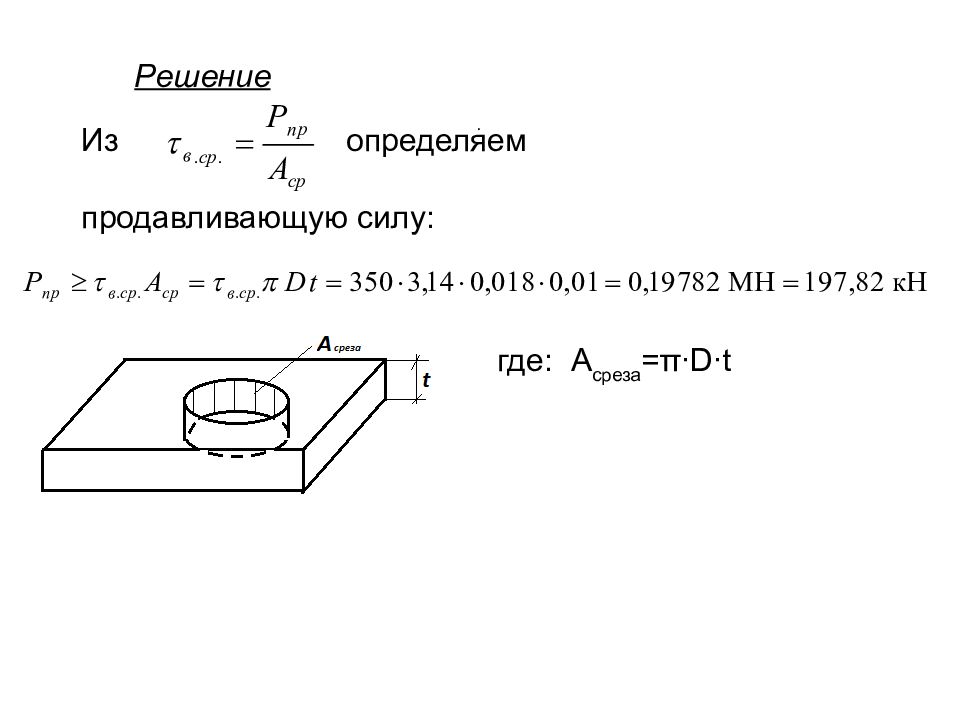
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ НА СДВИГ Задача 1 В стальном листе толщиной t = 10 мм необходимо продавить отверстие диаметром 18 мм. Определить силу, которую необходимо приложить к пуансону, продавливающему отверстие, если предел прочности материала листа на срез в.ср. =350 МПа.
Слайд 94
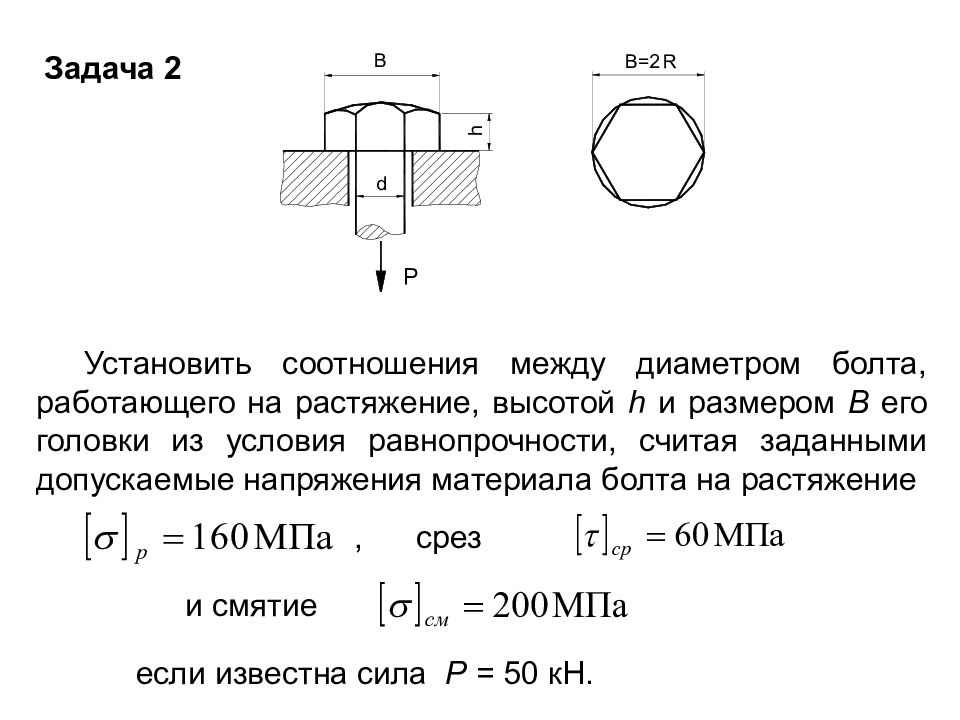
Задача 2 Установить соотношения между диаметром болта, работающего на растяжение, высотой h и размером В его головки из условия равнопрочности, считая заданными допускаемые напряжения материала болта на растяжение , срез и смятие если известна сила Р = 50 кН.
Слайд 95
Минимальный радиус болта определяется из условия прочности на растяжение: , отсюда Принимаем R =10 мм. Из условия прочности на срез головки болта определяем его высоту h : Принимаем h =14 мм.
Слайд 96
Из условия прочности на смятие определим размеры головки болта, для чего предварительно определяем площадь смятия: А см = Принимаем В =15 мм. Ответ: R =10 мм, h =14 мм, В =15 мм. Из условия прочности на смятие определим размеры головки болта
Слайд 97
Задача 3 Котел диаметром D =160 см подвергнут внутреннему давлению р =10 атм. Продольный шов осуществлен внахлестку с двумя рядами заклепок, толщина листов t = 10 мм, диаметр заклепок d = 20 мм, шаг заклепок а = 100 мм. Определить касательное, сжимающее и растягивающее напряжения в стыке. Определить предельное допускаемое давление в котле при следующих допускаемых напряжениях: . Рис. на срез на смятие на растяжение основного материала котла
Слайд 98
Решение Вырезаем из котла в области шва элемент шириной равной шагу заклепок «а» (рис. 3, а). Тангенциальные растягивающие усилия, действующие на этот элемент, определяются: где р =10 атм =10 6 Па. Сдвигающие касательные напряжения в поперечном сечении заклепки равны: Сминающие напряжения определяются:
Слайд 99
Растягивающие напряжения в листе котла: Следовательно, из условий прочности заклепок на срез и смятие котел на заданное давление не может работать. Из заданных условий прочностей заклепок и материала котла определяем предельное допускаемое давление в котле. Из условия среза заклепок: отсюда Из условия смятия заклепок: отсюда
Слайд 100
Из условия разрыва листа котла: отсюда Сравнивая результаты вычисления, предельное допускаемое давление в котле определяем из условия прочности заклепок на срез, при котором получаем наименьшее значение р доп :
Слайд 101
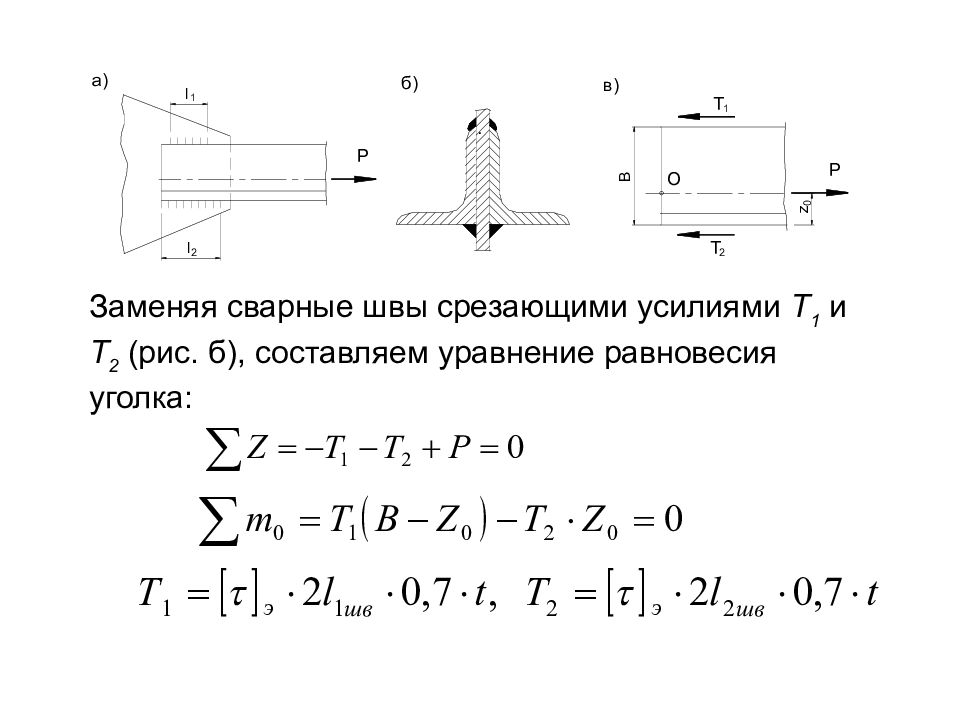
Задача 4 Растянутый стержень состоит из двух уголков 120 80 10. Они приварены к фасонке фланговыми швами, как показано на рис. 3.8, а. Определить длины швов l 1 и l 2, если допускаемое напряжение для сварки на срез, а допускаемое напряжение материала уголка на растяжение =160 МПа. Толщина швов равна толщине полок уголка. Решение Из таблицы сортаментов определяем для данного уголка Z 0 =3,93 см, А =19,2 см 2, t=10мм.
Слайд 102
Заменяя сварные швы срезающими усилиями Т 1 и Т 2 (рис. б), составляем уравнение равновесия уголка: .
Слайд 103
Из условия прочности уголков на растяжение определяем предельно допустимую нагрузку на узел: Из условия прочности сварного шва: определяем необходимую длину сварного шва: где – толщина полки уголков.
Слайд 104
Так как сварка производится с обеих сторон фасонки равными длинами: . Подставляя значение Т 1 и Т 2 в уравнение равновесия соединения получаем: . Окончательно с учетом недовара швов на концах принимаем: или . или .
Слайд 105
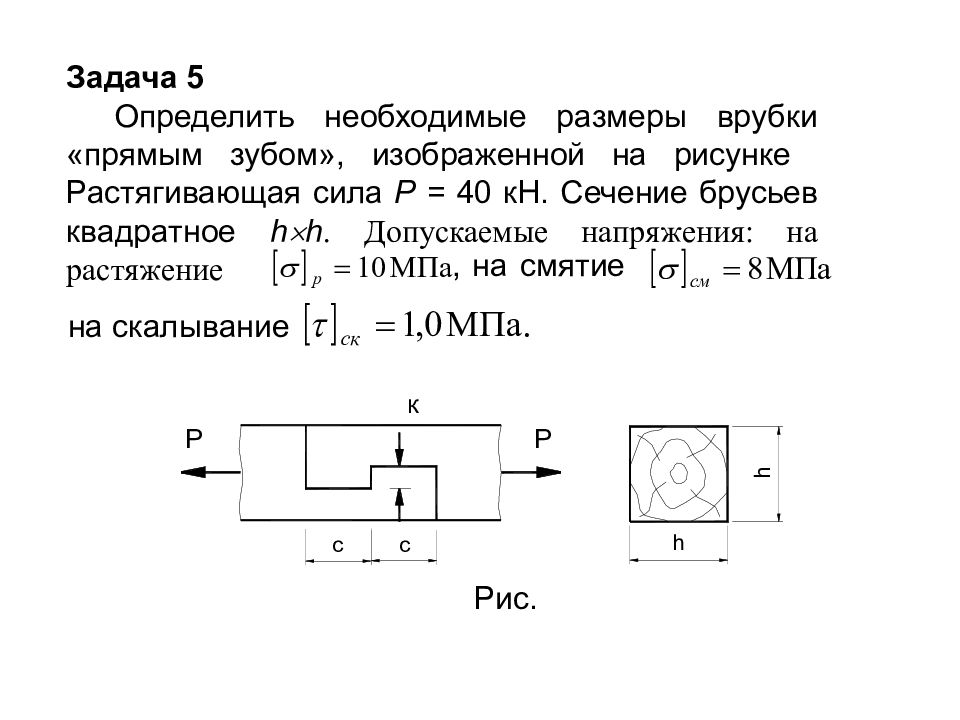
Задача 5 Определить необходимые размеры врубки «прямым зубом», изображенной на рисунке Растягивающая сила Р = 40 кН. Сечение брусьев квадратное h h. Допускаемые напряжения: на растяжение , на смятие на скалывание Рис.
Слайд 106
Решение Из условия прочности на смятие получаем зависимость между высотой зуба K и размерами сечения бруса h : отсюда Подставляем эту зависимость в условие прочности на растяжение: Подставляя значение K, получаем: , , принимаем h =12 см. Тогда K =4,2 см.
Слайд 107
Из условия прочности на скалывания зубов соединения определяем необходимую их длину С : , отсюда . Принимаем С =34 см.
Слайд 108
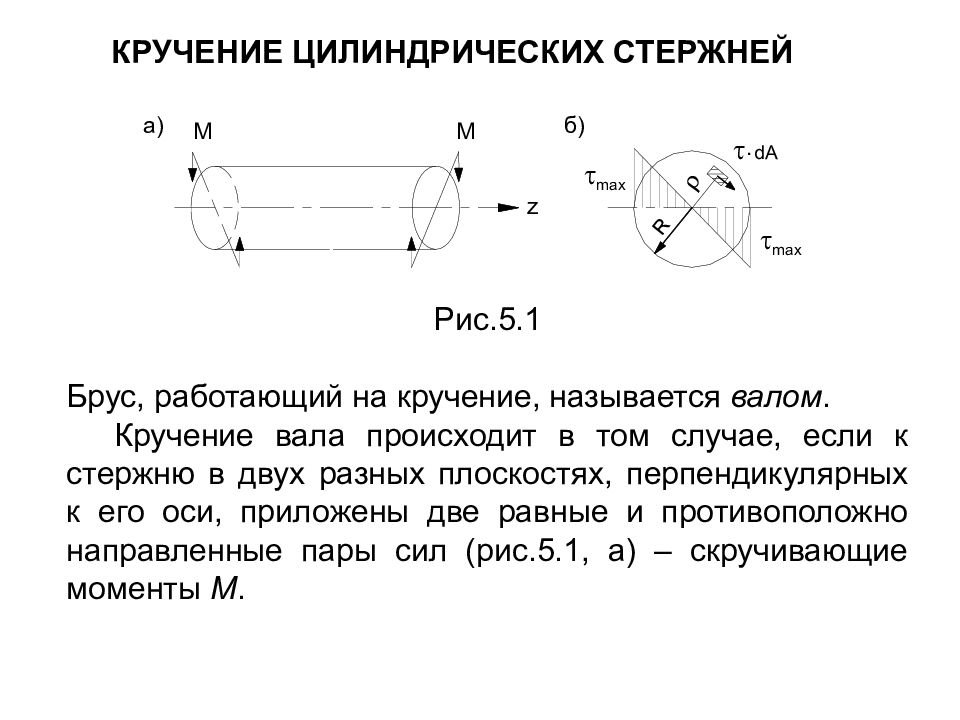
КРУЧЕНИЕ ЦИЛИНДРИЧЕСКИХ СТЕРЖНЕЙ Рис.5.1 Брус, работающий на кручение, называется валом. Кручение вала происходит в том случае, если к стержню в двух разных плоскостях, перпендикулярных к его оси, приложены две равные и противоположно направленные пары сил (рис.5.1, а) – скручивающие моменты М. Брус, работающий на кручение, называется валом. Кручение вала происходит в том случае, если к стержню в двух разных плоскостях, перпендикулярных к его оси, приложены две равные и противоположно направленные пары сил (рис.5.1, а) – скру
Слайд 109
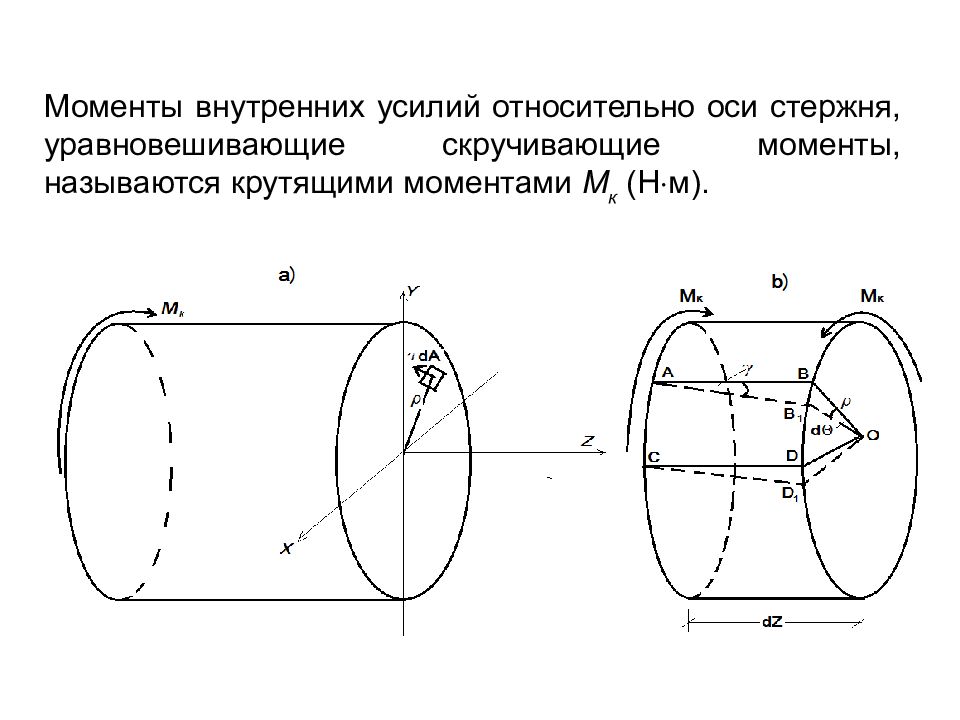
Моменты внутренних усилий относительно оси стержня, уравновешивающие скручивающие моменты, называются крутящими моментами М к ( Н м ).
Слайд 110
Проекция всех действующих сил на оси x, y, z равны нулю Сумма моментов всех сил относительно осей x, y тоже равны нулю сумма моментов относительно оси Z будет иметь вид .
Последний слайд презентации: ЛЕКЦИИ ПО КУРСУ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Из второго рисунка b ), деформированной схемы элемента dZ имеем: деформацию элемента АВСD, который принимает положение АВ 1 СD 1. (чистый сдвиг элемента) отсюда с другой стороны имеем Приравнивая выражения ВВ 1 получаем отсюда Поставляя это выражение в уравнение равновесия получаем