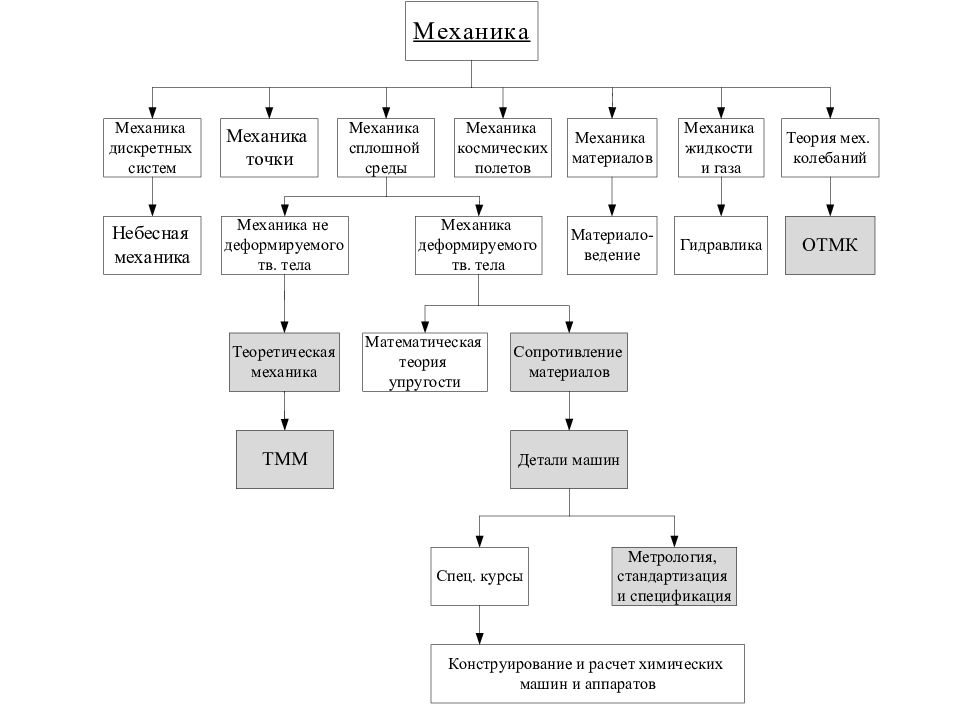
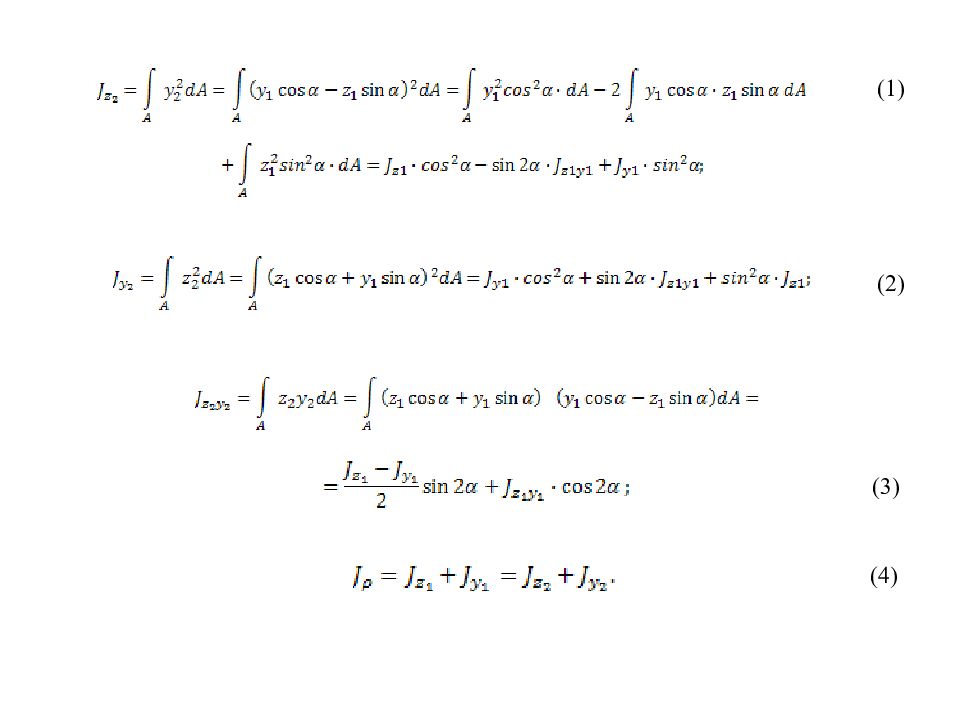Слайд 3: Вводная тема 1 Актуальность изучения курса
При проектировании различных строительных и машиностроительных конструкций, конструктор должен грамотно решить следующие два вопроса: 1 Правильно выбрать материал для всех элементов конструкции. 2 Определить геометрическую форму и размеры этих элементов. Основание для решения этих вопросов дает наука о сопротивлении материалов.
Слайд 4: 2 Основные задачи курса СМ
СМ – это наука о прочности, жесткости и устойчивости конструкции. 2.1 Конструкция должна быть прочной. Прочность – это способность конструкции воспринимать действия внешних нагрузок без признаков разрушения. 2.2 Конструкция должна быть жесткой. Жесткост ь – это способность конструкции сопротивляться действию внешних нагрузок без существенных изменений формы и размеров. 2.3 Конструкция должна быть устойчивой. Устойчивость – это способность конструкции при действии внешних нагрузок сохранять устойчивую форму равновесия.
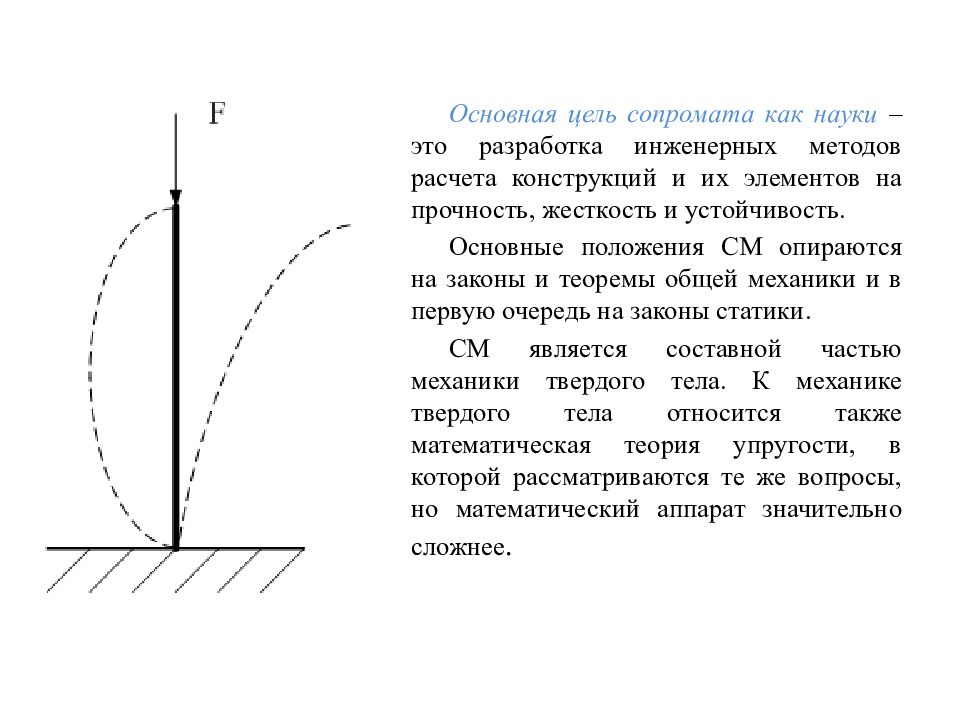
Слайд 5
Основная цель сопромата как науки – это разработка инженерных методов расчета конструкций и их элементов на прочность, жесткость и устойчивость. Основные положения СМ опираются на законы и теоремы общей механики и в первую очередь на законы статики. СМ является составной частью механики твердого тела. К механике твердого тела относится также математическая теория упругости, в которой рассматриваются те же вопросы, но математический аппарат значительно сложнее.
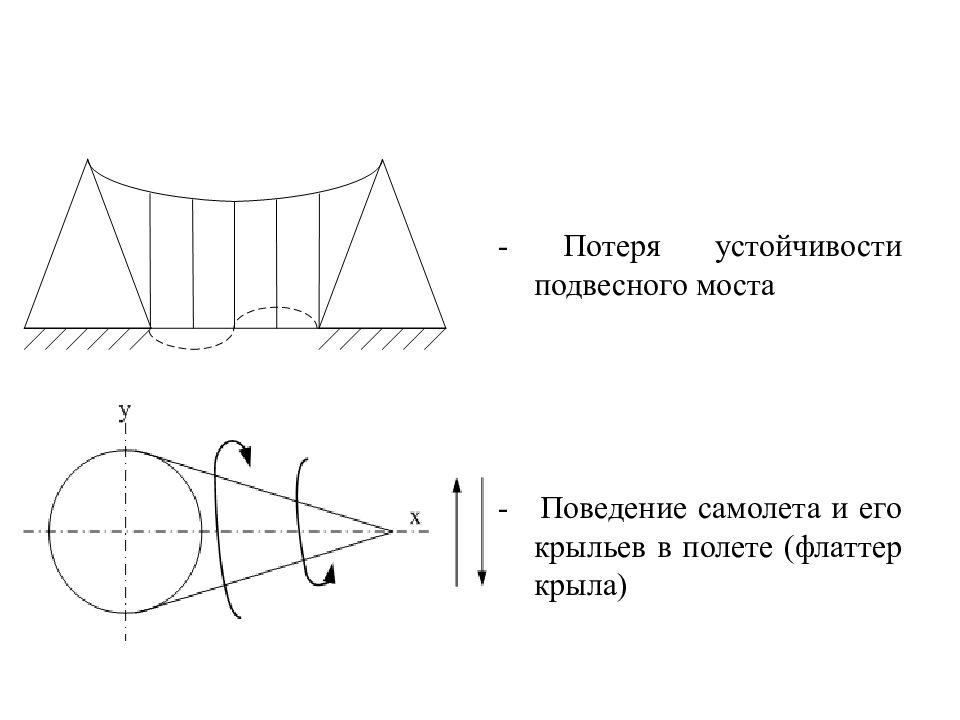
Слайд 6
- Потеря устойчивости подвесного моста - Поведение самолета и его крыльев в полете (флаттер крыла)
Все конструкции при проектировании обязательно рассчитываются на прочность, жесткость или устойчивость. Расчеты проводятся одновременно с конструированием. При расчетах конструктор использует расчетные схемы. Расчетная схема – реальная конструкция, освобожденная от несущественных подробностей, т.е. конструктор должен знать, что в конструкции существенно, а что менее существенно. Например, у вращающегося вала всегда должны быть две опоры. Чем подробнее расчетная схема, тем сложнее математическая модель, которая описывает поведение разрабатываемой машины.
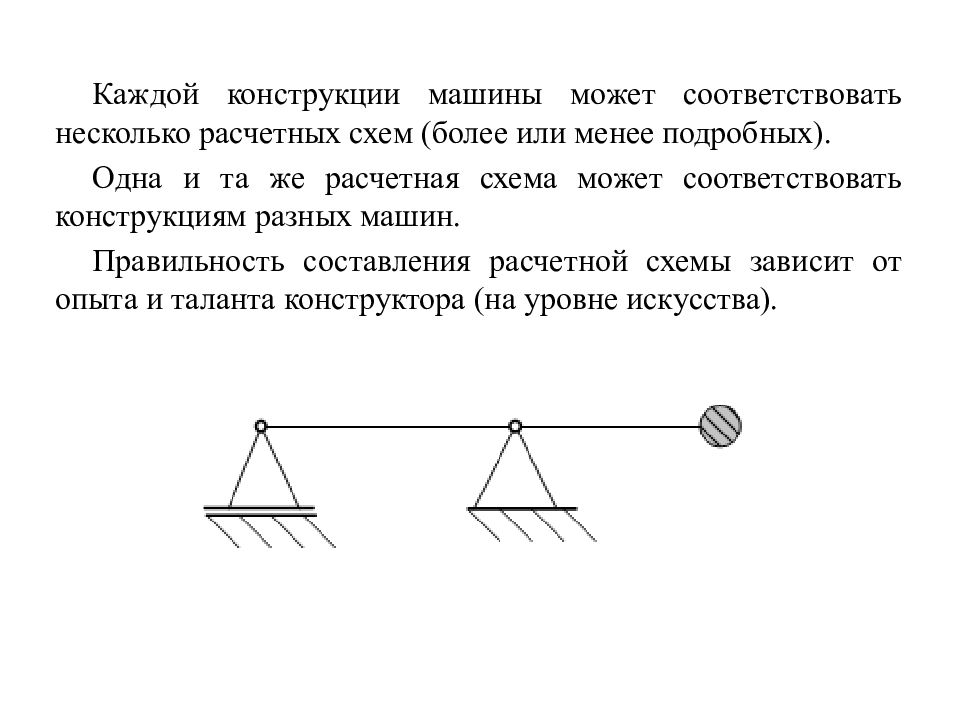
Слайд 8
Каждой конструкции машины может соответствовать несколько расчетных схем (более или менее подробных). Одна и та же расчетная схема может соответствовать конструкциям разных машин. Правильность составления расчетной схемы зависит от опыта и таланта конструктора (на уровне искусства).
Для упрощения расчетов в СМ используется целый ряд гипотез и допущений.
Слайд 10: 4.1 Допущения в свойствах материалов
Используется термин « тело » как элемент реальной конструкции. Предполагается, что материал тела является сплошным, однородным, изотропным и идеально упругим. Сплошность – весь объем тела заполнен материалом, пустоты отсутствуют. Прокат → литье → ковка. Наибольшую сплошность обеспечивает прокат. Однородность – все частицы тела обладают одинаковыми свойствами независимо от размеров тела. Наибольшую однородность дает прокат. Изотропность – свойства тела во всех направлениях - одинаковые. Анизотропия – это такие материалы, как дерево, бумага, фанера, ткань, композиты и др. Идеальная упругость – после снятия внешних нагрузок тело полностью восстанавливает свои первоначальные размеры и форму.
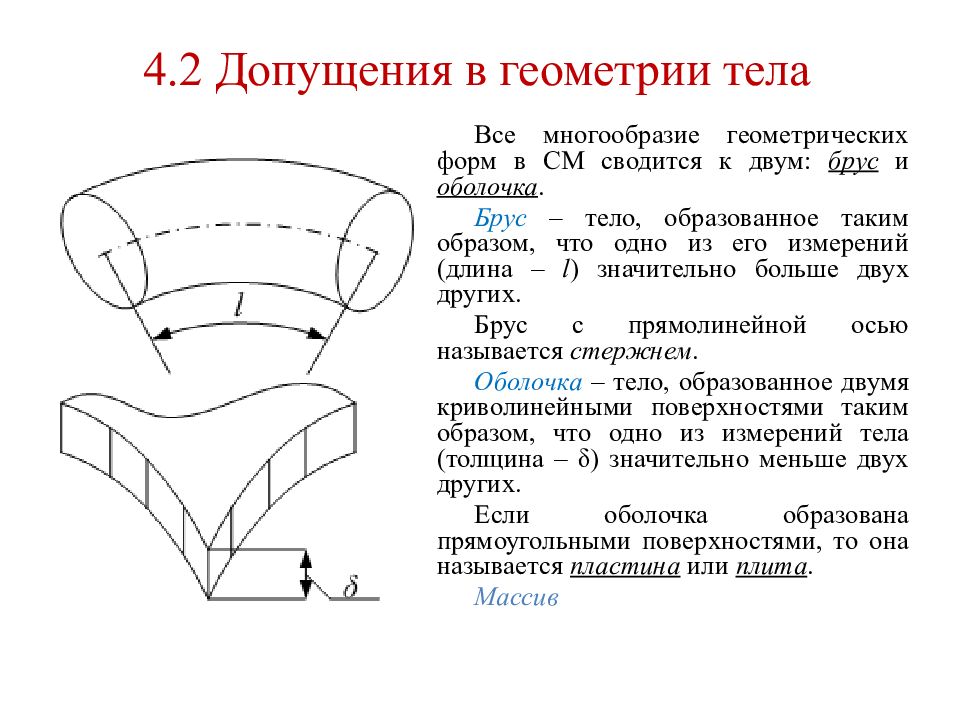
Слайд 11: 4.2 Допущения в геометрии тела
Все многообразие геометрических форм в СМ сводится к двум: брус и оболочка. Брус – тело, образованное таким образом, что одно из его измерений (длина – l ) значительно больше двух других. Брус с прямолинейной осью называется стержнем. Оболочка – тело, образованное двумя криволинейными поверхностями таким образом, что одно из измерений тела (толщина – δ) значительно меньше двух других. Если оболочка образована прямоугольными поверхностями, то она называется пластина или плита. Массив
Слайд 12: 4.3 Допущения во внешних силах, приложенных к телу
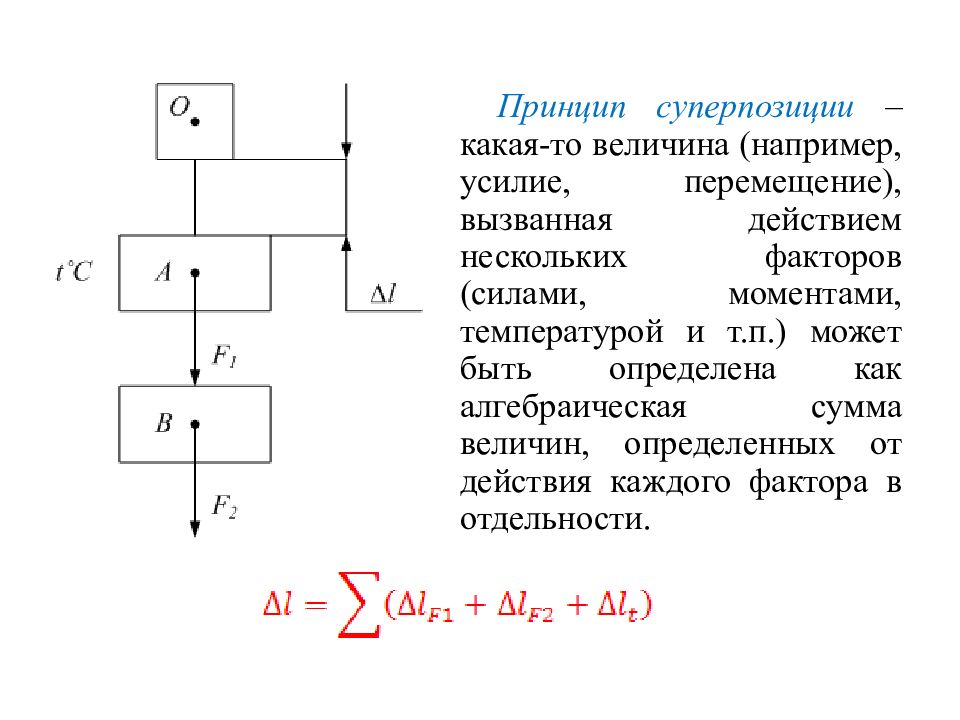
В СМ внешние силы могут быть распределенными и сосредоточенными. Согласно принципу Сен-Венана распределенные нагрузки могут быть заменены эквивалентными сосредоточенными. Это возможно в том случае, если площадь приложения распределенной нагрузки мала по сравнению с размерами самого тела. Силы могут быть статическими и динамическими. Статические – силы, которые очень медленно изменяют свою величину и достигнув конечного значения, практически не изменяется. Динамические – силы, которые быстро изменяют свою величину, их действие может сопровождаться колебаниями конструкции. В СМ используется принцип суперпозиции (принцип независимости действия сил).
Слайд 13
Принцип суперпозиции – какая-то величина (например, усилие, перемещение), вызванная действием нескольких факторов (силами, моментами, температурой и т.п.) может быть определена как алгебраическая сумма величин, определенных от действия каждого фактора в отдельности.
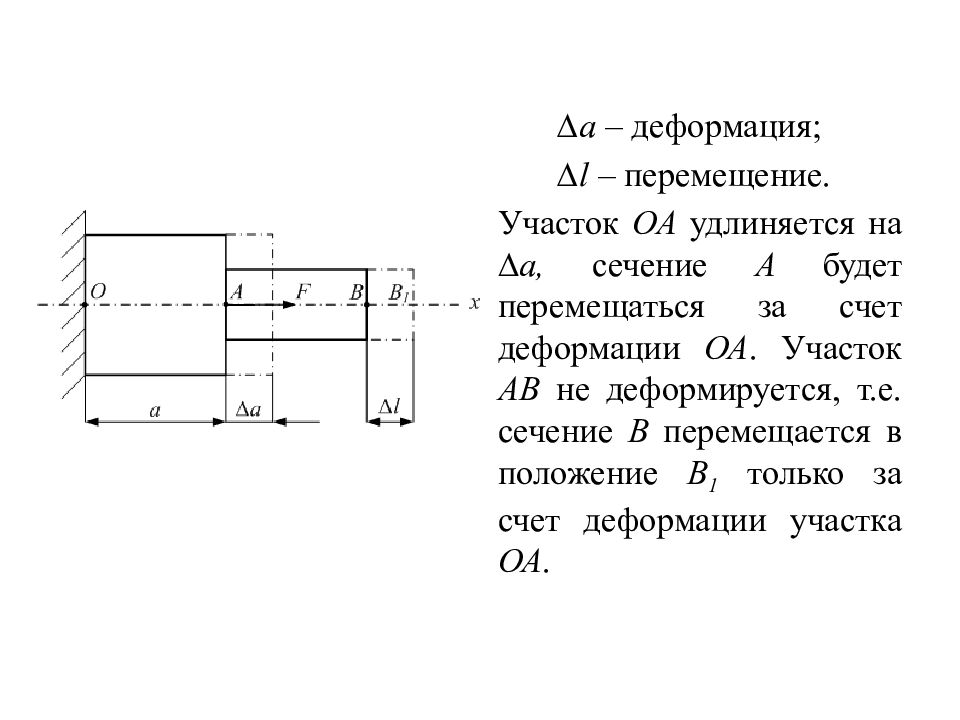
Слайд 14: 4.4 Допущения при определении деформаций
Гипотеза о малости деформаций (принцип начальных размеров). Согласно этому принципу, деформации считаются настолько малыми, что не влияют на взаимное расположение нагрузок, т.е. при определении реакций связи тело считается недеформируемым, следовательно, можно использовать уравнения статики общей механики. Гипотеза плоских сечений (гипотеза Бернулли) Сечения, плоские и перпендикулярные оси тела, остаются таковыми и после приложения внешних нагрузок. Гипотеза о линейной зависимости между перемещениями и нагрузками. Считается, что для большинства материалов сохраняется линейная зависимость между перемещениями(деформациями) и внешними нагрузками.
Слайд 15
∆а – деформация; ∆ l – перемещение. Участок ОА удлиняется на ∆ а, сечение А будет перемещаться за счет деформации ОА. Участок АВ не деформируется, т.е. сечение В перемещается в положение В 1 только за счет деформации участка ОА.
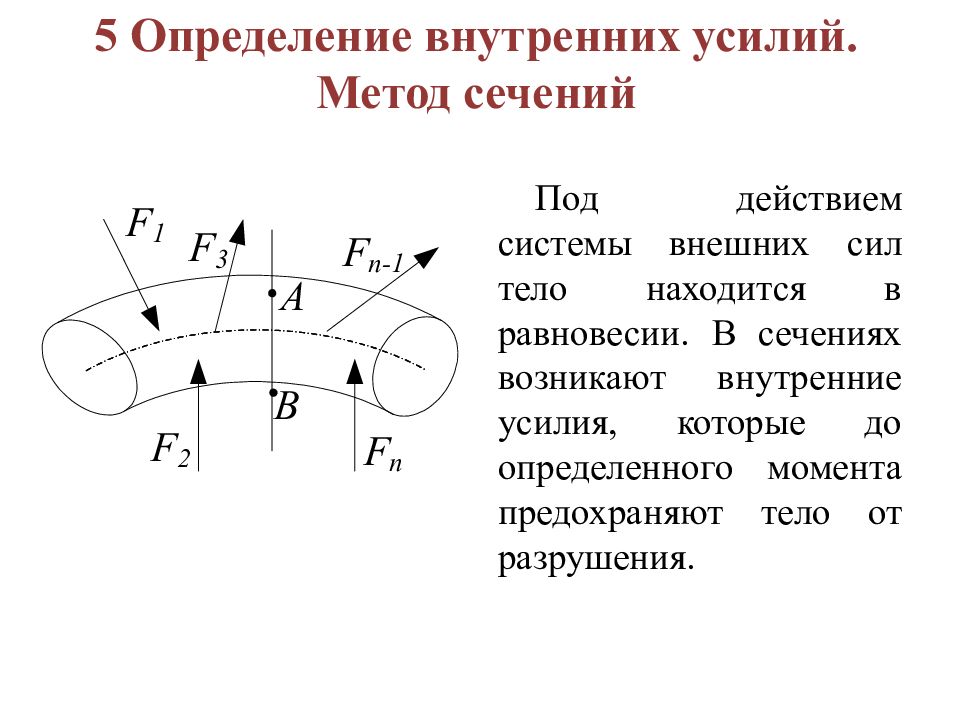
Слайд 16: 5 Определение внутренних усилий. Метод сечений
Под действием системы внешних сил тело находится в равновесии. В сечениях возникают внутренние усилия, которые до определенного момента предохраняют тело от разрушения.
Слайд 17
Для определения внутренних усилий в СМ используется метод сечений (РОЗУ). 4 этапа данного метода : 1 этап - тело мысленно Р ассекается в нужном нам сечении. 2 этап - мысленно О тбрасывается одна часть тела (как правило, наиболее нагруженная). 3 этап - действие отброшенной части тела З аменяется системой внутренних усилий. Под действием внешних сил и внутренних усилий оставленная часть тела должна находиться в равновесии. 4 этап - составляются У равнения равновесия, из которых определяются неизвестные внутренние усилия. РОЗУ – аббревиатура из слов (действий) на каждом этапе.
Слайд 18
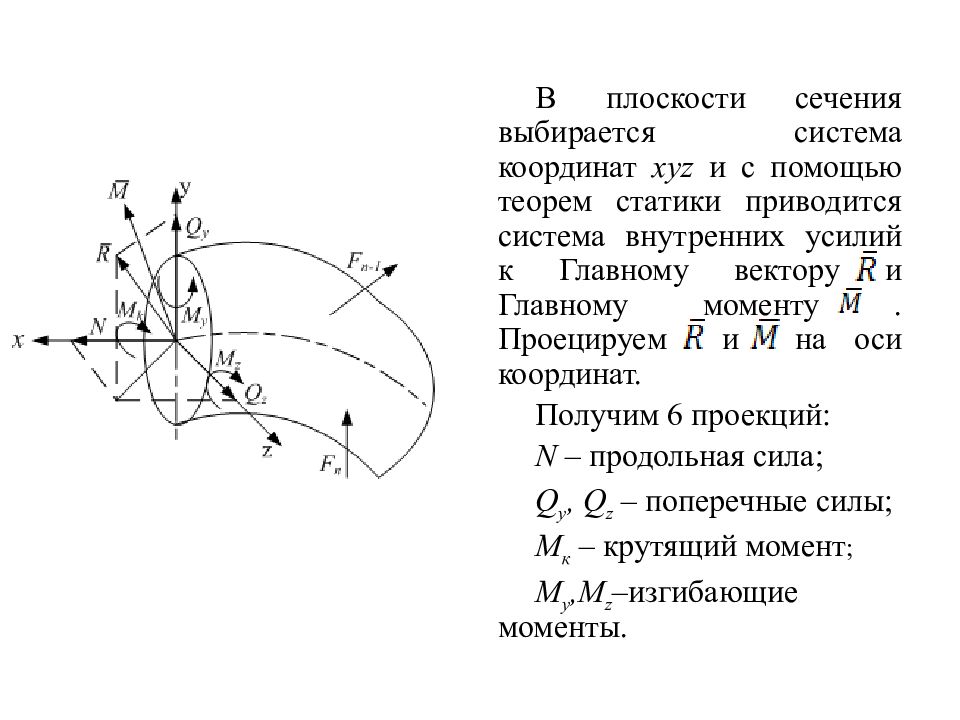
В плоскости сечения выбирается система координат xyz и с помощью теорем статики приводится система внутренних усилий к Главному вектору и Главному моменту. Проецируем и на оси координат. Получим 6 проекций: N – продольная сила; Q y, Q z – поперечные силы; М к – крутящий момент ; M y, M z –изгибающие моменты.
Слайд 19: 6 Классификация основных видов нагружения тела
– растяжение-сжатие; – сдвиг; - кручение; – чистый изгиб; – поперечный изгиб; – растяжение-сжатие с кручением; - кручение с чистым изгибом; - кручение с поперечным изгибом. Последние три случая показывают случаи сложных деформаций (сложного сопротивления ).
Слайд 20: 7 Напряжение и деформация в точке
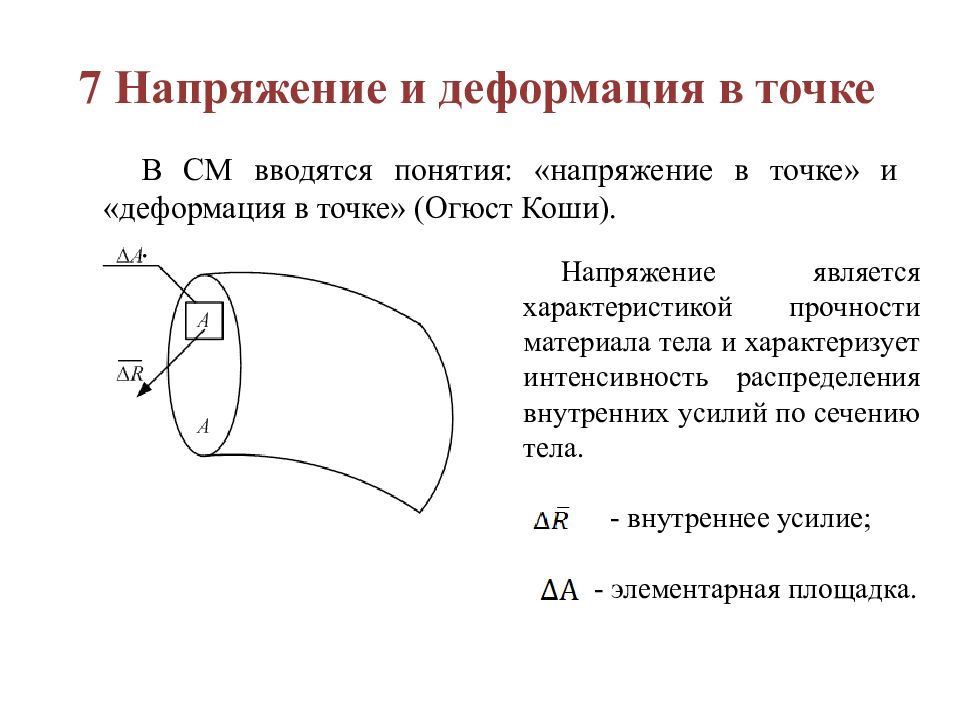
В СМ вводятся понятия: «напряжение в точке» и «деформация в точке» (Огюст Коши). . Напряжение является характеристикой прочности материала тела и характеризует интенсивность распределения внутренних усилий по сечению тела. - внутреннее усилие; - элементарная площадка.
Слайд 21
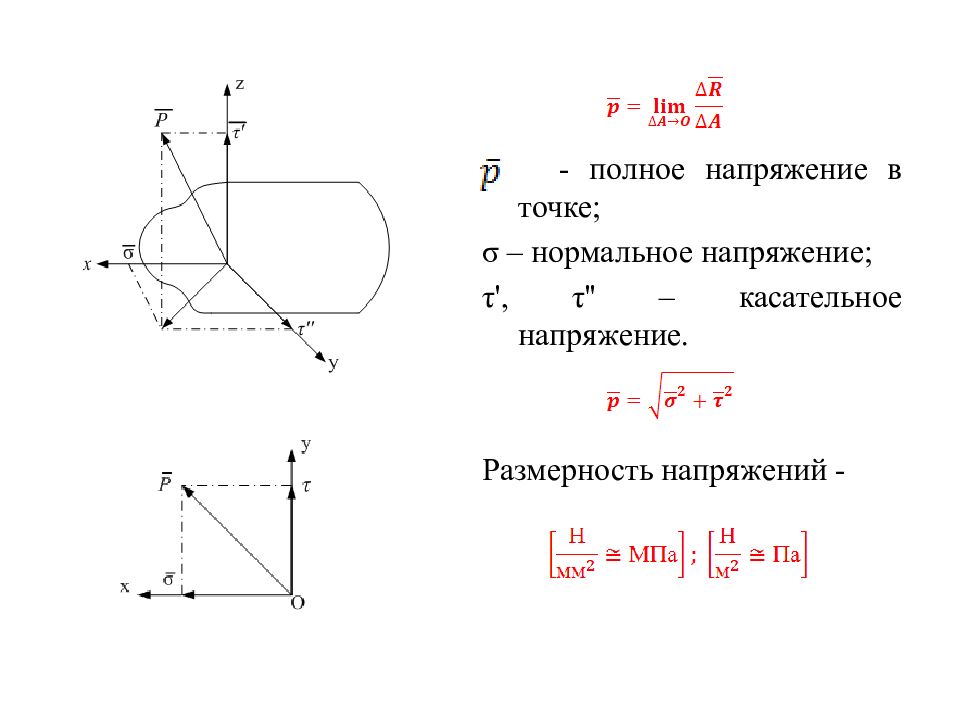
- полное напряжение в точке; σ – нормальное напряжение; τ', τ'' – касательное напряжение. Размерность напряжений -
Слайд 22
Деформация – изменение телом своей формы и размеров под действием внешних сил. Деформация : - линейная; - угловая.
Слайд 23
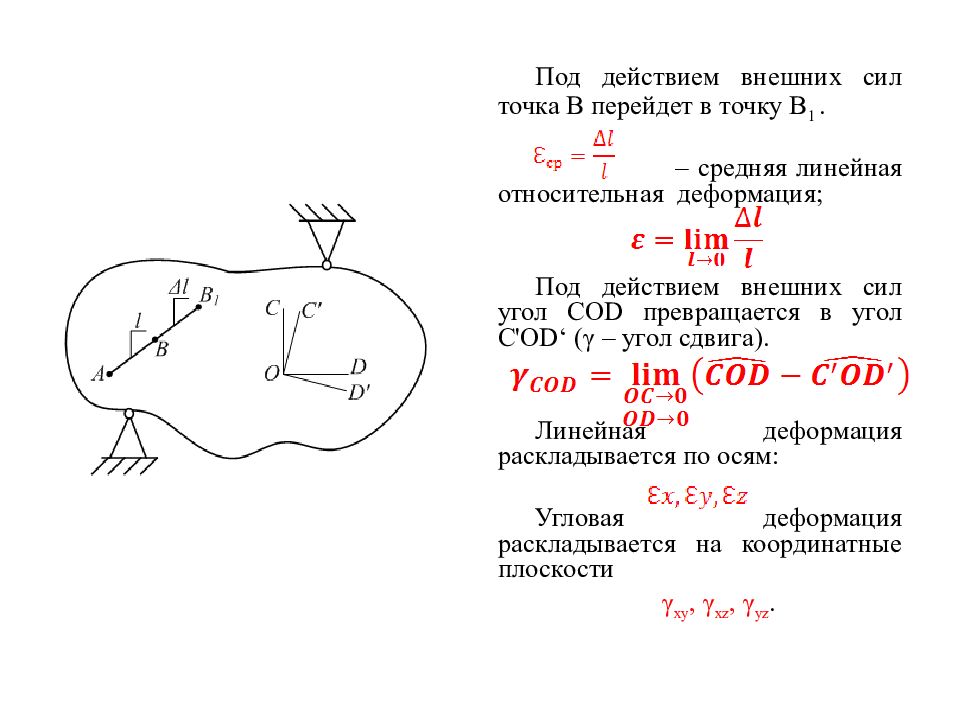
Под действием внешних сил точка В перейдет в точку В 1. – средняя линейная относительная деформация; Под действием внешних сил угол COD превращается в угол C ' OD ‘ (γ – угол сдвига). Линейная деформация раскладывается по осям: Угловая деформация раскладывается на координатные плоскости γ xy, γ xz, γ yz.
Слайд 24: 8 Центральное растяжение-сжатие
Центральным растяжением-сжатием называется такой вид нагружения бруса, когда в его поперечных сечениях возникает только одно внутреннее усилие – – продольная сила.
Слайд 25: 8. 1 Определение продольных сил
Если сила приложена не по оси бруса, то ее следует с помощью теоремы о параллельном переносе сил перенести на ось бруса. В этом случае получим растяжение с изгибом.
Слайд 26
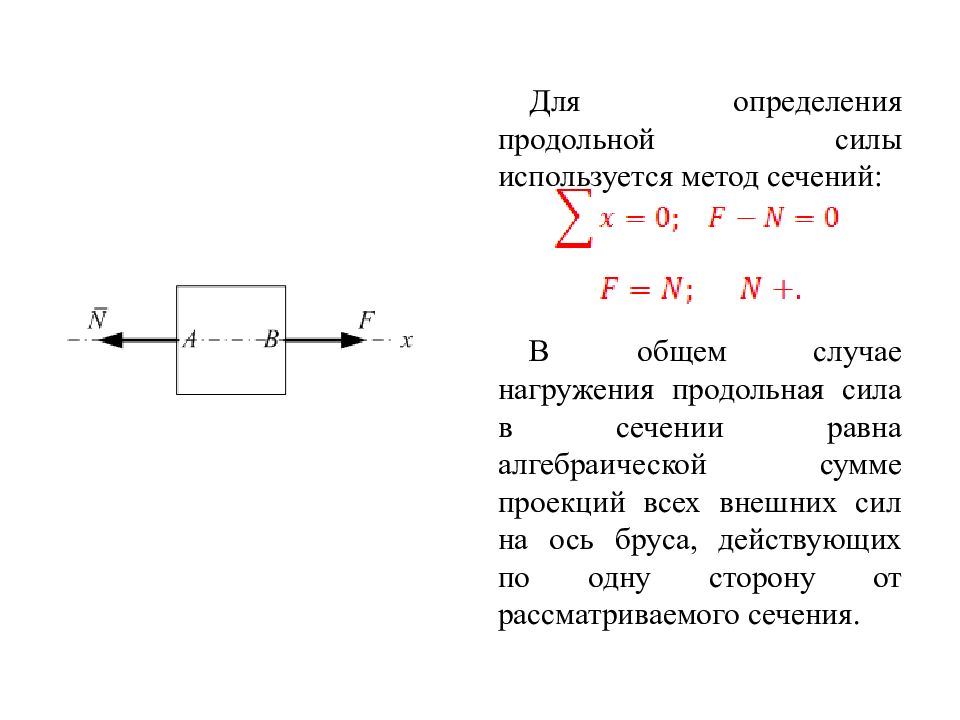
Для определения продольной силы используется метод сечений: В общем случае нагружения продольная сила в сечении равна алгебраической сумме проекций всех внешних сил на ось бруса, действующих по одну сторону от рассматриваемого сечения.
Слайд 27: 8. 2 Правило знаков для N
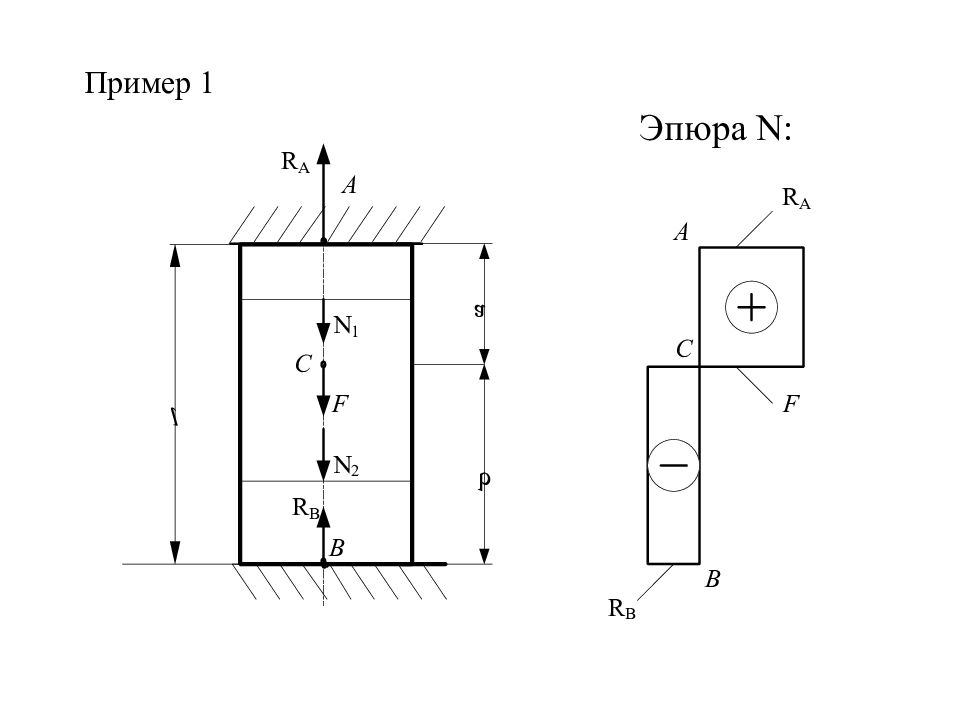
N считается положительной, если она направлена от сечения, т.е. как бы растягивает брус. N считается отрицательной, если она направлена к сечению, т.е. как бы сжимает брус. В сложных случаях нагружения, когда на брус действуют несколько внешних сил, для определения N в сечениях строятся эпюры продольных сил.
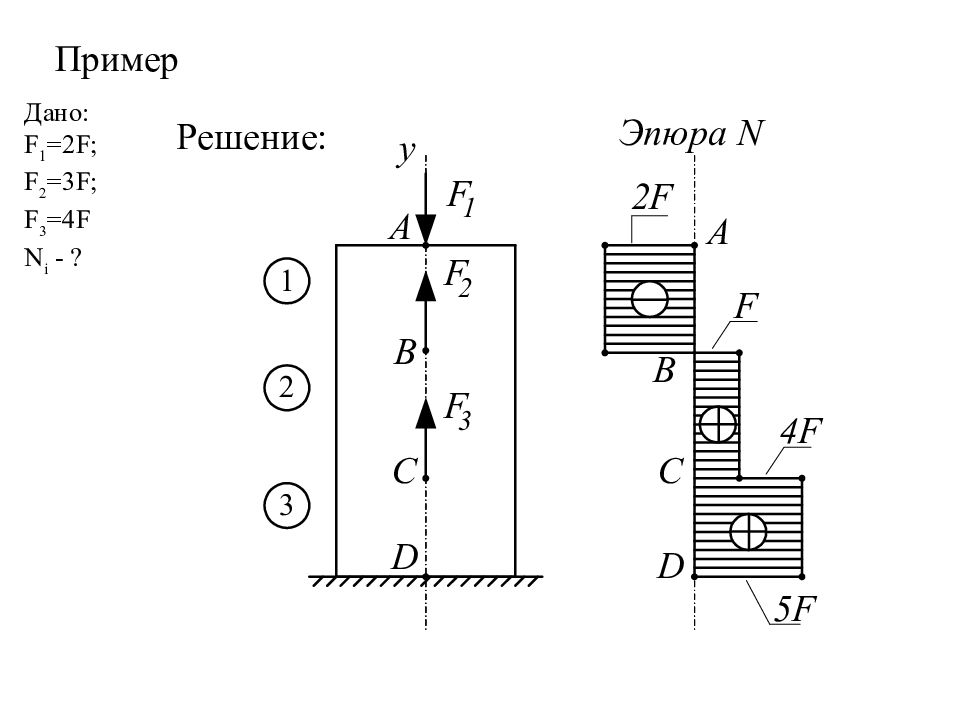
Слайд 28: 8. 3 Порядок построения эпюр
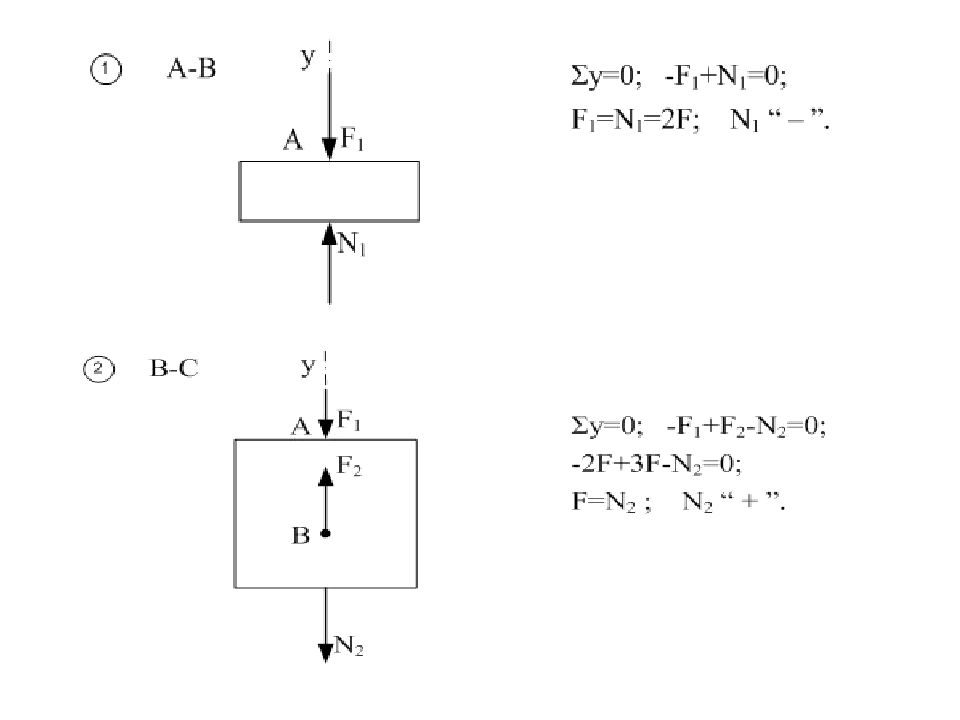
1 Проводится ось эпюры параллельно оси бруса. 2 Брус делится участки. Границами участков служат точки приложения внешних сил. 3 Методом сечений на каждом участке бруса определяются величина и знак N. При «+» N в выбранном масштабе эта величина откладывается вверх или вправо, при « - » N откладывается вниз или влево. 4 Делается штриховка линиями, перпендикулярными оси эпюры. 5 Проставляются все величины N на каждом участке эпюры. 6 Делается проверка согласно правилу: В точках приложения внешних сил на эпюре должны быть «скачки», величина «скачка» должна быть равна величине внешней силы, приложенной в данном сечении бруса. Эпюра должна быть замкнута, начинаться и заканчиваться на оси.
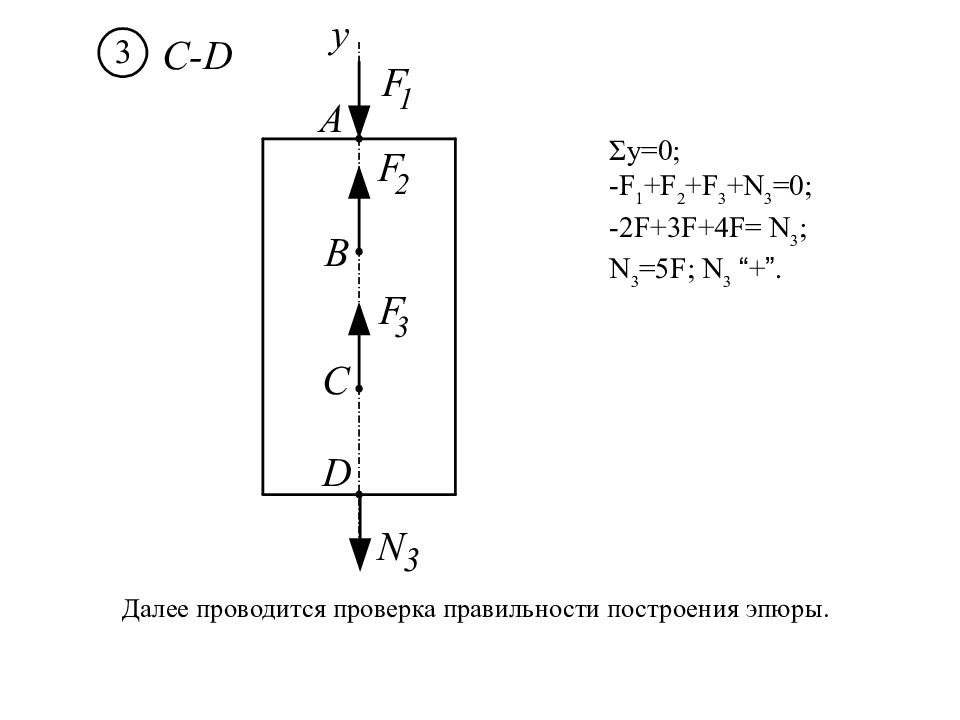
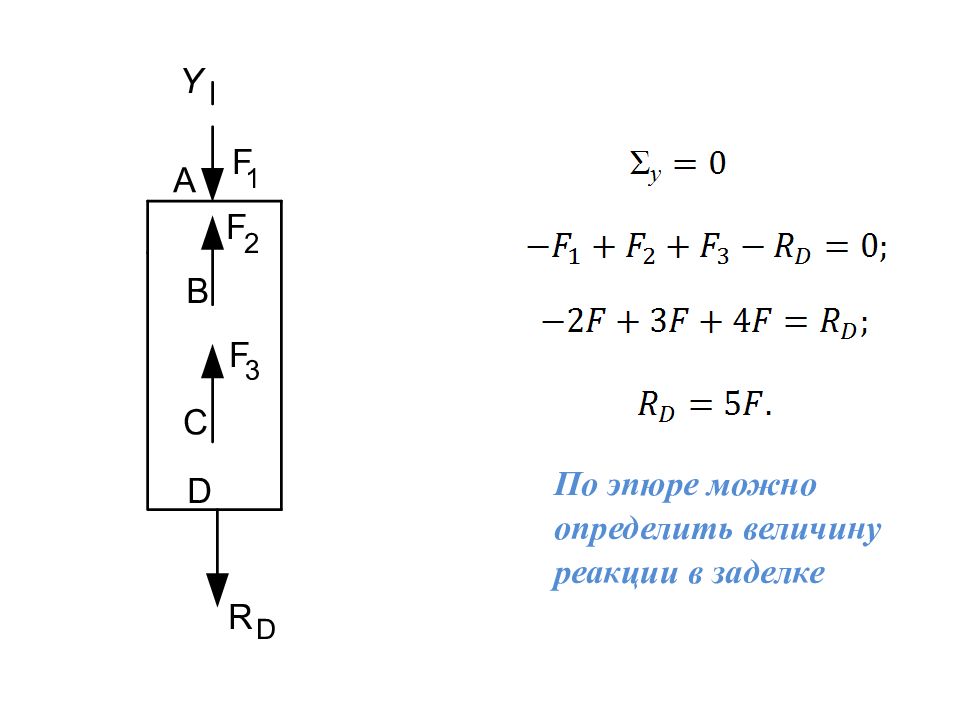
Слайд 31
Далее проводится проверка правильности построения эпюры. Σу =0; -F 1 +F 2 +F 3 +N 3 =0; -2F+3F+4F= N 3 ; N 3 =5F; N 3 “ + ”.
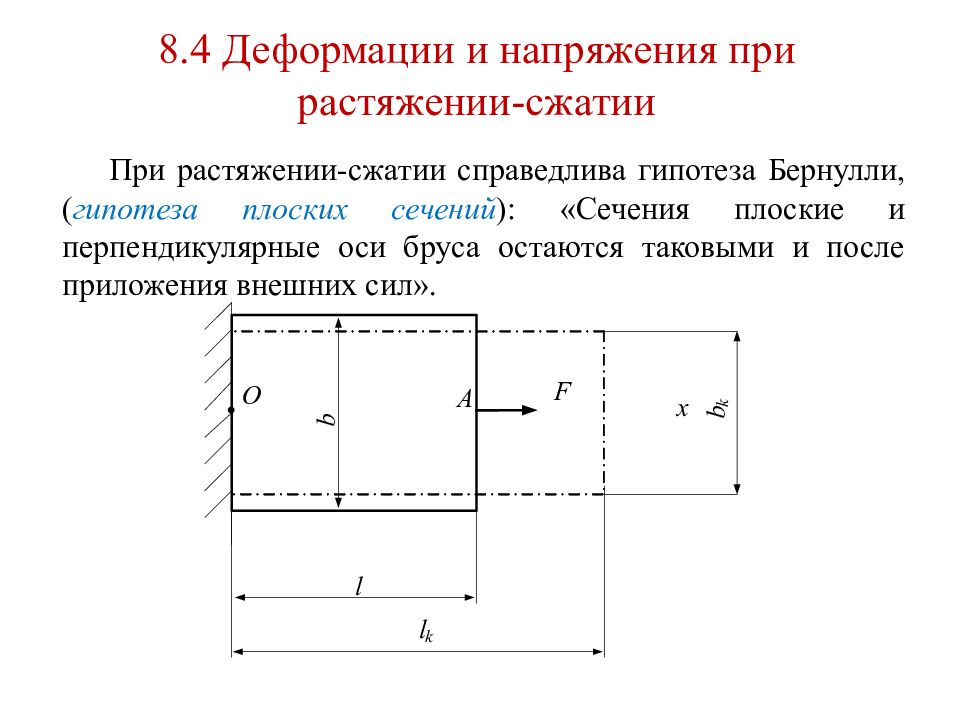
Слайд 33: 8. 4 Деформации и напряжения при растяжении-сжатии
При растяжении-сжатии справедлива гипотеза Бернулли, ( гипотеза плоских сечений ): «Сечения плоские и перпендикулярные оси бруса остаются таковыми и после приложения внешних сил».
Слайд 34
– абсолютная линейная продольная деформация; (1) – относительная линейная продольная деформация; (2) - абсолютная поперечная деформация; (3) – относительная поперечная деформация; (4) - коэффициент Пуассона; (5) - для изотропных материалов. Поскольку при центральном растяжении-сжатии справедлива гипотеза Бернулли, то предполагается, что внутренние усилия, т.е. продольные силы, равномерно распределены по поперечному сечению; при этом в сечениях возникают нормальные напряжения, которые также равномерно распределяются по сечению. (6)
Слайд 35: 8. 5 Закон Гука при растяжении-сжатии
В области малых упругих деформаций нормальные напряжения σ прямопропорциональны относительной линейной продольной деформации ε. где Е – модуль упругости первого рода (модуль Юнга) [ МПа, Па ]. Е – физическая константа, которая характеризует способность материала к продольной деформации. Она определяется экспериментально. (Сталь – Е=2∙10 5 МПа; Алюминий – Е=0,7∙10 5 МПа). (2) и (6)→(7) где ( ЕА) – жесткость бруса при растяжении-сжатии. (7) (6)
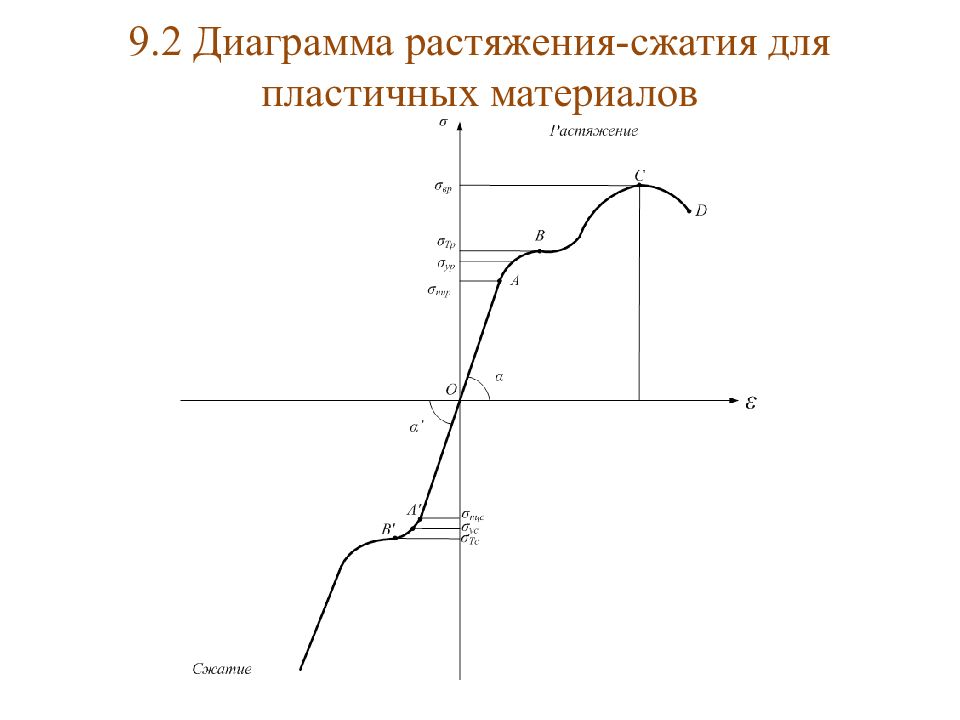
Слайд 36: 9 Механические испытания материалов 9.1 Цель механических испытаний
Условие прочности – где [σ] – допускаемое напряжение, которое определяется по результатам испытаний. Цель испытаний - определение механических характеристик материала (характеристик прочности, пластичности и упругости). Испытания проводятся на растяжение, сжатие, кручение и т.д. Наиболее полную картину можно получить при проведении испытаний на растяжение (при нормальных условиях, на специальных машинах и стандартных образцах). Нормальные условия: температура - 20˚С; давление - 760 мм.рт.ст. По результатам испытаний строятся диаграммы.
Слайд 38
Закон Гука соблюдается до точка А. σ ПЦ Р = σ ПЦ С ; σ У Р = σ У С ; σ В Р = σ В С ; σ 0,2 Р = σ 0,2 С ; E р =Е с. σ ПЦ - предел пропорциональности; σ У – предел упругости; σ Т – предел текучести; σ 0,2 – предел текучести ( ε ост =0.2%); σ 0,5 – предел текучести ( ε ост =0.5%); σ В – предел прочности (временное сопротивление). - относительное удлинение; - относительное сужение; где А – начальная площадь сечения; А ш – площадь шейки сечения.
Слайд 40
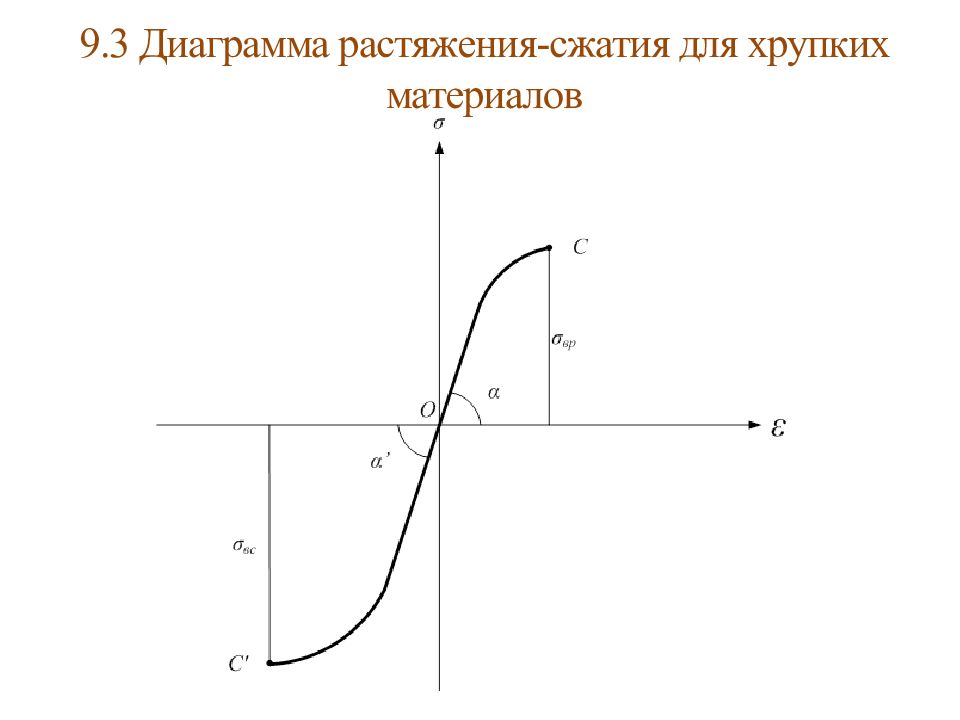
Хрупкие материалы работают неодинаково при растяжении и сжатии. Хрупкий материал разрушается при малых деформациях. Разрушение происходит внезапно, при этом Закон Гука не соблюдается, удается определить только предел прочности. - относительное удлинение; - относительное сужение; где А – начальная площадь сечения; А ш – площадь шейки сечения.
Слайд 41
Чем больше δ и ψ, тем пластичнее материал. К числу весьма пластичных материалов относятся отожженная медь, алюминий, латунь, малоуглеродистая сталь. Свойства пластичности имеют большое значение для технологических операций: - штамповка; - вытяжка; - волочение; - гибка. Модуль Юнга Е характеризует упругие свойства материала.
Слайд 42: 9.4 Условия прочности. Допускаемые напряжения. Коэффициент запаса прочности
Сечения в которых возникают максимальные расчетные напряжения, называются опасными. Условия прочности: (1 ) ( 2 ) где [ σ ], [ τ ] – допускаемые нормальные и касательные напряжения. Здесь σ пр, τ пр - это предельные (опасные) напряжения, при которых конструкция выходит из строя из-за потери прочности или жесткости. Для пластичных материалов, которые одинаково сопротивляются растяжению-сжатию σ пр = σ тр = σ тс : (3 ) Для хрупких материалов σ пр = σ вр ; ( 4 ) σ вс >> σ вр. [ n ] σ, [ n ] τ – нормативные коэффициенты запаса прочности, которые для каждого класса машин определяются из опыта эксплуатации.
Слайд 43
Существуют методы определения [ n ] σ, [ n ] τ : 1 Табличный метод [ n ] σ = n 1 ∙ n 2 ∙ n 3 ∙ …..∙n n (5) [ n ]=1.3 – наш коэффициент незнания [ n ] > 1. 2 Аналитический метод (более подробно – см. В.И. Феодосьев) Условие прочности может быть записано в виде: n ф ≥ [ n ]. ( 6 ) где n ф, - фактический коэффициент запаса прочности.
Слайд 44: 9.5 Условие прочности при растяжении-сжатии
(1) Три типа расчетов: 1 Проектный расчет (определение геометрических параметров): (2) 2 Проверочный расчет (в предположительно опасных сечениях) : (3) 3 Определение N max – максимальной грузоподъемности конструкции (4)
Слайд 45: 10 Статически неопределимые системы при растяжении-сжатии 10. 1 Основные понятия и определения
Это системы, в которых число неизвестных больше, чем число уравнений статики, которые можно составить для данной конструкции. Порядок решения статически неопределимых систем : 1 Определяется количество неизвестных усилий в стержнях или степень статической неопределенности. Пусть n – количество неизвестных; m – количество уравнений статики; k =( n - m ) – степень статической неопределимости. 2 Составляются дополнительные уравнения из условия совместности деформаций. Число дополнительных уравнений должно равняться k.
Слайд 46
Условие совместности деформаций Всякая конструкция деформируется таким образом, что не происходит разрыва стержней, их разъединения или их взаимного перемещения, не предусмотренного кинематической схемой конструкции. Общего метода решения таких задач не существует. Каждая задача требует индивидуального подхода.
Слайд 48
Дано : F, a, b; a + b = l; A, E. Определить: N i - ?; σ i - ?. Решение: n =2, m =1, k =1. Необходимо составить 1 дополнительное уравнение. (1) Δl – общая деформация; Δl = 0. (2) Мысленно убираем одну из заделок, например, нижнюю, действия заделки заменяем реакциями. Δl = Δl F + Δl R b = 0. (3) Используем закон Гука:
Слайд 49
Уравнение (4) подставляем в (3) Участок AC : N 1 = R А ( положительная); Участок BC : N 2 = - R B (отрицательная); F = R A + R B. (4) (5) (6)
Слайд 50
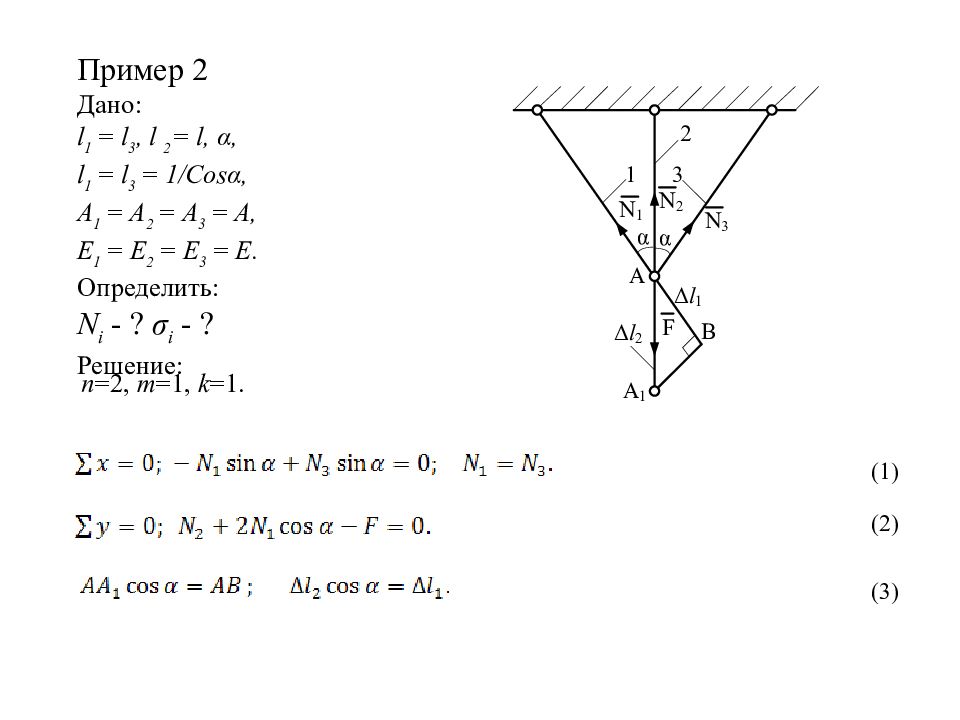
Пример 2 Дано : l 1 = l 3, l 2 = l, α, l 1 = l 3 = 1/Cosα, A 1 = A 2 = A 3 = A, E 1 = E 2 = E 3 = E. Определить: N i - ? σ i - ? Решение: n =2, m =1, k =1. (1) (2) (3)
Слайд 52: 11 Особенности СНС
В отличие от СОС, СНС обладают тремя особенностями: 1 Усилия в стержнях зависят от их жесткости (ЕА). 2 При изменении температуры в элементах системы возникают дополнительные температурные напряжения. 3 В случае неточности изготовления в элементах системы возникают дополнительные монтажные напряжения при сборке конструкции. Эти особенности являются недостатками СНС.
Слайд 53: 11. 1 Влияние жесткости отдельных элементов на усилия, возникающие в них
Дано: α, F, ,, ,. Найти: N i - ?. Анализируя предыдущее решение задачи видно, что n =3, m =2, k =1, все три стержня работают на растяжение и для них справедливы уравнения (1), (2) и (3).
Слайд 54
Вывод : Стержень (2) выполнен из Cu, т.е его жесткость уменьшили в 2 раза, В результате решения видно, что усилие N 2 уменьшилось в 2 раза. В СНС: «Чем больше жесткость элемента, тем больше внутреннее усилие, возникающее в нем, и наоборот». (1) (2) (3) По закону Гука: Тогда:
Слайд 55: 11. 2 Влияние изменения температуры на внутренние усилия, возникающие в элементах конструкции
α, F, Дано: Δ t = t 2 - t 1 Найти: N ti - ?. По закону линейного температурного расширения стержень 2 должен удлиниться на величину АА 1, но два других стержня не дадут это сделать. Стержень (2) на участке А 1 А 2 будет испытывать сжатие, стержни 1 и 3 будут растягиваться.
Слайд 56
По закону Гука : Решая уравнения (2) и (6) находим N 1 t, N 2 t. В СНС: При Изменении температуры в отдельных элементах СНС возникают дополнительные внутренние температурные усилия и, как следствие, дополнительные температурные напряжения. По закону Гука : Тогда: Подставив (4), (5)→(3). Получим: (1) ( 2 ) ( 3 ) ( 4 ) ( 5 ) ( 6 )
Слайд 57: 11. 3 Влияние неточности изготовления отдельных элементов конструкции на внутренние усилия, возникающие в СН С
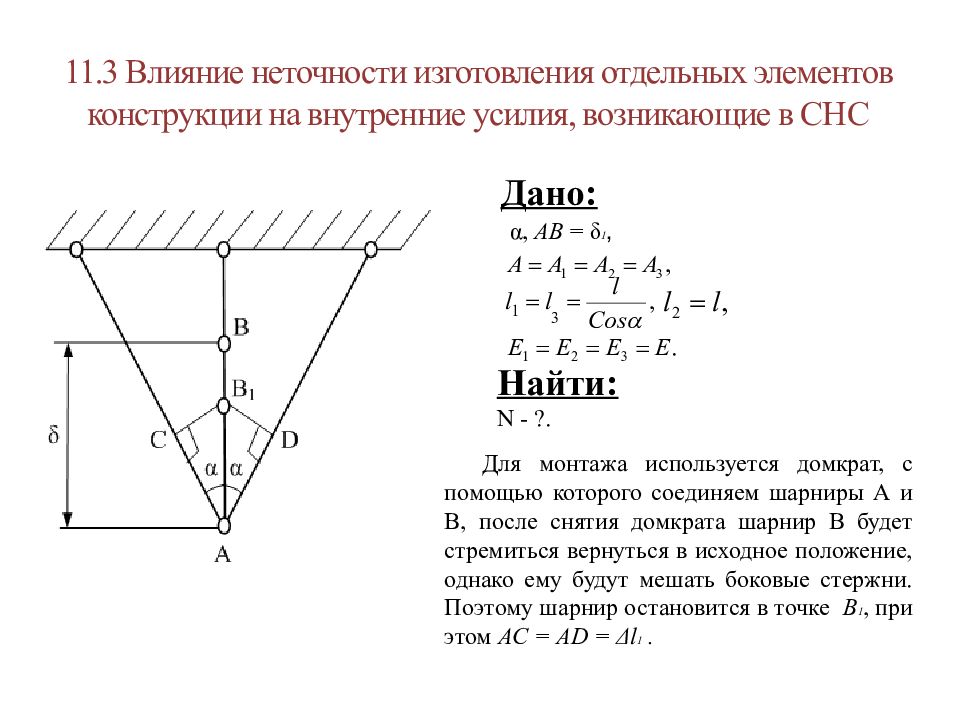
Дано: α, АВ = δ 1, Найти: N - ?. Для монтажа используется домкрат, с помощью которого соединяем шарниры А и В, после снятия домкрата шарнир В будет стремиться вернуться в исходное положение, однако ему будут мешать боковые стержни. Поэтому шарнир остановится в точке В 1, при этом АС = А D = Δ l 1.
Слайд 58
Для составления дополнительного уравнения из условия совместности деформаций рассмотрим треугольник АС : Применяем закон Гука: Решаем совместно (2) и (5), определяем N 1м и N 2м. (1) (2) (4) (5) (3) Вывод: Следует избегать неточностей изготовления, т.к. в СНС при сборке появляются дополнительные монтажные напряжения. или
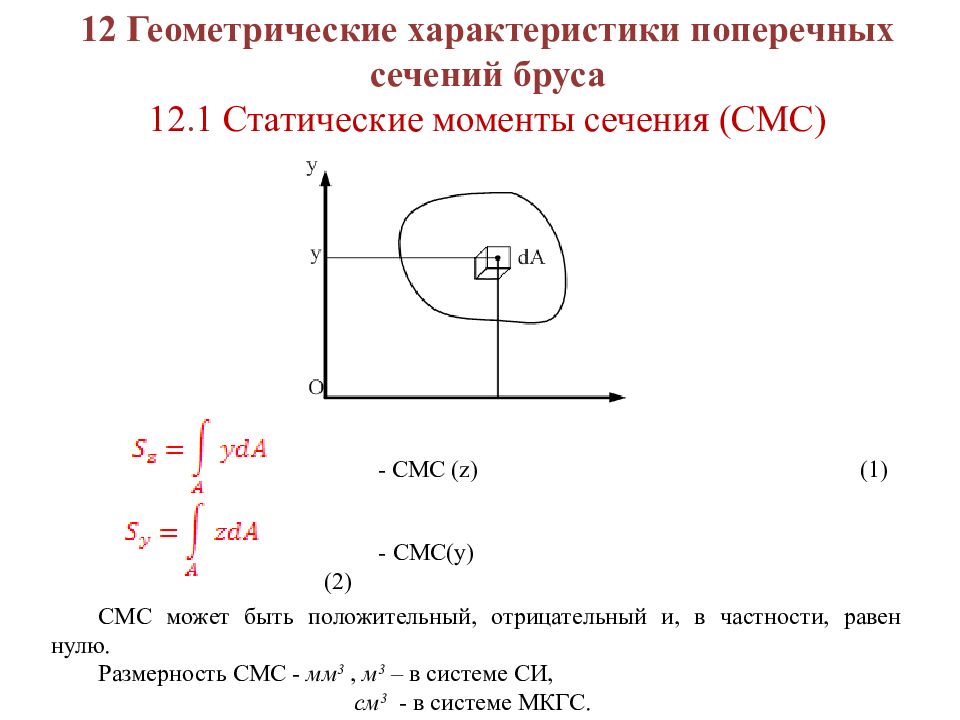
Слайд 59: 12 Геометрические характеристики поперечных сечений бруса 12. 1 Статические моменты сечения (СМС)
- СМС ( z ) (1) - СМС( y ) (2) СМС может быть положительный, отрицательный и, в частности, равен нулю. Размерность СМС - мм 3, м 3 – в системе СИ, см 3 - в системе МКГС.
Слайд 60: 12.2 Изменение СМС при параллельном переносе координатных осей
(3) (2) (1)
Слайд 61
(4) (5) (6) Вывод: при параллельном переносе координатных осей СМС изменяются на величину, равную произведению площади сечения А на расстояние между осями. Величины a, b можно подобрать таким образом, что СМС и будут равны 0. Оси, относительно которых СМС = 0, называются центральными осями. Точка пересечения центральных осей является центром тяжести сечения. Ось симметрии сечения – всегда центральная ось.
Слайд 62: 12.3 Определение центра тяжести сложных сечений
В этом случае сложное сечение разбивается на простые сечения, координаты центра тяжести которых известны.
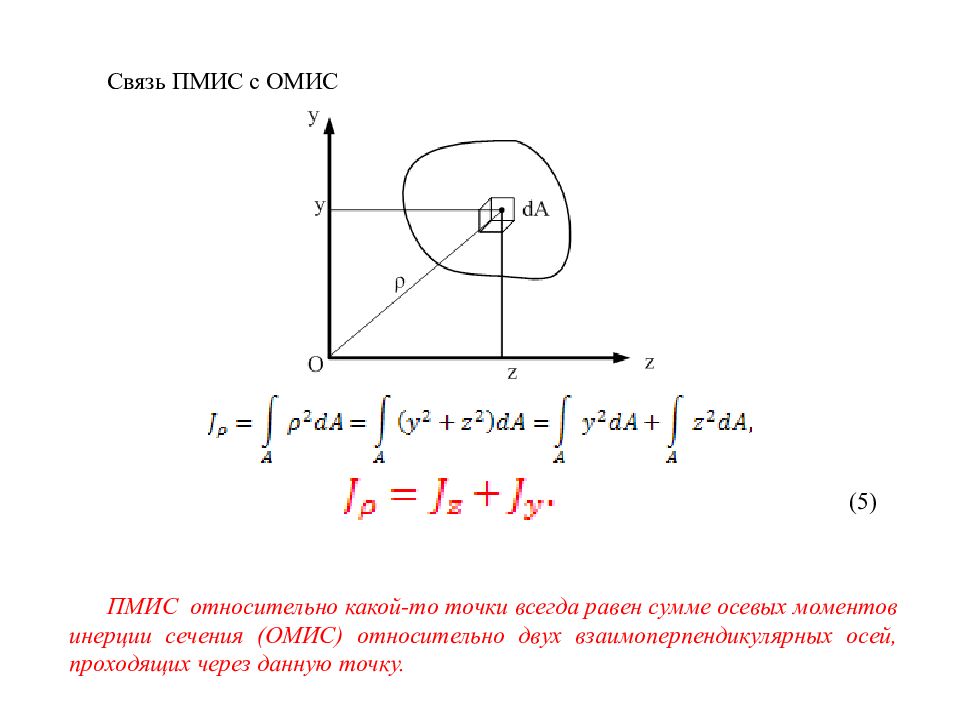
Слайд 63: 12.4 Моменты инерции сечения (МИС)
Осевой момент инерции сечения (ОМИС) - ОМИС относительно оси z ; (1) - ОМИС относительно оси y. (2) Центробежный момент инерции сечения (ЦМИС) ; (3) Полярный момент инерции сечения (ПМИС) ; (4)
Слайд 64
Связь ПМИС с ОМИС (5) ПМИС относительно какой-то точки всегда равен сумме осевых моментов инерции сечения (ОМИС) относительно двух взаимоперпендикулярных осей, проходящих через данную точку.
Слайд 65: 12.5 Изменение МИС при параллельном переносе осей
Пусть z 2, y 2 – центральные оси: S z1 =S y1 = 0. Тогда (6) (7) (8) (9)
Слайд 68: 14 Главные оси инерции сечения и главные моменты инерции сечения (ГОИС и ГМИС)
Формулы (1), (2) и (4) показывают, что при повороте координатных осей ОМИС изменяются, но сумма их остается постоянной. Следовательно, существует угол, при котором ОМИС относительно одной оси принимает m ах величину, а относительно другой min величину. ГОИС – такие оси, относительно которых один ОМИС принимает max значение, а другой, относительно другой оси, min значение. ЦМИС относительно этих осей равен нулю. Для нахождения положения главных осей используется понятие экстремума функции.
Слайд 69
Мы доказали, что относительно ГОИС ЦМИС должен быть равен 0. См. Писаренко Г.С. и др. «Справочник по сопромату». Если сечение имеет ось симметрии, то она всегда будет ГОИС. (5) (6) (7)
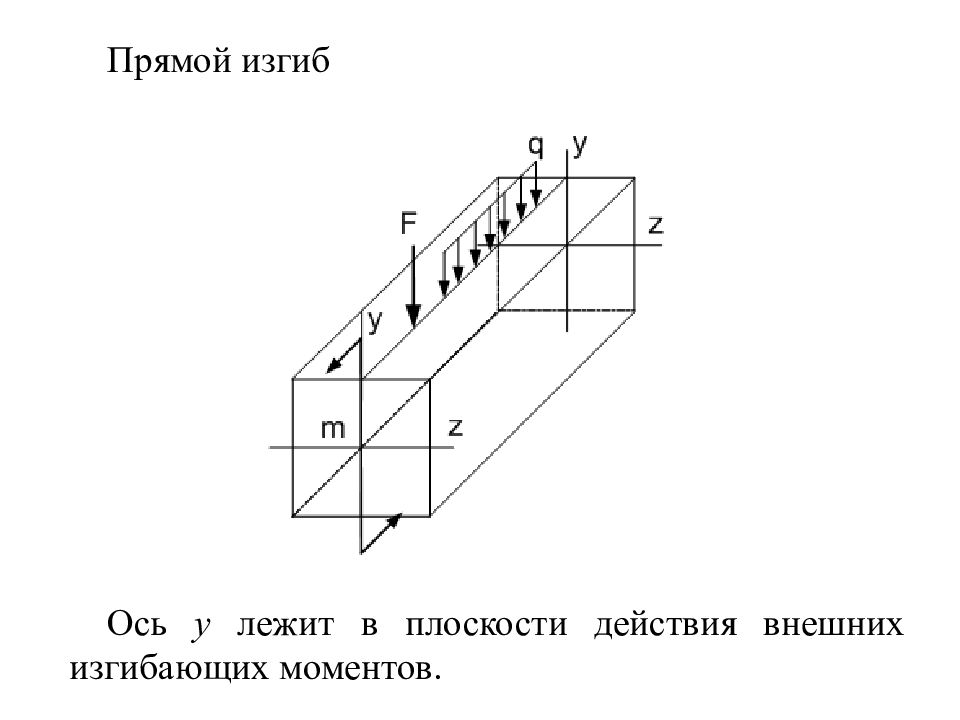
Слайд 70: 15 Изгиб
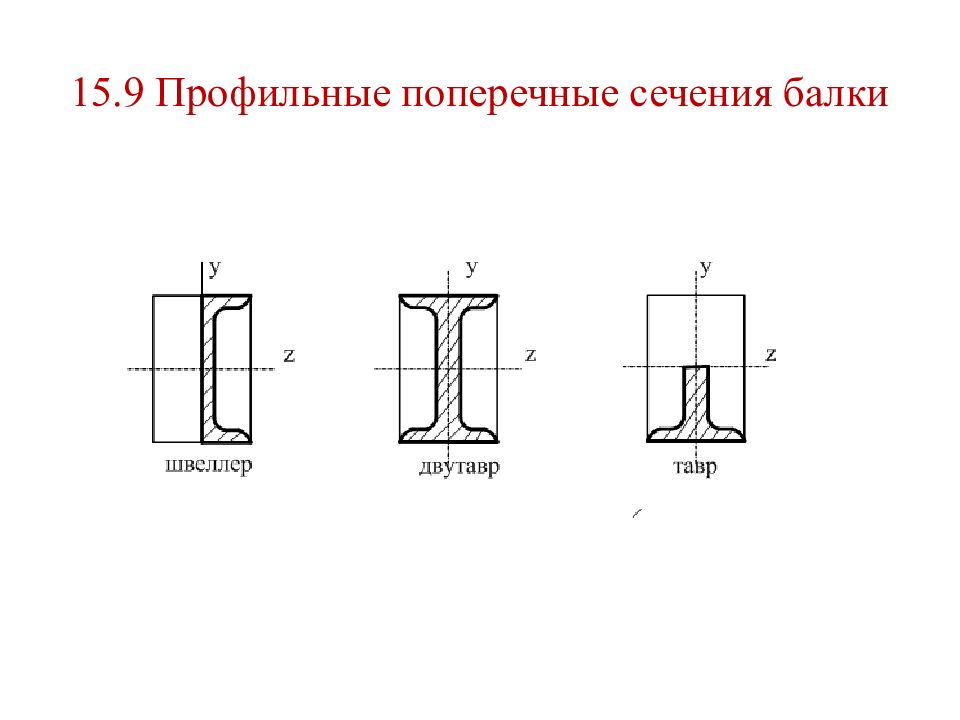
Изгиб – такой вид нагружения бруса, когда в его поперечных сечениях возникают: - изгибающие моменты M y или M z (чистый изгиб); - изгибающий момент M y и поперечная сила Q z или изгибающий момент M z и поперечная сила Q y (поперечный изгиб); Изгиб может быть прямым (плоским) и косым. Прямой изгиб возникает тогда, когда плоскость действующего внешнего изгибающего момента проходит через одну из ГОИС. Косой изгиб возникает тогда, когда ни одна из ГОИС не лежит в плоскости действия внешнего изгибающего момента. Это уже случай сложной деформации (сложного сопротивления). Брус, работающий на изгиб в технике называется балкой.
Слайд 71
Прямой изгиб Ось y лежит в плоскости действия внешних изгибающих моментов.
Слайд 72
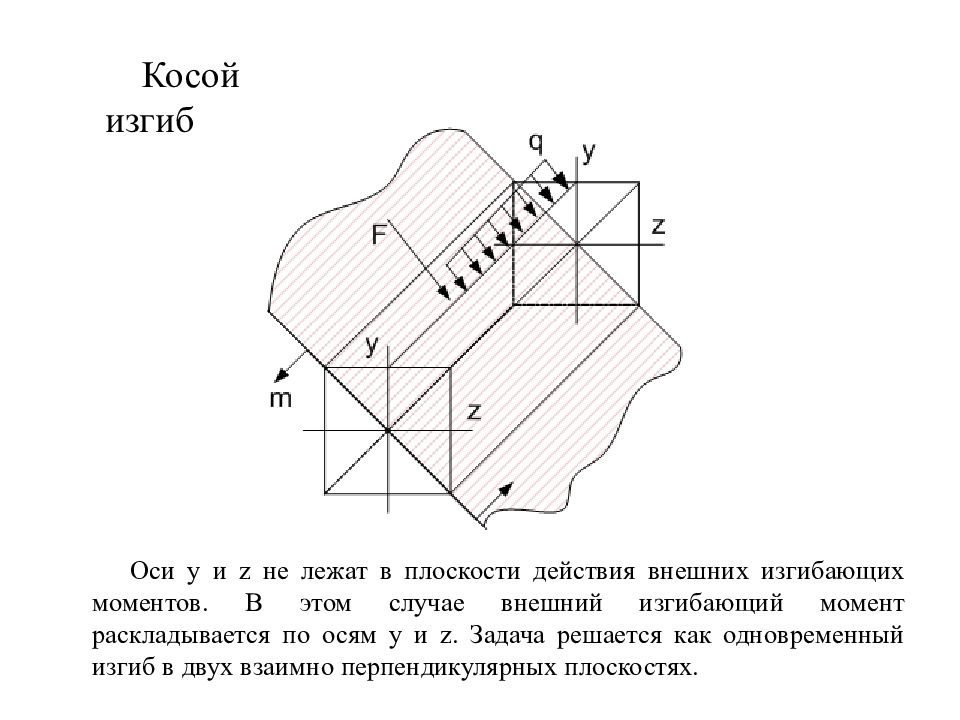
Косой изгиб Оси y и z не лежат в плоскости действия внешних изгибающих моментов. В этом случае внешний изгибающий момент раскладывается по осям y и z. Задача решается как одновременный изгиб в двух взаимно перпендикулярных плоскостях.
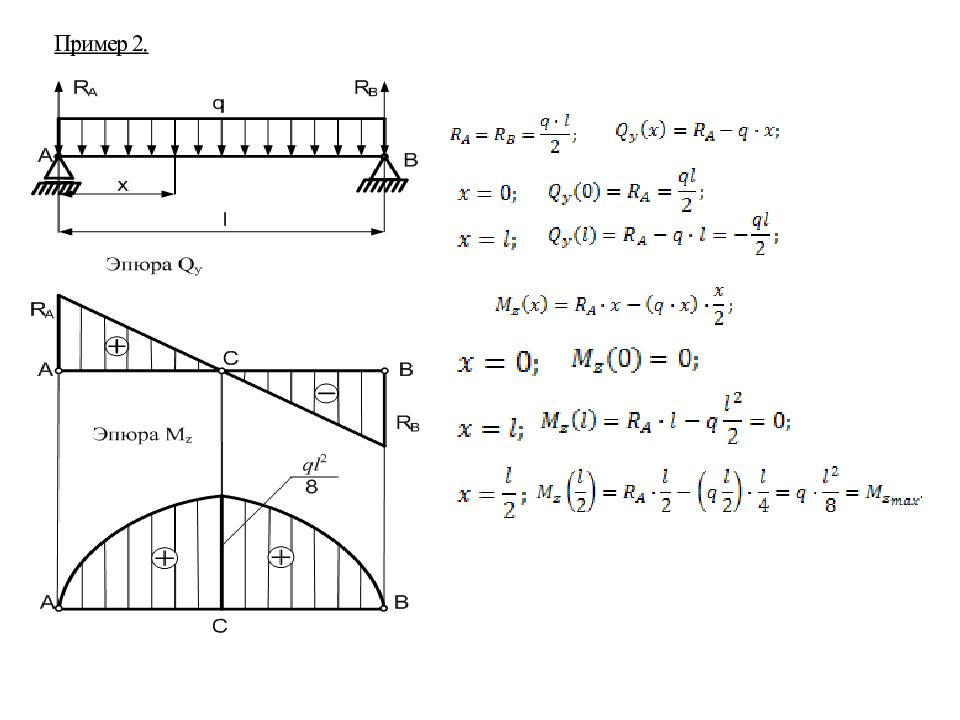
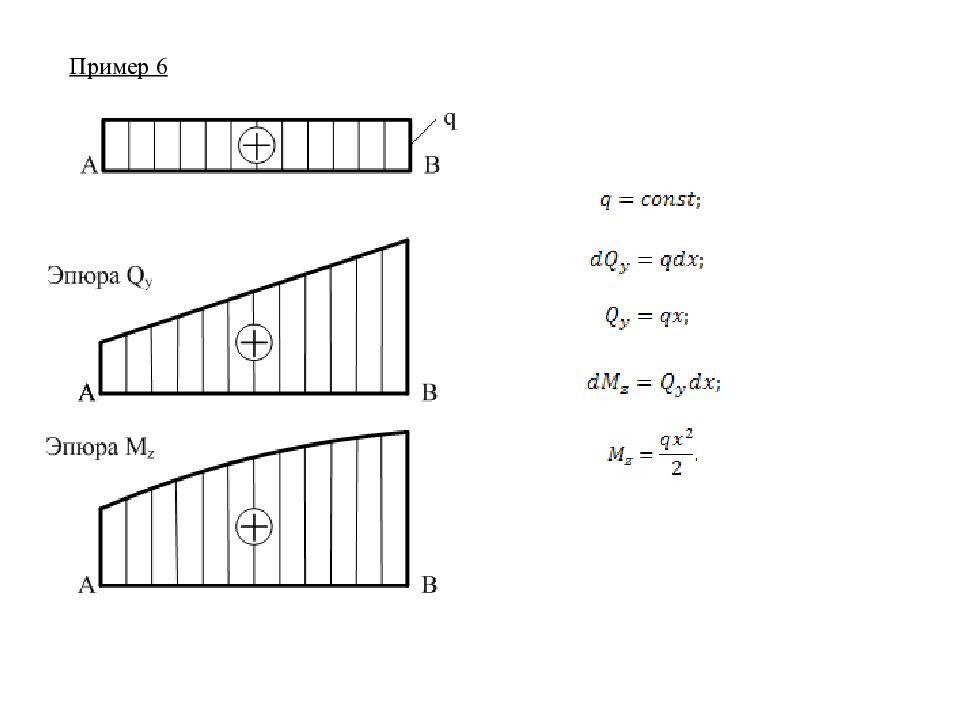
Слайд 73: 15.1Построение эпюр Q y и M z
M z – изгибающий момент, действующий относительно оси z (изгиб в пл. XOY ); Q y – поперечная сила, действующая по оси y. Для того, чтобы правильно рассчитывать балки на прочность, необходимо уметь строить эпюры Q y и M z.
Слайд 74
Построение эпюр следует проводить в следующем порядке : 1 Определить реакции опор. 2Разделить балку на участки, границами которых служат точки приложения внешних нагрузок. 3 Определить на каждом участке величину и знак Q y и M z, используя метод сечений. 4 Построить эпюры Q y и M z, (в выбранных масштабах). 5 Проверить правильность построенных эпюр согласно специальным правилам. При сложном нагружении балки поперечная сила Q y в сечении равна алгебраической сумме проекций всех внешних сил на плоскость сечения, действующих по одну сторону от рассматриваемого сечения. При сложном нагружении изгибающий момент M z в сечении равен алгебраической сумме моментов от всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
Слайд 75: 15.2 Правило знаков для Q y и M z
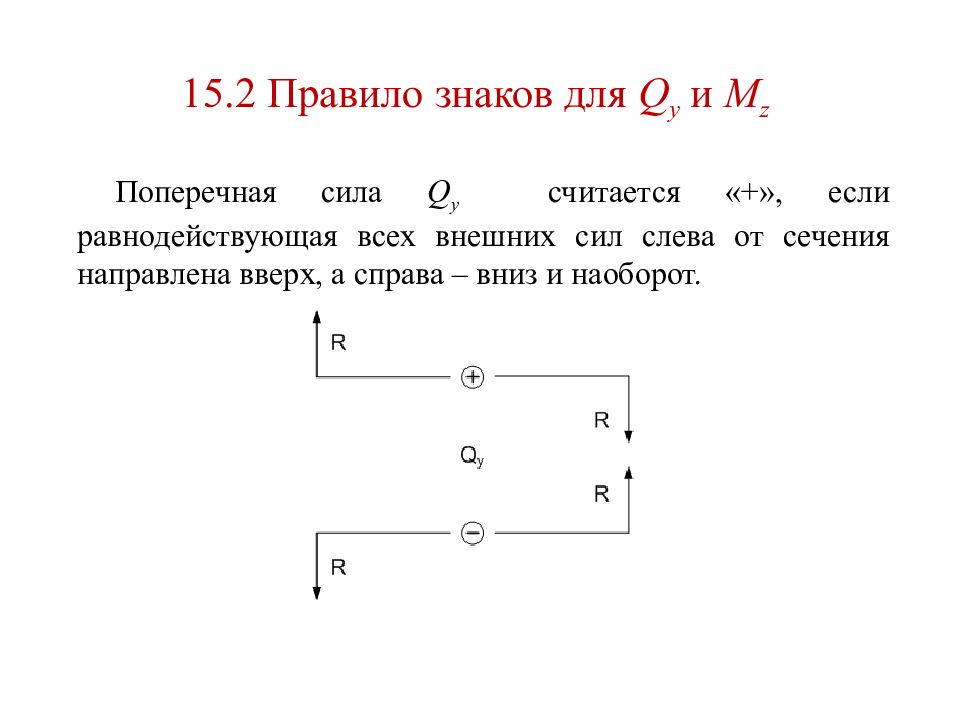
Поперечная сила Q y считается «+», если равнодействующая всех внешних сил слева от сечения направлена вверх, а справа – вниз и наоборот.
Слайд 76
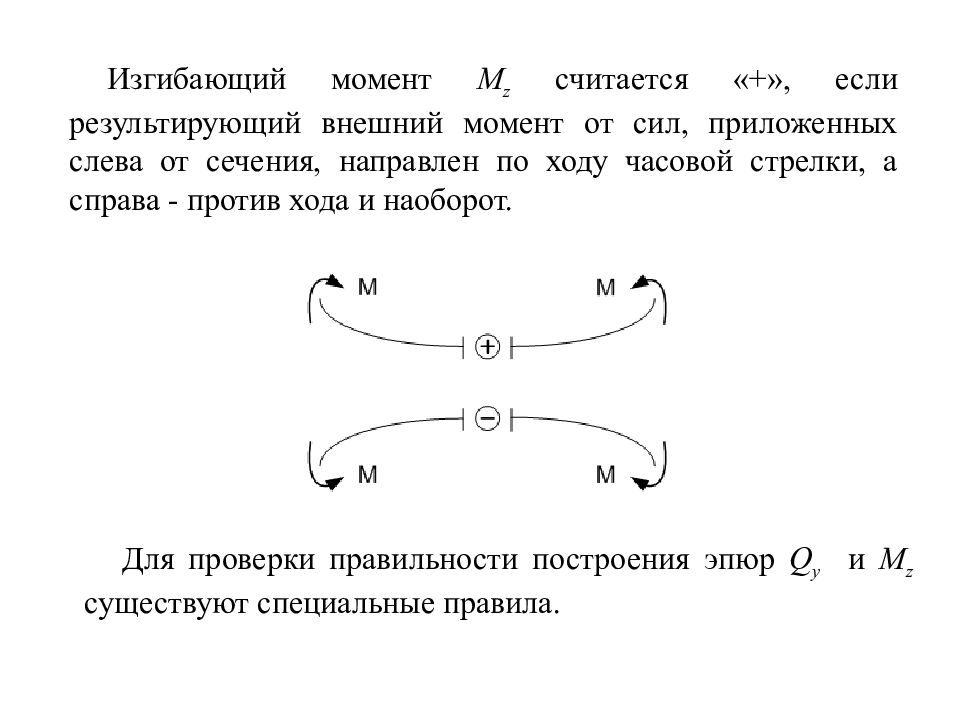
Изгибающий момент M z считается «+», если результирующий внешний момент от сил, приложенных слева от сечения, направлен по ходу часовой стрелки, а справа - против хода и наоборот. Для проверки правильности построения эпюр Q y и M z существуют специальные правила.
Слайд 77
15. 3 Дифференциальные зависимости между q, Q y и M z Используем метод сечений. Интенсивность распределенной нагрузки - первая производная поперечной силы по длине балки. Поперечная сила Q y - первая производная от изгибающего момента M z по длине балки. Выражения (1), (2), (3) используются для проверки правильности построения эпюр Q y и M z. Сформулируем основные правила для проверки правильности построения эпюр. Для этого рассмотрим несколько примеров построения эпюр Q y и M z (1) (2) (3)
Слайд 78
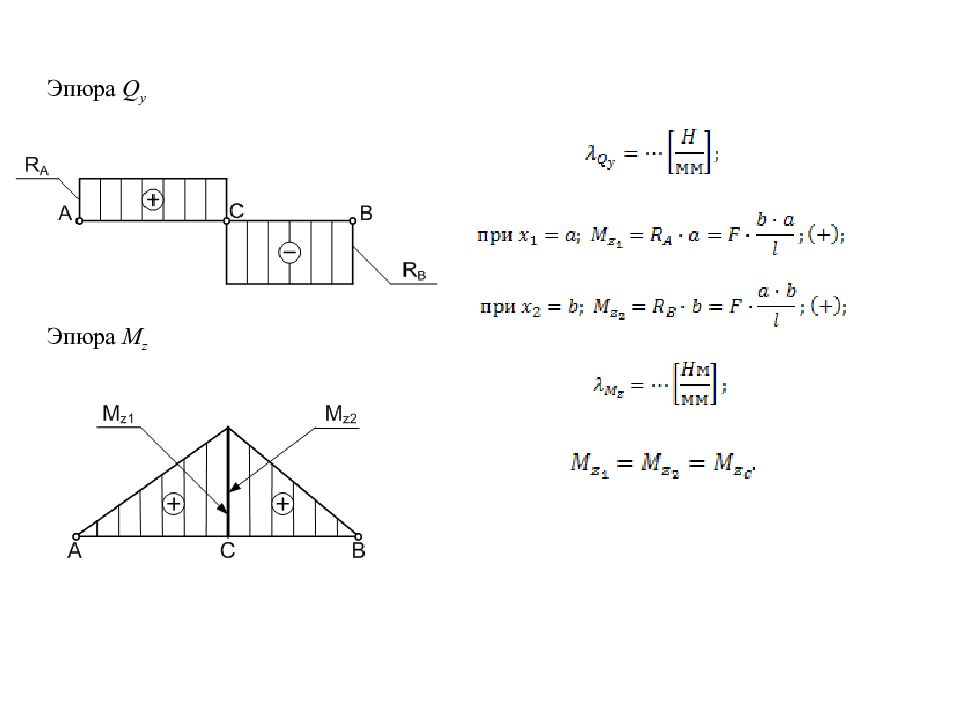
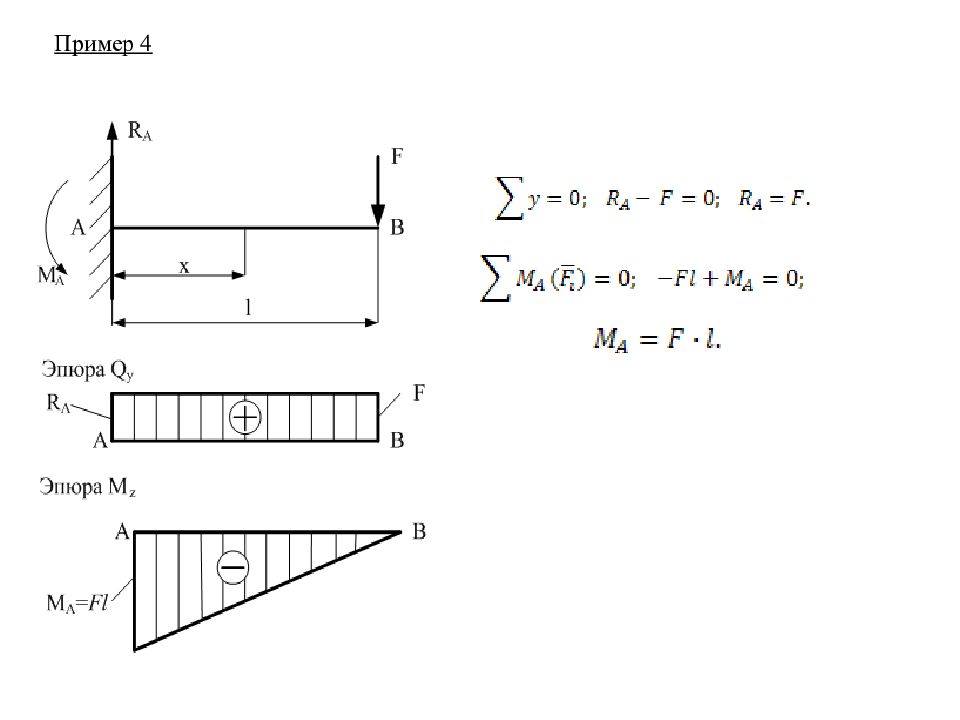
Пример 1 Определение реакций опор R A и R B : 15.4 Примеры построения эпюр Qy и M z Проверка: Сечение 1-1: Сечение 2-2:
Слайд 80
Правило 1 В точках приложения внешних сосредоточенных сил на эпюре Q y должны быть «скачки», равные по величине внешней силе, приложенной в данном сечении, а на эпюре M z должен быть излом функции. Направление излома – навстречу внешней силе.
Слайд 82
Правило 2 Если поперечная сила Q y проходит через ноль, то на эпюре M z будет экстремальное значение момента. Если Q y изменяется с « + » на « - », то на эпюре M z будет max. Если Q y изменяется с « - » на « + », то на эпюре M z будет min.
Слайд 84
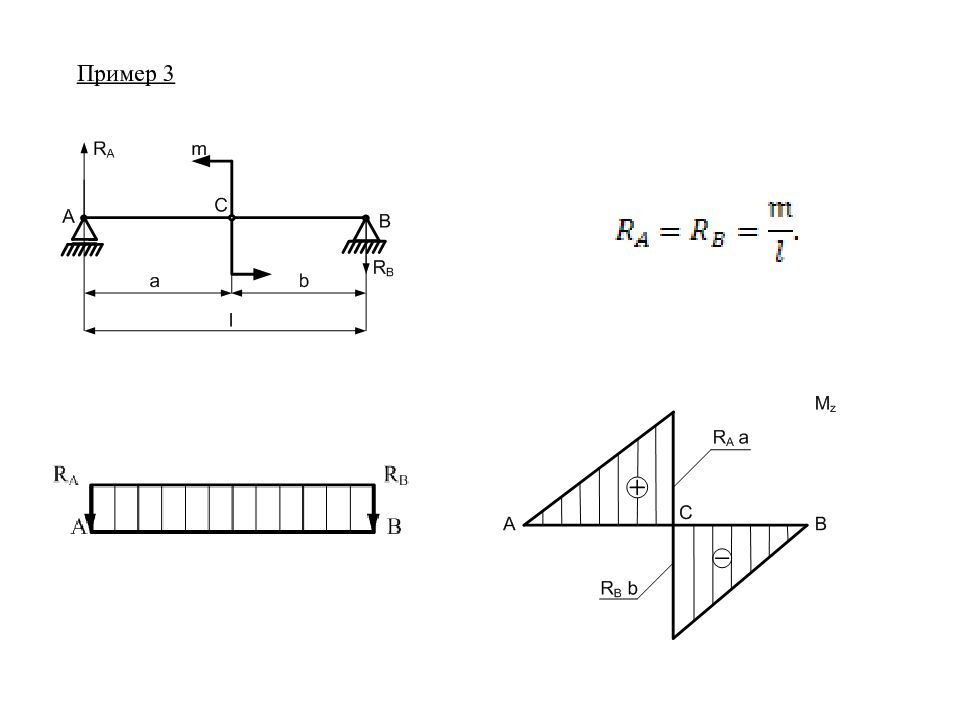
Правило 3 В точках приложения внешнего сосредоточенного момента m, на эпюре M z должен быть «скачок», равный внешнему сосредоточенному моменту, приложенному в данной точке.
Слайд 87
Правило 4 На участках балки, где отсутствует распределенная нагрузка, поперечная сила Q y ограничивается прямой, параллельной оси эпюры, а изгибающий момент M z ограничивается прямой, наклоненной к оси
Слайд 89
Правило 5 На участках балки, где q=const, эпюра поперечной силы ограничивается прямой, наклоненной к оси эпюры, а эпюра изгибающего момента ограничивается кривой второго порядка
Слайд 90: 15.5 Напряжения в балке при чистом изгибе
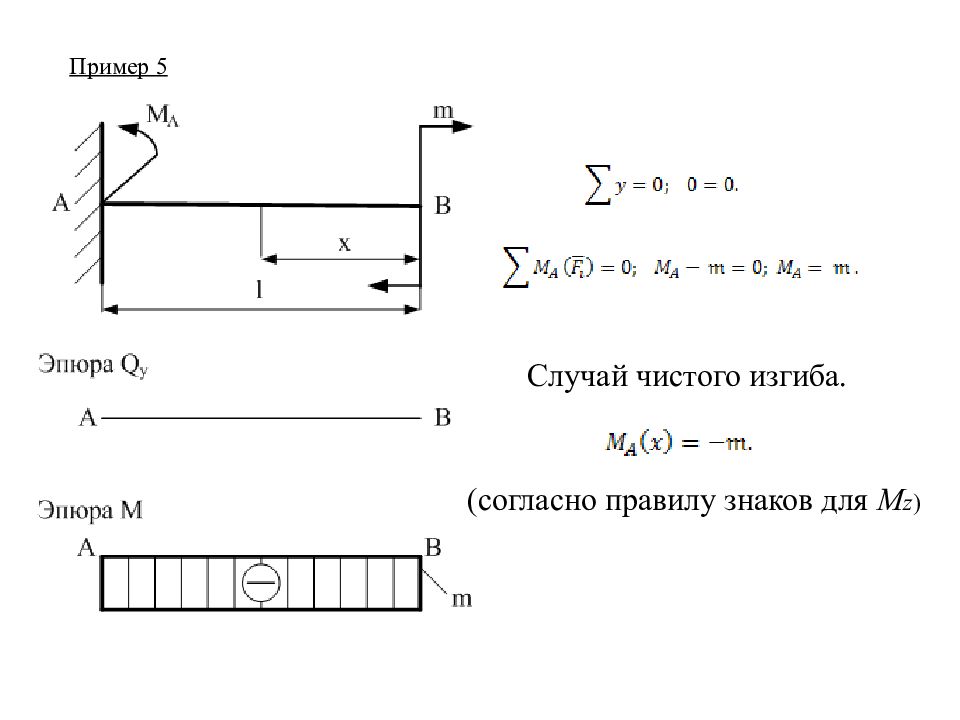
Возникновение изгибающего момента в сечении балки приводит к появлению нормальных напряжений – σ, а от действия поперечной силы появляются касательные напряжения τ. Чтобы исключить τ, рассмотрим чистый изгиб. На участке CD – чистый изгиб. Q y = 0; M z = const;
Слайд 91
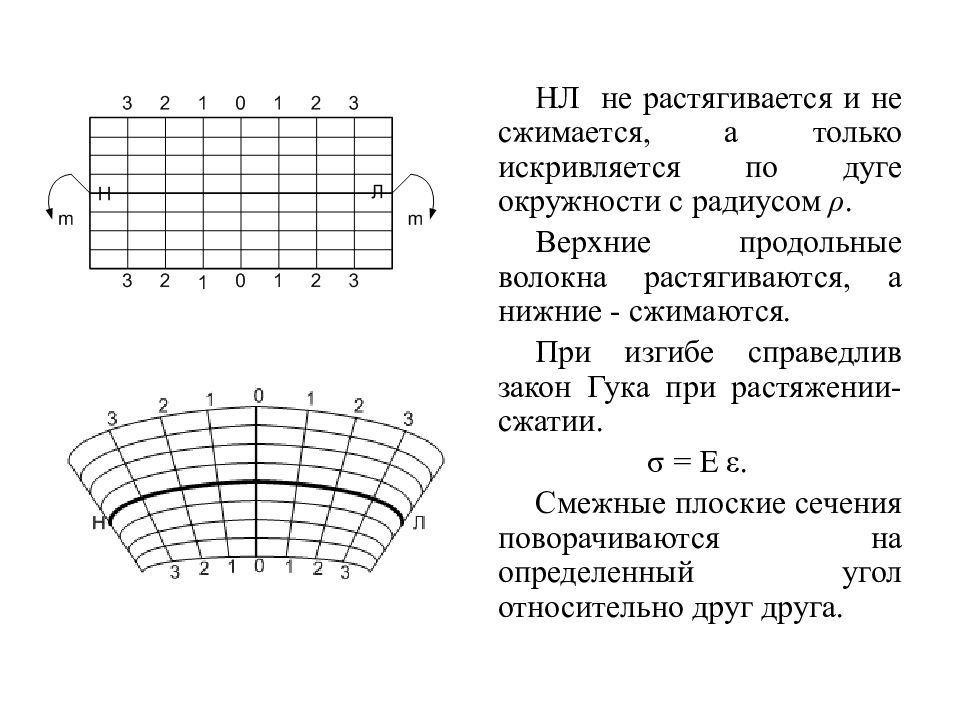
Экспериментально доказано, что при чистом изгибе справедлива гипотеза Бернулли (гипотеза плоских сечений), т.е. сечения плоские и перпендикулярные оси бруса остаются таковыми и после приложения внешних сил, при этом происходит поворот смежных сечений друг относительно друга. НЛ – нейтральная линия (слой) – геометрическое место точек, где напряжения σ равны нулю.
Слайд 92
НЛ не растягивается и не сжимается, а только искривляется по дуге окружности с радиусом ρ. Верхние продольные волокна растягиваются, а нижние - сжимаются. При изгибе справедлив закон Гука при растяжении-сжатии. σ = E ε. Смежные плоские сечения поворачиваются на определенный угол относительно друг друга.
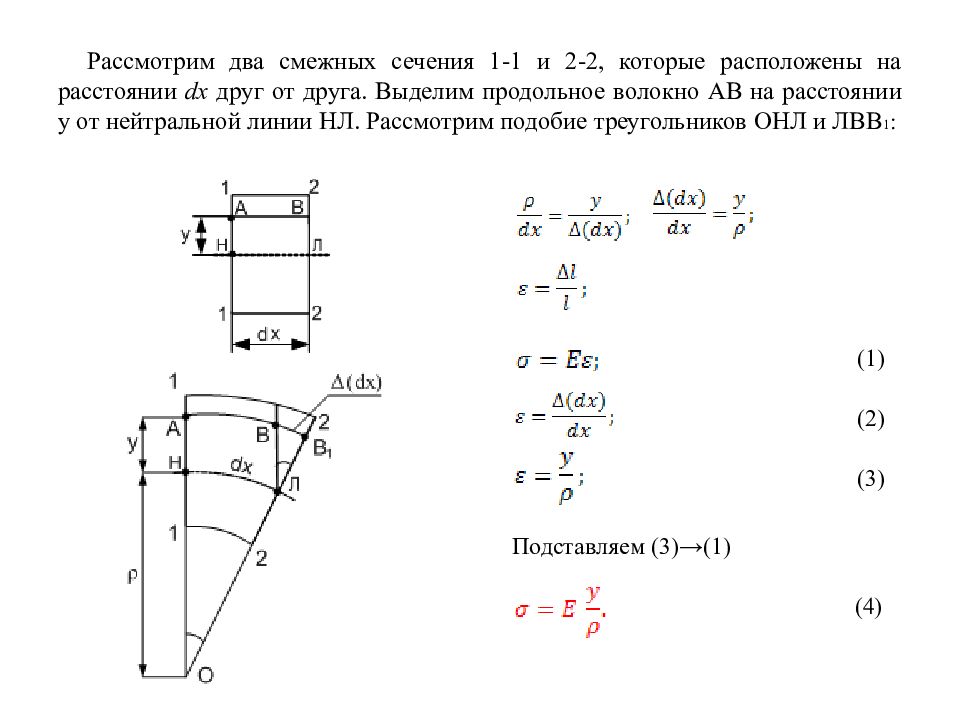
Слайд 93: Рассмотрим два смежных сечения 1-1 и 2-2, которые расположены на расстоянии dx друг от друга. Выделим продольное волокно АВ на расстоянии y от нейтральной линии НЛ. Рассмотрим подобие треугольников ОНЛ и ЛВВ 1 :
Подставляем (3)→(1) (1) (2) (3) (4)
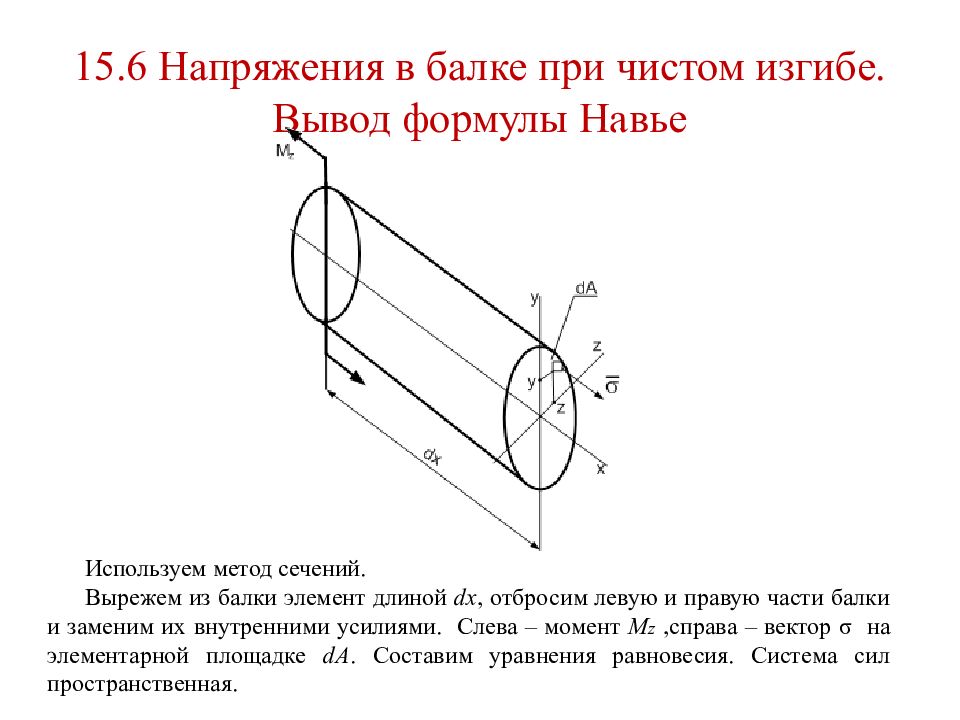
Слайд 94: 15.6 Напряжения в балке при чистом изгибе. Вывод формулы Навье
Используем метод сечений. Вырежем из балки элемент длиной dx, отбросим левую и правую части балки и заменим их внутренними усилиями. Слева – момент M z,справа – вектор σ на элементарной площадке dA. Составим уравнения равновесия. Система сил пространственная.
Слайд 95
S z =0 ; Ось z – центральная ось (проходит через центр тяжести сечения). (1) (2) (3)
Слайд 96
Для соблюдения условий равновесия необходимо, чтобы плоскость действия внутреннего изгибающего момента проходила через ось y, которая должна быть главной осью инерции сечения, т.е. рассматривается прямой (плоский ) изгиб. (5) (4) – закон Гука при изгибе. – формула Навье.
Слайд 98: 15.8 Условие прочности при чистом изгибе
- осевой момент сопротивления сечения; [ м 3, мм 3 ], [ см 3 ]. Виды расчетов: Проектный: Проверочный (10) (11) (12) (13)
Слайд 99
Определение M z max. Определение J z, W z простейших сечений. прямоугольник сплошной круг кольцо (16) (15) (14)
Слайд 101: 16 Поперечный изгиб балки
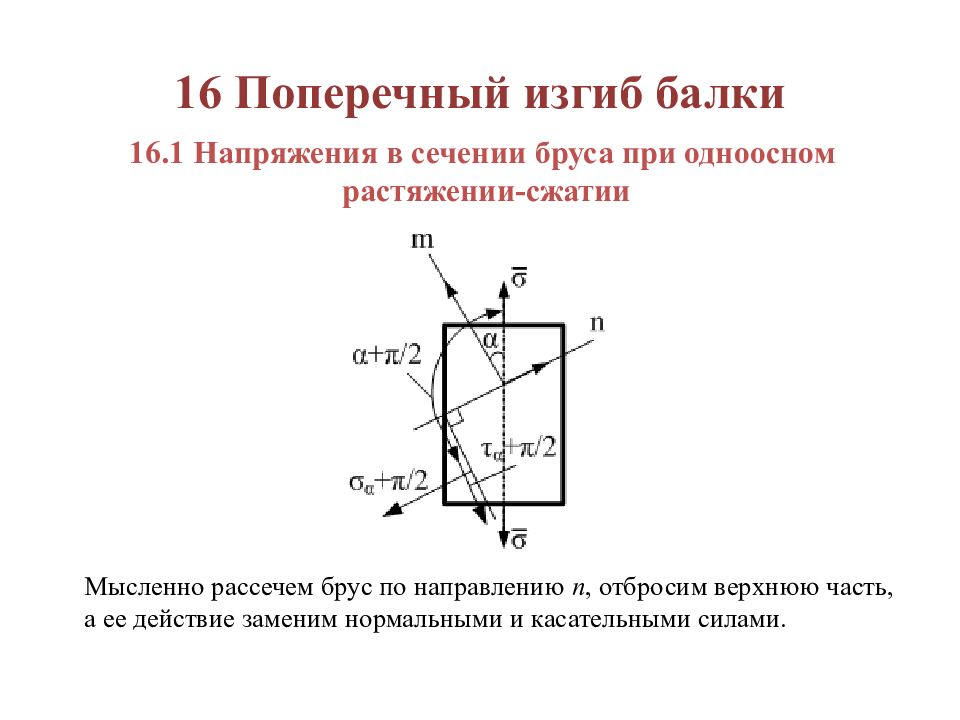
16.1 Напряжения в сечении бруса при одноосном растяжении-сжатии Мысленно рассечем брус по направлению n, отбросим верхнюю часть, а ее действие заменим нормальными и касательными силами.
Слайд 102
Вычислим σ и τ, действующие в сечении перпендикулярном n, (3) (4) (2) (5) (1) (6)
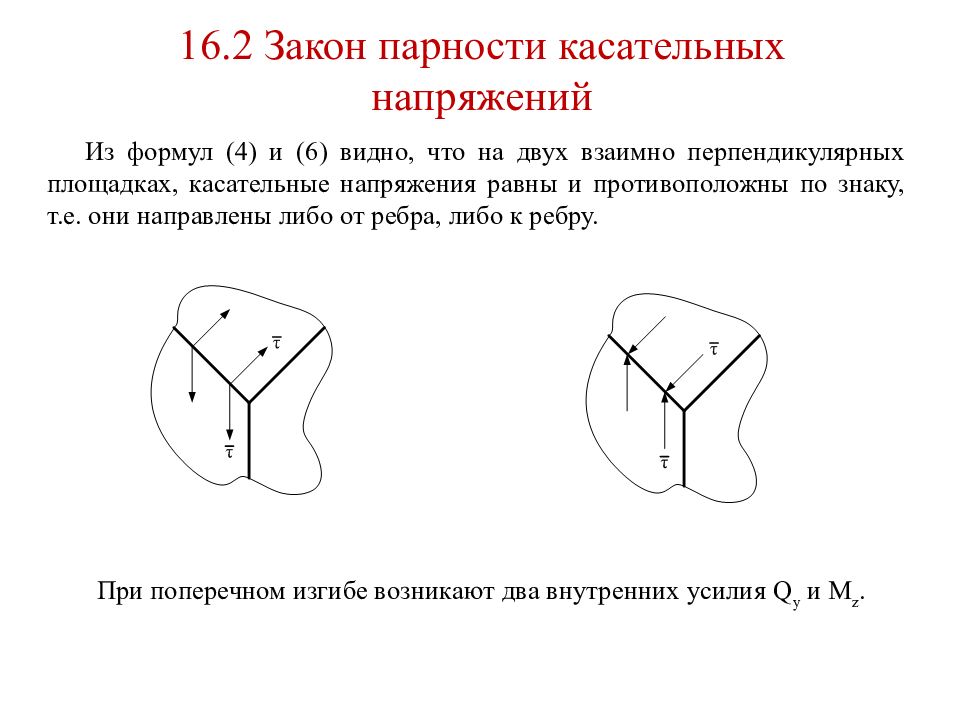
Слайд 103: 16.2 Закон парности касательных напряжений
Из формул (4) и (6) видно, что на двух взаимно перпендикулярных площадках, касательные напряжения равны и противоположны по знаку, т.е. они направлены либо от ребра, либо к ребру. При поперечном изгибе возникают два внутренних усилия Q y и M z.
Слайд 104
16.3 Особенности поперечного изгиба Q y является результирующей всех касательных сил, действующих в сечениях балки. По закону парности касательных напряжений, они будут возникать как в поперечных сечениях, так и в продольных. τ – касательное напряжение по сечению балки распределяется неравномерно, поэтому происходит искривление (депланация) поперечных сечений. Однако влияние τ невелико и формула Навье справедлива также для поперечного изгиба.
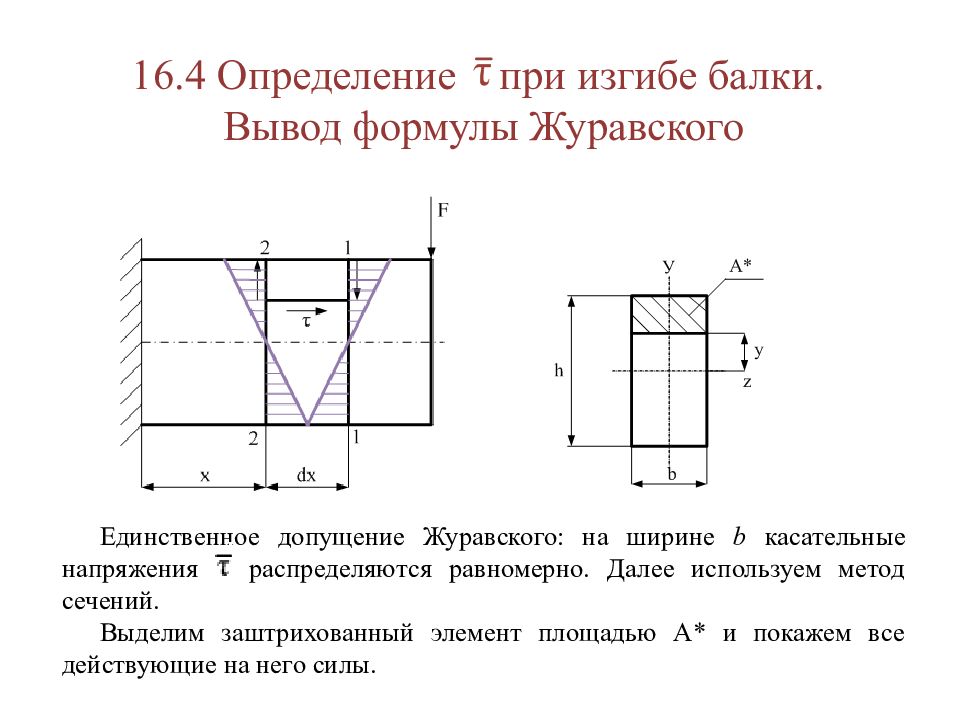
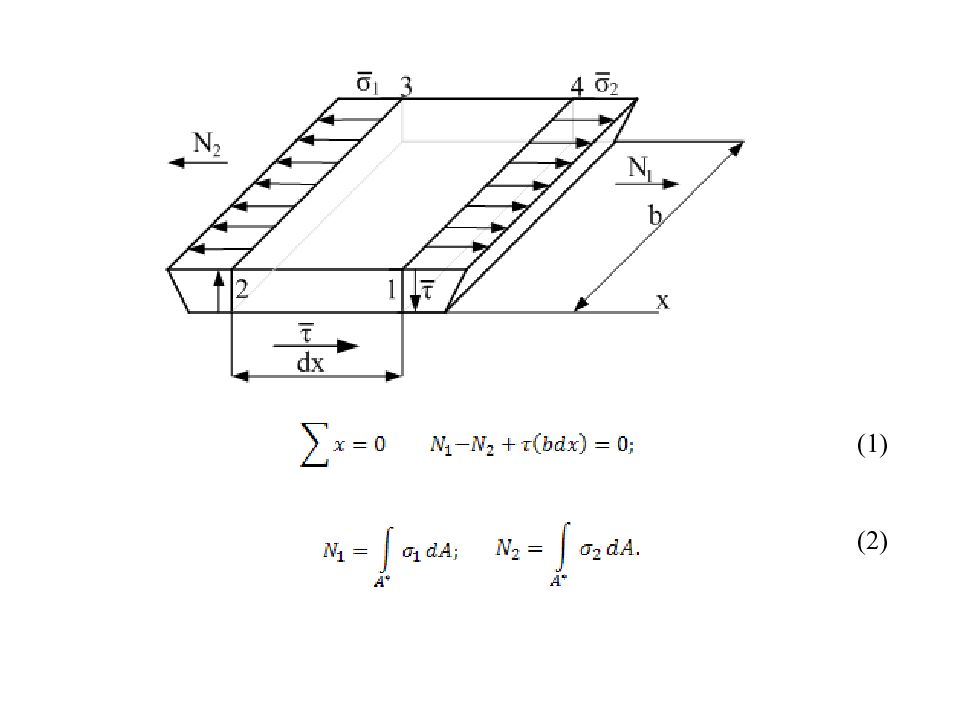
Слайд 105: 16.4 Определение при изгибе балки. Вывод формулы Журавского
Единственное допущение Журавского: на ширине b касательные напряжения распределяются равномерно. Далее используем метод сечений. Выделим заштрихованный элемент площадью А* и покажем все действующие на него силы.
Слайд 110
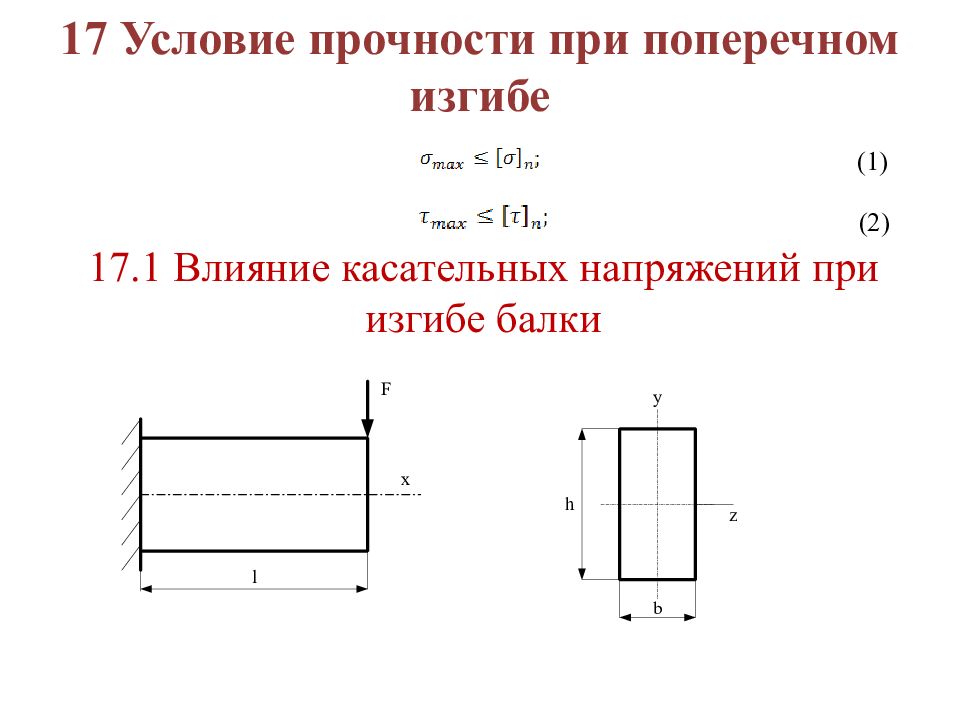
17 Условие прочности при поперечном изгибе (1) (2) 17.1 Влияние касательных напряжений при изгибе балки
Слайд 111
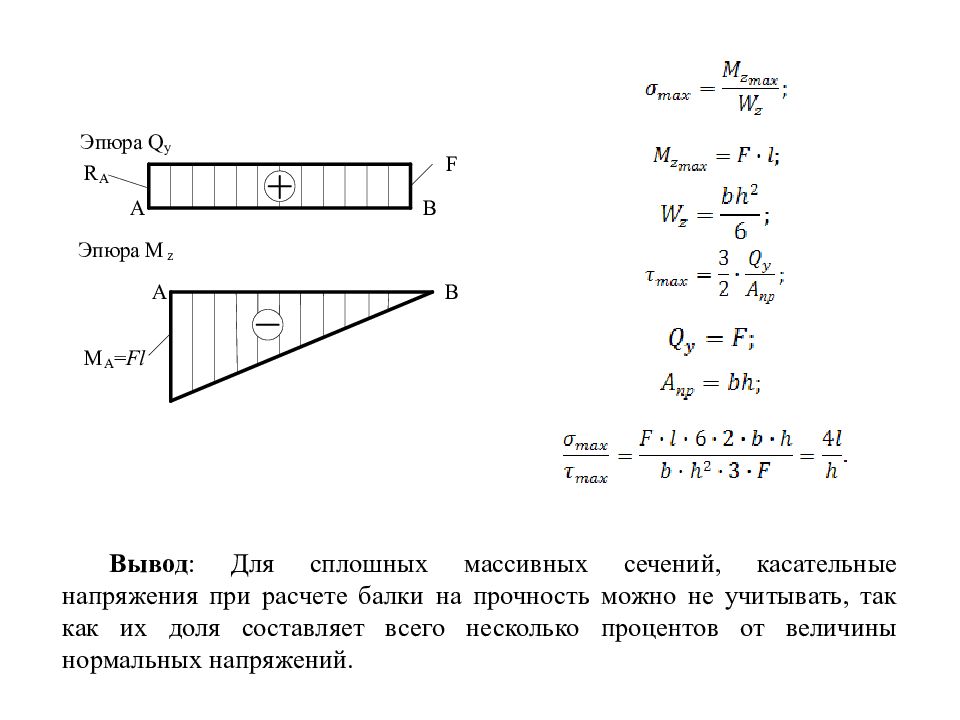
Вывод : Для сплошных массивных сечений, касательные напряжения при расчете балки на прочность можно не учитывать, так как их доля составляет всего несколько процентов от величины нормальных напряжений.
Слайд 112
17.2 Когда надо учитывать τ ? При одновременном учете σ и τ используют так называемые гипотезы прочности.
Слайд 113
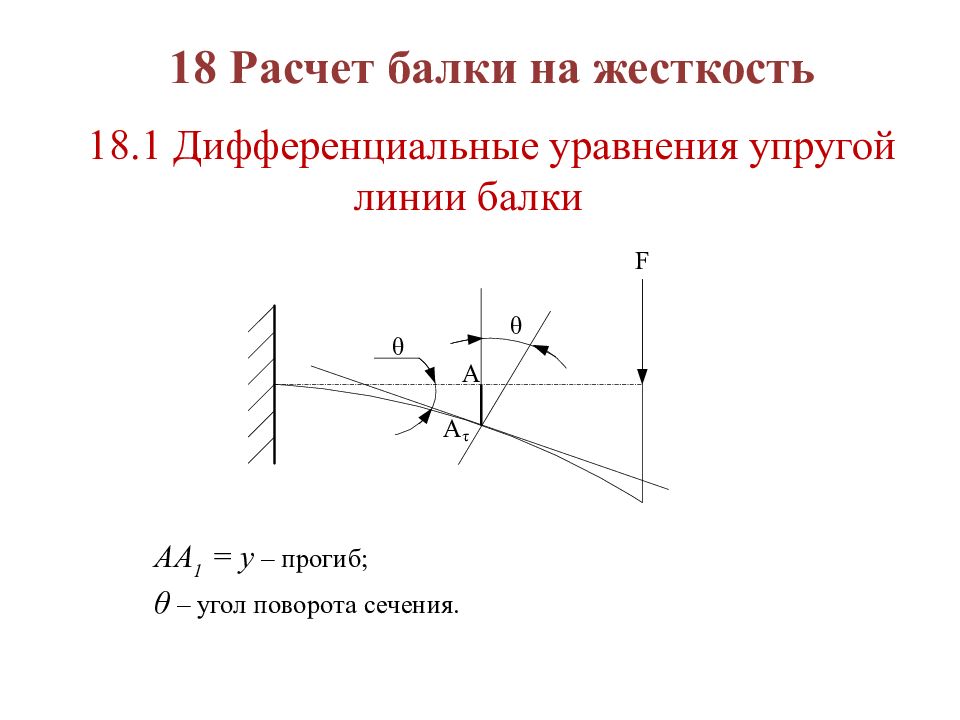
18 Расчет балки на жесткость 18.1 Дифференциальные уравнения упругой линии балки АА 1 = у – прогиб; θ – угол поворота сечения.
Слайд 114
(1) Вывод: у – прогиб балки; первая производная от прогиба – угол поворота сечения. (3) (2) и (3) – условия жесткости балки при изгибе. (5’) (5) – кривизна линии (см. курс ВМ) (4) (5)
Слайд 115
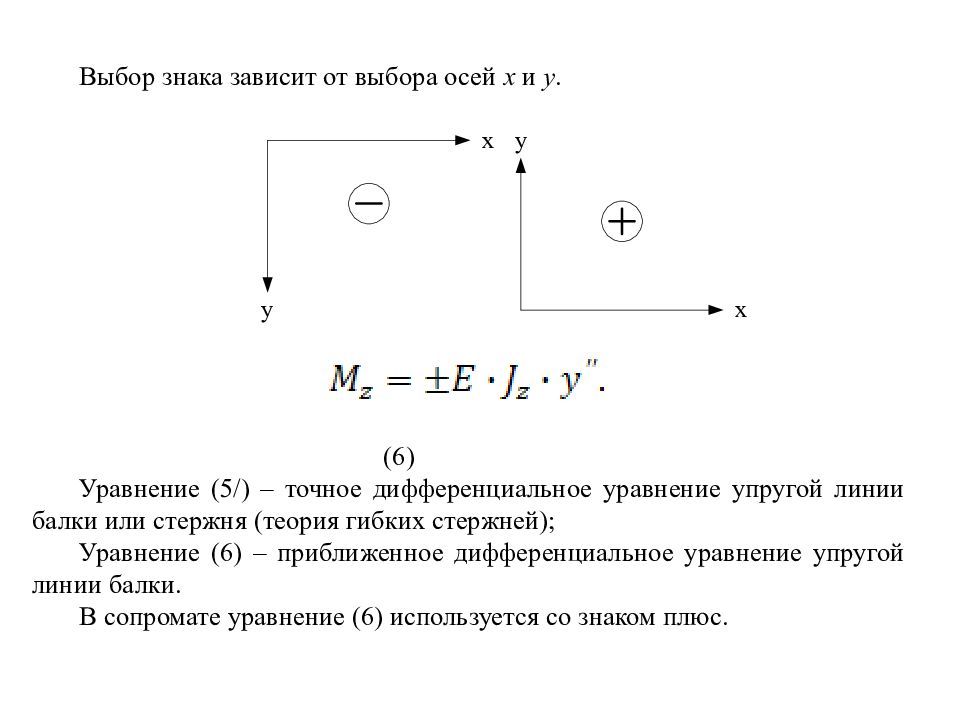
Выбор знака зависит от выбора осей x и y. (6) Уравнение (5/) – точное дифференциальное уравнение упругой линии балки или стержня (теория гибких стержней); Уравнение (6) – приближенное дифференциальное уравнение упругой линии балки. В сопромате уравнение (6) используется со знаком плюс.
Слайд 116
(7) (8) (9) где С и D – постоянные интегрирования, которые определяются из условий закрепления балки. Уравнение (8) позволяет определить углы поворота любого сечения балки. Уравнение (9) позволяет определить прогиб балки в любом сечении по её длине. 18. 2 Метод непосредственного интегрирования приближенного дифференциального уравнения
Слайд 117
Пример: OO 1 = y o = y max ; θ o = θ max. у – прогиб; у’ – угол поворота сечения; (1) (2) (3) (2) – уравнение углов поворота сечения балки; (3) – уравнение прогибов сечения балки.
Слайд 118
при х = l ; у( l ) = 0; (4) у’( l ) = 0; (5) (5) → (2) (7) (8) (9) Вывод : Мы рассмотрели балку, состоящую из одного участка, при этом получили две неизвестные постоянные интегрирования, которые определяются из условий закрепления балки. Если балка будет иметь n участков, то мы получим 2 n неизвестных постоянных интегрирования, для определения которых необходимо будет составить 2 n уравнений. Такая задача очень трудоемкая и решение ее методом непосредственного интегрирования неэффективно. Более эффективным является метод академика А.Н. Крылова и профессора Н.П. Пузыревского.
Слайд 119
18. 3 Метод начальных параметров. Составление универсальных уравнений Единственное допущение – изгибная жесткость балки по всей ее длине, является постоянной, т.е. EJ z = const. При интегрировании дифференциального уравнения используются следующие приемы: 1 Начало координат берется на левом конце балки и отсчет всех координат сечений ведется от одного и того же начала координат. 2 Интегрирование ведется без раскрытия скобок. 3 Внешний изгибающий момент m умножается на множитель ( х - а ) о, где а – координата точки приложения момента m. 4 Если на балку действует распределенная нагрузка q, не доходящая до правого конца балки, то q необходимо продлить до конца балки, а чтобы равновесие балки не нарушилось, надо приложить q той же интенсивности, но направленную в другую сторону.
Слайд 120
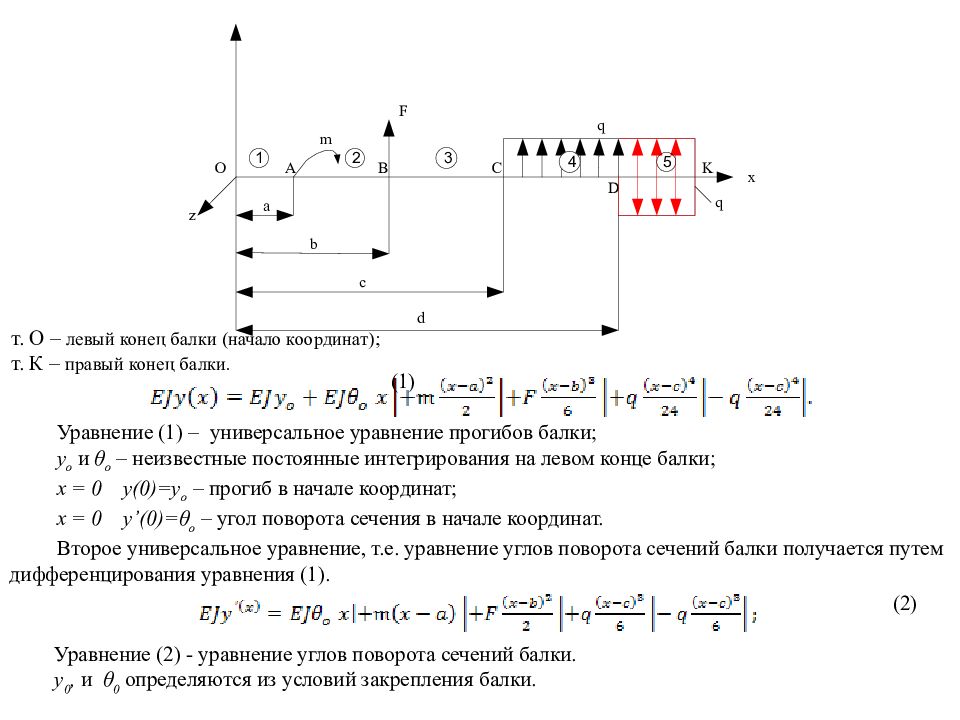
т. О – левый конец балки (начало координат); т. К – правый конец балки. (1) Уравнение (1) – универсальное уравнение прогибов балки; у о и θ о – неизвестные постоянные интегрирования на левом конце балки; х = 0 у(0)=у о – прогиб в начале координат; х = 0 у’(0)=θ о – угол поворота сечения в начале координат. Второе универсальное уравнение, т.е. уравнение углов поворота сечений балки получается путем дифференцирования уравнения (1). (2) Уравнение (2) - уравнение углов поворота сечений балки. y 0, и θ 0 определяются из условий закрепления балки.
Слайд 121
Пример ; (1’) Все сосредоточенные нагрузки, приложенные на правом конце балки, не учитываются. ; (2’) x=a y(a)=0 (3) x=a+2b y(a+2b)=0 (4)
Слайд 122
Уравнение (3) подставляем в (1’) до вертикальной черты с индексом 1. Уравнение (4) подставляем в (1’) до вертикальной черты с индексом 3. Получаем два уравнения с двумя неизвестными, из них определяем y 0 и θ 0. Далее строится форма упругой линии балки. Для этого в уравнение (1’) подставляются различные координаты x с определенным шагом и строится форма упругой линии балки ( ФУЛБ ), по которой определяется y max. Это значение y max подставляется в условие жесткости. Условие жесткости для балки при ее изгибе y max ≤ [ y ], (1) θ max ≤ [ θ ]. (2) [ y ] ≈ (0,01-0,03)∙ l – в общем машиностроении, [ θ ] ≈0,001 рад ≈ 3,5' – в опорных сечениях балки 1 рад = 57,3˚
Слайд 123
19 Сдвиг Сдвигом называется такой вид нагружения бруса, когда одно поперечное сечение бруса смещается относительно другого под действием двух равных по величине противоположно направленных, перпендикулярных оси бруса сил, лежащих достаточно близко друг от друга ( h – мало).
Слайд 124
19. 1 Деформация при сдвиге Под действием внешних сил прямоугольник АВСД превратится в параллелограмм АВС 1 Д 1. СС 1 = DD 1 = Δ a – абсолютный сдвиг (линейная деформация). (1) где γ – относительный сдвиг (угловая деформация).
Слайд 125
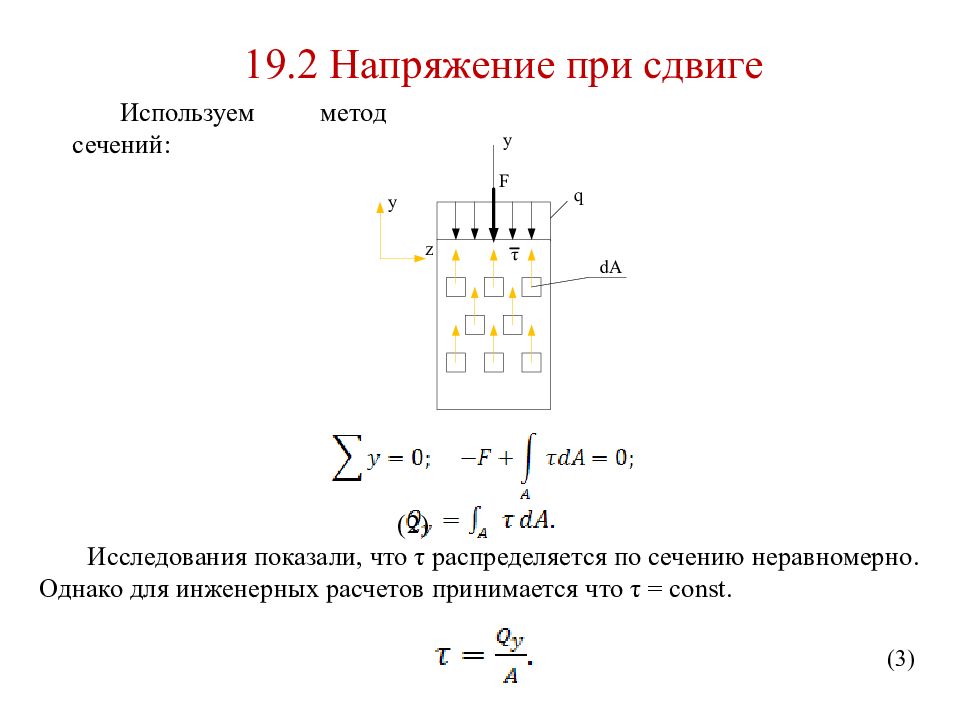
19. 2 Напряжение при сдвиге Используем метод сечений: (2) Исследования показали, что τ распределяется по сечению неравномерно. Однако для инженерных расчетов принимается что τ = const. ( 3 )
Слайд 126
19.3 Условия прочности при сдвиге (4) Три вида расчетов: 1 Проектный: 2 Проверочный: 3 Определение Q ymax :
Слайд 127
19.4 Закон Гука при сдвиге (5) В области малых упругих деформаций τ прямопропорциональны относительному сдвигу – γ. G – модуль упругости второго рода (модуль сдвига); [ G ] = [МПа, Па, кг/см 2 ] ; [ γ ] = [ рад ]. (6) где μ – коэффициент Пуассона; (1), (3) → (5) (7) Данные формулы используются в инженерных расчетах различных видов соединений.
Слайд 128
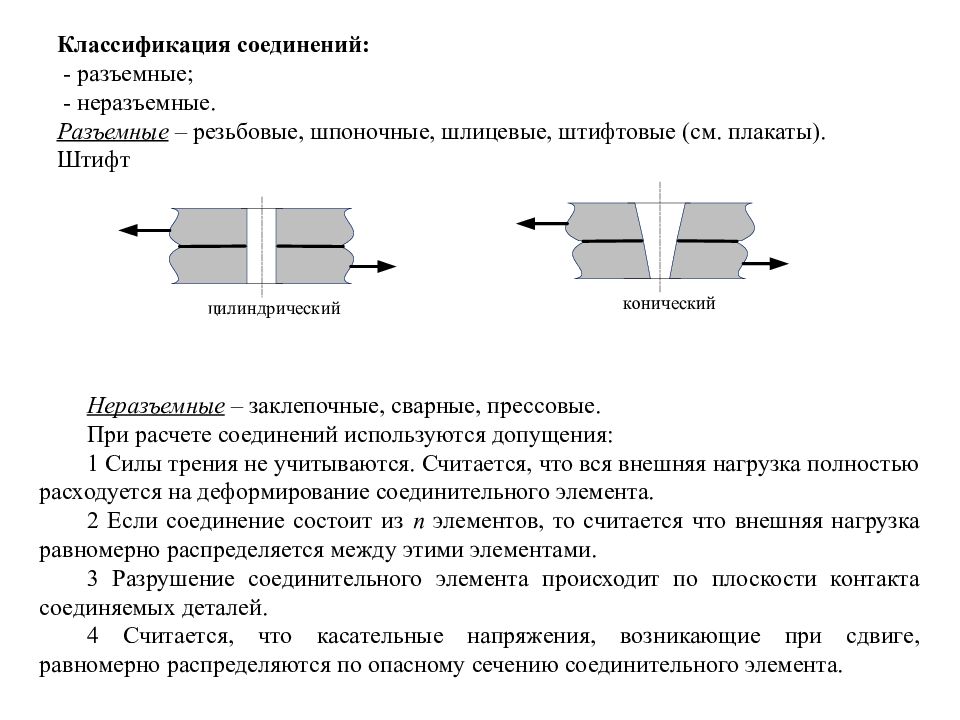
Классификация соединений: - разъемные; - неразъемные. Разъемные – резьбовые, шпоночные, шлицевые, штифтовые (см. плакаты). Штифт Неразъемные – заклепочные, сварные, прессовые. При расчете соединений используются допущения: 1 Силы трения не учитываются. Считается, что вся внешняя нагрузка полностью расходуется на деформирование соединительного элемента. 2 Если соединение состоит из n элементов, то считается что внешняя нагрузка равномерно распределяется между этими элементами. 3 Разрушение соединительного элемента происходит по плоскости контакта соединяемых деталей. 4 Считается, что касательные напряжения, возникающие при сдвиге, равномерно распределяются по опасному сечению соединительного элемента.
Слайд 130
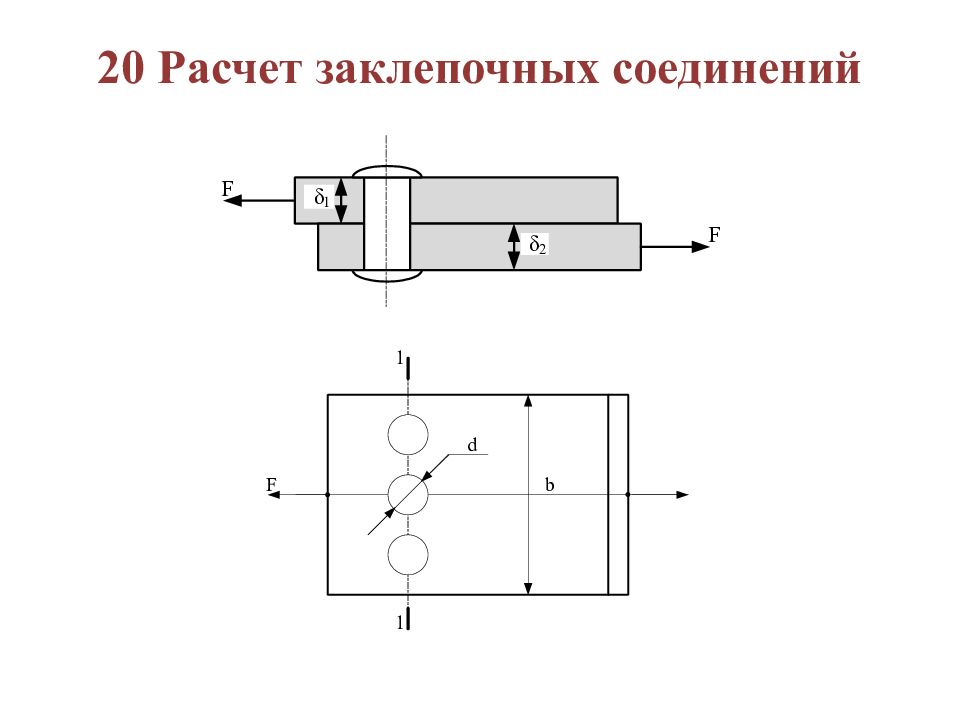
Виды разрушения данного соединения (δ 1 <δ 2 ): 1 Разрыв одного из листов по сечению 1-1 (1) где А р – площадь сечения разрыва; n – количество заклепок 2 Срез заклепок по плоскости контакта соединяемых деталей (2) где i – число плоскостей среза (если соединяются 3 листа, то i =2) 3 Смятие заклепок (частный случай деформации сжатия, когда площадка контакта деталей мала). (3)
Слайд 131
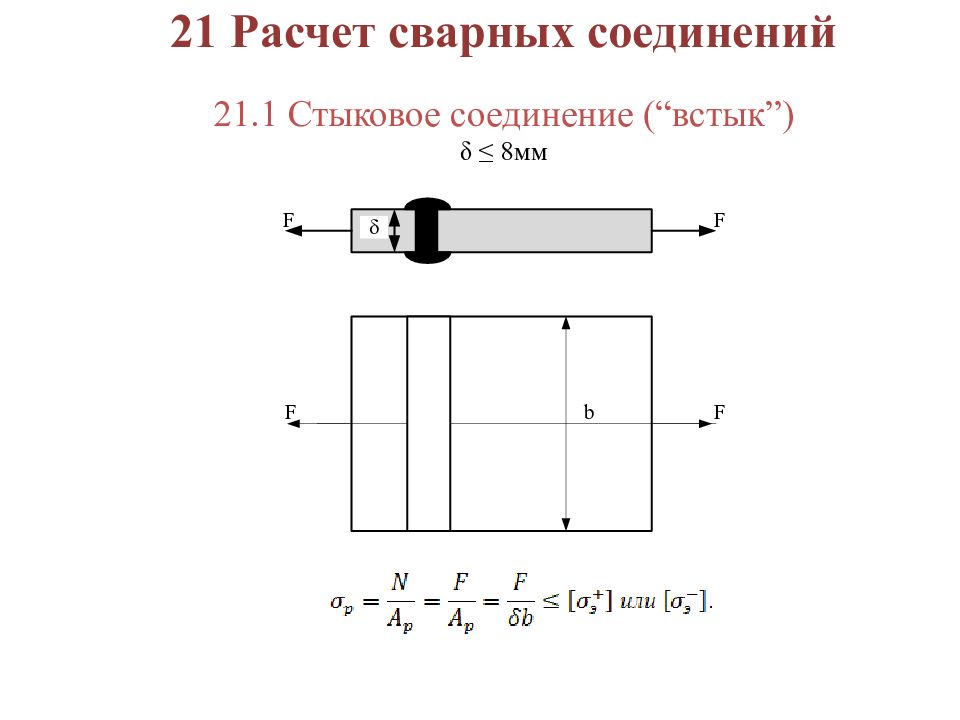
21 Расчет сварных соединений 21.1 Стыковое соединение (“встык”) δ ≤ 8мм
Слайд 132
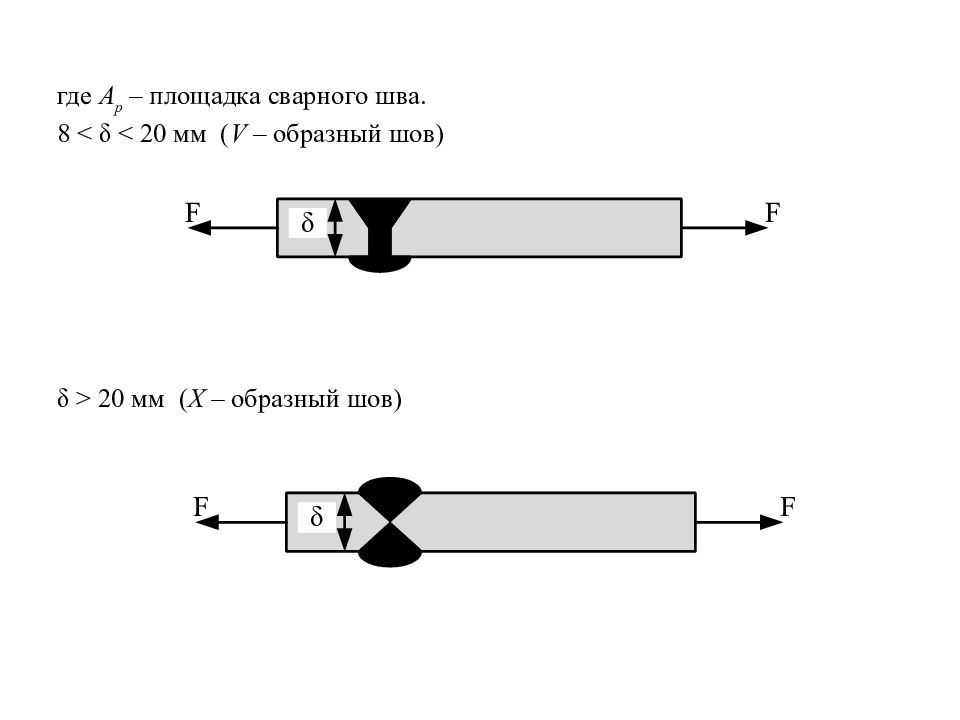
где А р – площадка сварного шва. 8 < δ < 20 мм ( V – образный шов) δ > 20 мм ( X – образный шов)
Слайд 133
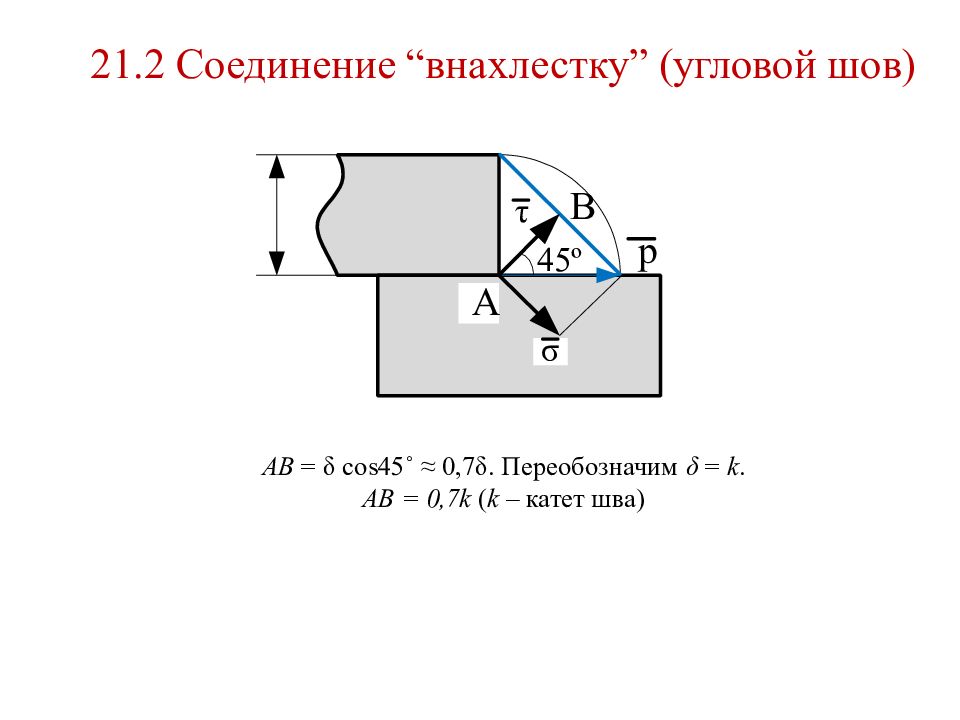
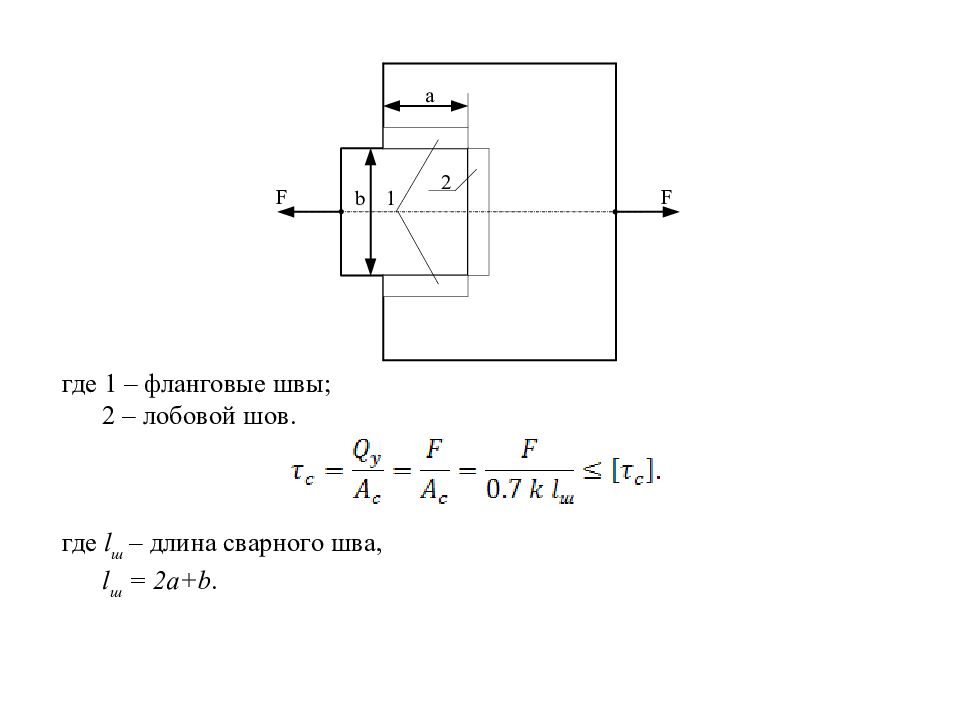
21. 2 Соединение “внахлестку” (угловой шов) АВ = δ cos 45˚ ≈ 0,7 δ. Переобозначим δ = k. АВ = 0,7 k ( k – катет шва)
Слайд 134
где 1 – фланговые швы; 2 – лобовой шов. где l ш – длина сварного шва, l ш = 2а+ b.
Слайд 135
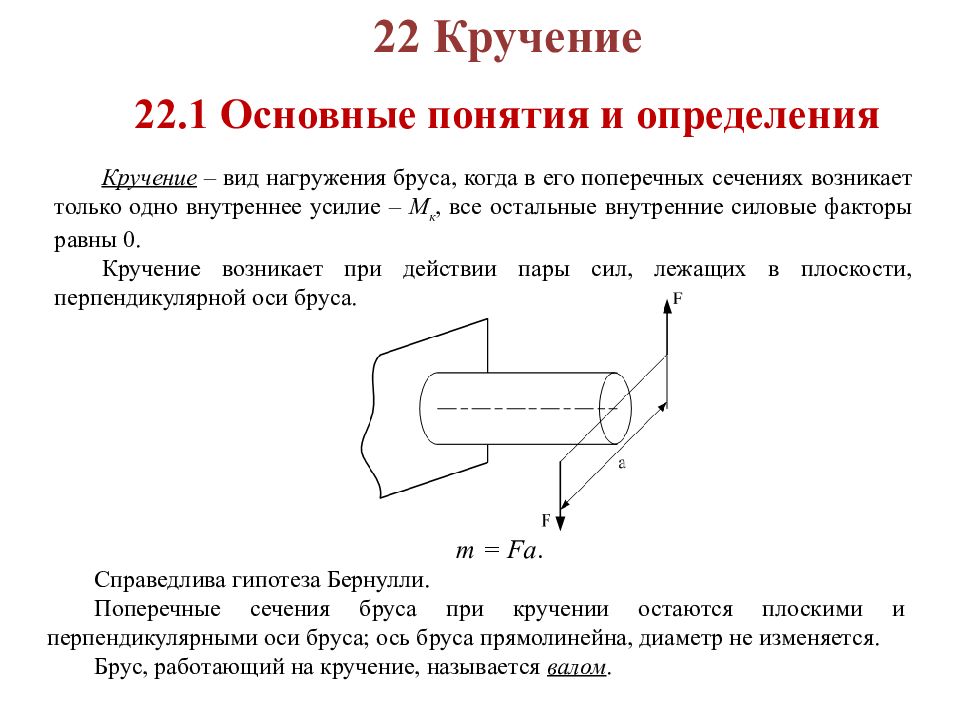
22 Кручение 22. 1 Основные понятия и определения Кручение – вид нагружения бруса, когда в его поперечных сечениях возникает только одно внутреннее усилие – М к, все остальные внутренние силовые факторы равны 0. Кручение возникает при действии пары сил, лежащих в плоскости, перпендикулярной оси бруса. m = Fa. Справедлива гипотеза Бернулли. Поперечные сечения бруса при кручении остаются плоскими и перпендикулярными оси бруса; ось бруса прямолинейна, диаметр не изменяется. Брус, работающий на кручение, называется валом.
Слайд 136
Ось не передает крутящий момент! Частицы материала, одновременно принадлежащие двум смежным сечениям, испытывают деформацию сдвига. Одновременно происходит поворот одного смежного сечения относительно другого вокруг оси на угол закрутки.
Слайд 137
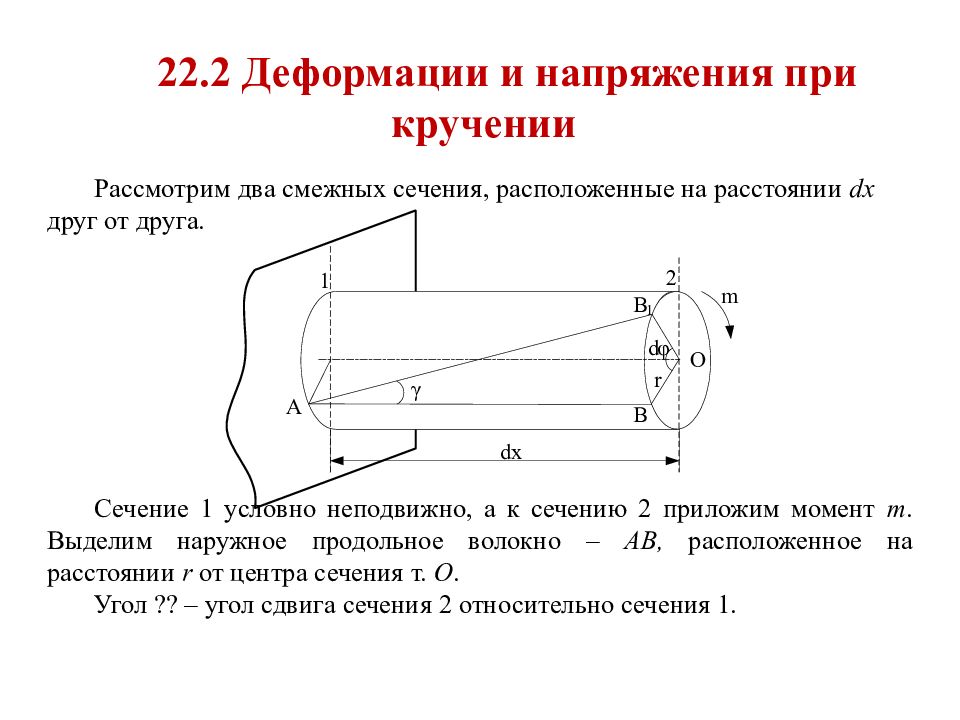
22. 2 Деформации и напряжения при кручении Рассмотрим два смежных сечения, расположенные на расстоянии dx друг от друга. Сечение 1 условно неподвижно, а к сечению 2 приложим момент m. Выделим наружное продольное волокно – АВ, расположенное на расстоянии r от центра сечения т. О. Угол ?? – угол сдвига сечения 2 относительно сечения 1.
Слайд 138
(1) (2) (3) (4) Поскольку при кручении справедлива гипотеза Бернулли, то в этом случае возникают только касательные напряжения, при этом нормальные напряжения отсутствуют. Кручение - частный случай деформации сдвига, т.е. при кручении справедлив закон Гука для сдвига. (5) (4) ↔ (5) (6)
Слайд 139
22. 3 Закон Гука при кручении Используем метод сечений. Мысленно рассечем вал в интересующем нас сечении, мысленно отбросим одну из частей, а действие ее заменим внутренним крутящим моментом. (7) (6) → (7) (8) где J ρ – полярный момент инерции (ПМИС), (9) где GJ p - жесткость вала при кручении. (10) (10) → (9) (11) (9), (11) – закон Гука при кручении (9) → (6) (12)
Слайд 140
ρ = 0 τ = 0 ρ = ρ max τ = τ max (13) где W ρ - полярный момент сопротивления сечения (ПМСС) (14)
Слайд 141
22. 4 Определение J ρ и W ρ для круглых сечений Сплошной круг: (15) (16) Кольцевое сечение (трубчатое): (17) (18) Самое рациональное сечение с точки зрения расхода материала – кольцевое (трубчатое).
Слайд 142
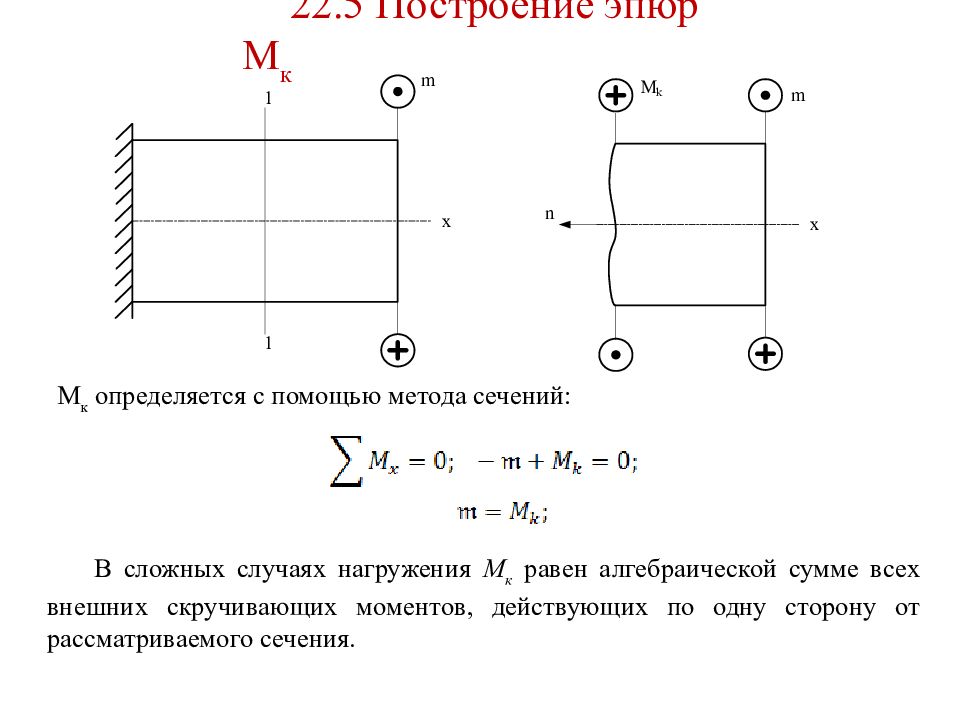
22. 5 Построение эпюр М к М к определяется с помощью метода сечений: В сложных случаях нагружения М к равен алгебраической сумме всех внешних скручивающих моментов, действующих по одну сторону от рассматриваемого сечения.
Слайд 143
22. 6 Правило знаков для М к М к в сечении считается «+», если m вращает отсеченную часть вала против хода часовой стрелки, если смотреть со стороны внешней нормали n к сечению.
Слайд 145
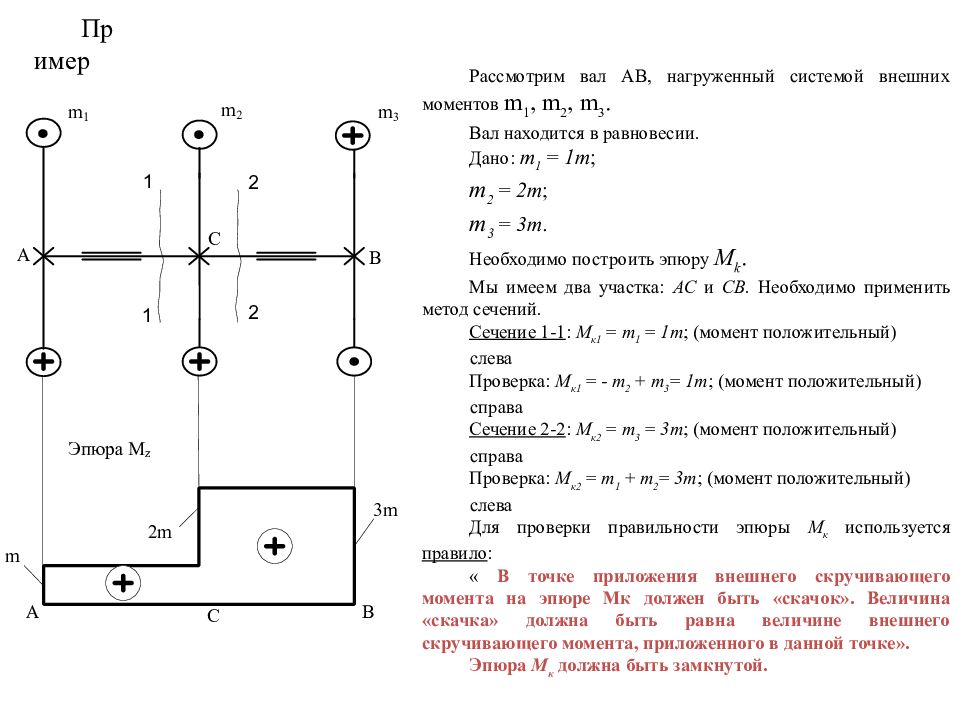
Пример Рассмотрим вал АВ, нагруженный системой внешних моментов m 1, m 2, m 3. Вал находится в равновесии. Дано: m 1 = 1 m ; m 2 = 2 m ; m 3 = 3 m. Необходимо построить эпюру M k. Мы имеем два участка: АС и СВ. Необходимо применить метод сечений. Сечение 1-1 : М к1 = m 1 = 1 m ; (момент положительный) слева Проверка: М к1 = - m 2 + m 3 = 1 m ; (момент положительный) справа Сечение 2-2 : М к2 = m 3 = 3 m ; (момент положительный) справа Проверка: М к2 = m 1 + m 2 = 3 m ; (момент положительный) слева Для проверки правильности эпюры М к используется правило : « В точке приложения внешнего скручивающего момента на эпюре Мк должен быть «скачок». Величина «скачка» должна быть равна величине внешнего скручивающего момента, приложенного в данной точке». Эпюра М к должна быть замкнутой.
Слайд 146
22. 7 Условие прочности при кручении (19) - проектный расчет, (20) – проверочный расчет;