Первый слайд презентации: Подготовка к экзамену
1 Подготовка к экзамену Способность конструкции воспринимать заданную нагрузку, не разрушаясь и без появления остаточных деформаций – прочность. Критерием прочности – напряжения в опасной точке тела ( нормальные, касательные, главные) Условия прочности: σ max ≤ [ σ ] ; τ max ≤ [ τ ] Из расчета Из расчета [ σ ] = σ оп / n [ τ ] = τ оп / n σ оп, τ оп = σ т, τ т – для пластичных матер. σ пч, τ пч – для хрупких матер. с диаграмм растяжения и сдвига
Слайд 2: Подготовка к экзамену
2 Подготовка к экзамену Способность конструкции под воздействием нагрузки сохранять свои размеры и форму в установленных пределах – жесткость. Критерием жесткости – перемещения (линейные, угловые) Условия жесткости:– максимальные перемещения сравниваются с допускаемыми
Слайд 3: К экзамену
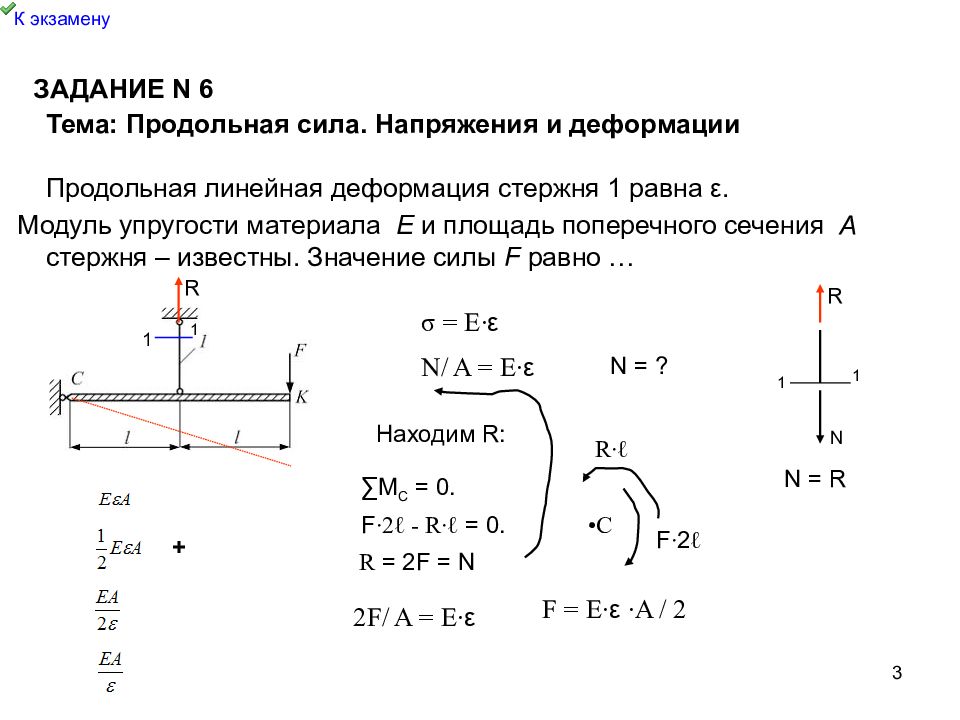
3 К экзамену ЗАДАНИЕ N 6 Тема: Продольная сила. Напряжения и деформации Продольная линейная деформация стержня 1 равна ε. Модуль упругости материала Е и площадь поперечного сечения А стержня – известны. Значение силы F равно … R σ = Е∙ ε N/ A = Е∙ ε N = ? 1 1 1 1 R N N = R Находим R : ∑М С = 0. F ∙2ℓ - R∙ℓ = 0. R = 2F = N 2F/ A = Е∙ ε F = Е∙ ε ∙ A / 2 + •С F ∙ 2 ℓ R∙ℓ
Слайд 4: К экзамену
4 К экзамену задание ЗАДАНИЕ N 16 Тема: Расчеты стержней на прочность и жесткость Система, показанная на рисунке, нагружена силой F. Известны величины: – перемещение шарнира С. Вес абсолютно жесткого элемента ВК в расчетах не учитывать. Значение силы F равно … + R=2F δ c ∆ ℓ 1 = δ c N ℓ / EA = δ c 2Fℓ / EA = δ c F = EA δ c / 2ℓ
Слайд 5: К экзамену
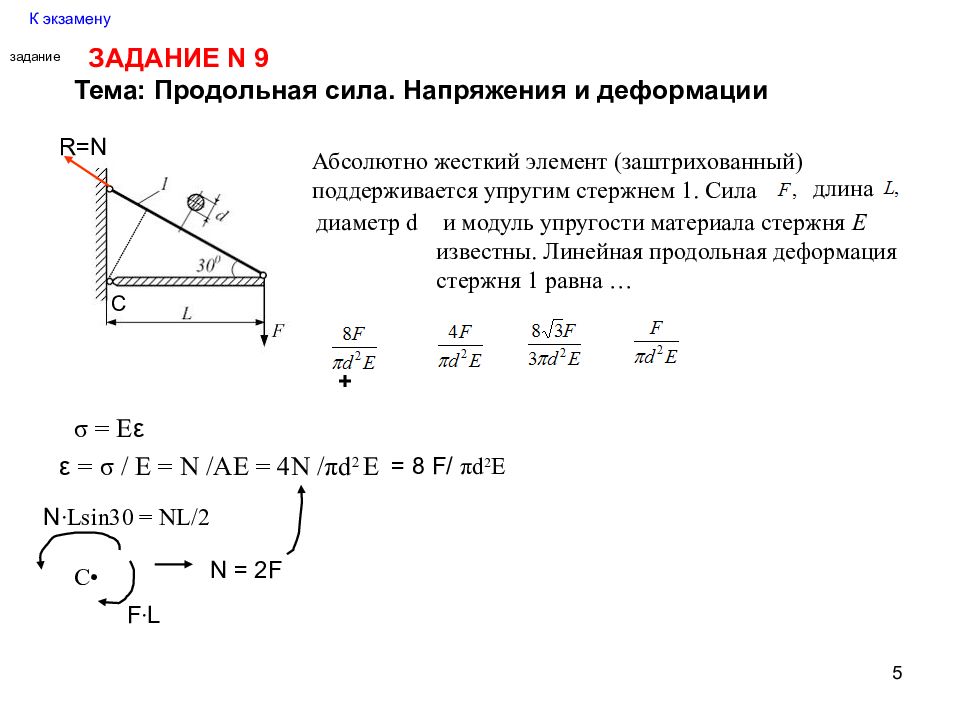
5 К экзамену задание ЗАДАНИЕ N 9 Тема: Продольная сила. Напряжения и деформации Абсолютно жесткий элемент (заштрихованный) поддерживается упругим стержнем 1. Сила длина диаметр d и модуль упругости материала стержня Е известны. Линейная продольная деформация стержня 1 равна … σ = Е ε ε = σ / Е = N /АЕ = 4 N / π d 2 Е С R=N C • F ∙ L N ∙Lsin30 = NL/2 N = 2F = 8 F/ π d 2 E +
Слайд 6: К экзамену
6 К экзамену ЗАДАНИЕ N 8 Тема: Расчеты стержней на прочность и жесткость Стержень растянут осевыми силами (см. рисунок). Задана допустимая величина нормального напряжения для материала стержня. Условие прочности имеет вид … σ max ≤ [ σ ] N max / A ≤ [ σ ] N max = 3F A = π d 2 /4 +
Слайд 7: К экзамену
7 К экзамену ЗАДАНИЕ N 7 Тема: Механические свойства и механические характеристики материалов На рисунке показана диаграмма растяжения образца диаметром 0,01 м. Масштаб нагрузки – 1 деление – 0,007 МН. Предел прочности материала равен ___ МПа. 446 112 357 268 σ пч = F max /A 0 = 0. 035 / 0.785(0.01) 2 =445.85МПа +
Слайд 8: К экзамену
8 К экзамену ЗАДАНИЕ N 9 Тема: Модели прочностной надежности В сопротивлении материалов все тела считаются … абсолютно упругими абсолютно твердыми вязко-упругими упруго-вязко-пластичными ЗАДАНИЕ N 10 Тема: Внутренние силы и напряжения Полное напряжение в точке сечения определяется Предельный переход позволила осуществить гипотеза … сплошной среды однородности материала изотропности материала начальных размеров + +
Слайд 9: К экзамену
9 К экзамену ЗАДАНИЕ N 11 Тема: Перемещение и деформация Если известны углы поворота малого прямолинейного отрезка в трех координатных плоскостях то полный угол поворота определяется по формуле φ = ЗАДАНИЕ N 12 Тема: Основные понятия, определения, допущения и принципы Древесина – материал … анизотропный кристалический аморфный изотропный + +
Слайд 10: К экзамену
10 К экзамену ЗАДАНИЕ N 5 Тема: Испытание конструкционных материалов на растяжение и сжатие Металлический образец, предназначенный для испытаний на сжатие, имеет форму короткого цилиндра, для того чтобы … он не изогнулся в процессе испытаний он не разрушился уменьшить влияние сил трения между поверхностями образца и поверхностями плит испытательной машины он разрушился +
Слайд 11: К экзамену
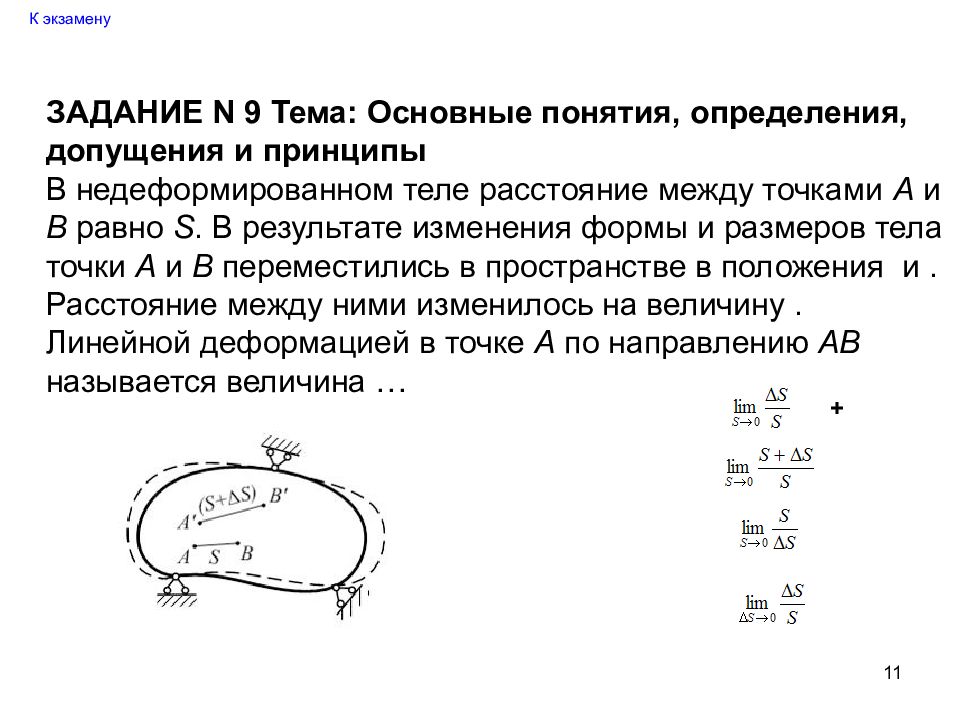
11 К экзамену ЗАДАНИЕ N 9 Тема: Основные понятия, определения, допущения и принципы В недеформированном теле расстояние между точками А и В равно S. В результате изменения формы и размеров тела точки А и В переместились в пространстве в положения и. Расстояние между ними изменилось на величину. Линейной деформацией в точке А по направлению АВ называется величина … +
Слайд 12: К экзамену
12 К экзамену Задание ЗАДАНИЕ N 10 Тема: Внутренние силы и напряжения Интегральная связь между изгибающим моментом и нормальными напряжениями имеет вид +
Слайд 13: К экзамену
13 К экзамену Задание ЗАДАНИЕ N 11 Тема: Перемещение и деформация Т очка К принадлежит деформируемому телу и перемещается в плоскости xoy (см. рисунок). Полное перемещение точки Перемещение вдоль оси x Перемещение вдоль оси y равно ___ мм. 4; 2; 2√2 ; 8. +
Слайд 14: К экзамену
14 К экзамену задание ЗАДАНИЕ N 14 Тема: Механические свойства и механические характеристики материалов Коэффициент Пуассона для изотропного материала изменяется в пределах … + ЗАДАНИЕ N 6 Тема: Внутренние силы и напряжения Значения полного и нормального напряжений в точке сечения соответственно равны 10 МПа и 8 МПа. Значение касательного напряжения в этой же точке сечения равно ____ МПа. 6; 2; 18; 1.41. +
Слайд 15: К экзамену
15 К экзамену задание ЗАДАНИЕ N 7 Тема: Модели прочностной надежности Первым этапом при расчете конструкции является … выбор расчетной схемы определение реакций опор составление условия прочности построение эпюр внутренних силовых факторов + ЗАДАНИЕ N 8 Тема: Перемещение и деформация До приложения к стержню сил F (см. рисунок) его длина равнялась 10 см. После приложения сил F длина стержня стала равна 9,95 см. Продольная линейная деформация стержня равна … 0.005; 0.995; 200; 1.005. + ε = ∆ ℓ / ℓ
Слайд 16: К экзамену
16 К экзамену задание ЗАДАНИЕ N 10 Тема: Испытание конструкционных материалов на растяжение и сжатие Основными видами испытаний материалов являются испытания на … растяжение и сжатие изгиб и кручение усталость и ударную вязкость на ползучесть и длительную прочность + ЗАДАНИЕ N 12 Тема: Механические свойства и механические характеристики материалов Наибольшее напряжение, до которого материал подчиняется закону Гука, называется пределом … пропорциональности упругости прочности текучести +
Слайд 17: К экзамену
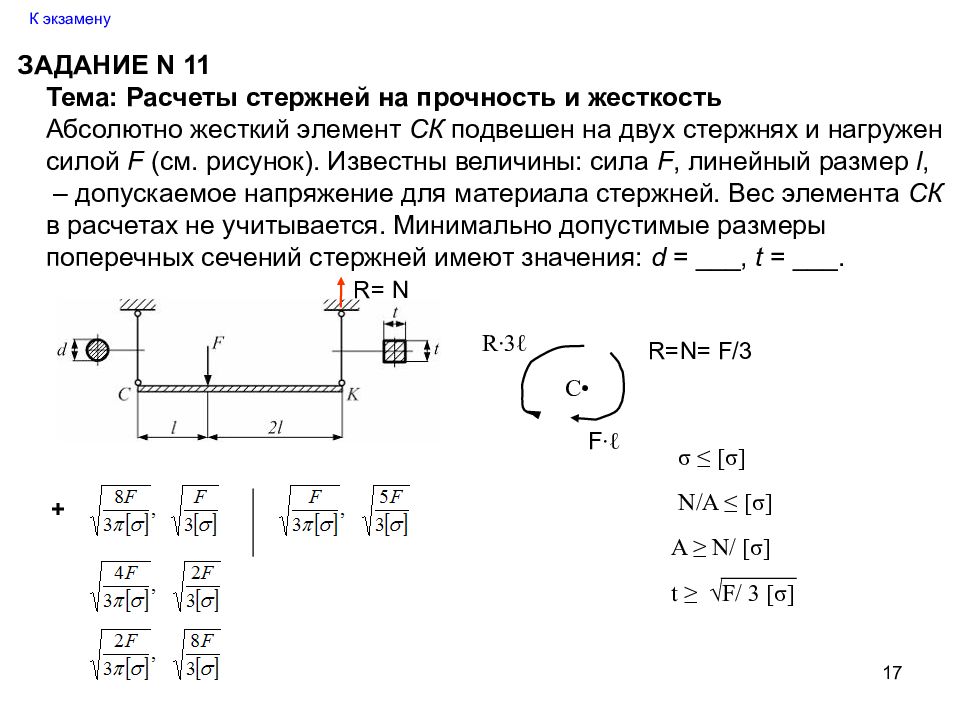
17 К экзамену ЗАДАНИЕ N 11 Тема: Расчеты стержней на прочность и жесткость Абсолютно жесткий элемент СК подвешен на двух стержнях и нагружен силой F (см. рисунок). Известны величины: сила F, линейный размер l, – допускаемое напряжение для материала стержней. Вес элемента СК в расчетах не учитывается. Минимально допустимые размеры поперечных сечений стержней имеют значения: d = ___, t = ___. + R= N C • F ∙ℓ R∙3ℓ R=N= F/3 σ ≤ [ σ ] N/A ≤ [ σ ] A ≥ N/ [ σ ] t ≥ √F/ 3 [ σ ]
Слайд 18: Перемещения при изгибе
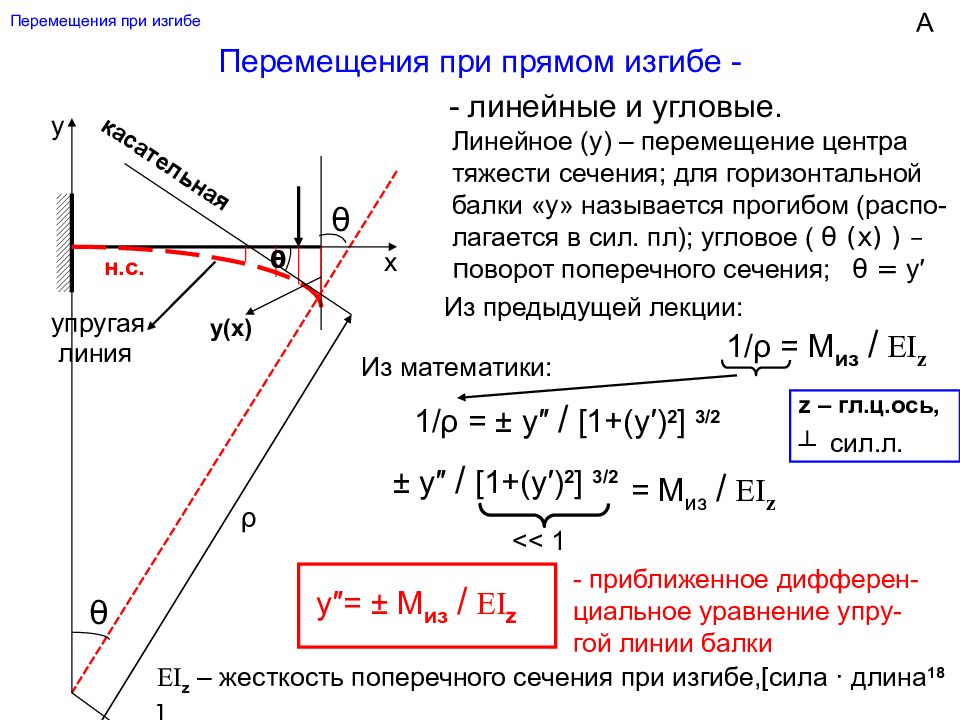
Перемещения при прямом изгибе - - линейные и угловые. θ y x θ ρ y(x) Линейное (у) – перемещение центра тяжести сечения; для горизонтальной балки «у» называется прогибом (распо-лагается в сил. пл); угловое ( θ (х) ) – п оворот поперечного сечения; Из предыдущей лекции: 1 / ρ = М из / Е I z 1 / ρ = ± у″ / [1+( у′) 2 ] 3 /2 ± у″ / [1+( у′) 2 ] 3 /2 н.с. << 1 θ у″= ± М из / Е I z - приближенное дифферен-циальное уравнение упру-гой линии балки упругая линия = М из / Е I z θ = у ′ Из математики: А EI z – жесткость поперечного сечения при изгибе, [ сила · длина 18 ] касательная z – гл.ц.ось, ┴ сил.л.
Слайд 19: К экзамену
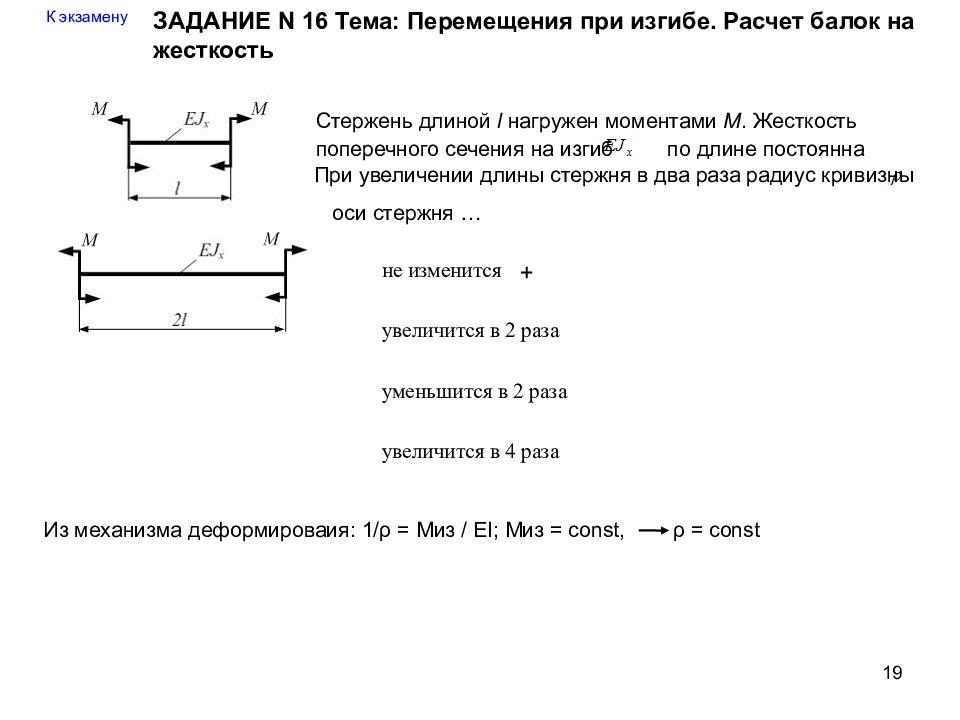
19 К экзамену Стержень длиной l нагружен моментами М. Жесткость поперечного сечения на изгиб по длине постоянна При увеличении длины стержня в два раза радиус кривизны оси стержня … не изменится увеличится в 2 раза уменьшится в 2 раза увеличится в 4 раза ЗАДАНИЕ N 16 Тема: Перемещения при изгибе. Расчет балок на жесткость + Из механизма деформироваия: 1/ ρ = Миз / Е I ; Миз = const, ρ = const
Слайд 20: Перемещения при изгибе
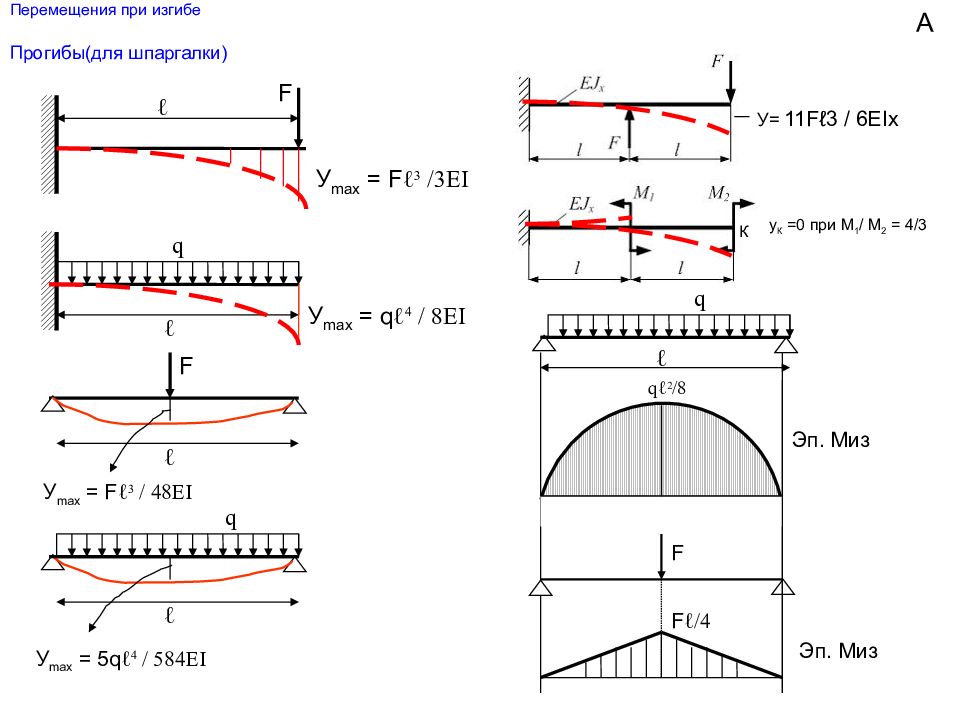
Прогибы(для шпаргалки) А F У max = F ℓ 3 /3EI ℓ ℓ q У max = q ℓ 4 / 8EI F ℓ У max = F ℓ 3 / 48EI ℓ q У max = 5q ℓ 4 / 584EI У = 11 Fℓ3 / 6EIx ℓ q Эп. Миз qℓ 2 /8 F F ℓ/4 Эп. Миз К у К =0 при М 1 / М 2 = 4/3
Слайд 21: Изгиб
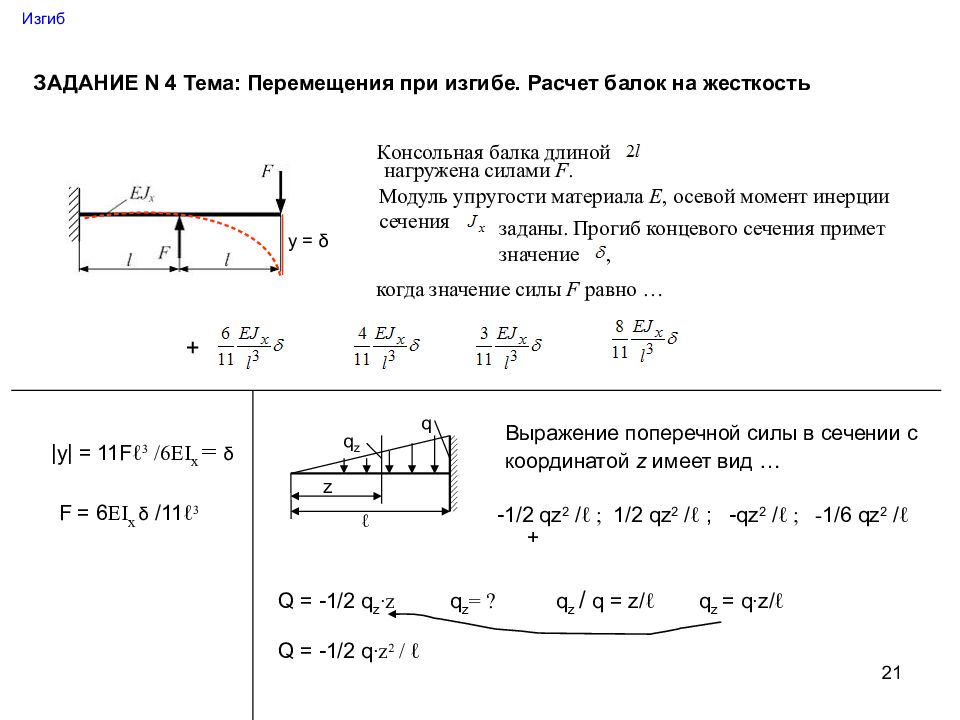
21 Изгиб ЗАДАНИЕ N 4 Тема: Перемещения при изгибе. Расчет балок на жесткость Консольная балка длиной нагружена силами F. Модуль упругости материала Е, осевой момент инерции сечения заданы. Прогиб концевого сечения примет значение, когда значение силы F равно … у = δ | у | = 11 F ℓ 3 /6EI x = δ F = 6 EI x δ / 1 1 ℓ 3 + q z ℓ Выражение поперечной силы в сечении с координатой z имеет вид … -1/2 qz 2 / ℓ ; 1/2 qz 2 / ℓ ; - qz 2 / ℓ ; - 1/6 qz 2 / ℓ Q = -1/2 q z ∙z q z q z = ? q z / q = z / ℓ q z = q ∙ z / ℓ Q = -1/2 q ∙z 2 / ℓ +
Слайд 22: Изгиб
22 Изгиб задание Тема: Перемещения при изгибе. Расчет балок на жесткость увеличится в 3 раза Однопролетная балка длиной l в середине пролета нагружена силой F. Жесткость поперечного сечения на изгиб постоянна по длине. При увеличении длины пролета в два раза максимальный прогиб … увеличится в 8 раз не изменится увеличится в 4 раза у max = F ℓ 3 / 48EI у max = F(2 ℓ) 3 / 48EI у max = F( ℓ) 3 / 6EI +
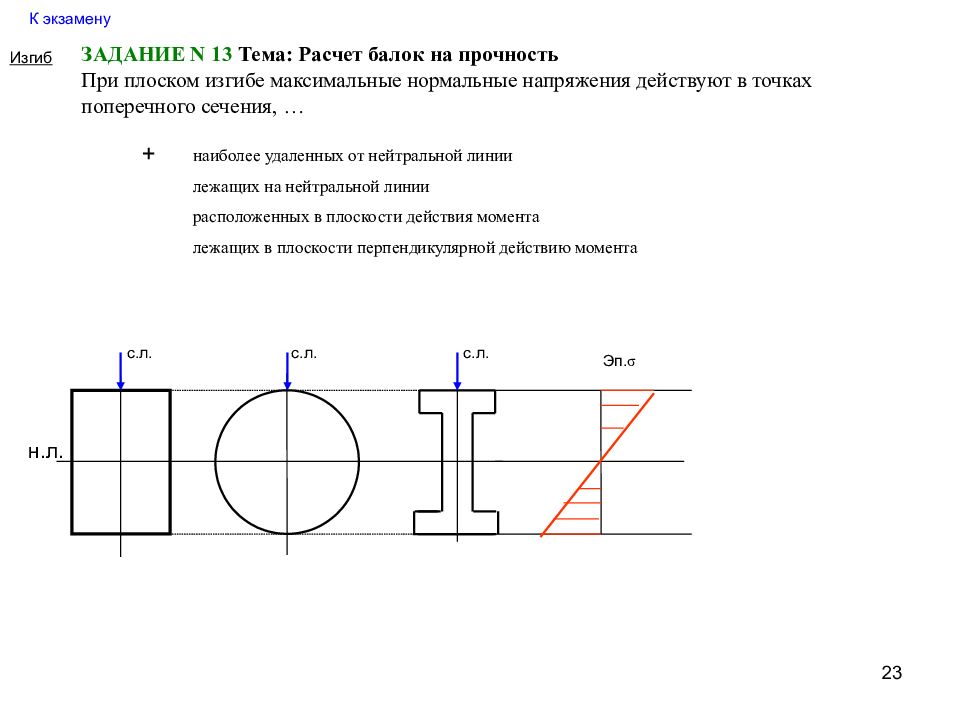
Слайд 23: К экзамену
23 К экзамену Изгиб ЗАДАНИЕ N 13 Тема: Расчет балок на прочность При плоском изгибе максимальные нормальные напряжения действуют в точках поперечного сечения, … наиболее удаленных от нейтральной линии лежащих на нейтральной линии расположенных в плоскости действия момента лежащих в плоскости перпендикулярной действию момента + н.л. с.л. с.л. с.л. Эп. σ
Слайд 24: К экзамену
24 К экзамену Изгиб ЗАДАНИЕ N 14 Тема: Поперечная сила, изгибающий момент и их эпюры На рисунке показана эпюра поперечных сил. Неверным является утверждение, что … на эпюре изгибающих моментов в сечении В излом; в сечении С изгибающий момент имеет экстремальное значение; распределенная нагрузка на участках AB и BD имеет противоположное направление; на участке балки AD действует равномерно распределенная нагрузка. +
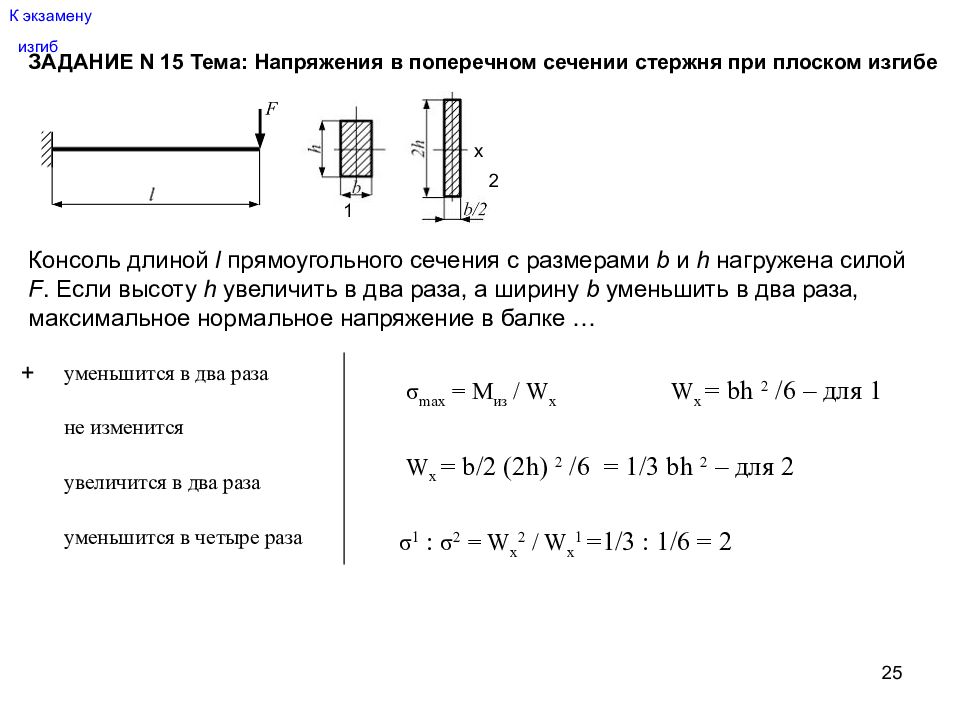
Слайд 25: изгиб
25 изгиб Консоль длиной l прямоугольного сечения с размерами b и h нагружена силой F. Если высоту h увеличить в два раза, а ширину b уменьшить в два раза, максимальное нормальное напряжение в балке … уменьшится в два раза не изменится увеличится в два раза уменьшится в четыре раза + ЗАДАНИЕ N 15 Тема: Напряжения в поперечном сечении стержня при плоском изгибе К экзамену σ max = M из / W x x W x = bh 2 /6 – для 1 1 2 W x = b /2 (2 h ) 2 /6 = 1/3 bh 2 – для 2 σ 1 : σ 2 = W x 2 / W x 1 =1/3 : 1/6 = 2
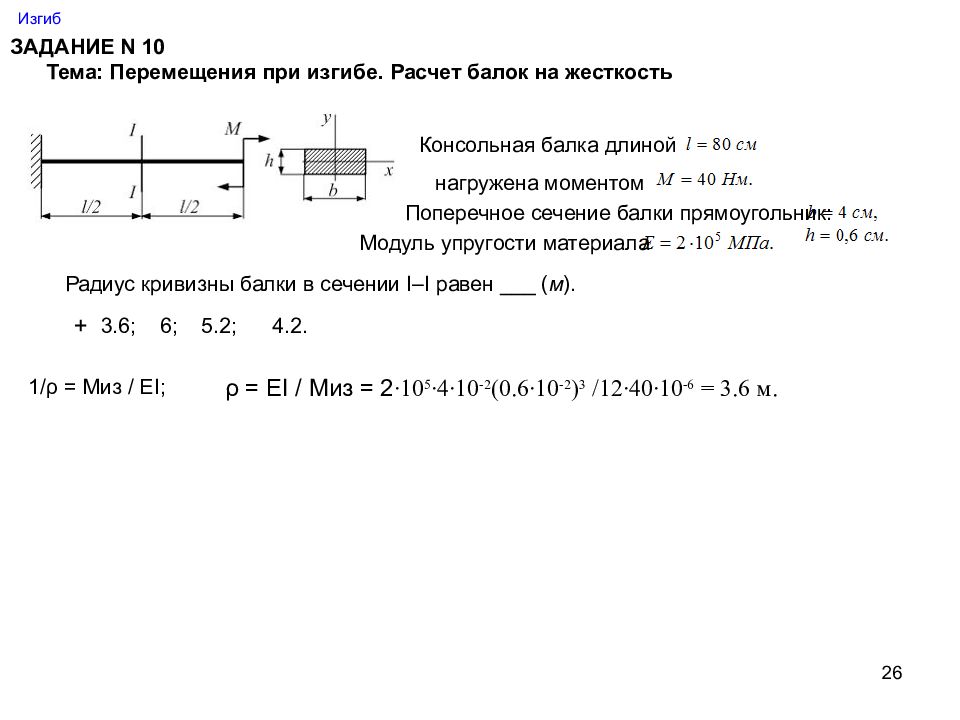
Слайд 26: Изгиб
26 Изгиб ЗАДАНИЕ N 10 Тема: Перемещения при изгибе. Расчет балок на жесткость Консольная балка длиной нагружена моментом Поперечное сечение балки прямоугольник: Модуль упругости материала Радиус кривизны балки в сечении I–I равен ___ ( м ). 3.6; 6; 5.2; 4.2. 1/ ρ = Миз / Е I ; ρ = Е I / Миз = 2 ∙10 5 ∙4∙10 -2 (0.6∙10 -2 ) 3 /12∙40∙10 -6 = 3.6 м. +
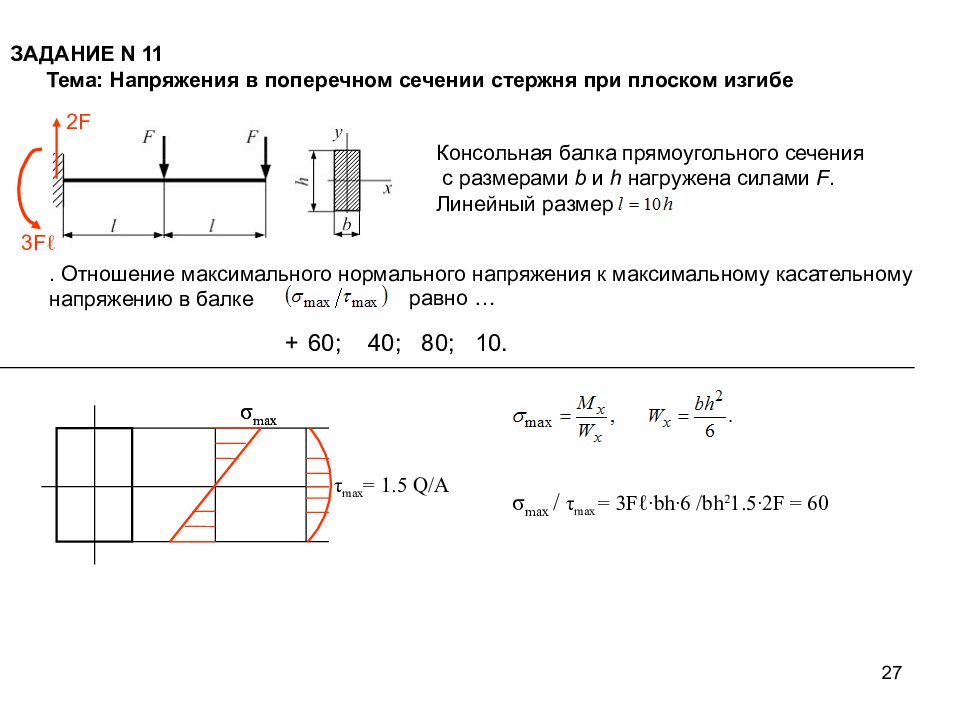
Слайд 27
27 ЗАДАНИЕ N 11 Тема: Напряжения в поперечном сечении стержня при плоском изгибе Консольная балка прямоугольного сечения с размерами b и h нагружена силами F. Линейный размер . Отношение максимального нормального напряжения к максимальному касательному напряжению в балке равно … 60; 40; 80; 10. 2F 3F ℓ τ max = 1.5 Q/A σ max σ max σ max / τ max = 3Fℓ∙bh∙6 /bh 2 1.5∙2F = 60 +
Слайд 28: Изгиб
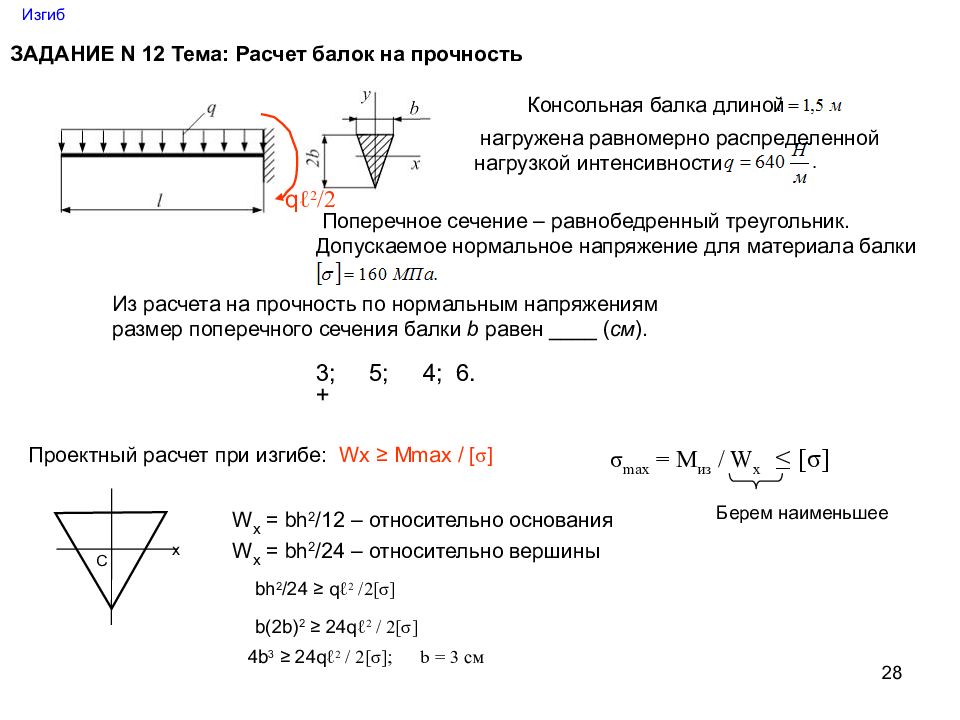
28 Изгиб ЗАДАНИЕ N 12 Тема: Расчет балок на прочность Консольная балка длиной нагружена равномерно распределенной нагрузкой интенсивности Поперечное сечение – равнобедренный треугольник. Допускаемое нормальное напряжение для материала балки Из расчета на прочность по нормальным напряжениям размер поперечного сечения балки b равен ____ ( см ). q ℓ 2 /2 Проектный расчет при изгибе: W х ≥ М max / [ σ ] 3; 5; 4; 6. σ max = M из / W x ≤ [ σ ] Берем наименьшее С х W x = bh 2 /12 – относительно основания W x = bh 2 / 24 – относительно вершины bh 2 /24 ≥ q ℓ 2 /2[ σ ] b(2b) 2 ≥ 24q ℓ 2 / 2[ σ ] 4b 3 ≥ 24q ℓ 2 / 2[ σ ] ; b = 3 см +
Слайд 29: Изгиб
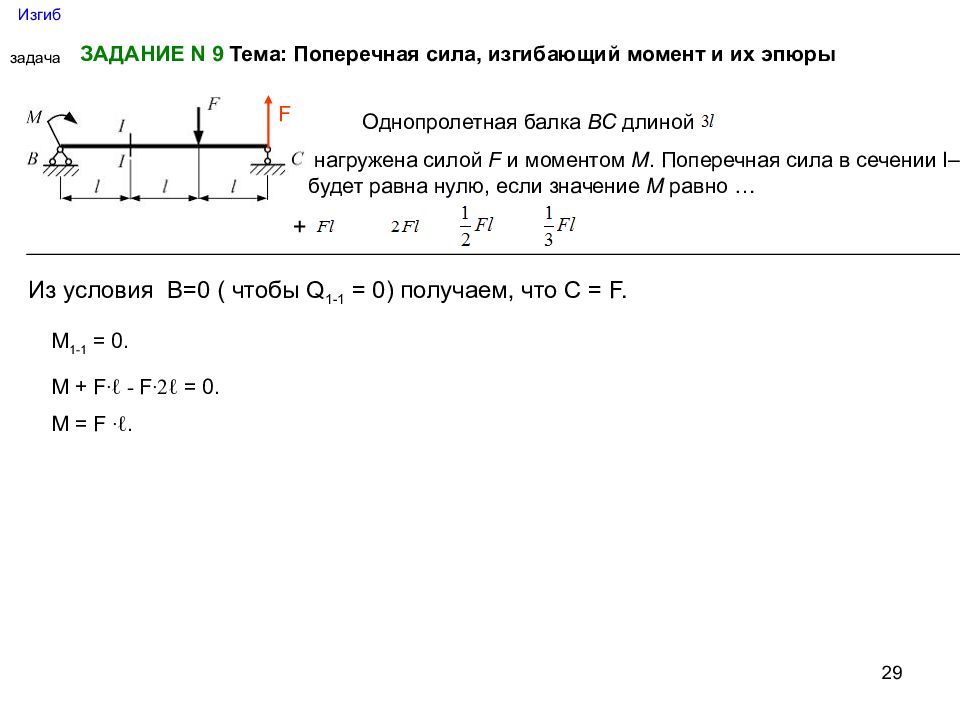
29 Изгиб задача ЗАДАНИЕ N 9 Тема: Поперечная сила, изгибающий момент и их эпюры Однопролетная балка ВС длиной нагружена силой F и моментом М. Поперечная сила в сечении I–I будет равна нулю, если значение М равно … F Из условия В=0 ( чтобы Q 1-1 = 0) получаем, что С = F. М 1-1 = 0. М + F ∙ℓ - F ∙2ℓ = 0. М = F ∙ℓ. +
Слайд 30: Изгиб
30 Изгиб ЗАДАНИЕ N 1 Тема: Поперечная сила, изгибающий момент и их эпюры На схеме показана отсеченная часть балки и нагрузка, действующая на нее. Неверным является утверждение, что изгибающий момент … на участке ВС постоянный на участке АВ меняется по закону квадратной параболы в сечении А имеет экстремальное значение на участке СD переменный +
Слайд 31: Изгиб
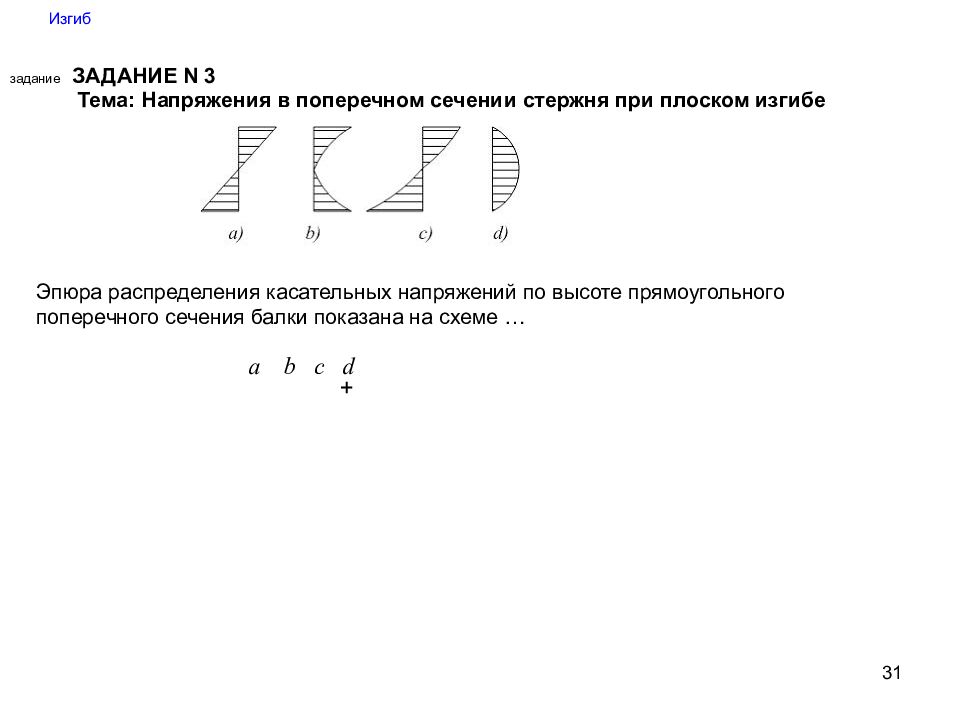
31 Изгиб задание ЗАДАНИЕ N 3 Тема: Напряжения в поперечном сечении стержня при плоском изгибе Эпюра распределения касательных напряжений по высоте прямоугольного поперечного сечения балки показана на схеме … a b c d +
Слайд 32: Изгиб
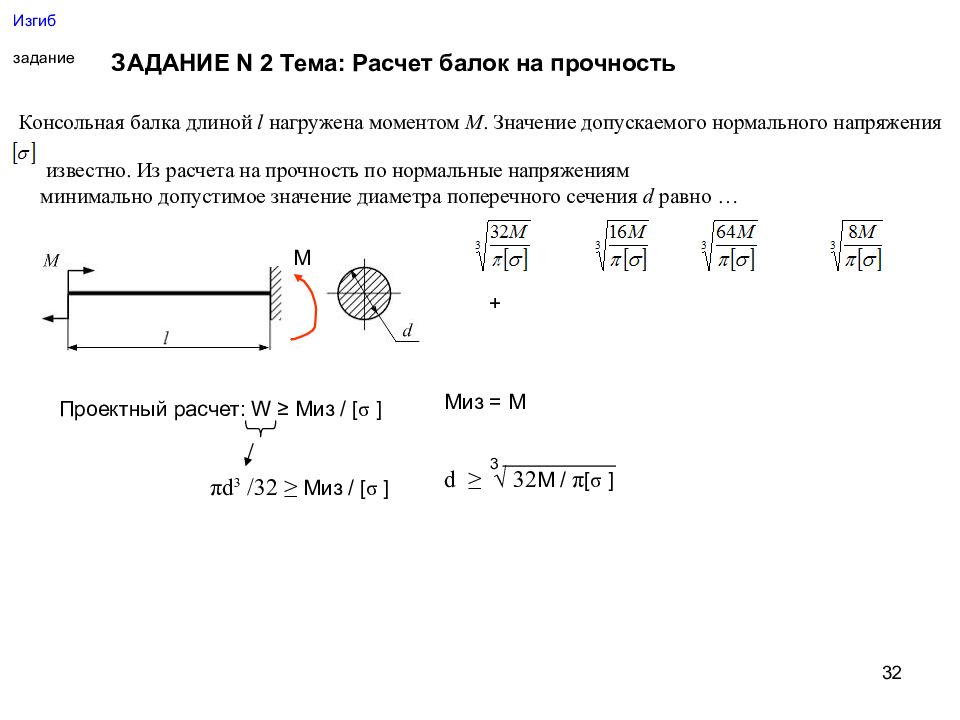
32 Изгиб задание ЗАДАНИЕ N 2 Тема: Расчет балок на прочность Консольная балка длиной l нагружена моментом М. Значение допускаемого нормального напряжения известно. Из расчета на прочность по нормальные напряжениям минимально допустимое значение диаметра поперечного сечения d равно … Проектный расчет: W ≥ Миз / [ σ ] М π d 3 /32 ≥ Миз / [ σ ] d ≥ √ 32 М / π [ σ ] 3 Миз = М +
Слайд 33: Изгиб
33 Изгиб задание ЗАДАНИЕ N 3 … Тема: Поперечная сила, изгибающий момент и их эпюры Однопролетная консольная балка нагружена силой F. Размер l задан. Значения изгибающего момента и поперечной силы по абсолютной величине в сечении I–I равны … + С А F/2 •с F ℓ A ∙ 2ℓ A =F/2
Слайд 34: Изгиб
34 Изгиб Задача ЗАДАНИЕ N 4 Тема: Напряжения в поперечном сечении стержня при плоском изгибе Для определения нормальных напряжений в точках поперечного сечения балки при плоском изгибе используется формула … + ЗАДАНИЕ N 12 Тема: Модели прочностной надежности Стержень изготовлен из пластичного материала c одинаковыми пределами текучести на растяжение и сжатие. Значения М и осевого момента сопротивления W заданы. Фактический коэффициент запаса прочности равен… n = σ т / σ max.. σ max. = М / W +
Слайд 35: Изгиб
35 Изгиб задача ЗАДАНИЕ N 2 : Тема: Напряжения в поперечном сечении стержня при плоском изгибе нормальные и касательные При плоском поперечном изгибе в точках поперечного сечения в общем случае возникают ______________ напряжения. главные касательные нормальные + Балка имеет прямоугольное поперечное сечение с размерами 2b и 3b. При повороте поперечного сечения из положения А в положение В грузоподъемность балки, из расчета по нормальным напряжениям, … Тема: Расчет балок на прочность уменьшится в 1,5 раза Не изменится уменьшится в 2 раза увеличится в 1,5 раза + W(A) / W(B) = 2b ∙(3b) 2 / 3b∙(2b) 2 = 1.5
Слайд 36: Изгиб
36 Изгиб задача на участке ВС меняется по линейному закону На рисунке показана отсеченная часть балки и нагрузка, действующая на нее. Неверным является утверждение, что поперечная сила … Тема: Поперечная сила, изгибающий момент и их эпюры на участке CD равна нулю на участке АВ постоянна в сечении В изменяется скачком + Тема: Расчет балок на прочность Однопролетная балка длиной l нагружена моментом М. К балке дополнительно прикладывается момент С изменением схемы нагружения прочность балки … Учесть только нормальные напряжения. не изменится уменьшится в два раза уменьшится в четыре раза увеличится в два раза + М М М Миз Миз Значение мах Миз не изменится Построить эп. Q + - Q F F
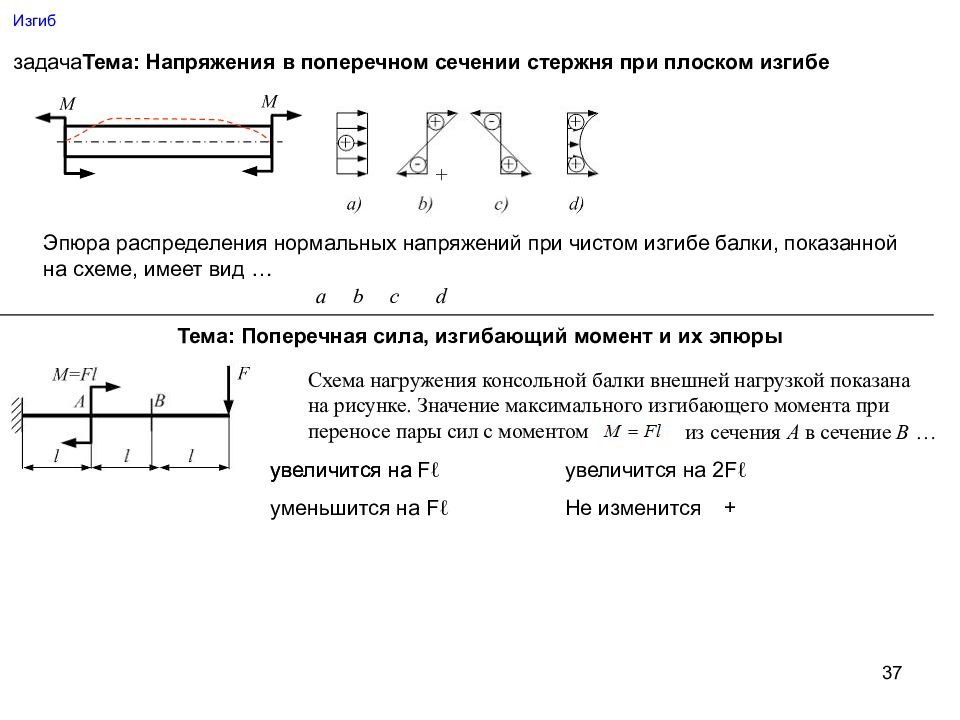
Слайд 37: Изгиб
37 Изгиб задача Тема: Напряжения в поперечном сечении стержня при плоском изгибе Эпюра распределения нормальных напряжений при чистом изгибе балки, показанной на схеме, имеет вид … a b c d + Тема: Поперечная сила, изгибающий момент и их эпюры Схема нагружения консольной балки внешней нагрузкой показана на рисунке. Значение максимального изгибающего момента при переносе пары сил с моментом из сечения А в сечение В … увеличится на увеличится на 2 F ℓ увеличится на F ℓ Не изменится уменьшится на F ℓ +
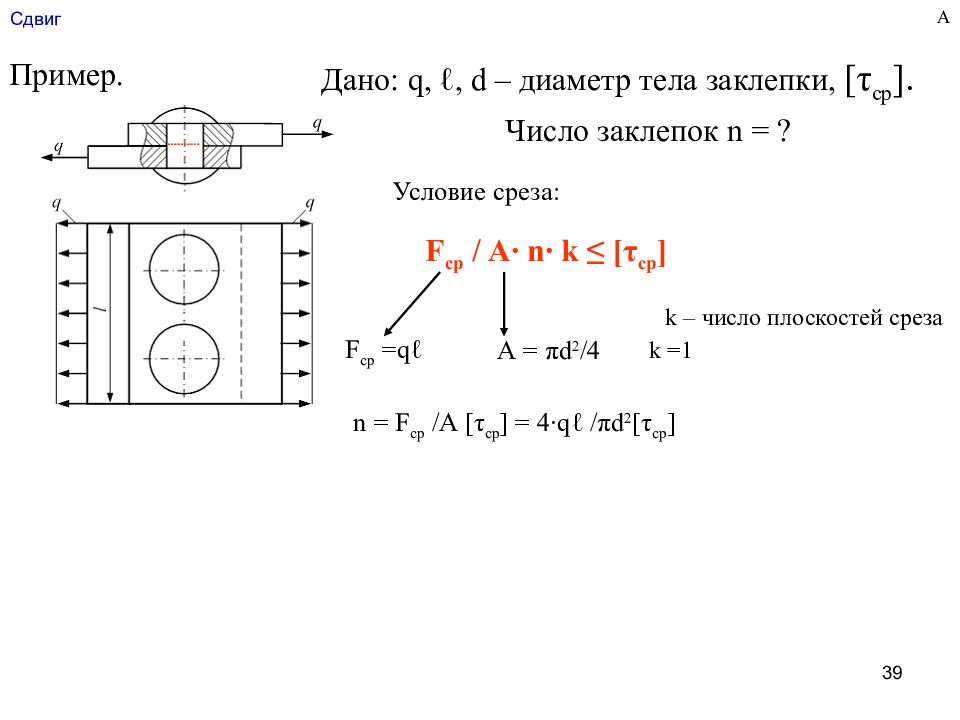
Слайд 39: Сдвиг
39 Сдвиг Дано: q, ℓ, d – диаметр тела заклепки, [ τ ср ]. Пример. Число заклепок n = ? Условие среза: F ср / А∙ n∙ k ≤ [ τ ср ] А = π d 2 /4 F ср = q ℓ n = F ср /А [ τ ср ] = 4 ∙ q ℓ / π d 2 [ τ ср ] k – число плоскостей среза k =1 А
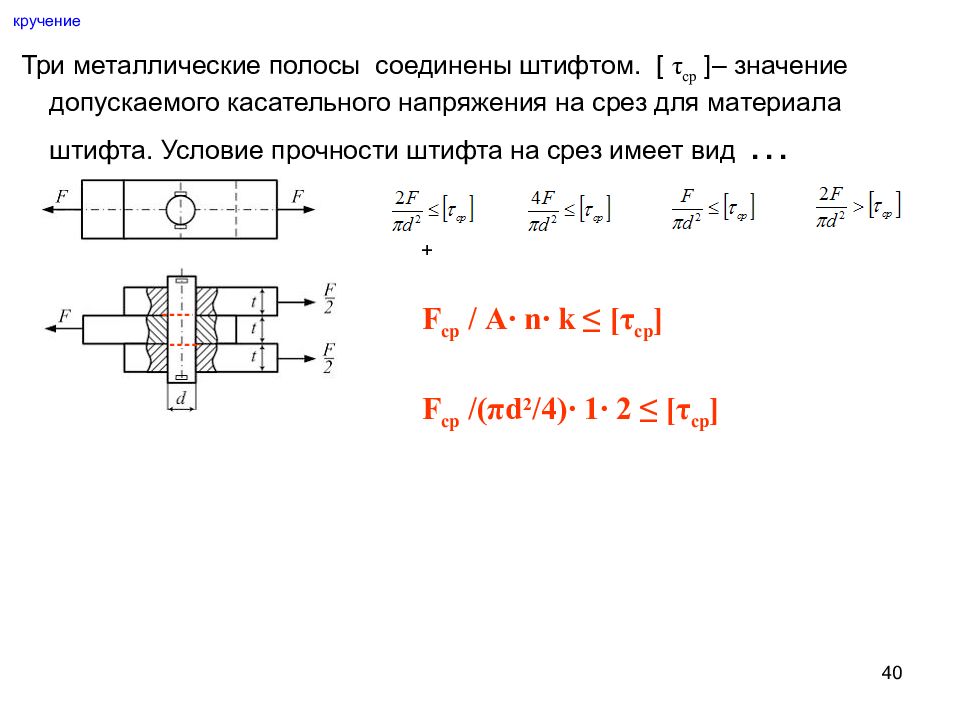
Слайд 40: кручение
40 кручение Три металлические полосы соединены штифтом. [ τ ср ] – значение допускаемого касательного напряжения на срез для материала штифта. Условие прочности штифта на срез имеет вид … + F ср / А∙ n∙ k ≤ [ τ ср ] F ср /( π d 2 /4) ∙ 1∙ 2 ≤ [ τ ср ]
Слайд 41: кручение
41 кручение допускаемое касательное Задача На рисунке показано клеевое соединение двух листов. Известно: Минимально допустимое значение l из расчета на срез клеевого слоя равно ___ см. - допускаемое напряжение на срез клеевого слоя. 1.5; 3; 0.75; 2 + А F ср / А ≤ [ τ c р ] F ср / b ∙ℓ ≤ [ τ c р ] ℓ ≥ F ср / b ∙ [ τ c р ] ℓ ≥ 4.5 кН ∙ / 2.5 см ∙ 1.2 кн/см 2 ℓ ≥ 1.5 см
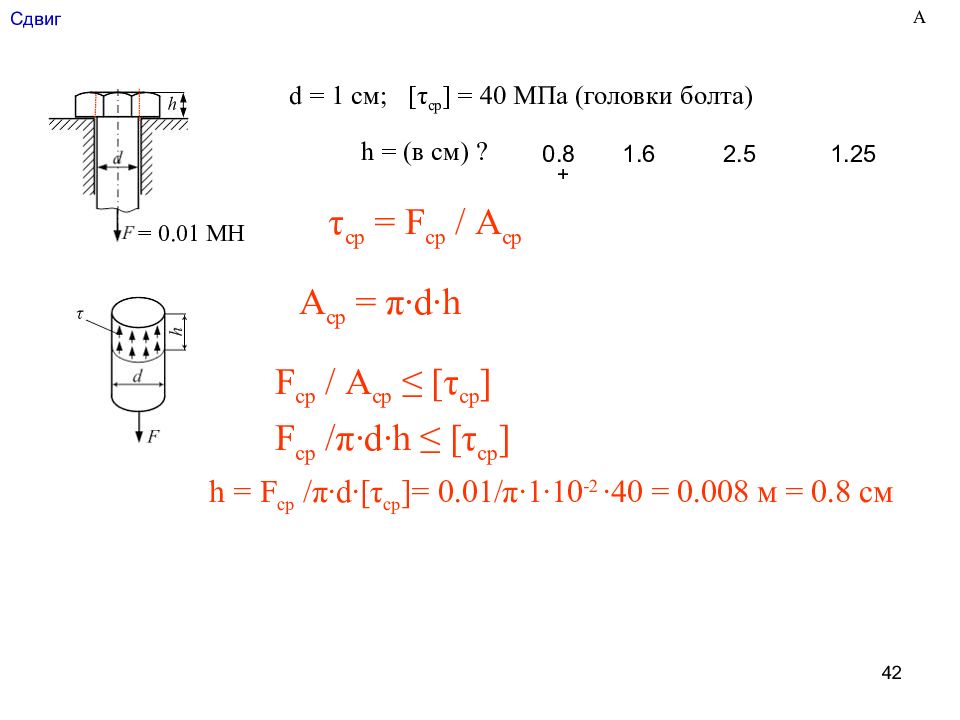
Слайд 42: C двиг
42 C двиг = 0.01 МН d = 1 см; [ τ ср ] = 40 МПа (головки болта) h = (в см) ? τ ср = F c р / А ср А ср = π∙ d∙h F c р / А ср ≤ [ τ ср ] F c р / π∙ d∙h ≤ [ τ ср ] h = F c р / π∙ d∙[ τ ср ]= 0.01/ π ∙ 1 ∙ 10 -2 ∙ 40 = 0.008 м = 0.8 см А 0.8 1.6 2.5 1.25 +
Слайд 43: кручение
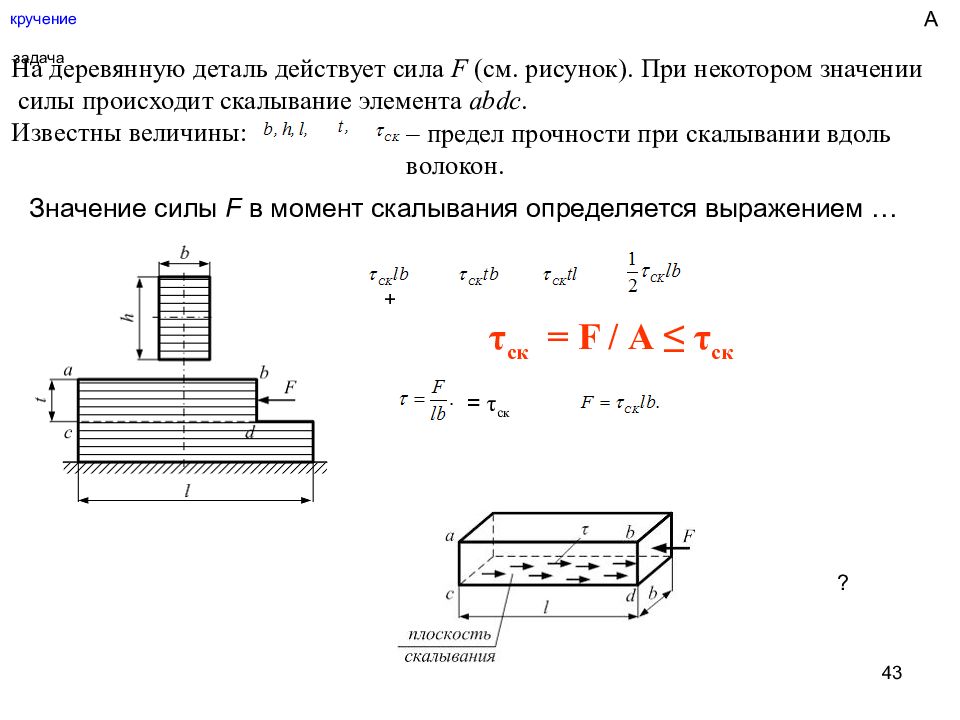
43 кручение задача На деревянную деталь действует сила F (см. рисунок). При некотором значении силы происходит скалывание элемента abdс. Известны величины: – предел прочности при скалывании вдоль волокон. Значение силы F в момент скалывания определяется выражением … + = τ ск ? τ ск = F / А ≤ τ ск А
Слайд 44: кручение
44 кручение Задача На рисунке показано клеевое соединение втулки с валом, передающее крутящий момент. Задано: М, d, l, – допускаемое касательное напряжение на срез клеевого слоя. Условие прочности на срез клеевого слоя имеет вид … + ∑ М Х =0 х τ А
Слайд 45: кручение
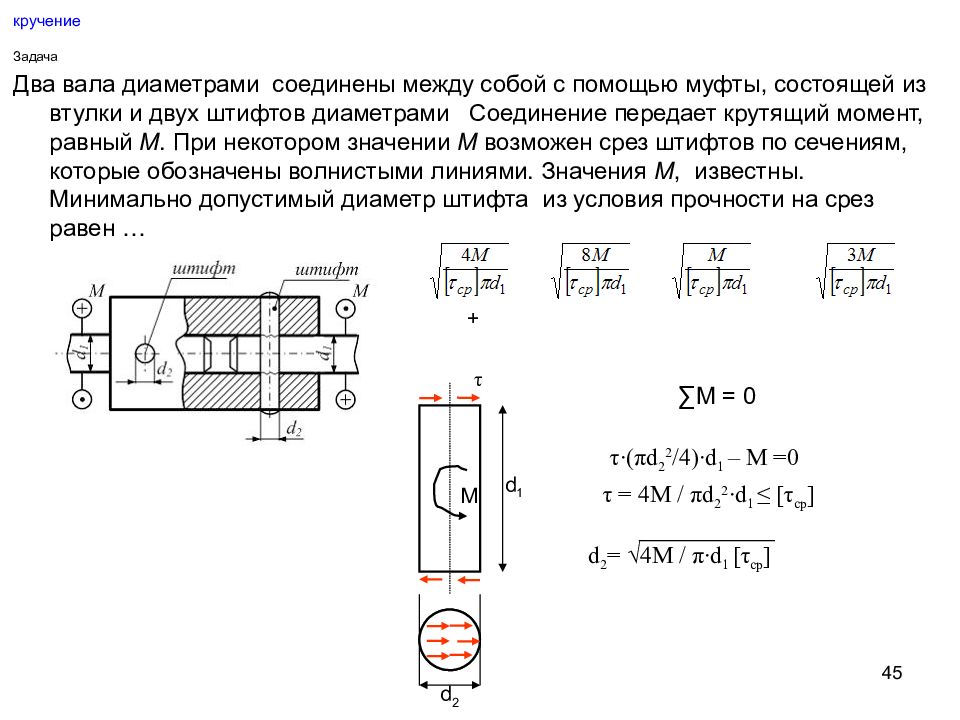
45 кручение Задача Два вала диаметрами соединены между собой с помощью муфты, состоящей из втулки и двух штифтов диаметрами Соединение передает крутящий момент, равный М. При некотором значении М возможен срез штифтов по сечениям, которые обозначены волнистыми линиями. Значения М, известны. Минимально допустимый диаметр штифта из условия прочности на срез равен … + М τ d 2 ∑М = 0 τ∙ ( π d 2 2 /4)∙d 1 – M =0 τ = 4M / π d 2 2 ∙d 1 ≤ [ τ ср ] d 2 = √4M / π ∙d 1 [ τ ср ] d 1
Слайд 46: Подготовка к экзамену - кручение
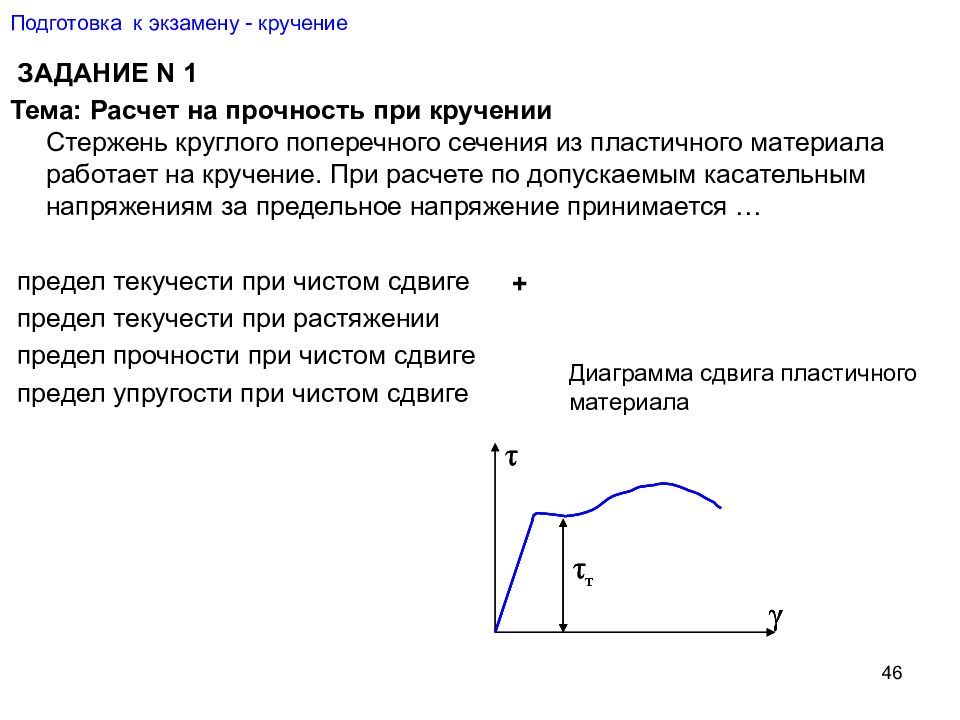
46 Подготовка к экзамену - кручение ЗАДАНИЕ N 1 Тема: Расчет на прочность при кручении Стержень круглого поперечного сечения из пластичного материала работает на кручение. При расчете по допускаемым касательным напряжениям за предельное напряжение принимается … предел текучести при чистом сдвиге предел текучести при растяжении предел прочности при чистом сдвиге предел упругости при чистом сдвиге τ γ τ т Диаграмма сдвига пластичного материала τ γ τ т τ γ τ т +
Слайд 47: Кручение
47 Кручение Стержень, работающий на кручение, нагружен равномерно распределенным по длине моментом с интенсивностью m и сосредоточенными моментами. Крутящий момент в среднем сечении стержня, по абсолютной величине, равен … 0 М = ? [M] = сила • длину [ m ] = ( сила • длину ) / длину ∑ М х = 0. 2М - m ∙2ℓ = 0. М = m ∙ ℓ = m ∙ ℓ = m ∙ ℓ 1 1 ℓ M кр 1 = М - m ∙ ℓ = 0 + х А
Слайд 48: кручение
48 кручение Задача На рисунке показаны два стержня из одного материала, работающие на кручение. Поперечное сечения стержня I – круг. Стержень II пустотелый с поперечным сечением в форме кольца. Отношение жесткости поперечного сечения стержня I к жесткости поперечного сечения стержня II равно … Жесткость поперечного сечения при кручении - EI P Для круга: EI P = Е ∙( π D 4 /64) Для кольца: EI P = Е ∙ π D 4 (1- α 4 ) /64) α = 0.8 D/D =0.8 Отношение: 1/(1-0.8 4 ) = 1.69 1.67; 2.42; 2.78; 0.6 +?
Слайд 49: кручение
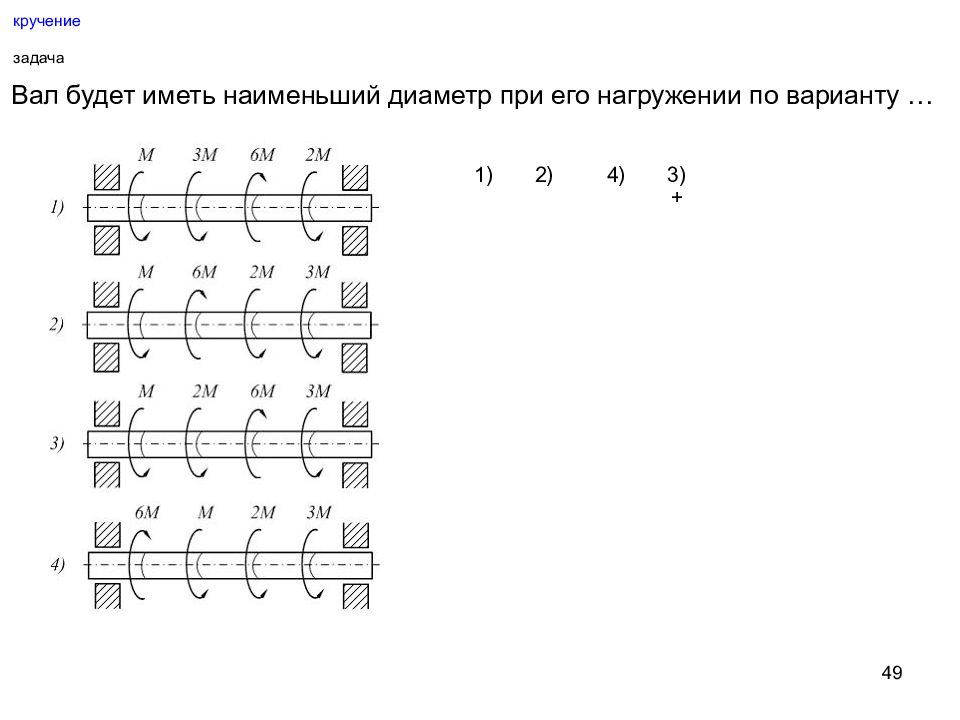
49 кручение задача Вал будет иметь наименьший диаметр при его нагружении по варианту … 1) 2) 4) 3) +
Слайд 50: кручение
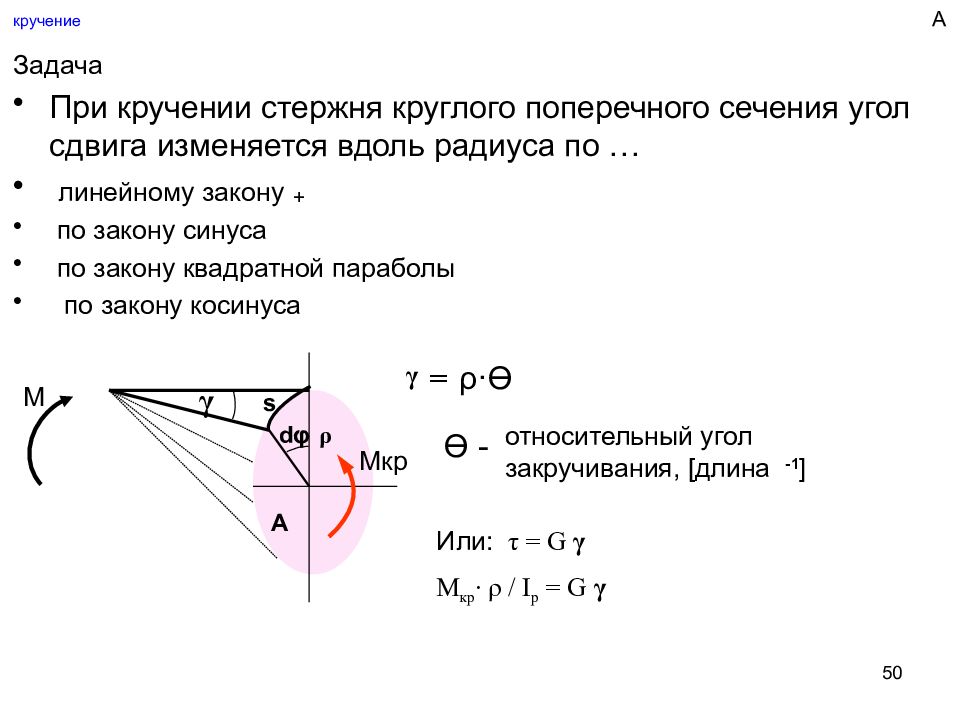
50 кручение Задача При кручении стержня круглого поперечного сечения угол сдвига изменяется вдоль радиуса по … линейному закону по закону синуса по закону квадратной параболы по закону косинуса d φ s ρ γ = Ө - относительный угол закручивания, [ длина -1 ] ρ · Ө A М Мкр Или: τ = G γ М кр ∙ ρ / I p = G γ γ А +
Слайд 51: кручение
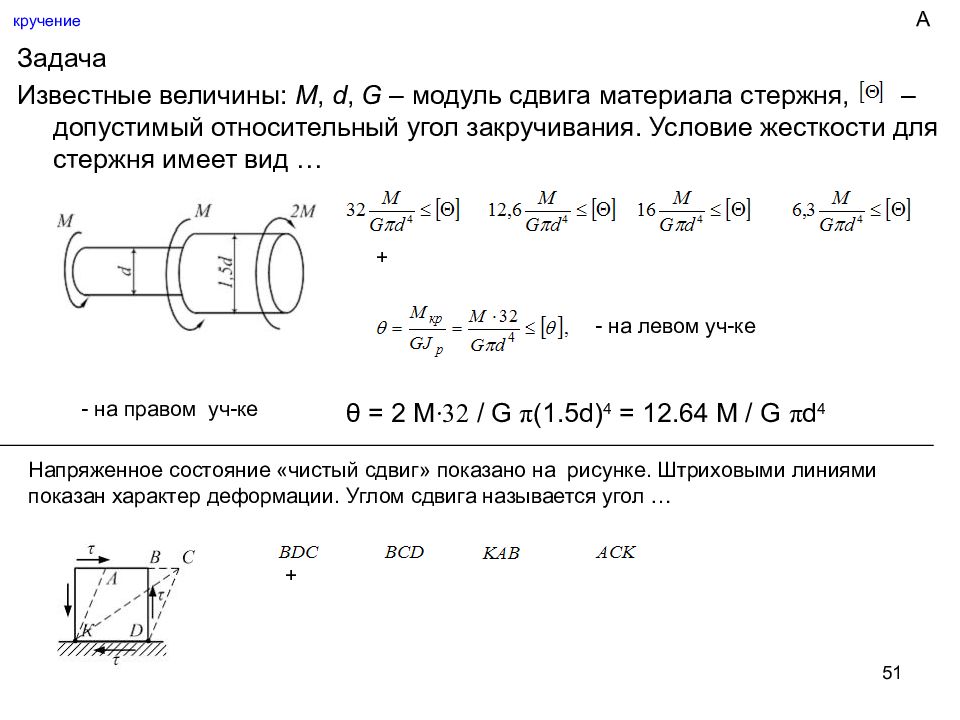
51 кручение Задача Известные величины: M, d, G – модуль сдвига материала стержня, – допустимый относительный угол закручивания. Условие жесткости для стержня имеет вид … + - на левом уч-ке - на правом уч-ке θ = 2 М ∙ 32 / G π (1.5 d) 4 = 12.64 М / G π d 4 А Напряженное состояние «чистый сдвиг» показано на рисунке. Штриховыми линиями показан характер деформации. Углом сдвига называется угол … +
Слайд 52: кручение
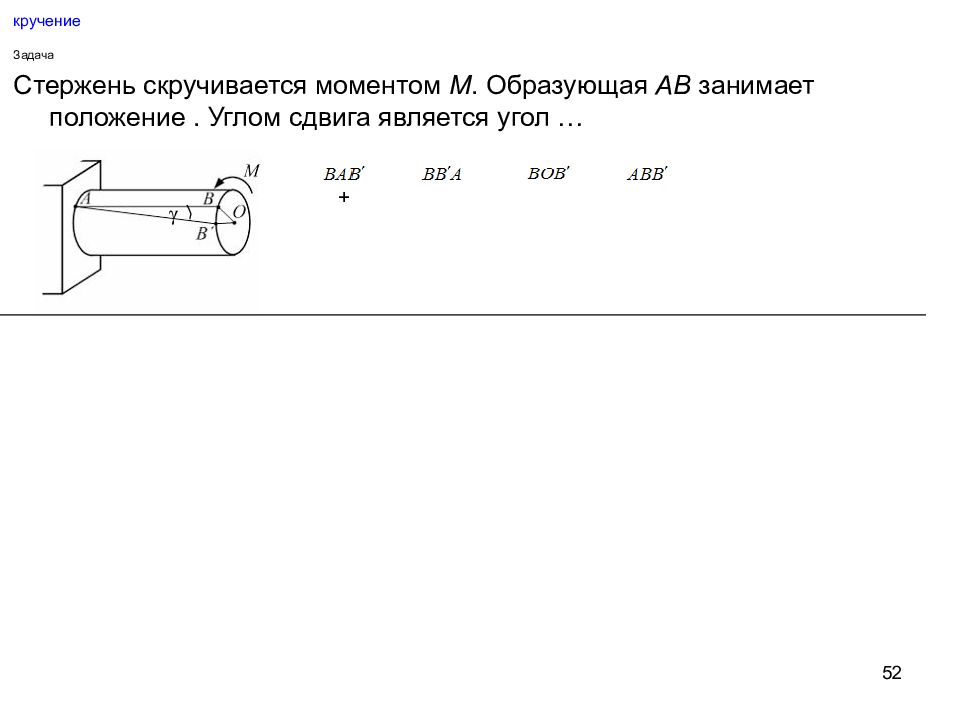
52 кручение Задача Стержень скручивается моментом М. Образующая АВ занимает положение. Углом сдвига является угол … + γ
Слайд 53: кручение
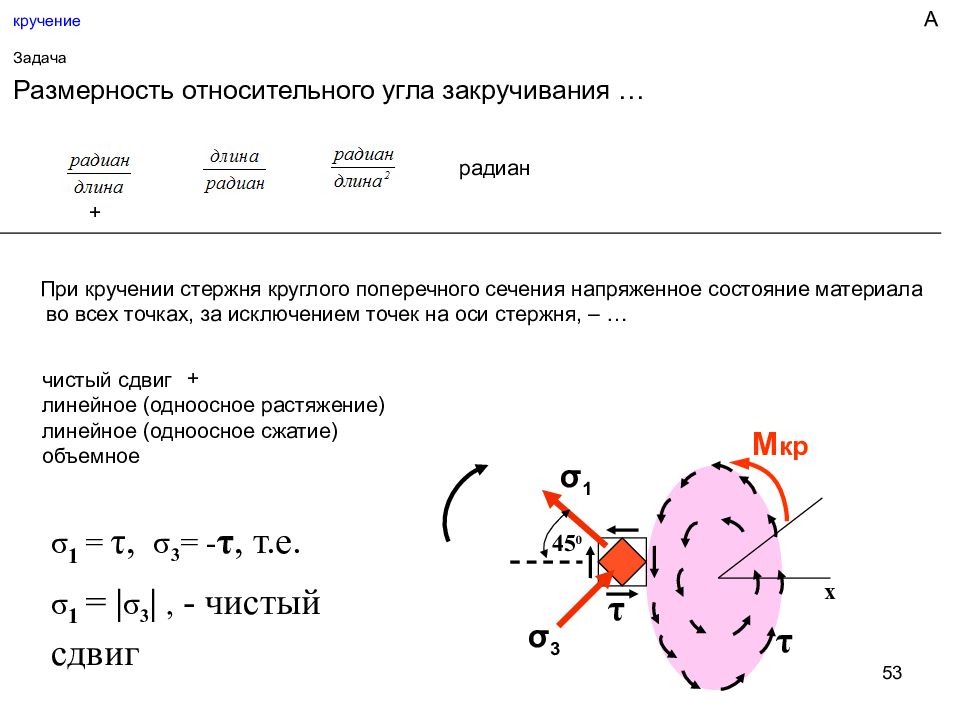
53 кручение Задача Размерность относительного угла закручивания … радиан + чистый сдвиг линейное (одноосное растяжение) линейное (одноосное сжатие) объемное При кручении стержня круглого поперечного сечения напряженное состояние материала во всех точках, за исключением точек на оси стержня, – … М кр τ τ σ 1 σ 3 45 0 х σ 1 = τ, σ 3 = - τ, т.е. σ 1 = | σ 3 |, - чистый сдвиг + А
Слайд 54: кручение
54 кручение Задача Стержень скручивается двумя моментами (см. рисунок). Из расчетов на прочность и жесткость максимально допустимая величина момента М равна ____ МН ∙м 0.0013; 0.0098; 0.0056; 0.0008. + ? А
Слайд 55: кручение
55 кручение Задача На рисунке показан стержень, работающий на кручение. Максимальные касательные напряжения в поперечном сечении стержня равны … + 1 участок 2участок 3 участок 1 участок τ max = 10M / π (2d) 3 /16 = 20M / π d 3 2участок τ max = 4M / π (3d) 3 /16 = 64M / 27 π d 3 = 2.37M / π d 3 3 участок τ max = M / π d 3 /16 = 16M / π d 3 Стержень круглого поперечного сечения из пластичного материала работает на кручение. В расчетах по допускаемым напряжениям условие прочности имеет вид … + А
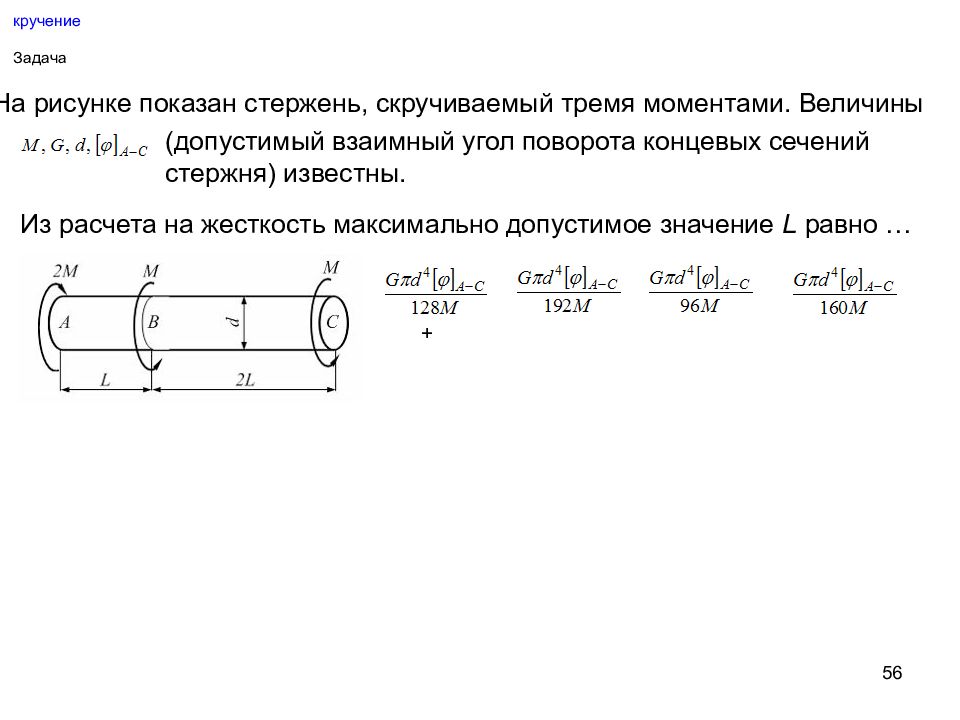
Слайд 56: кручение
56 кручение Задача На рисунке показан стержень, скручиваемый тремя моментами. Величины (допустимый взаимный угол поворота концевых сечений стержня) известны. Из расчета на жесткость максимально допустимое значение L равно … +
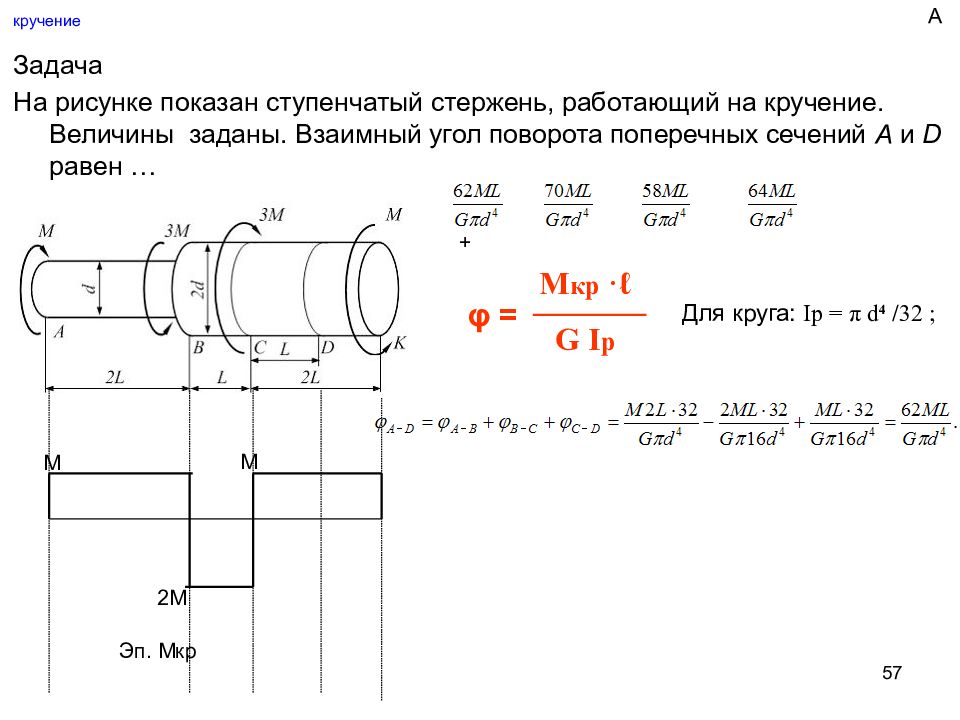
Слайд 57: кручение
57 кручение Задача На рисунке показан ступенчатый стержень, работающий на кручение. Величины заданы. Взаимный угол поворота поперечных сечений A и D равен … + φ = М кр ·ℓ G I p 2М М М Для круга: Ip = π d 4 / 32 ; Эп. Мкр А
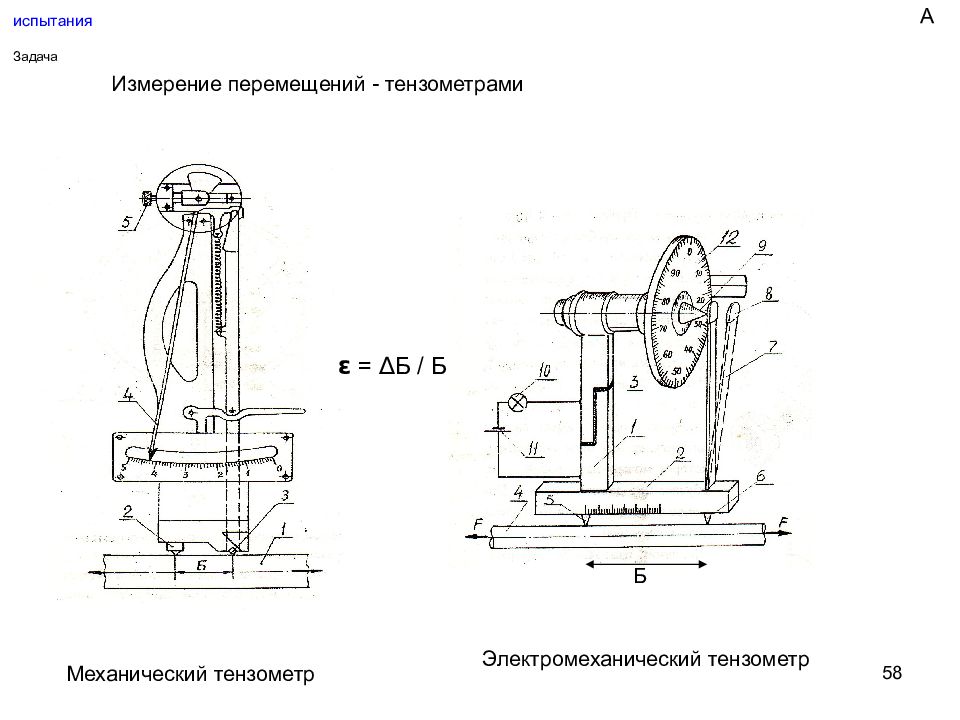
Слайд 58: испытания
58 испытания Задача Измерение перемещений - тензометрами Механический тензометр Электромеханический тензометр ε = ∆ Б / Б Б А
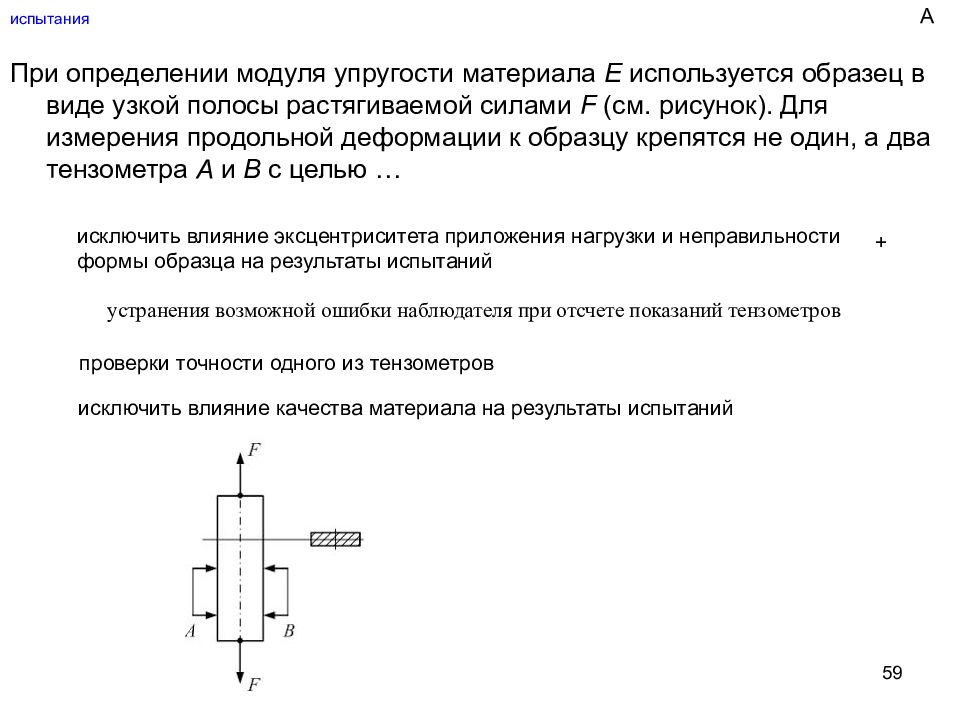
Слайд 59: испытания
59 испытания При определении модуля упругости материала Е используется образец в виде узкой полосы растягиваемой силами F (см. рисунок). Для измерения продольной деформации к образцу крепятся не один, а два тензометра А и В с целью … исключить влияние эксцентриситета приложения нагрузки и неправильности формы образца на результаты испытаний устранения возможной ошибки наблюдателя при отсчете показаний тензометров проверки точности одного из тензометров исключить влияние качества материала на результаты испытаний + А
Слайд 60: испытания
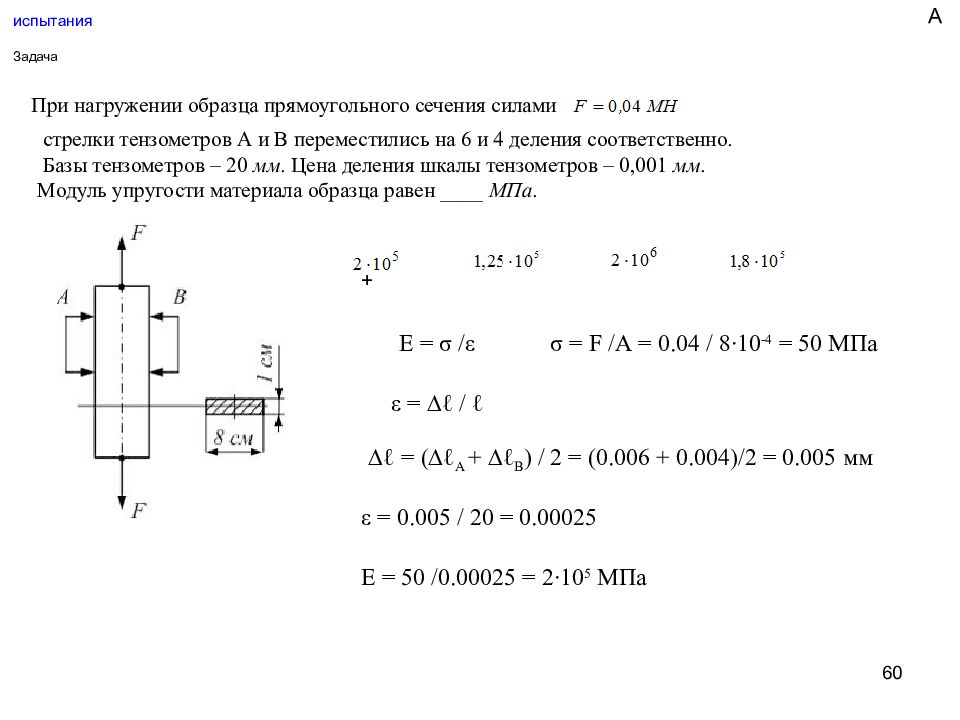
60 испытания Задача При нагружении образца прямоугольного сечения силами стрелки тензометров А и В переместились на 6 и 4 деления соответственно. Базы тензометров – 20 мм. Цена деления шкалы тензометров – 0,001 мм. Модуль упругости материала образца равен ____ МПа. ∆ℓ = (∆ℓ А + ∆ℓ В ) / 2 = (0.006 + 0.004)/2 = 0.005 мм Е = σ / ε σ = F /А = 0.04 / 8∙10 -4 = 50 МПа ε = ∆ℓ / ℓ ε = 0.005 / 20 = 0.00025 Е = 50 /0.00025 = 2∙10 5 МПа + А
Слайд 61: испытания
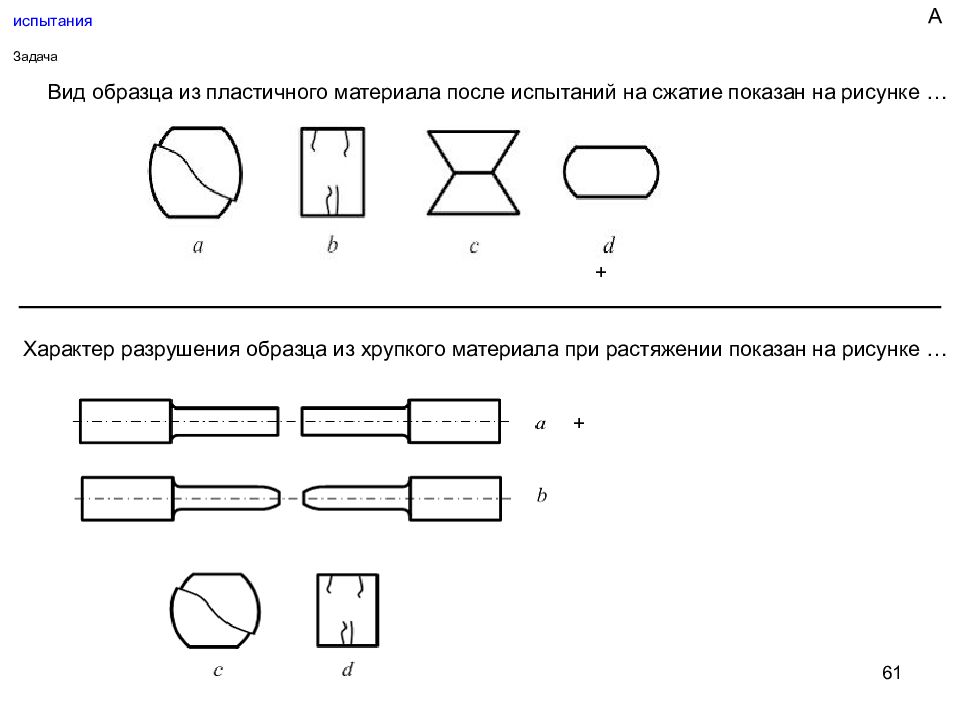
61 испытания Задача Вид образца из пластичного материала после испытаний на сжатие показан на рисунке … + Характер разрушения образца из хрупкого материала при растяжении показан на рисунке … + А
Слайд 62: испытания
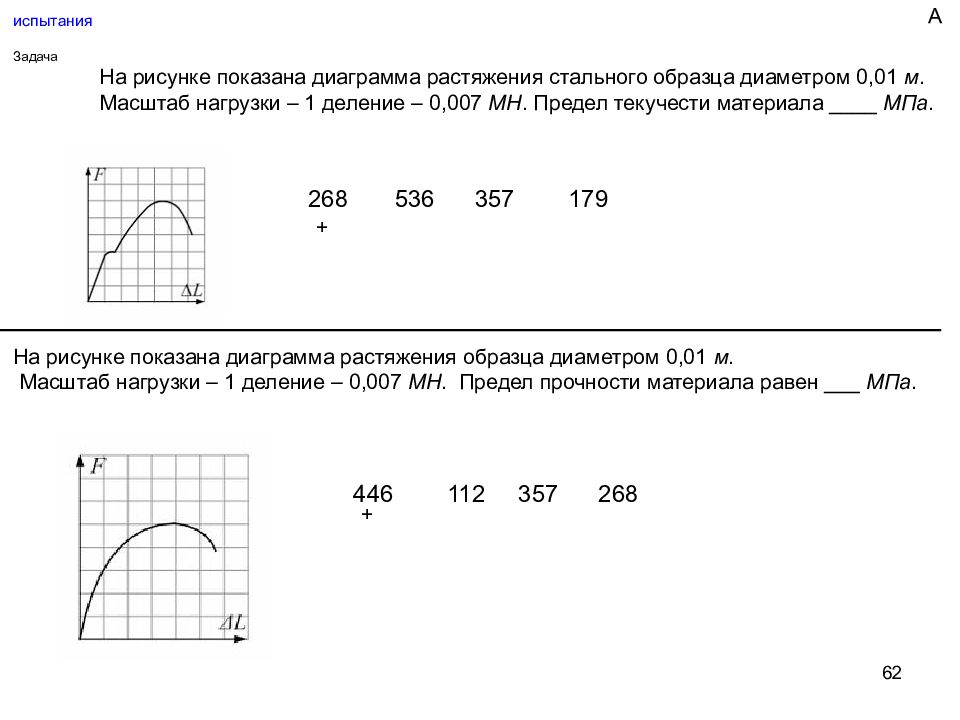
62 испытания Задача На рисунке показана диаграмма растяжения стального образца диаметром 0,01 м. Масштаб нагрузки – 1 деление – 0,007 МН. Предел текучести материала ____ МПа. 268 536 357 179 + На рисунке показана диаграмма растяжения образца диаметром 0,01 м. Масштаб нагрузки – 1 деление – 0,007 МН. Предел прочности материала равен ___ МПа. 446 112 357 268 + А
Слайд 63: испытания
63 испытания Задача Металлический образец, предназначенный для испытаний на сжатие, имеет форму короткого цилиндра, для того чтобы … он не изогнулся в процессе испытаний он не разрушился уменьшить влияние сил трения между поверхностями образца и поверхностями плит испытательной машины он разрушился + Вид образца после испытания показан на рисунке. Испытание проводилось по варианту … + А
Слайд 64: испытания
64 испытания Задача пропорциональности; упругости; прочности; текучести Коэффициент Пуассона для изотропного материала изменяется в пределах … + Наибольшее напряжение, до которого материал подчиняетс закону Гука, называется пределом … + Основными видами испытаний материалов являются испытания на … растяжение и сжатие изгиб и кручение усталость и ударную вязкость на ползучесть и длительную прочность + А
Слайд 65: испытания
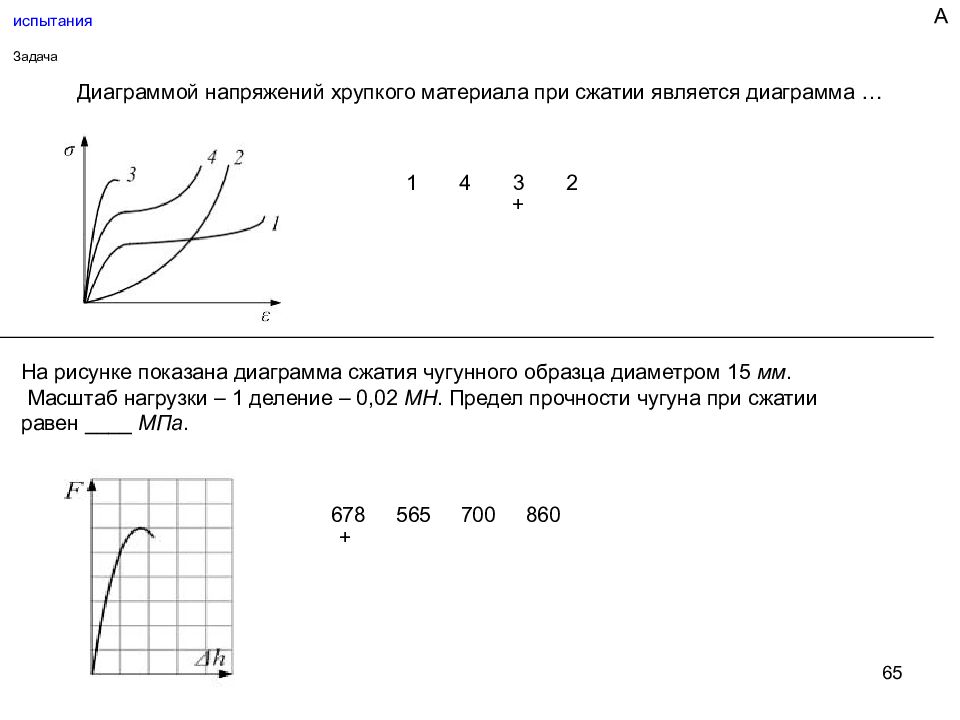
65 испытания Задача Диаграммой напряжений хрупкого материала при сжатии является диаграмма … 1 4 3 2 На рисунке показана диаграмма сжатия чугунного образца диаметром 15 мм. Масштаб нагрузки – 1 деление – 0,02 МН. Предел прочности чугуна при сжатии равен ____ МПа. + 678 565 700 860 + А
Последний слайд презентации: Подготовка к экзамену: испытания
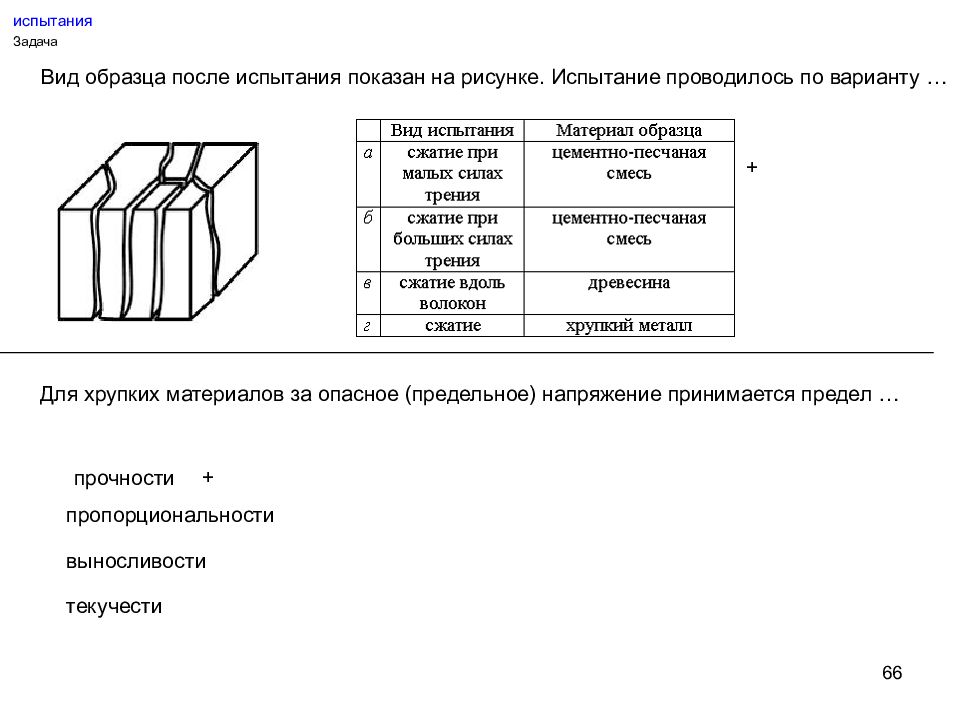
66 испытания Задача Вид образца после испытания показан на рисунке. Испытание проводилось по варианту … + Для хрупких материалов за опасное (предельное) напряжение принимается предел … прочности пропорциональности выносливости текучести +