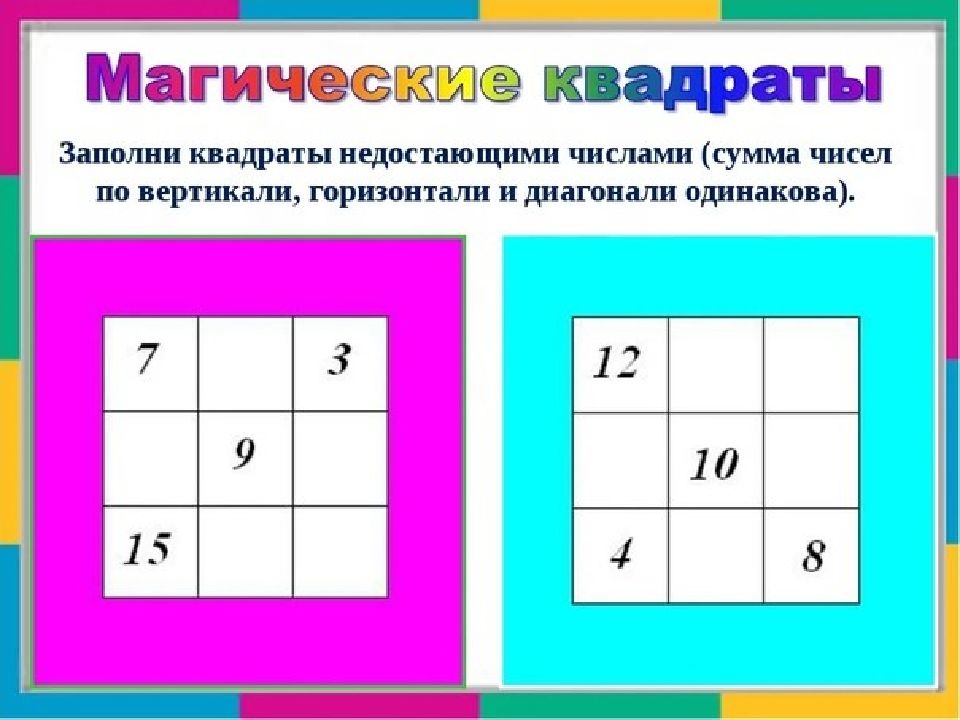
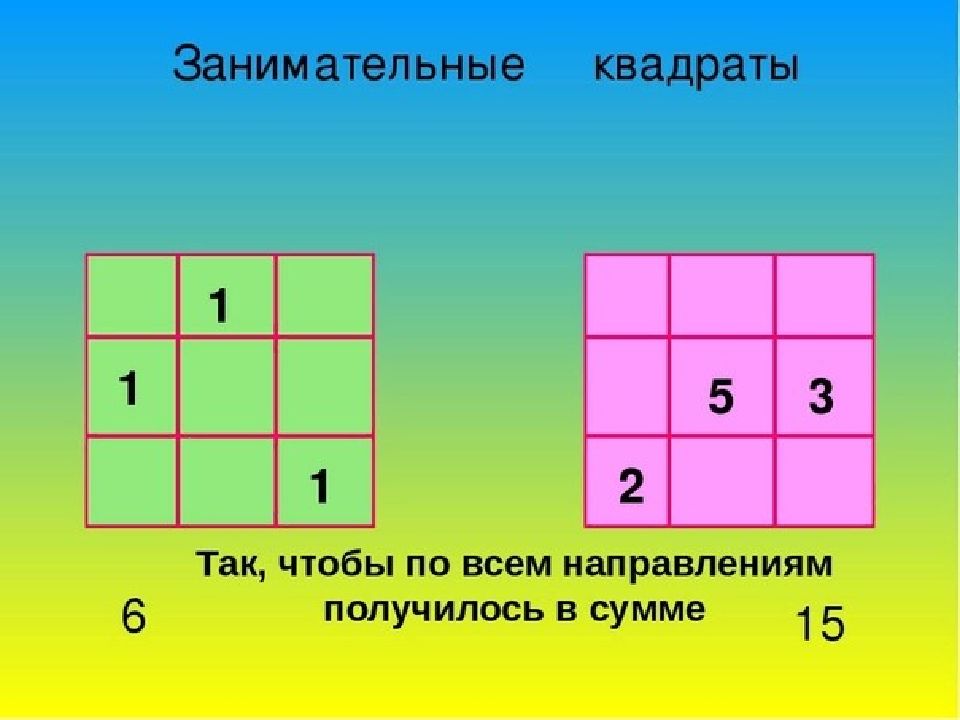
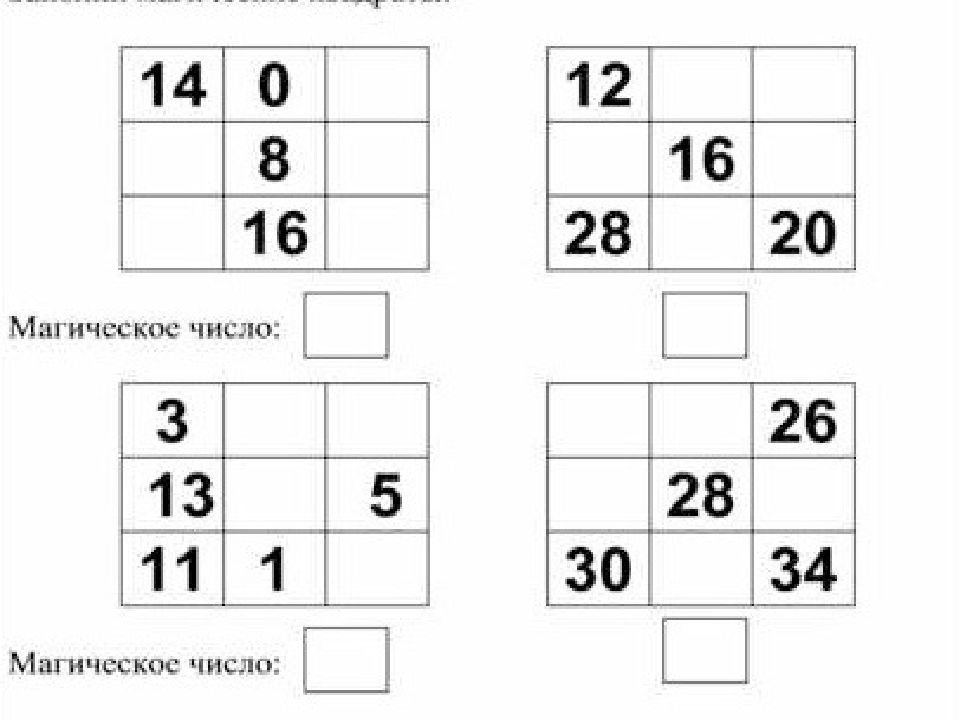
Магический квадрат представляет собой квадратную таблицу с числами, построенную так, что сумма чисел в каждой строке, каждом столбце и в каждой диагонали равна одному и тому же числу (магическая сумма). Магические квадраты бывают разных порядков — порядок квадрата определяет число столбцов/строк.
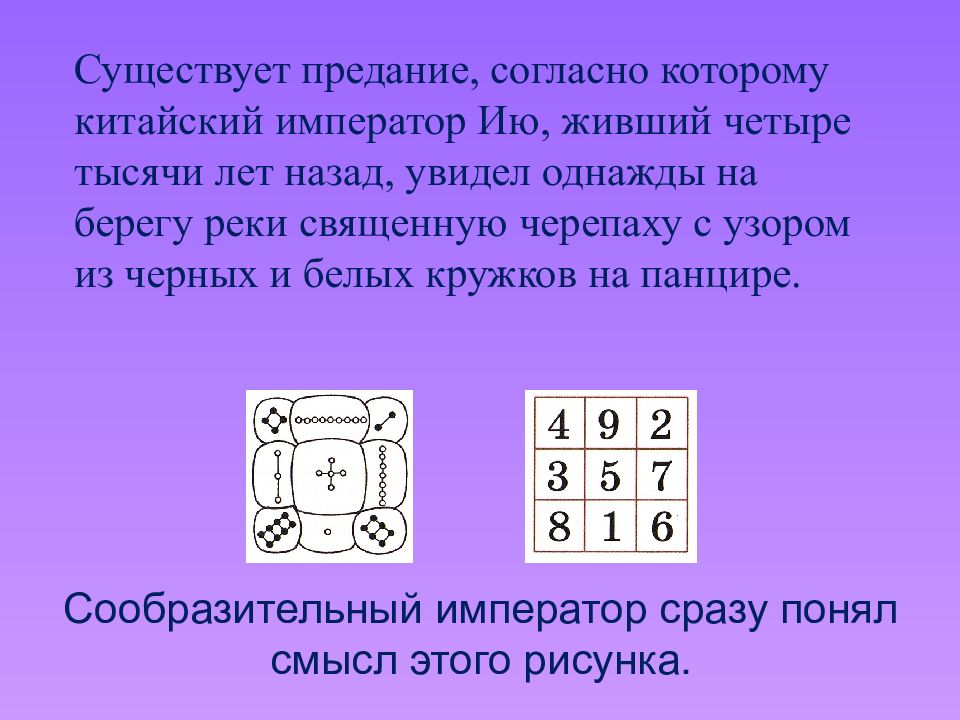
Существует предание, согласно которому китайский император Ию, живший четыре тысячи лет назад, увидел однажды на берегу реки священную черепаху с узором из черных и белых кружков на панцире.
4 9 2 3 5 7 8 1 6 Найдём сумму чисел в каждой строке. = 15 4+ 9+ 2 3+ 5+ 7 = 15 = 15 8+ 1+ 6
Найдём сумму чисел в каждом столбце. = 15 4+ 9+ 2+ 3+ 5+ 7+ = 15 = 15 8 1 6 4 9 2 3 5 7 8 1 6
Найдём сумму чисел в каждой диагонали. = 15 4+ 2+ 5+ = 15 8 6 4 9 2 3 5 7 8 1 6 5+
Все 8 различных магических квадратов из чисел от 1 до 9 ! 8 3 4 1 5 9 6 7 2 2 9 4 7 5 3 6 1 8 6 1 8 7 5 8 2 9 4 4 9 2 3 5 7 8 1 6 6 7 2 1 5 9 8 3 4 4 3 8 9 5 1 2 7 6 2 7 6 9 5 1 4 3 8 8 1 6 3 5 7 4 9 2
китайцы назвали « ло – шу» и считали магическим. Поэтому квадратные таблицы чисел, обладающие таким удивительным свойством, с тех пор называют магическими квадратами.
Полного описания всех возможных магических квадратов не получено и до сего времени. Известно, что магических квадратов 2х2 не существует (может быть, кто-нибудь это докажет?). Магический квадрат 3х3 только один, так как остальные магические квадраты 3 на 3 получаются из него либо поворотом вокруг центра, либо отражением относительно одной из его осей симметрии. Магических квадратов 4х4, как на картине Дюрера, составлено уже 800, а количество магических квадратов 5х5 близко к четверти миллиона!
16 2 8 14 14 42 23 24 ключ Решение
ключ 16 2 8 14 12 24 6 4 0 10 Получилось!
43 44 ключ 46 48 45 12 16 20 28 Решение
ключ 48 12 16 20 28 8 4 0 32 24 Молодец!
