Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори, Мурманской обл. 8 класс Теорема, обратная теореме Пифагора Л.С. Атанасян Геометрия 7-9
Повторение Найти S ABCD 30 0 45 0 А В С D 2 4 4 +
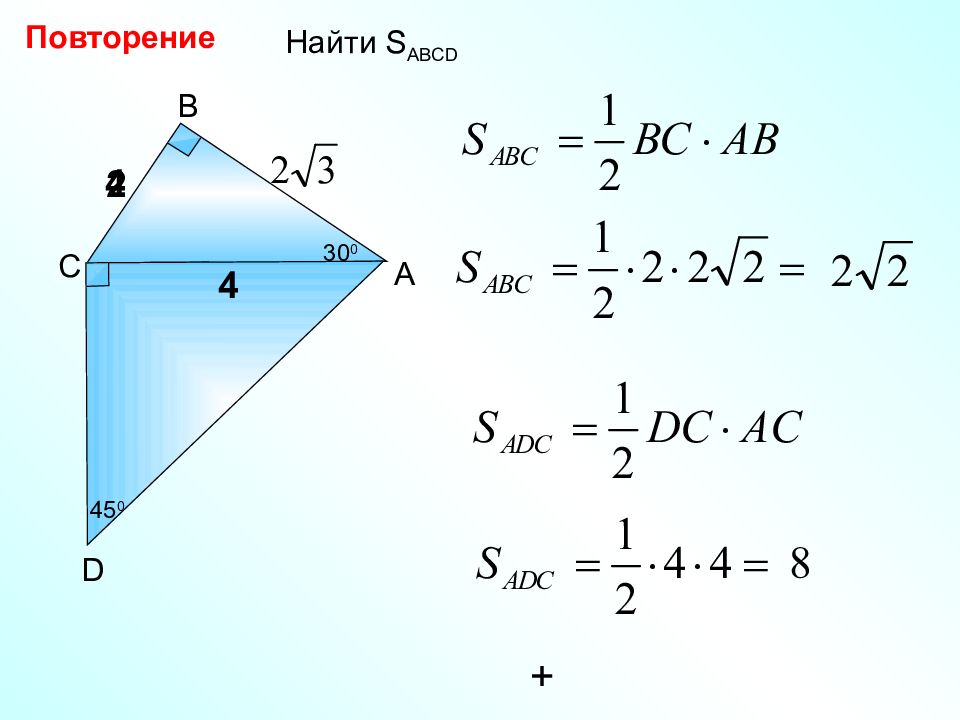
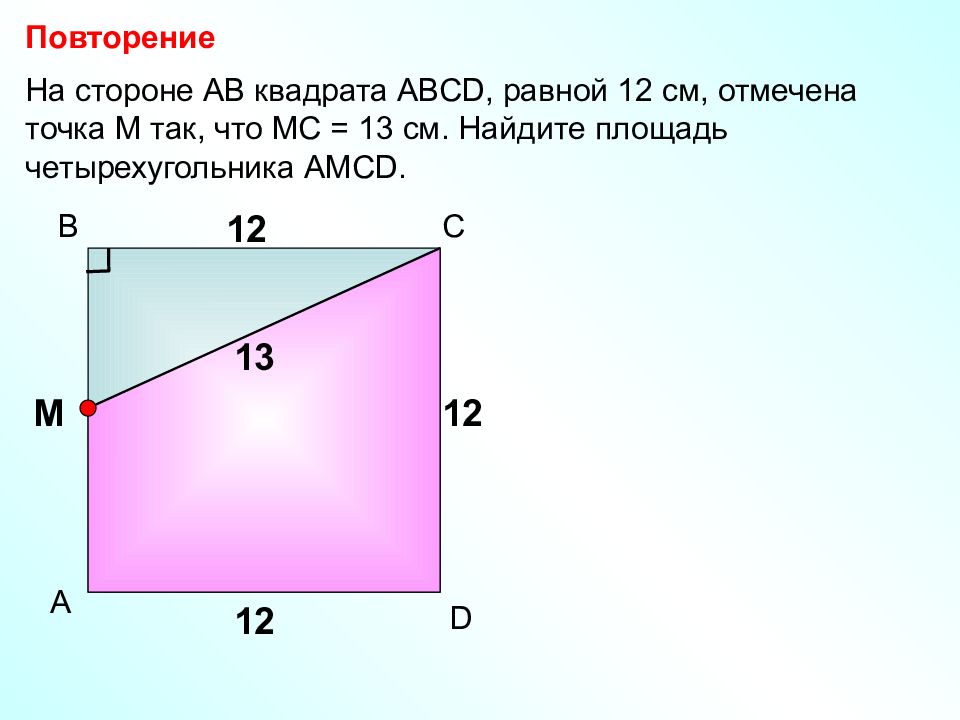
Повторение На стороне АВ квадрата АВС D, равной 12 см, отмечена точка М так, что МС = 13 см. Найдите площадь четырехугольника АМС D. А В С D 12 12 М 13 12
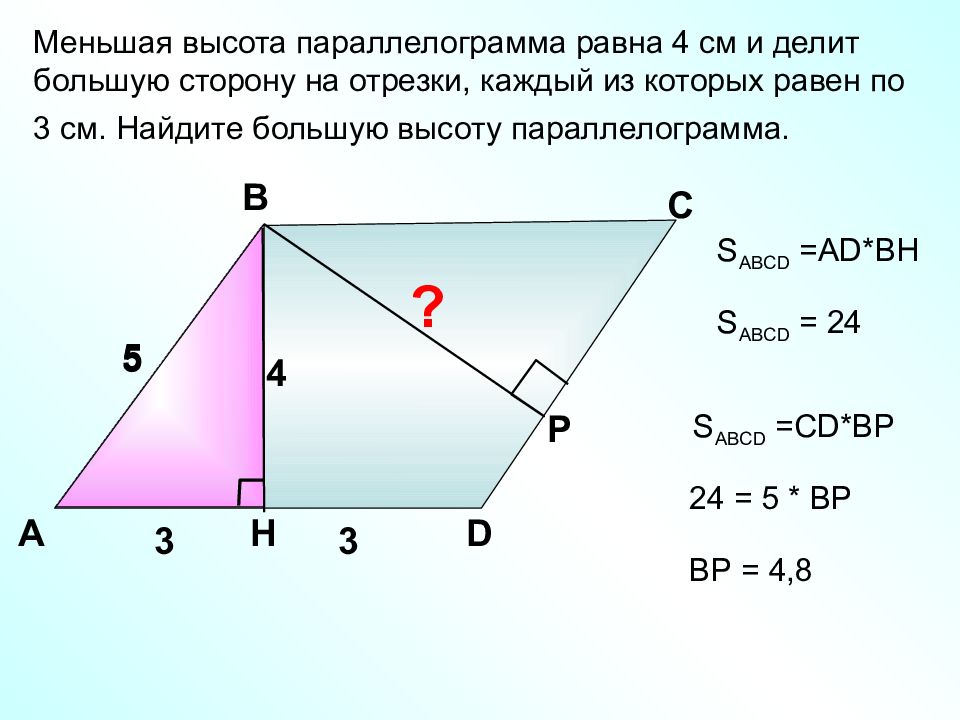
Меньшая высота параллелограмма равна 4 см и делит большую сторону на отрезки, каждый из которых равен по 3 см. Найдите большую высоту параллелограмма. А В С D H 5 3 3 4 S ABCD =AD*BH Р 5 S ABCD = 24 S ABCD = С D*B Р 24 = 5 * ВР ? ВР = 4,8
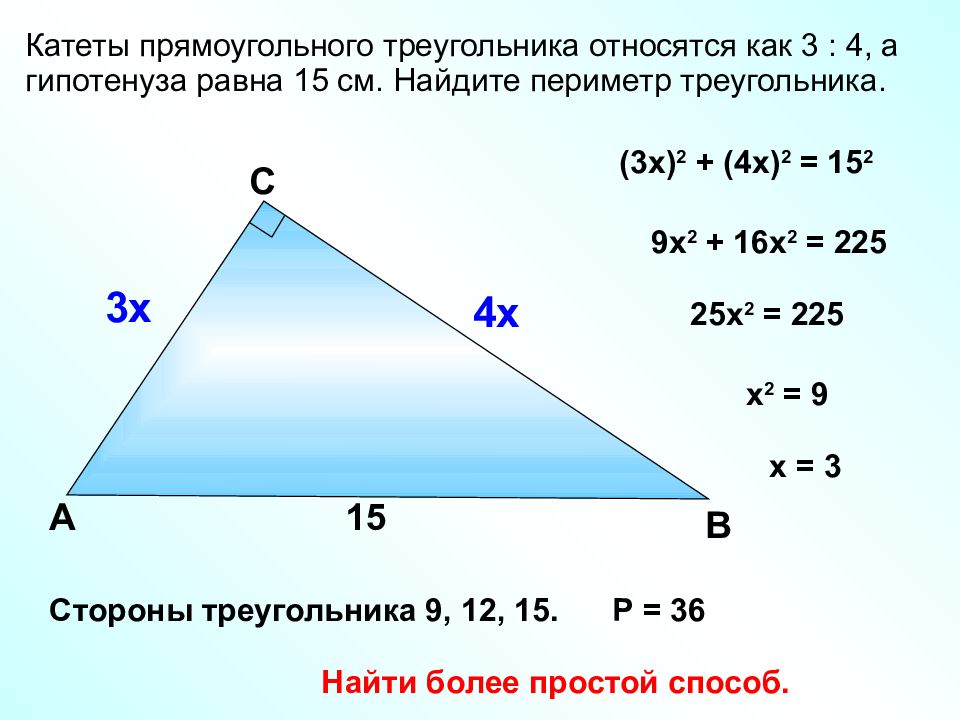
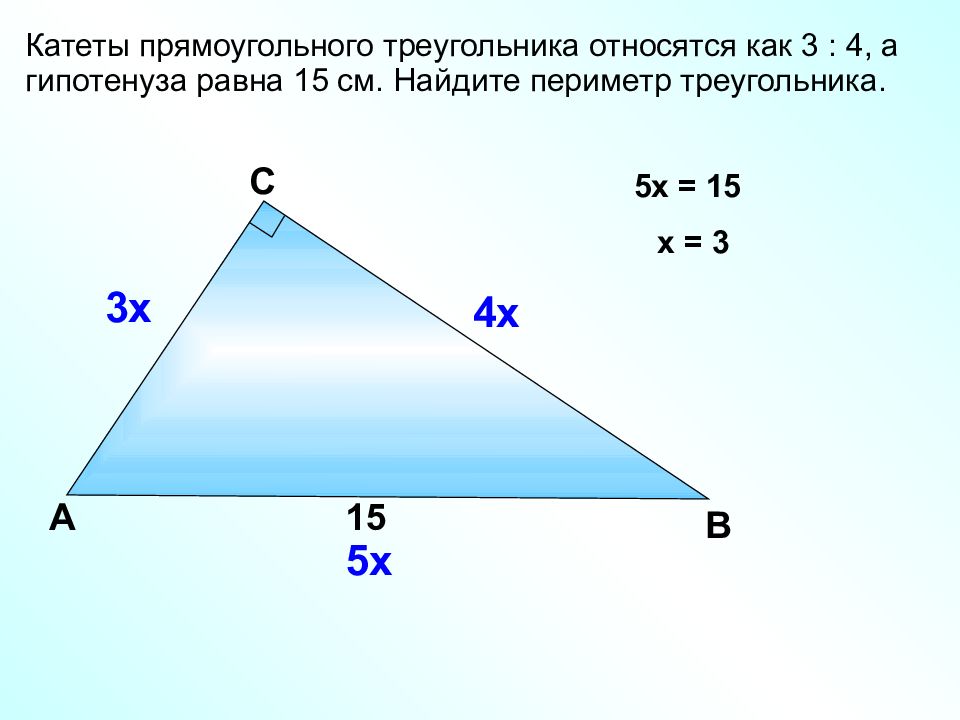
Катеты прямоугольного треугольника относятся как 3 : 4, а гипотенуза равна 15 см. Найдите периметр треугольника. В С A 15 3х 4х (3х) 2 + (4х) 2 = 15 2 9х 2 + 16х 2 = 225 25х 2 = 225 х 2 = 9 х = 3 Стороны треугольника 9, 12, 15. Р = 36 Найти более простой способ.
Построение прямого угла на местности Для построения прямоугольной площадки для игры в футбол следовало бы взять угольник и циркуль таких размеров.
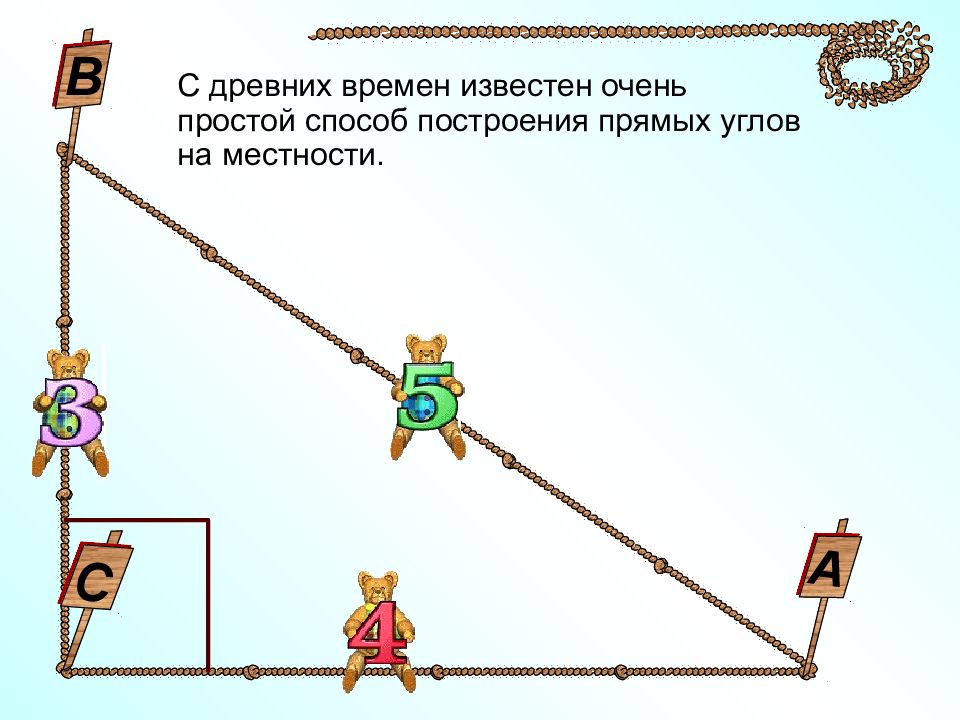
С древних времен известен очень простой способ построения прямых углов на местности. С В А
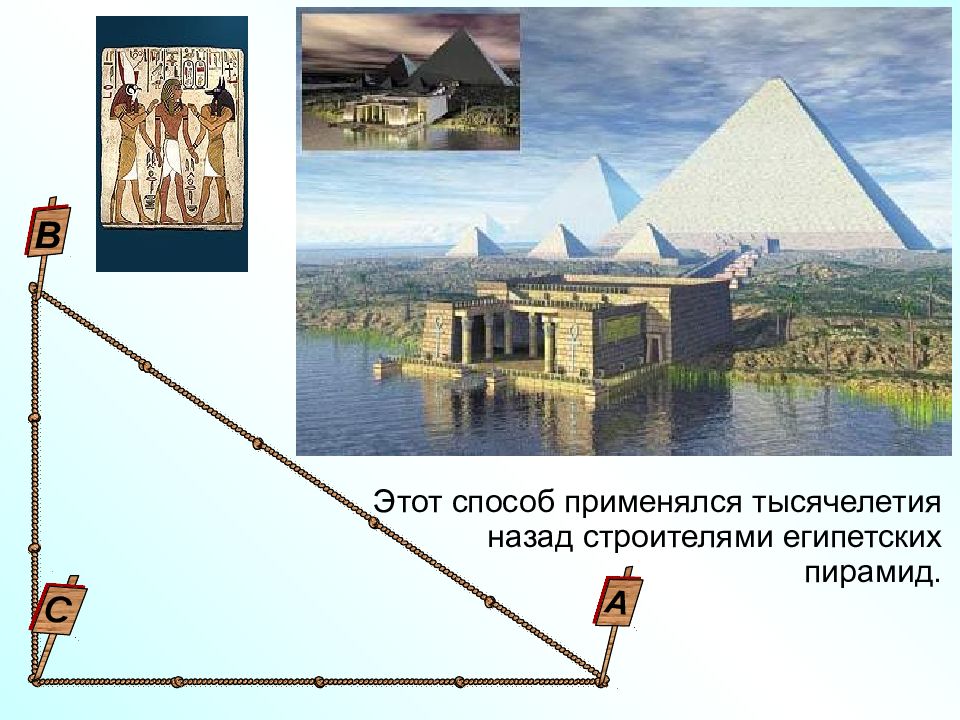
Этот способ применялся тысячелетия назад строителями египетских пирамид. С В А
Теорема, обратная теореме Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. Существует бесчисленное множество целых положительных чисел, удовлетворяющих соотношению с 2 = а 2 + b 2. Они называются п и ф а г о р о в ы м и ч и с л а м и
Вот несколько троек пифагоровых чисел. 3 2 + 4 2 = 5 2 5 2 + 12 2 = 13 2 7 2 + 24 2 = 25 2 9 2 + 40 2 = 41 2 11 2 + 60 2 = 61 2 13 2 + 84 2 = 85 2 6 2 + 8 2 = 10 2 9 2 + 12 2 = 15 2 12 2 + 16 2 = 20 2 Треугольник со сторонами 3, 4 и 5 часто называют египетским треугольником т. к. он был известен еще древним египтянам.
Катеты прямоугольного треугольника относятся как 3 : 4, а гипотенуза равна 15 см. Найдите периметр треугольника. В С A 15 3х 4х 5х = 15 х = 3 5х
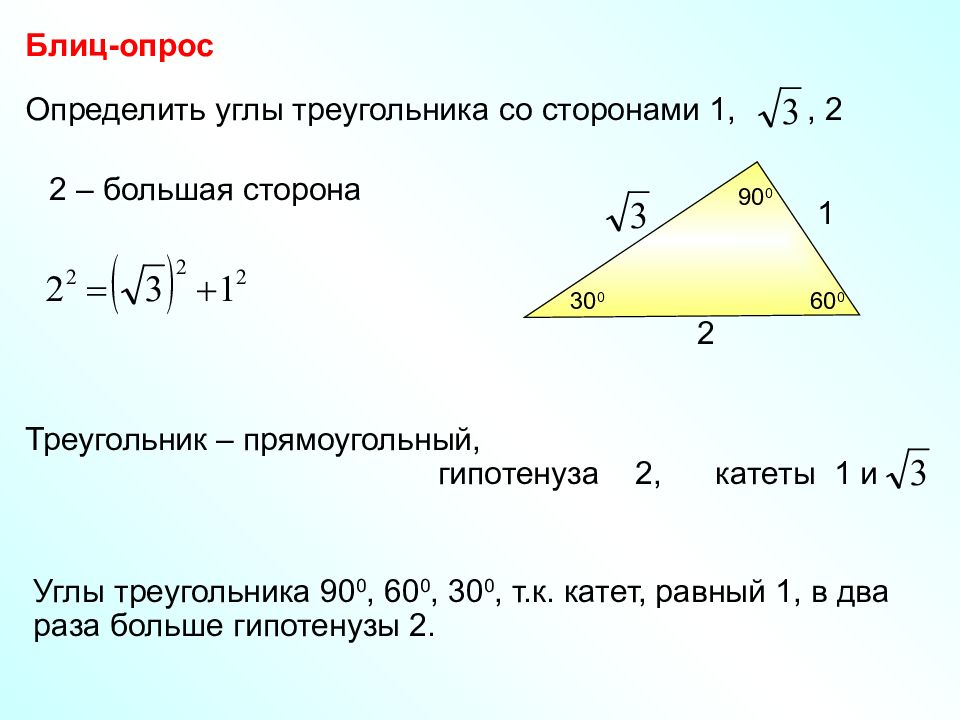
Определить углы треугольника со сторонами 1,, 2 Блиц-опрос 2 – большая сторона Треугольник – прямоугольный, гипотенуза 2, катеты 1 и Углы треугольника 90 0, 60 0, 30 0, т.к. катет, равный 1, в два раза больше гипотенузы 2. 2 1 90 0 30 0 60 0
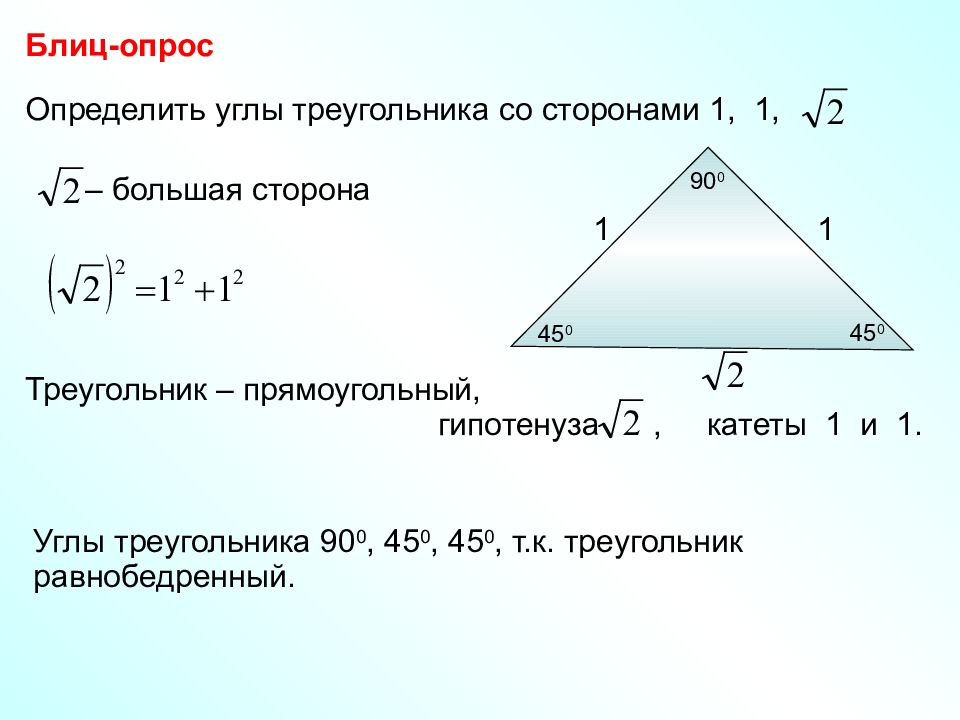
Определить углы треугольника со сторонами 1, 1, Блиц-опрос Углы треугольника 90 0, 45 0, 45 0, т.к. треугольник равнобедренный. – большая сторона Треугольник – прямоугольный, гипотенуза, катеты 1 и 1. 1 1 90 0 45 0 45 0
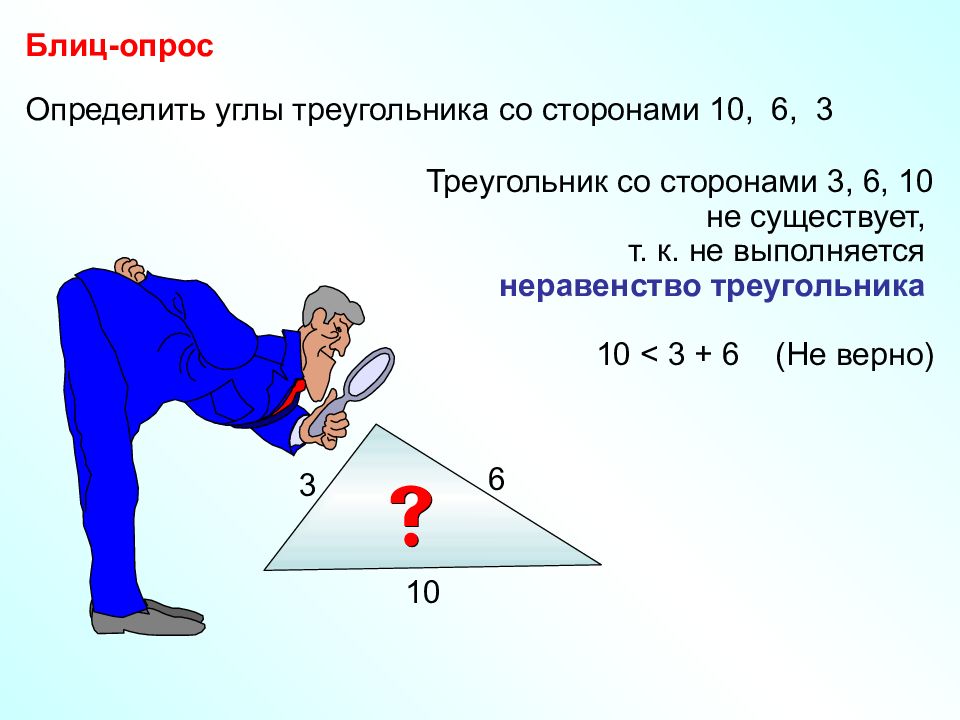
Определить углы треугольника со сторонами 10, 6, 3 Блиц-опрос Треугольник со сторонами 3, 6, 10 не существует, т. к. не выполняется неравенство треугольника 10 < 3 + 6 ( Не верно) 3 6 10
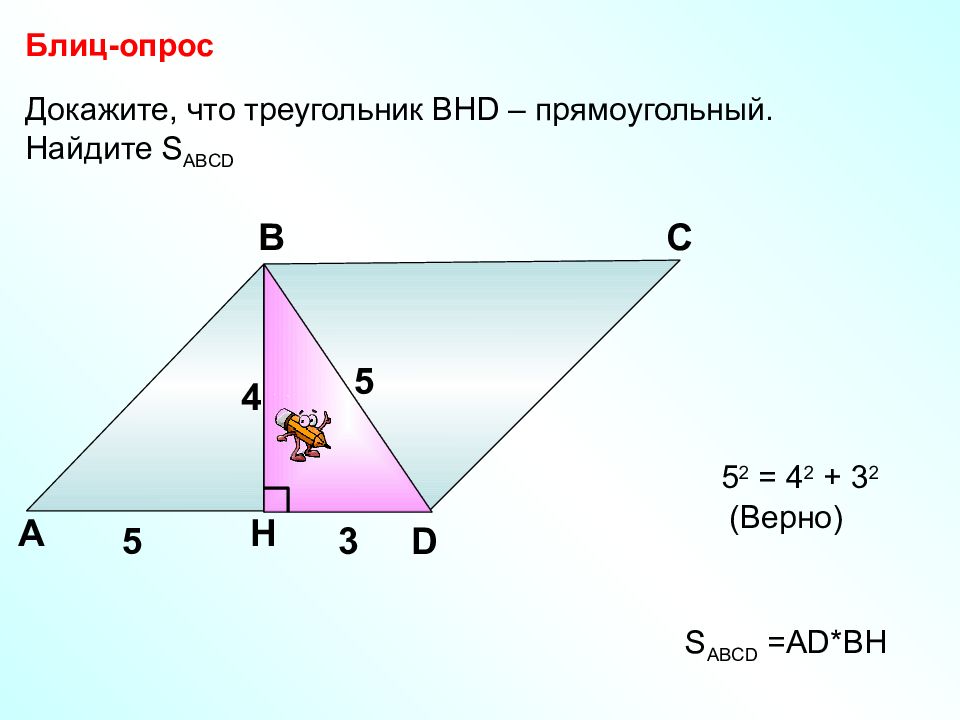
Докажите, что треугольник В HD – прямоугольный. Найдите S ABCD Блиц-опрос А В С D H 4 5 3 5 S ABCD =AD*BH 5 2 = 4 2 + 3 2 (Верно)
Найдите площадь трапеции АВ CD с основаниями А D и ВС. Блиц-опрос А В С D 10 5 8 10 2 = 8 2 + 6 2 (Верно) 6
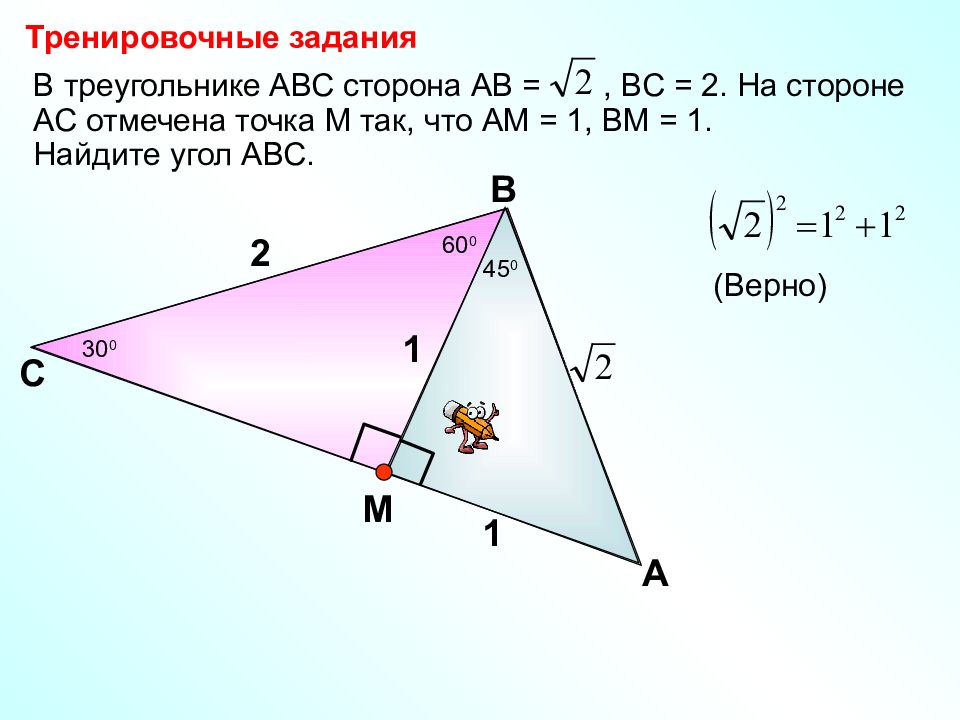
В треугольнике АВС сторона АВ =, ВС = 2. На стороне АС отмечена точка М так, что АМ = 1, ВМ = 1. Найдите угол АВС. С В А 2 1 М Тренировочные задания 1 (Верно) 30 0 60 0 45 0
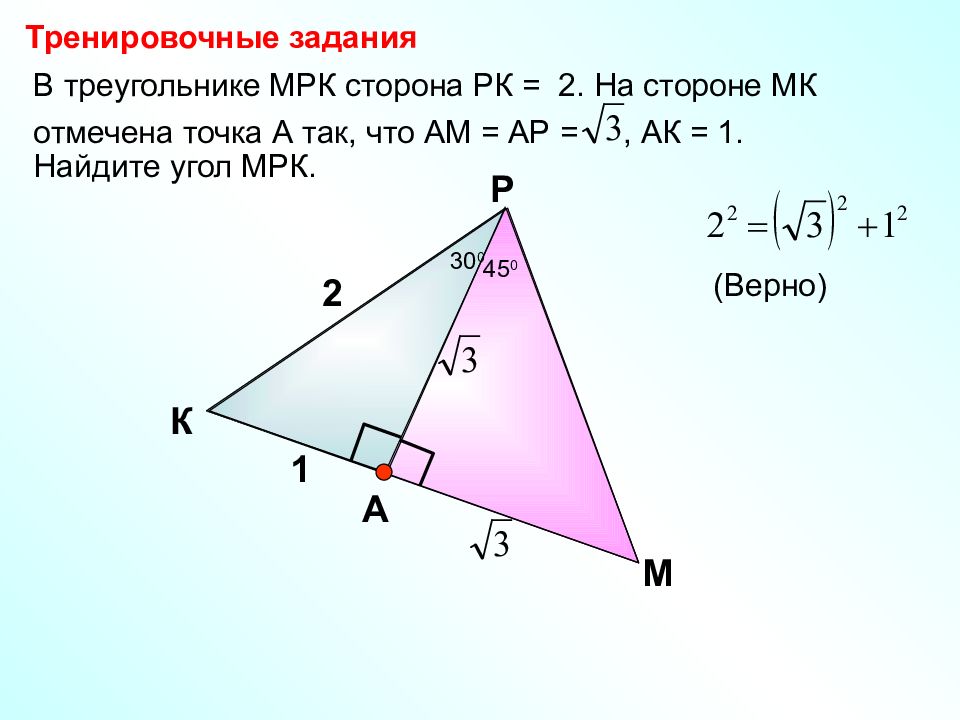
В треугольнике МРК сторона РК = 2. На стороне МК отмечена точка А так, что АМ = АР =, АК = 1. Найдите угол МРК. К Р М 2 1 А Тренировочные задания (Верно) 30 0 45 0
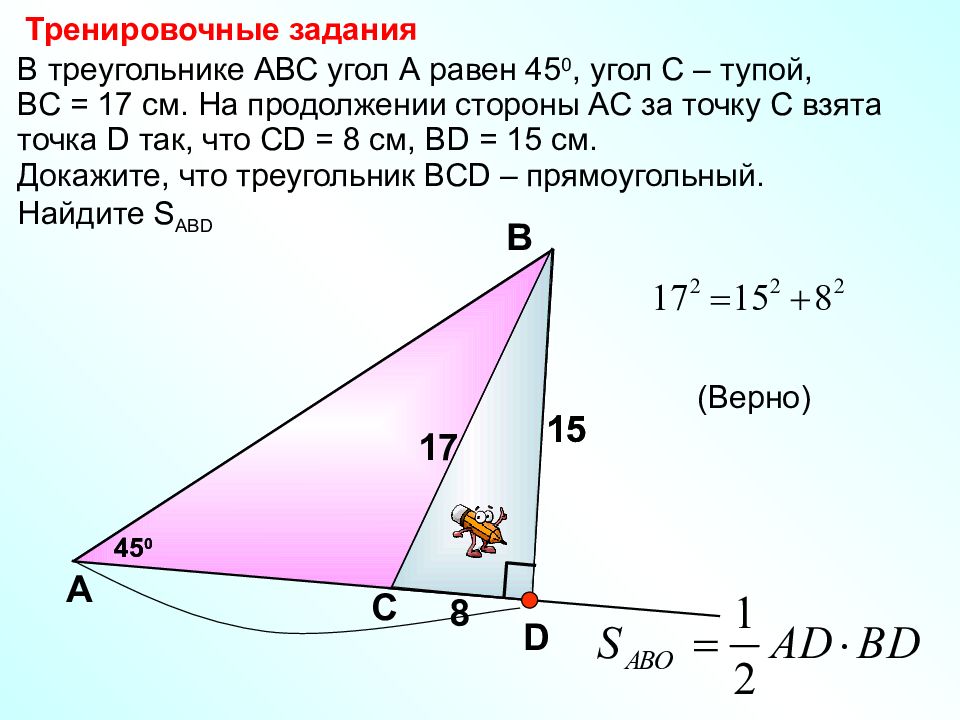
Докажите, что треугольник ВС D – прямоугольный. Найдите S ABD В треугольнике АВС угол А равен 45 0, угол С – тупой, ВС = 17 см. На продолжении стороны АС за точку С взята точка D так, что CD = 8 см, BD = 15 см. С А В Тренировочные задания 17 (Верно) 45 0 15 8 D 45 0 15
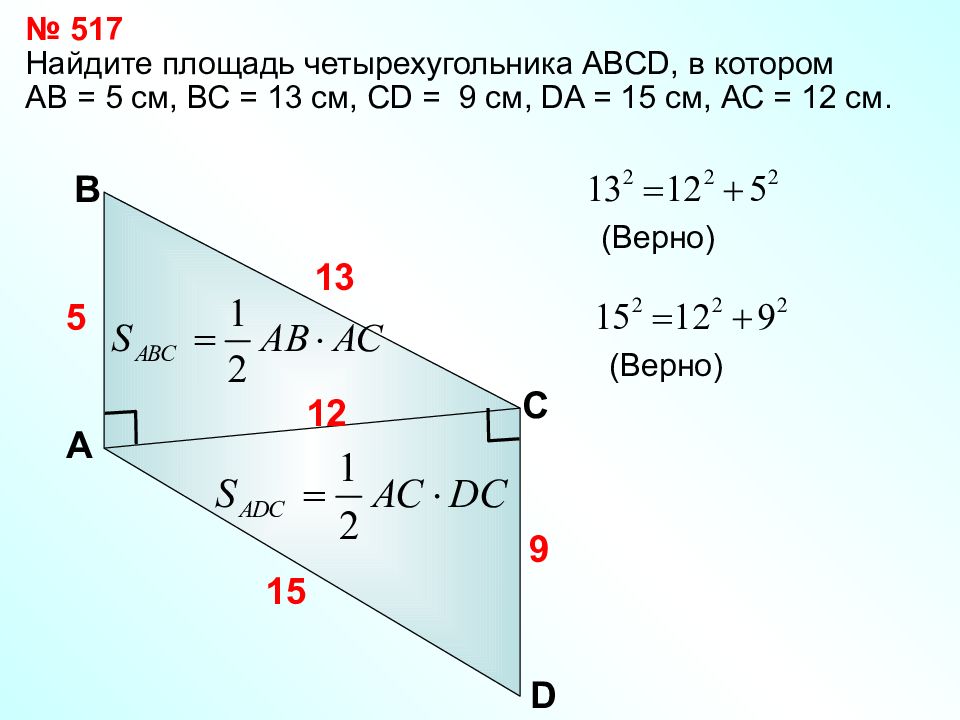
Найдите площадь четырехугольника АВС D, в котором АВ = 5 см, ВС = 13 см, С D = 9 см, DA = 15 см, АС = 12 см. С А В № 517 1 3 (Верно) 5 D 1 2 9 15 (Верно)
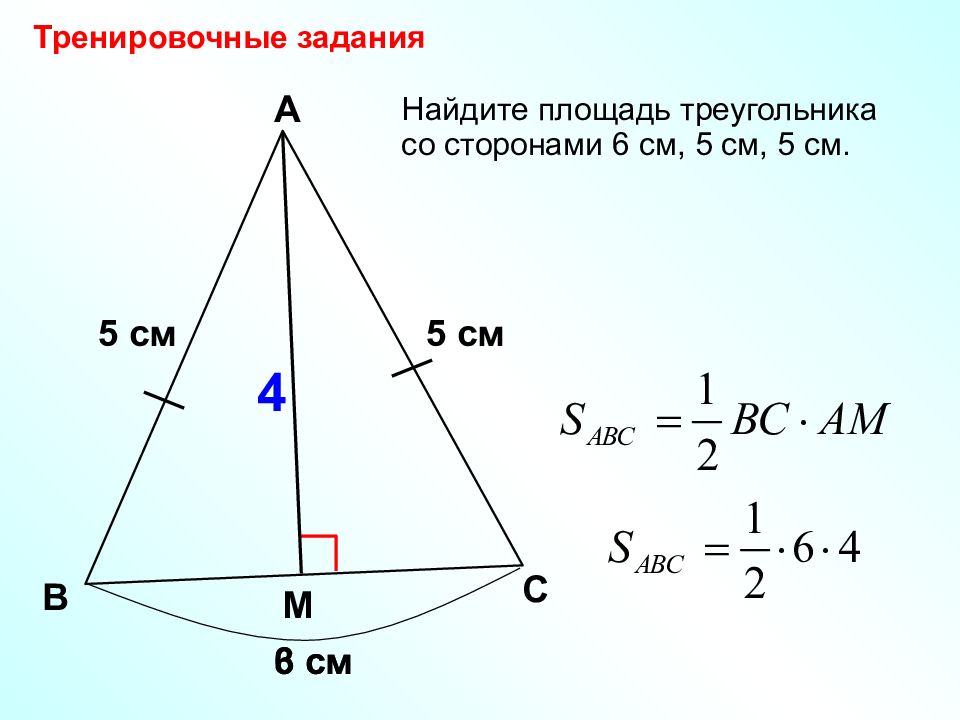
5 см Найдите площадь треугольника со сторонами 6 см, 5 см, 5 см. В А 5 см С Тренировочные задания 6 см М 3 см 4
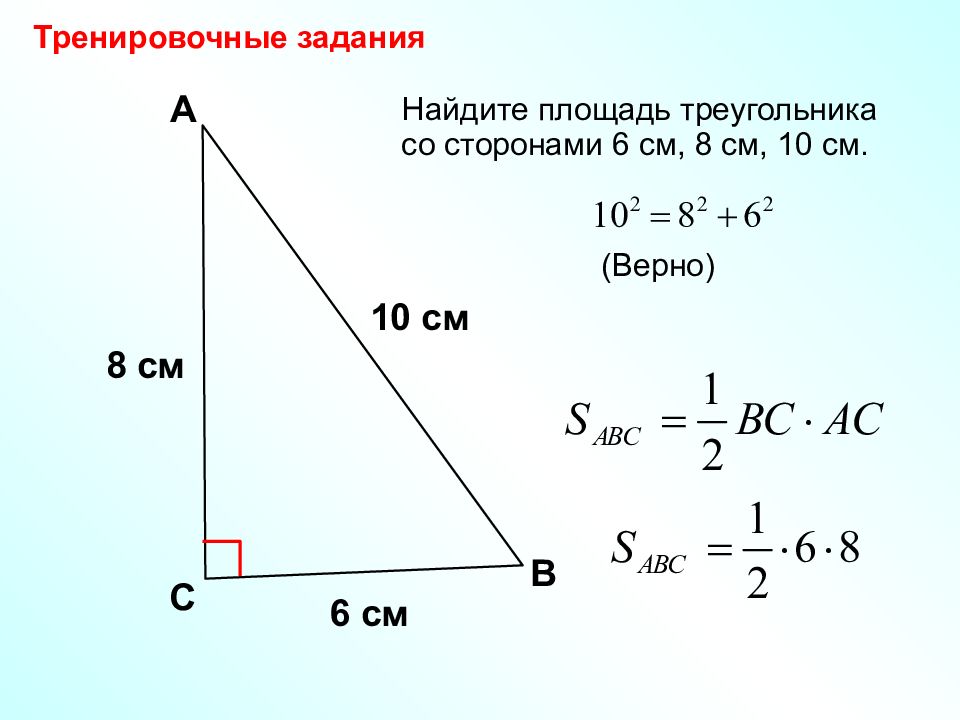
8 см Найдите площадь треугольника со сторонами 6 см, 8 см, 10 см. В А 10 см С Тренировочные задания 6 см (Верно)
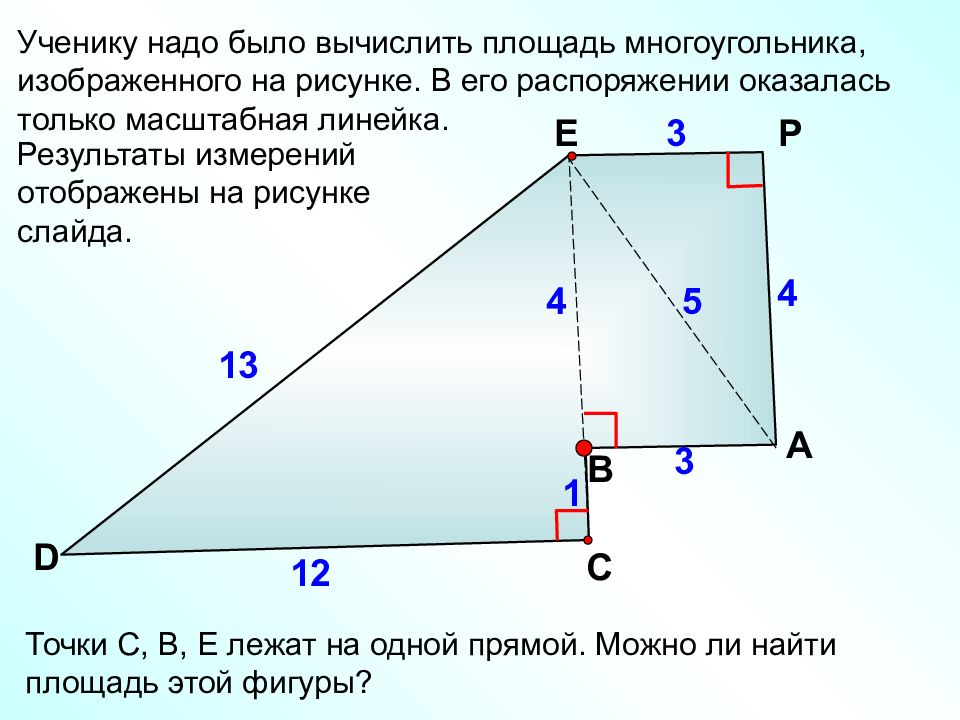
13 Ученику надо было вычислить площадь многоугольника, изображенного на рисунке. В его распоряжении оказалась только масштабная линейка. В P D 12 3 1 4 3 4 5 E C A Точки С, В, Е лежат на одной прямой. Можно ли найти площадь этой фигуры? Результаты измерений отображены на рисунке слайда.
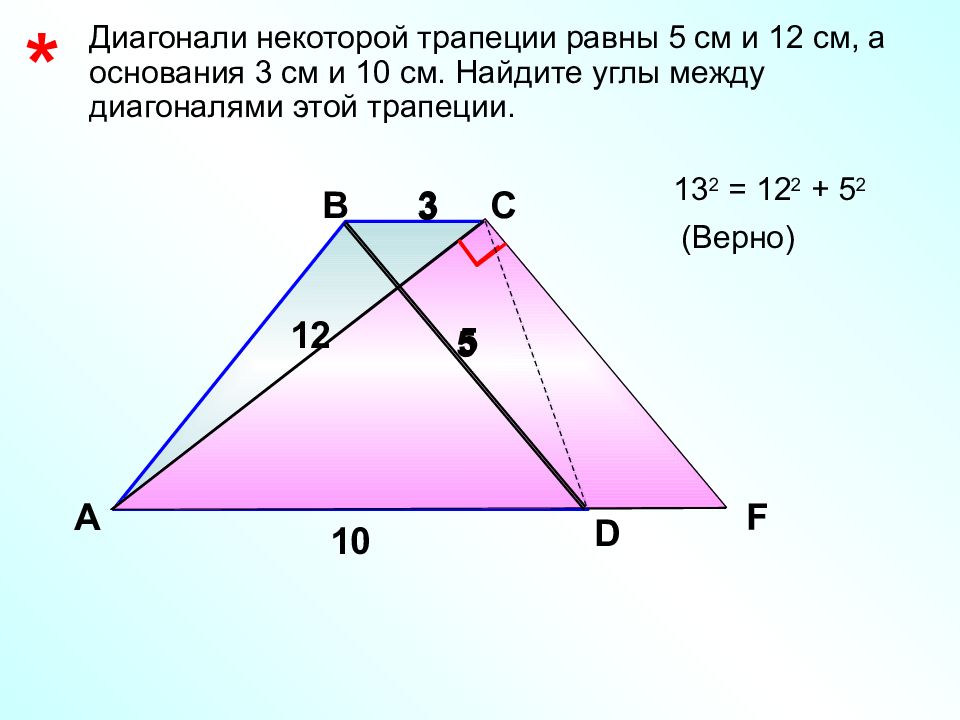
* Диагонали некоторой трапеции равны 5 см и 12 см, а основания 3 см и 10 см. Найдите углы между диагоналями этой трапеции. А В С D 12 10 3 13 2 = 12 2 + 5 2 (Верно) 5 5 3 F
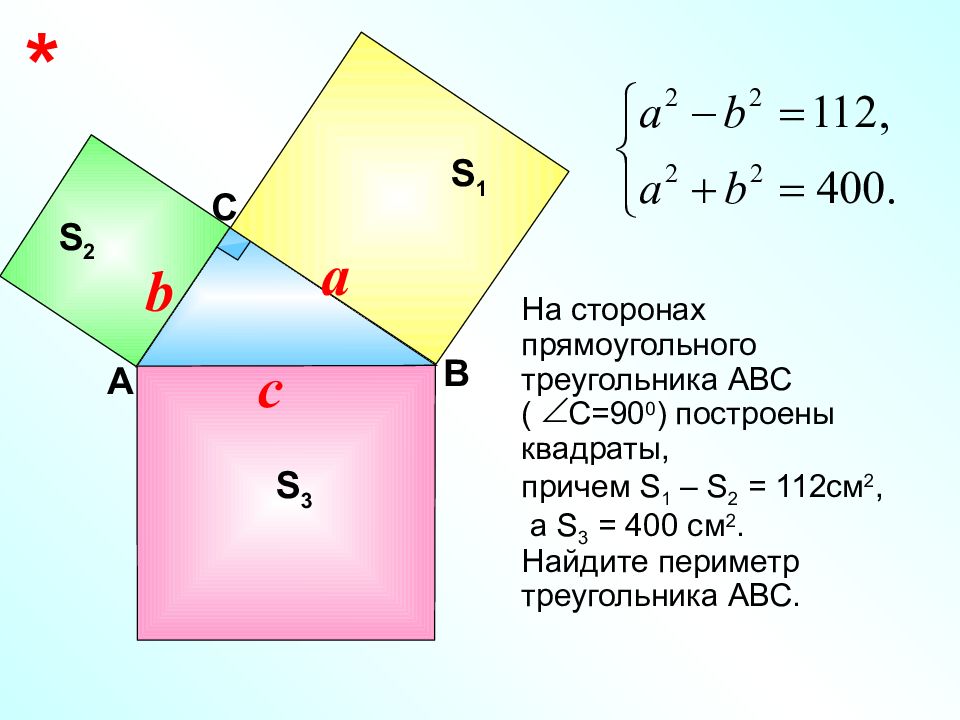
На сторонах прямоугольного треугольника АВС ( С=90 0 ) построены квадраты, причем S 1 – S 2 = 112 см 2, а S 3 = 400 см 2. Найдите периметр треугольника АВС. В S 2 С * A S 1 S 3 a b c
Докажите, что сумма квадратов медиан прямоугольного треугольника равна 3/2 квадрата гипотенузы. В С * A a b c N m 1 Из АС N M m 2 Из B С M F m 3 +
