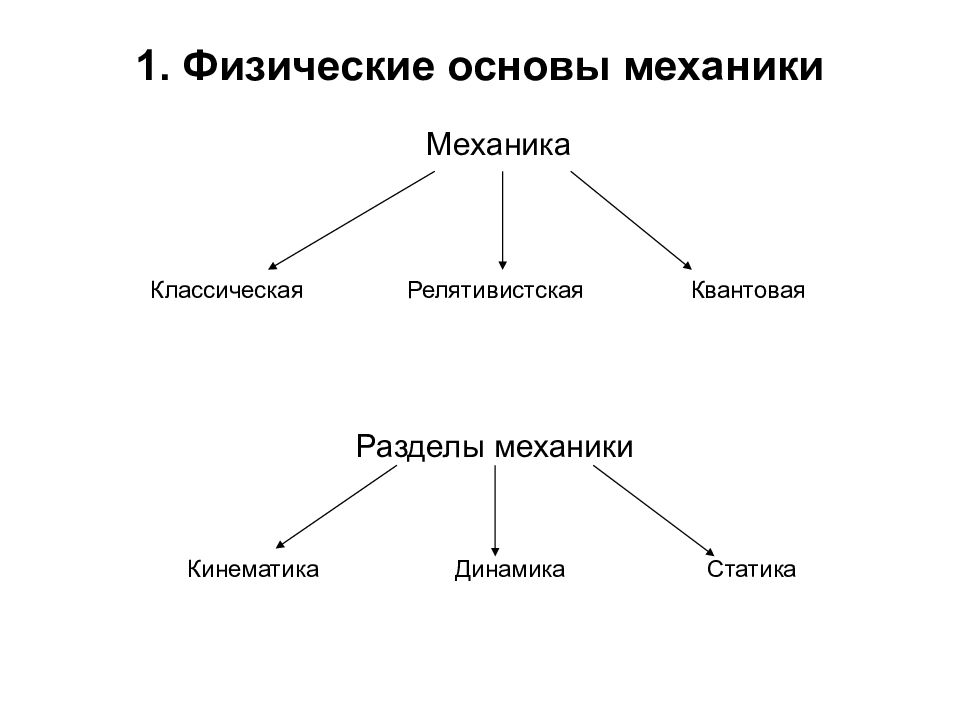
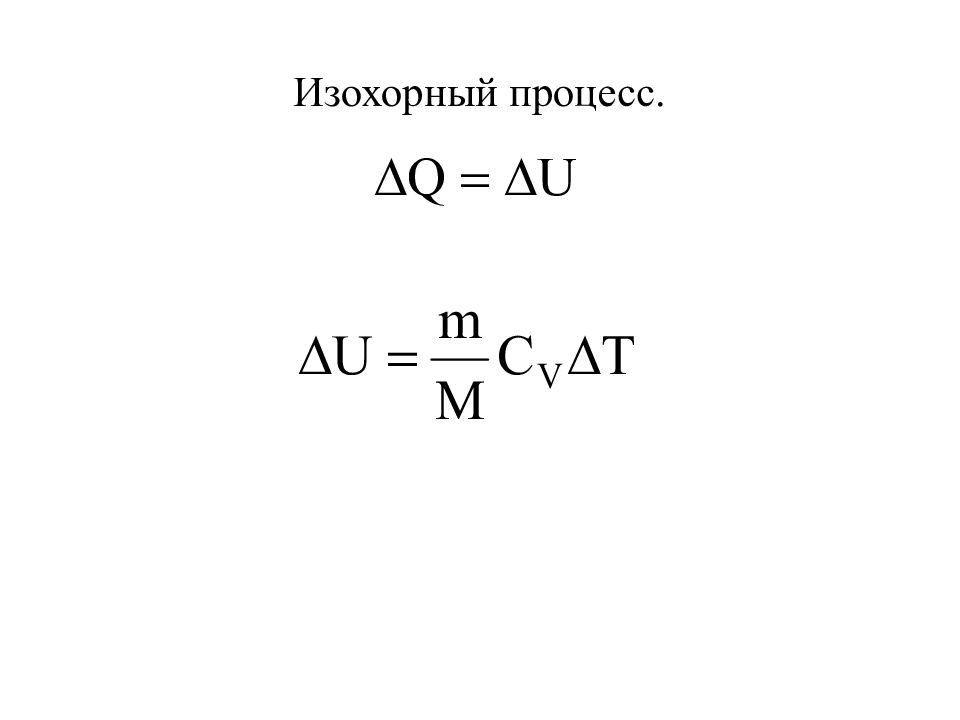Первый слайд презентации: Молекулярно-кинетическая теория идеальных газов
Доцент Кравцова О.С.
Слайд 15
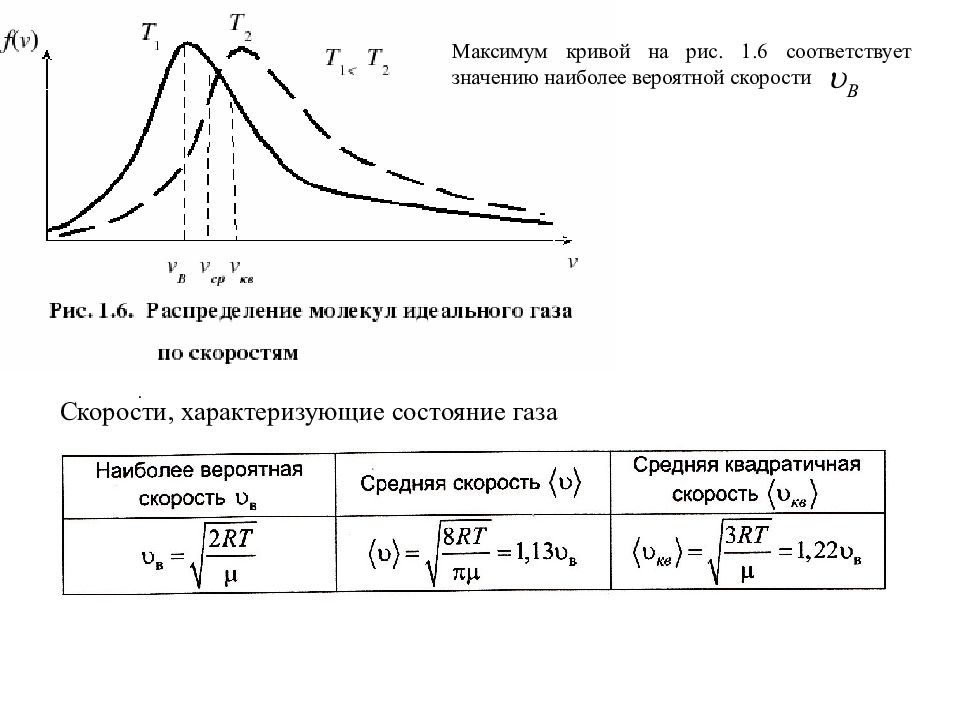
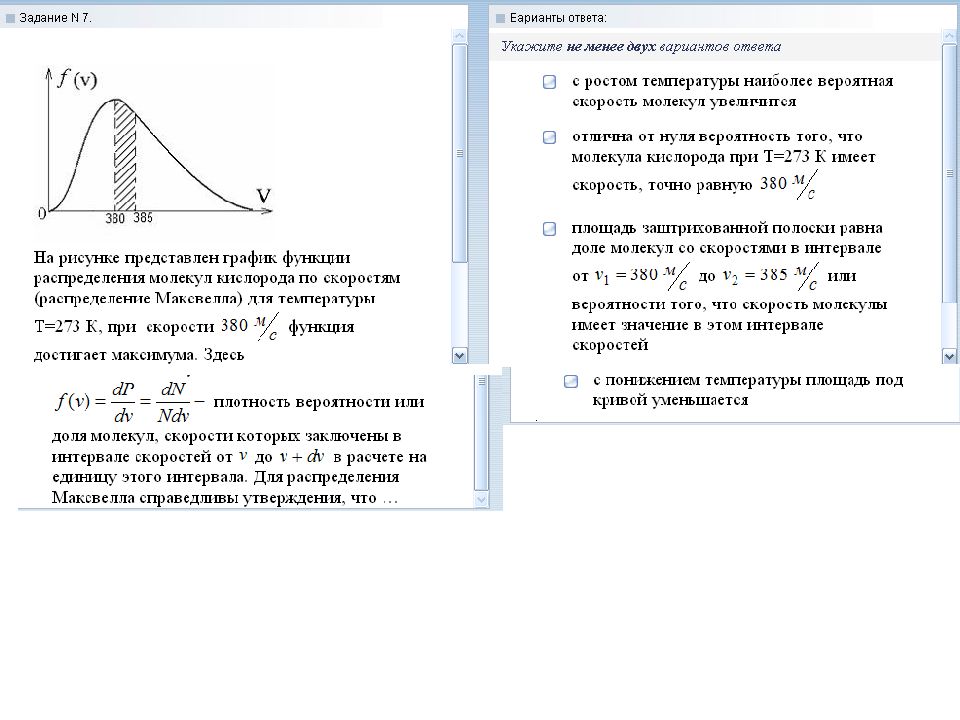
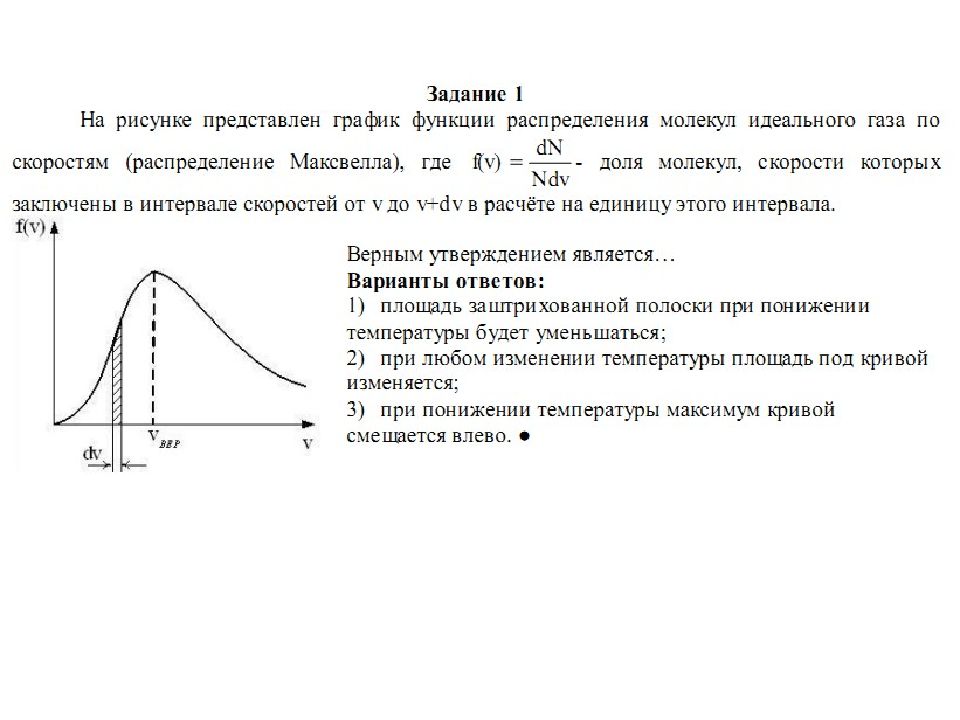
Скорости, характеризующие состояние газа Максимум кривой на рис. 1.6 соответствует значению наиболее вероятной скорости .
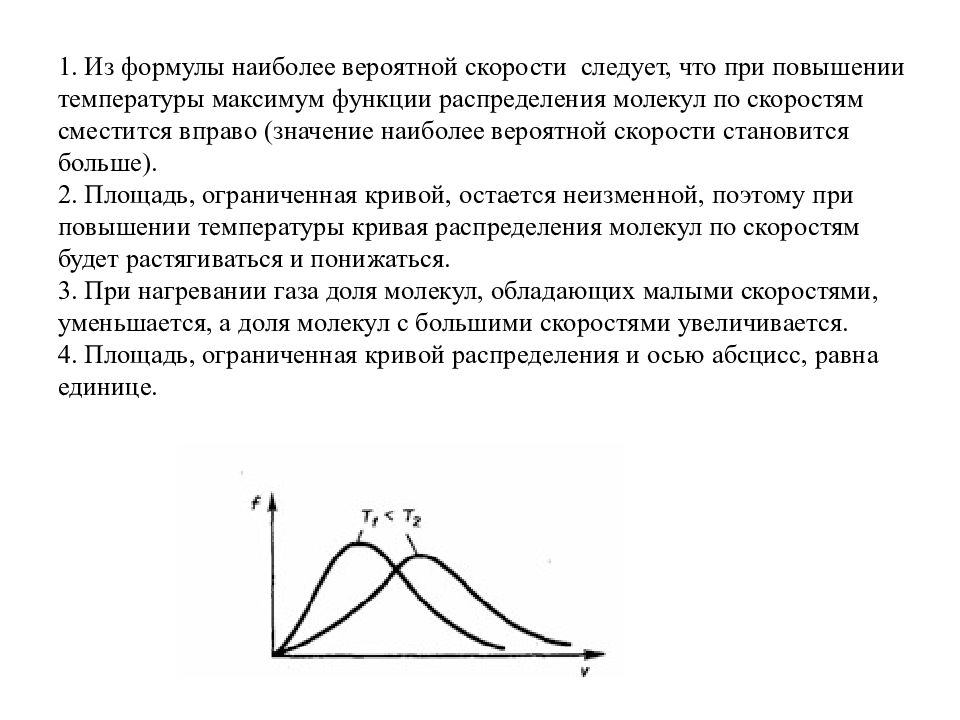
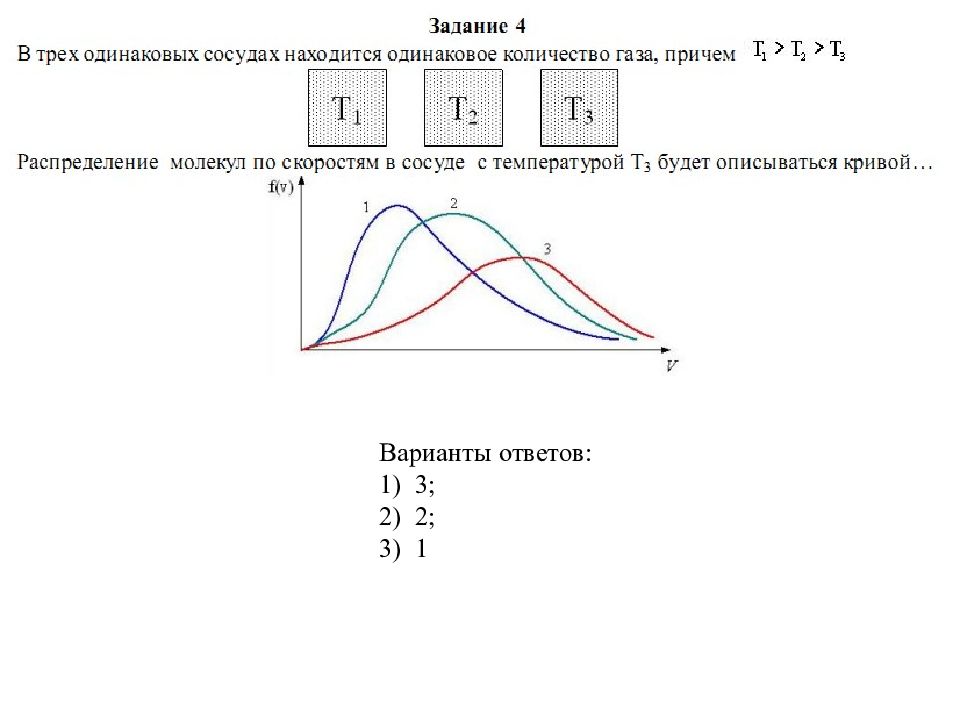
Слайд 16: 1. Из формулы наиболее вероятной скорости следует, что при повышении температуры максимум функции распределения молекул по скоростям сместится вправо (значение наиболее вероятной скорости становится больше). 2. Площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться. 3. При нагревании газа доля молекул, обладающих малыми скоростями, уменьшается, а доля молекул с большими скоростями увеличивается. 4. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице
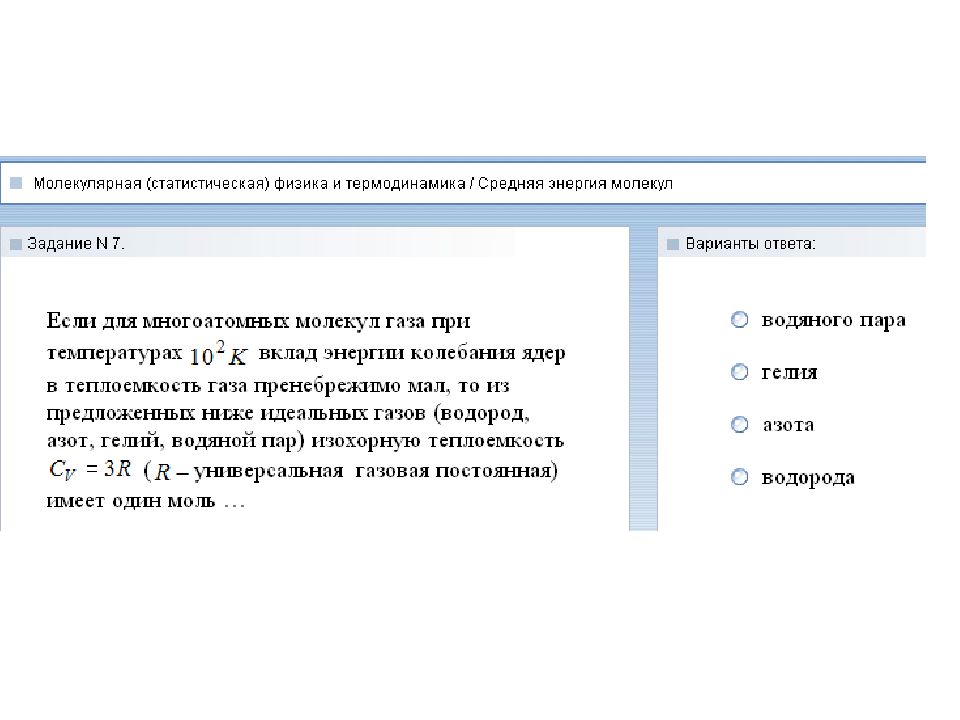
Слайд 25: Важной характеристикой термодинамической системы является ее внутренняя энергия. Внутренняя энергия - однозначная функция термодинамического состояния системы (при переходе системы из одного состояния в другое изменение внутренней энергии определяется разностью значений внутренней энергии этих состояний и не зависит от пути перехода). Положение тела в каждый момент времени характеризуется числом степеней свободы. Число степеней свободы молекулы – число независимых переменных (координат), полностью определяющих положение системы в пространстве. Средняя энергия молекулы равна:
Слайд 28: Закон сохранения и превращения энергии, получил название первого начала термодинамики: количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы
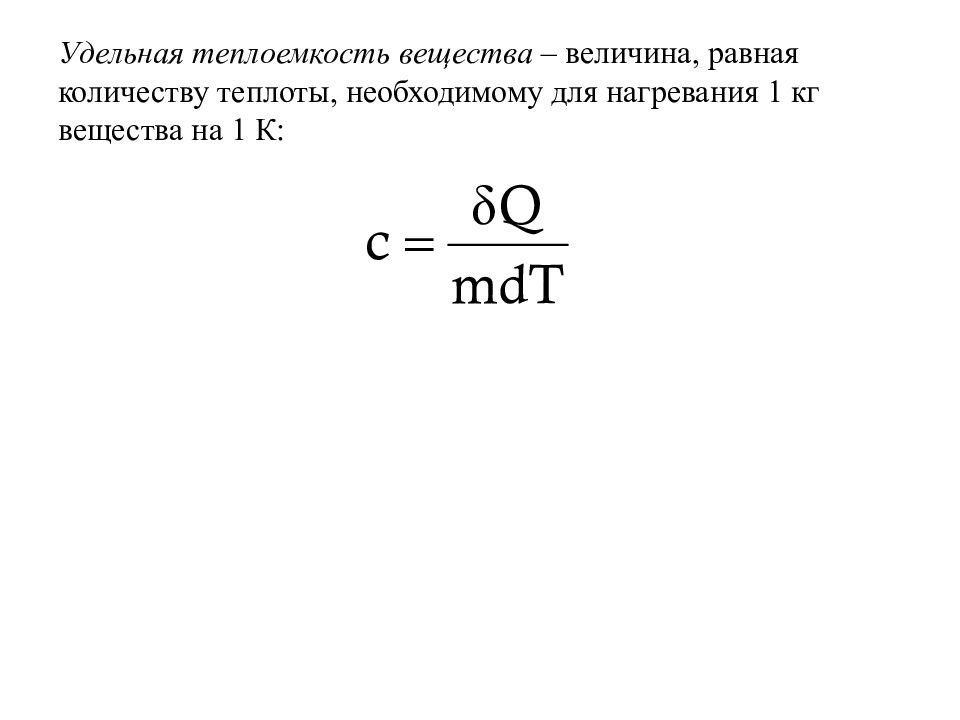
Слайд 29: Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Слайд 30: Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:
Связь удельной и молярной теплоемкости:
Слайд 36: Адиабатный процесс - процесс, при котором отсутствует теплообмен между системой и окружающей средой. Все быстропротекающие процессы можно отнести к адиабатным. Адиабатный процесс описывается уравнением Пуассона
Рис. Адиабатный процесс
Слайд 37: Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем, если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым
Слайд 38: Энтропией называется функция состояния системы, дифференциалом которой является :
Слайд 39: Для обратимых процессов изменение энтропии: - это выражение называется равенство Клаузиуса
Слайд 40: это неравенство Клаузиуса. При любом необратимом процессе в замкнутой системе энтропия возрастает ( dS > 0)
Слайд 41: Тогда для замкнутой системы – математическая запись второго начала термодинамики
Таким образом, для произвольного процесса, где, знак равенства – для обратимого процесса; знак больше для необратимого.
Слайд 42
Изохорический процесс: т. к. Изобарический процесс: т.к. P 1 = P 2 Изотермический процесс: т.к. Т 1 = Т 2 Адиабатический процесс: то изоэнтропийный процесс Изменение энтропии в изопроцессах:
Слайд 43: Второе начало термодинамики
1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к телу более нагретому.
Слайд 44: Математической формулировкой второго начала является выражение Энтропия замкнутой системы при любых происходивших в ней процессах не может убывать (или увеличивается или остается неизменной)
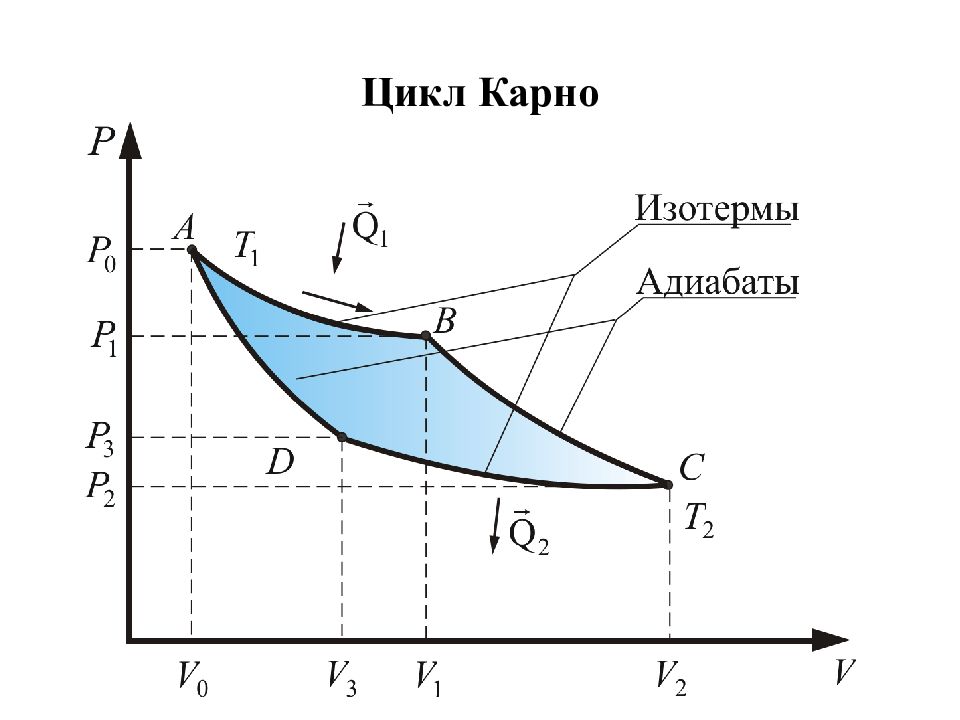
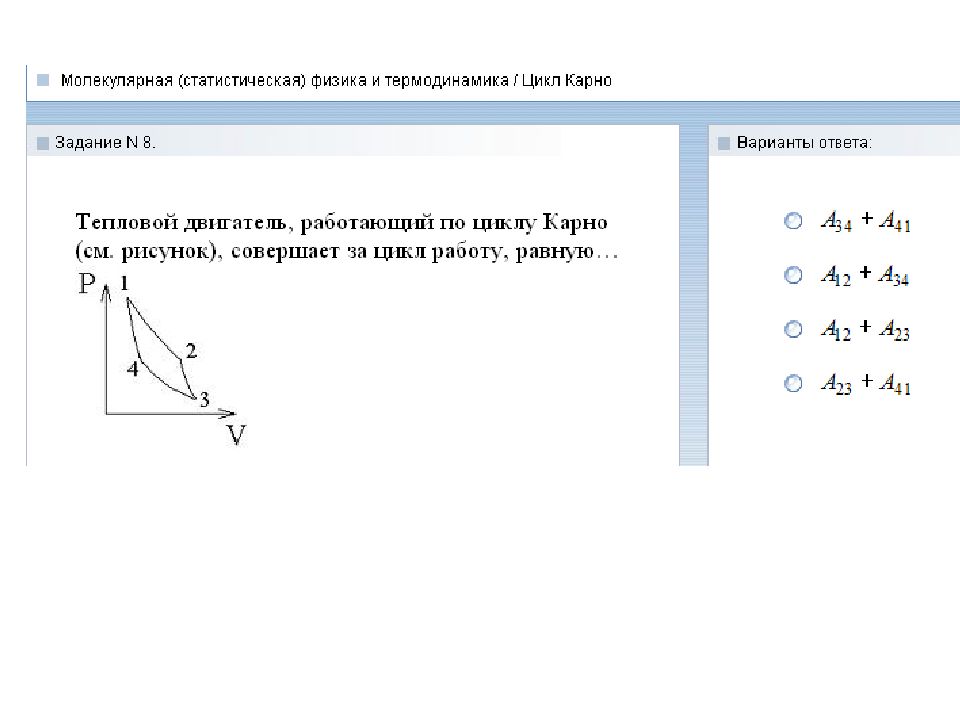
Слайд 46: Следствия: 1). КПД цикла Карно не зависит от рода рабочего тела. 2). КПД определяется только разницей температур нагревателя и холодильника. 3). КПД не может быть 100% даже у идеальной тепловой машины. 4). Невозможно создать вечный двигатель второго рода, работающий в тепловом равновесии без перепада температур
Слайд 54
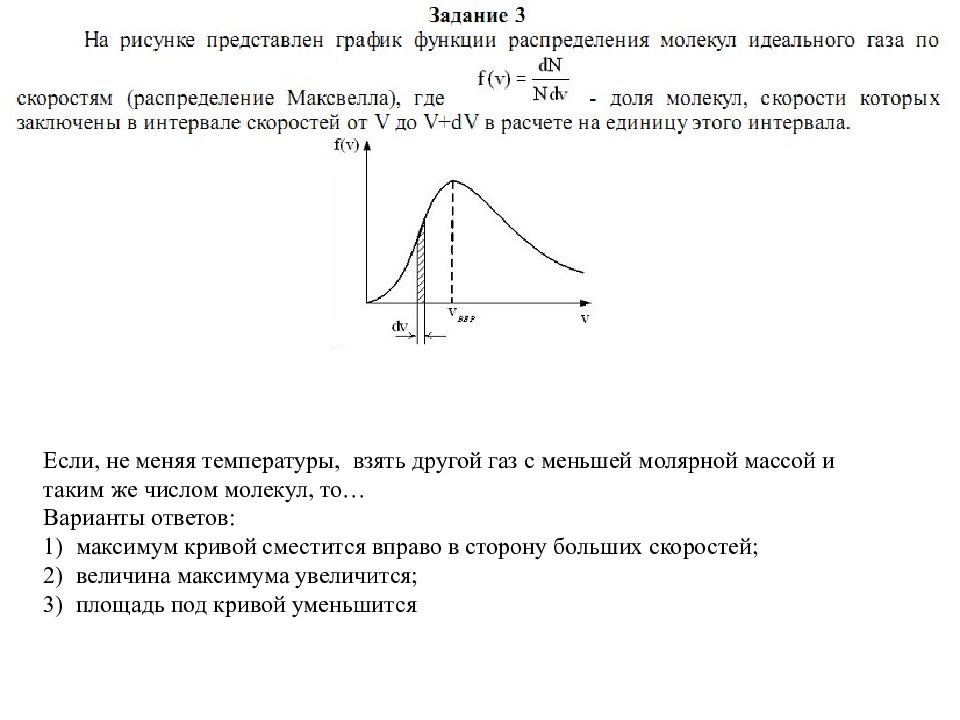
Если, не меняя температуры, взять другой газ с меньшей молярной массой и таким же числом молекул, то… Варианты ответов: 1) максимум кривой сместится вправо в сторону больших скоростей; 2) величина максимума увеличится; 3) площадь под кривой уменьшится