Первый слайд презентации: Раздел 2 Молекулярная физика. Статистическая физика и термодинамика
Курс лекций по общей физики Доцент Петренко Л.Г. Кафедра общей и экспериментальной физики НТУ «ХПИ» Харьков - 2013 год
Все тела в природе состоят из атомов и молекул, находящихся в непрерывном, хаотическом, тепловом движении. 2.1.1. Динамические и статистические закономерности в физике и их методологическое значение с точки зрения философских законов о соотношении случайности и необходимости. Открыто это явление было в 1827 году английским ботаником Р.Броуном, изучавшим движение цветочной пыльцы в воде, а его полная теория была разработана А.Эйнштейном и М.Смолуховским в 1905-1906 г.г. Экспериментальным подтверждением этого является так называемое броуновское движение - хаотическое движение взвешенных в жидкости или газе мельчайших (~10 -6 м) частичек твёрдого вещества под действием ударов окружающих их молекул, совершающих неупорядоченное тепловое движение.
Слайд 3
Количество атомов и молекул в любом теле огромно – от 10 23 м -3 (газы) до 10 28 м -3 (жидкости и твёрдые тела). В основе статистического метода лежат следующие утверждения: - поведение каждой молекулы подчиняется динамическим законам классической механики, а движение всей совокупности молекул является новой формой движения - тепловой, качественно отличающейся от механического движения; - совокупность множества молекул имеет такие свойства, которых нет у каждой молекулы в отдельности - давление, температура, теплопроводность и т.д., - существует определённая количественная связь между свойствами коллектива молекул ( макросвойствами ) и средними значениями физических величин, характеризующими поведение каждой молекулы ( микросвойствами ). Движение каждой отдельной частицы описывается динамическими закономерностями классической физики. Однако, описать поведение громадного числа частиц с помощью законов классической механики невозможно. Такая задача решается методами статистической физики.
Слайд 4
В статистических закономерностях однозначно связаны только вероятности обнаружения определённых значений тех или иных физических величин. Связи между самими величинами неоднозначны. Бесчисленное множество мгновенных случайных состояний молекул (микросостояний), усреднённое по всей системе, как необходимость приводит к вполне определённому состоянию (макросостоянию) этой системы, описываемому макроскопическими параметрами. Исторически вначале были открыты динамические, а затем статистические закономерности. Однако, статистические закономерности наиболее полно отражают объективные связи в природе и как частный случай содержат в себе динамические законы. Динамические теории - низший этап познания мира. В этом проявляется принцип соответствия Бора, согласно которому новая теория включает в себя старую как частный предельный случай.
Слайд 5
Термодинамический метод исследовани я, как и статистический, изучает свойства и процессы, происходящие в макро скопических системах, состоящих из большого числа частиц, однако, при этом не интересуется микро скопической картиной явлений. Термодинамический метод основан на нескольких фундаментальных законах, следующих из анализа опытных фактов. 2.1.2. Термодинамический метод исследования. Термодинамические параметры макроскопического состояния. Равновесные состояния и термодинамические процессы, их изображение на термодинамических диаграммах. Уравнения состояния идеального газа. Объектом исследования в термодинамике является термодинамическая система - совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами (внешней средой), обмениваясь с ними энергией и веществом.
Слайд 6
Массу атомов и молекул обычно выражают в атомных единицах массы. 1 а.е.м. = 1,6605402 10 -27 кг, что составляет 1/12 часть массы атома углерода-12. Количество вещества N выражают в молях. Моль - это количество вещества, в котором содержится столько структурных элементов, сколько атомов содержится в 12 граммах углерода-12. Количество структурных единиц, содержащихся в одном моле вещества, называется числом Авогадро : N A = 6,0221367 10 23 моль -1. Масса одного моля вещества называется молярной массой. Молярную массу удобно выражать через молекулярную : = М r кг/кмоль. Для характеристики состояний термодинамических систем вводятся термодинамические параметры – - экстенсивные ( пропорциональные массе системы) – объём V, внутренняя энергия U, энтропия S, энтальпия Н и т.д. - интенсивные ( не зависящие от массы системы) - давление Р, температура Т, концентрация n и т.д.
Слайд 7
При неизменных внешних условиях термодинамическая система через некоторое время приходит в равновесное состояние, в котором все параметры любой малой макроскопической части остаются постоянными сколь угодно долго. Термодинамическое равновесие включает в себя: механическое, термическое и химическое равновесие. Равновесное состояние можно задать с помощью ограниченного числа термодинамических параметров. Уравнение, устанавливающее связь между термодинамическими параметрами в условиях равновесия называется уравнением состояния : f(P,V,T)=0. Конкретный вид этой функции устанавливается опытным путём. В термодинамике широко используется модель идеального газа. В идеальном газе собственный объём молекул пренебрежимо мал по сравнению с объёмом сосуда, в котором находится газ, а взаимодействие молекул со стенками сосуда и друг с другом сводится лишь к упругим столкновениям.
Слайд 8
Уравнение состояния идеального газа можно представить в разных формах, введя такие параметры, как количество молей N, плотность , концентрация n, постоянная Больцмана k : , где ; , где ; , где,. На основе опытных законов Бойля-Мариотта и Гей-Люссака французский физик Б.Клапейрон и российский учёный Д.И.Менделеев записали уравнение состояния идеального газа : , где R = 8,31 Дж/моль. К - универсальная газовая постоянная.
Слайд 9
Изменение состояния термодинамической системы называется термодинамическим процессом. Процесс всегда приводит к нарушению равновесия. Однако, если процесс протекает бесконечно медленно, его можно рассматривать как смену одного равновесного состояния другим. Такие процессы называются квазистатическими или равновесными процессами. Термодинамические процессы удобно изображать на термодинамических диаграммах - графических изображениях соотношений между термодинамическими параметрами. Диаграммы процессов: изотермического ( Т=const ), изобарического ( Р=const ), изохорического ( V=const ). V Т Т V Т = const Р Р Р = const V = const
Слайд 10
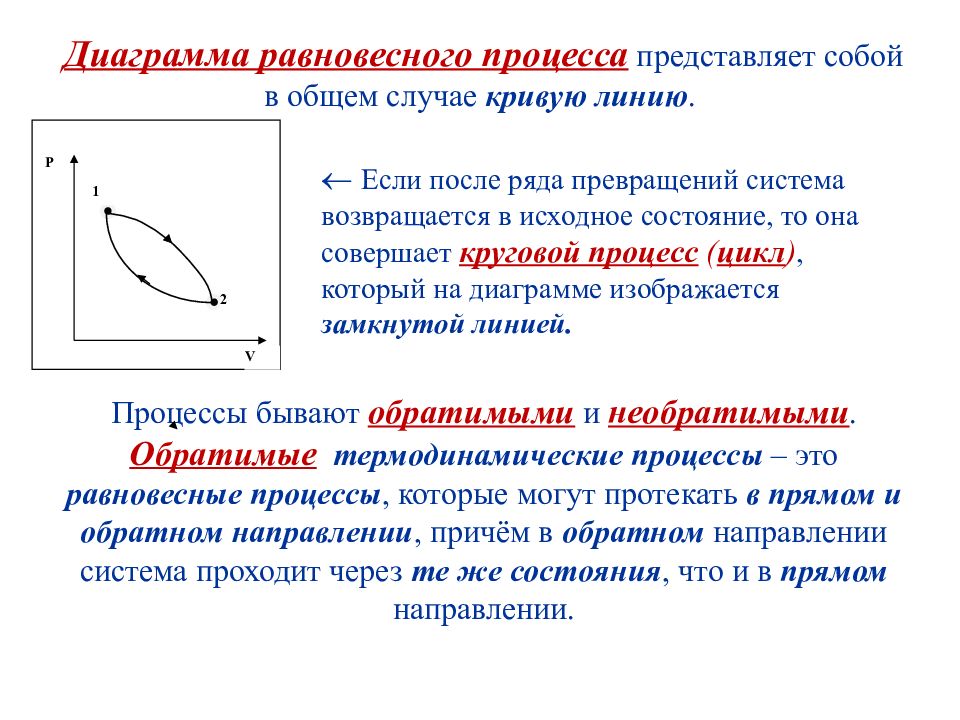
Процессы бывают обратимыми и необратимыми. Обратимые термодинамические процессы – это равновесные процессы, которые могут протекать в прямом и обратном направлении, причём в обратном направлении система проходит через те же состояния, что и в прямом направлении. V Р 2 1 Если после ряда превращений система возвращается в исходное состояние, то она совершает круговой процесс ( цикл ), который на диаграмме изображается замкнутой линией. Диаграмма равновесного процесса представляет собой в общем случае кривую линию.
Слайд 11
Все процессы в термодинамике обусловлены передачей энергии либо путём совершения работы, либо путём теплообмена, либо тем и другим одновременно. Количество энергии, полученное (отданное) системой в процессе совершения работы, называется работой и обозначается А. Количество энергии, полученное (отданное) системой в процессе теплообмена, называется теплотой и обозначается Q. 2.1. 3. Работа, количество теплоты и внутренняя энергия. Эквивалентность теплоты и работы. Общность и ограниченность термодинамического метода исследования. Изменить состояние термодинамической системы можно двумя способами: 1) заставить систему совершить работу над внешними телами ( А>0 ) или внешним телам совершить работу над системой ( А*<0 ); 2) осуществить теплообмен между системой и окружающей средой ; количество тепла, получаемое системой при теплообмене, положительно ( Q >0 ), а отдаваемое системой во внешнюю среду – отрицательно ( Q* <0 ).
Слайд 12
Связь между теплотой и работой была установлена экспериментально Ю.Майером и Дж.Джоулем, которые сформулировали принцип эквивалентности теплоты и работы (то есть их взаимопревращаемость) и установили Внутренней энергией U термодинамической системы называется сумма кинетической энергии хаотического движения молекул, потенциальной энергии их взаимодействия и внутримолекулярной энергии. Термодинамическая система состоит из большого числа микрочастиц, находящихся в непрерывном тепловом движении и взаимодействии между собой. Количественной мерой любого движения является энергия. механический эквивалент теплоты и тепловой эквивалент работы : 1 кал = 4,18 Дж и 1 Дж = 0,24 кал. В СИ теплота и работа выражаются в джоулях : [ Q ] = [ А ] = 1Дж.
Слайд 13
Внутренняя энергия может изменяться только при взаимодействии с внешними телами. Внутренняя энергия изолированной системы не изменяется. Внутренняя энергия является функцией состояния. Абсолютное значение внутренней энергии определить практически невозможно. Обычно при решении термодинамических задач достаточно знать изменение внутренней энергии U. Внутренняя энергия системы равна сумме внутренних энергий составляющих её частей, то есть обладает свойством аддитивности. Опыт показывает, что внутренняя энергия идеального газа в широком диапазоне температур пропорциональна абсолютной температуре : U ~ T, а значит изменение внутренней энергии пропорционально изменению температуры : U ~ T.
Слайд 14
Термодинамика изучает свойства тел, не опираясь на какие-либо представления об их структуре, исследует явления, непосредственно наблюдаемые на опыте, и оперирует величинами, измеряемыми либо непосредственно, либо вычисляемыми с помощью других величин, измеренных экспериментально. Термодинамика характеризует с количественной стороны закономерности превращения энергии в явлениях различной природы – тепловых, электрических, магнитных, оптических, химических и др. В этом состоит общность термодинамического метода исследований.
Слайд 15
Молекулярно-кинетическая теория основана на статистическом методе. 2.1.4. Развитие молекулярно-кинетической (статистической) теории. Вывод уравнения состояния идеального газа и его сравнение с экспериментальным уравнением Менделеева-Клапейрона. Средняя кинетическая энергия частицы. Постоянная Больцмана. Молекулярно-кинетический смысл температуры. Первые представления о кинетической природе теплоты высказал в 1745 г. М.В.Ломоносов в книге «Размышления о причинах теплоты и холода». Начало развитию теории было положено в1647г. французским учёным П.Гассенди, утверждавшим, что все вещества состоят из неделимых частиц, отличающихся формой, величиной, массой. Общие положения классической молекулярно-кинетической (статистической) теории состоят в следующем: 1) все частицы вещества являются « меченными » ; 2) каждая частица может иметь совершенно произвольные значения координат и компонент скорости, независимо от других частиц системы; 3) все физические процессы протекают в пространстве и времени непрерывно ; 4) во всех процессах выполняются законы сохранения - энергии, импульса, момента импульса, электрического заряда и числа частиц.
Слайд 16
В молекулярно-кинетической теории используется модель идеального газа. Основным уравнением молекулярно-кинетической теории газов является уравнение, устанавливающее связь давления Р газа на стенки сосуда со средней кинетической энергией молекул : Сравнение этого уравнения с уравнением состояния идеального газа: P = nkT позволяет определить температурные зависимости средней квадратичной скорости и средней кинетической энергии молекул: где n - концентрация молекул в сосуде; m - масса молекулы газа; < v кв > - средняя квадратичная скорость молекул. Постоянная Больцмана играет роль коэффициента пропорциональности между средней кинетической энергией молекул и абсолютной температурой. , . , Таким образом, согласно молекулярно-кинетическим представлениям абсолютная температура – это мера средней кинетической энергии поступательного движения молекул идеального газа.
Слайд 17
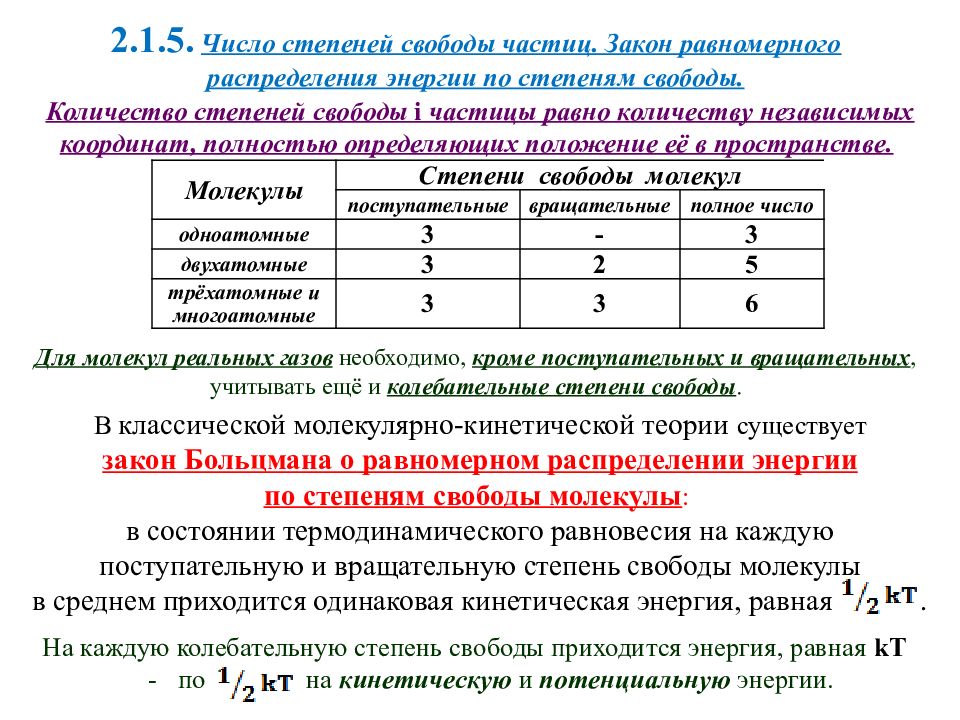
Количество степеней свободы i частицы равно количеству независимых координат, полностью определяющих положение её в пространстве. 2.1.5. Число степеней свободы частиц. Закон равномерного распределения энергии по степеням свободы. На каждую колебательную степень свободы приходится энергия, равная kT - по на кинетическую и потенциальную энергии. В классической молекулярно-кинетической теории существует закон Больцмана о равномерном распределении энергии по степеням свободы молекулы : в состоянии термодинамического равновесия на каждую поступательную и вращательную степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная. Для молекул реальных газов необходимо, кроме поступательных и вращательных, учитывать ещё и колебательные степени свободы. Молекулы Степени свободы молекул поступательные вращательные полное число одноатомные 3 - 3 двухатомные 3 2 5 трёхатомные и многоатомные 3 3 6
Слайд 18
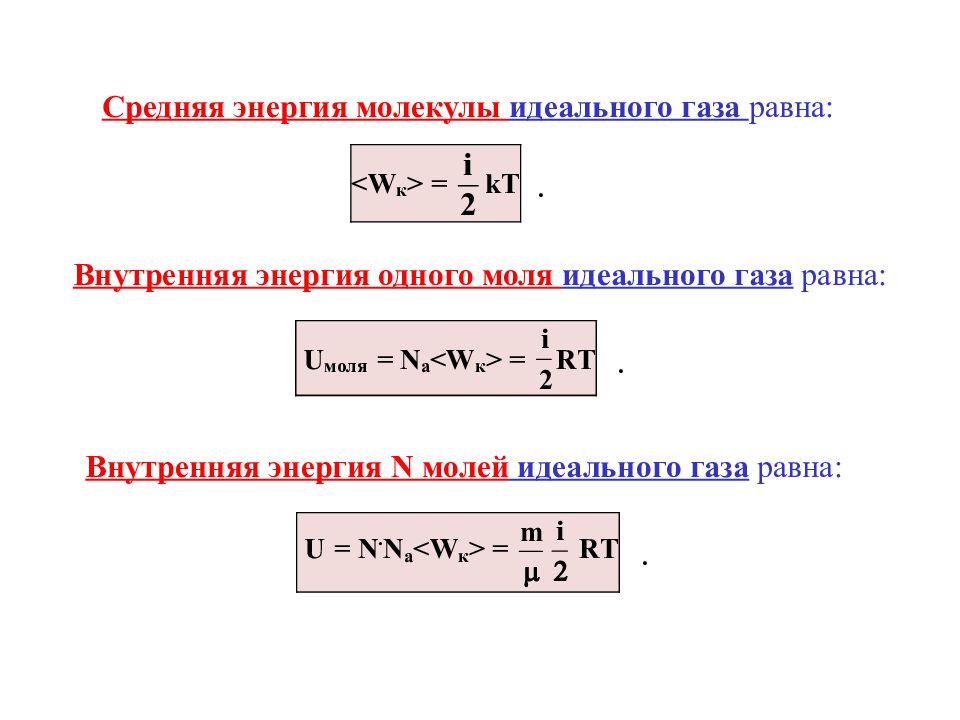
Средняя энергия молекулы идеального газа равна: Внутренняя энергия одного моля идеального газа равна: Внутренняя энергия N молей идеального газа равна: . . .
Слайд 19: 2.2. КЛАССИЧЕСКИЕ СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
Из-за непрерывного хаотического движения молекул газа, многократных их столкновений друг с другом скорости этих молекул непрерывно изменяются по величине и направлению. Но, если газ находится в равновесном состоянии, то существует вполне определённое стационарное (не изменяющееся со временем) распределение молекул по скоростям, подчиняющееся статистическим закономерностям. 2.2.1. Распределения Максвелла. Распределение частиц по абсолютным значениям скорости. Скорости теплового движения частиц. Такое состояние газа называется подвижным равновесием. При этом соблюдается принцип детального равновесия – количество частиц 1 2, перешедших из состояния 1 в состояние 2 в любой промежуток времени, равно числу частиц 2 1, перешедших из состояния 2 в состояние 1 : 1 2 = 2 1. Поскольку такие переходы имеют вероятностный характер, то выполняется равенство: где 1 и 2 - число частиц, находящихся в состоянии 1 и 2 соответственно; Р 1 2 и Р 2 1 - вероятности переходов частицы из состояния 1 в 2 и из состояния 2 в 1 соответственно. ,
Слайд 20
Таким образом, в состоянии подвижного равновесия при постоянной температуре ( Т=const ) как бы не изменялась скорость молекул при столкновениях, средняя квадратичная скорость молекул массой m остаётся постоянной и равной: Распределение же молекул по скоростям подчиняется статистическому закону, теоретически выведенному в 1859 году Дж.Максвеллом. . Закон Максвелла описывается некоторой функцией f ( v ), называемой функцией распределения молекул по скоростям : В газе, содержащем N молекул с разными скоростями (в интервале [0, ] ), относительное число молекул, имеющих скорости в интервале [ v, v + dv ], равно: . . (1)
Слайд 21
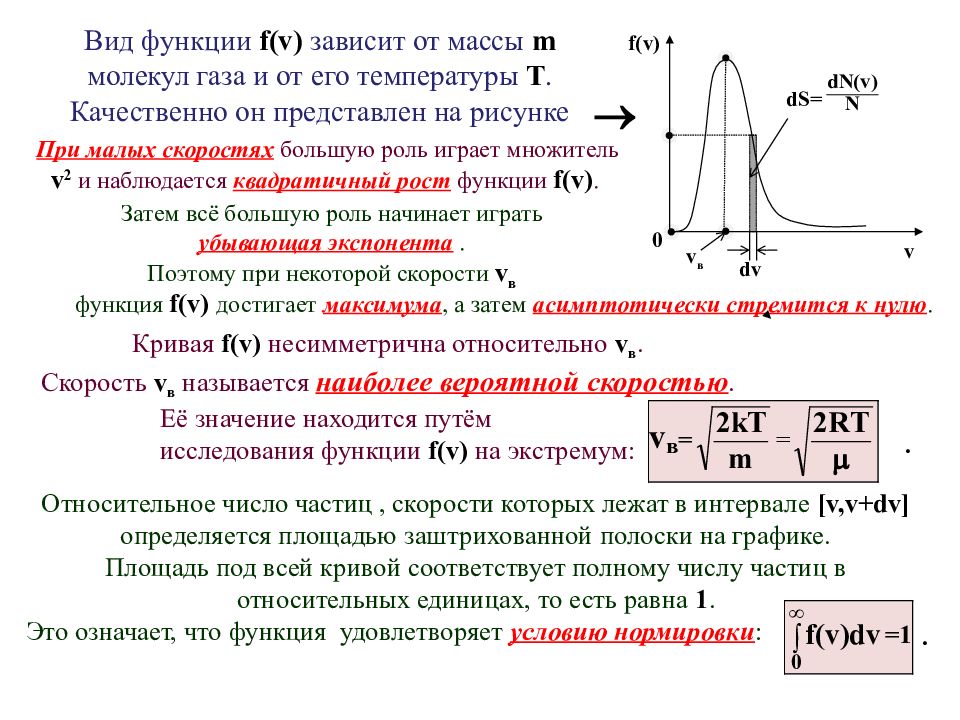
Вид функции f(v) зависит от массы m молекул газа и от его температуры Т. Качественно он представлен на рисунке Относительное число частиц, скорости которых лежат в интервале [ v, v + dv ] определяется площадью заштрихованной полоски на графике. Площадь под всей кривой соответствует полному числу частиц в относительных единицах, то есть равна 1. Это означает, что функция удовлетворяет условию нормировки : При малых скоростях большую роль играет множитель v 2 и наблюдается квадратичный рост функции f ( v ). Затем всё большую роль начинает играть убывающая экспонента. Поэтому при некоторой скорости v в Кривая f(v) несимметрична относительно v в. Скорость v в называется наиболее вероятной скоростью. Её значение находится путём исследования функции f(v) на экстремум: функция f(v) достигает максимума, а затем асимптотически стремится к нулю. . . v в 0 dv f(v) v dS=
Слайд 22
Функцию распределения можно выразить в более простом виде, если ввести относительные скорости u = v / v в и du = dv / v в : С повышением температуры наиболее вероятная скорость v в, а значит и максимум на кривой f ( v ) смещается в область больших скоростей. Площадь под кривой при этом остаётся неизменной, так как полное число частиц не меняется (выполняется условие нормировки). Поэтому кривая растягивается и высота максимума на ней уменьшается. . Зная распределение молекул по скоростям f ( v ), можно рассчитать среднюю арифметическую скорость молекул : (2) . v в1 f(v) v Т 2 >T 1 v в2 Т 1 0
Слайд 23
Таким образом, получен известный ранее результат. От распределения молекул по скоростям можно перейти к распределению Максвелла молекул по кинетическим энергиям : где d N ( W к ) - число молекул, имеющих кинетические энергии в интервале [ W к, W к + dW к ]. , Распределение Максвелла молекул по кинетическим энергиям позволяет определить среднюю кинетическую энергию молекул : Между наиболее вероятной, средней арифметической и средней квадратичной скоростями существует соотношение: v в : < v > : < v кв > = 1 : 1,13 : 1,22. Это следует из соотношений , , .
Слайд 24
При выводе основного уравнения молекулярно-кинетической теории и Максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа не действуют внешние силы. В этом случае плотность (концентрация) газа в сосуде постоянна. 2.2.2. Распределения Больцмана. Здесь Р и Р 0 – давление газа на высоте h и на поверхности Земли ( h =0 ) соответственно; - молярная масса газа; m – масса молекулы газа; g - ускорение свободного падения; R - универсальная газовая постоянная; k – постоянная Больцмана; Т – абсолютная температура. . Если газ находится в силовом поле, то его плотность (концентрация) неоднородна и зависит от особенностей силового поля. Например, в однородном поле силы тяжести, плотность (концентрация) воздуха зависит от расстояния до поверхности Земли, что обусловлено уменьшением давления при увеличении этого расстояния. Закон изменения давления газа с высотой над поверхностью Земли определяется барометрической формулой : Барометрическую формулу можно преобразовать, если учесть, что Р = nkT : . Здесь n и n 0 – концентрация молекул газа на высоте h и на поверхности Земли ( h =0 ) соответственно.
Слайд 25
В формуле распределения концентрации газа вблизи поверхности Земли в показателе экспоненты величина mgh = W п является потенциальной энергией молекулы в поле силы тяжести. Таким образом, уравнение можно представить в виде: Из распределения Больцмана следует, что концентрация (плотность) газа больше там, где потенциальная энергия его молекул меньше. Эта формула называется распределением Больцмана молекул по потенциальным энергиям в силовом поле. . Чем выше температура, тем медленнее убывает с высотой давление и концентрация газа. 0 h Р T 1 >T 2 T 2 Р 0 0 h Р 1 < 2 2 Р 0 Чем тяжелее молекулы газа (больше его молярная масса), тем быстрее убывает с высотой давление и концентрация газа. Существование атмосферы обусловлено двумя причинами: 1) гравитационным притяжением и 2) тепловым движением молекул. Распределение Больцмана для хаотически движущихся частиц с одинаковой массой справедливо в любом внешнем потенциальном поле, а не только в поле силы тяжести.
Слайд 26: 2.3. ЯВЛЕНИЯ ПЕРЕНОСА
В физической кинетике рассматриваются процессы, происходящие в системах с пространственными неоднородностями либо плотности, либо температуры, либо скорости упорядоченного движения частиц или слоёв вещества. Такие системы являются неравновесными, в них медленно и необратимо происходит самопроизвольное выравнивание этих неоднородностей - возникают потоки либо вещества, либо энергии, либо импульса упорядоченного движения частиц. Такие процессы называются кинетическими явлениями или явлениями переноса. 2.3.1. Понятие о физической кинетике. Время релаксации. Время выравнивания. Эффективное сечение рассеяния. Среднее число столкновений, средняя длина свободного пробега и эффективный диаметр молекул. Общие представления о явлениях переноса. К ним относятся: диффузия (перенос массы вещества), теплопроводность (перенос энергии молекул), электропроводность (перенос электрического заряда), внутреннее трение (перенос импульса молекул). 2.3. ЯВЛЕНИЯ ПЕРЕНОСА
Слайд 27
Процесс перехода термодинамической системы из неравновесного состояния в равновесное называется процессом релаксации. Время, за которое первоначальное отклонение какой-либо физической величины от равновесного значения уменьшится в е раз ( е ≈2,71 – основание натурального логарифма), называется временем релаксации. Процессы выравнивания неоднородностей являются медленными. Время релаксации в газах значительно меньше, чем в жидкостях, а в жидкостях – значительно меньше, чем в твёрдых телах. Молекулы газа, двигаясь хаотически, непрерывно сталкиваются друг с другом. Расстояние, проходимое молекулой между двумя последовательными столкновениями, называется длиной свободного пробега . Это расстояние всё время меняется. Поэтому вводится понятие средней длины свободного пробега молекул < >, являющейся характеристикой всех молекул системы при заданных значениях температуры Т и давления газа Р. Для вычисления < > в молекулярно-кинетической теории выбирается модель химически однородного газа, молекулы которого представляют собой шарики диаметром d 10 -10 м, движущиеся среди других «застывших» шариков-молекул ( d зависит от химической природы газа).
Слайд 28
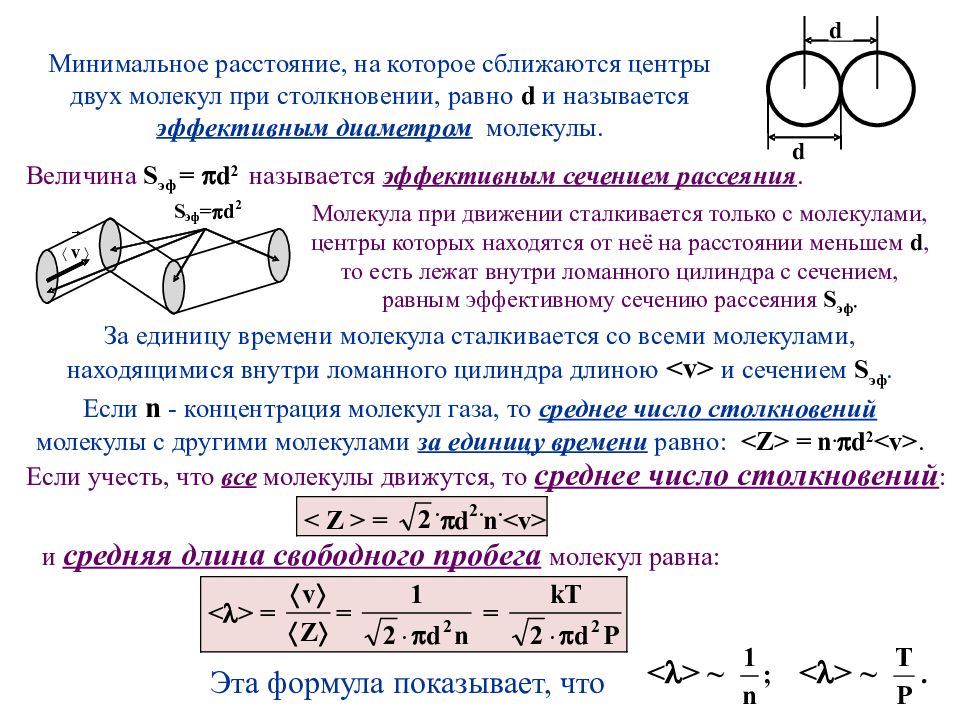
Минимальное расстояние, на которое сближаются центры двух молекул при столкновении, равно d и называется эффективным диаметром молекулы. За единицу времени молекула сталкивается со всеми молекулами, находящимися внутри ломанного цилиндра длиною < v > и сечением S эф. Если n - концентрация молекул газа, то среднее число столкновений молекулы с другими молекулами за единицу времени равно: < Z > = n. d 2 < v >. Молекула при движении сталкивается только с молекулами, центры которых находятся от неё на расстоянии меньшем d, то есть лежат внутри ломанного цилиндра с сечением, равным эффективному сечению рассеяния S эф. Величина S эф = d 2 называется эффективным сечением рассеяния. Если учесть, что все молекулы движутся, то среднее число столкновений : и средняя длина свободного пробега молекул равна: Эта формула показывает, что
Слайд 29
1. Диффузия - это обусловленное тепловым движением молекул самопроизвольное выравнивание плотности (концентрации) молекул в смеси двух или нескольких веществ (твёрдых, жидких, газообразных). 2.3.2. Понятие о молекулярно-кинетической теории явлений переноса. Явление диффузии. Коэффициент диффузии. Диффузия в газах и твёрдых телах. Явление теплопроводности. Коэффициент теплопроводности. Температуропроводность. Вязкость. Коэффициент вязкости газов и жидкостей. Динамическая и кинематическая вязкости. В химически однородном газе диффузия подчиняется закону Фика, установленному экспериментально в 1855 году: , где J m - плотность потока массы - это масса вещества, переносимого за единицу времени через единичную площадку, перпендикулярную оси Х, что можно представить в виде: «-» означает, что перенос массы происходит в направлении убывания плотности; - градиент плотности в направлении нормали к единичной площадке (ось Х ) ; D - коэффициент диффузии, согласно МКТ равный:, , где < > - средняя длина свободного пробега молекул, < v > - их средняя арифметическая скорость.
Слайд 30
2. Теплопроводность - это направленный перенос внутренней энергии вещества, возникающий при наличии разности температур, вызванной какими-либо внешними причинами. , Скорость выравнивания температуры в среде при нестационарной теплопроводности характеризует коэффициент температуропроводности : Перенос энергии в виде теплоты подчиняется закону Фурье, установленному экспериментально в 1822 году : где J U - плотность теплового потока - это количество тепла, переносимого за единицу времени через единичную площадку, перпендикулярную оси Х, что можно представить в виде: « - » означает, что перенос теплоты происходит в направлении убывания температуры; - градиент температуры Т в направлении нормали к единичной площадке (ось Х ) ; - коэффициент теплопроводности, согласно МКТ равный: ( < > - средняя длина свободного пробега молекул, < v > - их средняя арифметическая скорость, - плотность вещества; с v - его удельная теплоёмкость при постоянном объёме). ( с р - удельная теплоёмкость при постоянном давлении).
Слайд 31
3. Внутреннее трение (вязкость) - это возникновение сил трения между слоями вещества, перемещающимися параллельно друг другу с различными по модулю скоростями. Силы трения направлены по касательной к поверхности соприкасающихся слоёв. С точки зрения МКТ причиной вязкости является наложение упорядоченного движения слоёв и хаотического теплового движения отдельных молекул. . Сила внутреннего трения согласно закону Ньютона, установленному им экспериментально в 1687 году, равна: где - градиент скорости слоёв в направлении, перпендикулярном направлению движения этих слоёв (в направлении оси Z ), S - площадь, на которой действует сила трения F тр, - коэффициент вязкости или динамическая вязкость. Взаимодействие слоёв можно рассматривать как процесс передачи импульса р от слоя к слою. Тогда закон Ньютона можно представить в виде:
Слайд 32
В уравнении J р - плотность потока импульса р - это импульс, переносимый за единицу времени через единичную площадку, перпендикулярную оси Z : . Согласно выводам МКТ коэффициент вязкости (динамическая вязкость) равен: В гидродинамике, кроме динамической вязкости, используется также кинематическая вязкость, характеризующая степень ламинарности потока вещества: По найденным экспериментально одним величинам можно рассчитать другие. «-» означает, что перенос импульса происходит в направлении убывания скорости. Из сопоставления формул, описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были открыты задолго до создания молекулярно-кинетической теории, позволившей установить, что все эти явления обусловлены механизмом перемешивания молекул в процессе их хаотического движения и столкновения друг с другом. Коэффициенты диффузии, теплопроводности и вязкости связаны друг с другом простыми соотношениями: Кинематическая вязкость вещества тем больше, чем больше динамическая вязкость и меньше плотность. .
Слайд 33
Систематизация параметров и уравнений, описывающих явления переноса. Процесс Кинетический параметр Плотность потока Уравнения процессов Коэффициенты в кинетических уравнениях Диффузия Масса m Внутреннее трение Импульс р Тепло- проводность Внутренняя энергия U Здесь: - средняя длина свободного пробега молекул; - средняя арифметическая скорость молекул; - плотность вещества; - удельная теплоёмкость вещества, измеренная при постоянном объёме.
Слайд 34: 2.4. ОСНОВЫ ТЕРМОДИНАМИКИ
Первоначально термодинамика возникла как теория тепловых машин, которые в начале 19 века уже широко использовались в производстве. 2.4.1. Первое начало термодинамики. Закон сохранения и превращения энергии доказан экспериментально для ограниченного круга явлений с точностью, не превышающей погрешность измерений. Французский физик и инженер С. Карно в 1824 году опубликовал труд, в котором положено начало развитию термодинамики. Немецкий физик Р.Клаузиус в 1850 году и независимо от него английский физик У.Томсон (лорд Кельвин) в 1851 году дали теоретическое обоснование идеям Карно, связав их с установленным незадолго до того (в 40-е годы) Майером, Джоулем и Гельмгольцем законом сохранения и превращения энергии. Этот закон, являющийся одним из фундаментальных законов природы, лежит в основе термодинамики и носит название первого начала термодинамики.
Слайд 35
Первое начало термодинамики устанавливает закономерности взаимодействия термодинамической системы с окружающей средой. Это взаимодействие сводится к двум процессам – совершению работы и теплообмену. В результате внутренняя энергия системы изменяется. Первое начало термодинамики можно представить в нескольких формах в зависимости от конкретных условий энергообмена. 3) В любом периодическом процессе (цикле) термодинамическая система не может совершить работу без подведения энергии извне или работу большую, чем количество подводимого тепла : А Q. Иными словами - вечный двигатель первого рода невозможен. 1) Количество тепла Q, сообщённое системе, расходуется на приращение внутренней энергии U системы и на совершение системой работы А> 0 над внешними телами : Q = U + А. 2) Изменение внутренней энергии U может происходить в результате передачи системе количества тепла Q и совершения внешними телами работы А < 0 над системой : U = Q + А'.
Слайд 36
Р При взаимодействии термодинамической системы с внешними телами изменяются её термодинамические параметры. Работу, изменение внутренней энергии системы и количество теплоты можно рассчитывать, зная изменение параметров этой системы. Например, газ, находящийся в замкнутом цилиндре под поршнем, при расширении действует на поршень силой F = PS, где P - давление газа, S - площадь поверхности поршня. Эта сила перемещает поршень на расстояние dl и объём газа увеличивается на величину: dV = Sdl. При этом газ совершает работу: dA = Fdl = PSdl = PdV. Если в термодинамическом процессе давление Р изменяется, то при изменении объёма от V 1 до V 2 совершается работа: 0 1 V Р 2 V 2 V 1 d V S F dl Р Таким образом, элементарная работа равна:. Эта формула верна только в обратимом процессе. На Р V -диаграмме элементарная работа соответствует затемнённой полосе, а полная работа соответствует площади, ограниченной кривой P = f ( V ), осью V и прямыми, параллельными оси ординат и проведенными через точки V 1 и V 2.
Слайд 37
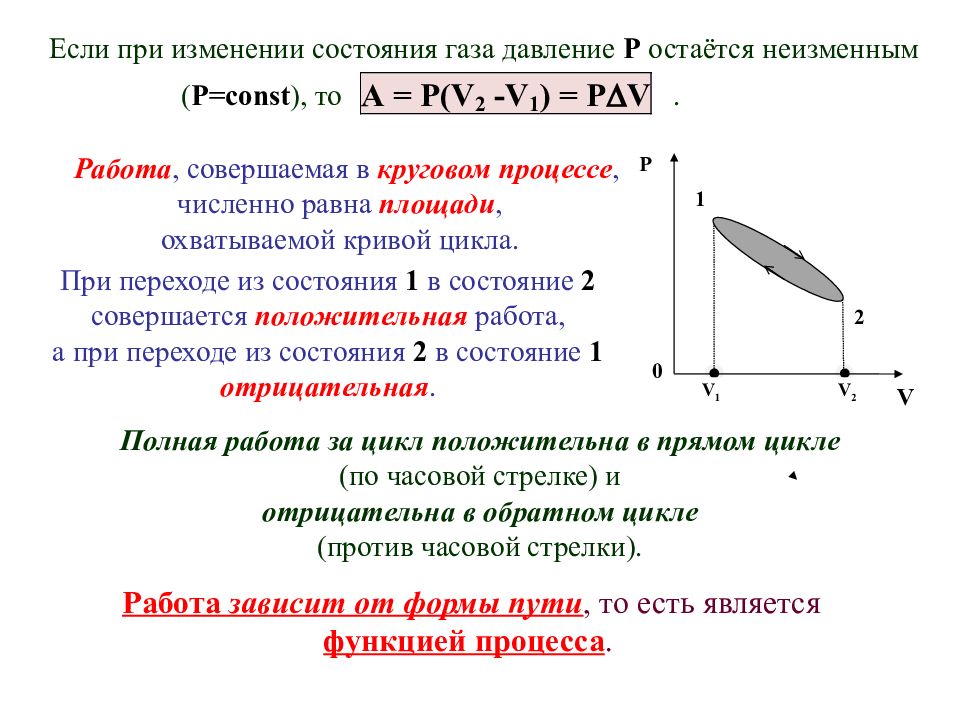
При переходе из состояния 1 в состояние 2 совершается положительная работа, а при переходе из состояния 2 в состояние 1 отрицательная. Работа, совершаемая в круговом процессе, численно равна площади, охватываемой кривой цикла. 0 V Р 2 1 V 2 V 1 Если при изменении состояния газа давление Р остаётся неизменным ( P=const ), то. Работа зависит от формы пути, то есть является функцией процесса. Полная работа за цикл положительна в прямом цикле (по часовой стрелке) и отрицательна в обратном цикле (против часовой стрелки).
Слайд 38
Поскольку m = N. , то между молярной и удельной теплоёмкостями существует простая связь: Теплоёмкостью тела называется величина, равная количеству тепла, которое нужно сообщить этому телу, чтобы повысить его температуру на 1 К : Изменение параметров термодинамической системы при передаче ей теплоты зависит от таких свойств системы как теплоёмкость. Теплоёмкость единицы массы вещества называется удельной теплоёмкостью : Теплоёмкость моля вещества называется молярной теплоёмкостью : Теплоёмкость газов зависит от условий, в которых она измеряется. Различают теплоёмкость, измеренную при постоянном объёме газа: С v, и теплоёмкость, измеренную при постоянном давлении : С p. . . . .
Слайд 39
2.4.2. Применение первого начала термодинамики к изопроцессам и адиабатному процессу. Молярная теплоёмкость, измеренная в изохорном процессе равна: В результате взаимодействия термодинамической системы с внешними телами в общем случае могут меняться все параметры. Однако, особый интерес представляют процессы, протекающие при неизменном каком-либо параметре, так называемые изопроцессы : изохорный ( V = const ), изобарный ( Р = const ), изотермный ( Т = const ), а также адиабатный, протекающий без теплообмена с окружающей средой. Изохорный процесс. В изохорном процессе V = const, dV = 0, поэтому работа не совершается: dA = PdV = 0. Всё тепло, подведенное к системе, расходуется на увеличение её внутренней энергии. Первое начало термодинамики в изохорном процессе представляется в виде:. Р 2 Р 1 0 V Р 2 1 V .
Слайд 40
Из формулы для C V следует закон Джоуля для идеального газа, определяющий изменение внутренней энергии идеального газа в любых процессах : Изобарный процесс В изобарном процессе Р = const, d Р = 0, поэтому совершаемая работа равна: А = Р( V 2 - V 1 ) = P V. Если система переходит из состояния 1, описываемого уравнением PV 1 = NRT 1, в состояние 2, описываемое уравнением PV 2 = NRT 2, то изменение её объёма можно выразить . . V 2 Р V 1 0 V Р 2 1 Графически работа представляется затемнённым прямоугольником. через изменение её температуры: P(V 2 - V 1 ) = NR(T 2 -T 1 ) или P V = NR T. Тогда работу в изобарном процессе можно выразить следующим образом: А = P V = NR T = ( m/ ) R T. Или в дифференциальной форме: d А = PdV = NRdT = ( m/ ) RdT. Из этой формулы следует физический смысл универсальной газовой постоянной - универсальная газовая постоянная численно равна работе изобарического расширения одного моля идеального газа при нагреве его на 1К : R = A / N T.
Слайд 41
Первое начало термодинамики для изобарного процесса может быть выражено следующим образом: . Молярная теплоёмкость, измеренная в изобарном процесс е, равна: или Это уравнение выражает закон Майера – для нагревания одного моля идеального газа на 1 К при постоянном давлении, кроме затраты тепла на увеличение внутренней энергии газа необходимо также совершить работу расширения газа, численно равную R.
Слайд 42
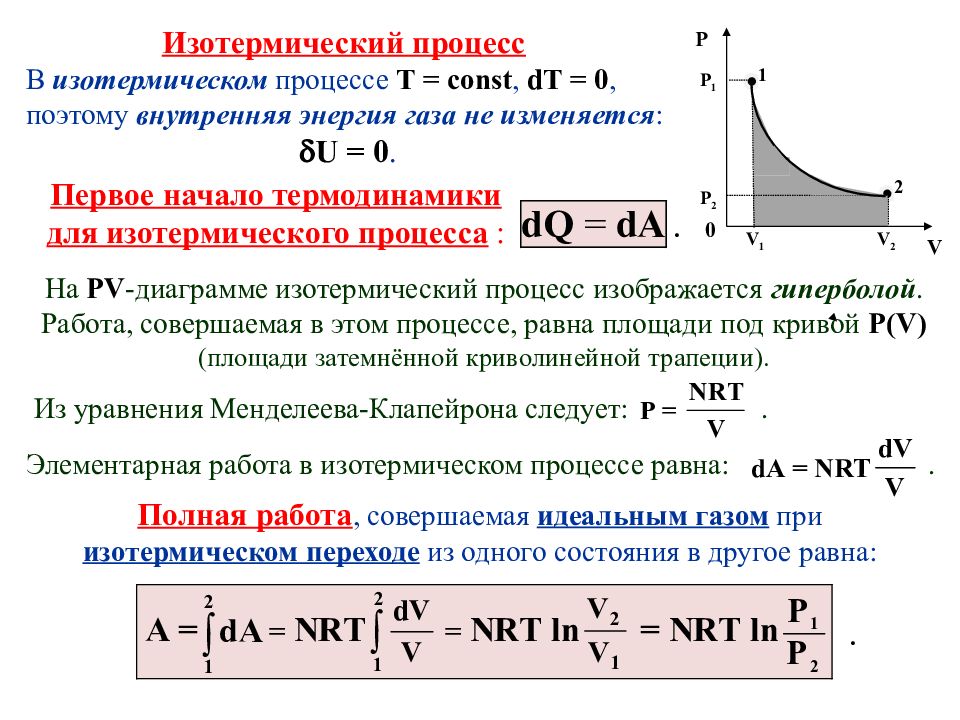
V 2 Р 2 V 1 0 V Р 2 1 Р 1 Изотермический процесс В изотермическом процессе Т = const, d Т = 0, поэтому внутренняя энергия газа не изменяется : U = 0. . Полная работа, совершаемая идеальным газом при изотермическом переходе из одного состояния в другое равна: Из уравнения Менделеева-Клапейрона следует:. Первое начало термодинамики для изотермического процесса : На PV -диаграмме изотермический процесс изображается гиперболой. Работа, совершаемая в этом процессе, равна площади под кривой P ( V ) (площади затемнённой криволинейной трапеции). Элементарная работа в изотермическом процессе равна:. .
Слайд 43
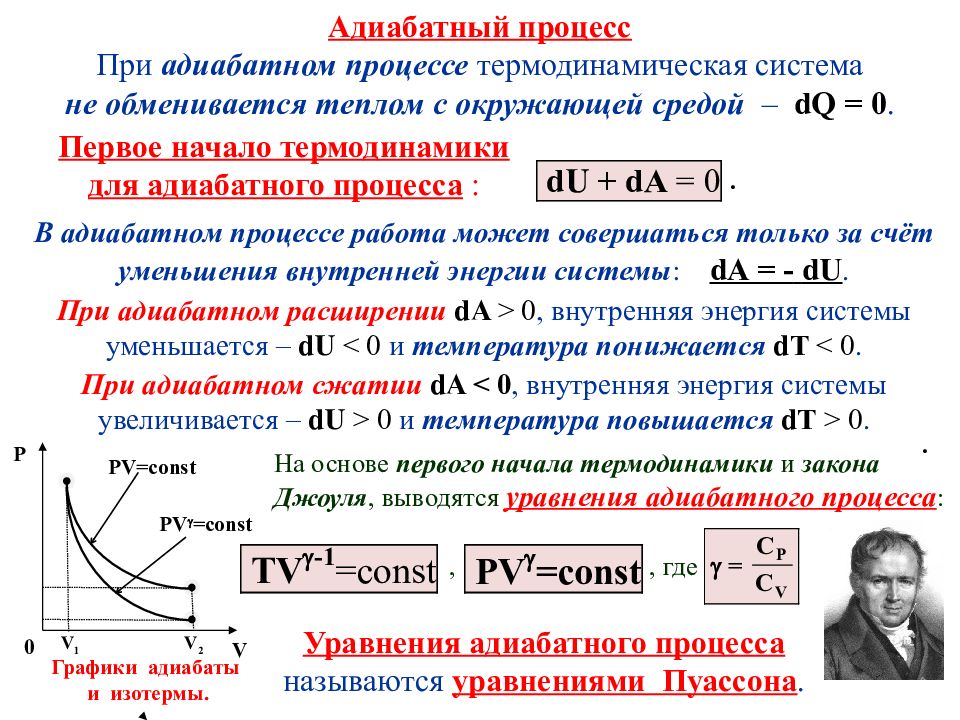
Адиабатный процесс При адиабатном процессе термодинамическая система не обменивается теплом с окружающей средой – dQ = 0. . Уравнения адиабатного процесса называются уравнениями Пуассона. Первое начало термодинамики для адиабатного процесса : В адиабатном процессе работа может совершаться только за счёт уменьшения внутренней энергии системы : dA = - dU. При адиабатном расширении dA > 0, внутренняя энергия системы уменьшается – dU < 0 и температура понижается d Т < 0. При адиабатном сжатии dA < 0, внутренняя энергия системы увеличивается – dU > 0 и температура повышается d Т > 0. На основе первого начала термодинамики и закона Джоуля, выводятся уравнения адиабатного процесса : , V 2 V 1 0 V Р PV=const PV =const . Графики адиабаты и изотермы. , где
Слайд 44
2.4.3. Теплоёмкость одноатомных и многоатомных газов. Недостаточность классической теории теплоёмкостей. Границы применимости классического закона распределения энергии по степеням свободы. при постоянном объёме : В классической молекулярно-кинетической теории ( МКТ ) существует закон равномерного распределения энергии по степеням свободы молекулы, согласно которой в состоянии теплового равновесия средняя энергия молекулы идеального газа, имеющей i степеней свободы, равна: <W к >= ( i/2 ) kT. Внутренняя энергия одного моля идеального газа : U моля =N a <W к >= ( i/2 ) RT, а внутренняя энергия N молей идеального газа равна: Молярная теплоёмкость идеального газа, измеренная: при постоянном давлении : Постоянная Пуассона равна: . , . .
Слайд 45
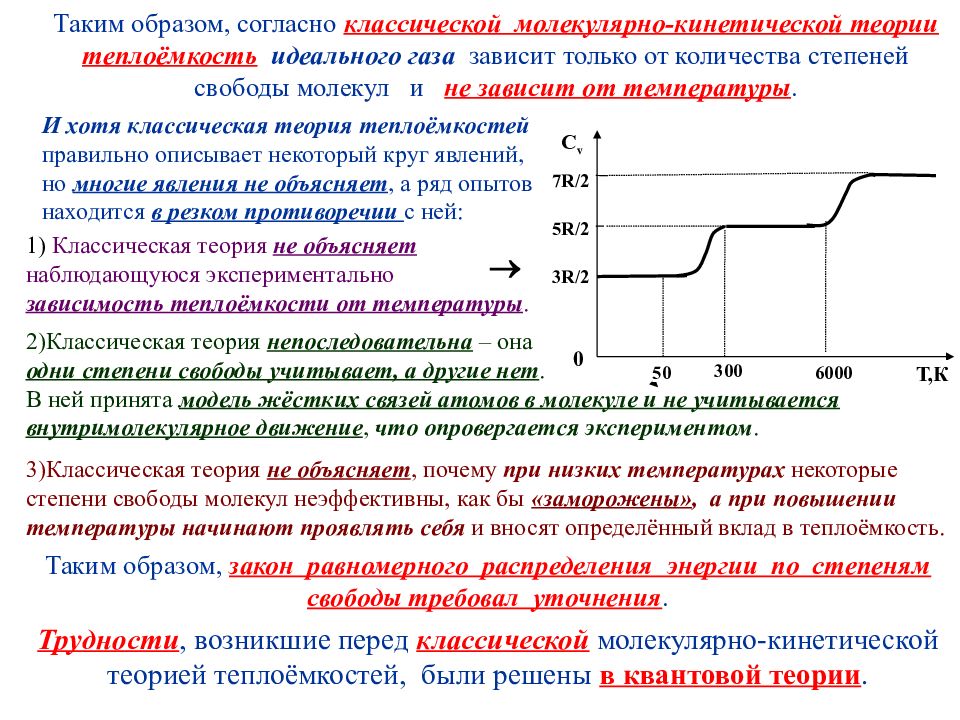
Таким образом, согласно классической молекулярно-кинетической теории теплоёмкость идеального газа зависит только от количества степеней свободы молекул и не зависит от температуры. И хотя классическая теория теплоёмкостей правильно описывает некоторый круг явлений, но многие явления не объясняет, а ряд опытов находится в резком противоречии с ней: 3)Классическая теория не объясняет, почему при низких температурах некоторые степени свободы молекул неэффективны, как бы «заморожены», а при повышении температуры начинают проявлять себя и вносят определённый вклад в теплоёмкость. Таким образом, закон равномерного распределения энергии по степеням свободы требовал уточнения. Трудности, возникшие перед классической молекулярно-кинетической теорией теплоёмкостей, были решены в квантовой теории. 1) Классическая теория не объясняет наблюдающуюся экспериментально зависимость теплоёмкости от температуры. С v 0 Т,К 50 300 6000 7 R/2 5R/2 3R/2 2)Классическая теория непоследовательна – она одни степени свободы учитывает, а другие нет. В ней принята модель жёстких связей атомов в молекуле и не учитывается внутримолекулярное движение, что опровергается экспериментом.
Слайд 46
Процесс Уравнение процесса I начало ΔU A Q Теплоёмкость молярная удельная Изохорный V = const = const Q = ΔU ΔU = NC v ΔT= = VΔP 0 Изобарный Р = const = const Q=ΔU+A ΔU = NC v ΔT= = PΔV A = PΔV = NRΔT Изотермный Т = const PV= const Q = A 0 (формально) Адиабатный Q = 0 PV γ = const ΔU = - A ΔU = NC v ΔT A = - NC v ΔT 0 0 (формально) Термодинамика изопроцессов и адиабатного процесса
Слайд 47
2.4.4. Круговой процесс (цикл). Тепловые двигатели и холодильные установки. Обратимый и необратимый процессы. Первое начало термодинамики, выражая всеобщий закон сохранения и превращения энергии, не позволяет определять направление протекания процессов. Все произвольно протекающие в природе процессы являются необратимыми, так как сопровождаются преодолением сил трения, сопротивления среды. При обратимом процессе система может вернуться в исходное состояние, не внося в окружающую среду какие-либо изменения. При необратимом процессе для возвращения системы в исходное состояние необходимо совершить некоторый компенсирующий процесс, в результате которого в окружающей среде произойдут изменения - состояния внешних тел изменятся. Любые тепловые двигатели и холодильные машины - паровые и газовые турбины, тепловые насосы, двигатели внутреннего сгорания, холодильники и др. совершают круговые процессы (циклы).
Слайд 48
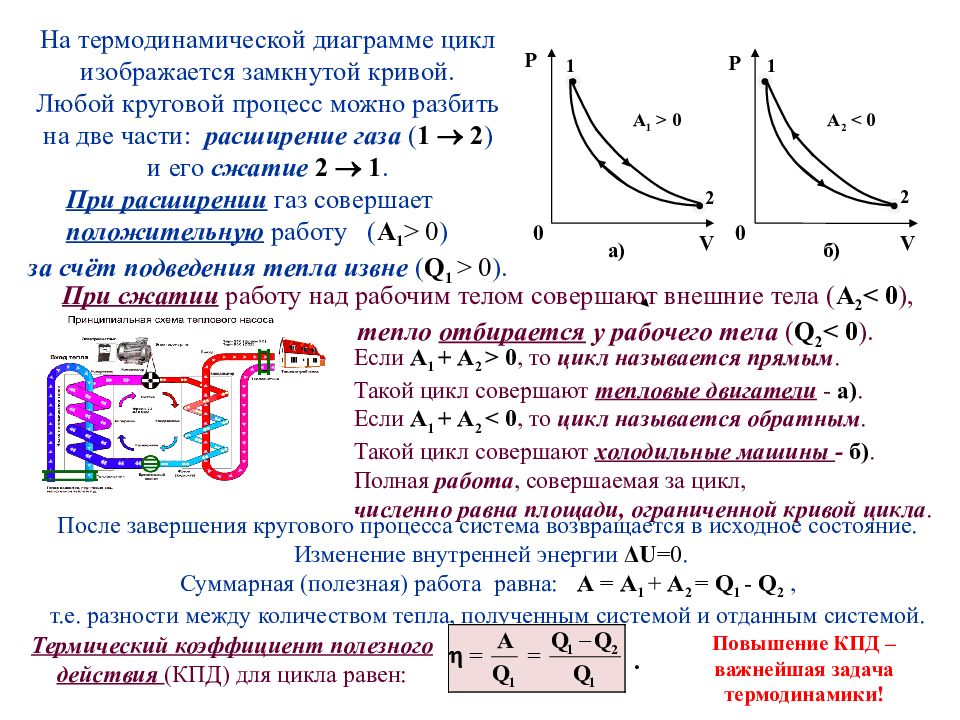
После завершения кругового процесса система возвращается в исходное состояние. Изменение внутренней энергии Δ U =0. Суммарная (полезная) работа равна: А = А 1 + А 2 = Q 1 - Q 2, т.е. разности между количеством тепла, полученным системой и отданным системой. Если А 1 + А 2 > 0, то цикл называется прямым. Такой цикл совершают тепловые двигатели - а). Если А 1 + А 2 < 0, то цикл называется обратным. Такой цикл совершают холодильные машины - б). Полная работа, совершаемая за цикл, численно равна площади, ограниченной кривой цикла. 0 0 V V А 1 > 0 Р Р А 2 < 0 а) б) 2 2 1 1 На термодинамической диаграмме цикл изображается замкнутой кривой. Любой круговой процесс можно разбить на две части: расширение газа ( 1 2 ) и его сжатие 2 1. При расширении газ совершает положительную работу ( А 1 > 0 ) за счёт подведения тепла извне ( Q 1 > 0 ). При сжатии работу над рабочим телом совершают внешние тела ( А 2 < 0 ), тепло отбирается у рабочего тела ( Q 2 < 0 ). Термический коэффициент полезного действия (КПД) для цикла равен: . Повышение КПД – важнейшая задача термодинамики!
Слайд 49
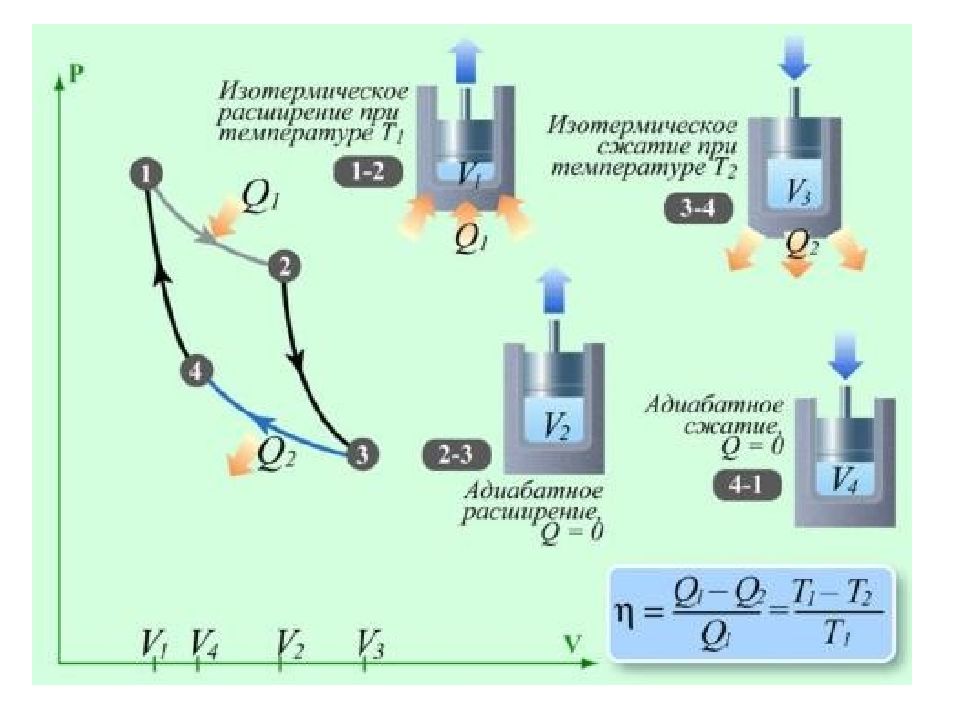
2.4.5. Цикл Карно. Максимальный КПД тепловых машин. Тепловые машины достаточно широко начали использоваться в промышленности уже во второй половине 18-го века. Обратимый круговой процесс, совершаемый тепловой машиной, впервые теоретически рассмотрел французский физик и инженер С.Карно в 1824 году. Цикл Карно сыграл большую роль в термодинамике и теплотехнике, так как позволил проанализировать КПД тепловых машин и установить условия его повышения. Карно рассмотрел наиболее экономичный цикл, состоящий из четырёх обратимых процессов - двух изотермических и двух адиабатных. На рисунке изображён прямой цикл Карно. Газ, заключённый в цилиндр с подвижным поршнем, в процессе изотермического расширения ( 1 2 ) находится в тепловом контакте с телом, называемым нагревателем, имеющим температуру Т н, и получает от него тепло Q н. Q 2 =0 Q 4 =0 4 0 V Р 2 1 Т н 3 Т х Q 1 =Q н Q 3 =Q х Затем газ теплоизолируется и совершается адиабатное расширение ( 2 3 ). Температура газа понижается до Т х. В этот момент газ приводят в тепловой контакт с телом, называемым холодильником, имеющим температуру Т х, и отдаёт ему тепло Q х. На следующем этапе газ изотермически сжимают ( 3 4 ), теплоизолируют и сжимают адиабатно ( 4 1 ). На этом цикл завершается.
Слайд 51
Рассчитывая работу, совершаемую в каждом процессе (рабочим телом или внешними телами), Карно определил соотношение между полезной работой и затраченным в цикле теплом, то есть коэффициент полезного действия (КПД) цикла: Эта формула выражает теорему Карно - КПД всех обратимых машин, работающих в идентичных условиях (одинаковых Т н и Т х ), одинаков, не зависит от природы рабочего тела, а зависит только от температуры нагревателя и холодильника. Для повышения КПД тепловых машин необходимо увеличивать разность температур нагревателя и холодильника. КПД всех реальных тепловых машин из-за неизбежных тепловых потерь и трения в механических их частях значительно меньше определяемого формулой Карно. . Для холодильных машин аналогичный вывод позволяет получить выражение для холодильного коэффициента обратного цикла Карно : .
Слайд 52
2.4.6. Второе начало термодинамики. Первое начало термодинамики допускает построение такой тепловой машины, которая бы совершала работу за счёт охлаждения одного источника теплоты (например, за счёт внутренней энергии мирового океана). Опыт показывает невозможность построения вечного двигателя второго рода. Это утверждение является вторым законом термодинамики и называется вторым началом термодинамики. Существует несколько эквивалентных формулировок второго начала термодинамики. Формулировка Р.Клаузиуса - невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему. Такая тепловая машина называется вечным двигателем второго рода. Такую формулировку впервые ввёл в 1888 году немецкий учёный В.Оствальд. Формулировка У.Томсона (Кельвина) - невозможен процесс, единственным результатом которого является совершение работы за счёт охлаждения одного тела.
Слайд 53
2.4.7. Энтропия. Определение энтропии системы через статистический вес её макросостояния. Теорема Нернста и её следствия. Закон возрастания энтропии. Для получения аналитического выражения второго начала термодинамики и общей его формулировки Клаузиус в 1865 году ввёл понятие энтропии. К необходимости введения новой функции состояния термодинамической системы - энтропии Клаузиус пришёл, анализируя работу тепловых машин. Верхний предел КПД тепловых машин в соответствии с теоремой Карно равен: Отсюда следует: Т.о., алгебраическая сумма приведенного количества теплоты, полученного и отданного рабочим телом в идеальном цикле Карно равна 0. Отношение количества тепла Q, полученного ( + ) или отданного ( - ) термодинамической системой в изотермическом процессе при температуре Т, к этой температуре - называется приведенным количеством тепла -. . .
Слайд 54
Клаузиус показал, что, если любой квазистатический (бесконечно медленно протекающий) процесс представить как сумму бесконечного числа элементарных циклов Карно, в которых система последовательно получает или отдаёт количество тепла d Q при температуре Т, то приведенное количество тепла, получаемое системой в любом обратимом круговом процессе равно 0 : Это уравнение называется равенством Клаузиуса. Равенство Клаузиуса выполняется, если подынтегральное выражение представляет собой полный дифференциал от некоторой функции S, которая называется энтропией : . Из равенства Клаузиуса следует, что в обратимых процессах изменение энтропии не происходит : .
Слайд 55
Физический смысл имеет не сама энтропия, а её изменение. Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии равно: которое означает, что энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов). Эти соотношения можно представить в виде неравенства Клаузиуса : . Все реальные процессы необратимы. Энтропия изолированной системы, совершающей необратимый цикл, всегда возрастает : , Неравенство Клаузиуса выражает закон возрастания энтропии : в любой реальной замкнутой системе процессы происходят в направлении возрастания энтропии. Таким образом, энтропия является функцией состояния и указывает направленность процессов в природе. .
Слайд 56
С точки зрения первого начала термодинамики в изолированной системе возможны любые процессы, при которых сохраняется внутренняя энергия системы. Однако, различные состояния с одинаковой энергией, обладают разной вероятностью. Естественно, что изолированная система самопроизвольно будет переходить из менее вероятных состояний в более вероятные или пребывать преимущественно в состояниях, вероятность которых максимальна. Энтропия является величиной, характеризующей вероятность состояния системы. Глубокий физический смысл понятия энтропия может быть разъяснён в статистической физике.
Слайд 57
То есть, энтропия - это мера неупорядоченности системы ( мера беспорядка ). Больцман в 1875 году предложил в качестве меры или степени молекулярного беспорядка системы использовать энтропию системы и установил связь её с W : Качественным отличием теплового движен ия от других видов движения является его беспорядочность, хаотичность. Для характеристики теплового движения вводится количественная мера степени молекулярного беспорядка – так называемый статистический вес макросостояния системы W или термодинамическая вероятность состояния системы. Статистический вес - это число способов, которыми может быть реализовано данное состояние макроскопической системы ( число микросостояний, осуществляющих данное макросостояние ): W 1 ( в математике вероятность всегда меньше единицы! ). Чем более неупорядочена система, тем больше статистический вес макросостояния ( например, газ более неупорядочен, чем жидкость ). , где k = 1,38. 10 -23 Дж/К – постоянная Больцмана.
Слайд 58
Или другими словами - при помощи конечной последовательности термодинамических процессов нельзя достичь температуры абсолютного нуля. Первое и второе начала термодинамики не определяют поведение термодинамических систем при Т=0 К. . Теорема Нернста-Планка дополняет их и называется третьим началом термодинамики - энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к абсолютному нулю : Таким образом, второе начало термодинамики является статистическим законом. Эта формулировка позволила понять, почему реальные процессы идут самопроизвольно в одном направлении, а для прохождения их в другом направлении нужен компенсирующий процесс.
Слайд 59
2.4.8. Философский смысл второго начала термодинамики. Критика концепции «тепловой смерти» Вселенной. Второе начало термодинамики указывает на то, что процесс перехода упорядоченного движения тела как целого в неупорядоченное движение его частиц необратим и любая замкнутая система стремится к наиболее вероятному равновесному состоянию с максимальной энтропией. Опровергая фаталистический вывод Р.Клаузиуса Л.Больцман в 1872 году выдвинул так называемую флуктуационную гипотезу, согласно которой, хотя Вселенная как целое постоянно пребывает в равновесном изотермическом состоянии, но существует отличная от нуля вероятность случайных отклонений от этого состояния в отдельных её частях. . . Основываясь на этом выводе, Р.Клаузиус в 1865 году пришёл к ошибочному заключению о неизбежности «тепловой смерти» Вселенной – все виды энергии во Вселенной в конце концов должны перейти в энергию теплового движения, которая равномерно распределится по Вселенной, и все процессы в ней прекратятся.
Последний слайд презентации: Раздел 2 Молекулярная физика. Статистическая физика и термодинамика
Современной космологией установлено, что в выводе о «тепловой смерти» Вселенной и в попытках его опровержения не учитывалась нестационарность Вселенной и наличие в ней сил тяготения. . . Вселенная расширяется, почти однородное в начале расширения вещество в дальнейшем под действием гравитации образует скопления в виде галактик, звёзд, планет, астероидов, космической пыли. Эти процессы протекают с ростом энтропии и не противоречат второму началу термодинамики. И в дальнейшем Вселенная будет эволюционировать, оставаясь всегда нестатичной, и её «тепловая смерть» не наступит.