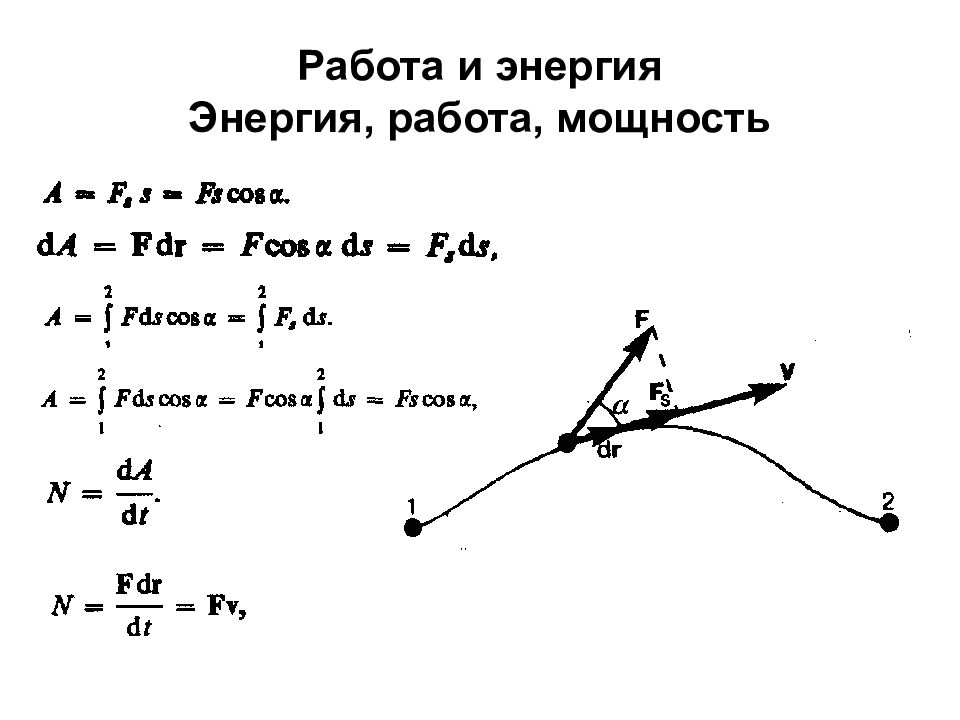
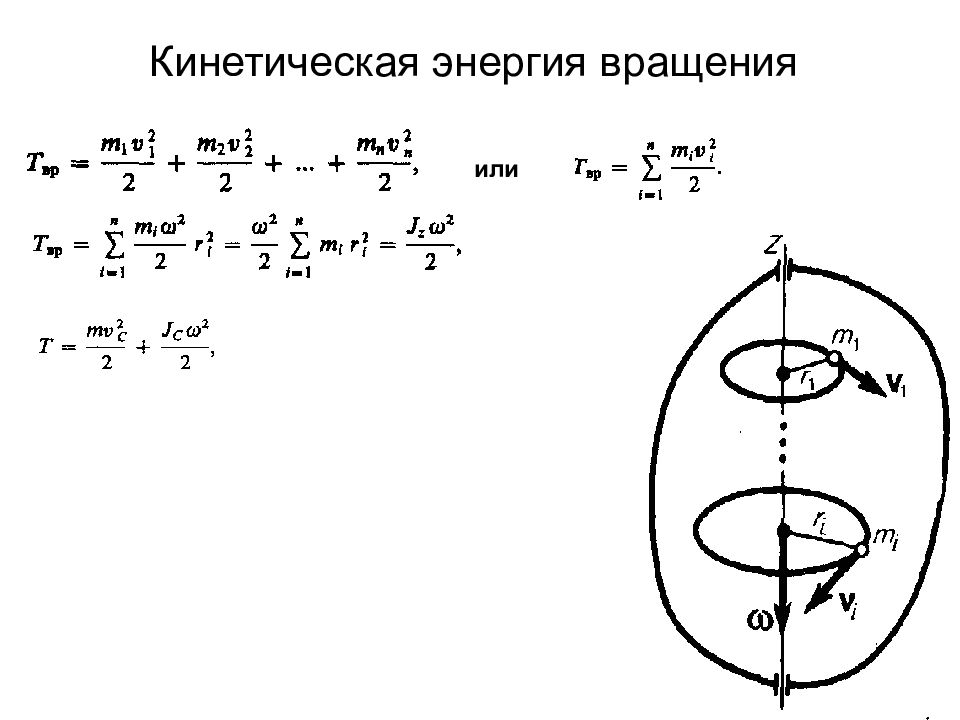
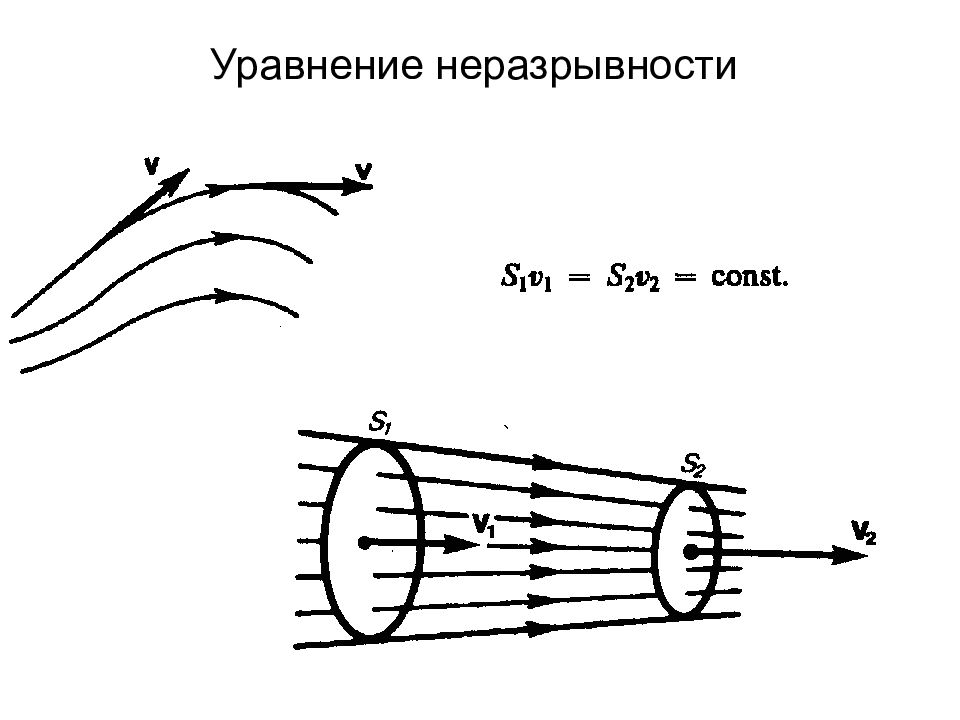
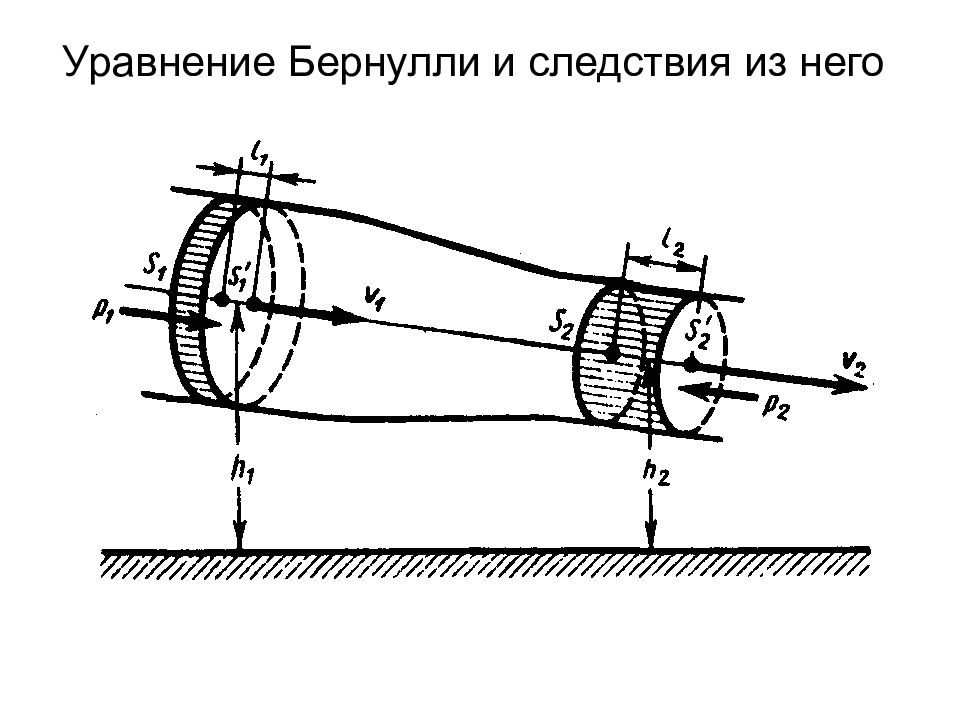
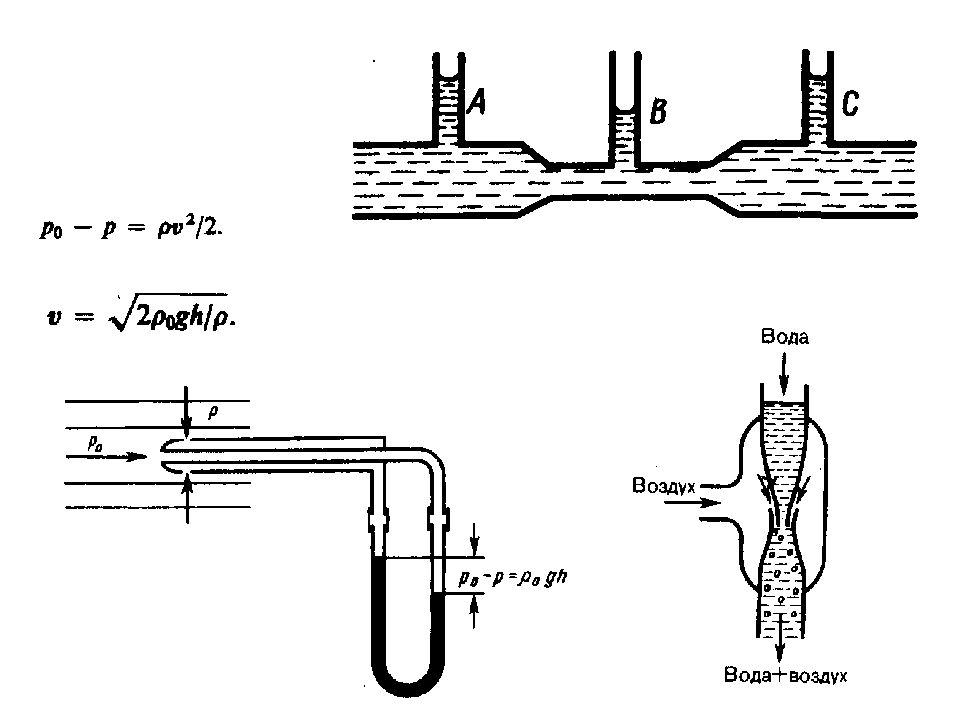
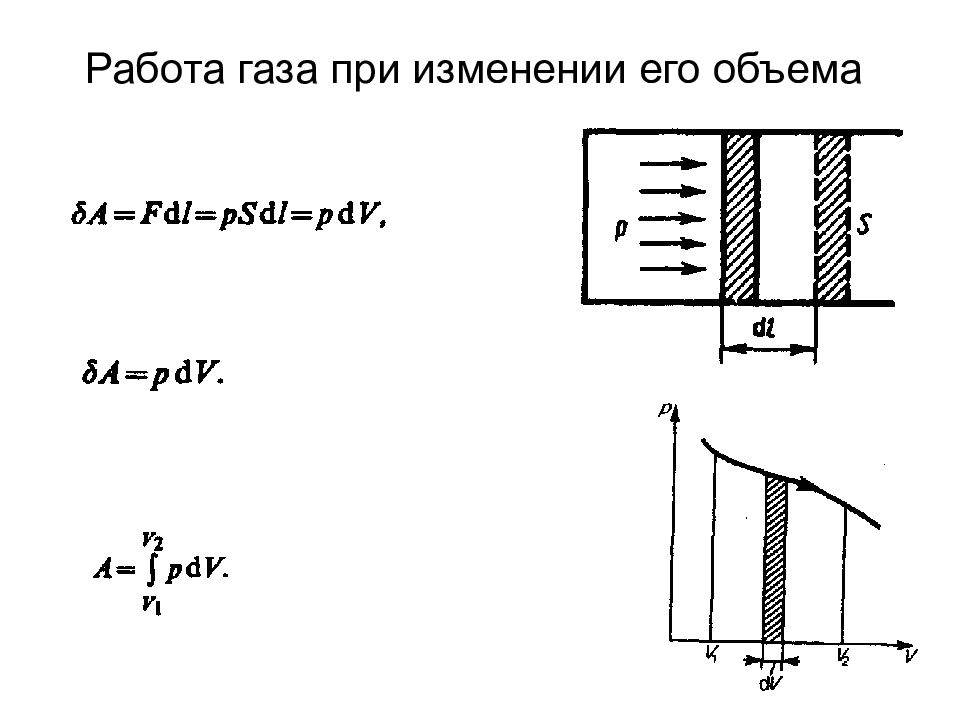
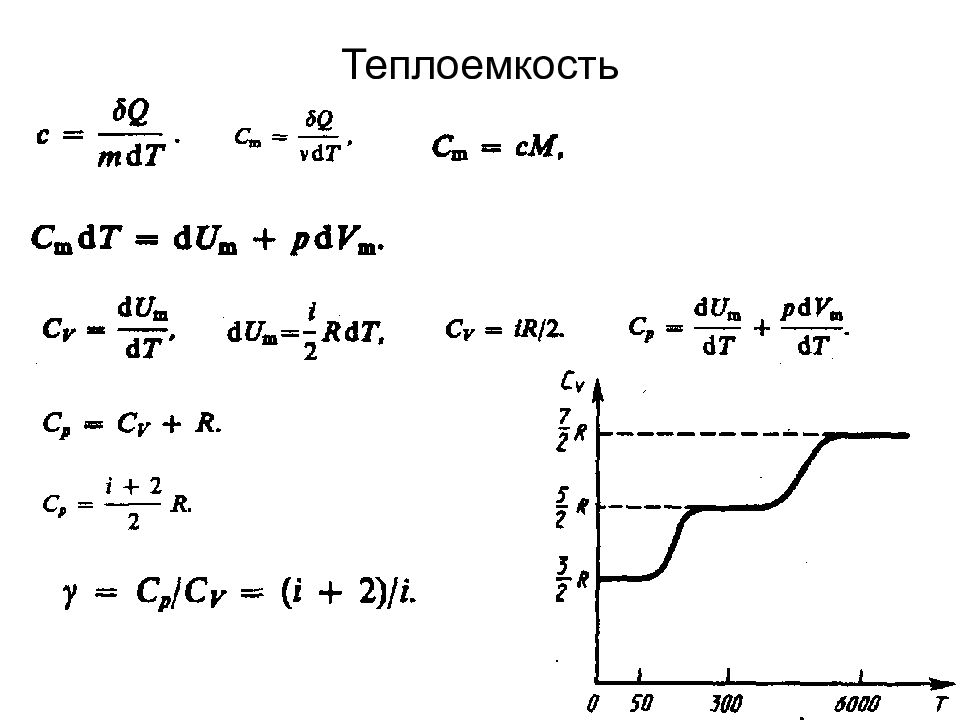
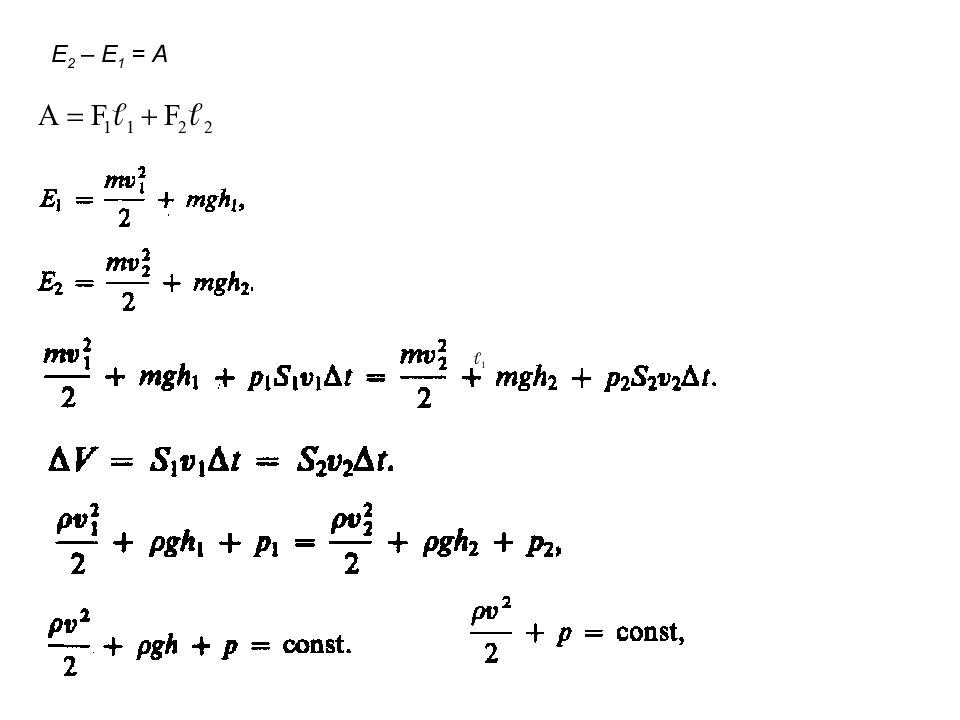Первый слайд презентации: 1. Физические основы механики
Механика Классическая Релятивистская Квантовая Разделы механики Кинематика Динамика Статика
Слайд 2: Физические модели в механике
Физические модели Материальная точка Система материальных точек Абсолютно твердое тело Абсолютно упругое тело Абсолютно неупругое тело
Слайд 3: 2. Механическое движение
Тело отсчёта Система координат Система отсчёта Кинематические уравнения движения материальной точки X=x(t) Y=y(t) или r=r(t) Z=z(t)
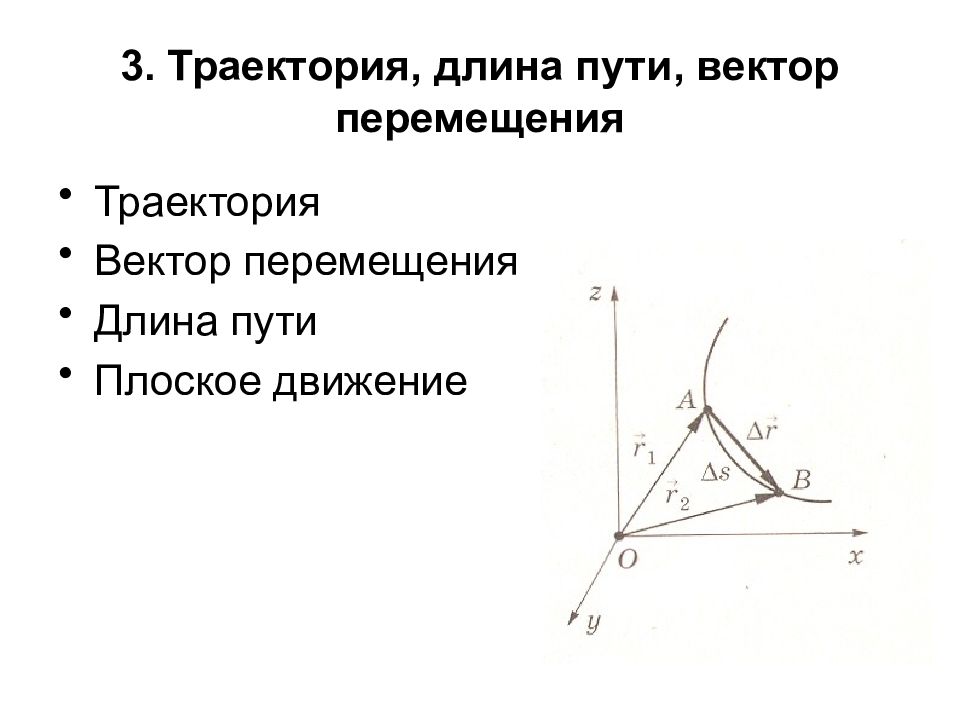
Траектория Вектор перемещения Длина пути Плоское движение
Слайд 5: 4. Поступательное и вращательное движение твердого тела
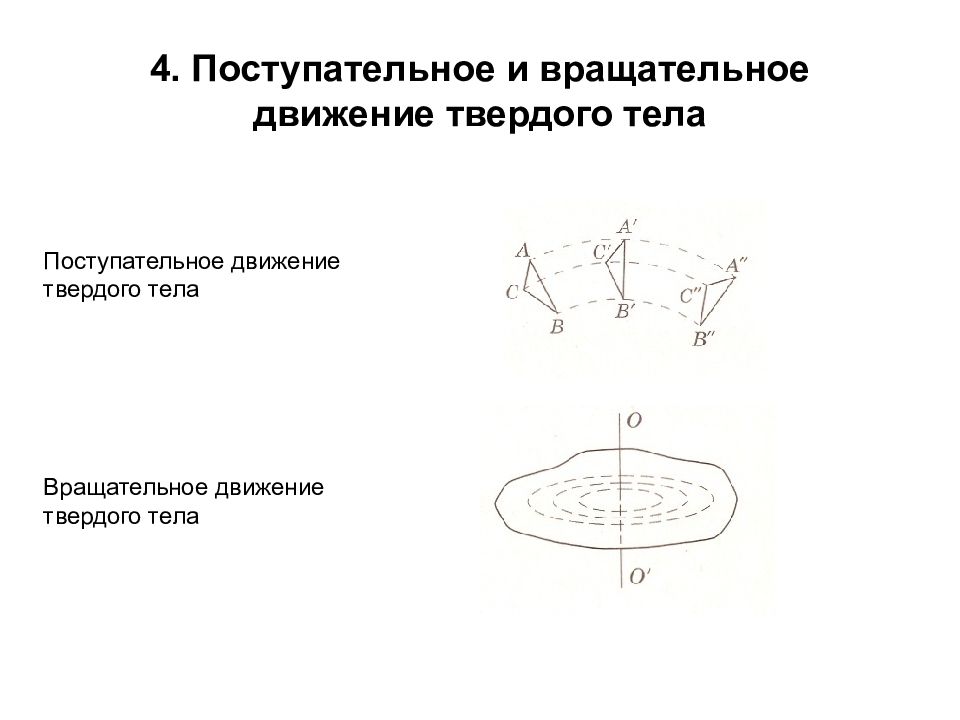
Поступательное движение твердого тела Вращательное движение твердого тела
Слайд 6: 5. Кинематика поступательного движения
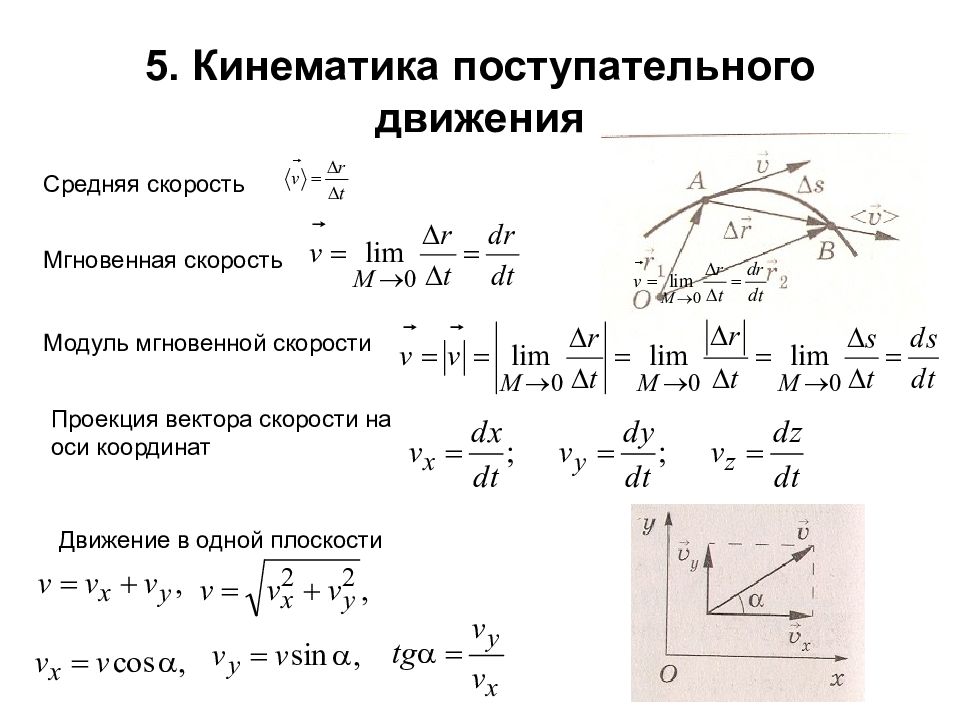
Средняя скорость Мгновенная скорость Модуль мгновенной скорости Проекция вектора скорости на оси координат Движение в одной плоскости
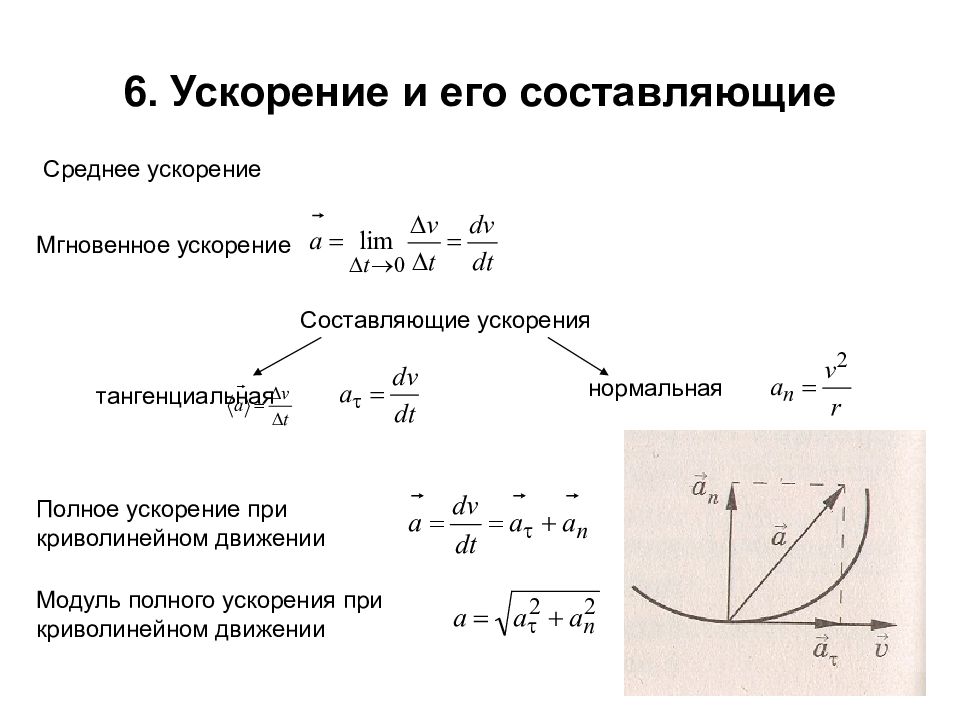
Слайд 7: 6. Ускорение и его составляющие
Среднее ускорение Мгновенное ускорение Составляющие ускорения тангенциальная нормальная Полное ускорение при криволинейном движении Модуль полного ускорения при криволинейном движении
Слайд 9: 7. Равномерное движение материальной точки по окружности
Равномерное движение по окружности Период вращения Частота вращения Ускорение материальной точки, равномерно движущейся по окружности Угловое ускорение
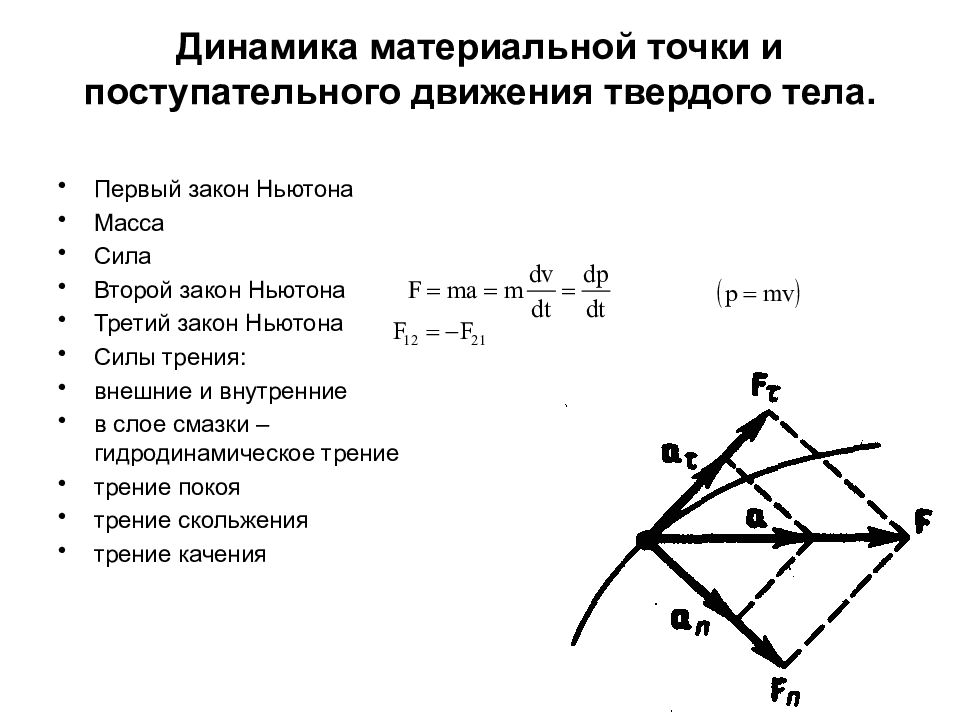
Слайд 11: Динамика материальной точки и поступательного движения твердого тела
Первый закон Ньютона Масса Сила Второй закон Ньютона Третий закон Ньютона Силы трения: внешние и внутренние в слое смазки – гидродинамическое трение трение покоя трение скольжения трение качения
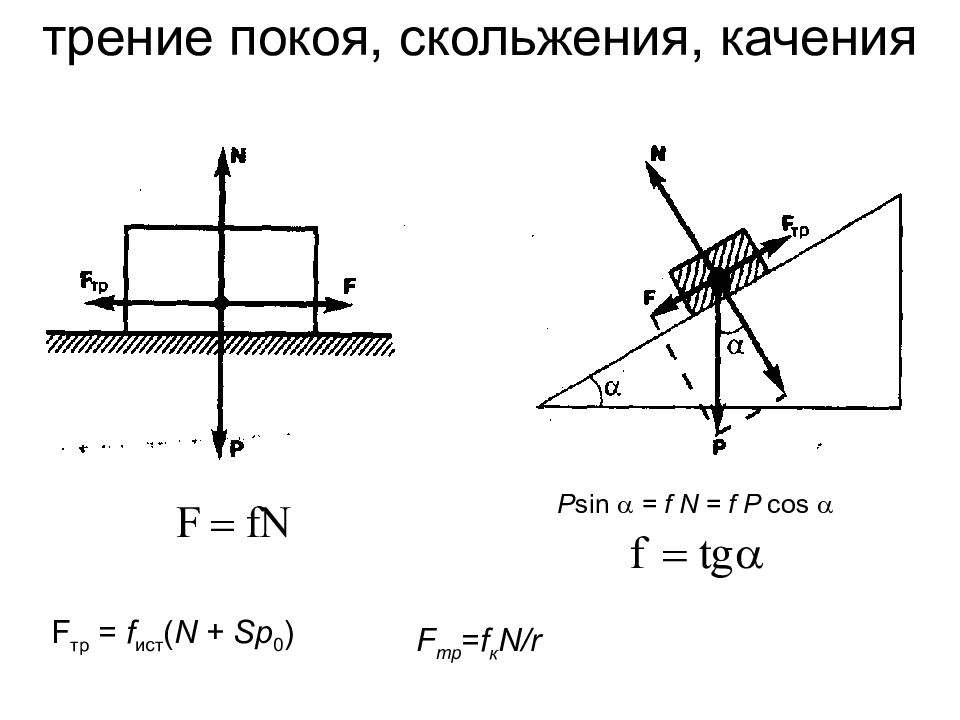
Слайд 12: трение покоя, скольжения, качения
P sin = f N = f P cos F тр = f ист ( N + Sp 0 ) F тр = f к N / r
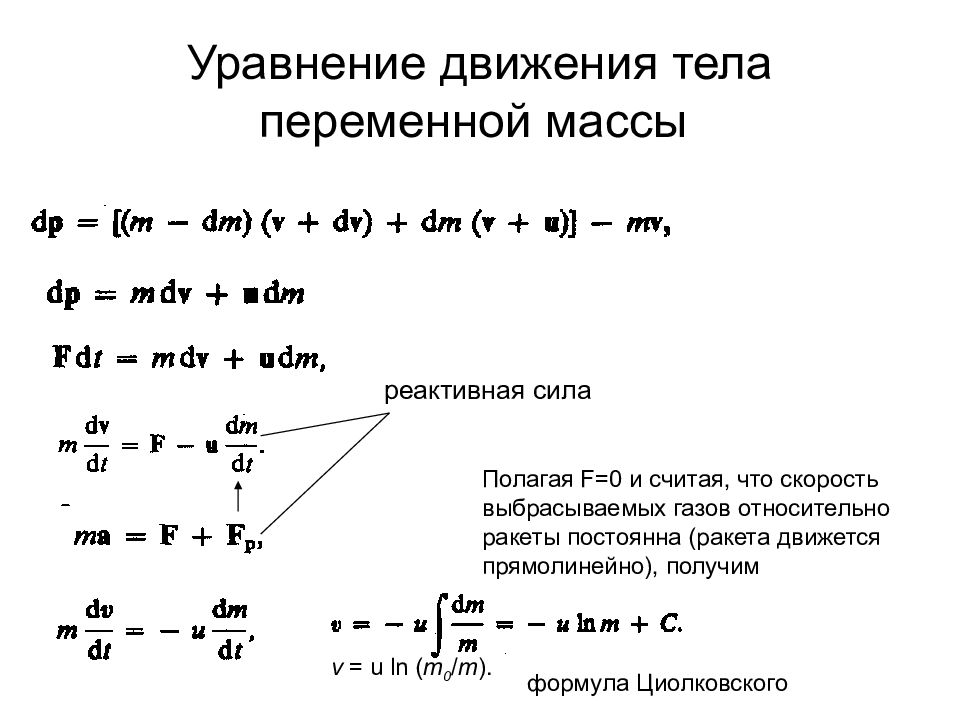
Слайд 14: Уравнение движения тела переменной массы
реактивная сила Полагая F =0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим формула Циолковского v = u ln ( m 0 / m ).
Слайд 18: Удар абсолютно упругих и неупругих тел
Отношение нормальных составляющих относительной скорости тел после и да удара называется коэффициентом восстановления :
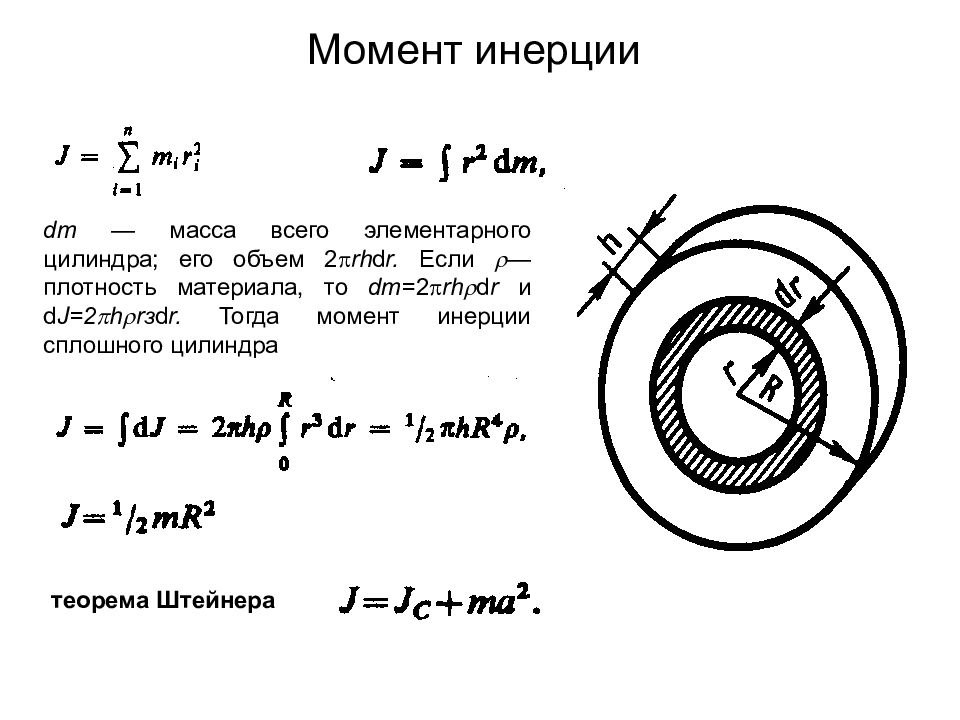
Слайд 19: Момент инерции
dm — масса всего элементарного цилиндра; его объем 2 rh d r. Если — плотность материала, то dm = 2 rh d r и d J=2 h r з d r. Тогда момент инерции сплошного цилиндра теорема Штейнера
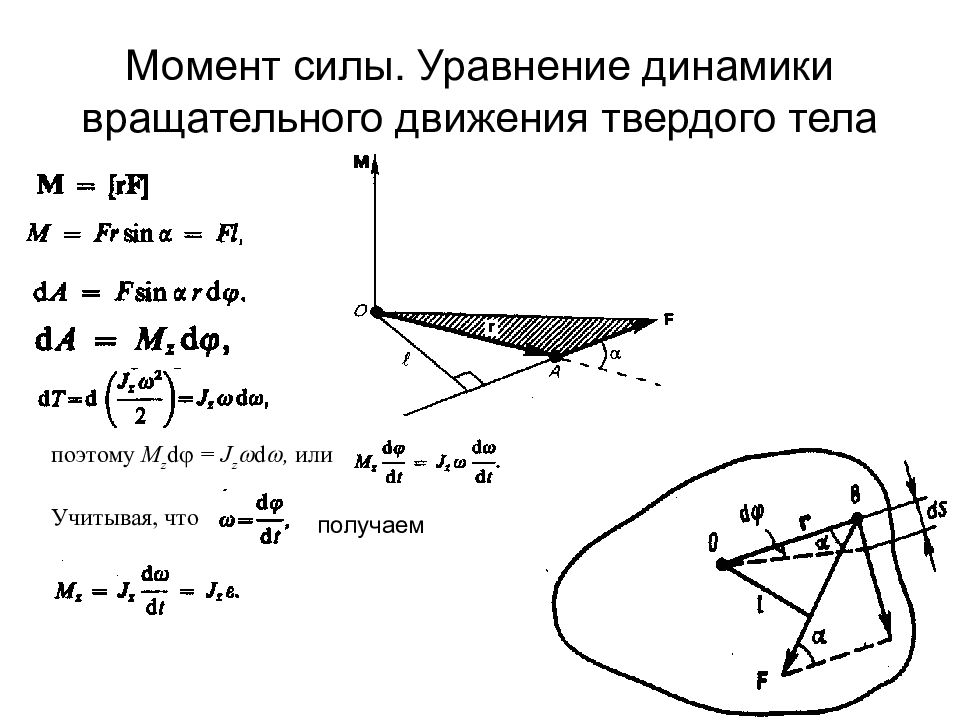
Слайд 22: Момент силы. Уравнение динамики вращательного движения твердого тела
поэтому M z d = J z d , или Учитывая, что получаем
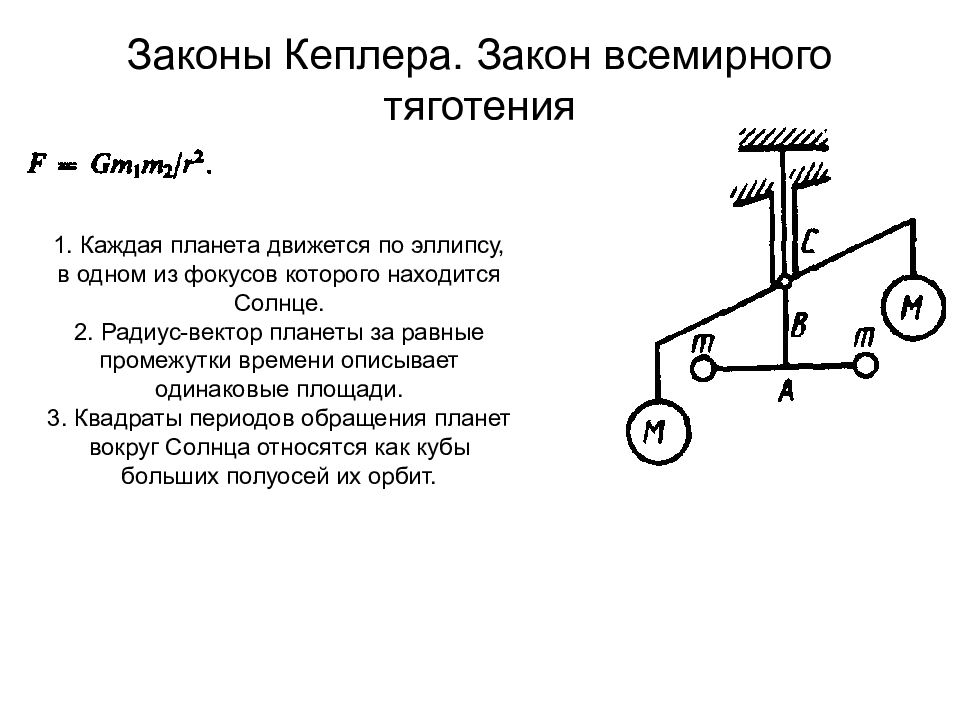
Слайд 28: Законы Кеплера. Закон всемирного тяготения
1. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. 2. Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади. 3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.
Слайд 30: Поле тяготения и то напряженность
Работа в поле тяготения. Потенциал поля тяготения
Слайд 31: Космические скорости
- первая космическая скорость - вторая космическая скорость v 3 =16,7 км/с – третья космическая скорость
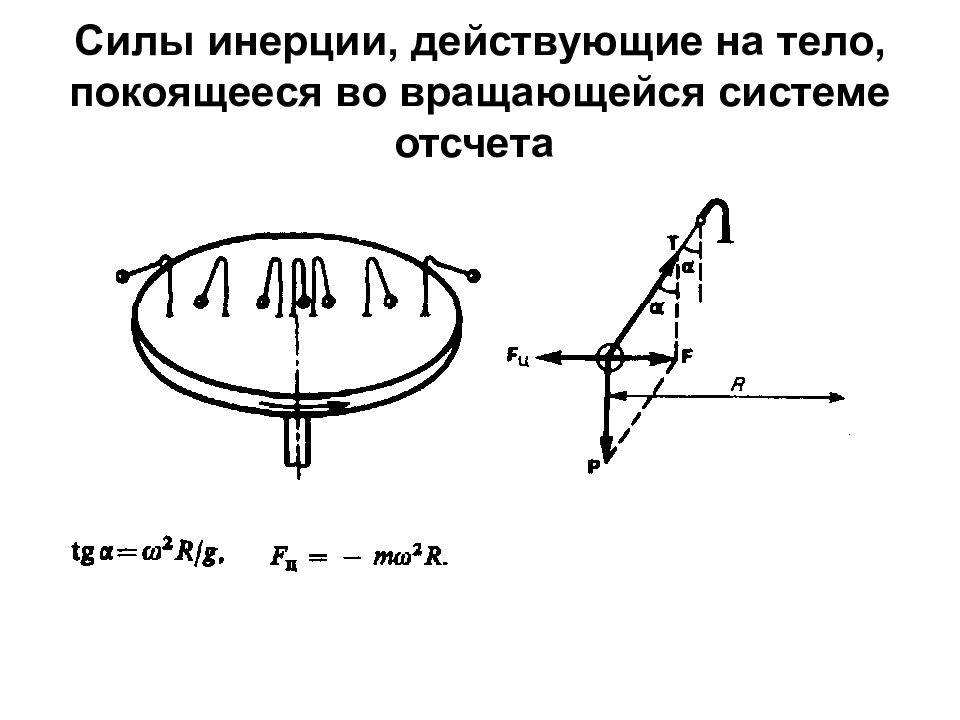
Слайд 33: Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета
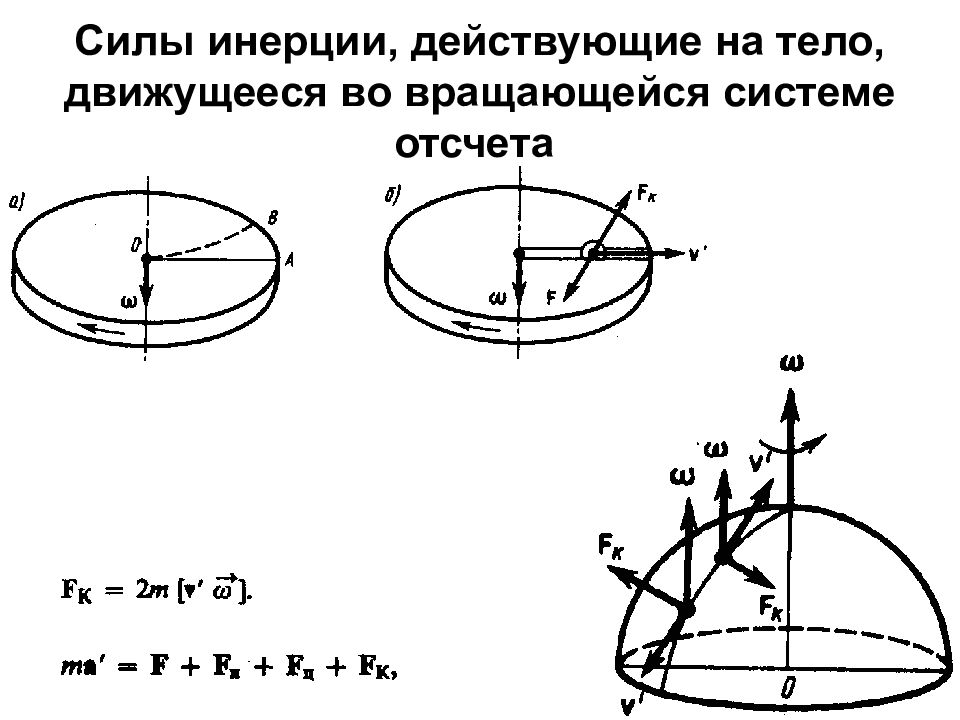
Слайд 34: Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета
Слайд 41
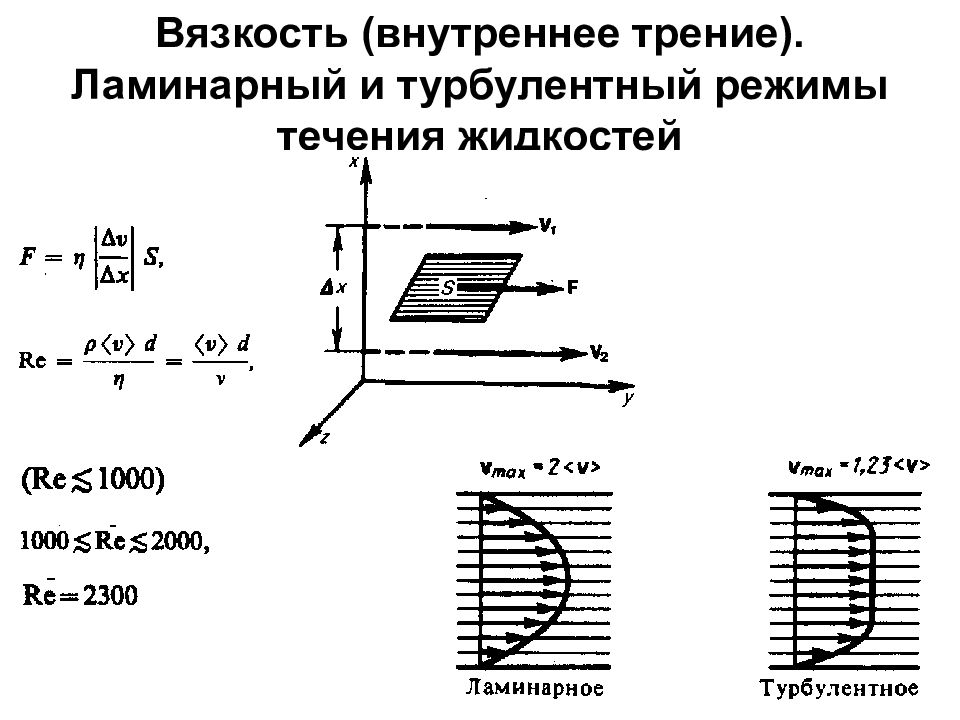
Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкостей
Слайд 45
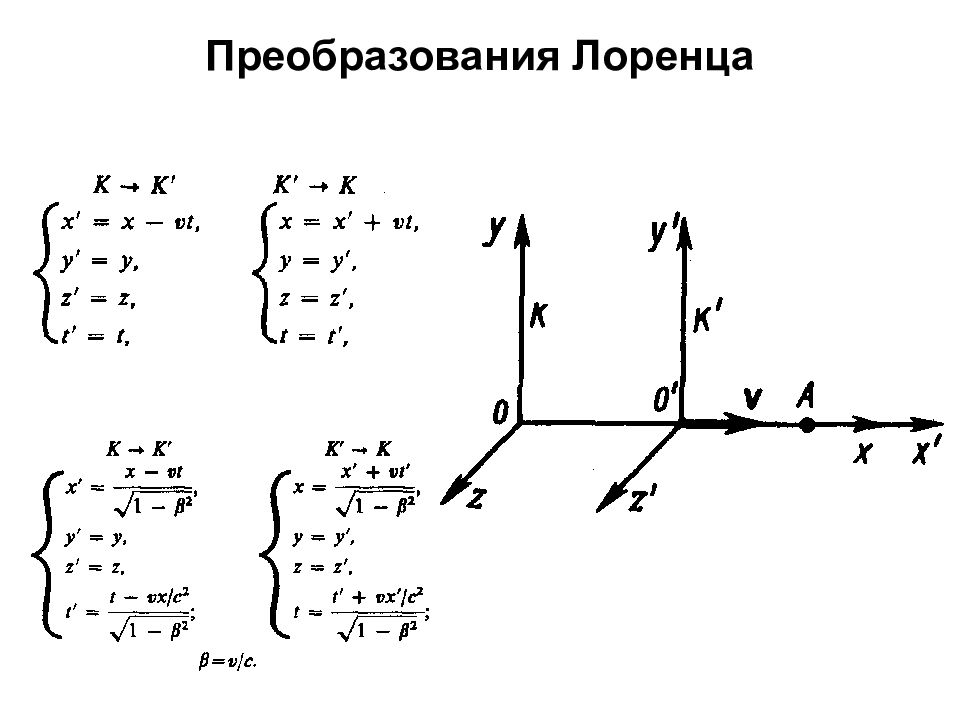
Постулаты специальной (частной) теории относительности I. Принцип относительности: никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. II. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
Слайд 47
Следствия из преобразований Лоренца 1. Одновременность событий в разных системах отсчета. 2. Длительность событий в разных системах отсчета.
Слайд 48
3. Длина тел в разных системах отсчета. 4. Релятивистский закон сложения скоростей. Действительно, если u ' = c, то
Слайд 51
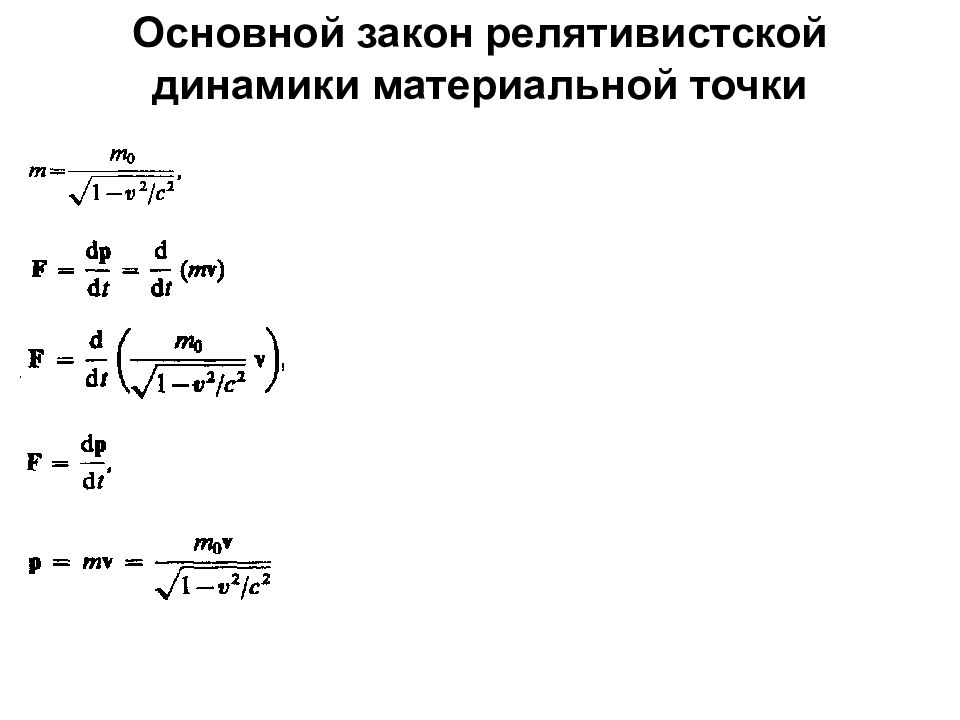
Закон взаимосвязи массы и энергии Покоящееся тело обладает Т=0, следовательно Энергия связи системы равна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например, атомное ядро — на протоны и нейтроны).
Слайд 52: ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
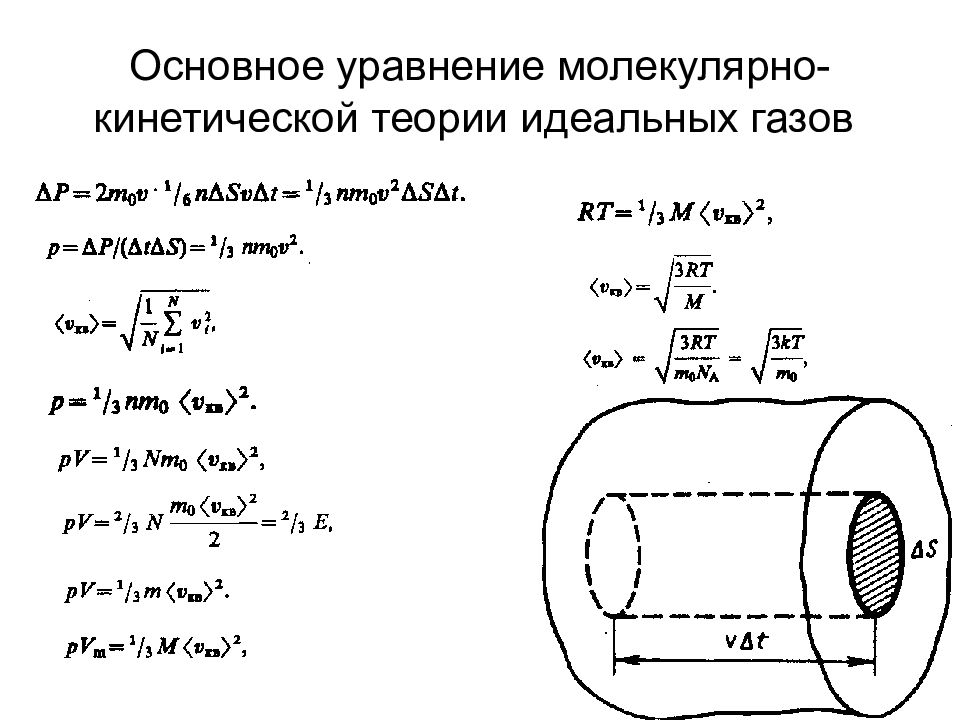
Молекулярно-кинетическая теория идеальных газов Статистический и термодинамический методы. Опытные законы идеального газа Молекулярная физика Термодинамика Термодинамическая температурная шкала определяется по одной реперной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давления 609 Па находятся в термодинамическом равновесии).
Слайд 53
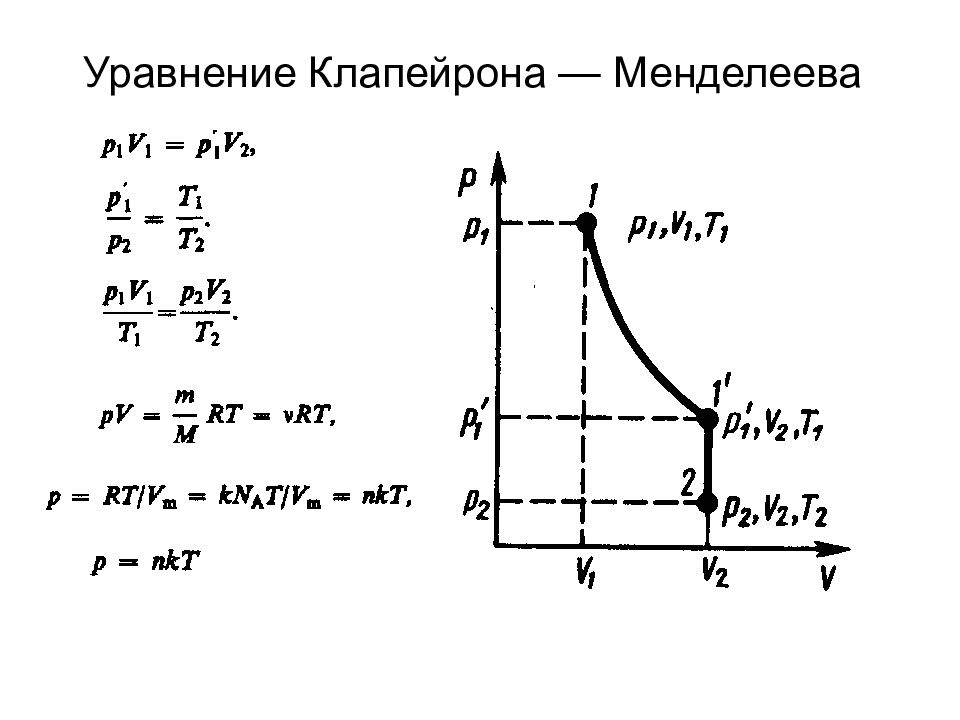
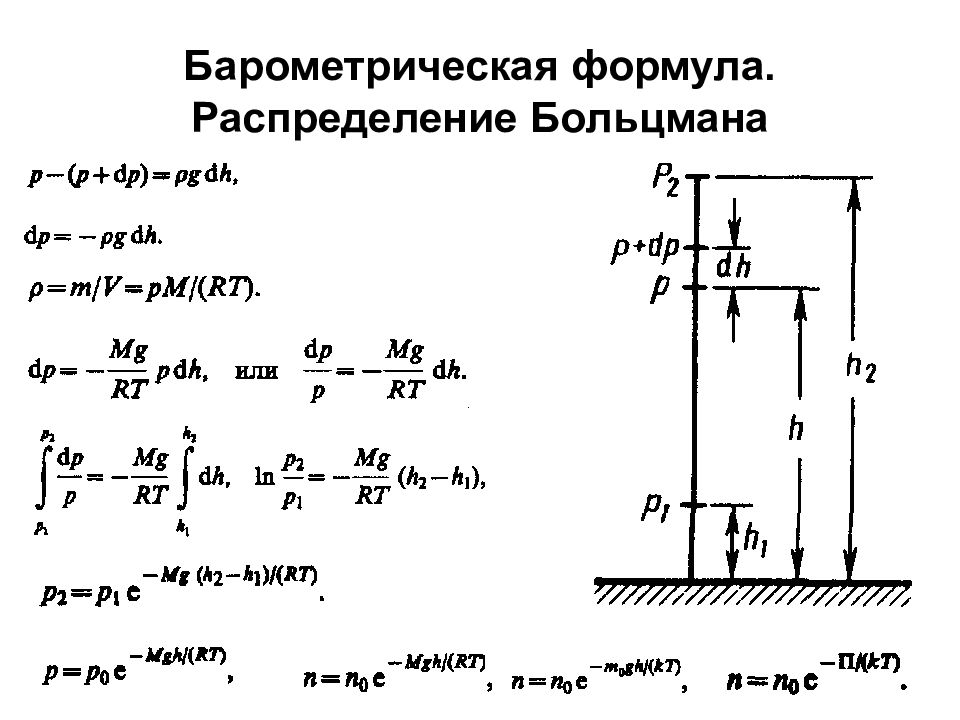
Закон Бойля—Мариотта: pV=const Законы Гей-Люссака : объем данной массы газа при постоянном давлении изменяется линейно с температурой давление данной массы газа при постоянном объеме изменяется линейно с температурой Закон Дальтона Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре
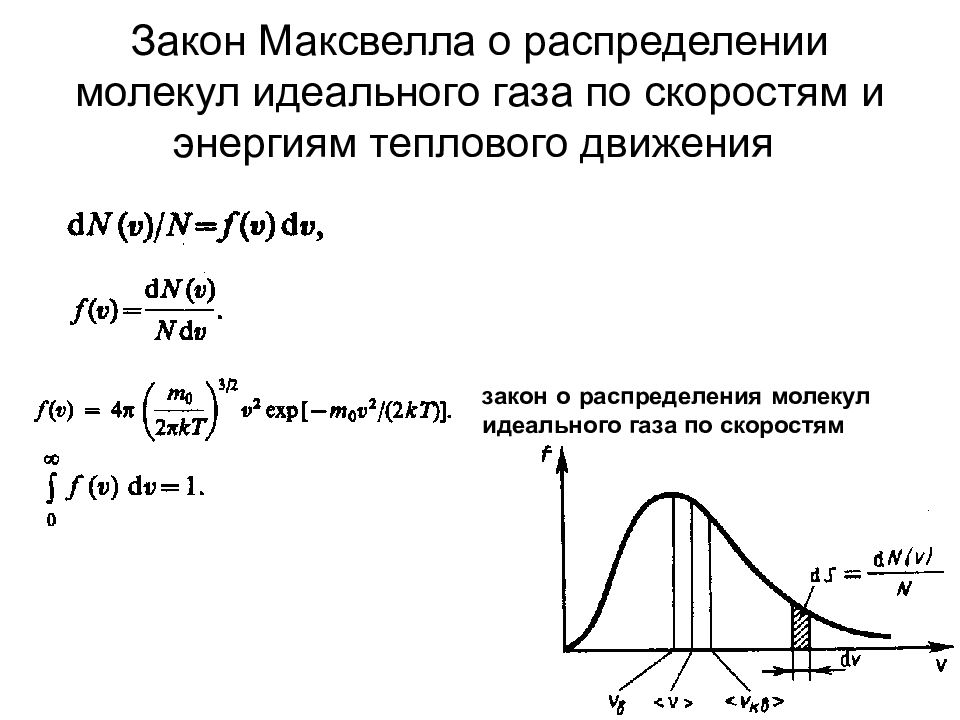
Слайд 56: Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения
закон о распределения молекул идеального газа по скоростям
Слайд 58
Исходя из распределения молекул по скоростям можно найти распределение молекул газа по значениям кинетической энергии . Для этого перейдем от переменной v к переменной =m 0 v 2 / 2. Подставив в v = и d v = d , получим и d v = Таким образом, функция распределения молекул по энергиям теплового движения Средняя кинетическая энергия < > молекулы идеального газа
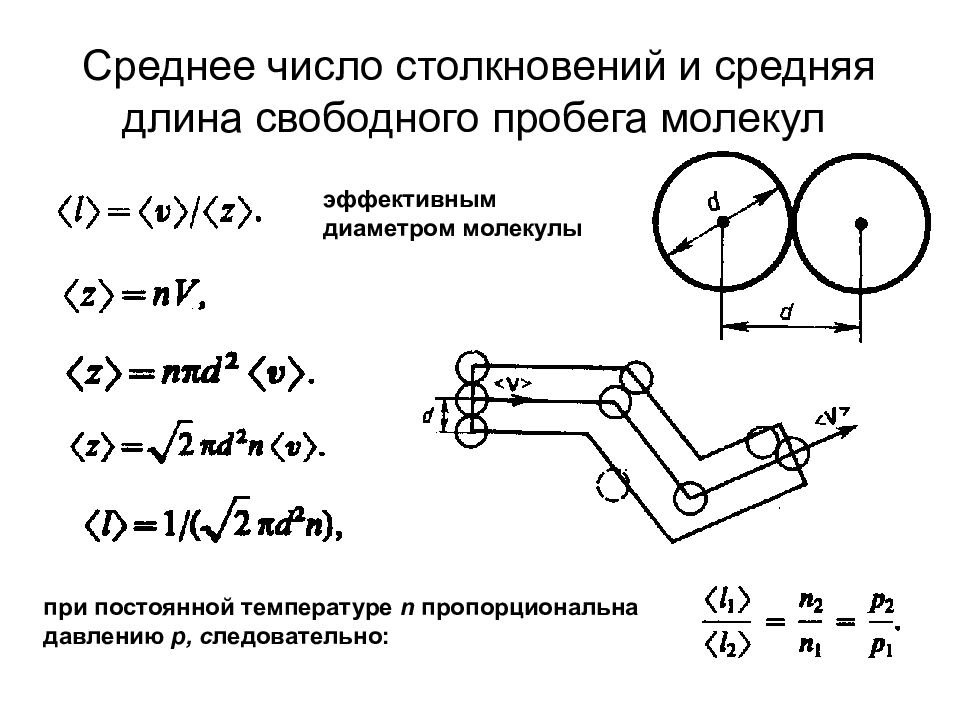
Слайд 60: Среднее число столкновений и средняя длина свободного пробега молекул
эффективным диаметром молекулы при постоянной температуре n пропорциональна давлению р, с ледовательно:
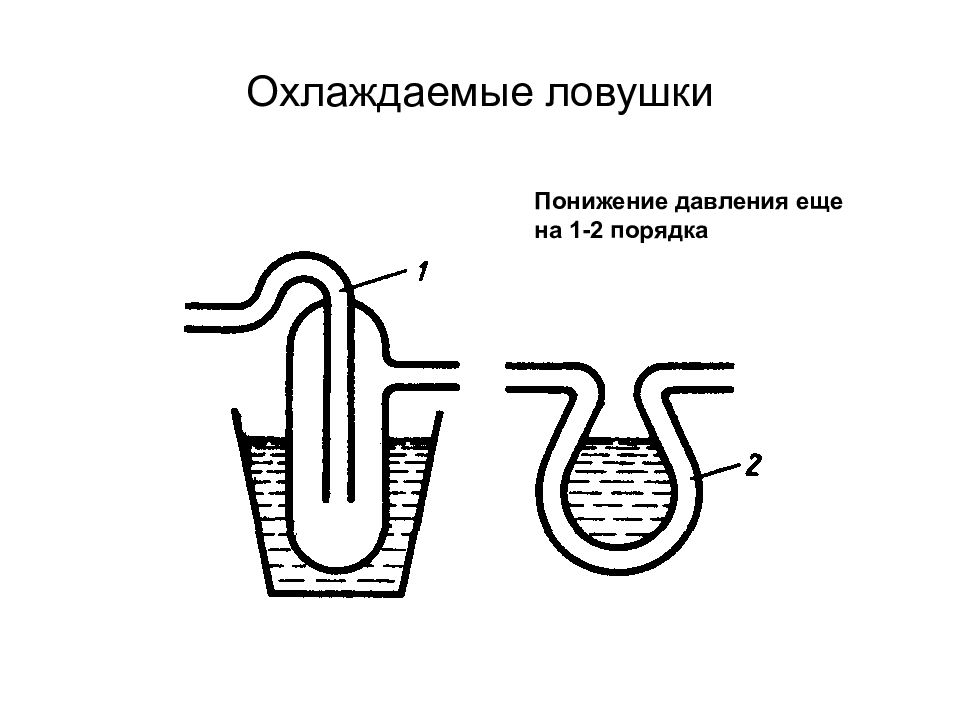
Слайд 61: Явления переноса в термодинамически неравновесных системах
1. Теплопроводность закон Фурье 2. Диффузия закон Фука 3. Внутреннее трение (вязкость) закон Ньютона
Слайд 62: Вакуум и методы его получения. Свойства ультраразреженных газов
низкий (< l > << d ), средний (< l > d ), высокий (< l > > d ) сверхвысокий (< l > >> d ) вакуум. Газ в состоянии высокого вакуума называется ультраразреженным.
Слайд 63
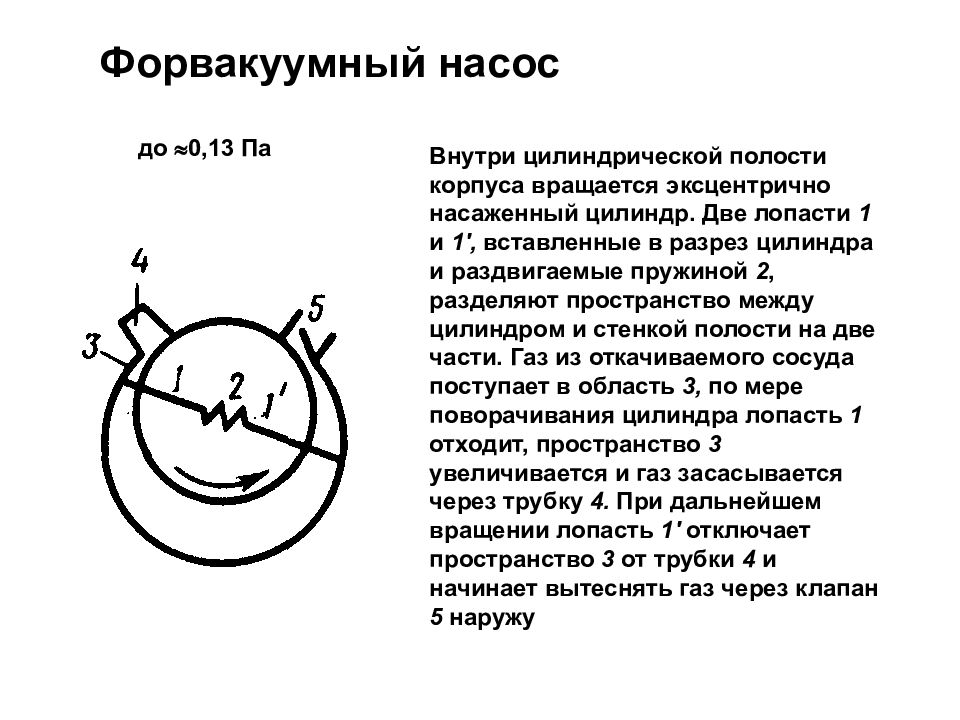
Внутри цилиндрической полости корпуса вращается эксцентрично насаженный цилиндр. Две лопасти 1 и 1', вставленные в разрез цилиндра и раздвигаемые пружиной 2, разделяют пространство между цилиндром и стенкой полости на две части. Газ из откачиваемого сосуда поступает в область 3, по мере поворачивания цилиндра лопасть 1 отходит, пространство 3 увеличивается и газ засасывается через трубку 4. При дальнейшем вращении лопасть 1' отключает пространство 3 от трубки 4 и начинает вытеснять газ через клапан 5 наружу Форвакуумный насос до 0,13 Па
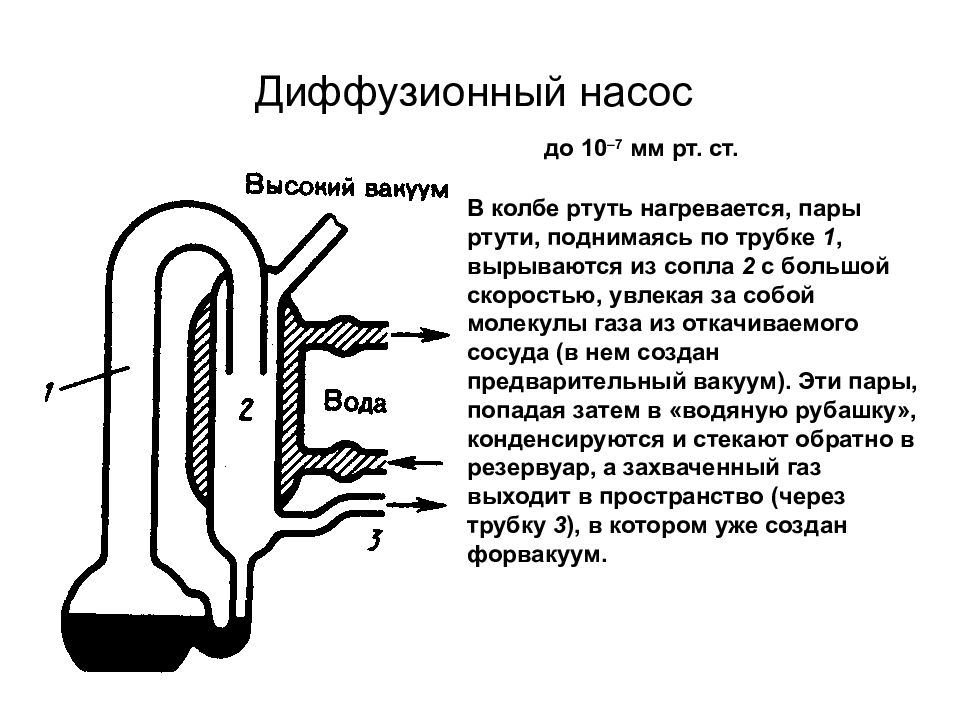
Слайд 64: Диффузионный насос
В колбе ртуть нагревается, пары ртути, поднимаясь по трубке 1, вырываются из сопла 2 с большой скоростью, увлекая за собой молекулы газа из откачиваемого сосуда (в нем создан предварительный вакуум). Эти пары, попадая затем в «водяную рубашку», конденсируются и стекают обратно в резервуар, а захваченный газ выходит в пространство (через трубку 3 ), в котором уже создан форвакуум. до 10 –7 мм рт. ст.
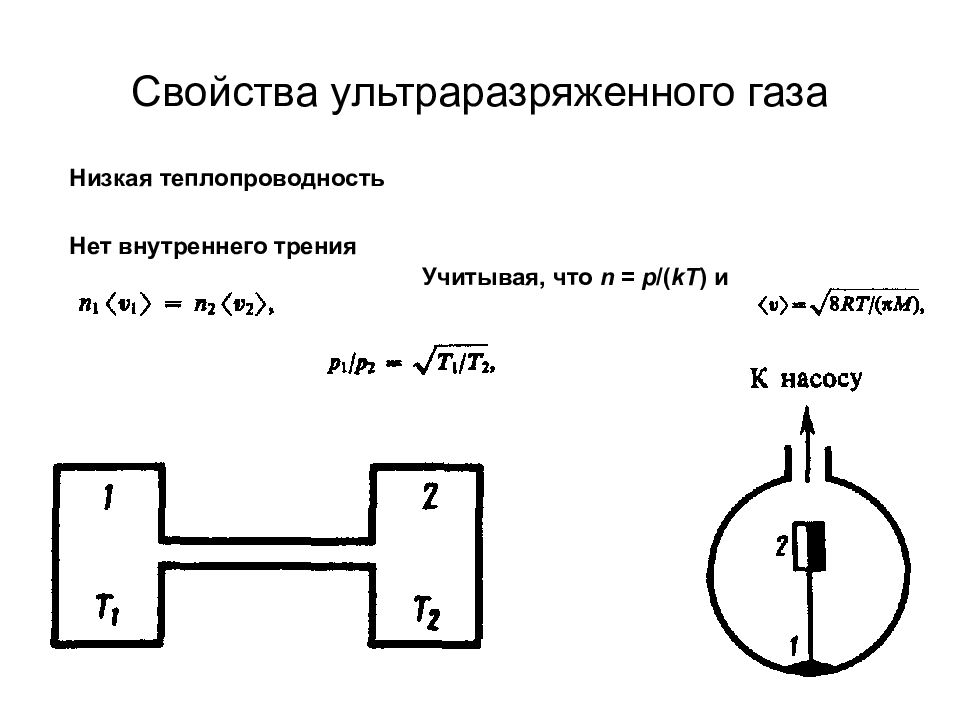
Слайд 66: Свойства ультраразряженного газа
Учитывая, что n = p /( kT ) и Низкая теплопроводность Нет внутреннего трения
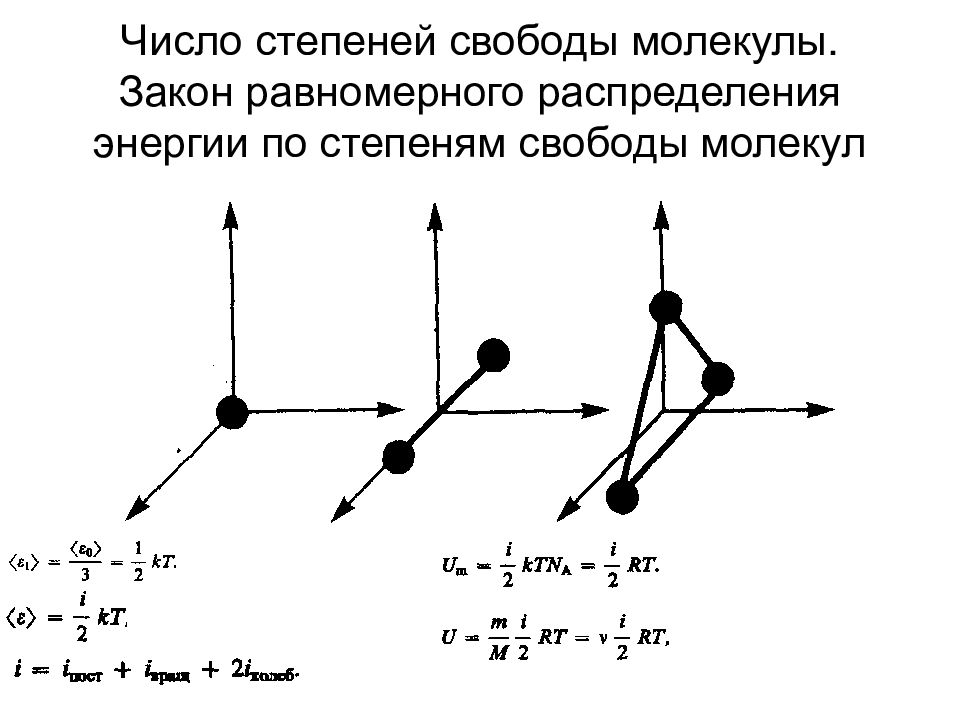
Слайд 67: Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул
Слайд 68: Первое начало термодинамики
Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии U =0. Тогда, согласно первому началу термодинамики, А= Q
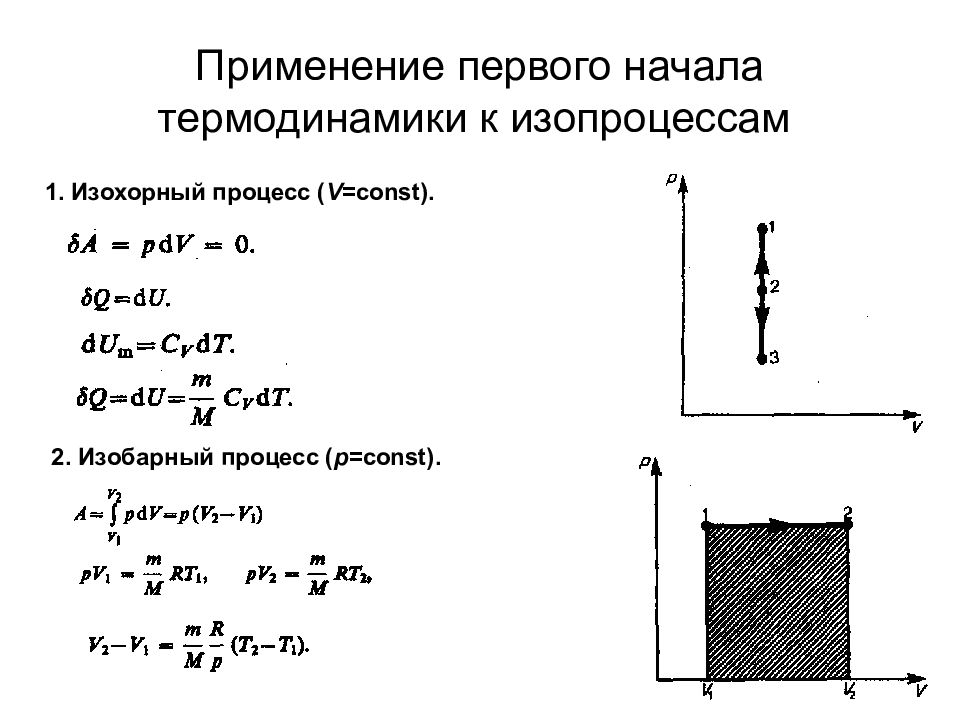
Слайд 71: Применение первого начала термодинамики к изопроцессам
1. Изохорный процесс ( V = const ). 2. Изобарный процесс ( p = const ).
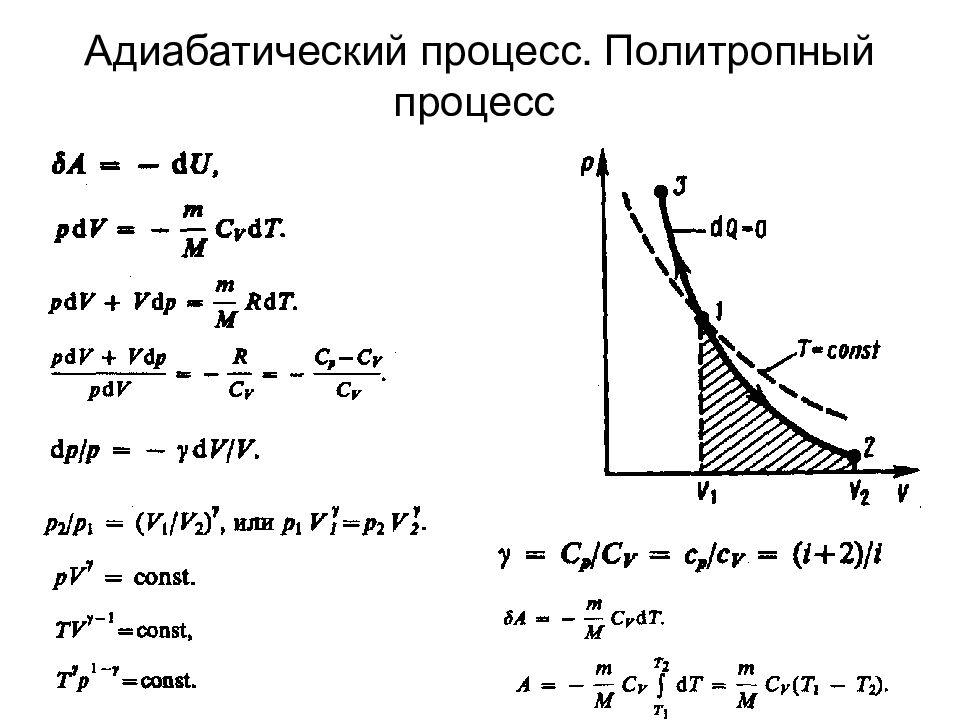
Слайд 74
где n =(С—С p )/(С—С V )— показатель политропы. Очевидно, что при С =0, n = - уравнение адиабаты, при С = , n = 1 — уравнение изотермы; при С = С p, n =0 —уравнение изобары, при С=С V, n =± — уравнение изохоры.
Слайд 76: Энтропия, ее статистическое толкование и связь с термодинамической вероятностью
Уравнение Клаузиуса при изотермическом процессе при изохорном процессе
Слайд 77: Второе и третье начало термодинамики
второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает. по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому. третье начало термодинамика, или теорема Нернста-Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:
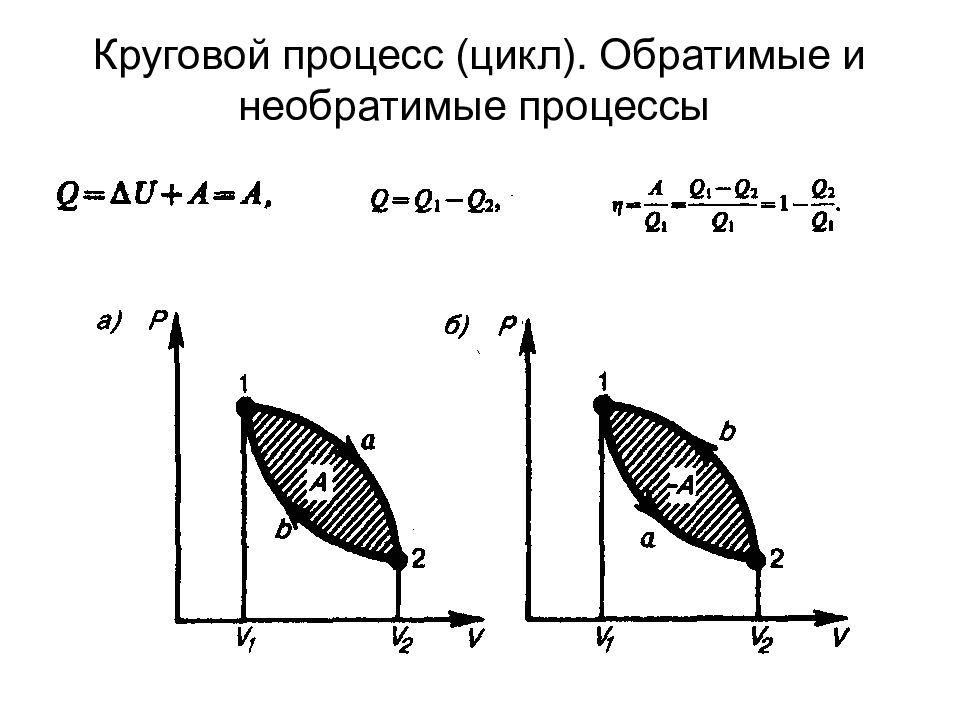
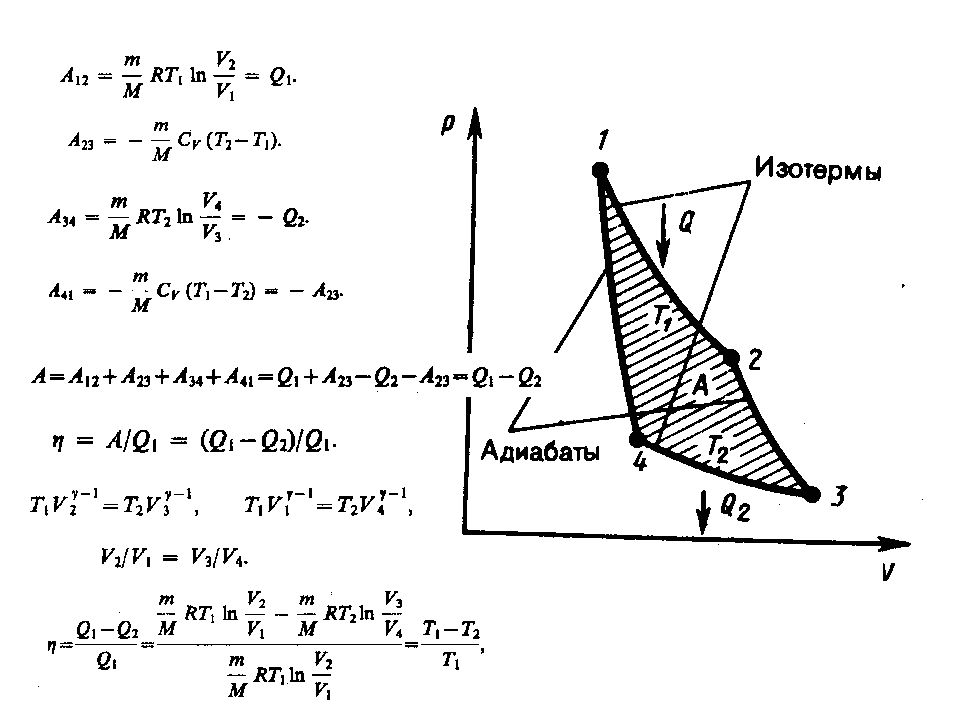
Слайд 78: Тепловые двигатели и холодильные машины. Цикл Карно и его к. п. д. для идеального газа
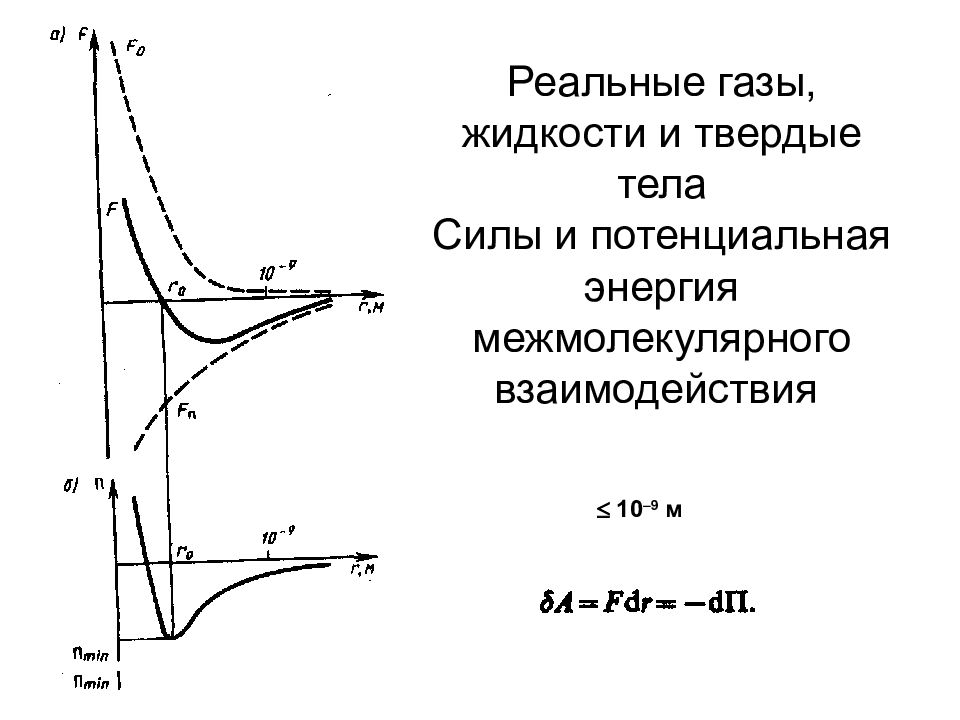
Слайд 80: Реальные газы, жидкости и твердые тела Силы и потенциальная энергия межмолекулярного взаимодействия
10 –9 м
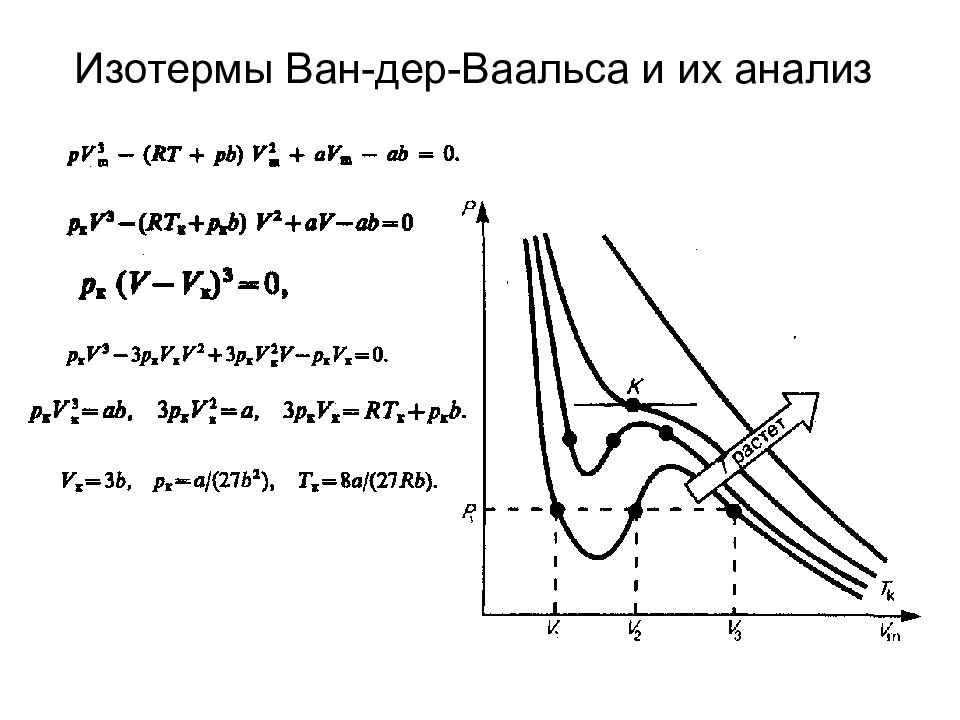
Слайд 81: Уравнение Ван-дер-Ваальса
1. Учет собственного объема молекул. V m — b, где b — объем, занимаемый самими молекулами. 2. Учет притяжения молекул. где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, V m — молярный объем. V = V m
Слайд 84: Внутренняя энергия реального газа
адиабатический процесс, т. е. Q =0 (расширение газа в вакуум, т. е. А= 0), Так как V 2 > V 1, то Т 1 > Т 2, т. е. реальный газ при адиабатическом расширении в вакуум охлаждается. При адиабатическом сжатии в вакуум реальный газ нагревается.
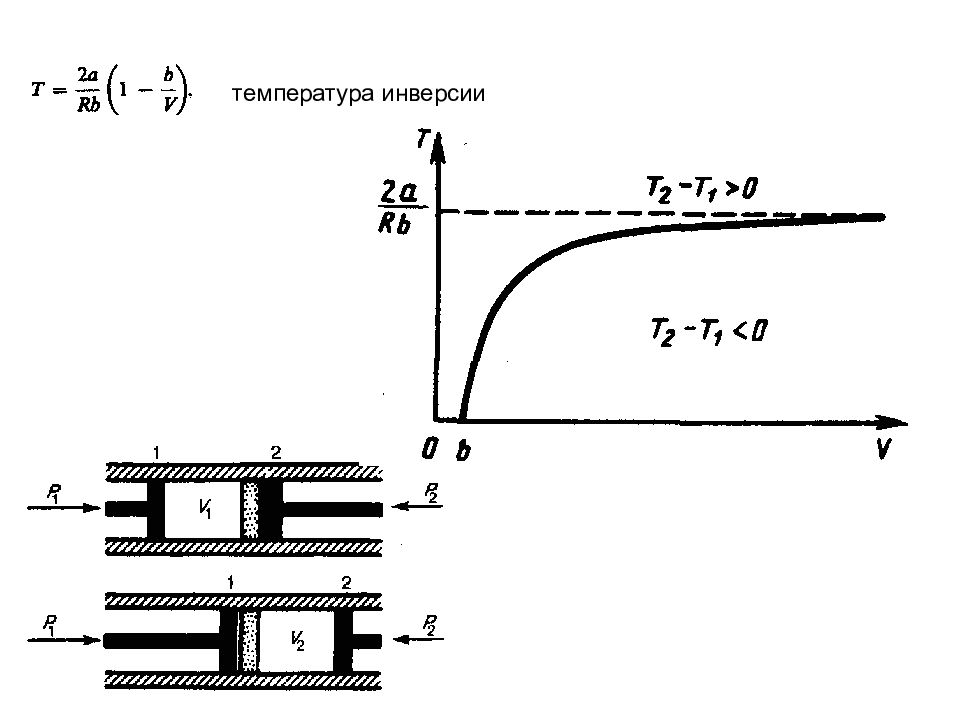
Слайд 85: Эффект Джоуля — Томсона
Проанализируем данное выражение, сделав допущение, что p 2 << p 1 и V 2 >> V 1 : 1) а 0 2) b 0 3) учитываем обе поправки т. е. знак разности температур зависит от значений начального объема V 1 и начальной температуры Т 1. Эффект Джоуля — Томсона принято называть положительным, если газ в процессе дросселирования охлаждается ( T <0), и отрицательным, если газ нагревается ( T > 0).
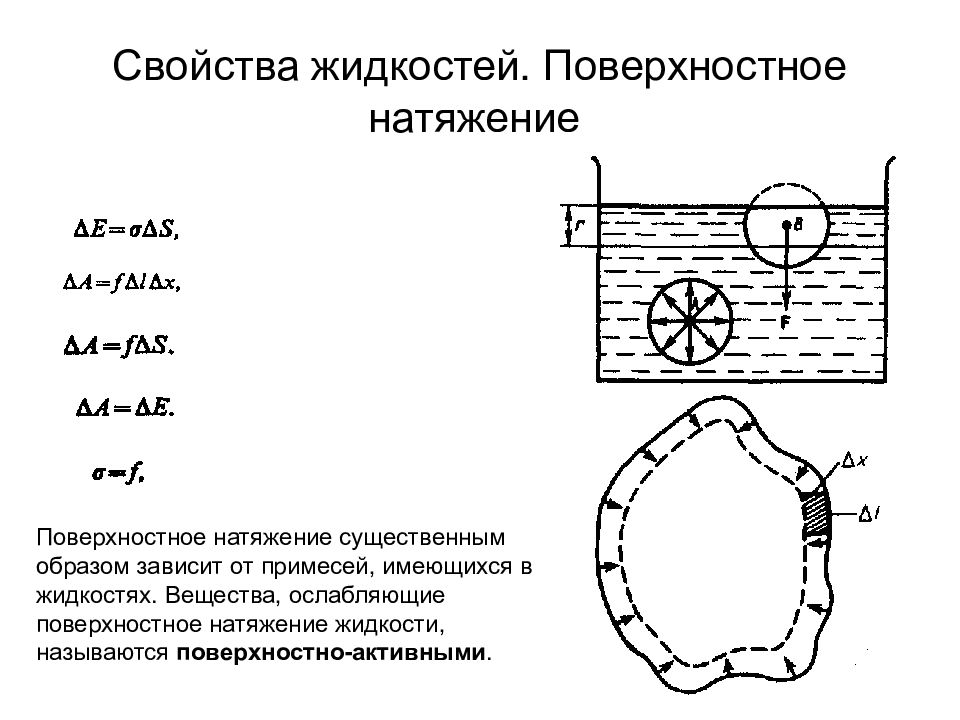
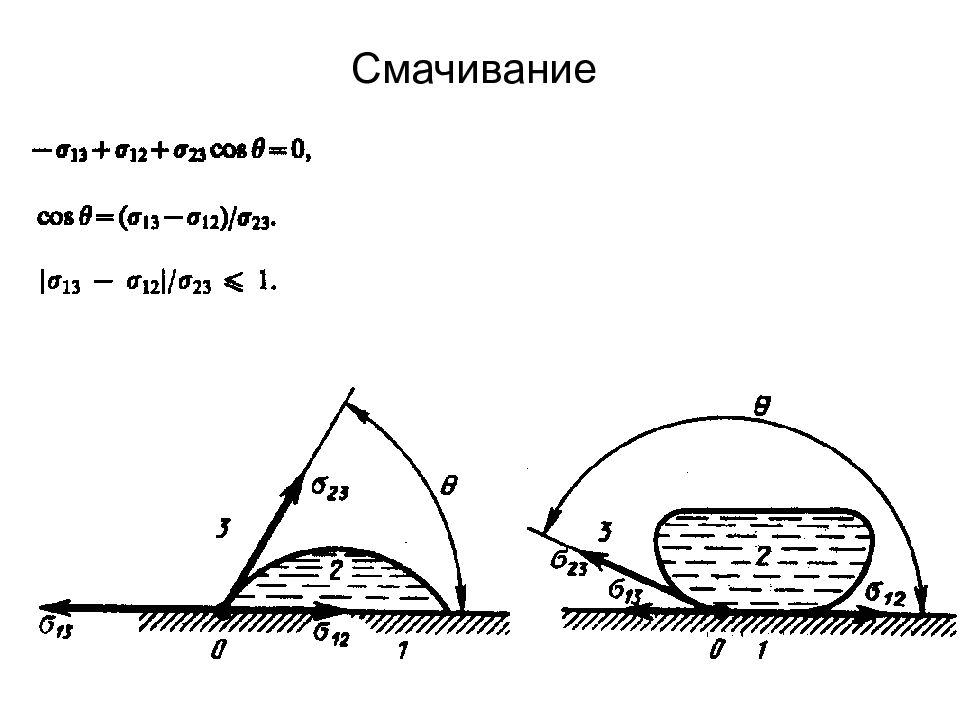
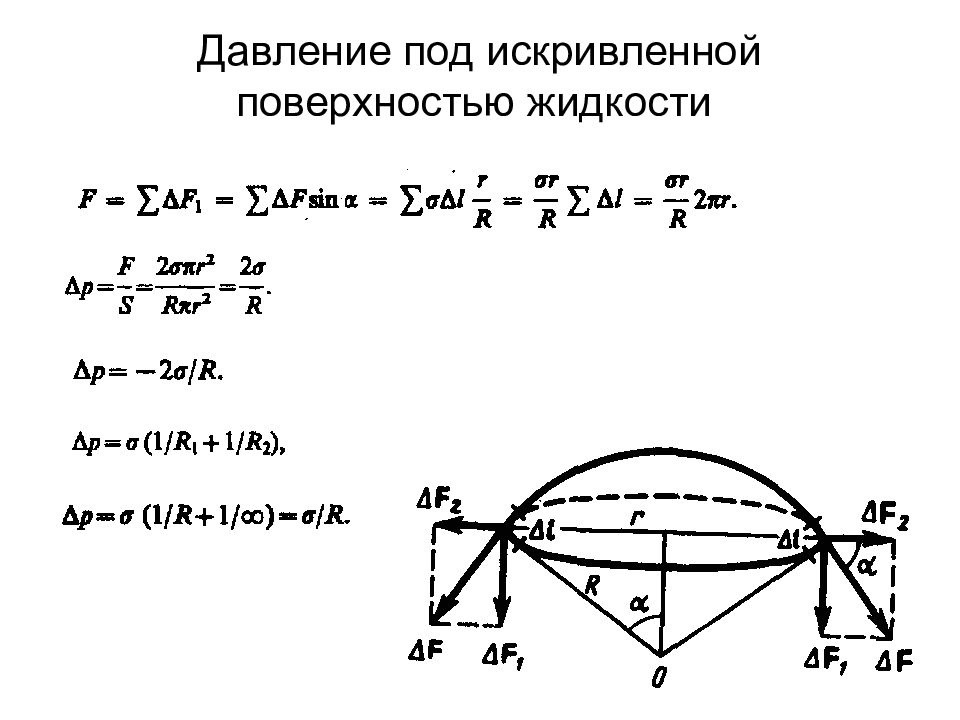
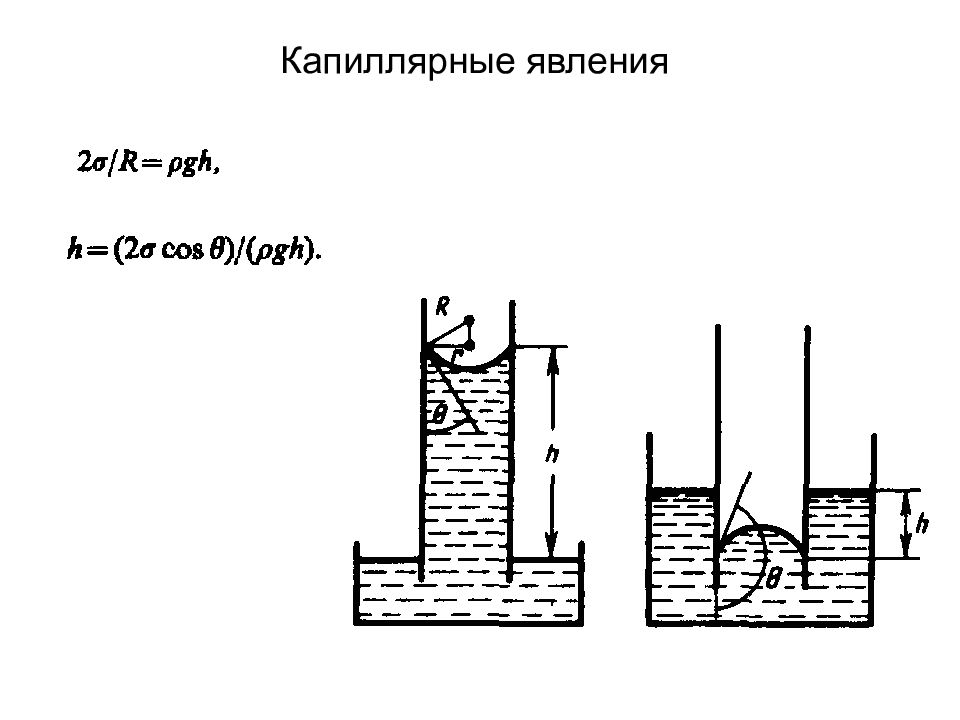
Слайд 88: Свойства жидкостей. Поверхностное натяжение
Поверхностное натяжение существенным образом зависит от примесей, имеющихся в жидкостях. Вещества, ослабляющие поверхностное натяжение жидкости, называются п o ве px ностно-активными.
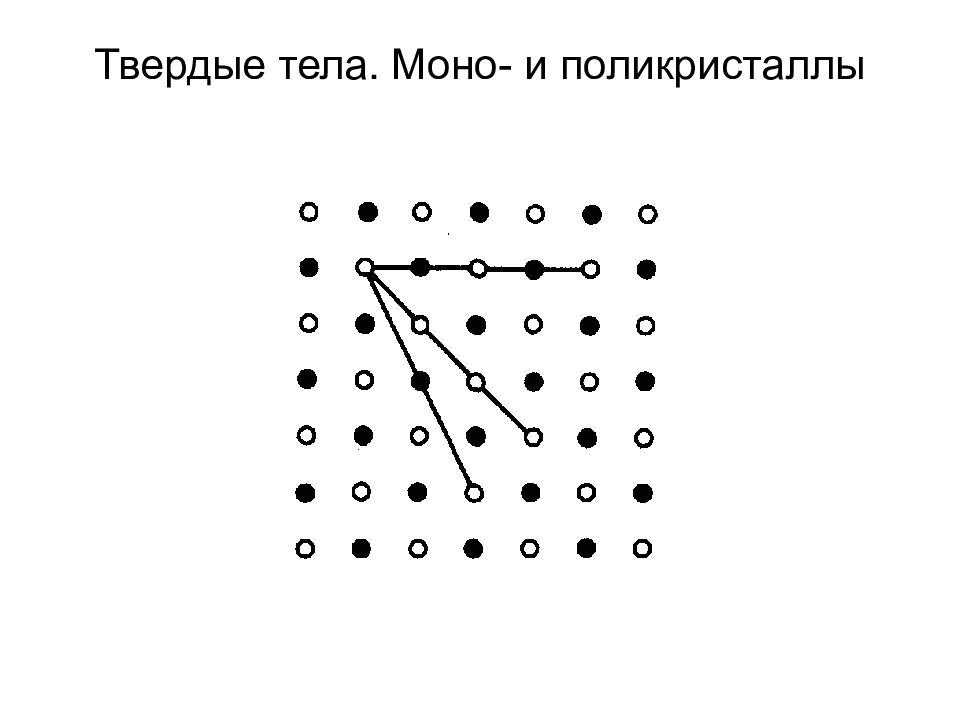
Слайд 93: Типы кристаллических твердых тел
1. Кристаллографический признак кристаллов Симметрия кристаллической решетки — ее свойство совмещаться с собой при некоторых пространственных перемещениях, например параллельных переносах, поворотах, отражениях или их комбинациях и т. д. Существует 230 пространственных групп. Всего существует 14 типов решеток Бравэ. Они распределяются по семи кристаллографическим системам, или сингониям.
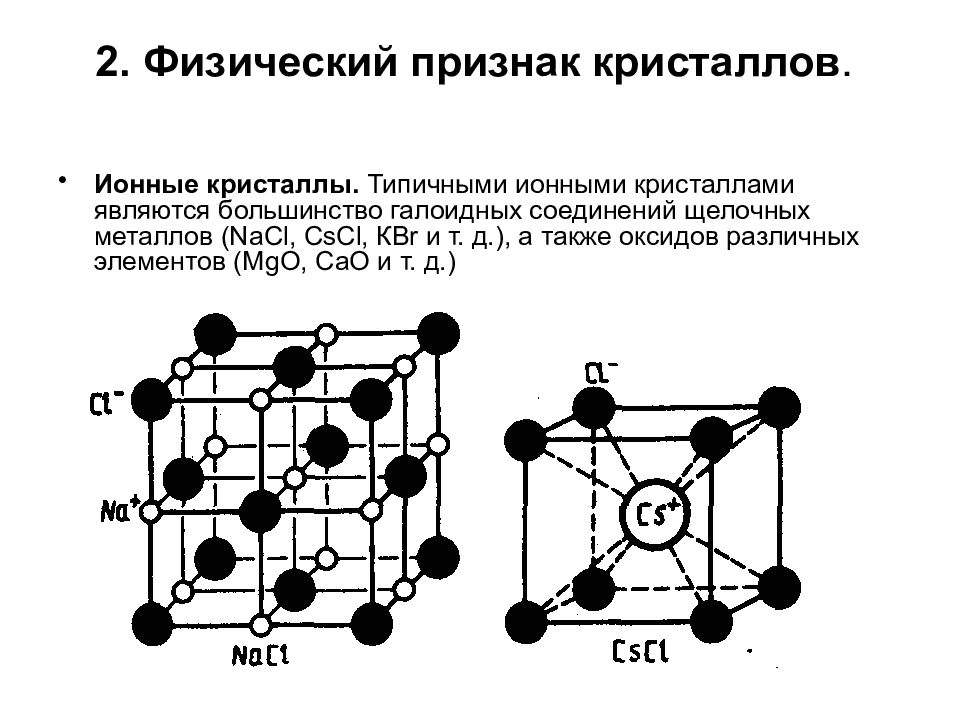
Слайд 94: 2. Физический признак кристаллов
Ионные кристаллы. Типичными ионными кристаллами являются большинство галоидных соединений щелочных металлов ( NaCl, CsCl, КВ r и т. д.), а также оксидов различных элементов ( MgO, СаО и т. д.)
Слайд 95
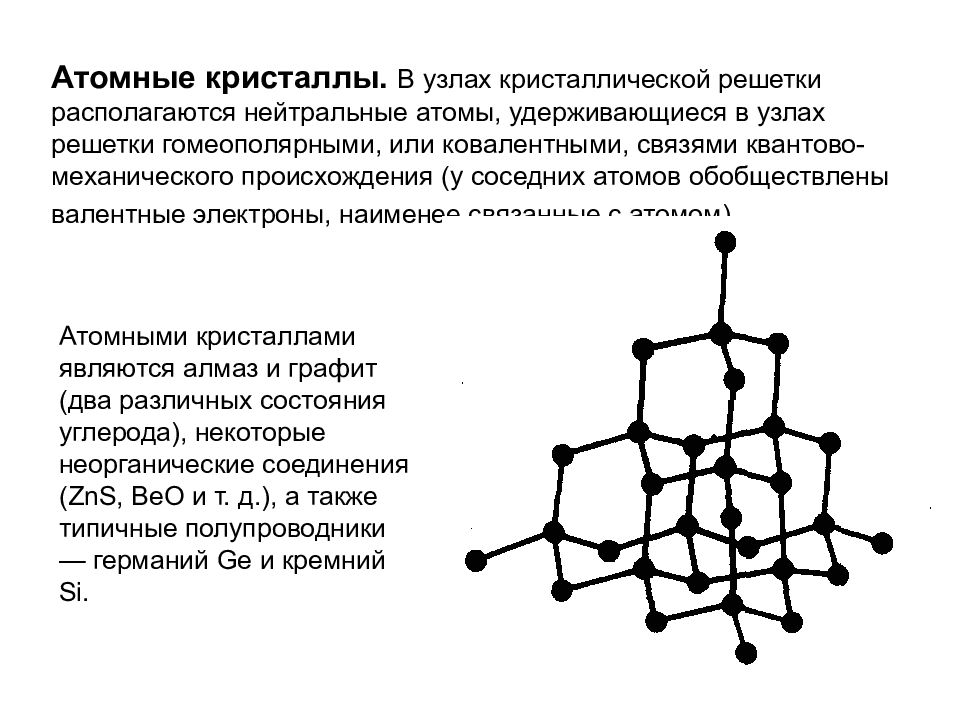
Атомные кристаллы. В узлах кристаллической решетки располагаются нейтральные атомы, удерживающиеся в узлах решетки гомеополярными, или ковалентными, связями квантово-механического происхождения (у соседних атомов обобществлены валентные электроны, наименее связанные с атомом). Атомными кристаллами являются алмаз и графит (два различных состояния углерода), некоторые неорганические соединения ( ZnS, ВеО и т. д.), а также типичные полупроводники — германий Ge и кремний Si.
Слайд 96
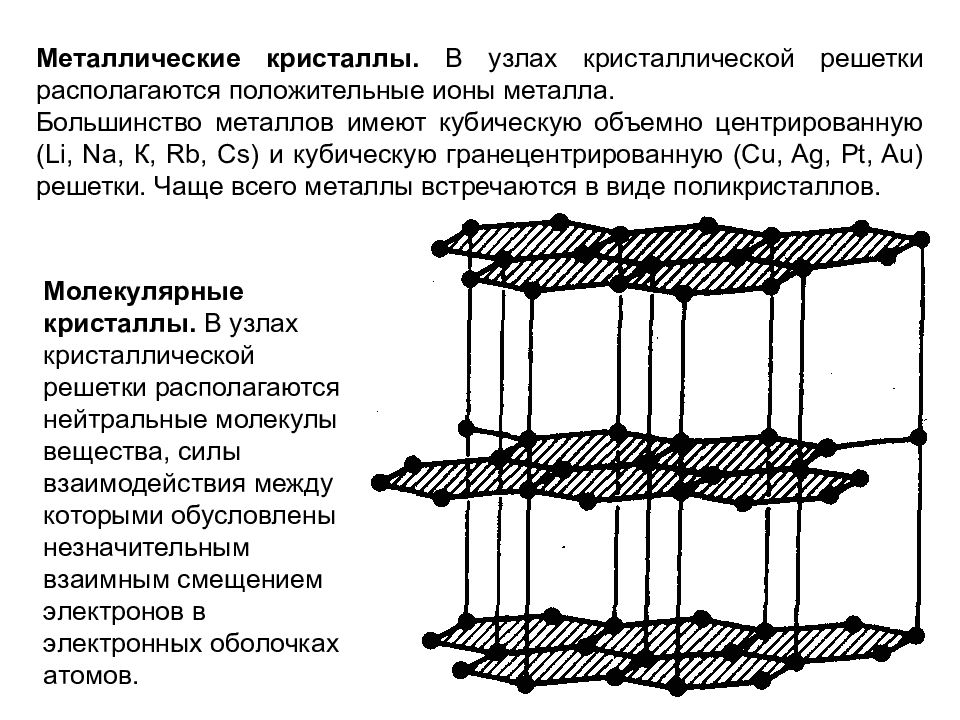
Металлические кристаллы. В узлах кристаллической решетки располагаются положительные ионы металла. Большинство металлов имеют кубическую объемно центрированную (Li, Na, К, Rb, Cs) и кубическую гранецентрированную (С u, Ag, Pt, Au ) решетки. Чаще всего металлы встречаются в виде поликристаллов. Молекулярные кристаллы. В узлах кристаллической решетки располагаются нейтральные молекулы вещества, силы взаимодействия между которыми обусловлены незначительным взаимным смещением электронов в электронных оболочках атомов.
Слайд 97
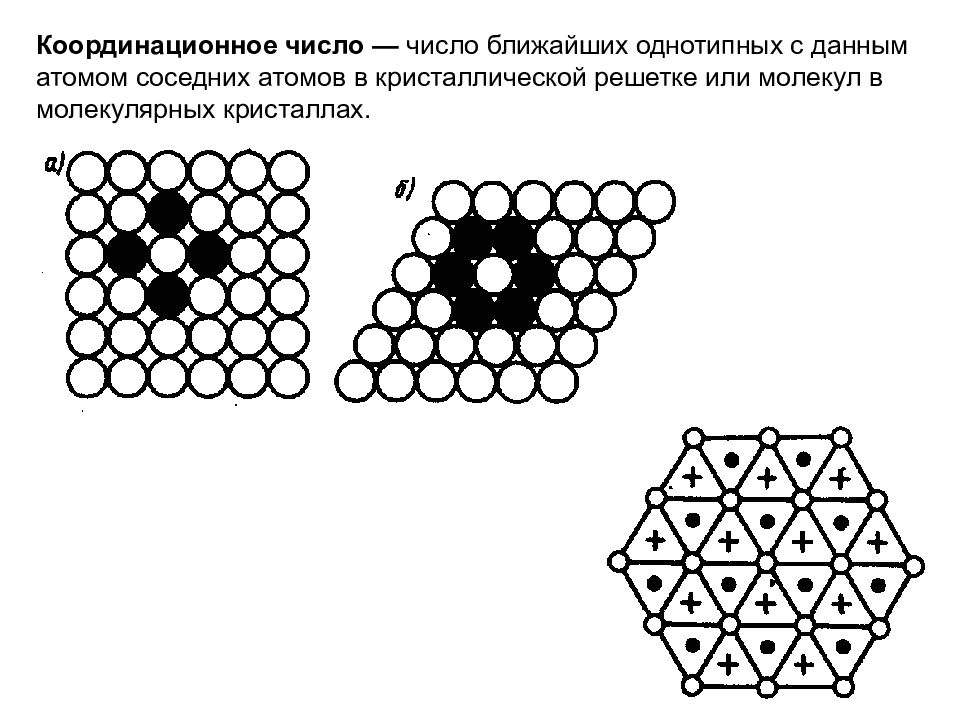
Координационное число — число ближайших однотипных с данным атомом соседних атомов в кристаллической решетке или молекул в молекулярных кристаллах.
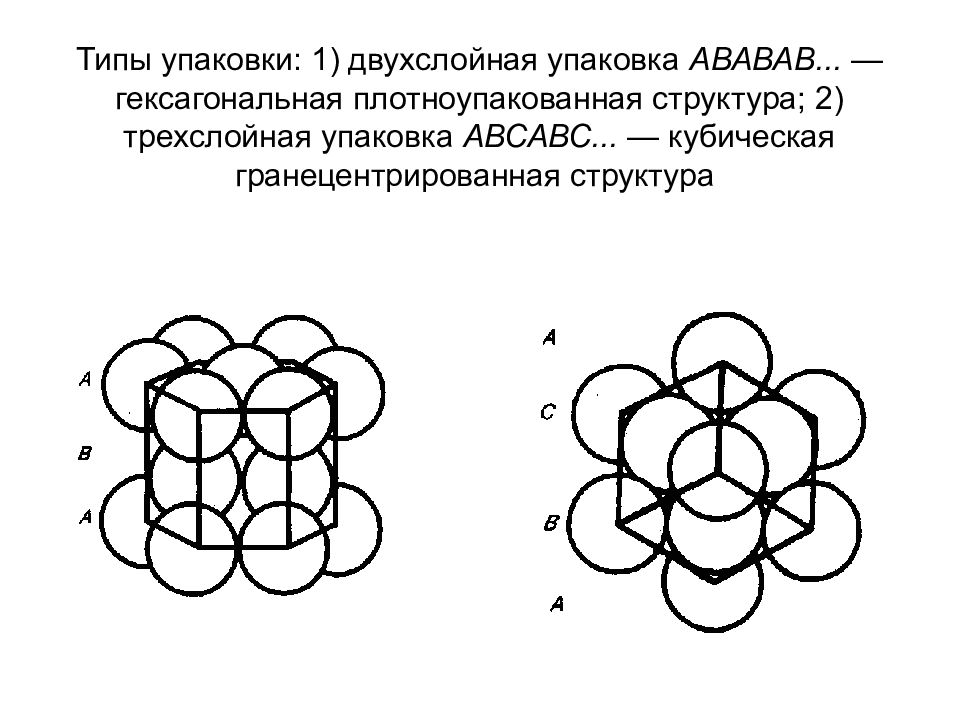
Слайд 98: Типы упаковки: 1) двухслойная упаковка АВАВАВ... — гексагональная плотноупакованная структура; 2) трехслойная упаковка АВСАВС... — кубическая гранецентрированная структура
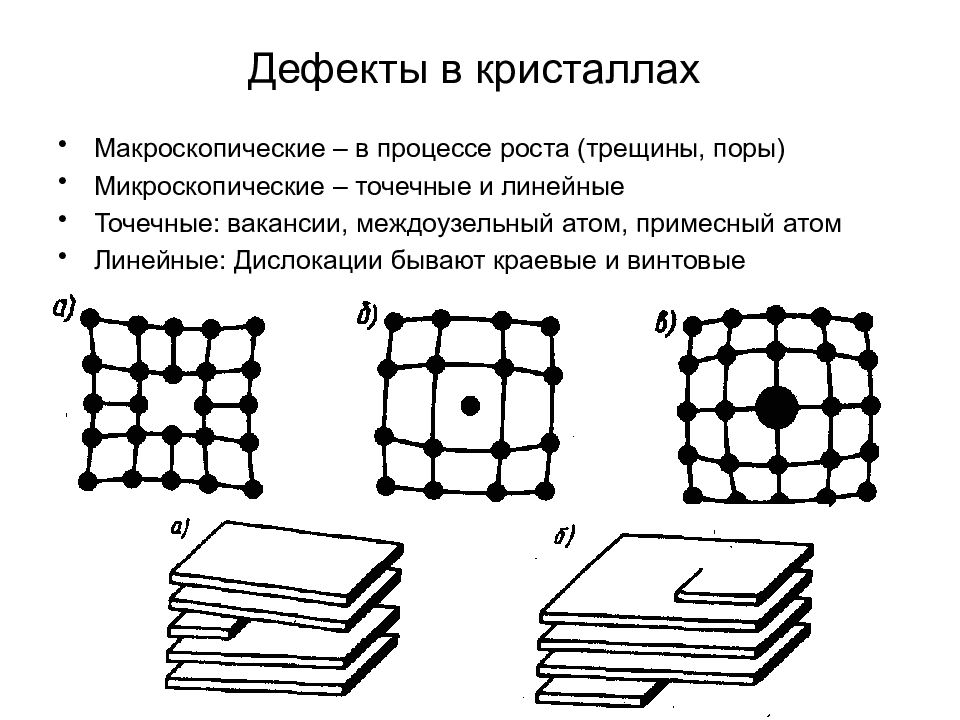
Слайд 99: Дефекты в кристаллах
Макроскопические – в процессе роста (трещины, поры) Микроскопические – точечные и линейные Точечные: вакансии, междоузельный атом, примесный атом Линейные: Дислокации бывают краевые и винтовые
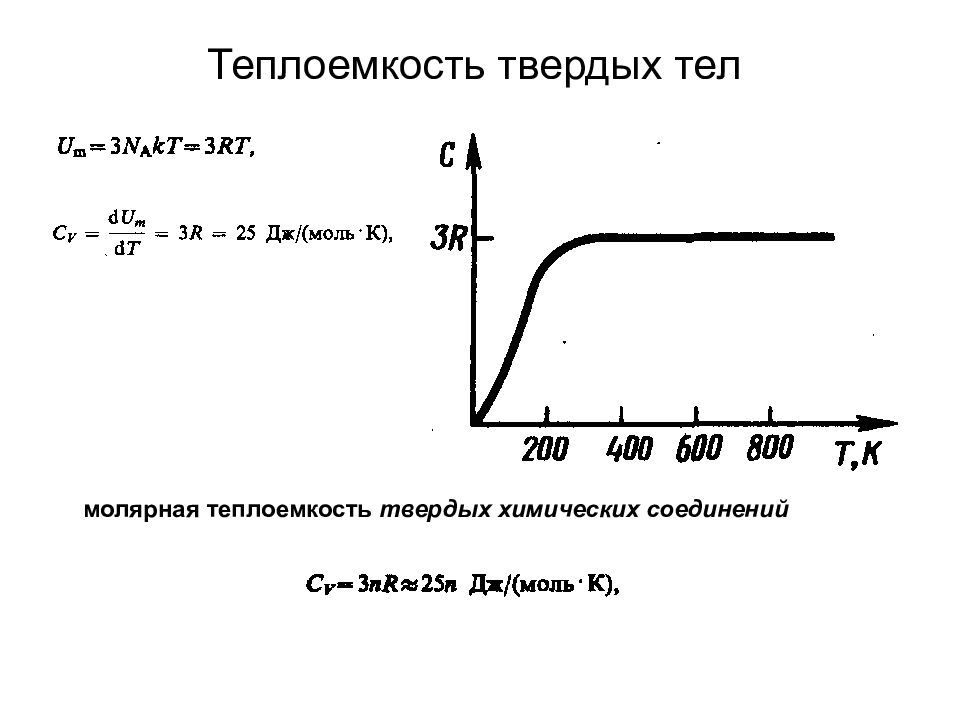
Слайд 100: Теплоемкость твердых тел
молярная теплоемкость твердых химических соединений
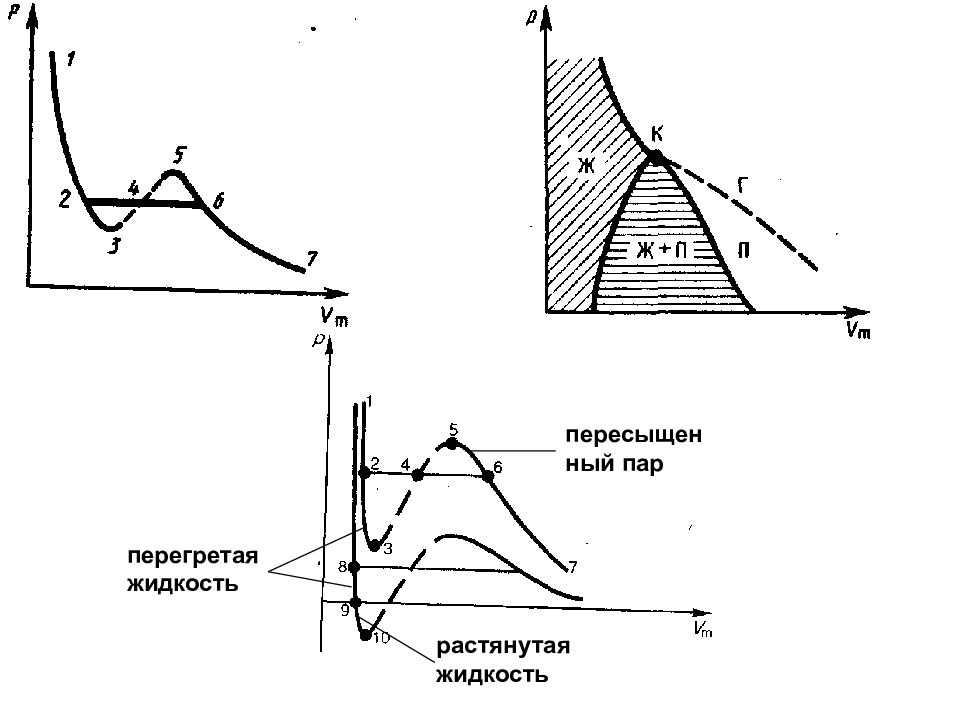
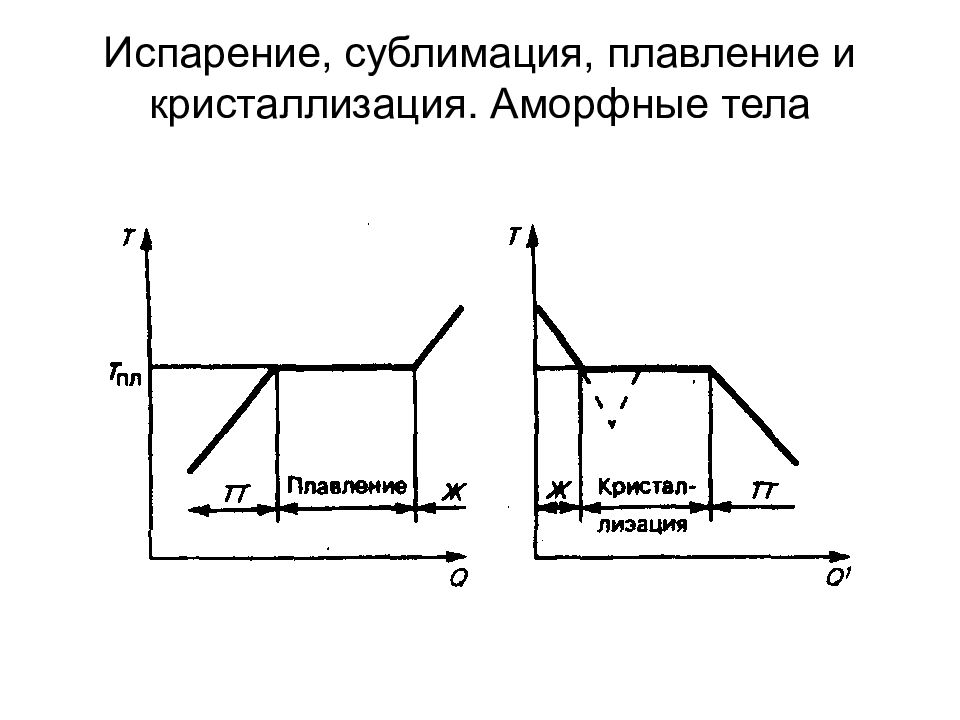
Слайд 102: Фазовые переходы I и II рода
Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Переход вещества из одной фазы в другую — фазовый переход — всегда связан с качественными изменениями свойств вещества Фазовый переход I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода.
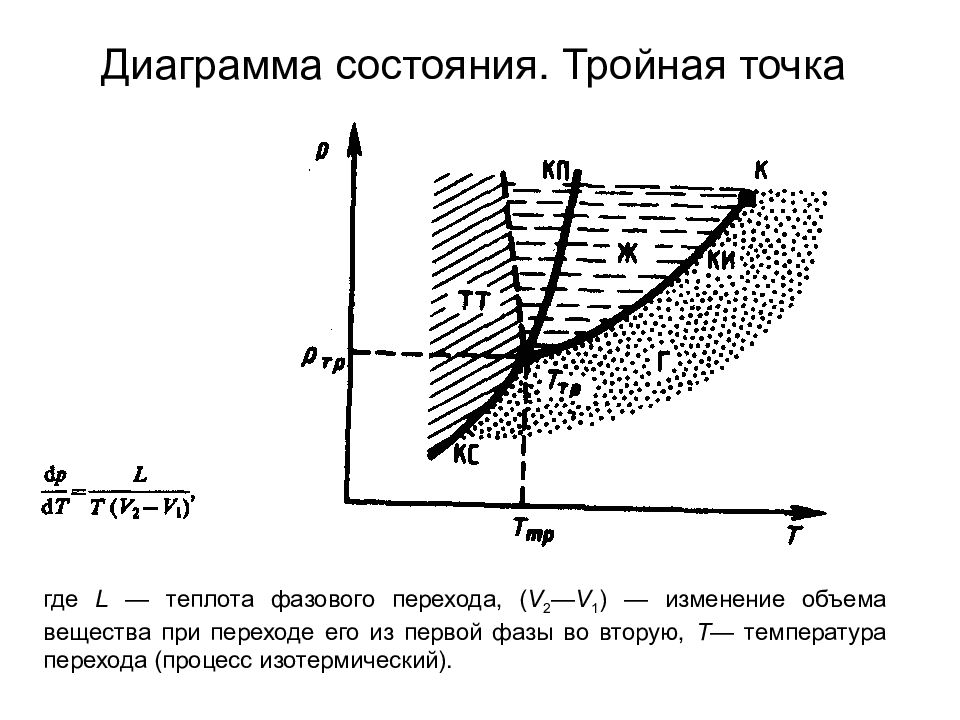
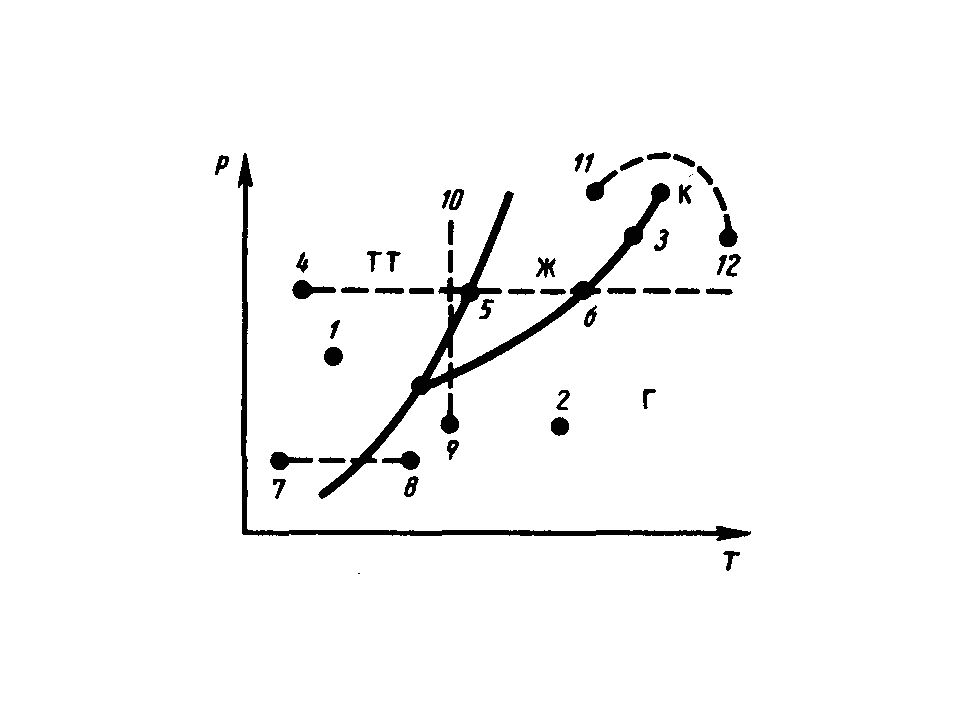
Слайд 103: Диаграмма состояния. Тройная точка
где L — теплота фазового перехода, ( V 2 — V 1 ) — изменение объема вещества при переходе его из первой фазы во вторую, Т — температура перехода (процесс изотермический).