Первый слайд презентации: Молекулярная физика и термодинамика
Курс лекций по общей физике Вечерний факультет МГАКХиС Бахтина Елена Юрьевна, к.ф-м.н., доц. каф. физики
Слайд 2: Методы исследования
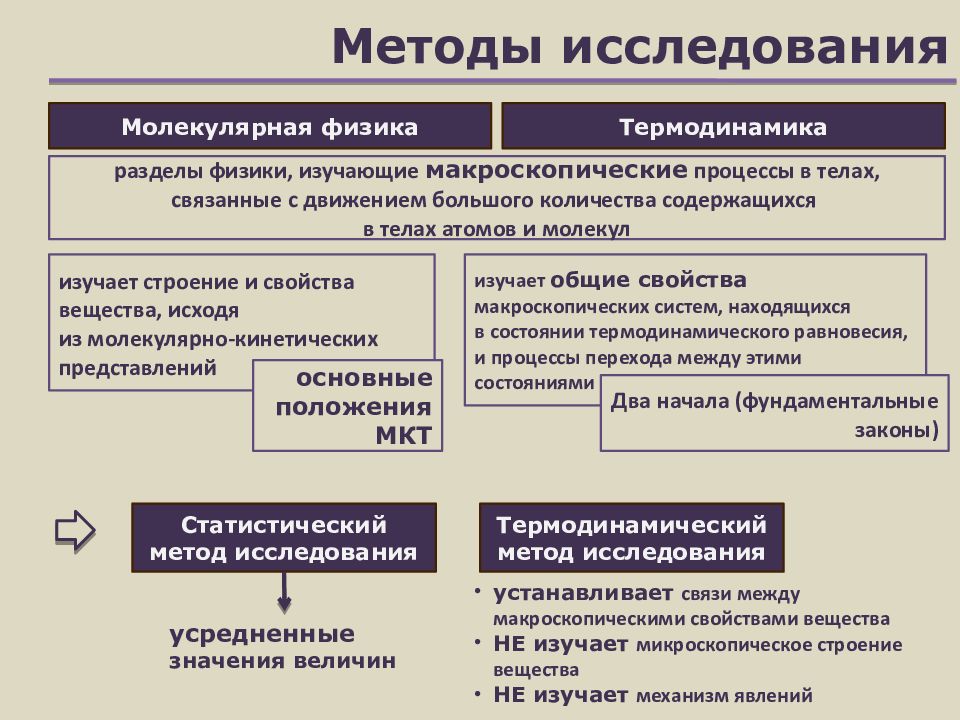
Термодинамический метод исследования Статистический метод исследования разделы физики, изучающие макроскопические процессы в телах, связанные с движением большого количества содержащихся в телах атомов и молекул Молекулярная физика Термодинамика изучает строение и свойства вещества, исходя из молекулярно-кинетических представлений основные положения МКТ усредненные значения величин изучает общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями Два начала (фундаментальные законы) устанавливает связи между макроскопическими свойствами вещества НЕ изучает микроскопическое строение вещества НЕ изучает механизм явлений
Слайд 3: Основные понятия
T = 273,15 + t Термодинамическая система совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами Термодинамические параметры давление P объем V температура Т Моль количество вещества, содержащее столько же частиц, сколько содержится атомов в 0,012 кг углерода 12 C N A = 6,022·10 23 моль –1 число Авогадро абсолютным нулем температуры – точка нулевого давления газа Реперные точки температура тройной точки воды: лед, вода и пар – в тепловом равновесии в шкале Кельвина 0,01° С 273,16 К
Слайд 4: Основные положения МКТ
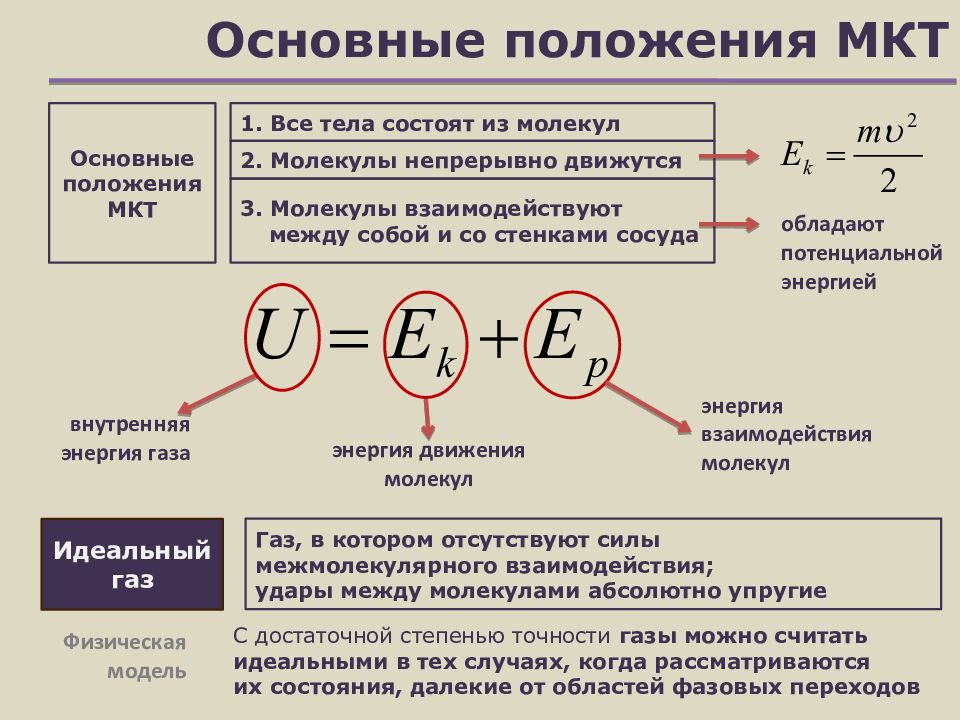
Идеальный газ 1. Все тела состоят из молекул Основные положения МКТ Газ, в котором отсутствуют силы межмолекулярного взаимодействия; удары между молекулами абсолютно упругие 2. Молекулы непрерывно движутся 3. Молекулы взаимодействуют между собой и со стенками сосуда энергия движения молекул энергия взаимодействия молекул внутренняя энергия газа С достаточной степенью точности газы можно считать идеальными в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых переходов Физическая модель обладают потенциальной энергией
Слайд 5: Основное уравнение МКТ
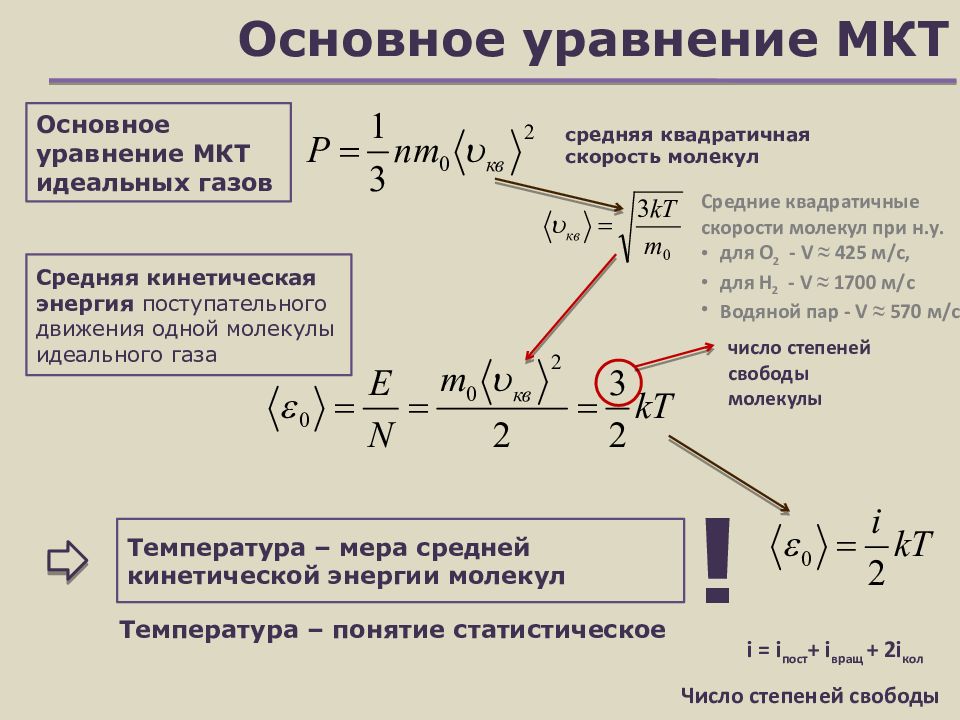
Основное уравнение МКТ идеальных газов средняя квадратичная скорость молекул Средние квадратичные скорости молекул при н.у. для О 2 - V ≈ 425 м/с, для Н 2 - V ≈ 1700 м/с Водяной пар - V ≈ 570 м/с Средняя кинетическая энергия поступательного движения одной молекулы идеального газа Температура – мера средней кинетической энергии молекул Температура – понятие статистическое ! число степеней свободы молекулы i = i пост + i вращ + 2 i кол Число степеней свободы
Слайд 6: Уравнение состояния идеального газа
Уравнение Менделеева- Клапейрона М – молярная масса – количество вещества R =8,31 Дж/(моль∙К) – универсальная газовая постоянная k = R/N A = 1,38 ∙10 -23 Дж/К – постоянная Больцмана n – концентрация молекул
Слайд 7: Внутренняя энергия идеального газа
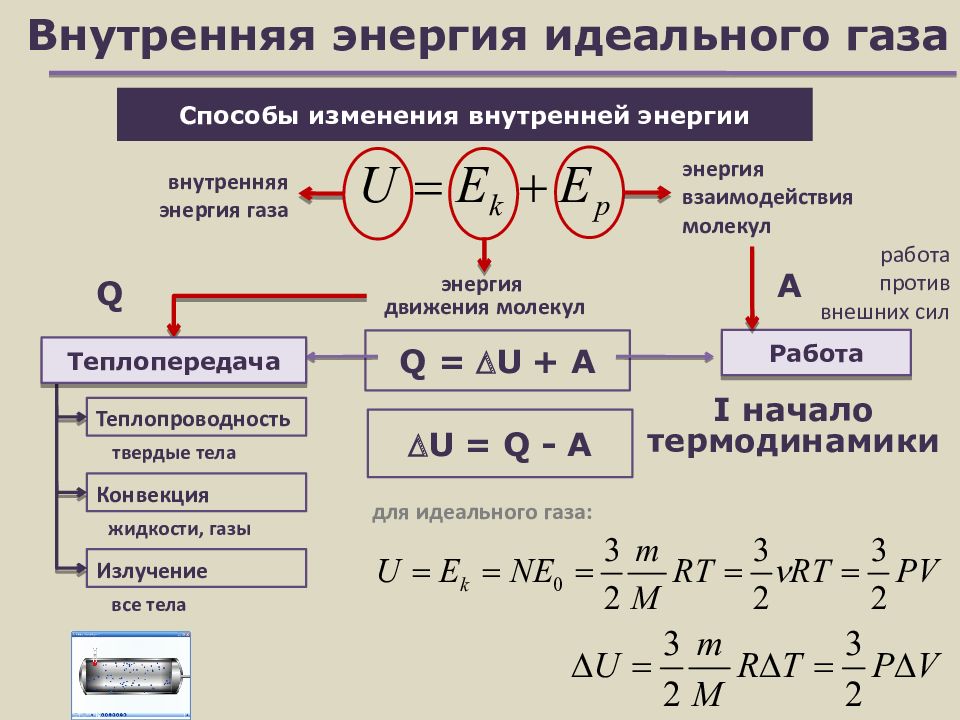
Способы изменения внутренней энергии Работа Теплопроводность энергия движения молекул энергия взаимодействия молекул внутренняя энергия газа Q A Конвекция Излучение твердые тела жидкости, газы все тела Q = U + A I начало термодинамики для идеального газа: U = Q - A Теплопередача работа против внешних сил
Слайд 8: Работа газа при изменении его объема
Р S d l Q справедливо при любых изменениях объема твердых, жидких и газообразных тел Графически можно изображать только равновесные процессы (последовательности равновесных состояний) Все реальные процессы неравновесны !
Слайд 9: Первое начало термодинамики
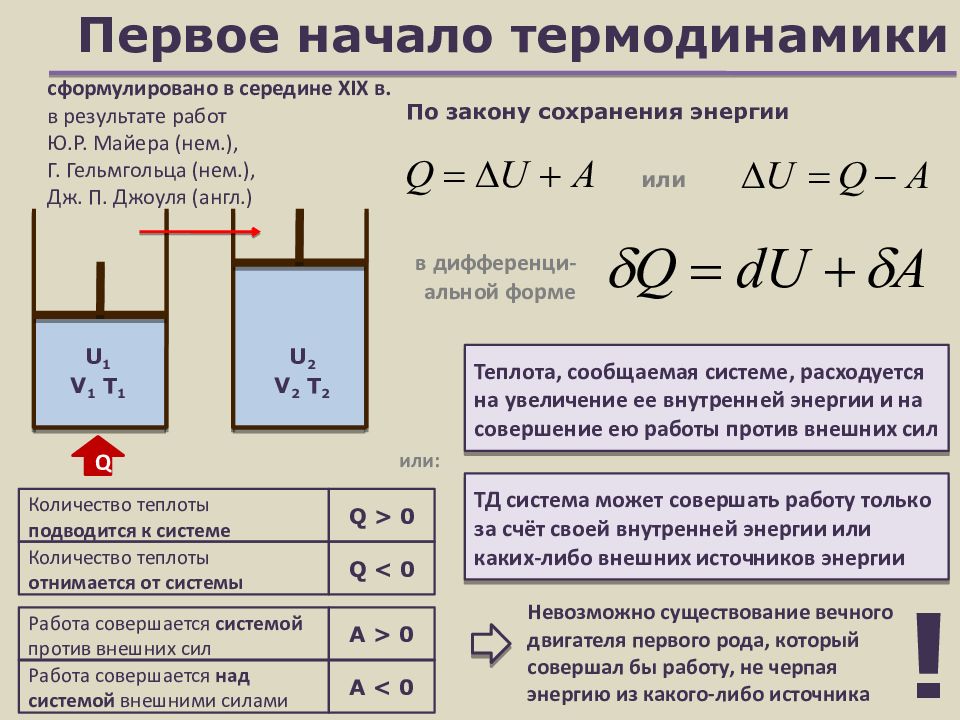
U 1 V 1 T 1 или Q > 0 Количество теплоты подводится к системе Q < 0 Количество теплоты отнимается от системы Работа совершается системой против внешних сил Работа совершается над системой внешними силами А > 0 А < 0 По закону сохранения энергии U 2 V 2 T 2 Q в дифференци-альной форме Теплота, сообщаемая системе, расходуется на увеличение ее внутренней энергии и на совершение ею работы против внешних сил ТД система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии сформулировано в середине XIX в. в результате работ Ю.Р. Майера (нем.), Г. Гельмгольца (нем.), Дж. П. Джоуля (англ.) Невозможно существование вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника или: !
Слайд 10: Теплоемкость
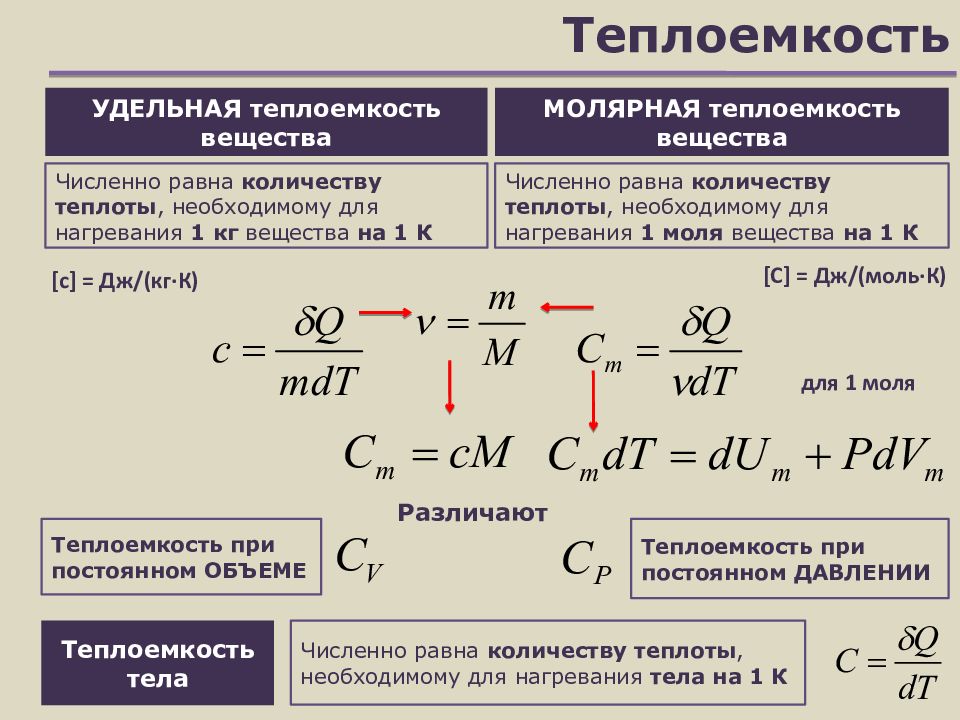
УДЕЛЬНАЯ теплоемкость вещества Численно равна количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К Теплоемкость при постоянном ОБЪЕМЕ Теплоемкость при постоянном ДАВЛЕНИИ [ с ] = Дж/(кг∙К) МОЛЯРНАЯ теплоемкость вещества Численно равна количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К [ С ] = Дж/(моль∙К) Различают для 1 моля Теплоемкость тела Численно равна количеству теплоты, необходимому для нагревания тела на 1 К
Слайд 11: Изопроцессы
Изохорный V=const =0 Молярная теплоемкость при постоянном объеме С учетом Все количество теплоты, полученное телом, идет на изменение внутренней энергии равна Q, необходимому для нагревания 1 моль вещества на 1 К Жак Александр Сезар Шарль, 1808 г.
Слайд 12: Изопроцессы
Изобарный Р =const = C V = R работа при изобарном нагревании 1 моля на 1 К Жозеф Луи Гей-Люссак, 1862 г. уравнение Майера Все количество теплоты, полученное телом, идет на изменение внутренней энергии и совершение работы телом
Слайд 13: Изопроцессы
Изотермический Роберт Бойль, 1662 г. Эдм Мариотт, 1676 г. Т =const =0 Для того, чтобы при расширении газа Т не понижалась, к газу в течение изотермического процесса необходимо подводить Q, эквивалентное внешней работе расширения Все количество теплоты, полученное телом, идет на совершение работы телом
Слайд 14: Адиабатический процесс
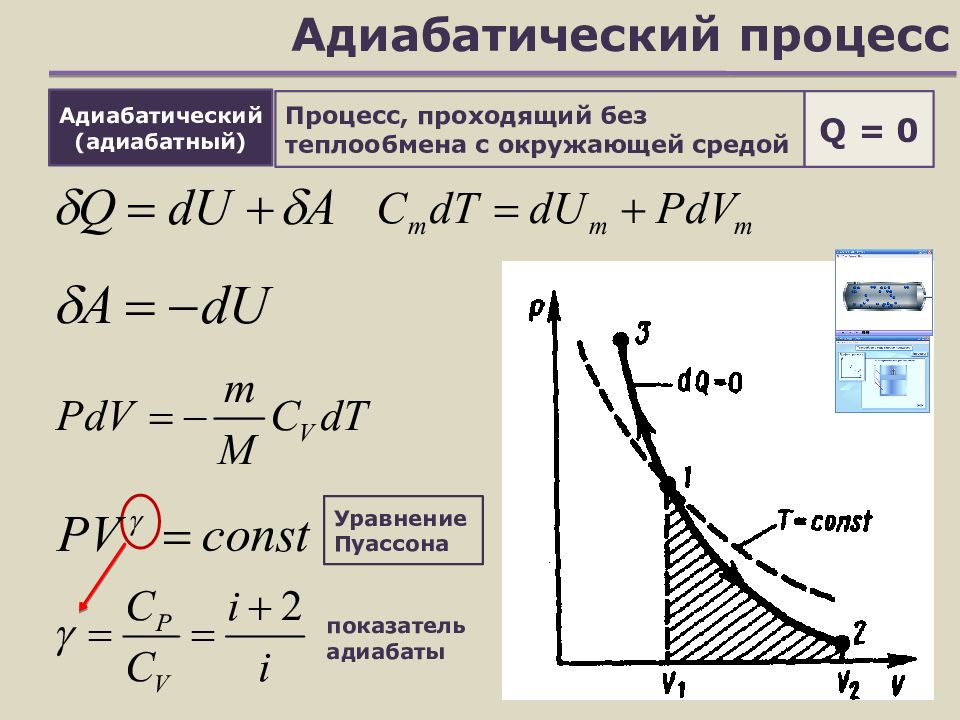
Процесс, проходящий без теплообмена с окружающей средой показатель адиабаты Адиабатический (адиабатный) Q = 0 Уравнение Пуассона
Слайд 15: Термодинамический цикл
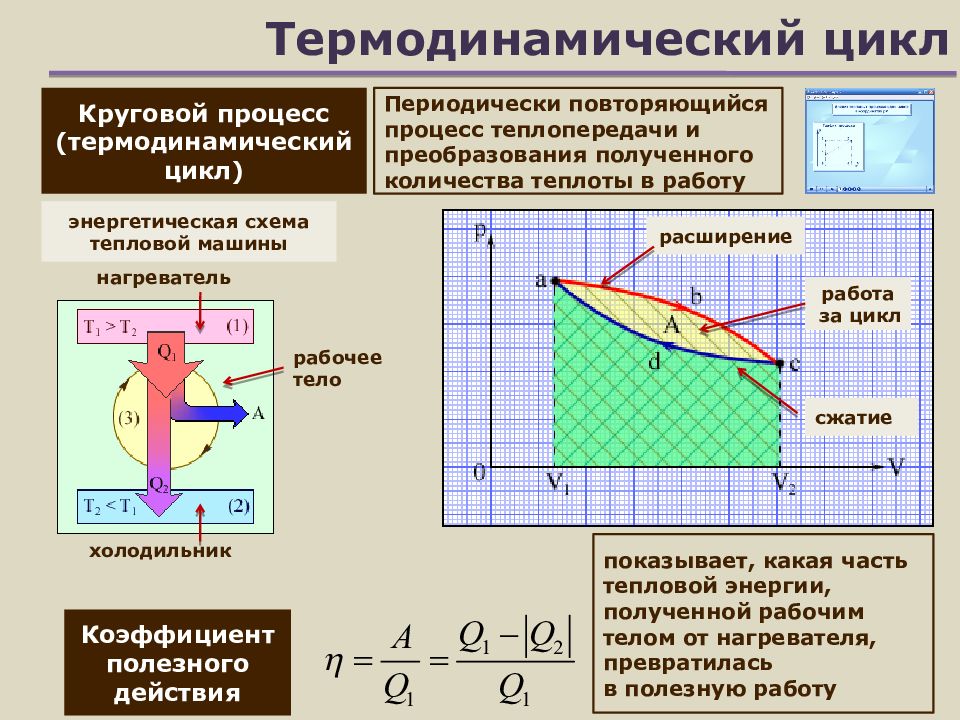
Круговой процесс (термодинамический цикл) Периодически повторяющийся процесс теплопередачи и преобразования полученного количества теплоты в работу Коэффициент полезного действия рабочее тело нагреватель холодильник расширение сжатие работа за цикл показывает, какая часть тепловой энергии, полученной рабочим телом от нагревателя, превратилась в полезную работу энергетическая схема тепловой машины
Слайд 16: Использование циклов
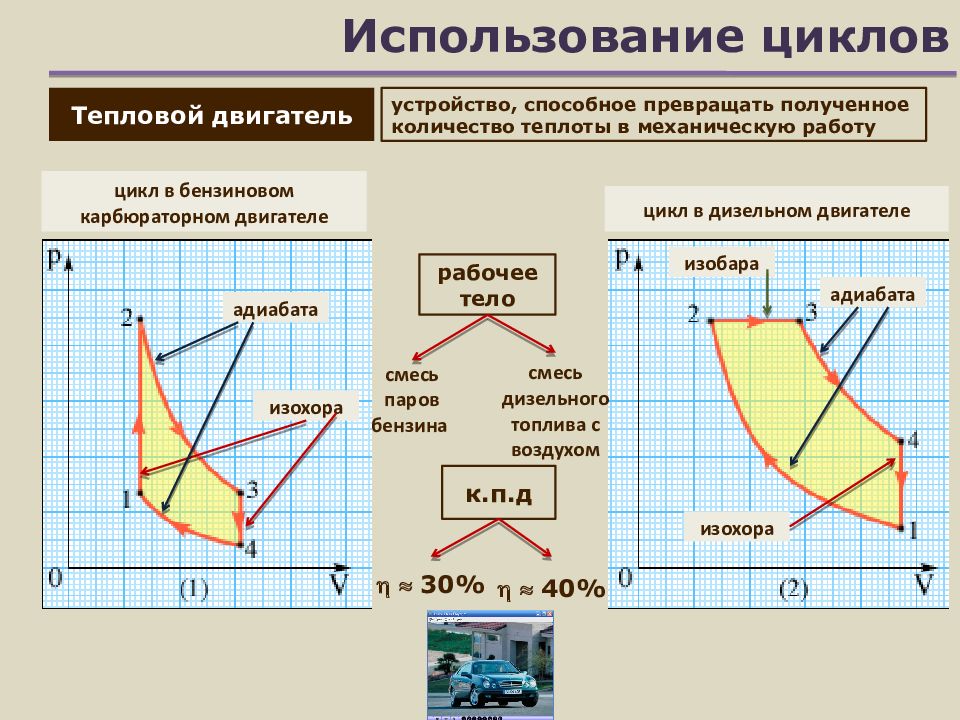
рабочее тело Тепловой двигатель устройство, способное превращать полученное количество теплоты в механическую работу цикл в бензиновом карбюраторном двигателе цикл в дизельном двигателе смесь паров бензина смесь дизельного топлива с воздухом изохора адиабата адиабата изохора изобара 30% 40% к.п.д
Слайд 17: Цикл Карно
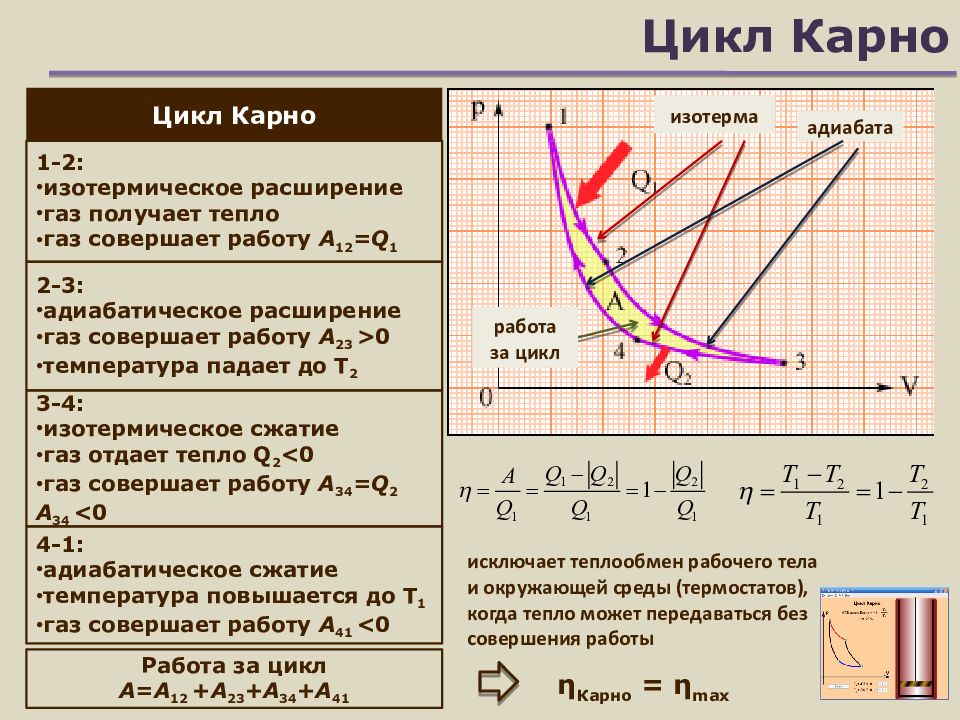
Цикл Карно изотерма адиабата 1-2: изотермическое расширение газ получает тепло газ совершает работу A 12 =Q 1 2-3: адиабатическое расширение газ совершает работу A 2 3 >0 температура падает до T 2 3 - 4 : изотермическое сжатие газ отдает тепло Q 2 <0 газ совершает работу А 34 = Q 2 A 3 4 <0 4-1 : адиабатическое сжатие температура повышается до T 1 газ совершает работу A 4 1 <0 Работа за цикл A = A 1 2 +А 23 +А 34 +А 4 1 работа за цикл η Карно = η max исключает теплообмен рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы
Слайд 18: Использование цикла Карно
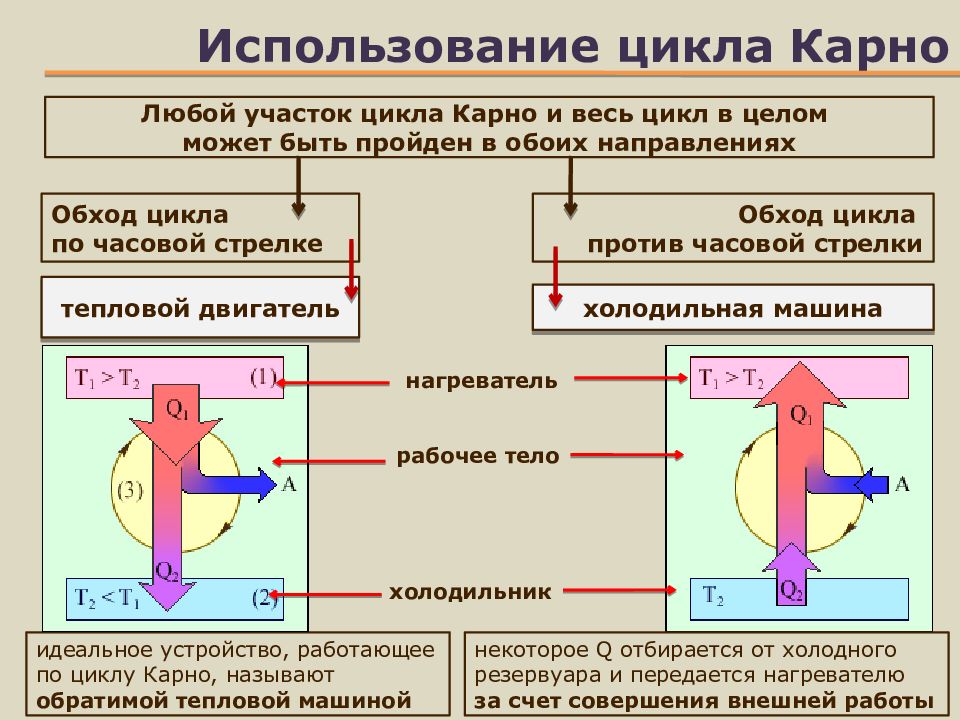
холодильник Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной Обход цикла по часовой стрелке некоторое Q отбирается от холодного резервуара и передается нагревателю за счет совершения внешней работы тепловой двигатель Обход цикла против часовой стрелки холодильная машина рабочее тело нагреватель
Слайд 19: Второе начало термодинамики
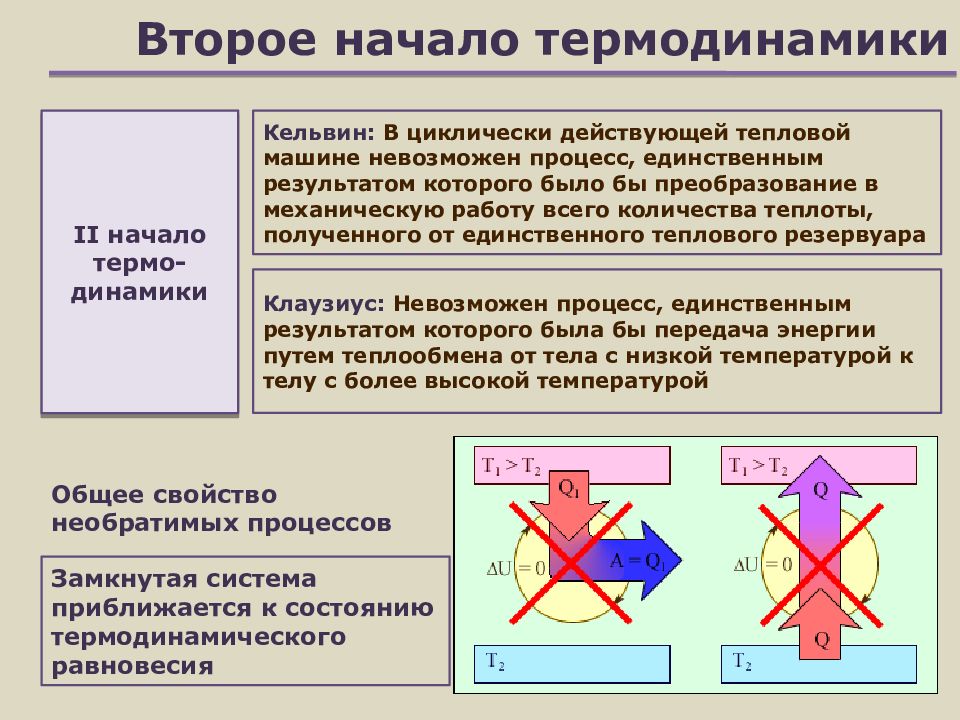
Клаузиус : Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой II начало термо -динамики З амкнутая система приближается к состоянию термодинамического равновесия Общее свойство необратимых процессов Кельвин: В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара
Слайд 20: Энтропия
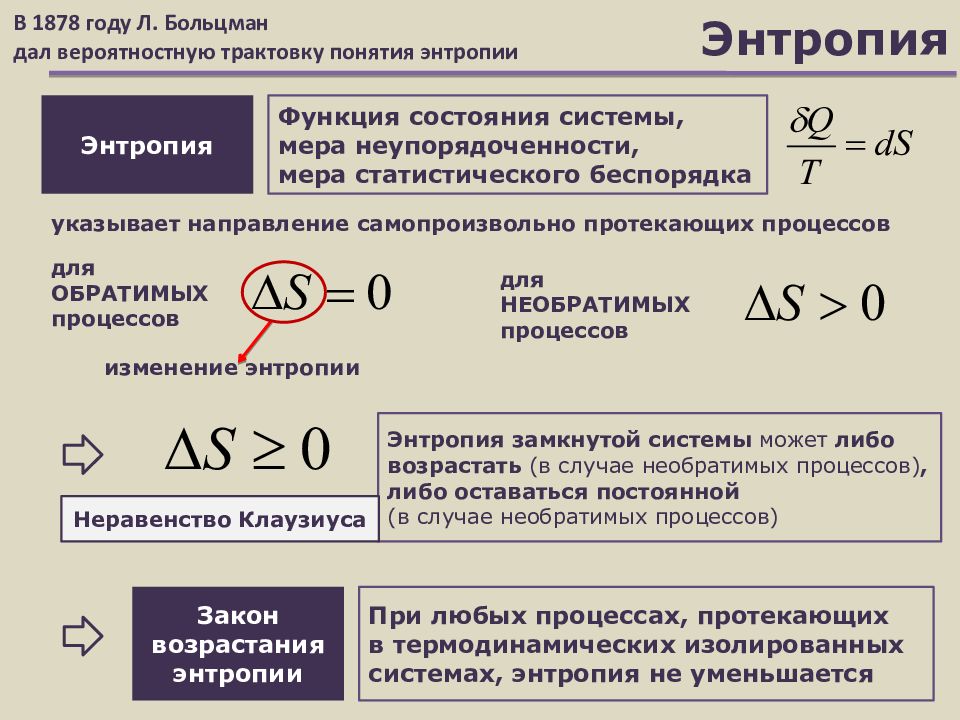
Энтропия Функция состояния системы, мера неупорядоченности, мера статистического беспорядка указывает направление самопроизвольно протекающих процессов В 1878 году Л. Больцман дал вероятностную трактовку понятия энтропии д ля ОБРАТИМЫХ процессов Закон возрастания энтропии При любых процессах, протекающих в термодинамических изолированных системах, энтропия не уменьшается изменение энтропии д ля НЕОБРАТИМЫХ процессов Энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае необратимых процессов) Неравенство Клаузиуса
Слайд 21: Явления переноса в термодинамически неравновесных системах
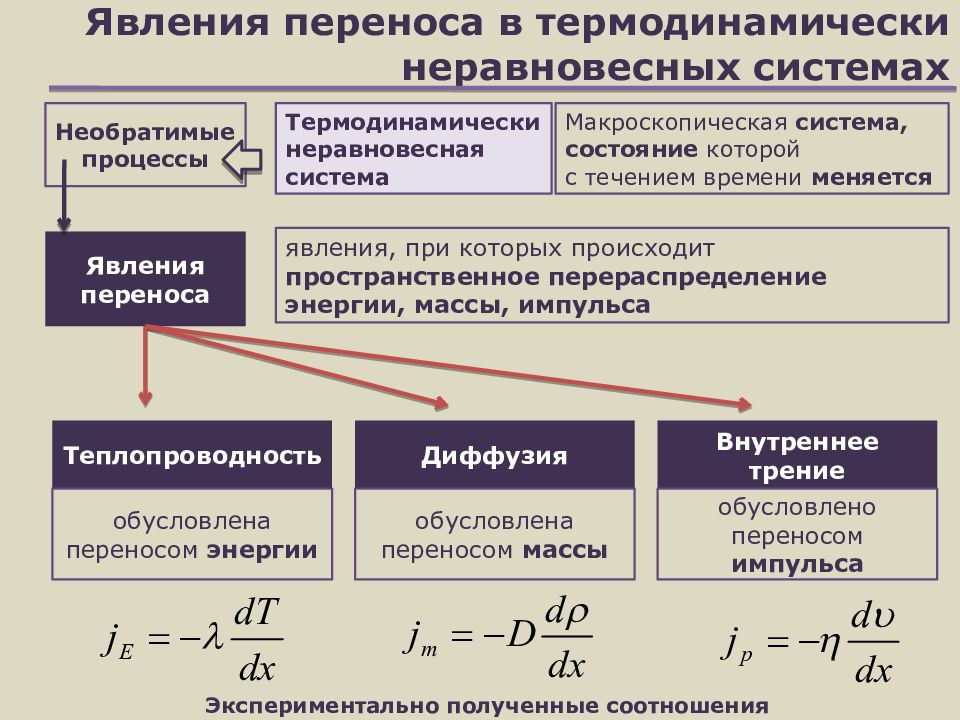
Теплопроводность обусловлена переносом энергии Внутреннее трение обусловлено переносом импульса Диффузия обусловлена переносом массы Необратимые процессы Макроскопическая система, состояние которой с течением времени меняется Термодинамически неравновесная система Явления переноса явления, при которых происходит пространственное перераспределение энергии, массы, импульса Экспериментально полученные соотношения
Слайд 22: Теплопроводность
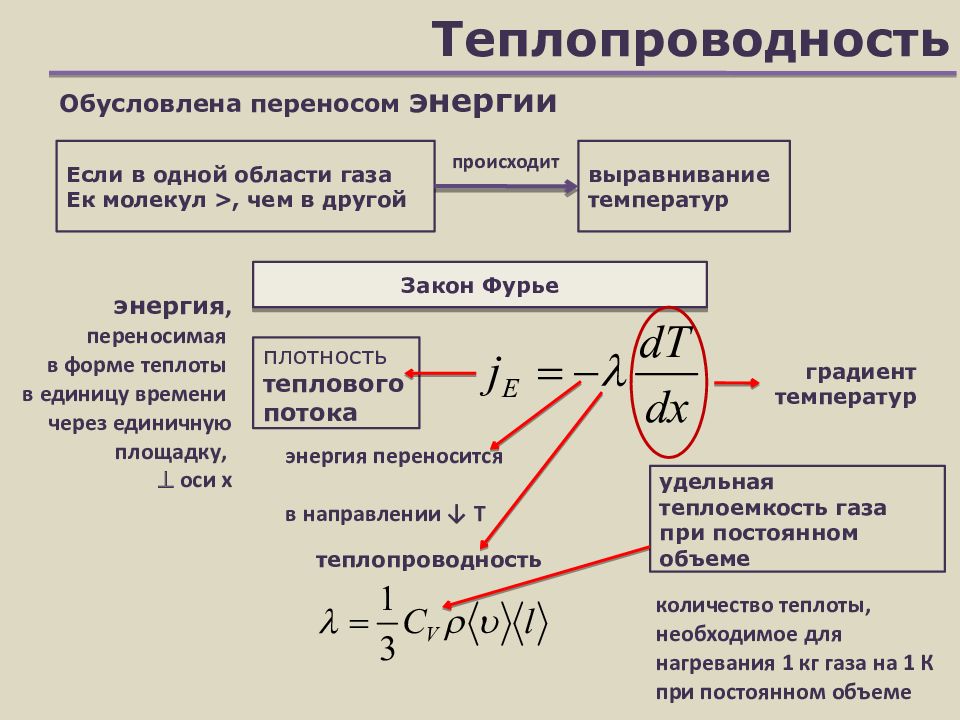
Обусловлена переносом энергии Закон Фурье Если в одной области газа Ек молекул >, чем в другой выравнивание температур плотность теплового потока градиент температур энергия переносится в направлении ↓ Т теплопроводность происходит удельная теплоемкость газа при постоянном объеме количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме энергия, переносимая в форме теплоты в единицу времени через единичную площадку, оси х
Слайд 23: Диффузия
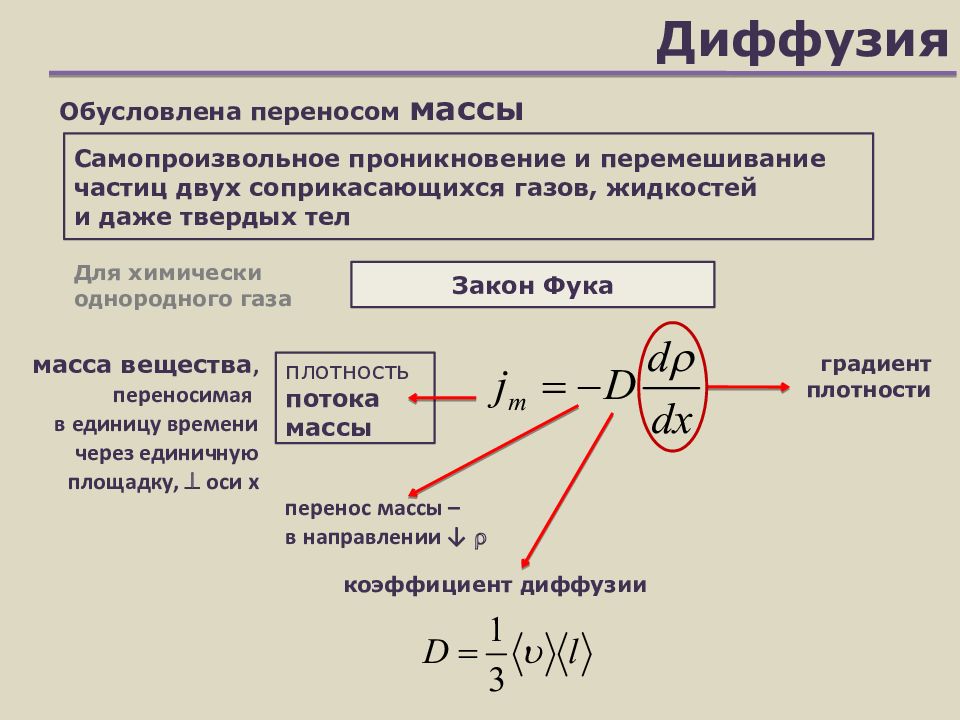
Закон Фука Самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел плотность потока массы градиент плотности Для химически однородного газа коэффициент диффузии Обусловлена переносом массы масса вещества, переносимая в единицу времени через единичную площадку, оси х перенос массы – в направлении ↓
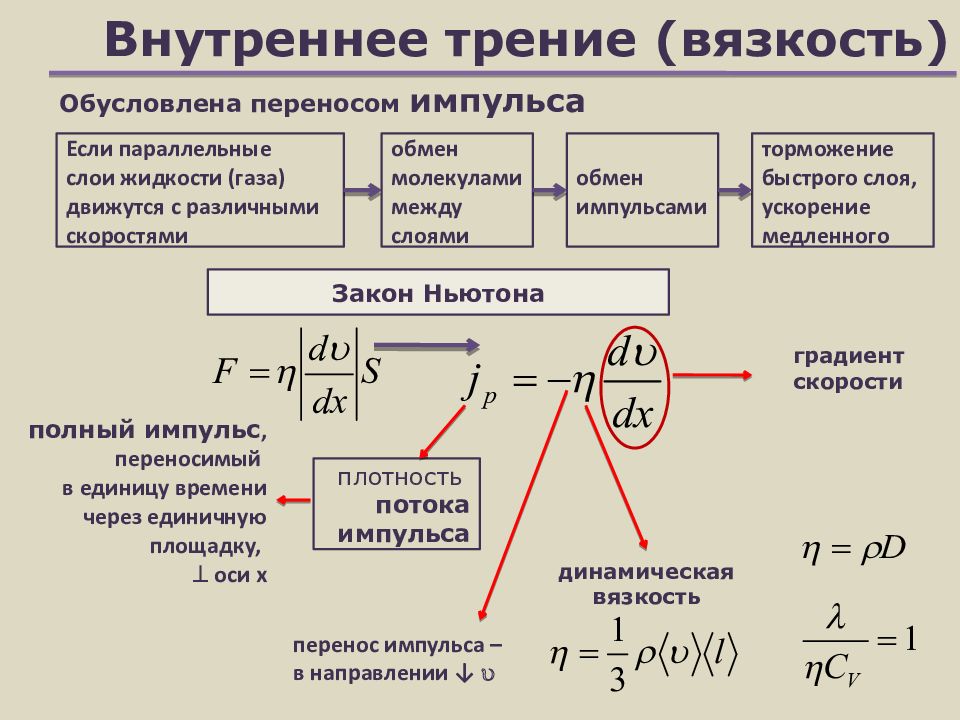
Слайд 24: Внутреннее трение (вязкость)
Закон Ньютона Если параллельные слои жидкости (газа) движутся с различными скоростями плотность потока импульса градиент скорости динамическая вязкость Обусловлена переносом импульса перенос импульса – в направлении ↓ обмен молекулами между слоями обмен импульсами торможение быстрого слоя, ускорение медленного п олный импульс, переносимый в единицу времени через единичную площадку, оси х
Последний слайд презентации: Молекулярная физика и термодинамика: Вязкость
Вязкость (внутреннее трение) Свойство жидкостей (газов) оказывать сопротивление перемещению одной части жидкости относительно другой Градиент скорости П оказывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, направлению движения слоев – коэффициент пропорциональности зависит от: химических свойств жидкости температуры (для жидкостей зависимость обратная, для газов – прямая пропорциональность) Динамическая вязкость ( вязкость ) [] = Па∙с 1 Па с – динамическая вязкости среды, в которой при ламинарном течении и градиенте скорости, равным 1 м/с на 1 м, возникает сила внутреннего трения 1 Н на 1 м 2 поверхности касания слоев (1 Па с = 1 Н с /м 2 )