Урок 27 Новикова В.Л. МБОУ «Школа №2 города Ясиноватая»
Повторить понятия «эксперимент», «событие», «исход», «благоприятный исход», типы событий, их вероятности. Познакомить с понятием «модель теории вероятности». Изучить роль классических вероятностных моделей (монета, игральная кость) в теории вероятностей. Рассмотреть задачи, связанные с бросанием монеты, кубика.
Какова вероятность того, что на светофоре загорится синий цвет? Какой тип этого события? У бабушки 2 гуся (белый и серый), какова вероятность того, что первым к кормушке прибежит белый гусь? Определите тип события «скорость движущегося автомобиля будет > 0 км/ч». Ситуация: на столе лежат перевёрнутые 2 белые и 3 чёрные карточки. А) Определите тип события: наугад взятая карточка окажется белой. Б) Найдите вероятность того, что взятая наугад карточка окажется чёрной.
1) Назовите внутренние воздействия на исход событий, связанных с выпадением определённой грани, карты, цвета шарика, стороны монеты (орла-решка). (несимметричность формы, веса кубика, краплёность карт, отличающиеся фактура спрятанных шариков, кривизна монеты и т.д.) 2) Назовите внешние воздействия на исход событий, связанных с выпадением определённой грани, карты, цвета шарика, стороны монеты (орла-решка). (неровность поверхности, желание вытащить определённую карту, желание подсмотреть в мешок и выбрать шарик, навык выбрасывания определённой стороны монеты)
Задание: перечислите все элементарные события, которые произойдут в результате подбрасывания монеты, кубика.
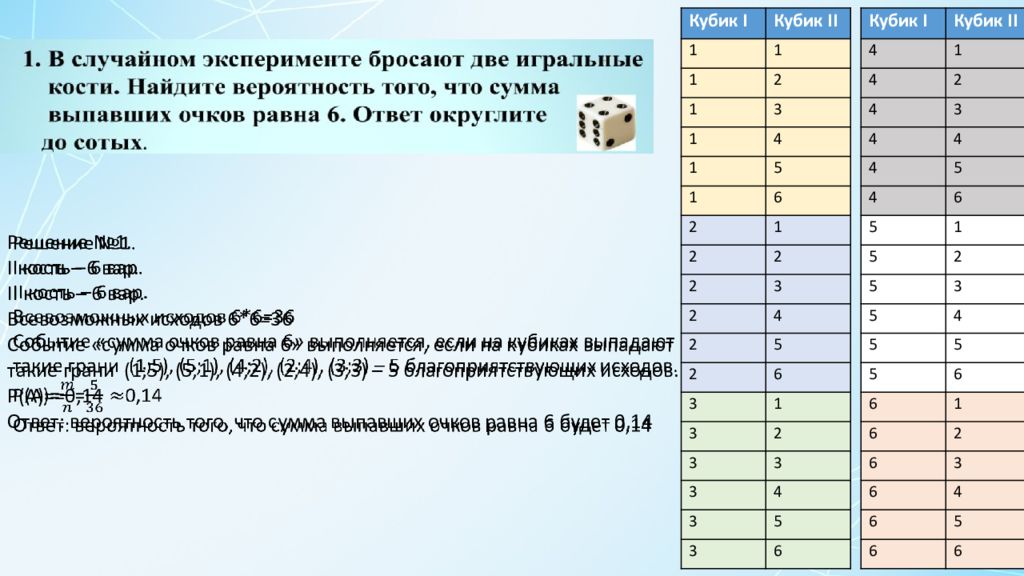
Решение №1. I кость – 6 вар. II кость – 6 вар. Всевозможных исходов 6*6=36 Событие «сумма очков равна 6» выполняется, если на кубиках выпадают такие грани (1;5), (5;1), (4;2), (2;4), (3;3) – 5 благоприятствующих исходов. Р(А)= = 0,14 Ответ: вероятность того, что сумма выпавших очков равна 6 будет 0,14 Кубик I Кубик II 1 1 1 2 1 3 1 4 1 5 1 6 2 1 2 2 2 3 2 4 2 5 2 6 3 1 3 2 3 3 3 4 3 5 3 6 Кубик I Кубик II 4 1 4 2 4 3 4 4 4 5 4 6 5 1 5 2 5 3 5 4 5 5 5 6 6 1 6 2 6 3 6 4 6 5 6 6
Решение. Найдём n – количество всех возможных исходов. ОО ОР РО РР Значит n =4. Благоприятный исход 1 = m, это ОО. P(A)= =0,25 - вероятность того, что подбросив монету два раза, оба раза выпадут орлы.
По образцу №1 решить задачи №2,3. По образцу №4 решить №5. Выучить понятие «вероятностная модель». 5. Монету подбрасывают 2 раза. Какова вероятность того, орёл выпадет только 1 раз?
