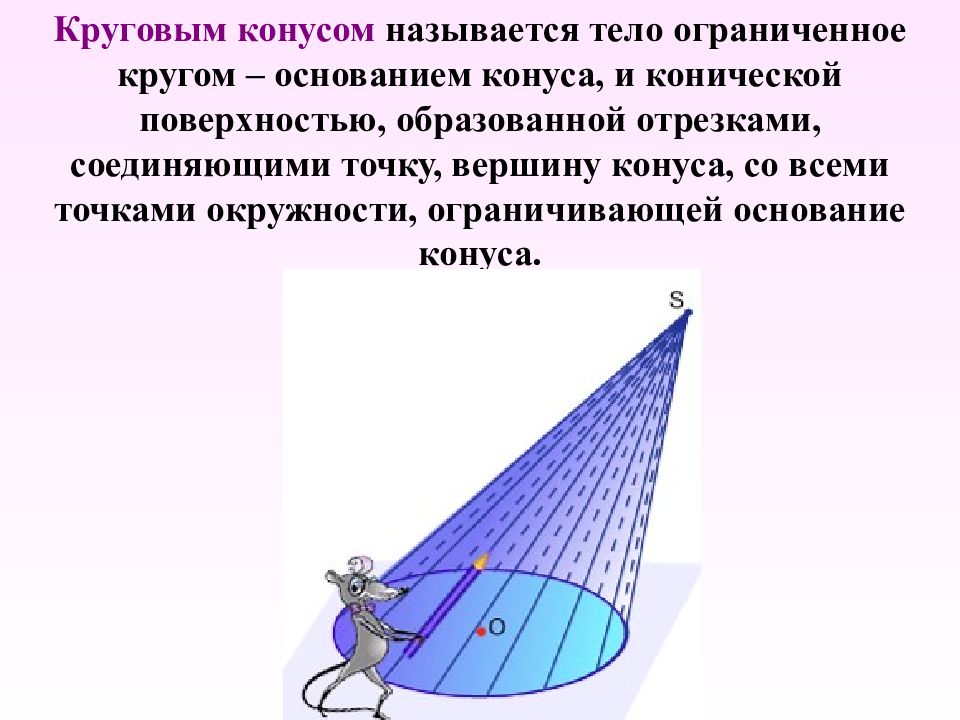
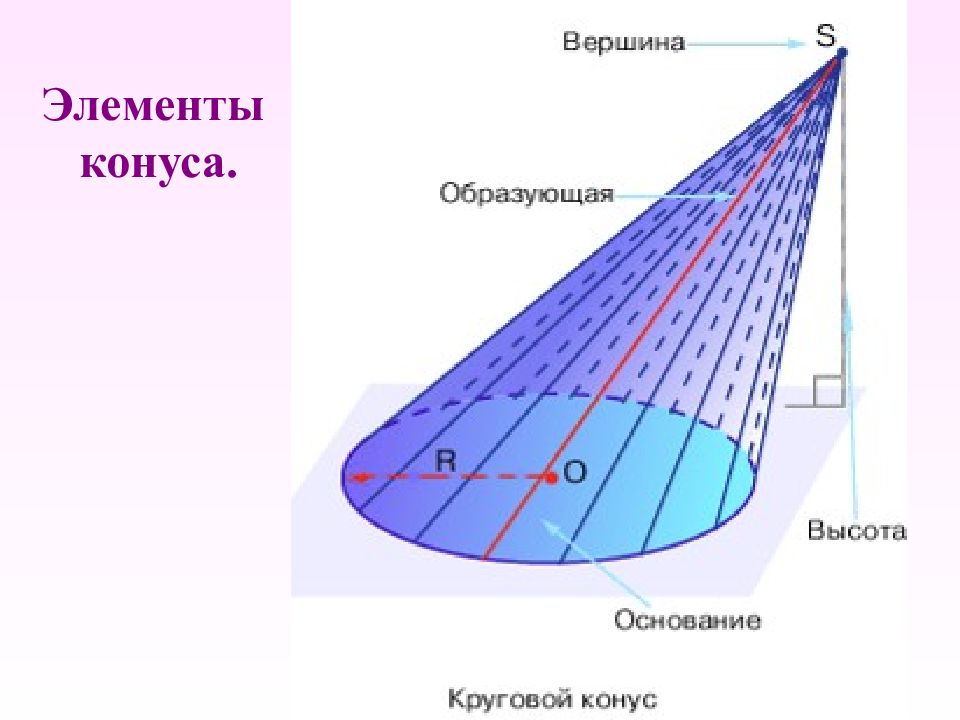
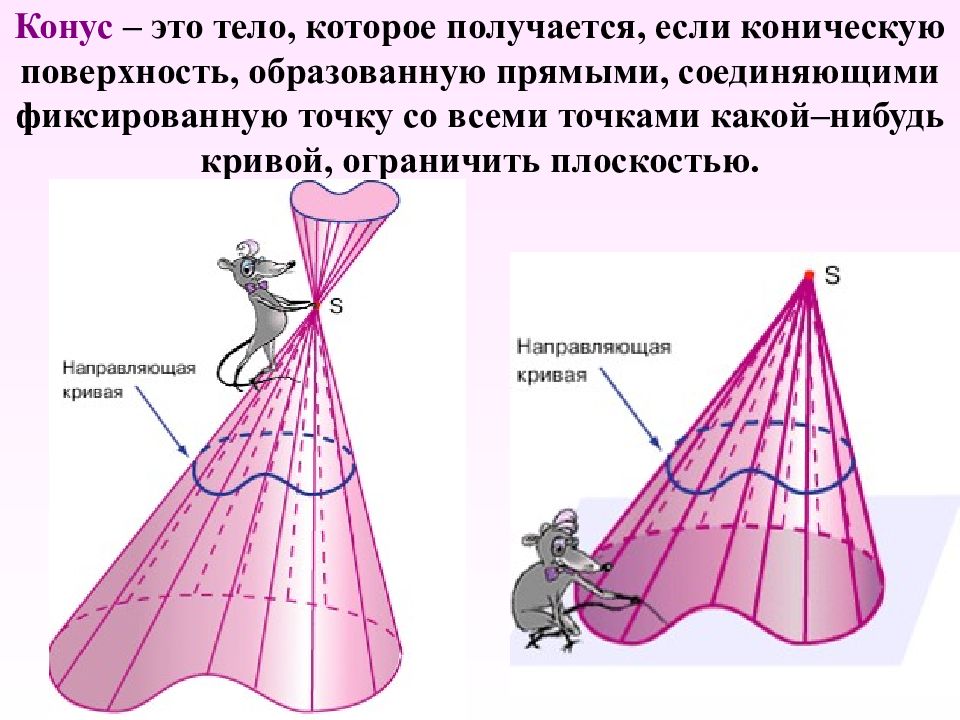
Слайд 3: Элементы конуса
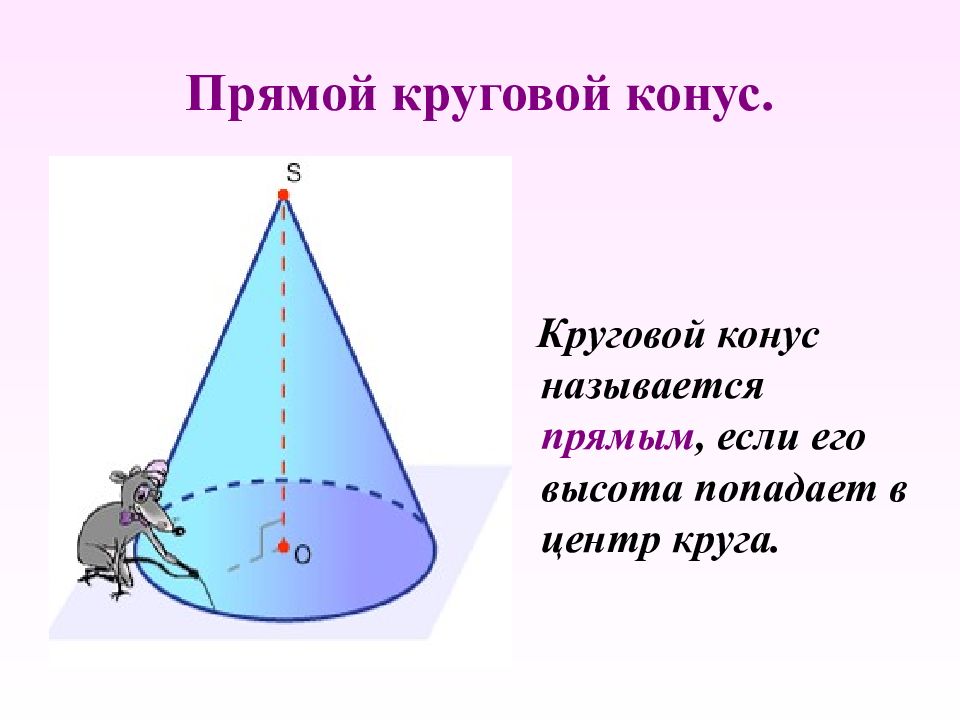
Слайд 5: Прямой круговой конус
Круговой конус называется прямым, если его высота попадает в центр круга.
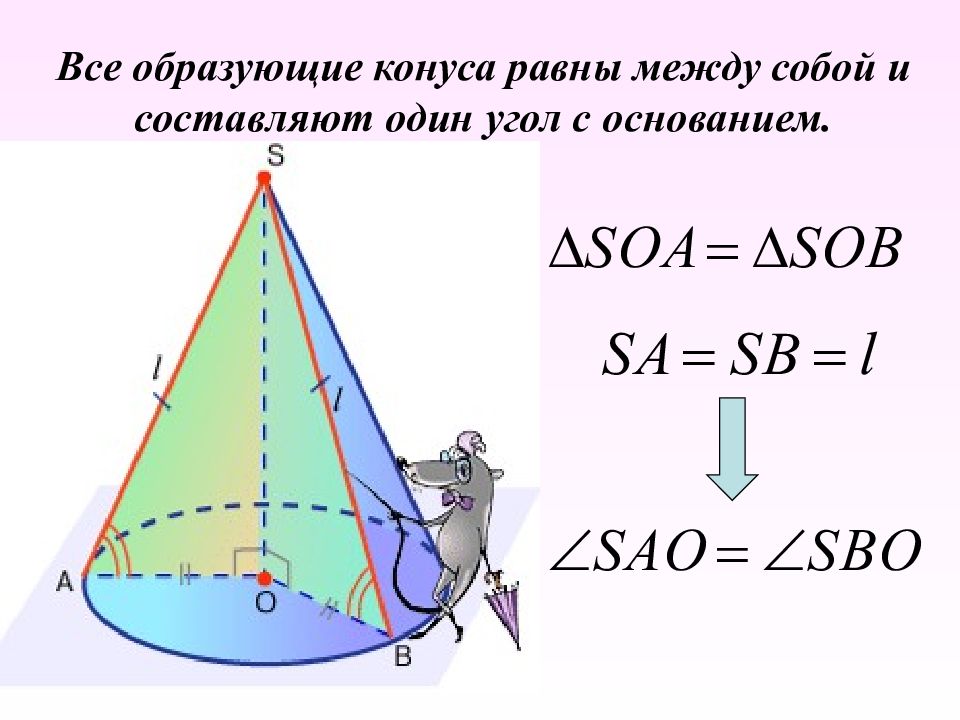
Слайд 6: Все образующие конуса равны между собой и составляют один угол с основанием
Слайд 7
Чему равен угол между образующей и основанием конуса, если известен угол между высотой и образующей. ? 65 0
Слайд 8
Конус можно получить, вращая прямоугольный треугольник вокруг одного из катетов. При этом осью вращения будет прямая, содержащая высоту конуса. Эта прямая так и называется – осью конуса.
Слайд 9
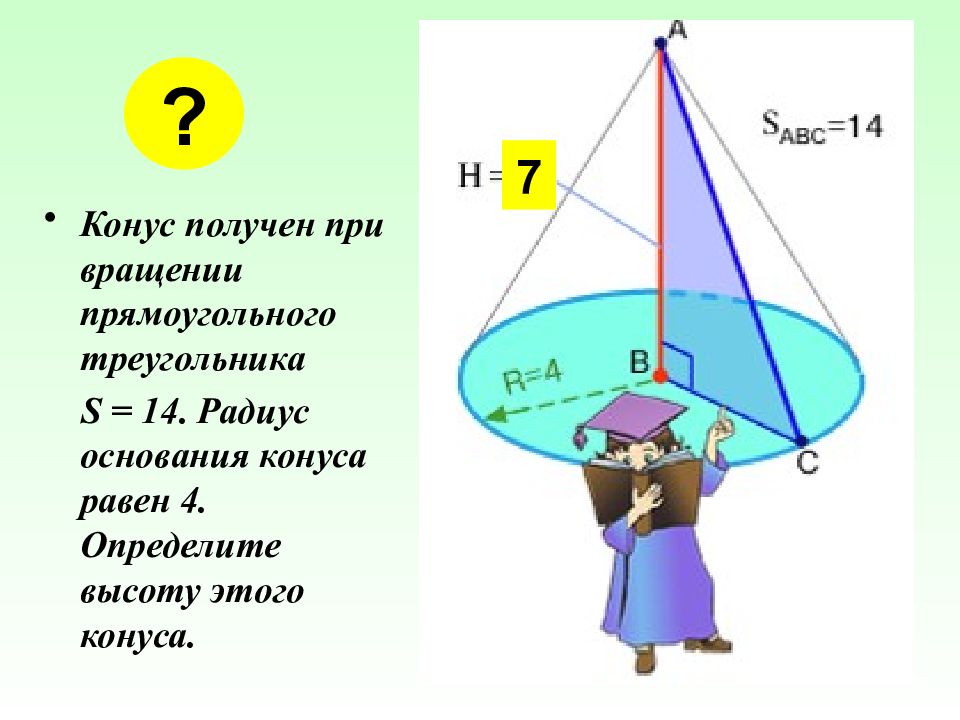
Конус получен при вращении прямоугольного треугольника S = 14. Радиус основания конуса равен 4. Определите высоту этого конуса. ? 7
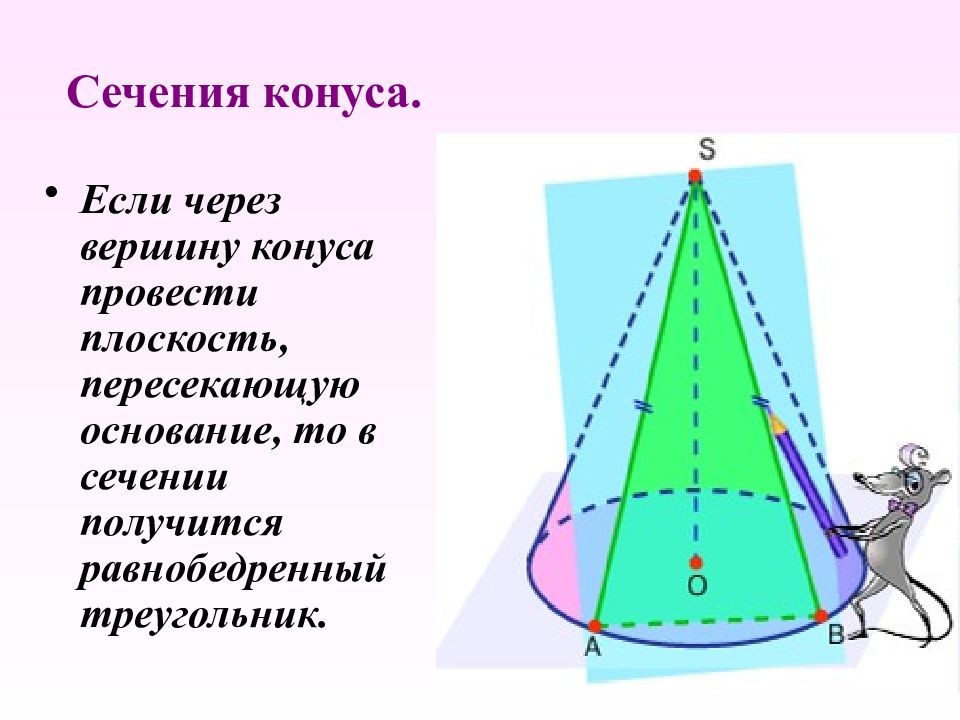
Слайд 10: Сечения конуса
Если через вершину конуса провести плоскость, пересекающую основание, то в сечении получится равнобедренный треугольник.
Слайд 11: Сечения конуса
Сечение конуса, проходящее через ось, называется осевым. В основании осевого сечения лежит диаметр – максимальная хорда, поэтому угол при вершине осевого сечения – это максимальный угол между образующими конуса. ( Угол при вершине конуса ). Сечения конуса.
Слайд 12
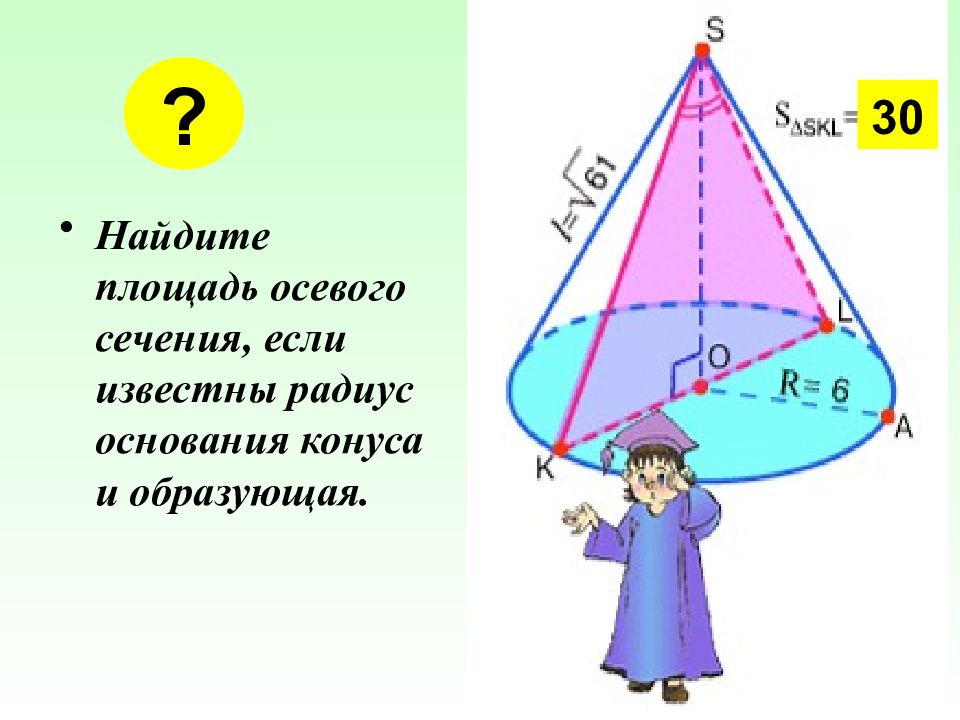
Найдите площадь осевого сечения, если известны радиус основания конуса и образующая. ? 30
Слайд 13
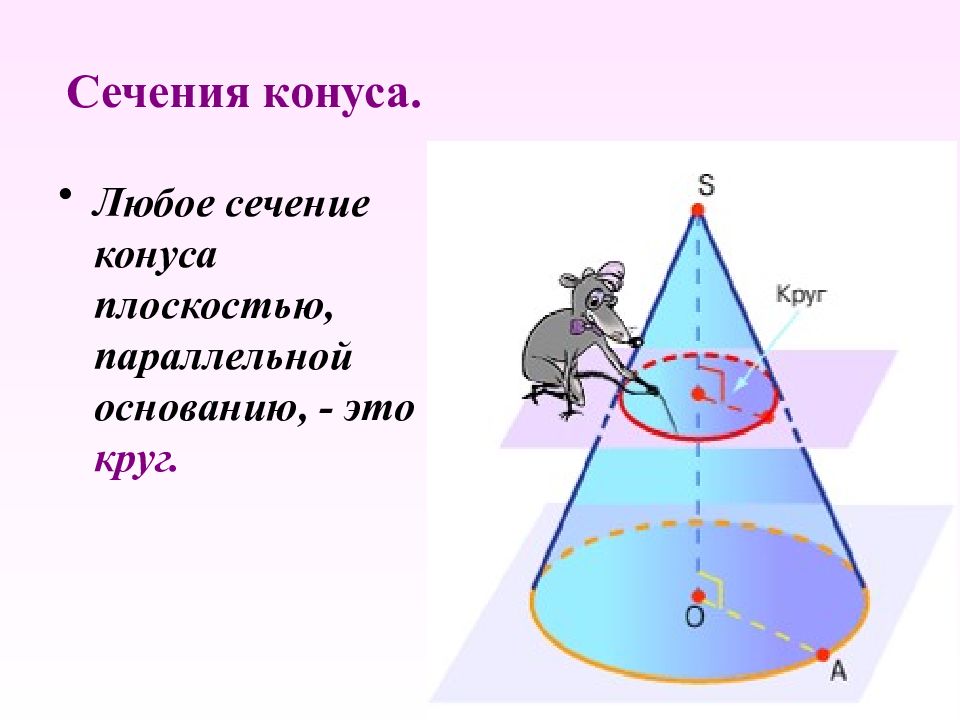
Любое сечение конуса плоскостью, параллельной основанию, - это круг. Сечения конуса.
Слайд 14
Через середину высоты конуса провели плоскость, перпендикулярную оси, и получили круг R = 5. Чему равна площадь основания конуса? ? 100 π
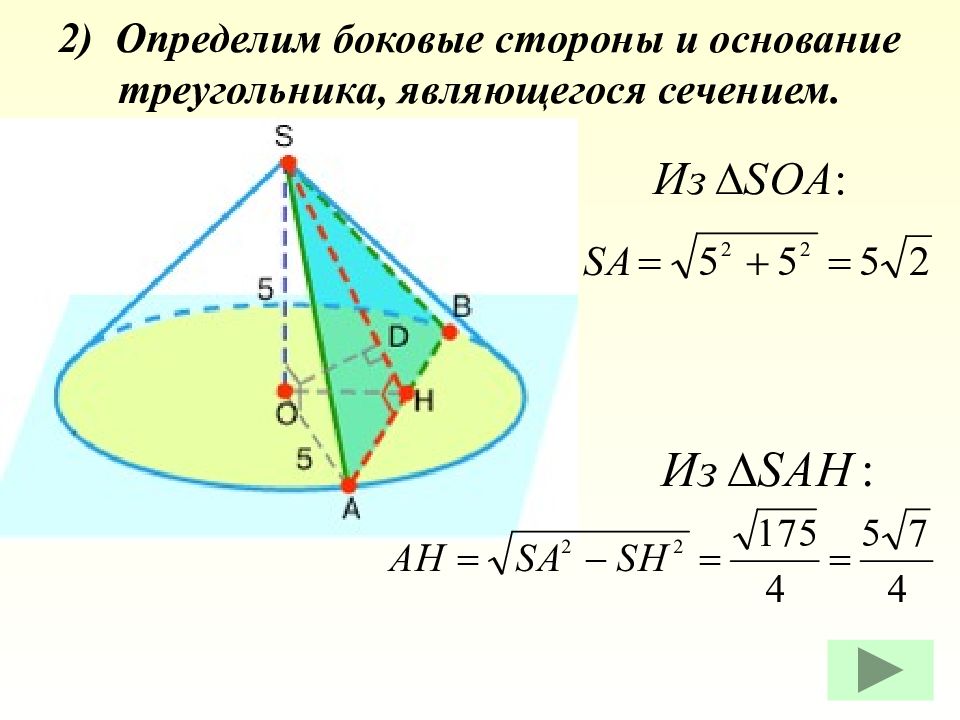
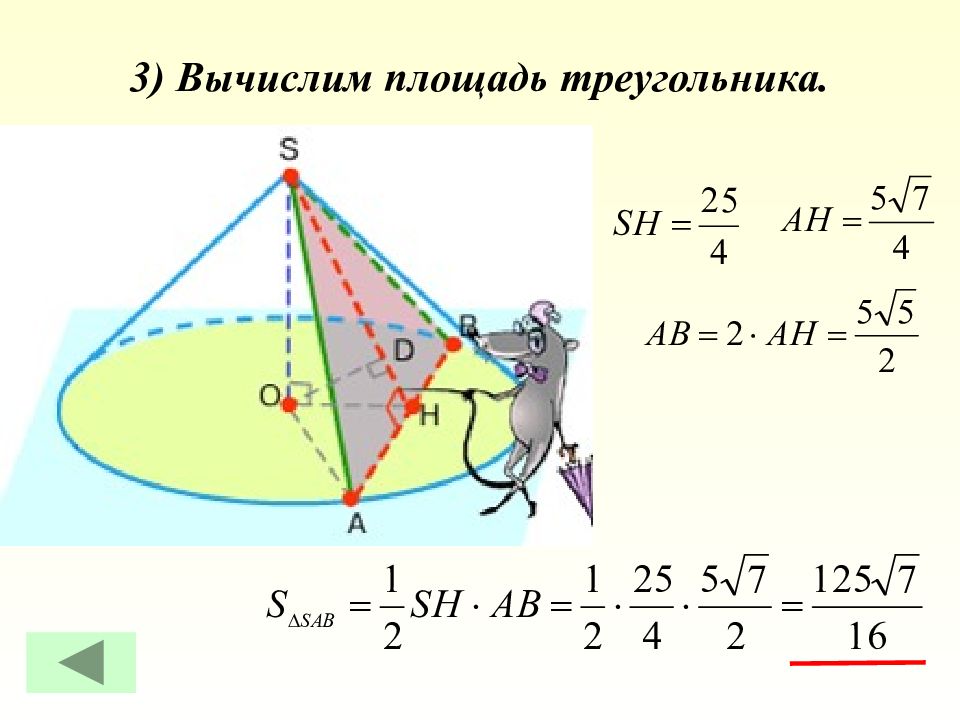
Слайд 17: 2) Определим боковые стороны и основание треугольника, являющегося сечением
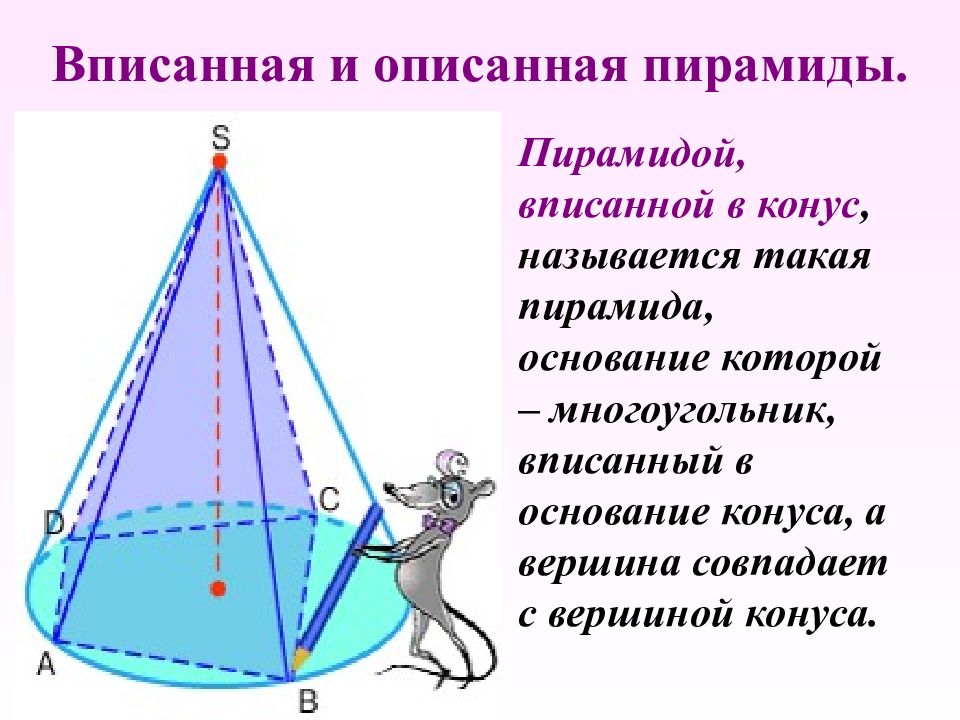
Слайд 19: Вписанная и описанная пирамиды
Пирамидой, вписанной в конус, называется такая пирамида, основание которой – многоугольник, вписанный в основание конуса, а вершина совпадает с вершиной конуса.
Слайд 20
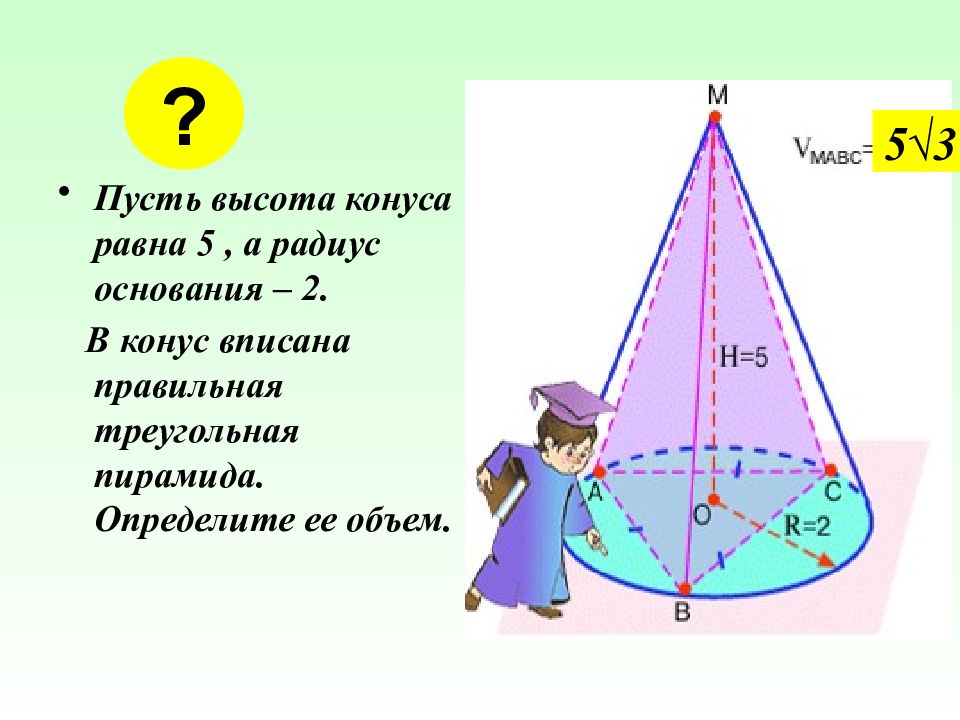
Пусть высота конуса равна 5, а радиус основания – 2. В конус вписана правильная треугольная пирамида. Определите ее объем. ? 5 √3
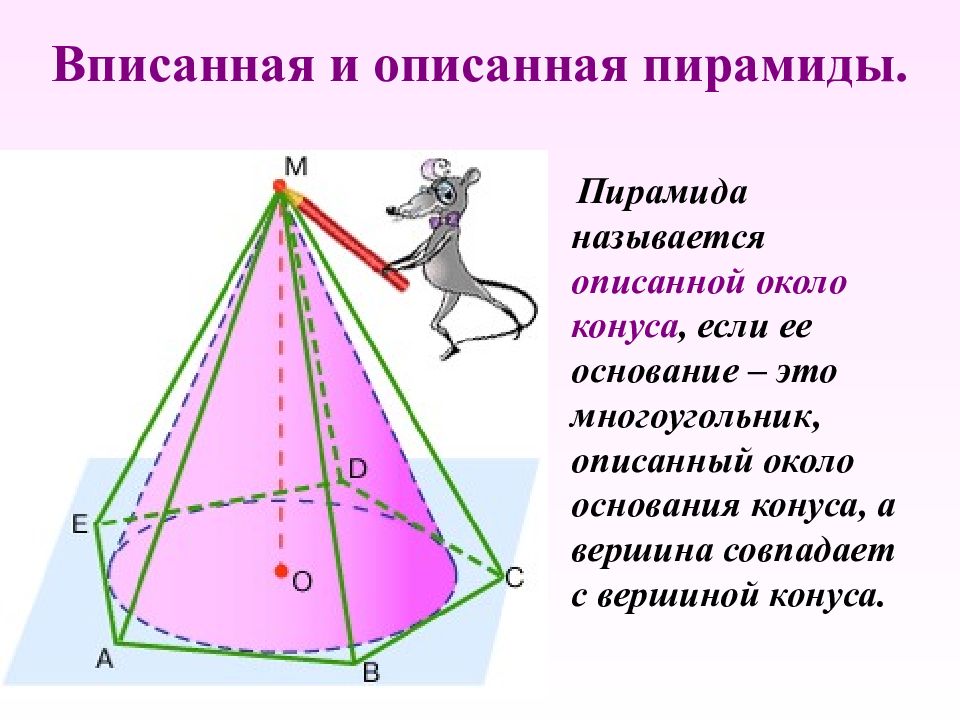
Слайд 21: Вписанная и описанная пирамиды
Пирамида называется описанной около конуса, если ее основание – это многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Вписанная и описанная пирамиды.
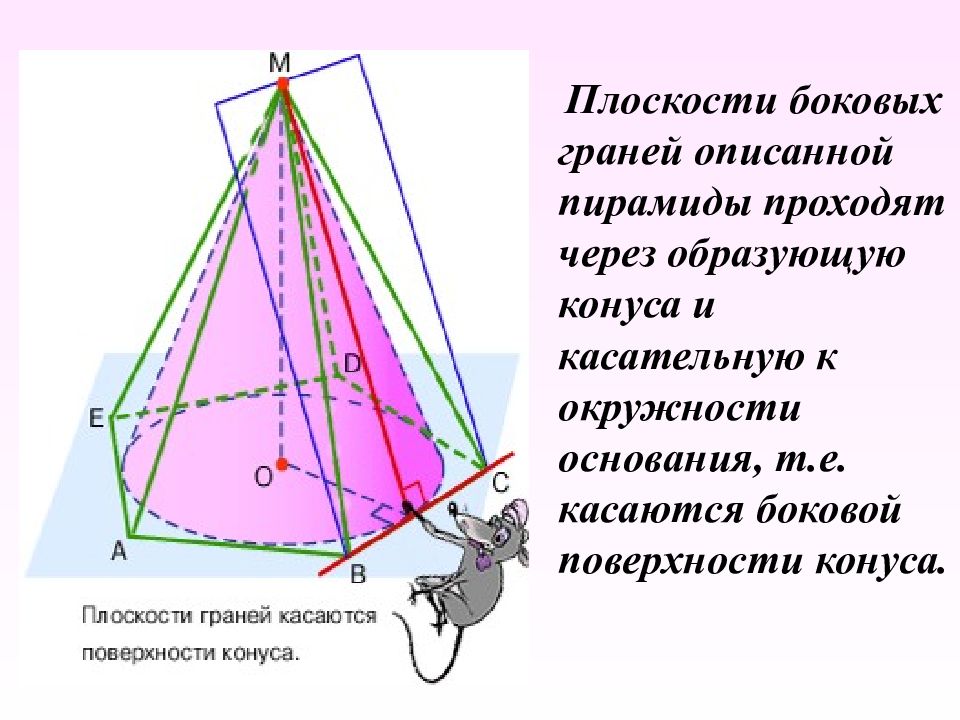
Слайд 22
Плоскости боковых граней описанной пирамиды проходят через образующую конуса и касательную к окружности основания, т.е. касаются боковой поверхности конуса.
Слайд 23
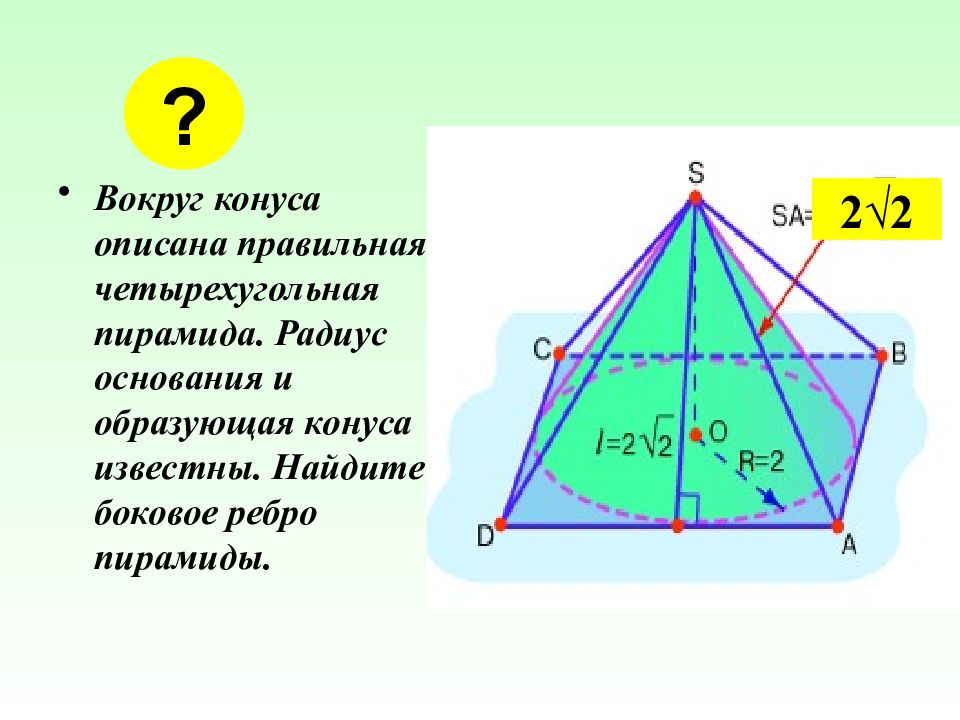
Вокруг конуса описана правильная четырехугольная пирамида. Радиус основания и образующая конуса известны. Найдите боковое ребро пирамиды. ? 2√2
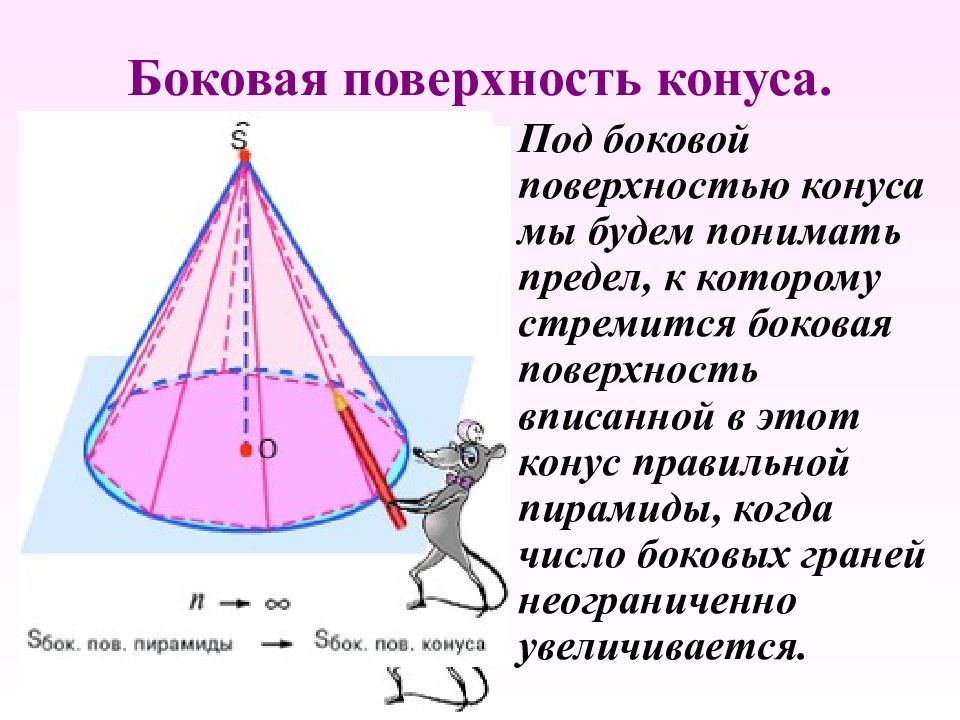
Слайд 24: Боковая поверхность конуса
Под боковой поверхностью конуса мы будем понимать предел, к которому стремится боковая поверхность вписанной в этот конус правильной пирамиды, когда число боковых граней неограниченно увеличивается.
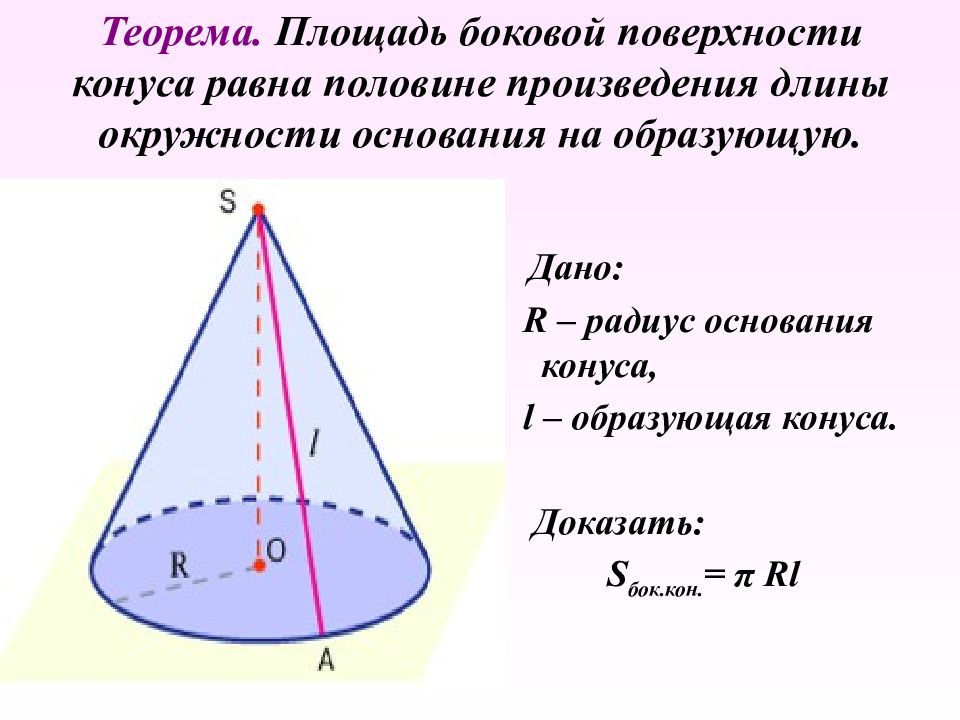
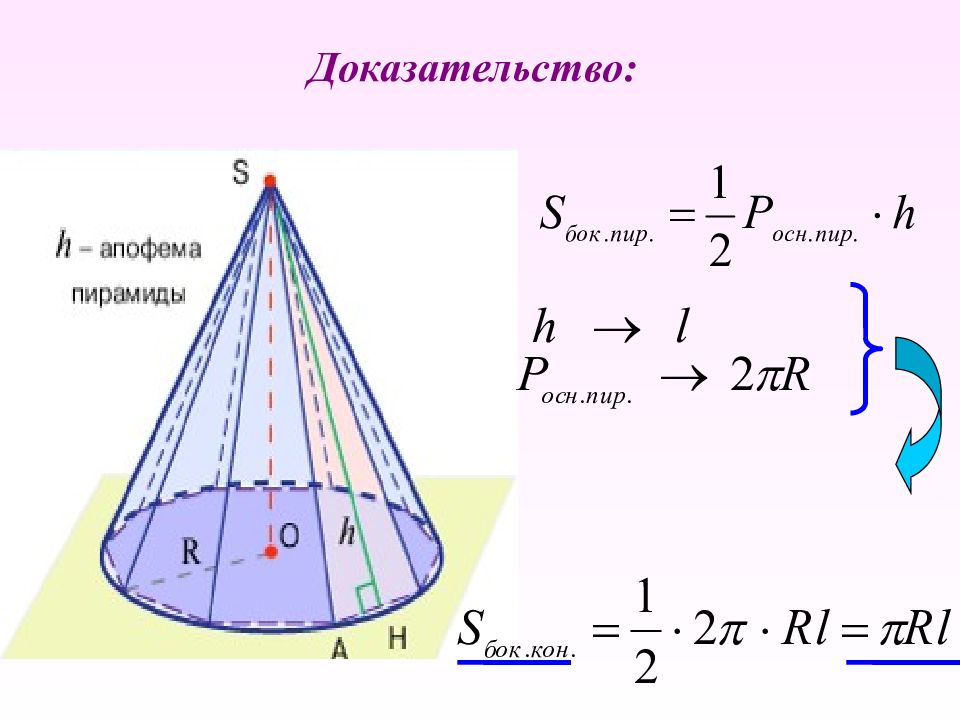
Слайд 25: Теорема. Площадь боковой поверхности конуса равна половине произведения длины окружности основания на образующую
Дано: R – радиус основания конуса, l – образующая конуса. Доказать: S бок.кон. = π Rl
Слайд 27
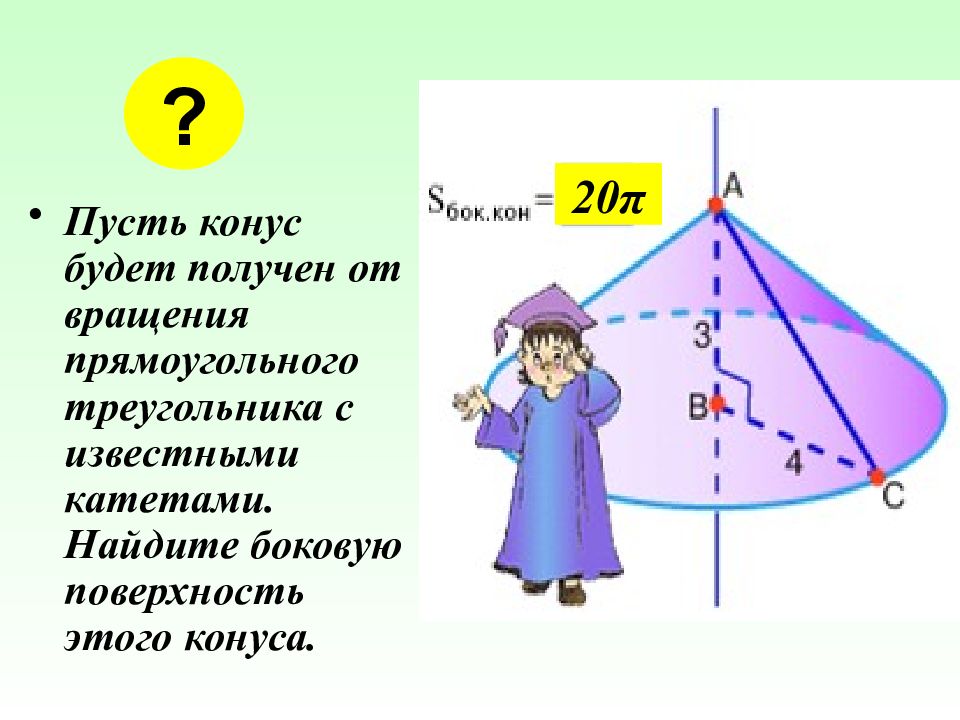
Пусть конус будет получен от вращения прямоугольного треугольника с известными катетами. Найдите боковую поверхность этого конуса. ? 20 π
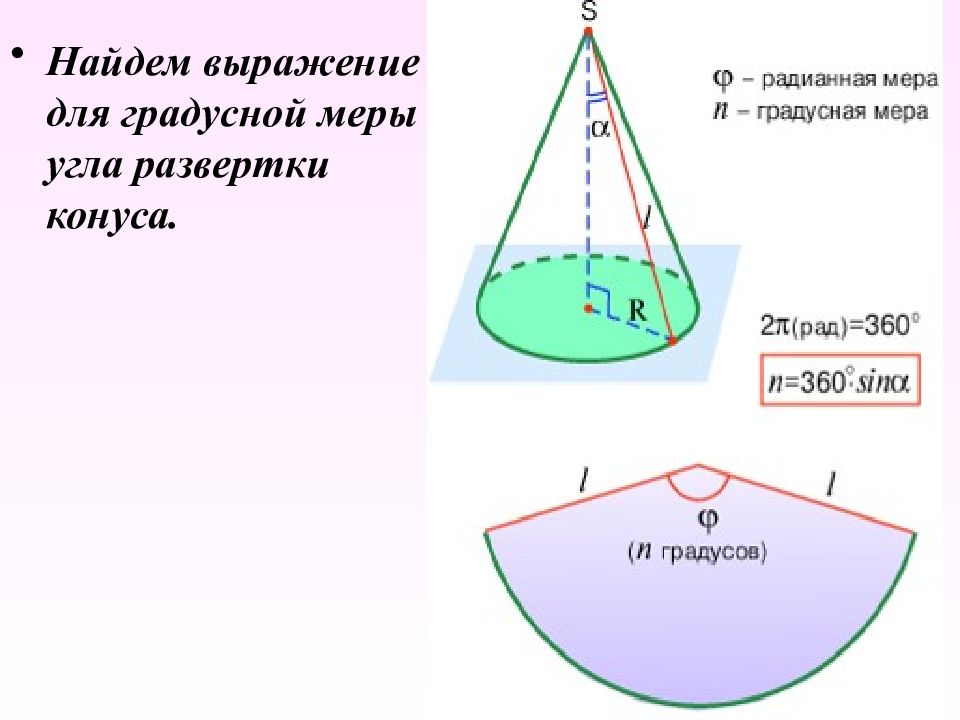
Слайд 28: Развертка конуса
Развертка конуса – это круговой сектор. Его можно рассматривать как развертку боковой поверхности вписанной правильной пирамиды, у которой число боковых граней бесконечно увеличивается.
Слайд 29
Зная угол, образованный высотой и образующей конуса, можно вычислить угол сектора, полученного при развертке конуса, и наоборот.
Слайд 31
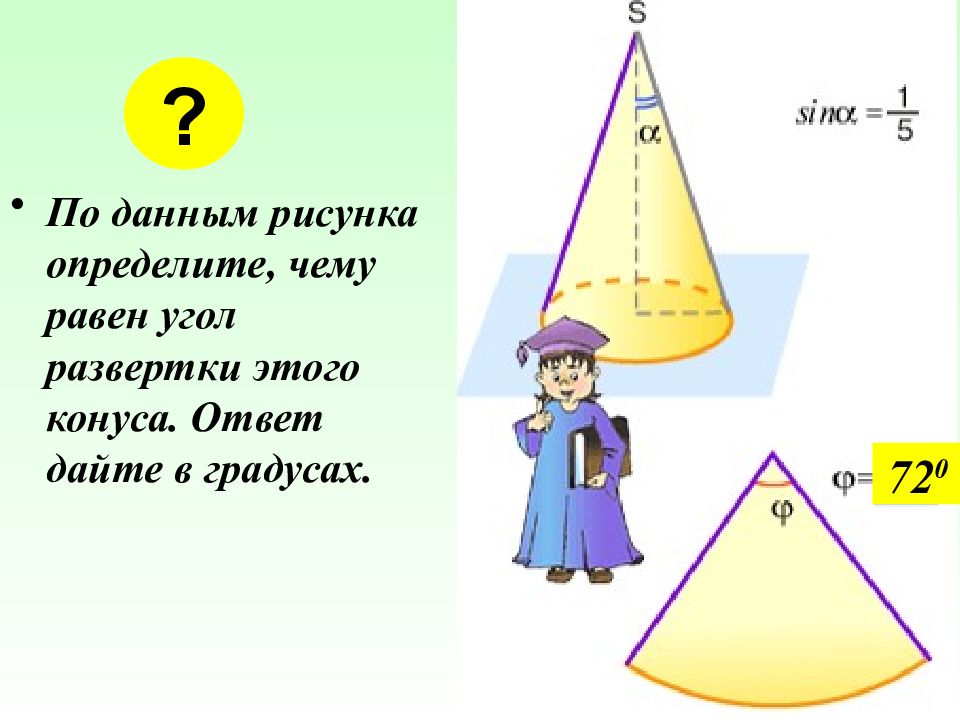
По данным рисунка определите, чему равен угол развертки этого конуса. Ответ дайте в градусах. ? 72 0
Слайд 32
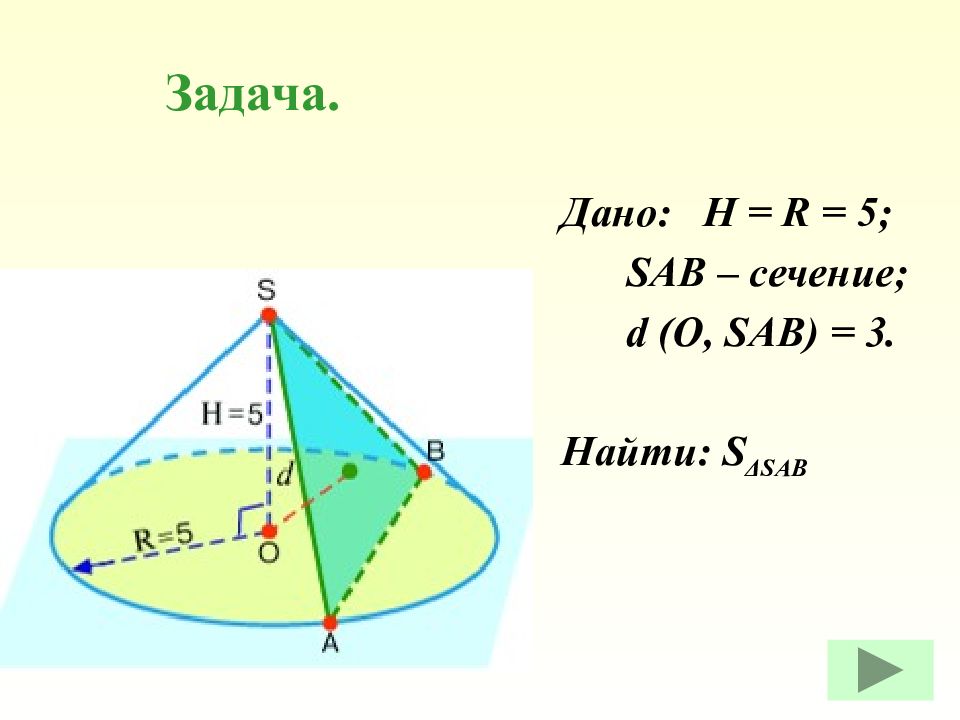
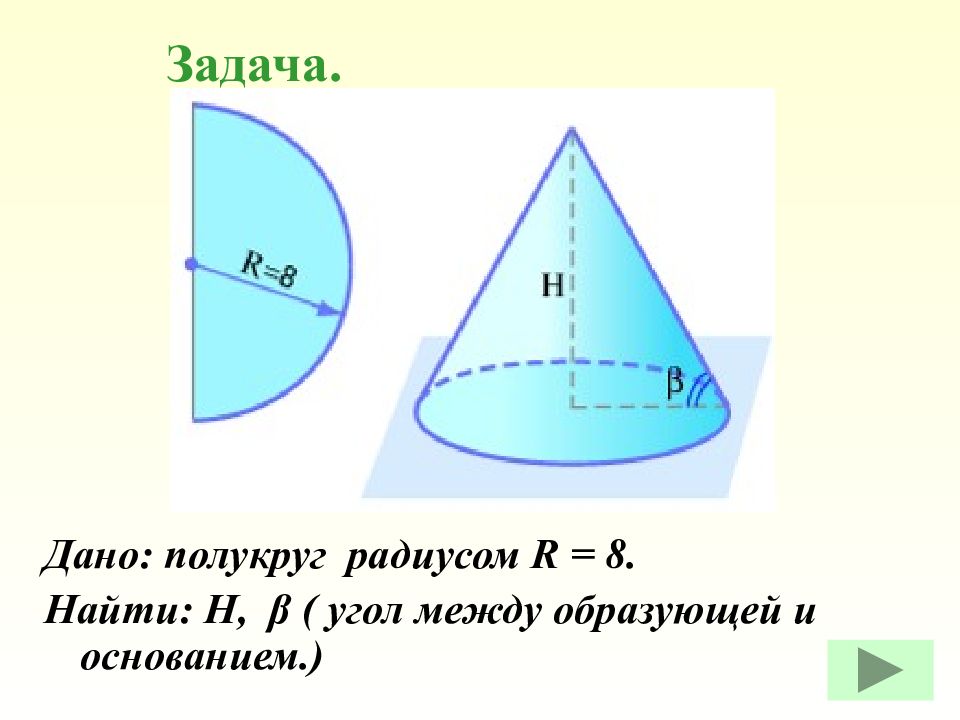
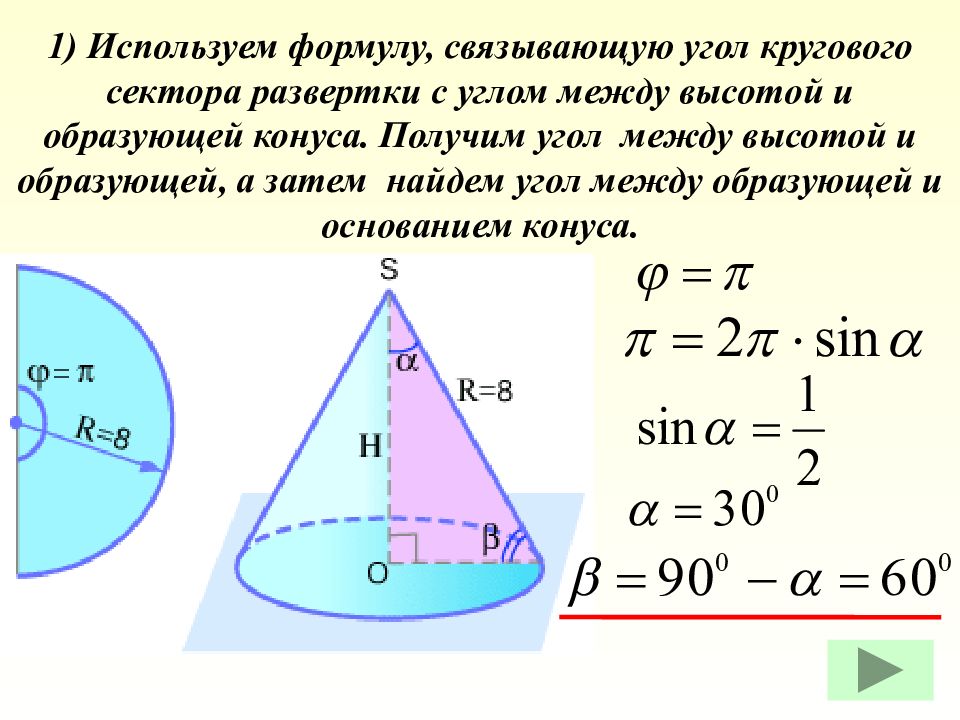
Дано: полукруг радиусом R = 8. Найти: Н, β ( угол между образующей и основанием.) Задача.
Слайд 33: 1) Используем формулу, связывающую угол кругового сектора развертки с углом между высотой и образующей конуса. Получим угол между высотой и образующей, а затем найдем угол между образующей и основанием конуса
Слайд 34: 2) Найдем высоту конуса, используя определение тангенса угла в прямоугольном треугольнике
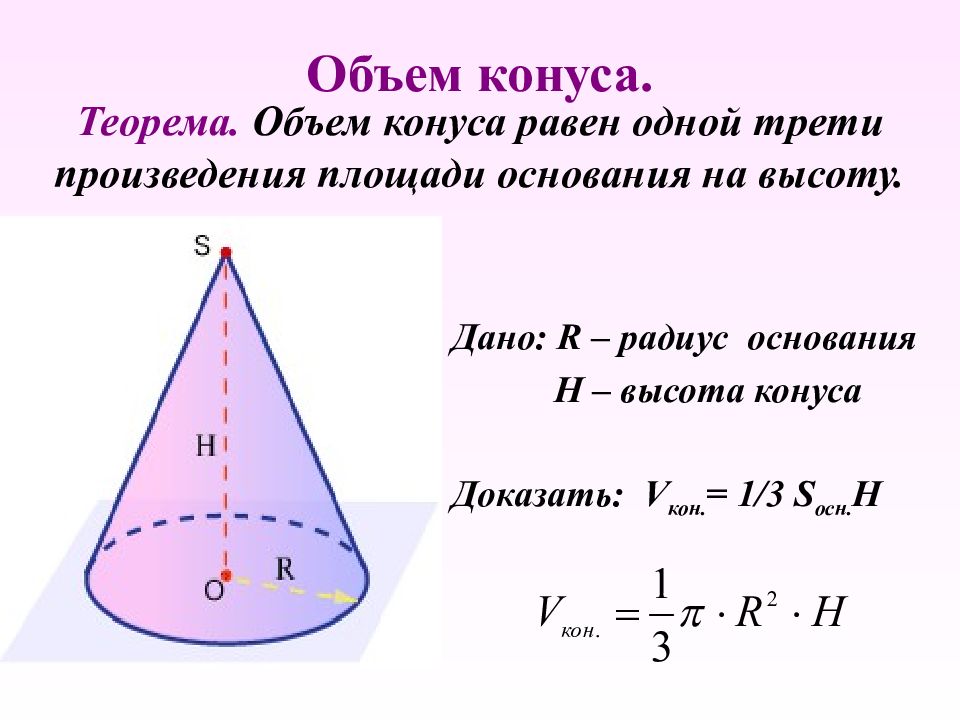
Слайд 35: Объем конуса
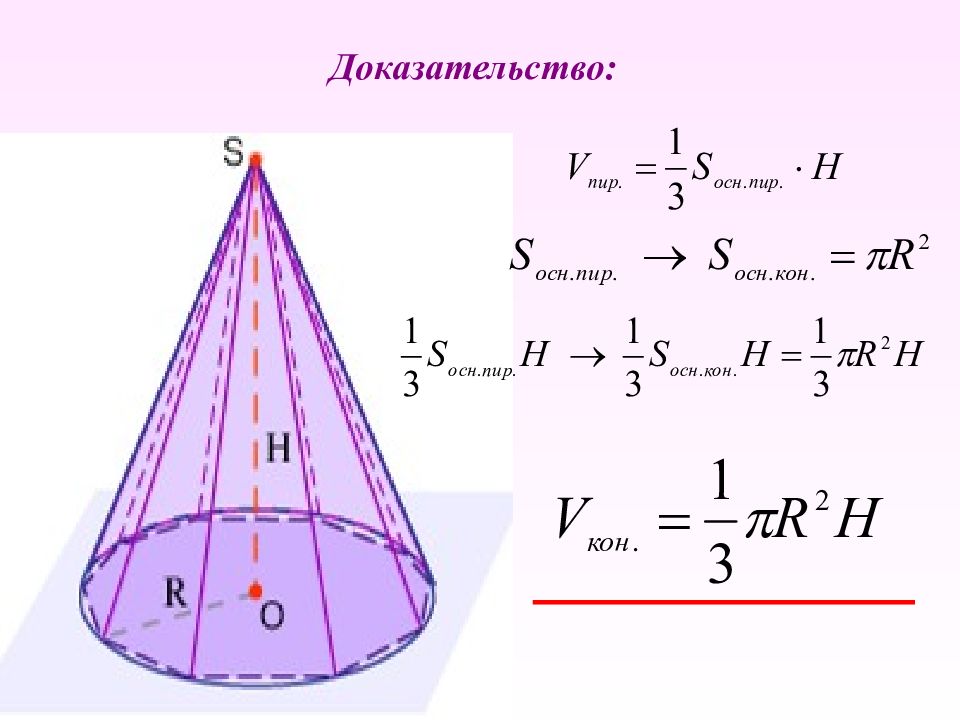
Дано: R – радиус основания Н – высота конуса Доказать: V кон. = 1/3 S осн. H Теорема. Объем конуса равен одной трети произведения площади основания на высоту.
Слайд 36
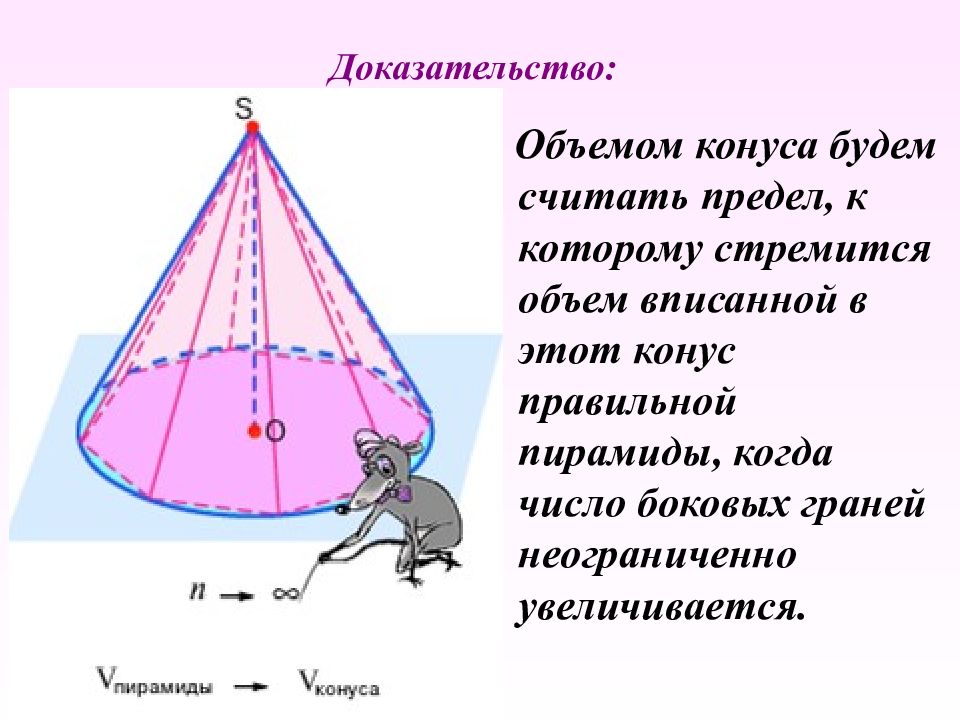
Объемом конуса будем считать предел, к которому стремится объем вписанной в этот конус правильной пирамиды, когда число боковых граней неограниченно увеличивается. Доказательство:
Слайд 38
Найдите объем конуса, если радиус его основания равен трем, а образующая равна пяти. ? 1 2 π
Слайд 39
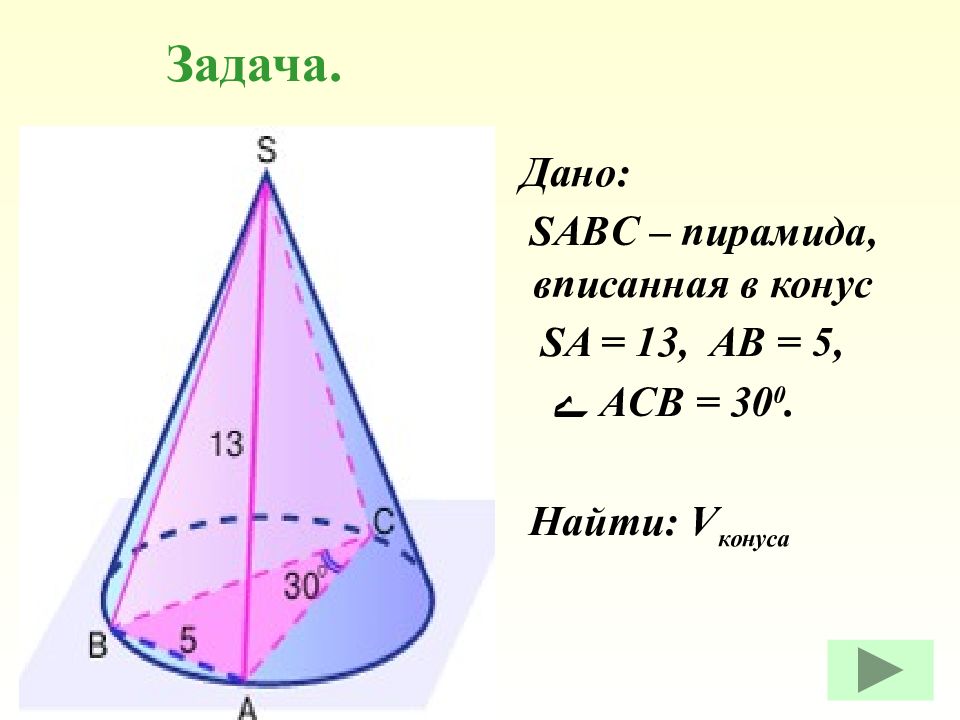
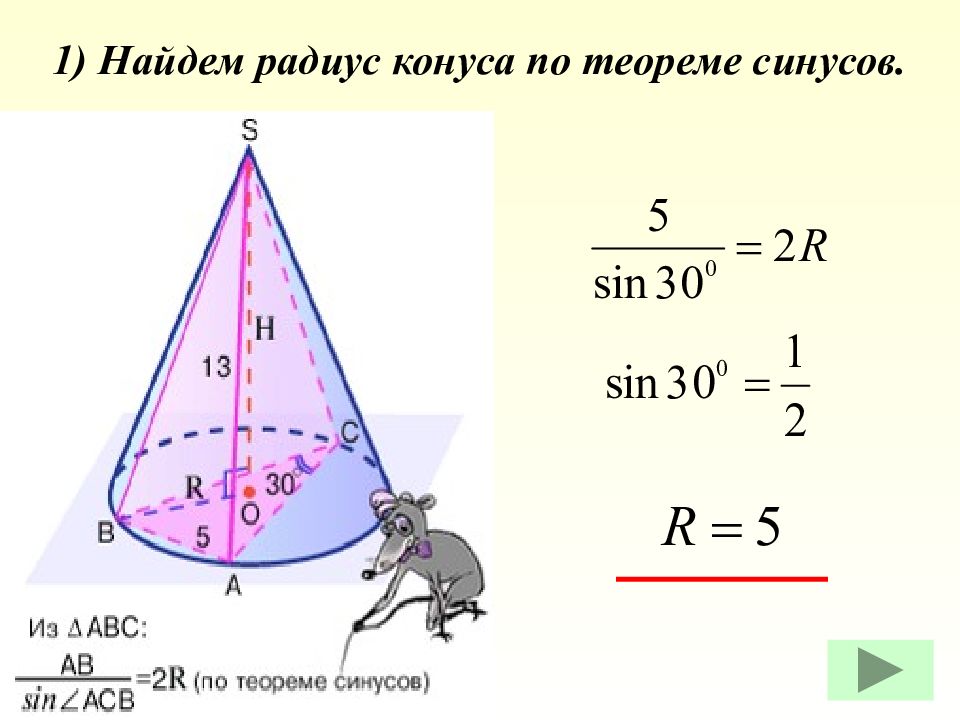
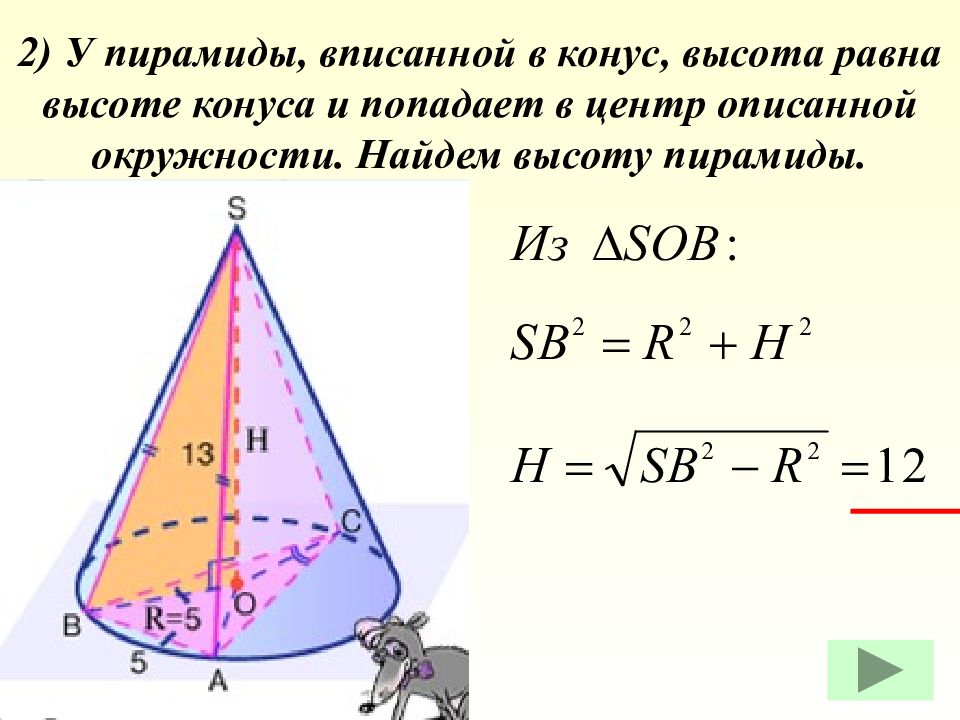
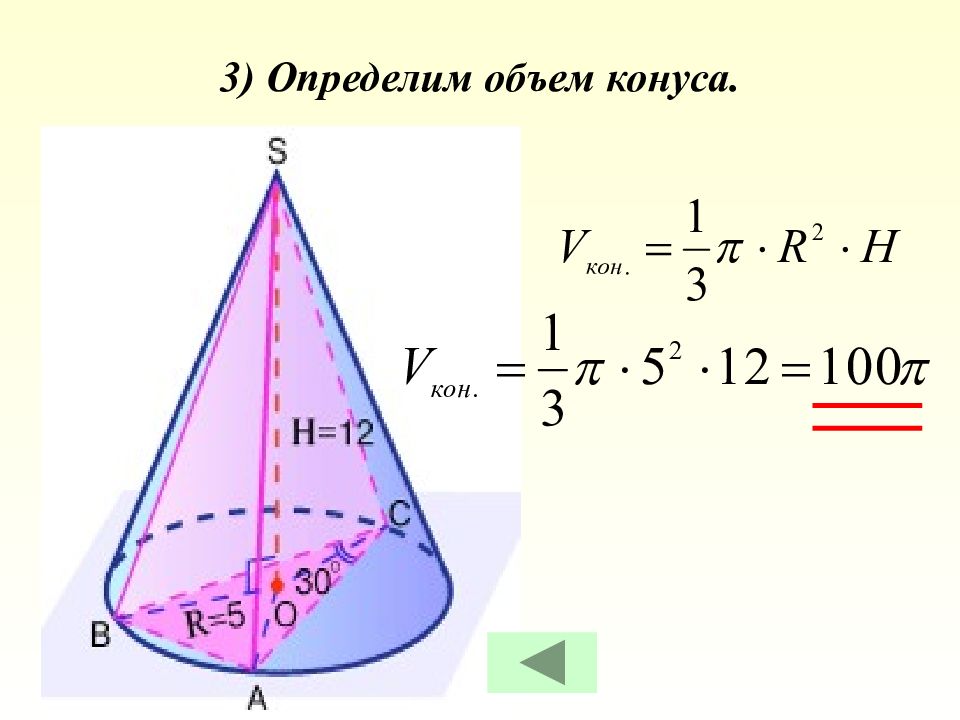
Дано: SABC – пирамида, вписанная в конус SA = 13, AB = 5, ے ACB = 30 0. Найти: V конуса Задача.