Первый слайд презентации: Многогранники, описанные около сферы
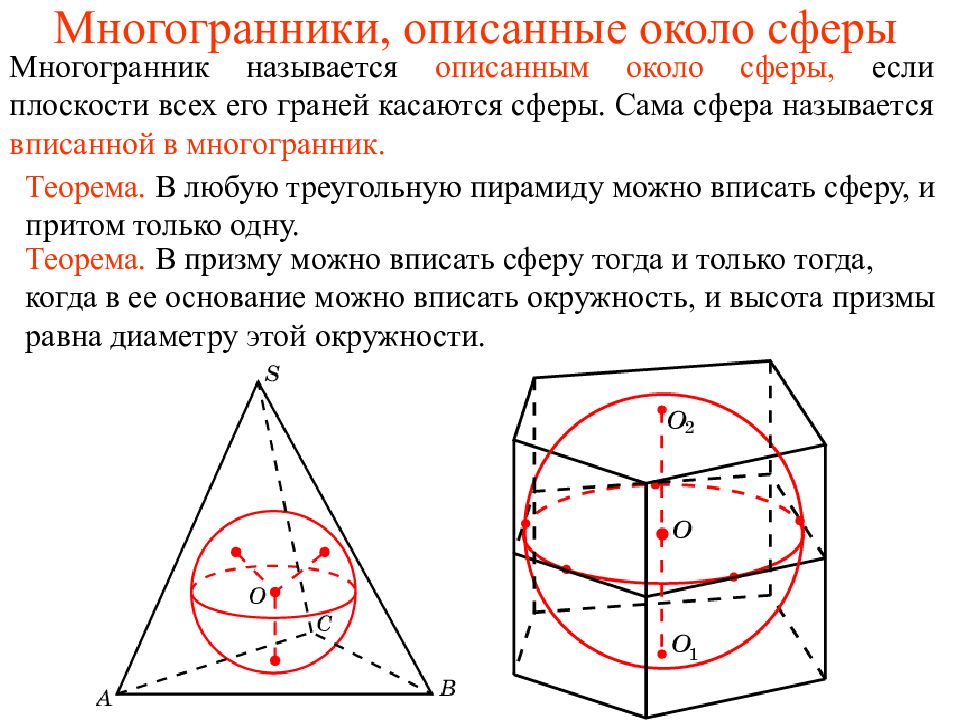
Многогранник называется описанным около сферы, если плоскости всех его граней касаются сферы. Сама сфера называется вписанной в многогранник. Теорема. В призму можно вписать сферу тогда и только тогда, когда в ее основание можно вписать окружность, и высота призмы равна диаметру этой окружности. Теорема. В любую треугольную пирамиду можно вписать сферу, и притом только одну.
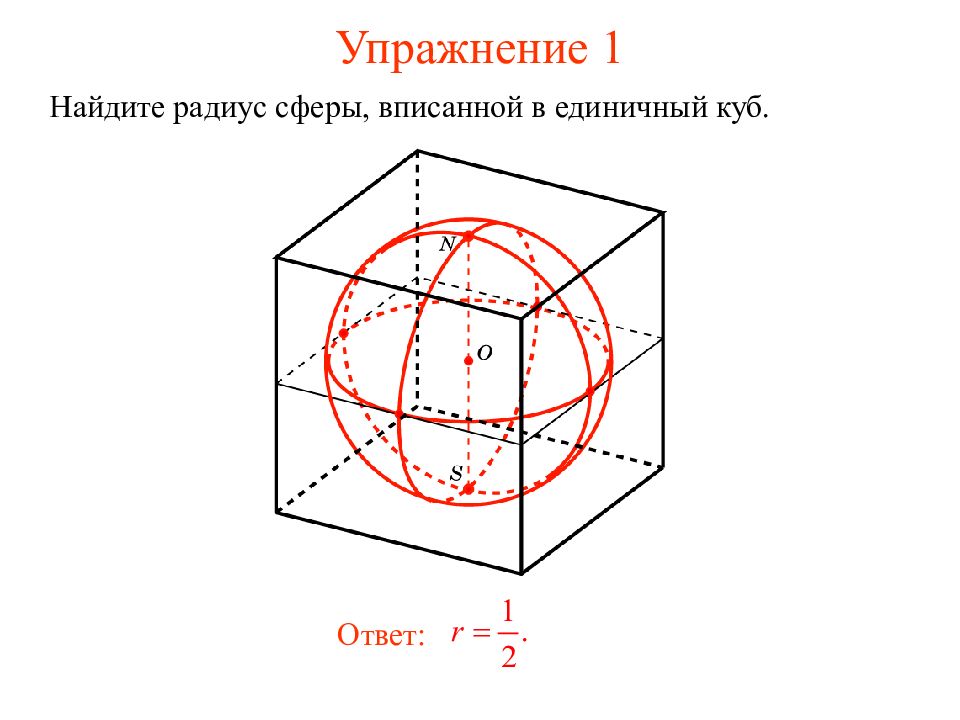
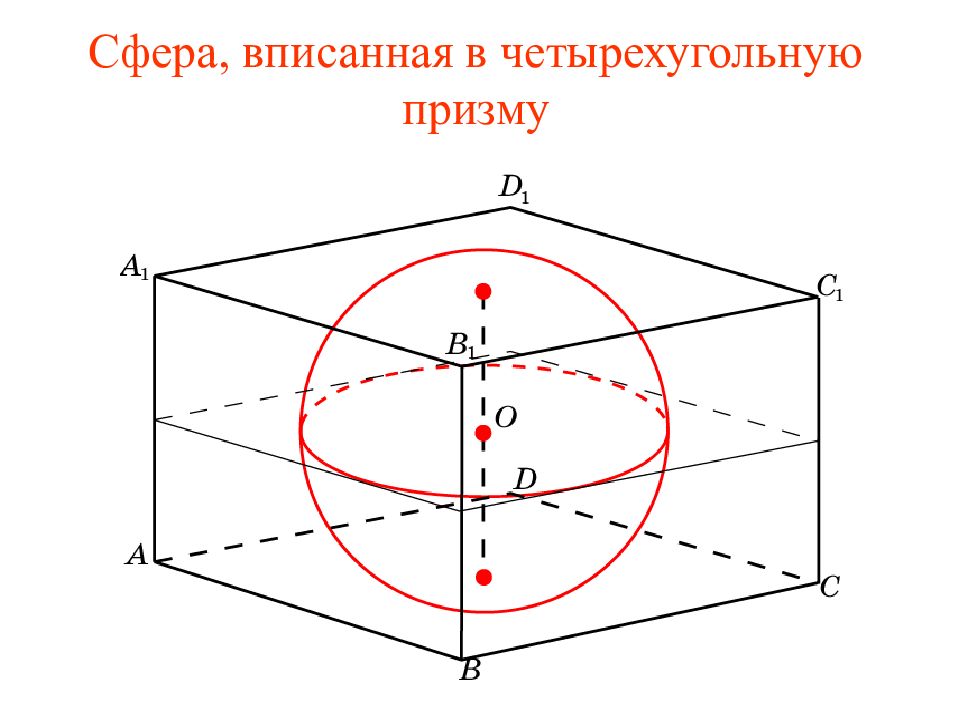
Слайд 2: Сфера, вписанная в куб
Слайд 4: Упражнение 2
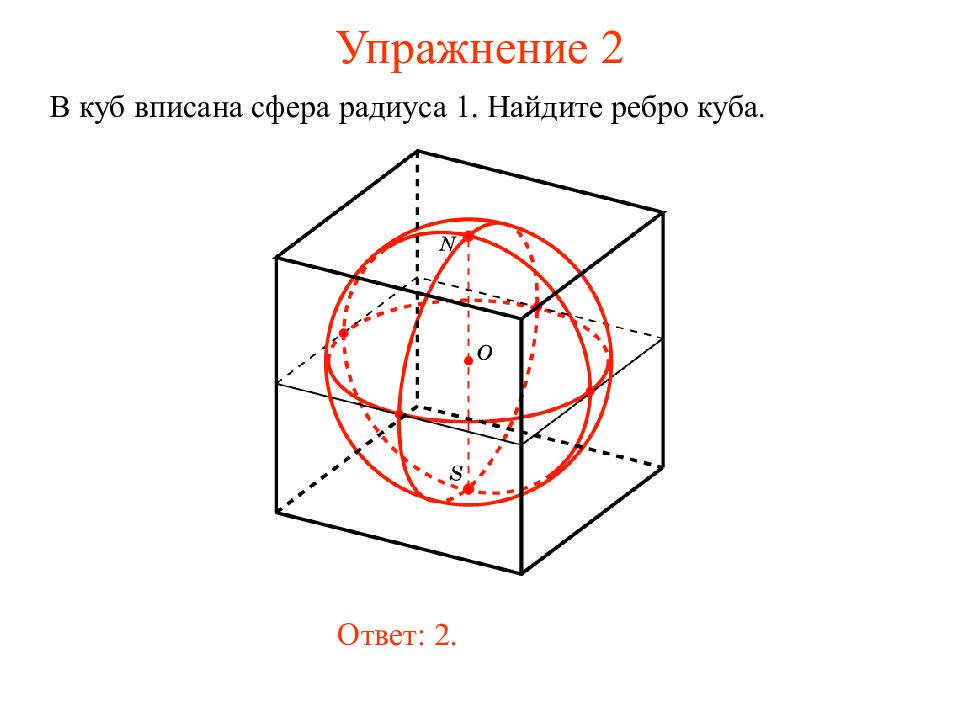
В куб вписана сфера радиуса 1. Найдите ребро куба. Ответ: 2.
Слайд 5: Упражнение 3
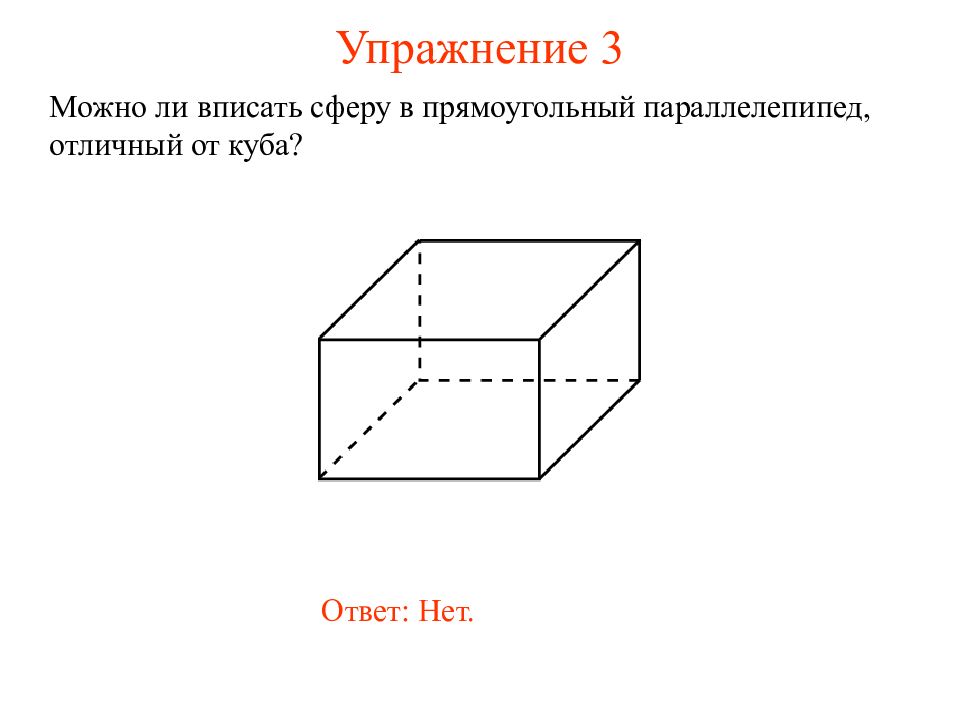
Можно ли вписать сферу в прямоугольный параллелепипед, отличный от куба? Ответ: Нет.
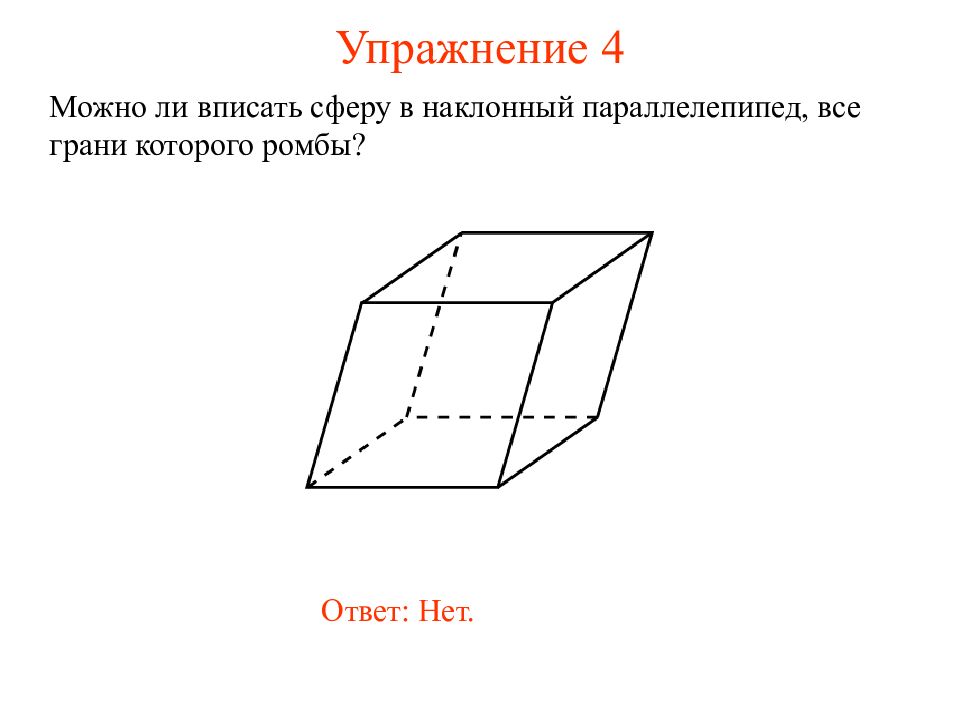
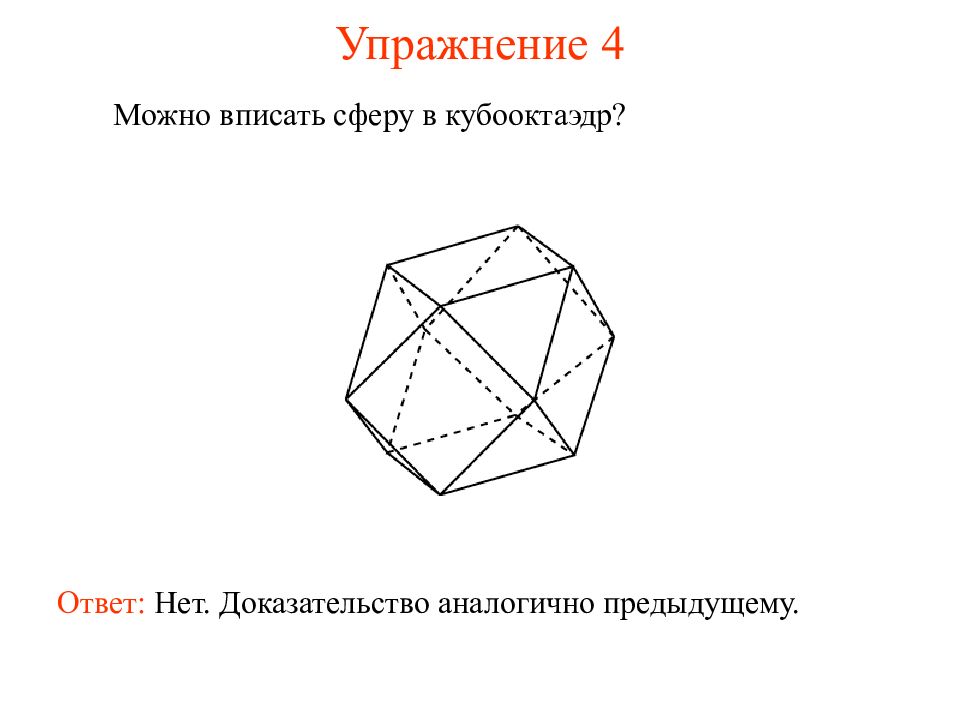
Слайд 6: Упражнение 4
Можно ли вписать сферу в наклонный параллелепипед, все грани которого ромбы? Ответ: Нет.
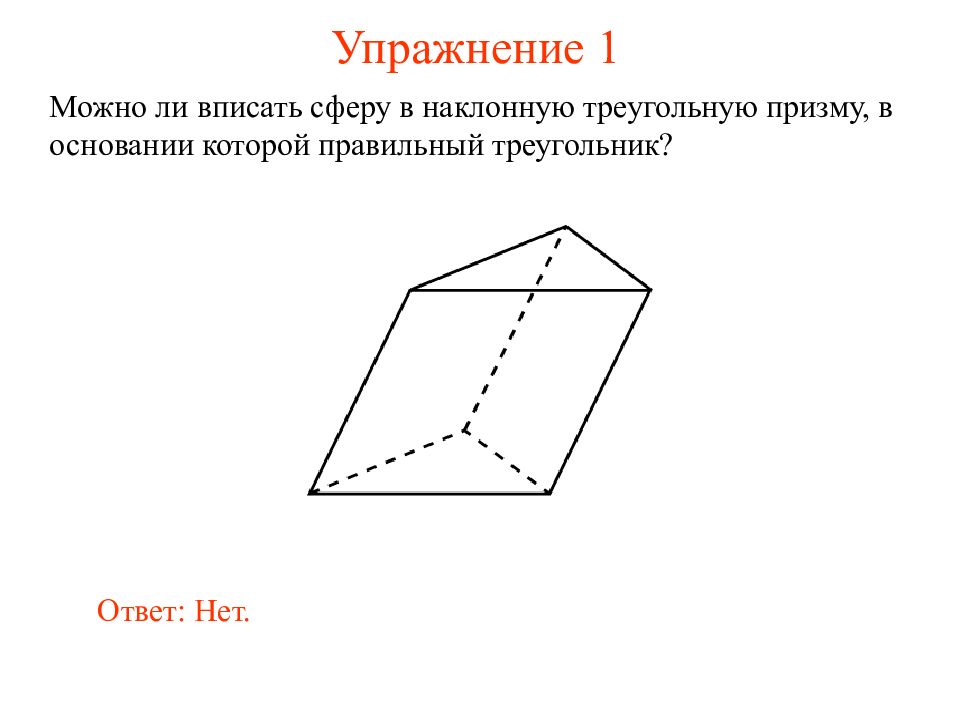
Слайд 8: Упражнение 1
Можно ли вписать сферу в наклонную треугольную призму, в основании которой правильный треугольник? Ответ: Нет.
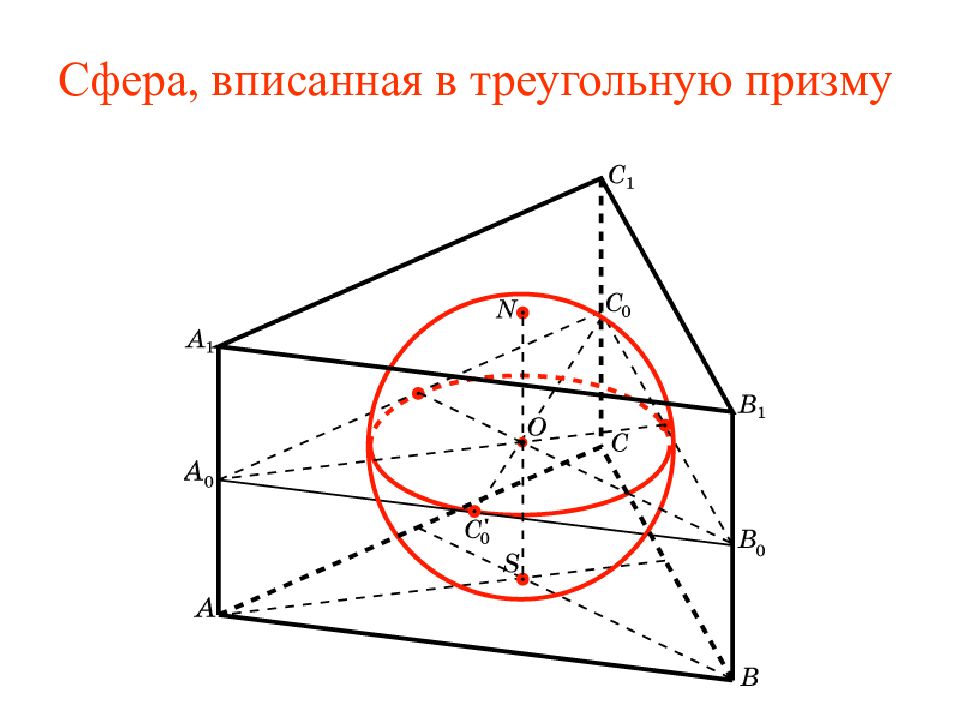
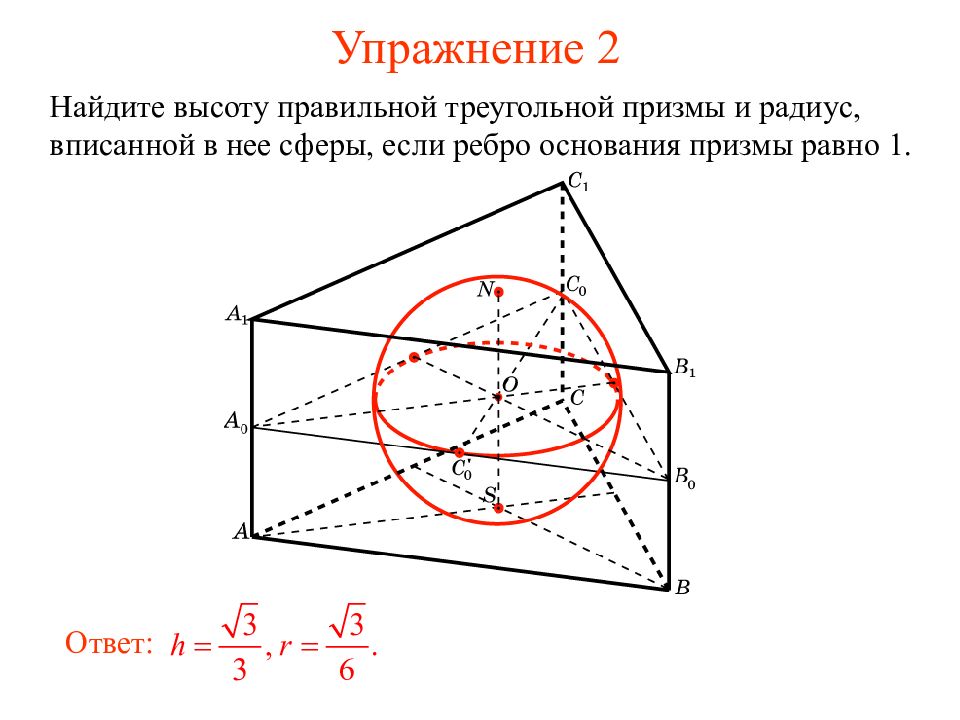
Слайд 9: Упражнение 2
Найдите высоту правильной треугольной призмы и радиус, вписанной в нее сферы, если ребро основания призмы равно 1. Ответ:
Слайд 10: Упражнение 3
В правильную треугольную призму вписана сфера радиуса 1. Найдите сторону основания и высоту призмы. Ответ:
Слайд 11: Упражнение 4
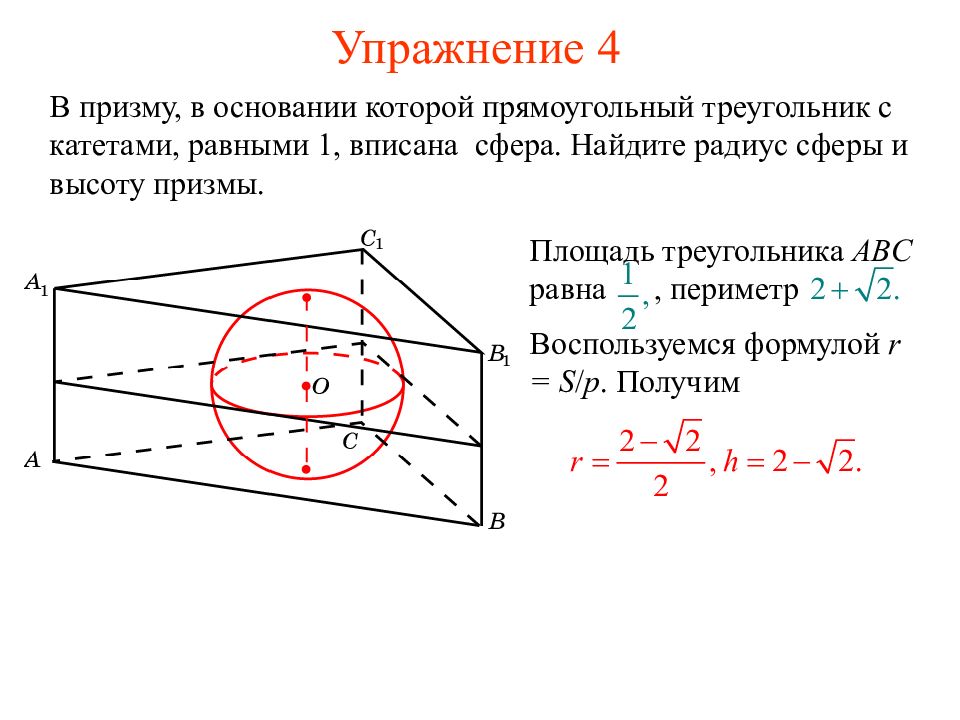
В призму, в основании которой прямоугольный треугольник с катетами, равными 1, вписана сфера. Найдите радиус сферы и высоту призмы. Площадь треугольника ABC равна, периметр Воспользуемся формулой r = S / p. Получим
Слайд 12: Упражнение 5
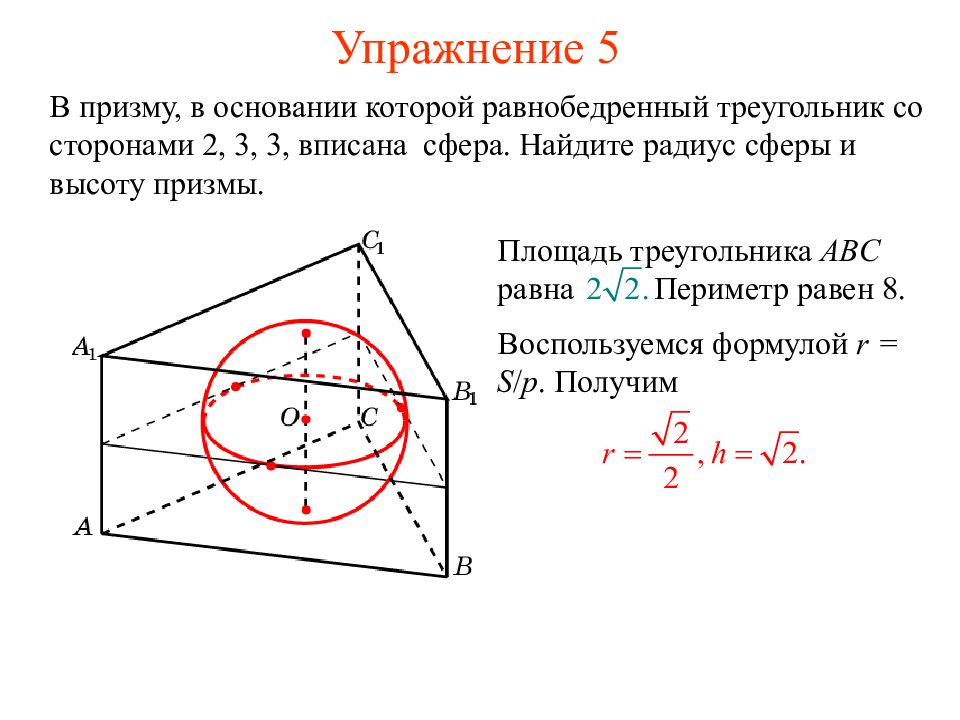
В призму, в основании которой равнобедренный треугольник со сторонами 2, 3, 3, вписана сфера. Найдите радиус сферы и высоту призмы. Площадь треугольника ABC равна Периметр равен 8. Воспользуемся формулой r = S / p. Получим
Слайд 14: Упражнение 1
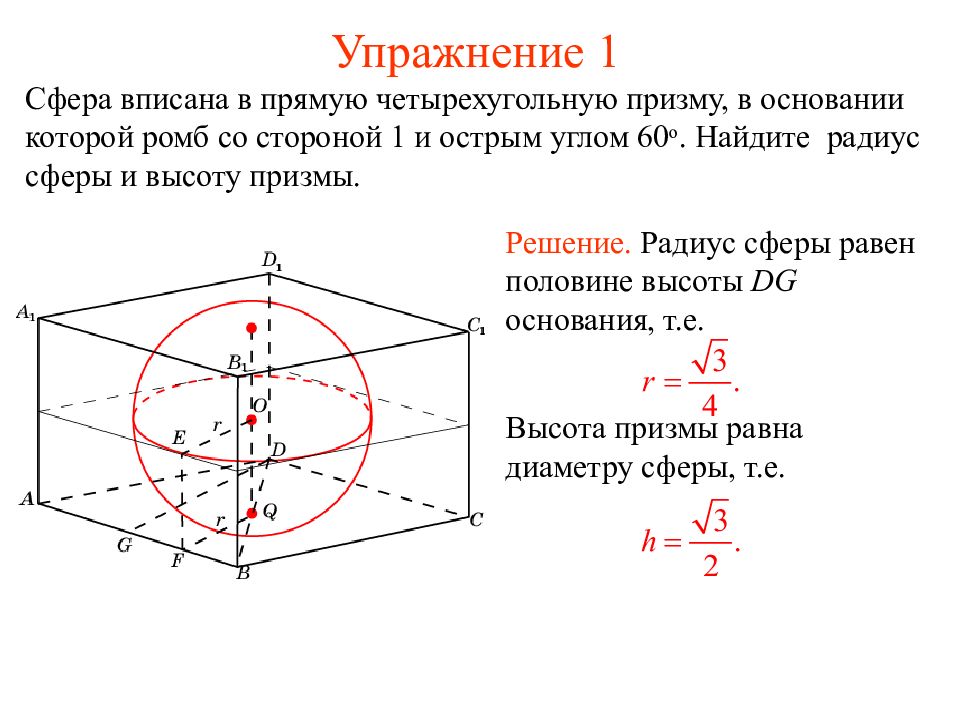
Сфера вписана в прямую четырехугольную призму, в основании которой ромб со стороной 1 и острым углом 60 о. Найдите радиус сферы и высоту призмы. Решение. Радиус сферы равен половине высоты DG основания, т.е. Высота призмы равна диаметру сферы, т.е.
Слайд 15: Упражнение 2
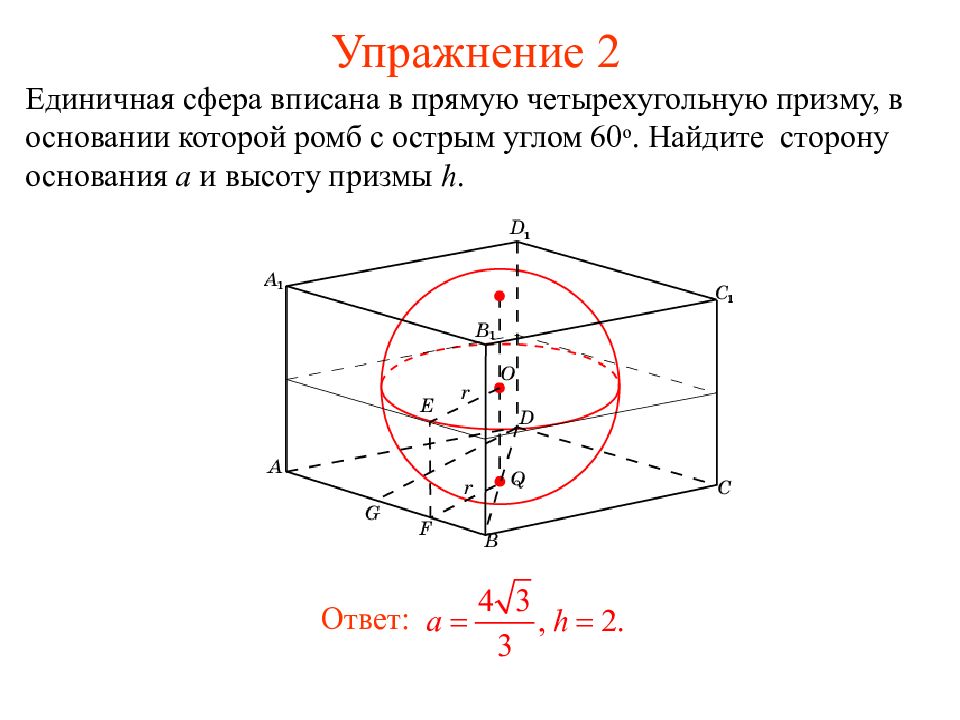
Единичная сфера вписана в прямую четырехугольную призму, в основании которой ромб с острым углом 60 о. Найдите сторону основания a и высоту призмы h. Ответ:
Слайд 16: Упражнение 3
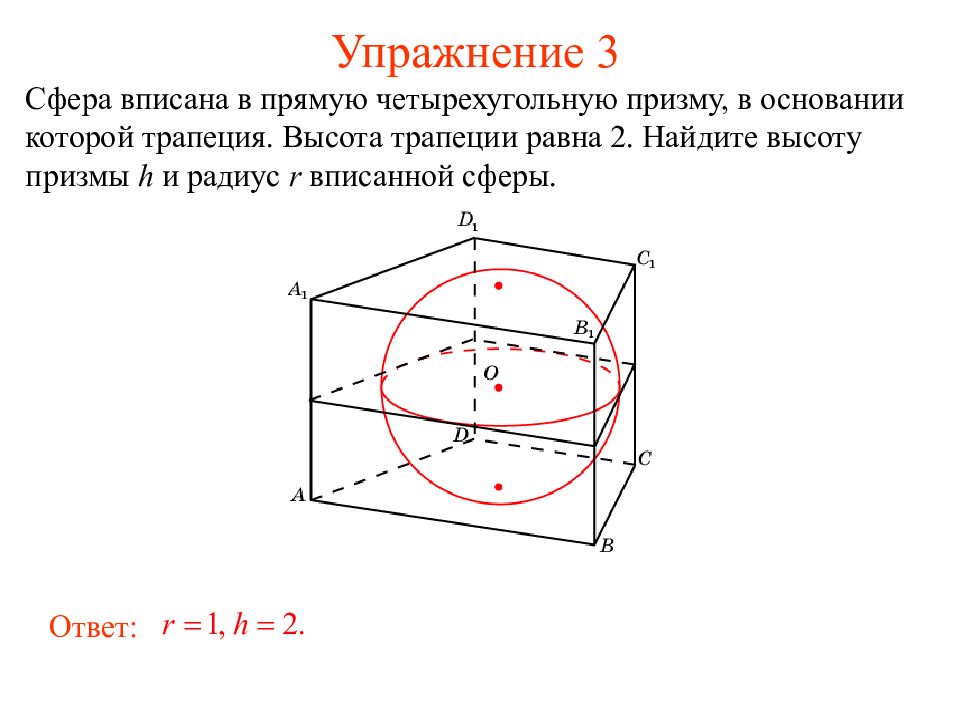
Сфера вписана в прямую четырехугольную призму, в основании которой трапеция. Высота трапеции равна 2. Найдите высоту призмы h и радиус r вписанной сферы. Ответ:
Слайд 17: Упражнение 4
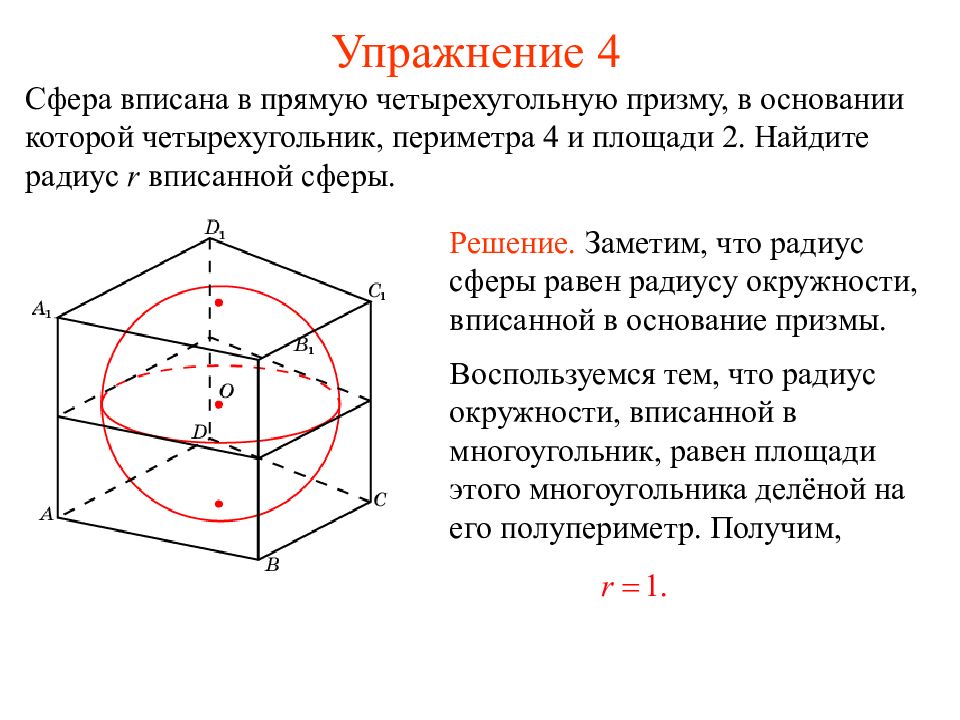
Сфера вписана в прямую четырехугольную призму, в основании которой четырехугольник, периметра 4 и площади 2. Найдите радиус r вписанной сферы. Решение. Заметим, что радиус сферы равен радиусу окружности, вписанной в основание призмы. Воспользуемся тем, что радиус окружности, вписанной в многоугольник, равен площади этого многоугольника делёной на его полупериметр. Получим,
Слайд 19: Упражнение 1
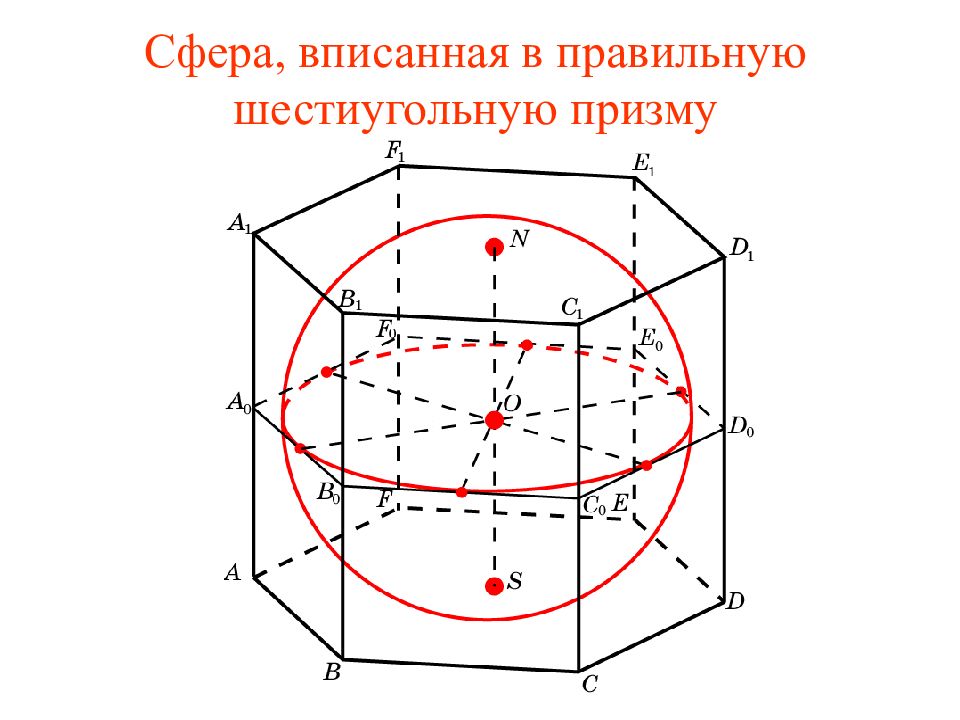
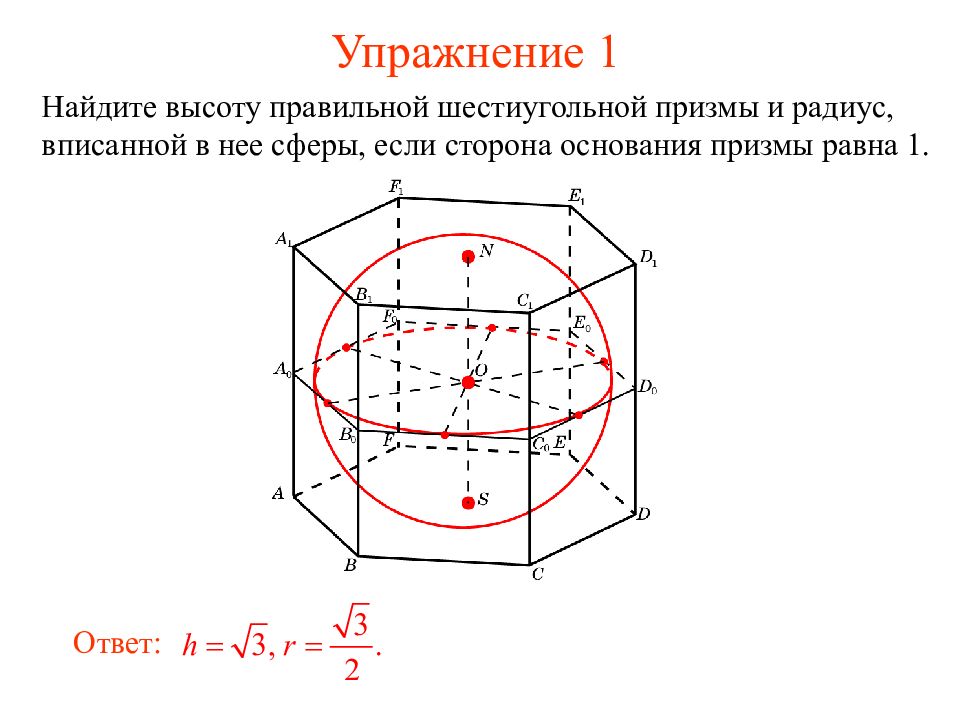
Найдите высоту правильной шестиугольной призмы и радиус, вписанной в нее сферы, если сторона основания призмы равна 1. Ответ:
Слайд 20: Упражнение 2
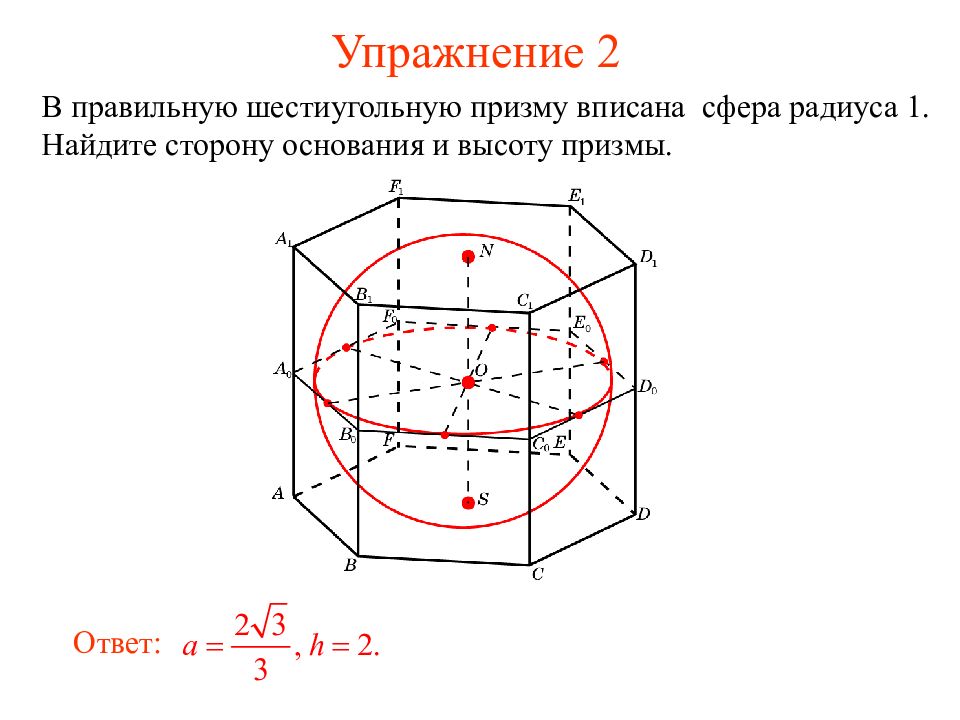
В правильную шестиугольную призму вписана сфера радиуса 1. Найдите сторону основания и высоту призмы. Ответ:
Слайд 22: Упражнение 1
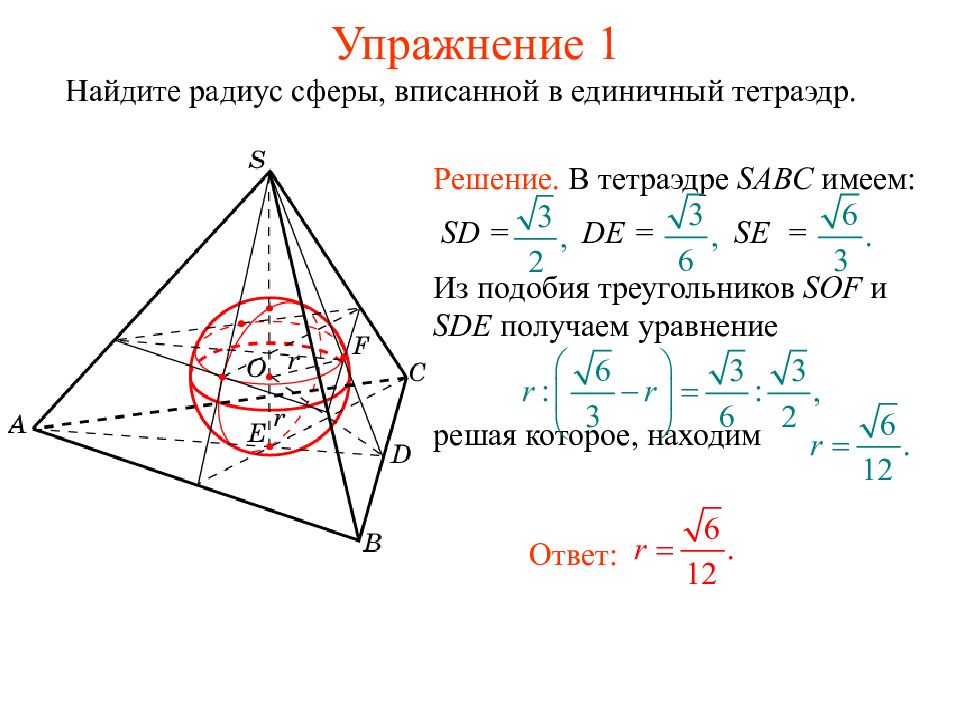
Найдите радиус сферы, вписанной в единичный тетраэдр. Ответ: Решение. В тетраэдре SABC имеем: SD = DE = SE = Из подобия треугольников SOF и SDE получаем уравнение решая которое, находим
Слайд 23: Упражнение 2
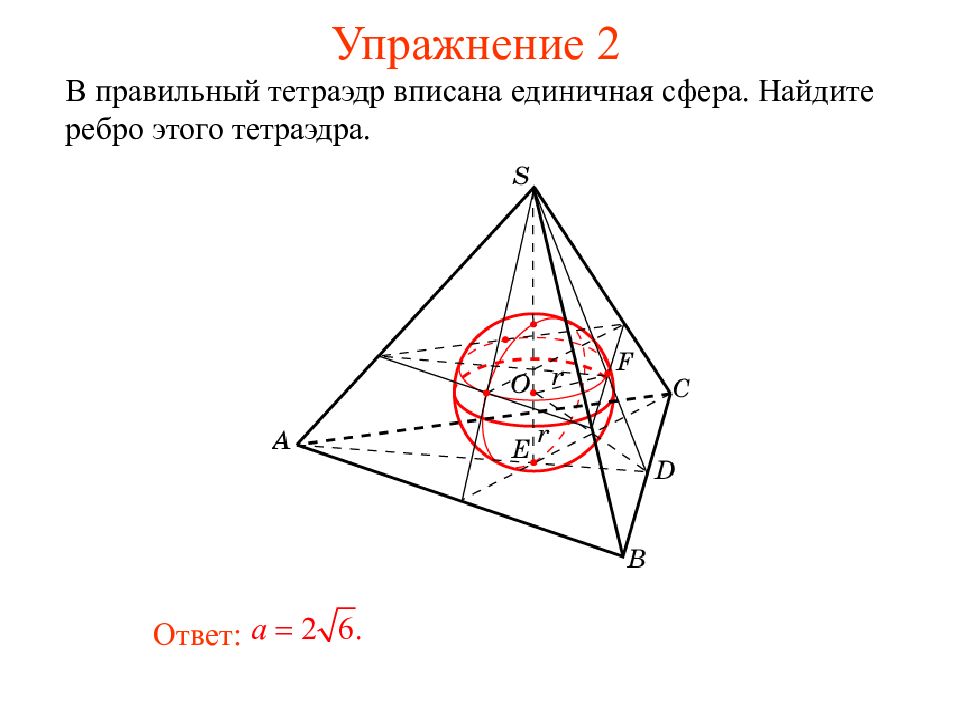
В правильный тетраэдр вписана единичная сфера. Найдите ребро этого тетраэдра. Ответ:
Слайд 24: Упражнение 3
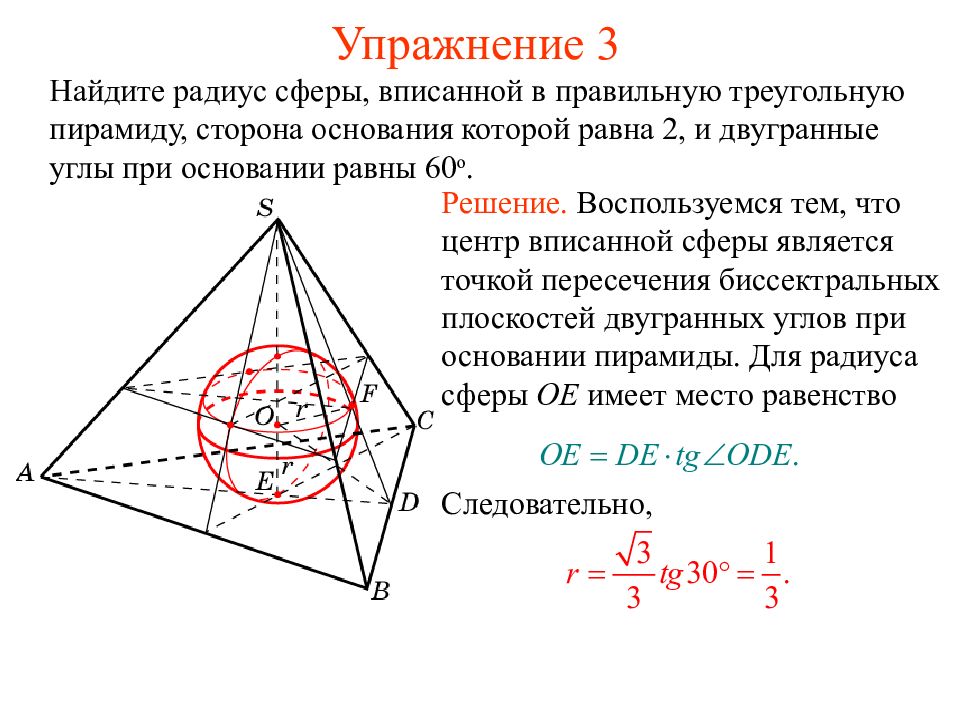
Найдите радиус сферы, вписанной в правильную треугольную пирамиду, сторона основания которой равна 2, и двугранные углы при основании равны 60 о. Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов при основании пирамиды. Для радиуса сферы OE имеет место равенство Следовательно,
Слайд 25: Упражнение 4
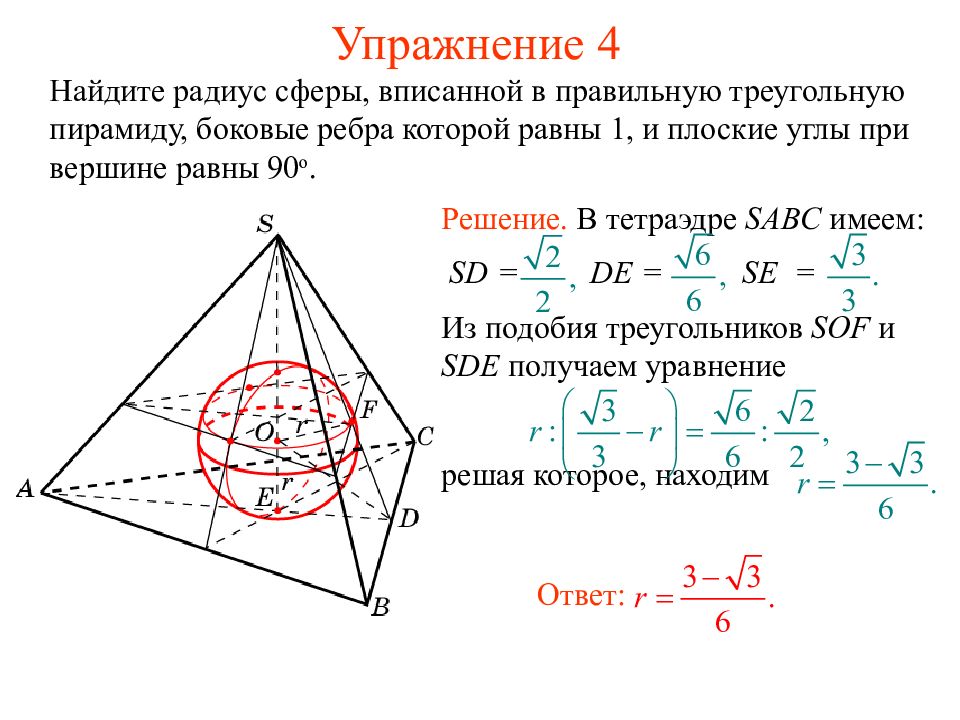
Найдите радиус сферы, вписанной в правильную треугольную пирамиду, боковые ребра которой равны 1, и плоские углы при вершине равны 90 о. Ответ: Решение. В тетраэдре SABC имеем: SD = DE = SE = Из подобия треугольников SOF и SDE получаем уравнение решая которое, находим
Слайд 27: Упражнение 1
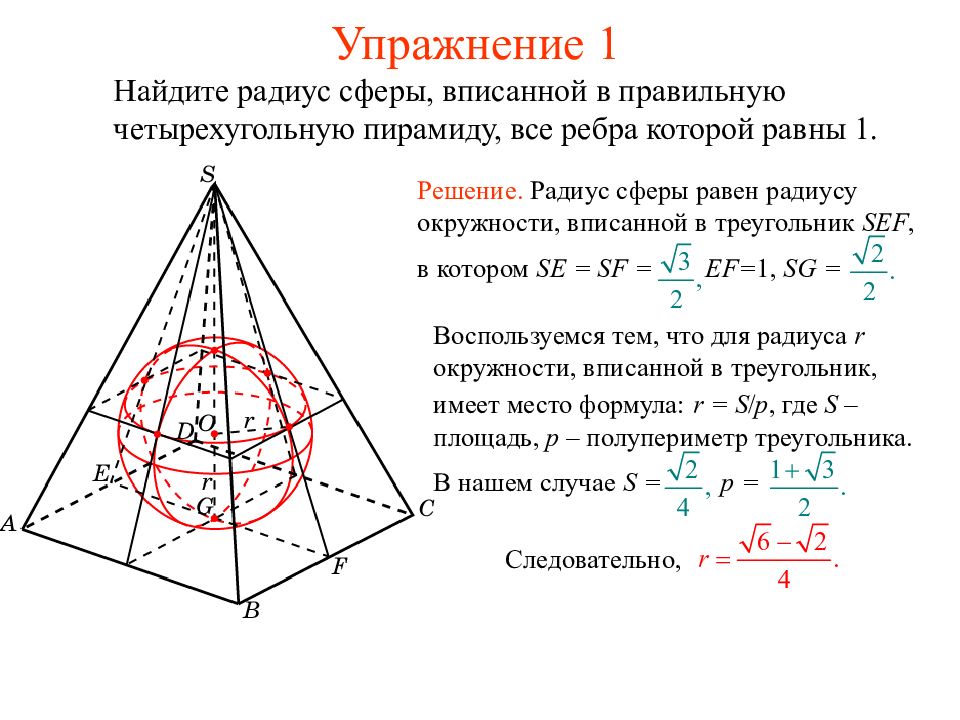
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, все ребра которой равны 1. Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S / p, где S – площадь, p – полупериметр треугольника. В нашем случае S = p = Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF, в котором SE = SF = EF= 1, SG = Следовательно,
Слайд 28: Упражнение 2
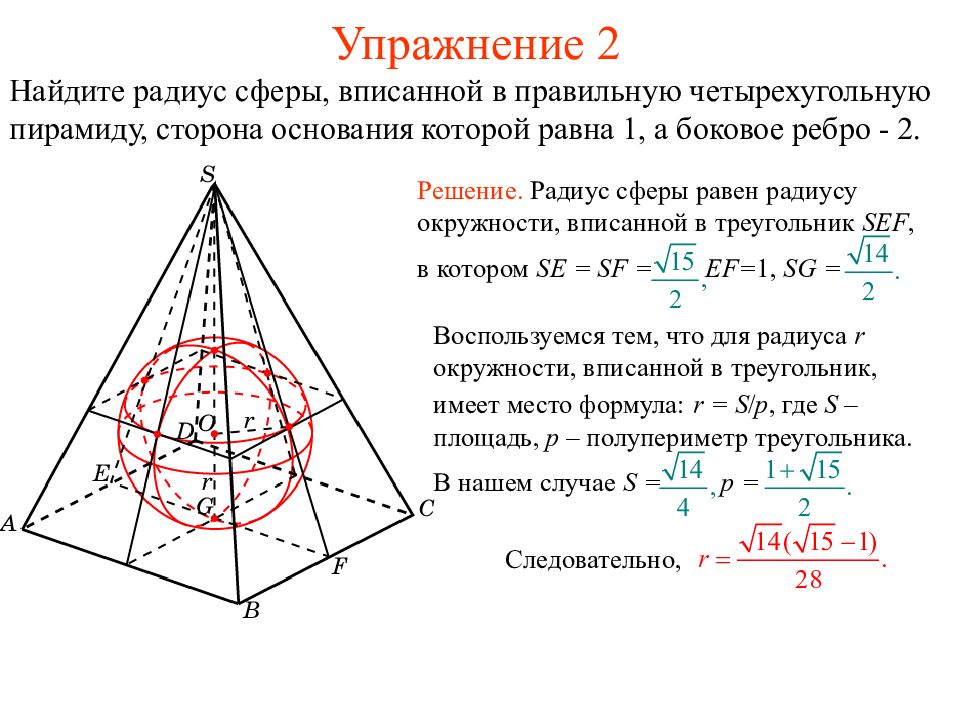
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 1, а боковое ребро - 2. Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S / p, где S – площадь, p – полупериметр треугольника. В нашем случае S = p = Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF, в котором SE = SF = EF= 1, SG = Следовательно,
Слайд 29: Упражнение 3
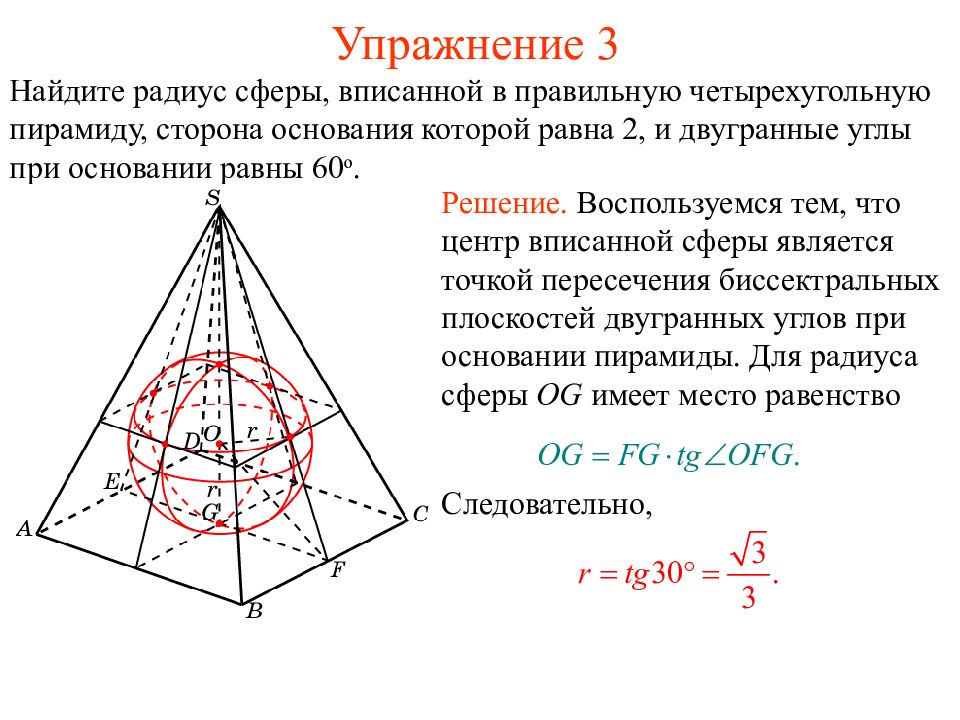
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 2, и двугранные углы при основании равны 60 о. Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов при основании пирамиды. Для радиуса сферы OG имеет место равенство Следовательно,
Слайд 30: Упражнение 4
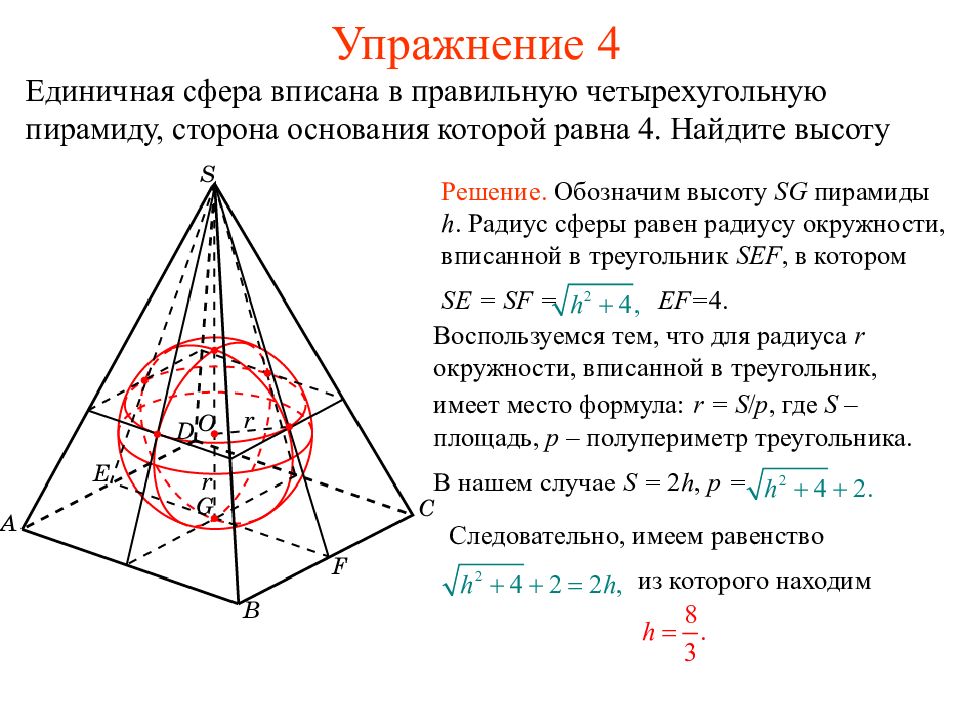
Единичная сфера вписана в правильную четырехугольную пирамиду, сторона основания которой равна 4. Найдите высоту пирамиды. Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S / p, где S – площадь, p – полупериметр треугольника. В нашем случае S = 2 h, p = Решение. Обозначим высоту SG пирамиды h. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF, в котором SE = SF = EF= 4. Следовательно, имеем равенство из которого находим
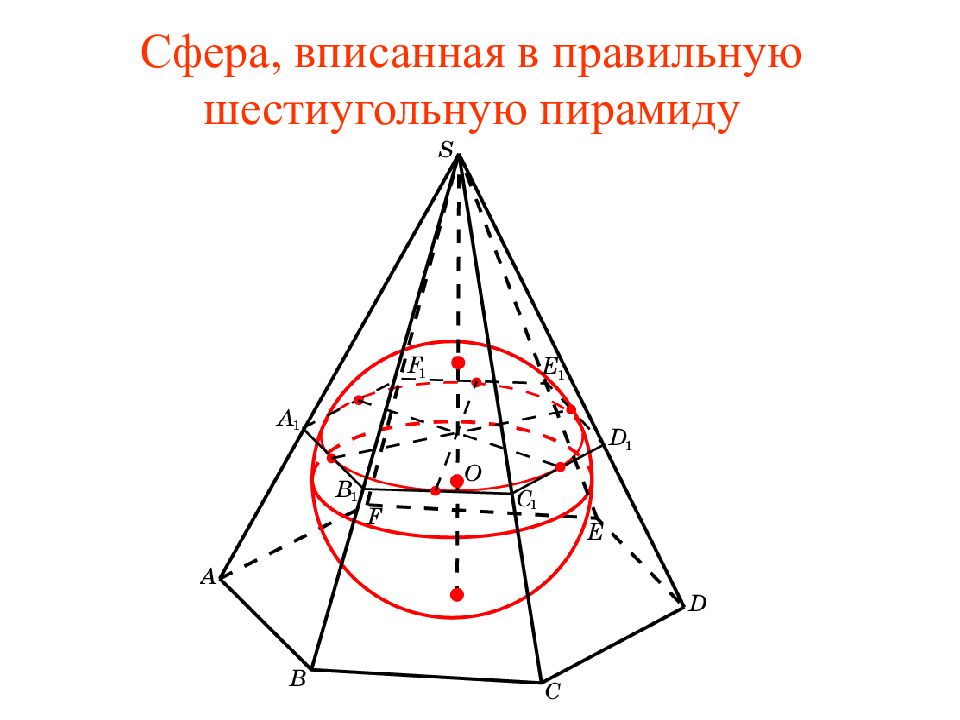
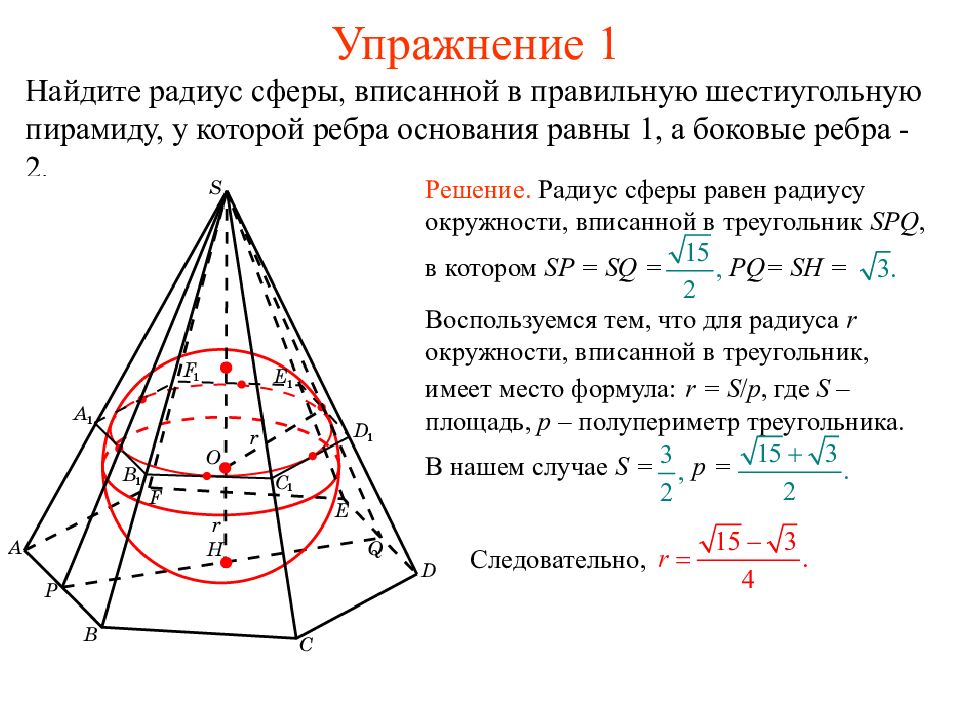
Слайд 32: Упражнение 1
Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду, у которой ребра основания равны 1, а боковые ребра - 2. Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S / p, где S – площадь, p – полупериметр треугольника. В нашем случае S = p = Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SPQ, в котором SP = SQ = PQ= SH = Следовательно,
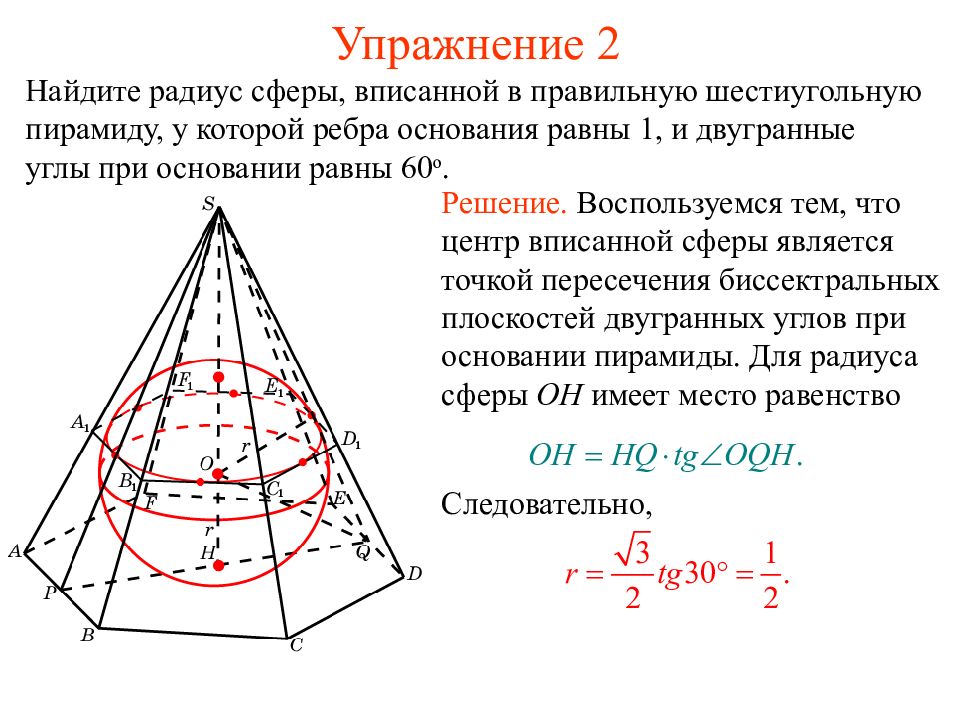
Слайд 33: Упражнение 2
Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду, у которой ребра основания равны 1, и двугранные углы при основании равны 60 о. Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов при основании пирамиды. Для радиуса сферы OH имеет место равенство Следовательно,
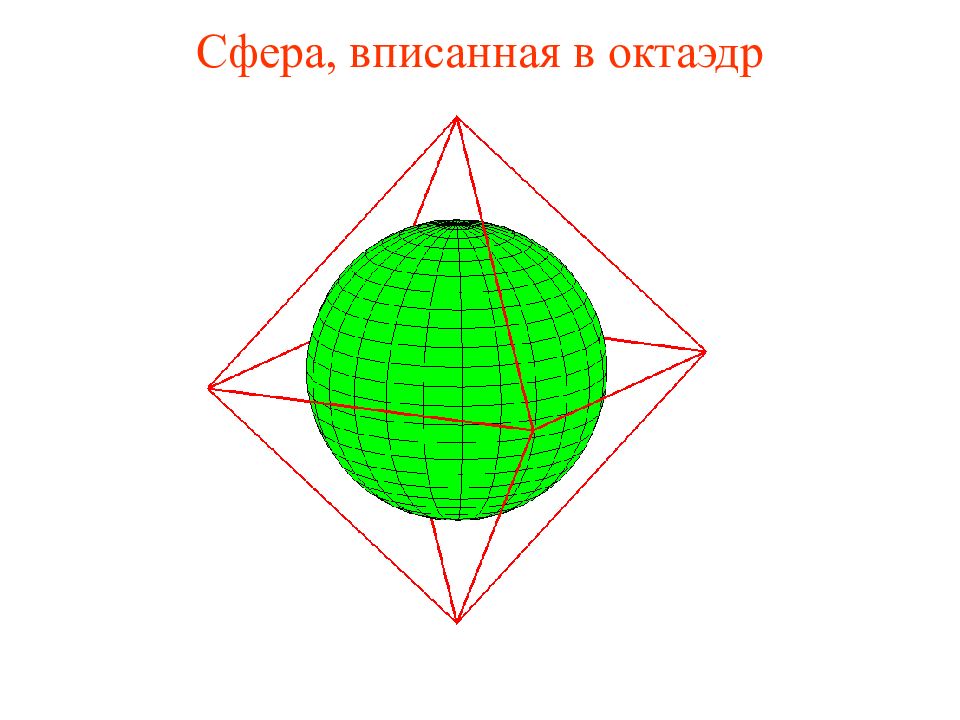
Слайд 35: Упражнение
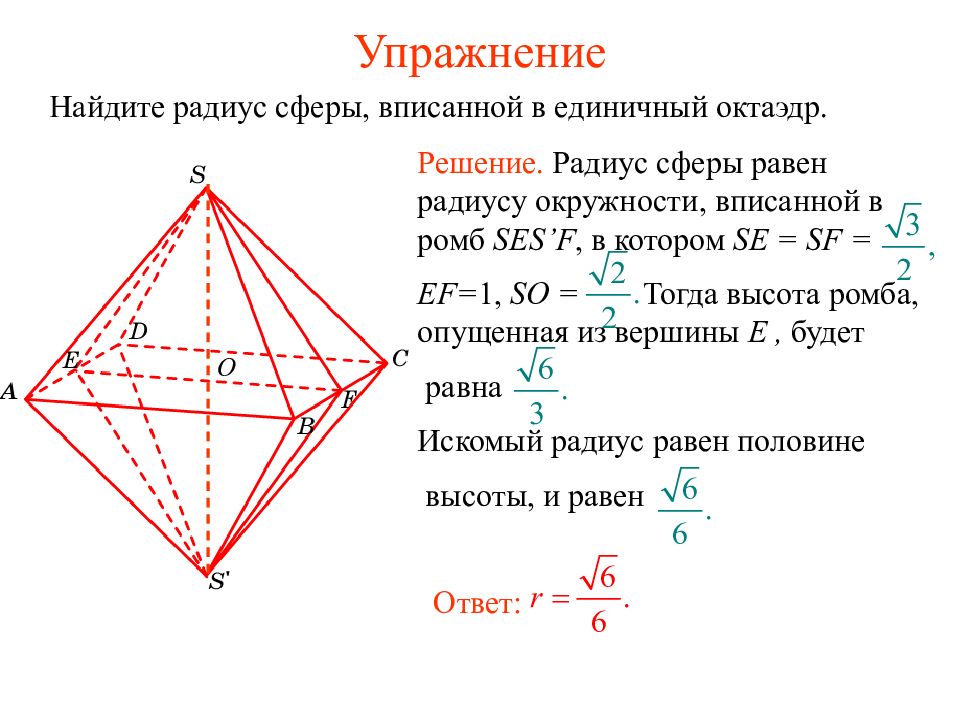
Найдите радиус сферы, вписанной в единичный октаэдр. Ответ: Решение. Радиус сферы равен радиусу окружности, вписанной в ромб SES’F, в котором SE = SF = EF= 1, SO = Тогда высота ромба, опущенная из вершины E, будет равна Искомый радиус равен половине высоты, и равен O
Слайд 37: Упражнение
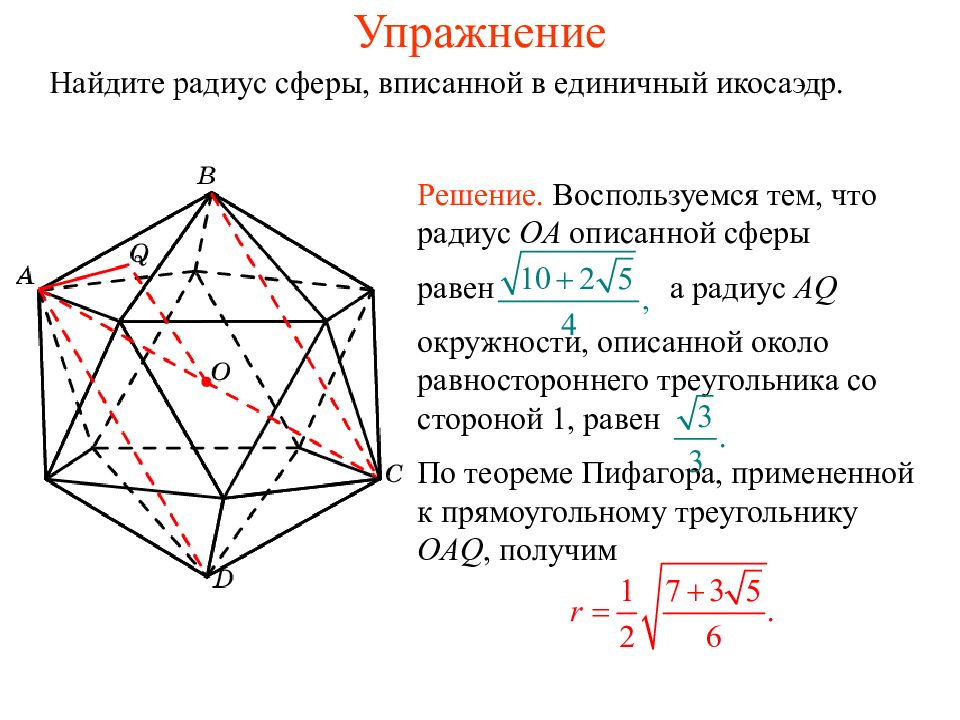
Найдите радиус сферы, вписанной в единичный икосаэдр. Решение. Воспользуемся тем, что радиус OA описанной сферы равен а радиус AQ окружности, описанной около равностороннего треугольника со стороной 1, равен По теореме Пифагора, примененной к прямоугольному треугольнику OAQ, получим
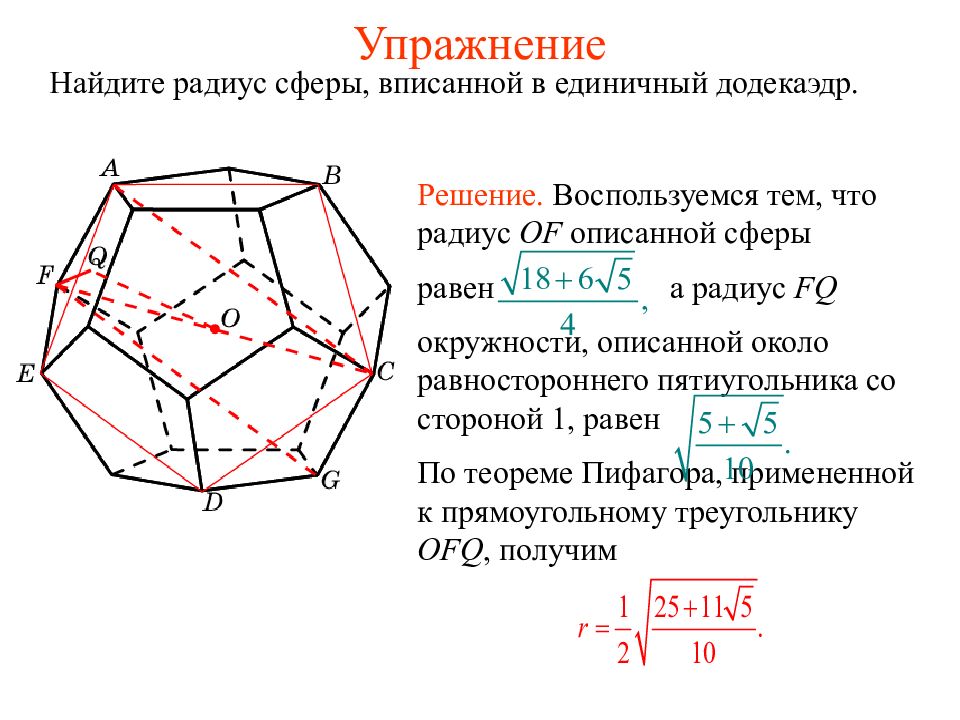
Слайд 39: Упражнение
Найдите радиус сферы, вписанной в единичный додекаэдр. Решение. Воспользуемся тем, что радиус OF описанной сферы равен а радиус FQ окружности, описанной около равностороннего пятиугольника со стороной 1, равен По теореме Пифагора, примененной к прямоугольному треугольнику OFQ, получим
Слайд 40: Упражнение 1
Можно вписать сферу в усеченный тетраэдр? Решение. Заметим, что центр O сферы, вписанной в усеченный тетраэдр должен совпадать с центром сферы, вписанной в тетраэдр, который совпадает с центром сферы, полувписанной в усеченный тетраэдр. Расстояния d 1, d 2 от точки O до шестиугольной и треугольной граней вычисляются по теореме Пифагора: где R – радиус полувписанной сферы, r 1, r 2 – радиусы окружностей, вписанных в шестиугольник и треугольник, соответственно. Поскольку r 1 > r 2, то d 1 < d 2 и, следовательно, сферы, вписанной в усеченный тетраэдр, не существует.
Слайд 41: Упражнение 2
Можно вписать сферу в усеченный куб ? Ответ: Нет. Доказательство аналогично предыдущему.
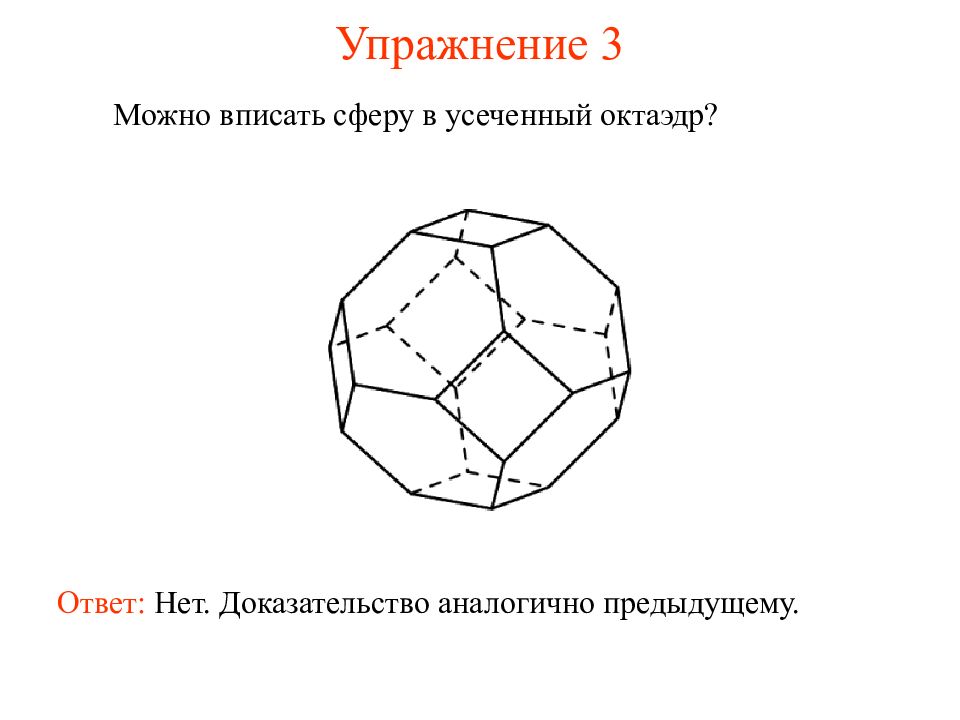
Слайд 42: Упражнение 3
Можно вписать сферу в усеченный октаэдр ? Ответ: Нет. Доказательство аналогично предыдущему.