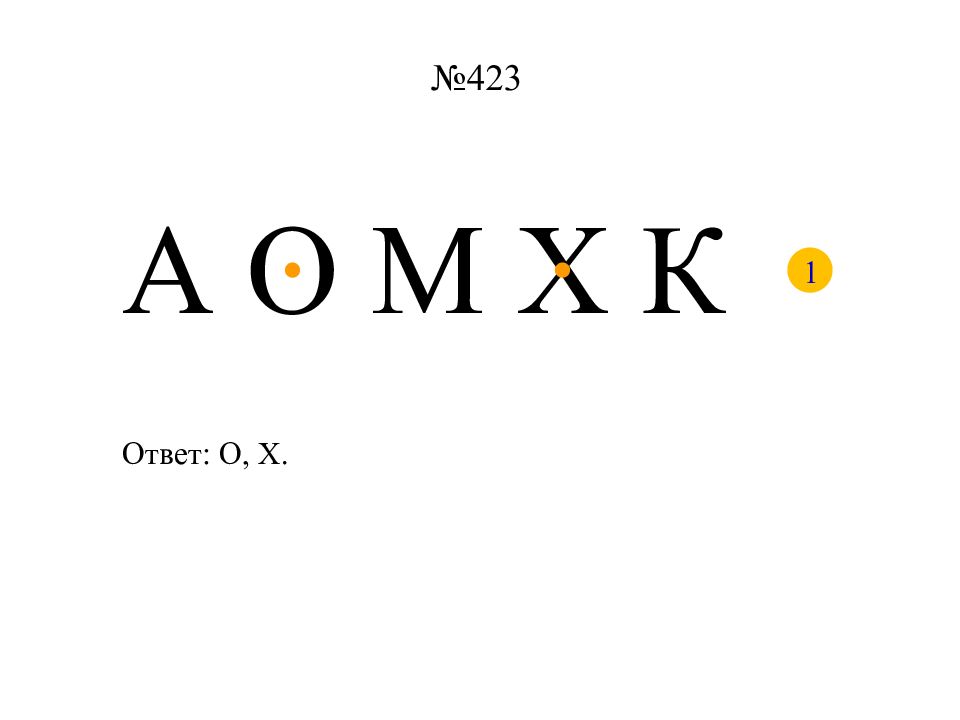"Осевая и центральная симметрии" Тема урока
Симметрия в окружающем нас мире Взгляните на снежинку, бабочку, морскую звезду, листья растений, паутинку – это лишь некоторые про-явления симметрии в природе. Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии.
С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Так фасады многих зданий обладают осевой симметрией. В большин-стве случаев симметрич-ны относительно оси или центра узоры на коврах, тканях, комнатных обо-ях. Симметричны многие детали механизмов.
Слово «симметрия» греческое ( συμμετρία), оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”, неизменность при каких-либо преобразованиях.
Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. Л.Н.Толстой. Русский художник Илья Ефимович Репин Портрет писателя Л.Н.Толстого. 1887 г. http://ilya-repin.ru/master/repin9.php
В японском городе Никко находятся красивейшие ворота страны. Они необычайно сложные, со множеством фронтонов и изумительной резьбой. Но в сложном и искусном рисунке на одной из колонн некоторые из его мелких деталей вырезаны вверх ногами. В остальном, рисунок полностью симметричен. Для чего это было нужно? http://www.walls-world.ru/download-wallpapers-4109-original.html
Как говорит предание, симметрия была нарушена намеренно, чтобы боги не заподозрили человека в совершенстве и не разгневались на него. http://www.walls-world.ru/download-wallpapers-4109-original.html
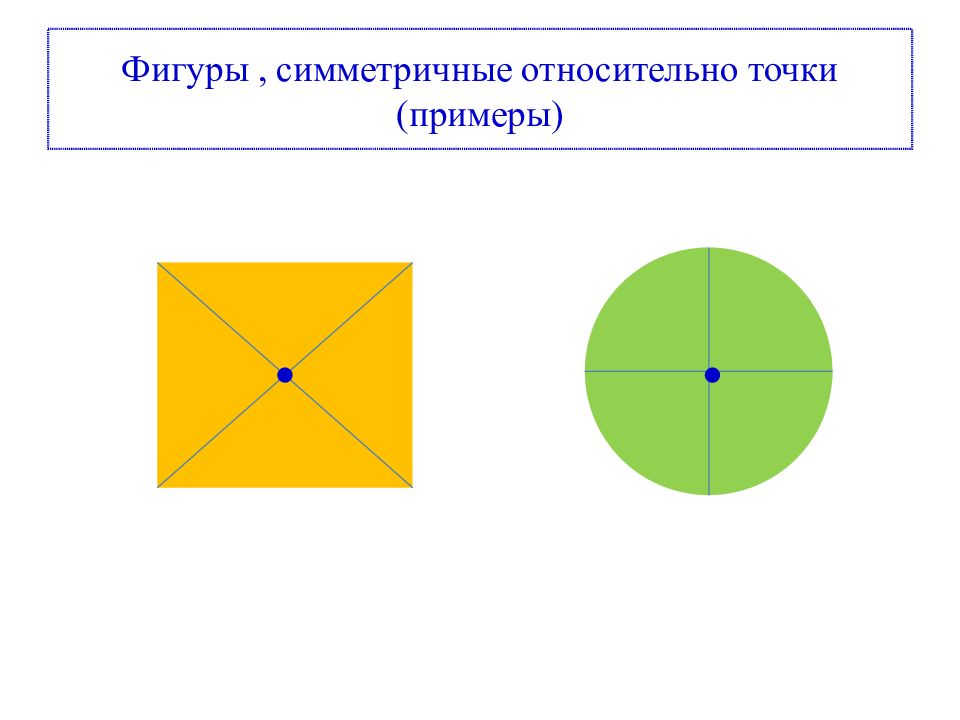
Центральная симметрия Центральная симметрия является одним из видов симметрии. Фигура называется симметричной относительно точки O, если для каждой точки фигуры симметричная ей точка относительно точки O также принадлежит этой фигуре. Точка O называется центром симметрии.
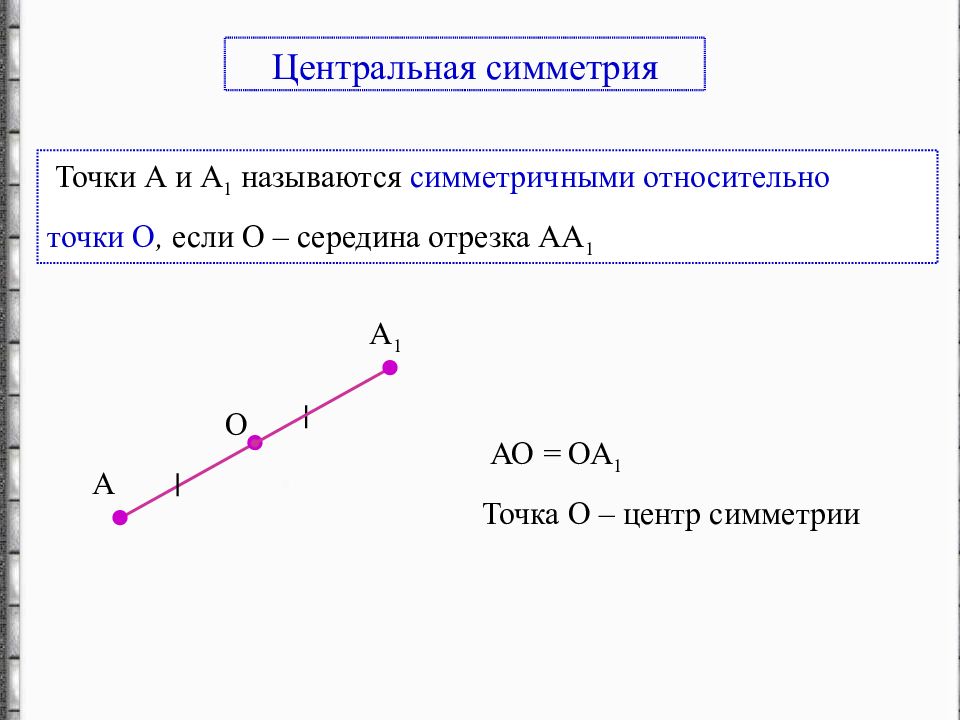
Точки А и А 1 называются симметричными относительно точки О, если О – середина отрезка АА 1 А А 1 О АО = ОА 1 Точка О – центр симметрии Центральная симметрия
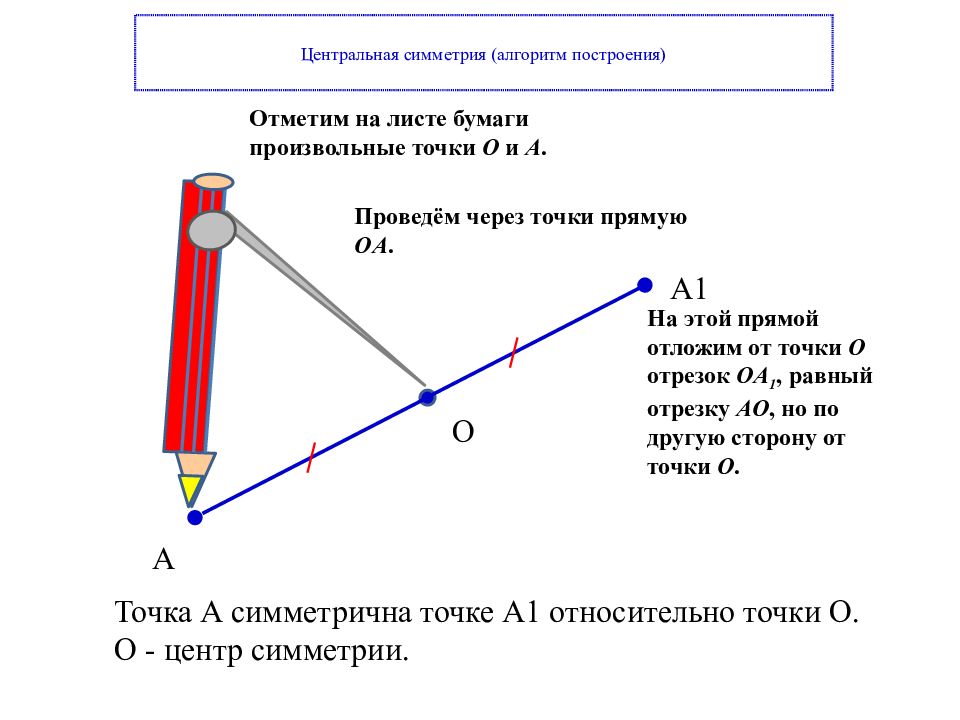
А А1 О Точка А симметрична точке А1 относительно точки О. О - центр симметрии. Отметим на листе бумаги произвольные точки O и A. Проведём через точки прямую OA. На этой прямой отложим от то ч ки O отрезок OA 1, равный отрезку AO, но по другую сторону от точки O.
Если внимательно рассмотреть данные орнаменты и фигуры, можно заметить, что все они имеют центр симметрии. Задание. На рисунке изображены различные геометричес-кие фигуры. Выберите из них те, которые име-ют центр симметрии, и изобразите их в тет-ради. Отметьте центр симметрии и точки, симметричные отмечен-ным точкам. б) в) г) а) д) е)
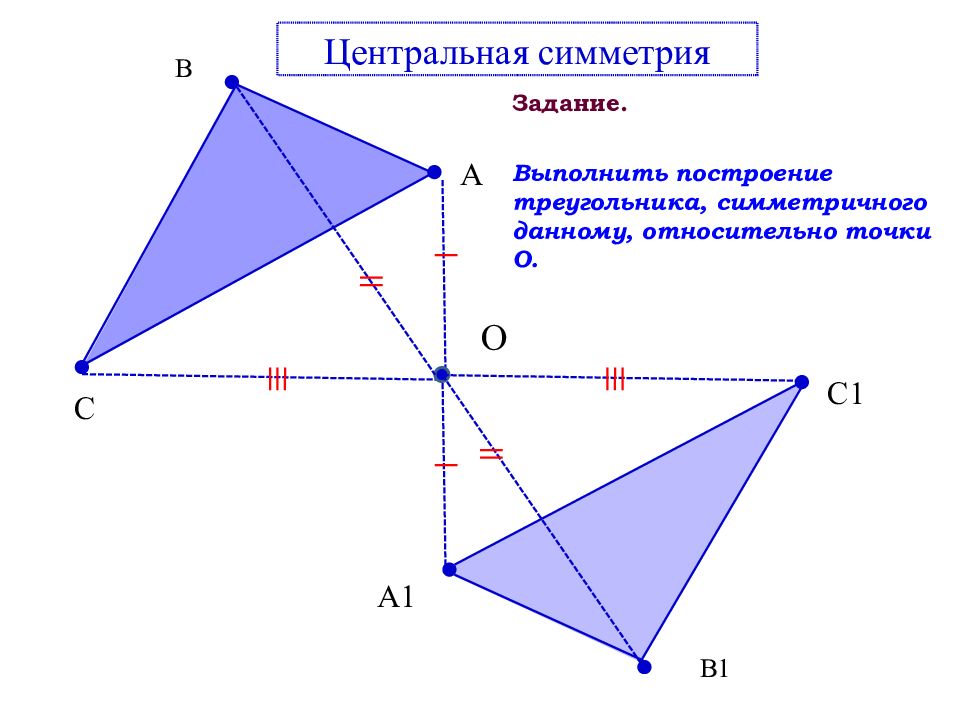
В А С О Центральная симметрия В1 А1 С1 Задание. Выполнить построение треугольника, симметричного данному, относительно точки O.
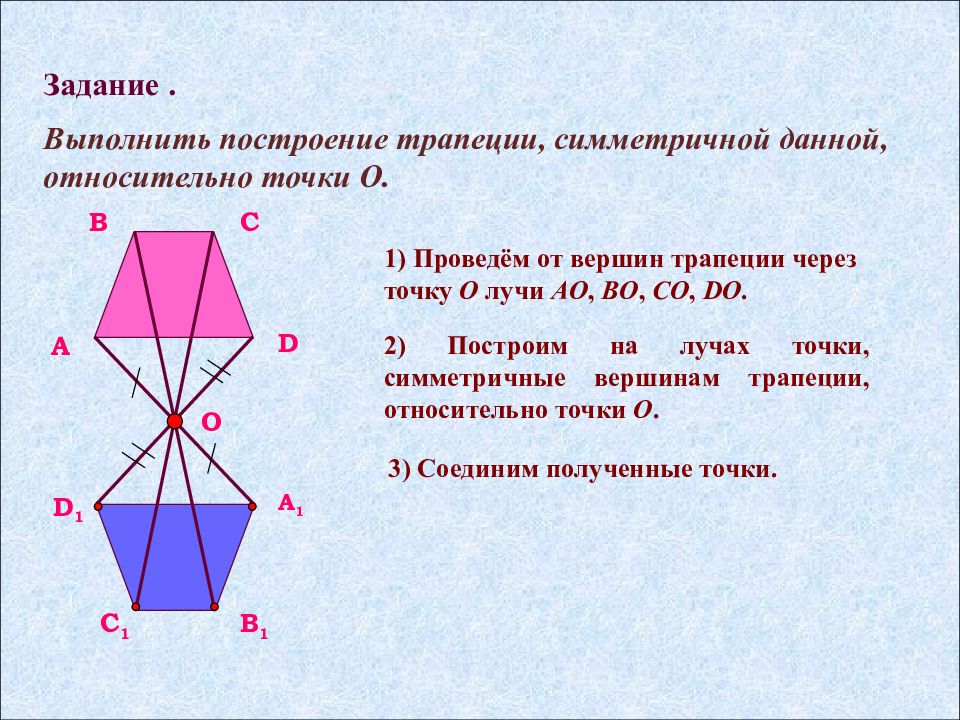
Задание. Выполнить построение трапеции, симметричной данной, относительно точки O. A B C D A 1 B 1 C 1 D 1 O 1) Проведём от вершин трапеции через точку O лучи AO, BO, CO, DO. 2) Построим на лучах точки, симметричные вершинам трапеции, относительно точки O. 3) Соединим полученные точки.
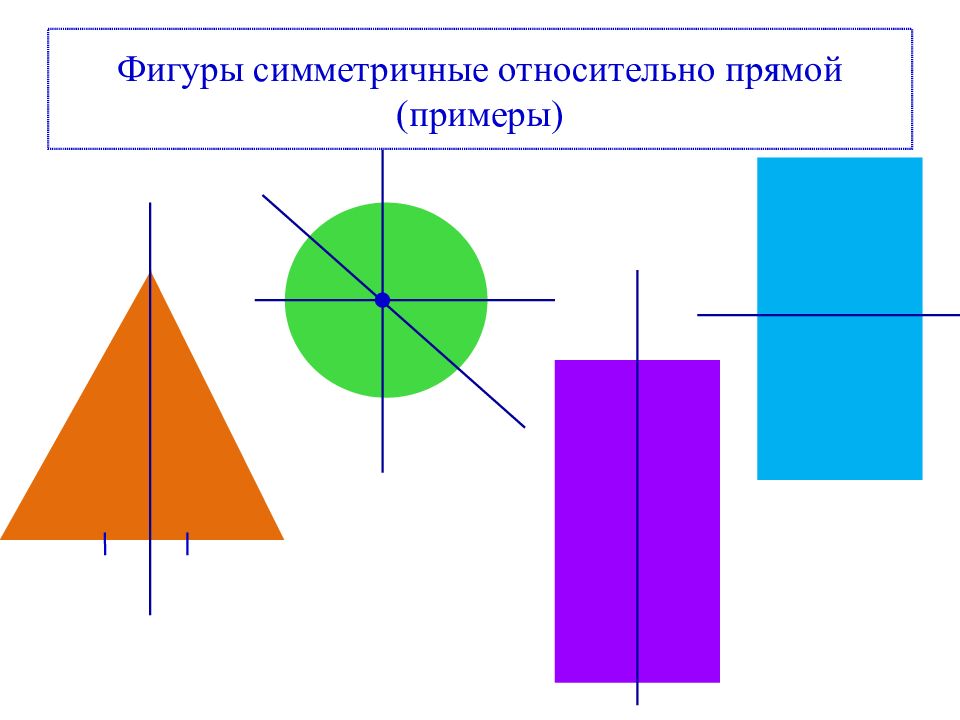
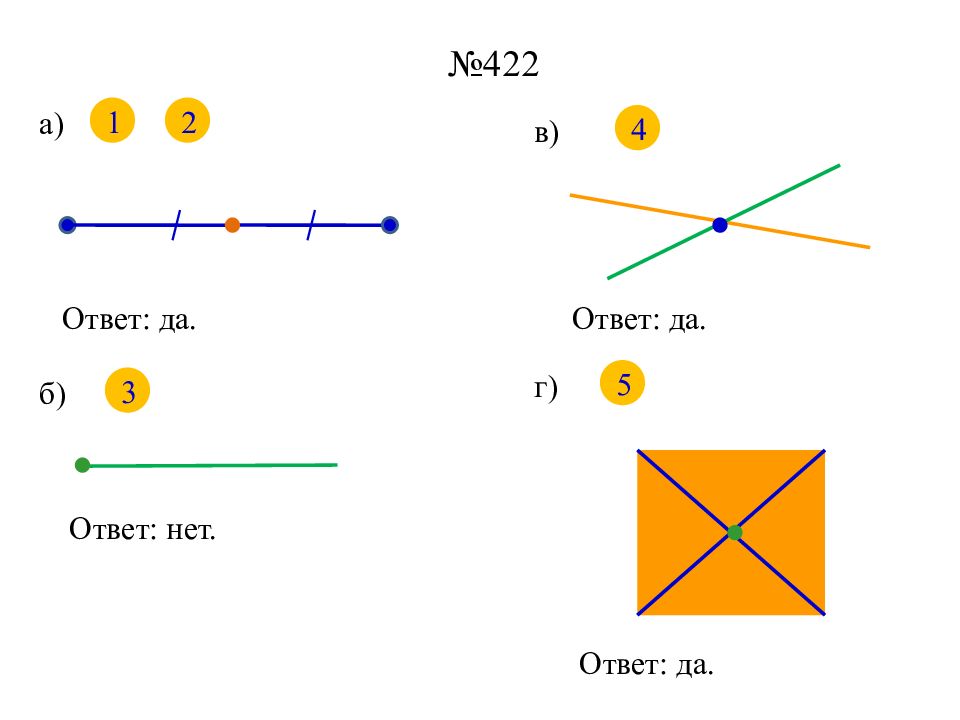
Осевая симметрия Фигура называется симмет-ричной относительно прямой a, если для каждой точки фигуры симметричная ей точка отно-сительно прямой a также при-надлежит этой фигуре. Прямая a называется осью симметрии фигуры. Рассмотрите данные фигуры. Каждая из них состоит как бы из двух полови-нок, одна из ко-торых является зеркальным отра-жением другой. Каждую из этих фигур можно сог-нуть «пополам» так, что эти поло-винки совпадут. Говорят, что эти фигуры симмет-ричны относи-тельно прямой – линии сгиба.
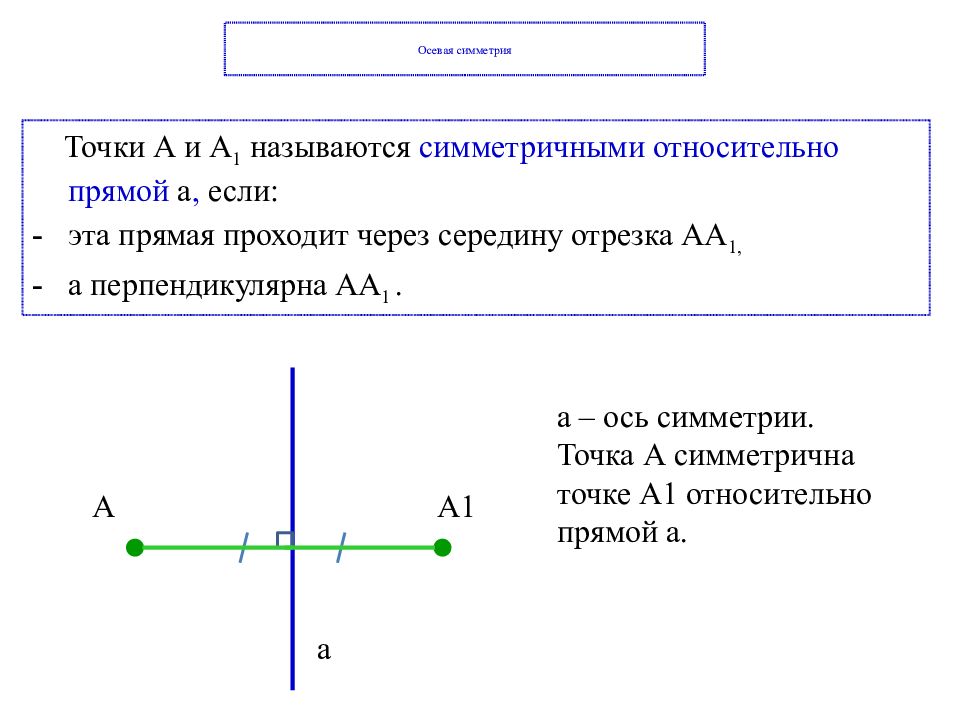
Точки А и А 1 называются симметричными относительно прямой а, если: эта прямая проходит через середину отрезка АА 1, а перпендикулярна АА 1. А А1 а a – ось симметрии. Точка А симметрична точке А1 относительно прямой а.
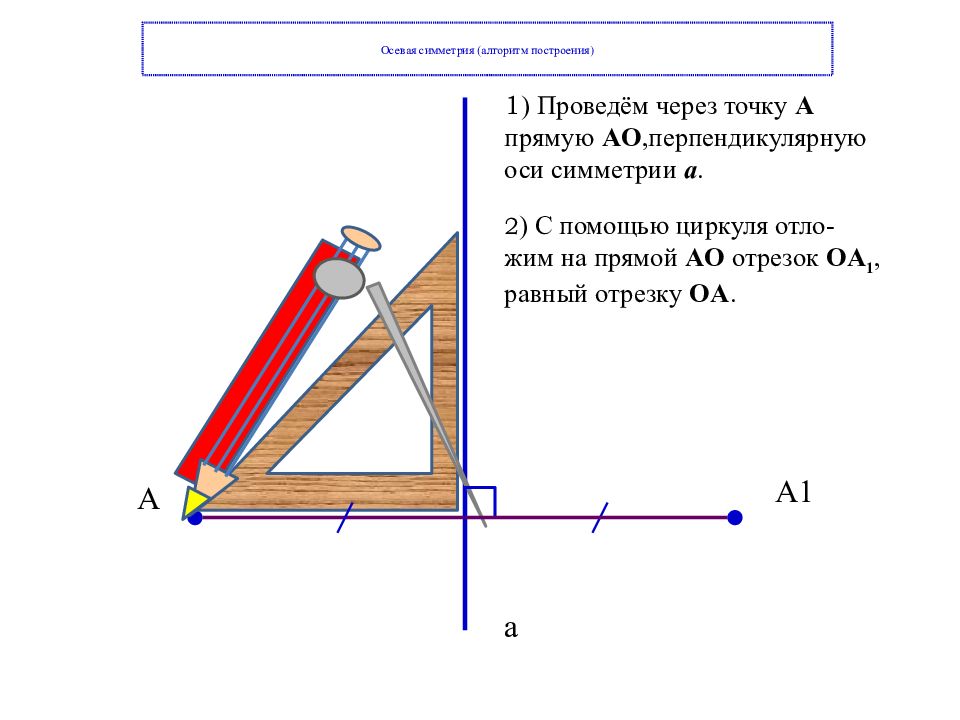
А А1 а 1 ) Проведём через точку А прямую А O,перпендикулярную оси симметрии a. 2 ) С помощью циркуля отло-жим на прямой А O отрезок O А 1, равный отрезку O А.
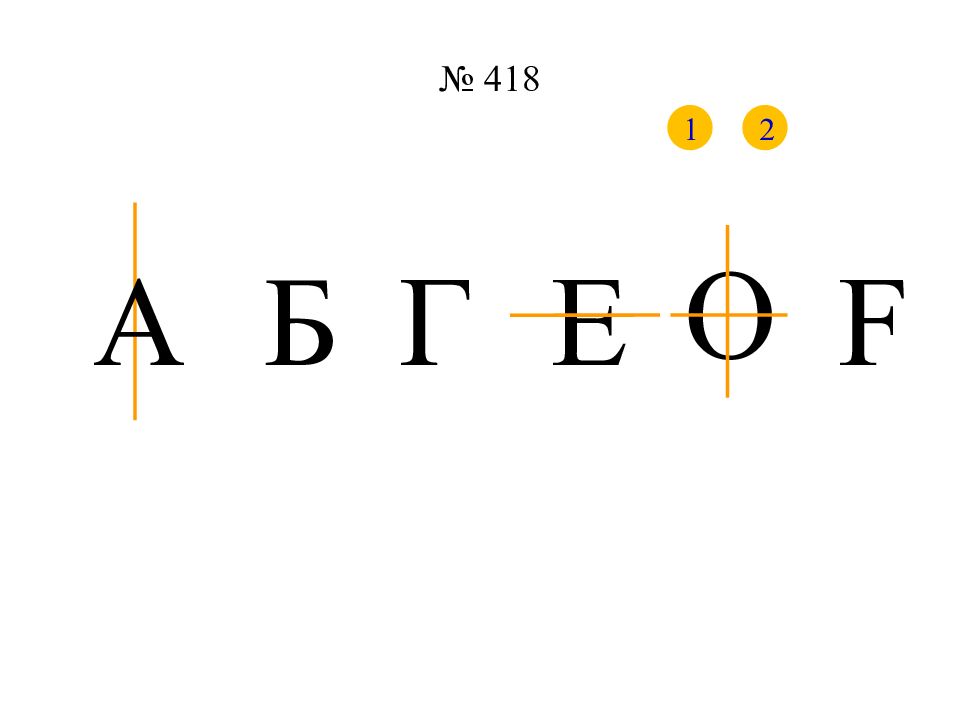
Ось симметрии имеют плоские и пространственные фигуры. Например: Некоторые фигуры имеют не одну ось симметрии. Задание. Из данных фигур выберите те, которые имеют ось симметрии. Есть ли среди них такие, которые имеют более одной оси симметрии? а) б) в) г) На листе бумаги изображена «ёлочка». Концы её нижних «веток» обозначены буквами A и A 1. Если перегнуть «ёлочку» по прямой l, то точки A и A 1 совпадут. Если посмотреть на рисунок сверху, то точки A и A 1 будут расположены на пер-пендикуляре к прямой l по разные стороны и на равных расстояниях от неё. Такие точки называют симмет-ричными относительно пря-мой l.
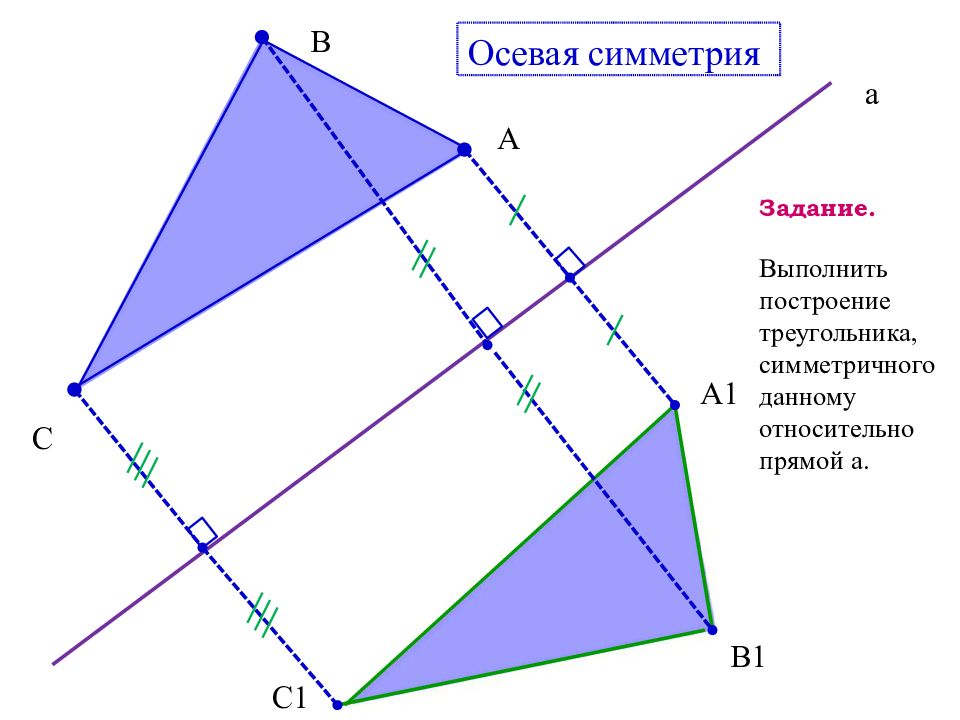
B C А C1 B1 A1 а Осевая симметрия Задание. Выполнить построение треугольника, симметричного данному относительно прямой a.
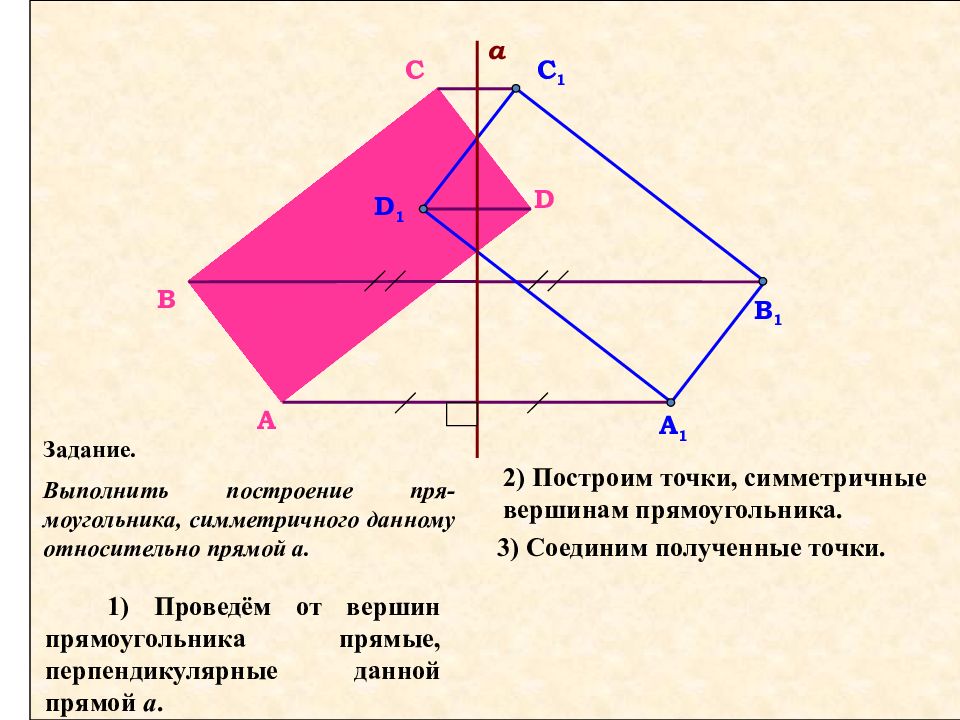
Задание. Выполнить построение пря-моугольника, симметричного данному относительно прямой a. 1) Проведём от вершин прямоугольника прямые, перпендикулярные данной прямой a. B B 1 a A C D A 1 C 1 D 1 2) Построим точки, симметричные вершинам прямоугольника. 3) Соединим полученные точки.
1 2 3 Ответ: две прямые.
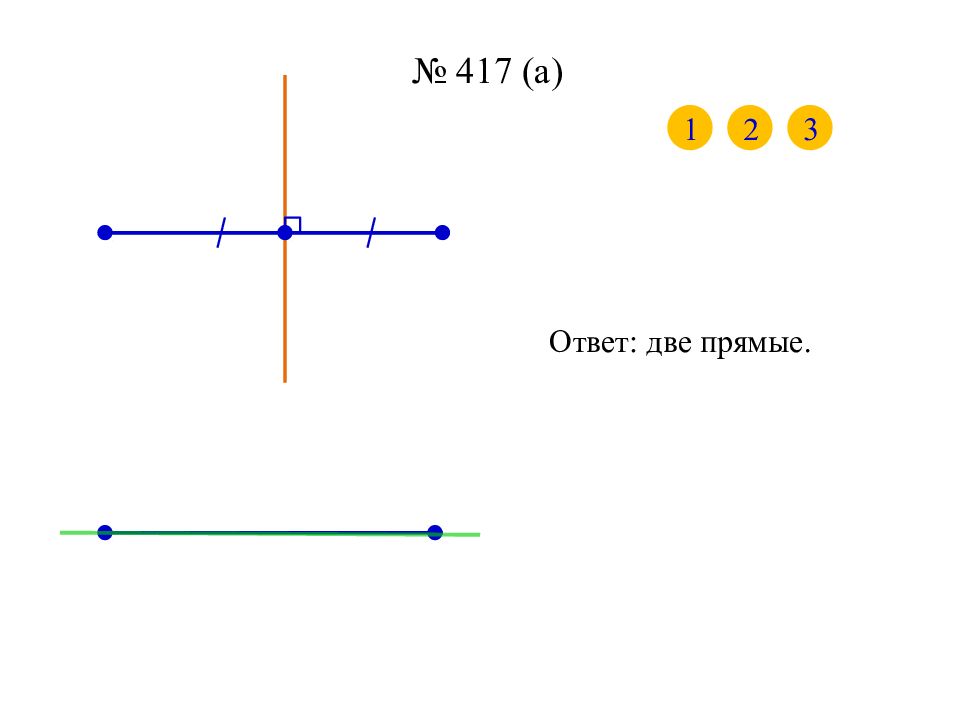
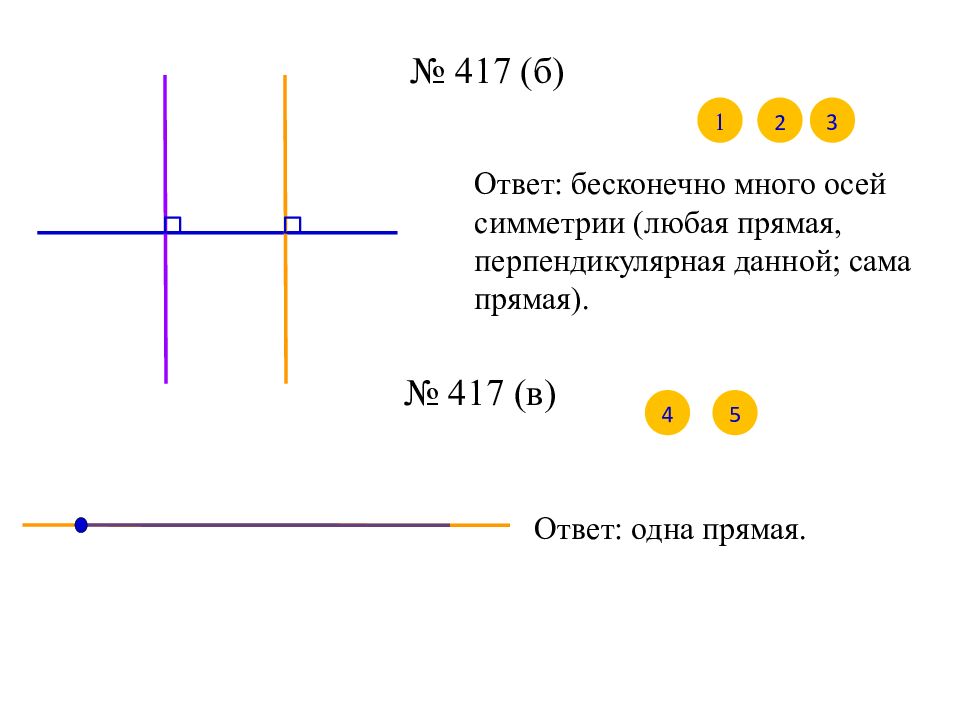
1 2 Ответ: бесконечно много осей симметрии (любая прямая, перпендикулярная данной; сама прямая). № 417 (в) Ответ: одна прямая. 3 4 5
F А Б E Г O 1 2
а) в) б) 1 2 Ответ: да. Ответ: нет. 3 4 Ответ: да. г) 5 Ответ: да.
А О М Х К 1 Ответ: О, Х.
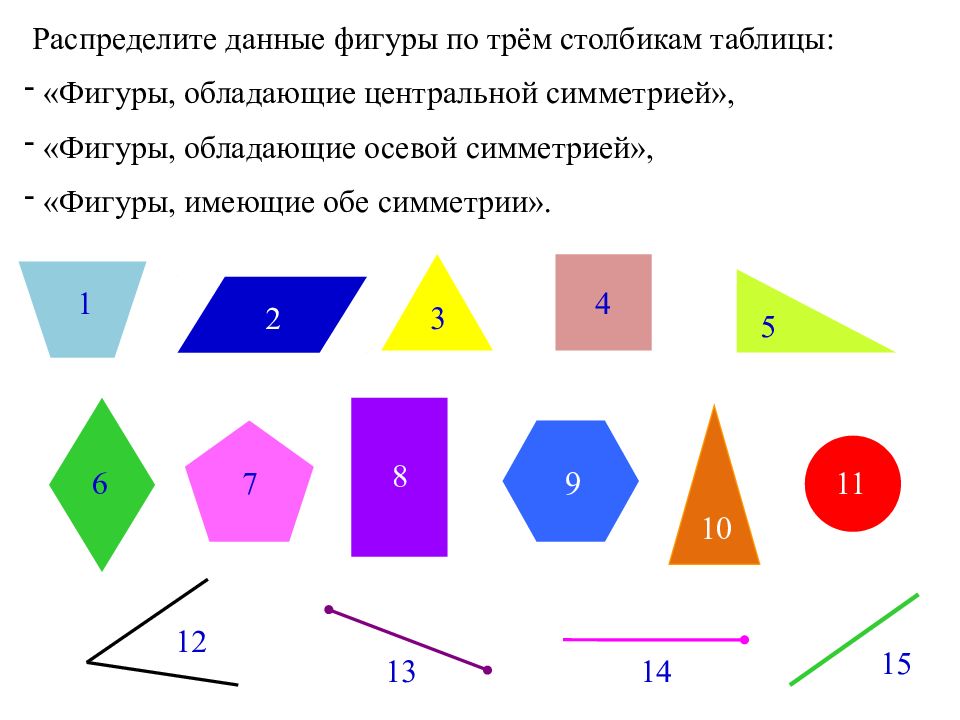
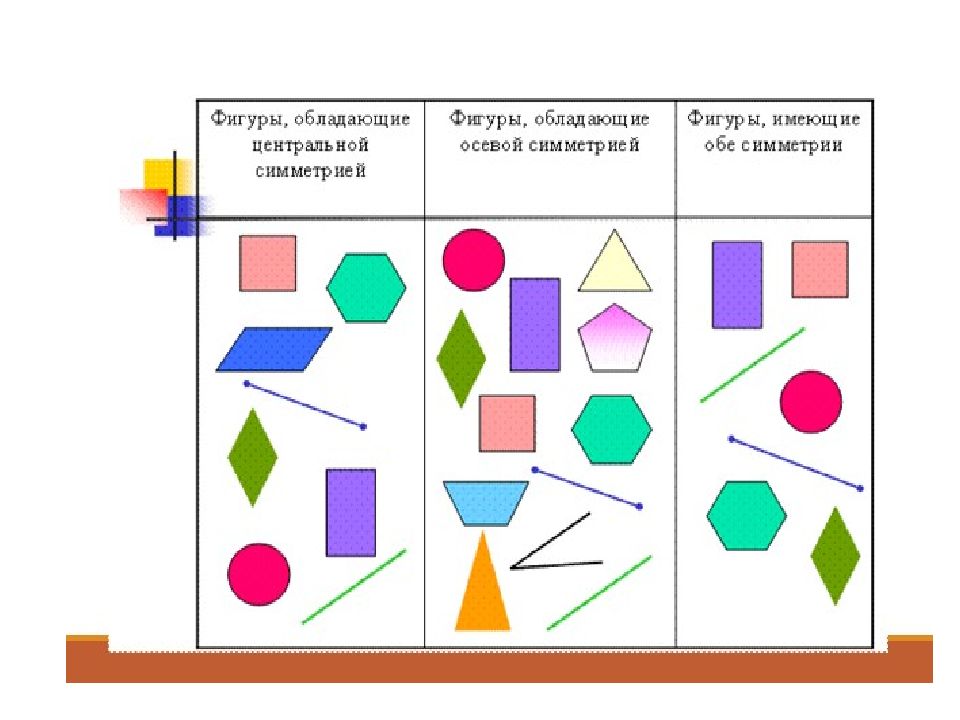
Распределите данные фигуры по трём столбикам таблицы: «Фигуры, обладающие центральной симметрией», «Фигуры, обладающие осевой симметрией», «Фигуры, имеющие обе симметрии». 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
П.46,47,48 №401(б), 405 (а), 421
