Первый слайд презентации: Симметрия в пространстве
Работа Морозовой Алёны 14 группа.
Слайд 2: Что такое симметрия?
Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной в пространстве или на плоскости, заключающееся в закономерном повторении равных её частей
Слайд 3
«Симметрия… есть идея с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». Герман Вейль «Что может быть более похоже на мою руку или моё ухо, чем их собственное отражение в зеркале? И все же руку, которую я вижу в зеркале, нельзя поставить на место постоянной руки…» Иммануил Кант
Слайд 4: Виды симметрии
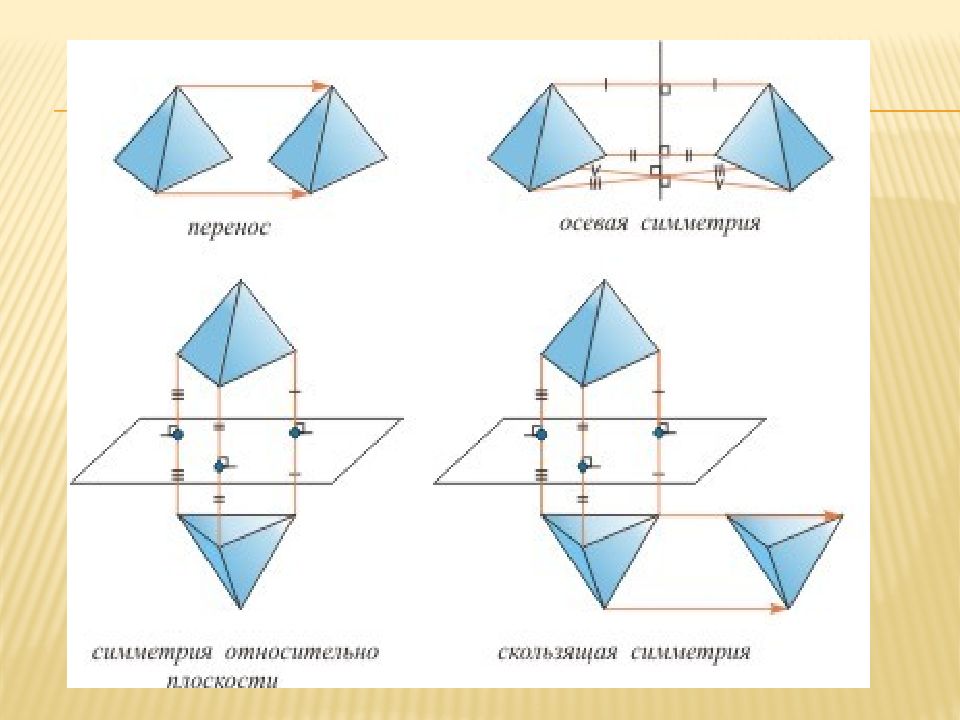
Центральная симметрия Осевая симметрия Зеркальная симметрия Поворот параллельный Перенос Скользящая симметрия Винтовая симметрия
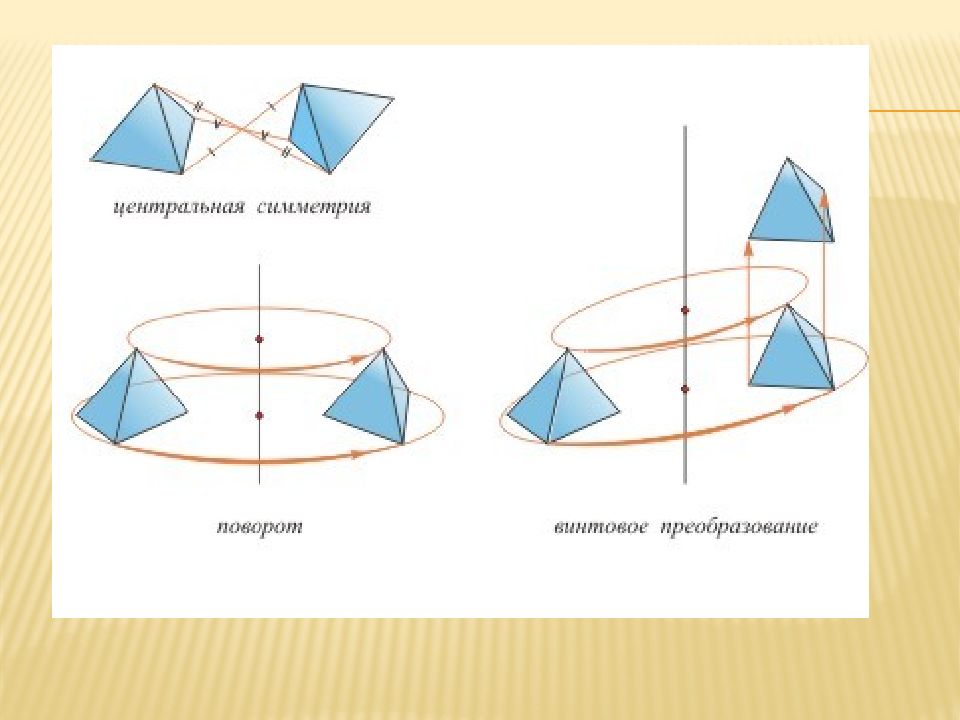
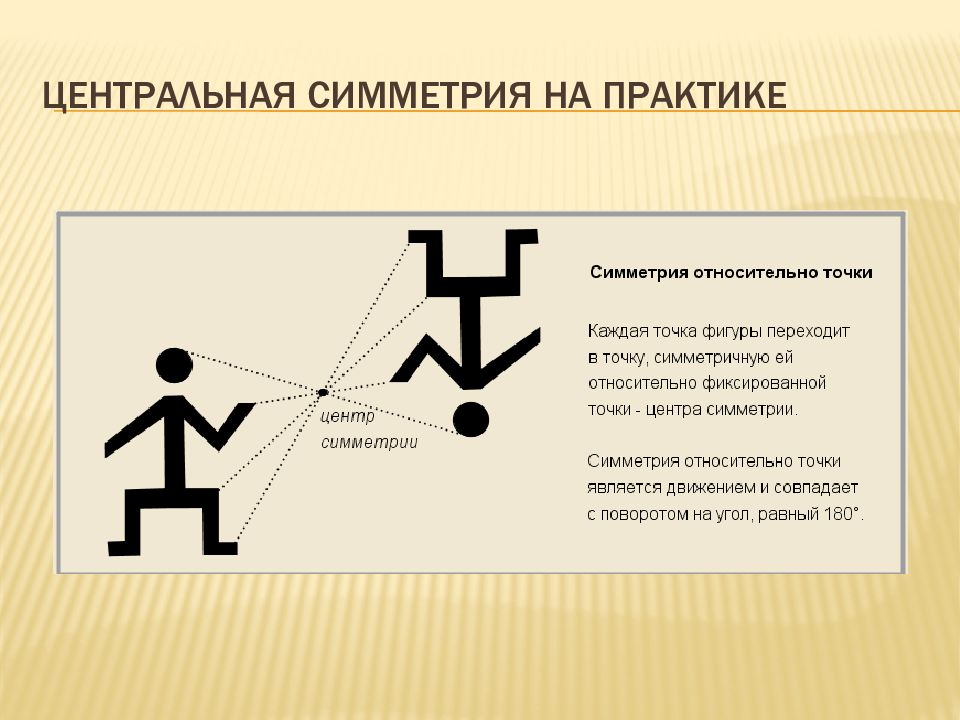
Центральная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно центра О. Точки A и A1 называются симметричными относительно точки О (центр симметрии), если О - середина отрезка АА1. Точка О считается симметричной самой себе.
Слайд 9: Теорема – центральная симметрия является движением
Доказательство : Пусть точки М1 и N1 получены центральной симметрией относительно точки О точек М и N. Тогда треугольники NOM и N1OM1 равны и по первому признаку равенства треугольников( по двум сторонам и углу между ними) и, значит, NM=N1M1.Таким образом, центральная симметрия сохраняет расстояния и, следовательно, является движением.
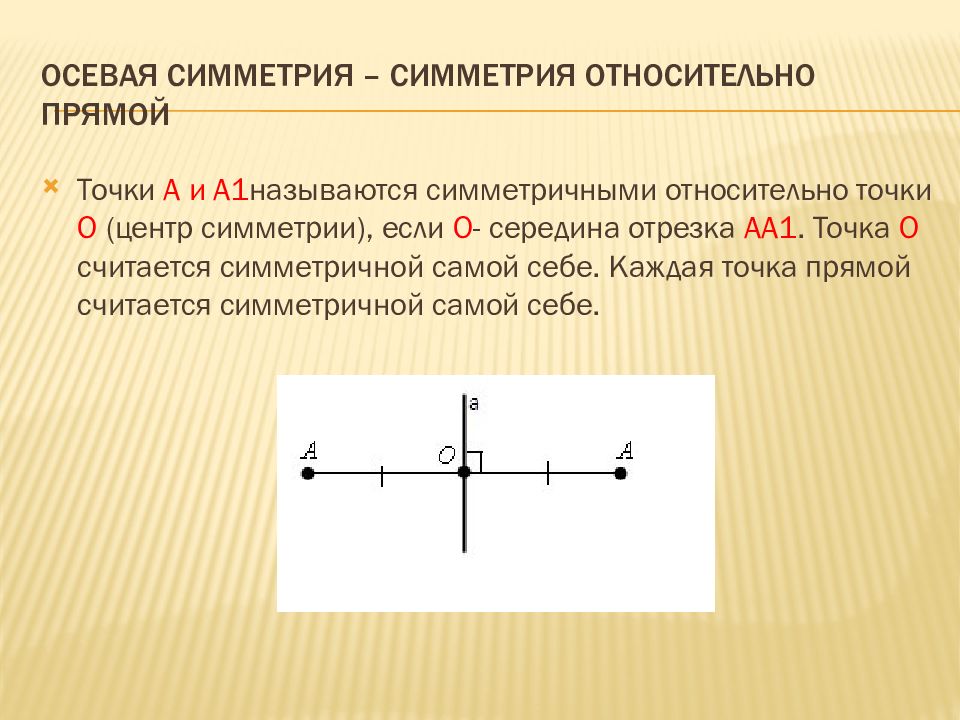
Слайд 10: Осевая симметрия – симметрия относительно прямой
Точки A и A1 называются симметричными относительно точки О (центр симметрии), если О - середина отрезка АА1. Точка О считается симметричной самой себе. Каждая точка прямой считается симметричной самой себе.
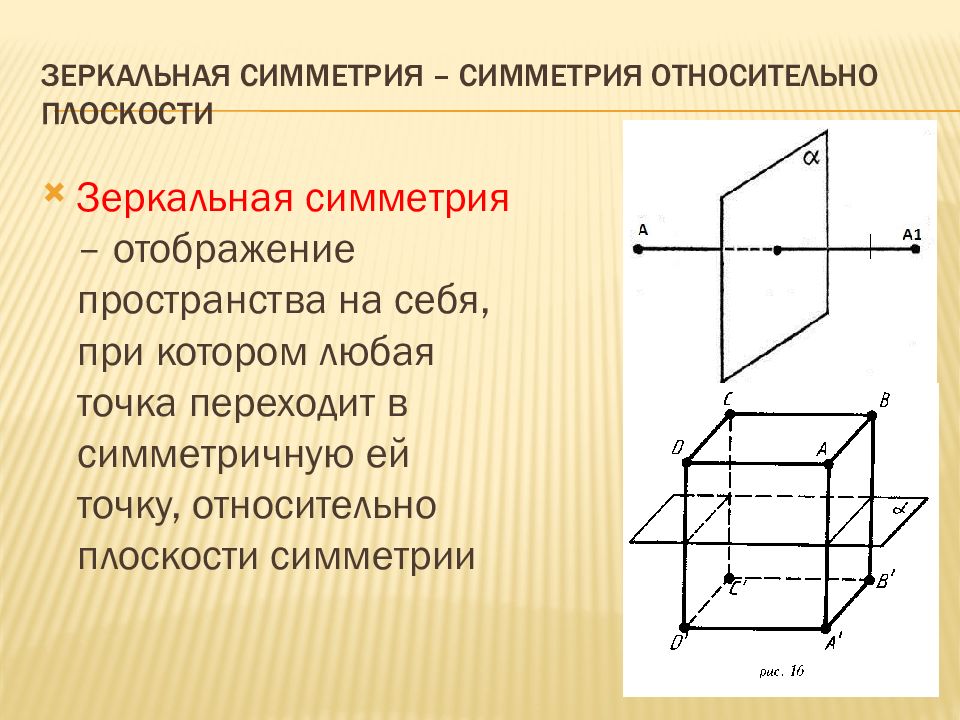
Слайд 12: Зеркальная симметрия – симметрия относительно плоскости
Зеркальная симметрия – отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно плоскости симметрии
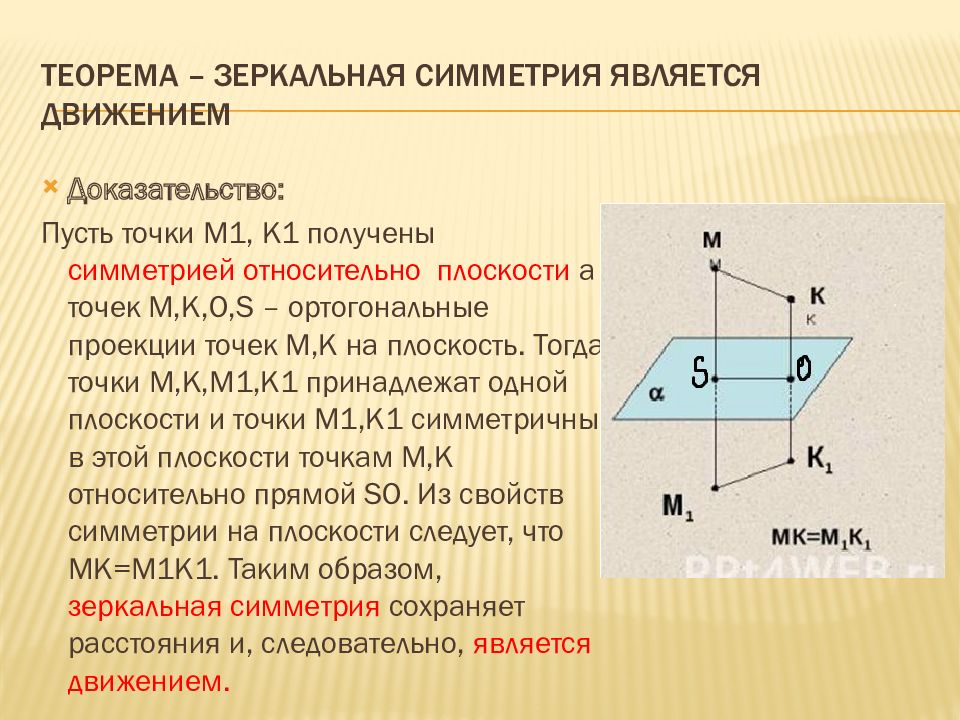
Слайд 13: Теорема – зеркальная симметрия является движением
Доказательство: Пусть точки М1, К1 получены симметрией относительно плоскости a точек M,К,О, S – ортогональные проекции точек M,К на плоскость. Тогда точки М,К,М1,К1 принадлежат одной плоскости и точки М1,К1 симметричны в этой плоскости точкам М,К относительно прямой SO. Из свойств симметрии на плоскости следует, что МК=М1К1. Таким образом, зеркальная симметрия сохраняет расстояния и, следовательно, является движением.
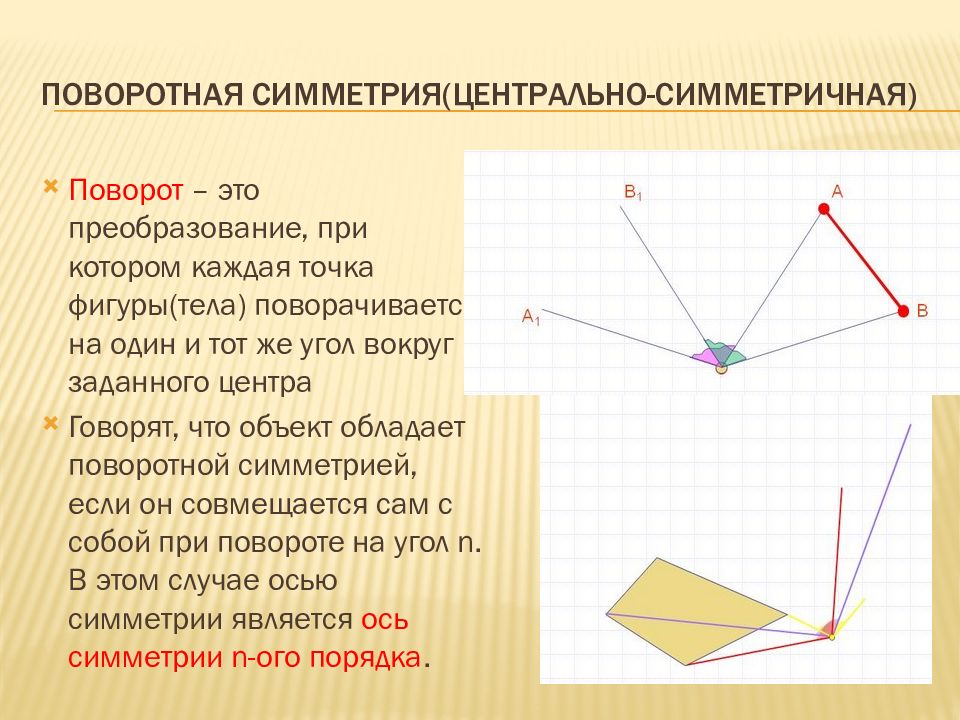
Слайд 14: Поворотная симметрия(центрально-симметричная)
Поворот – это преобразование, при котором каждая точка фигуры(тела) поворачивается на один и тот же угол вокруг заданного центра Говорят, что объект обладает поворотной симметрией, если он совмещается сам с собой при повороте на угол n. В этом случае осью симметрии является ось симметрии n- ого порядка.
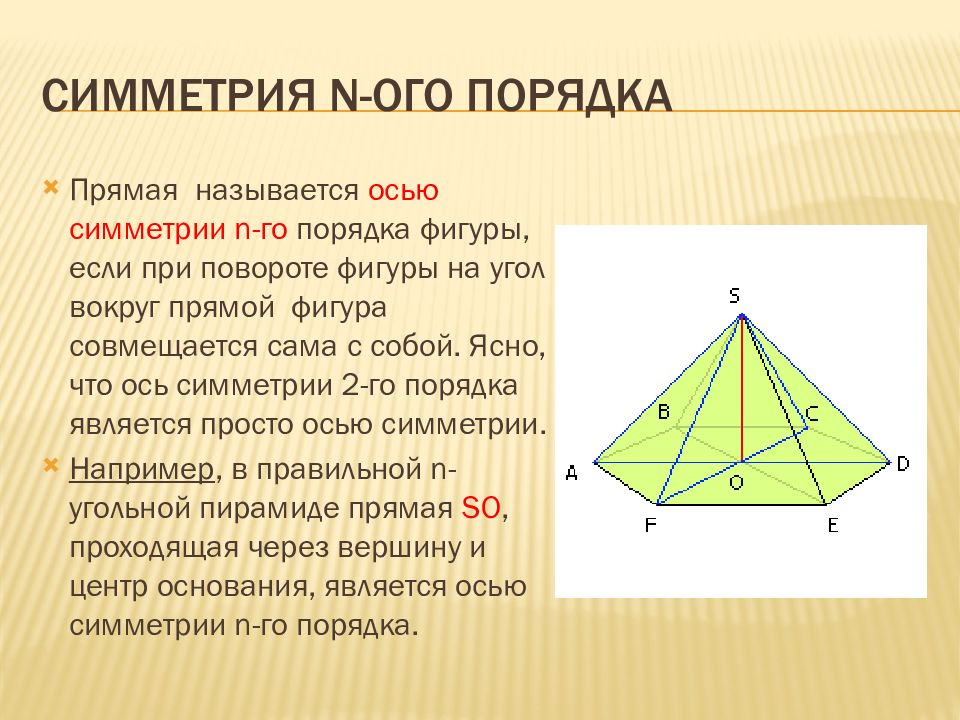
Слайд 15: Симметрия n- ого порядка
Прямая называется осью симметрии n-го порядка фигуры, если при повороте фигуры на угол вокруг прямой фигура совмещается сама с собой. Ясно, что ось симметрии 2-го порядка является просто осью симметрии. Например, в правильной n-угольной пирамиде прямая SO, проходящая через вершину и центр основания, является осью симметрии n-го порядка.
Слайд 16: Параллельный перенос
Параллельный перенос - это преобразование, при котором каждая точка фигуры(тела) перемещается в одном и том же направлении на одно и то же расстояние
Слайд 17: Скользящая симметрия
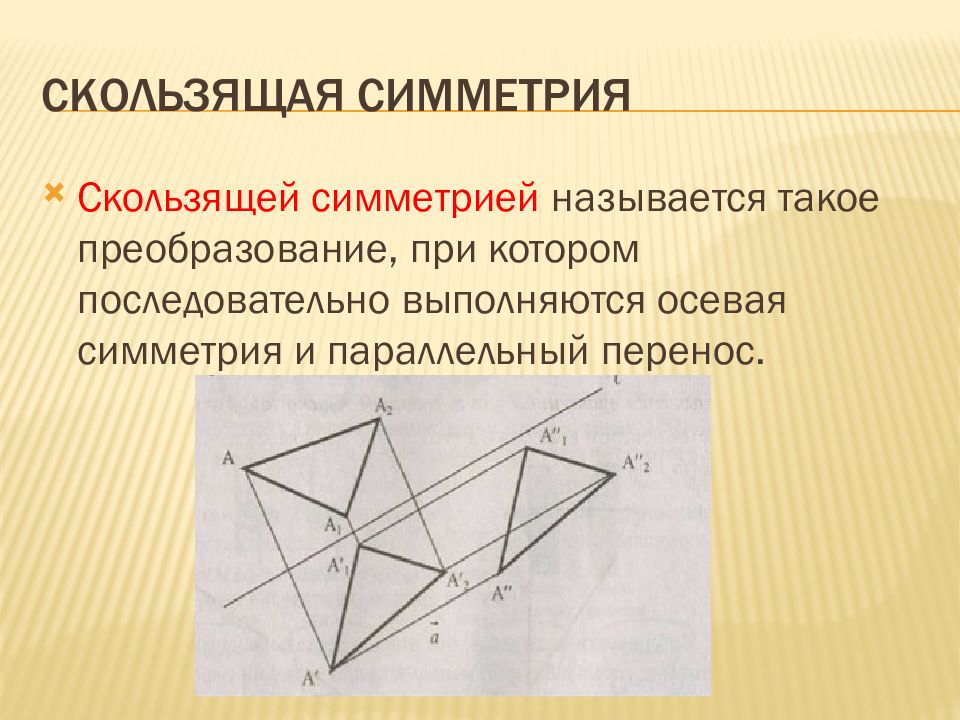
Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.
Слайд 18: Винтовая симметрия
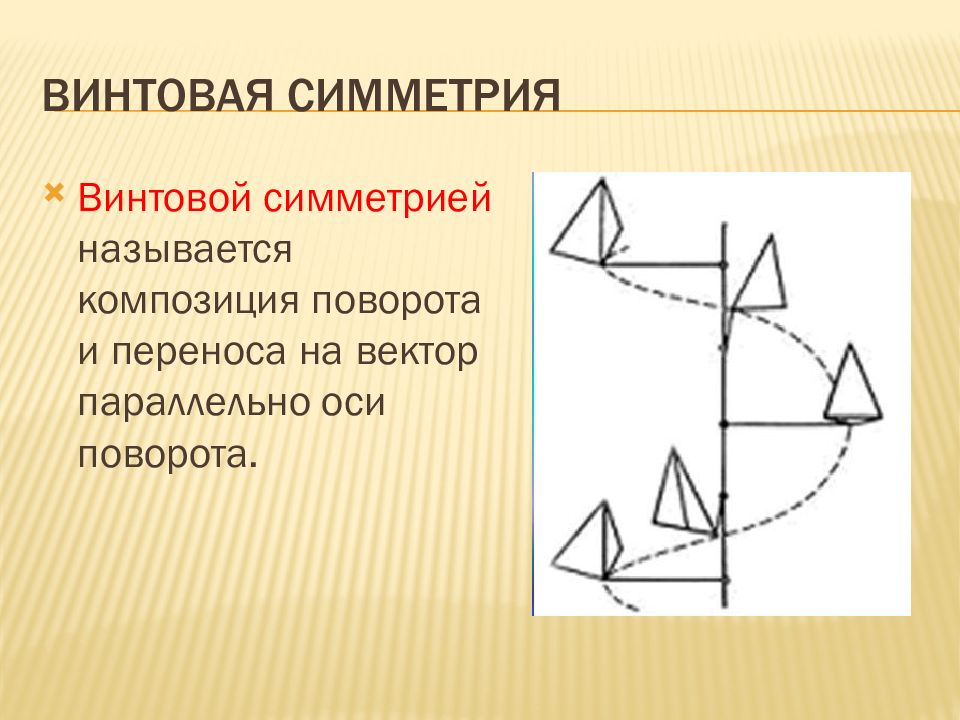
Винтовой симметрией называется композиция поворота и переноса на вектор параллельно оси поворота.
Слайд 19: Симметрия в жизни
«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни есть симметрия?» Л. Толстой «Отрочество»
Слайд 23: Симметрия в алфавите
Буквы русского алфавита тоже можно рассматривать с точки зрения симметрии Вертикальная ось симметрии : А; Д; Л; М; П; Т; Ф; Ш; Ж; Н; О; Х; Горизонтальная ось симметрии : В; Е; З; К; С; Э; Ю; Ж; Н; О; Х;
Слайд 24: Симметрия в литературе
В русском языке есть «симметричные» слова – палиндромы, которые можно читать родинаково в двух направлениях: Шалаш, казак, радар, Алла, Анна, кок, поп. Могут быть палиндромическими и предложения: А роза упала на лапу Азора. Я иду с мечём судия. Г.Р. Державин
Последний слайд презентации: Симметрия в пространстве: Для учащихся 10 и 13 групп
Гогов оценить Ваше творчество по теме главы «Многогранники» ( работа может выполняться индивидуально или группой учащихся(3-5 чел., с указанием ответственных за вид деятельности) В оформлении учитывать: Дизайн. Материал. Оригинальность. ( думаю 3 недели будет достаточно ) Не забывай те и о моделях правильных многогранников!