СИММЕТРИЯ И АСИММЕТРИЯ
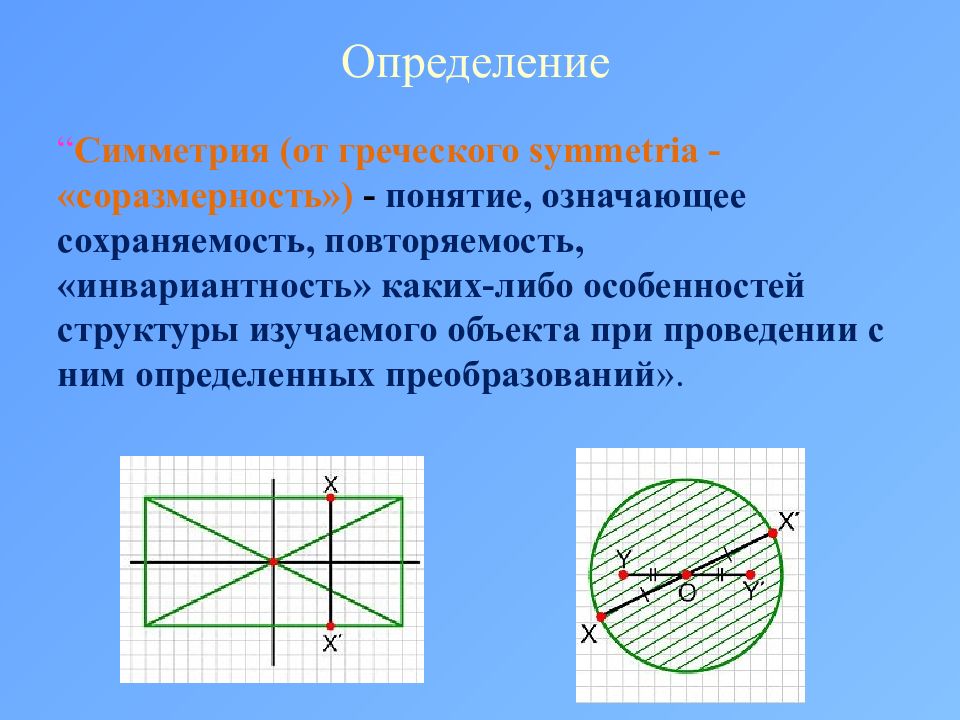
Определение “ Симметрия (от греческого symmetria - «соразмерность») - понятие, означающее сохраняемость, повторяемость, «инвариантность» каких-либо особенностей структуры изучаемого объекта при проведении с ним определенных преобразований ».
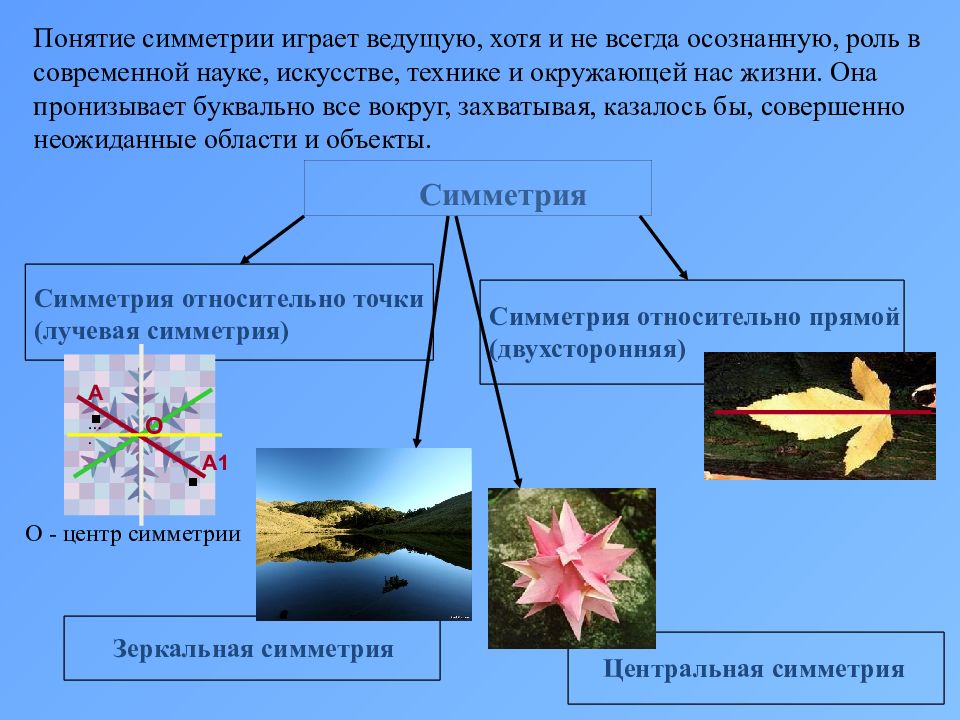
Понятие симметрии играет ведущую, хотя и не всегда осознанную, роль в современной науке, искусстве, технике и окружающей нас жизни. Она пронизывает буквально все вокруг, захватывая, казалось бы, совершенно неожиданные области и объекты. Симметрия относительно точки (лучевая симметрия) Симметрия относительно прямой (двухсторонняя) Центральная симметрия Зеркальная симметрия …. . . А А1 О О - центр симметрии Симметрия
Особое внимание следует заострить на зеркальной симметрии. Такой подход вполне правомерен. Достаточно взглянуть на окружающий нас реальный мир, чтобы убедиться в первостепенном значении именно зеркальной симметрии с соответствующим симметричным элементом — плоскостью симметрии. Комбинируя зеркальные отражения, можно вывести все возможные симметричные операции. Исходя из этих комбинаций, можно полностью вывести все элементы классической симметрии — простые, сложные и винтовые оси, плоскости простого и скользящего отражения, трансляции. Это движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). При отражении объект переходит сам в себя.
ПРИМЕРЫ Отработанные параллельно танцевальные движения
Отражение природных ландшафтов в воде
Отражение архитектурных построек в воде
Отражение непосредственно в зеркале Ладони, ступни; аксессуары для рук и ног
Если при отражении изображение искажено, зеркальная симметрия неполная. В таком случае явление называется просто отражение
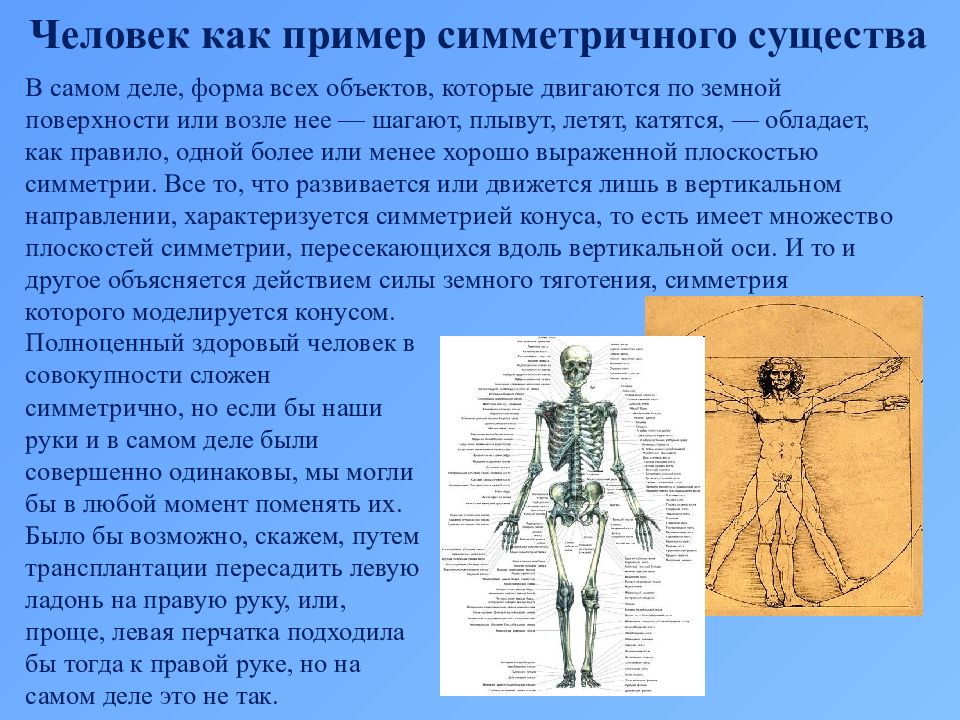
В самом деле, форма всех объектов, которые двигаются по земной поверхности или возле нее — шагают, плывут, летят, катятся, — обладает, как правило, одной более или менее хорошо выраженной плоскостью симметрии. Все то, что развивается или движется лишь в вертикальном направлении, характеризуется симметрией конуса, то есть имеет множество плоскостей симметрии, пересекающихся вдоль вертикальной оси. И то и другое объясняется действием силы земного тяготения, симметрия которого моделируется конусом. Полноценный здоровый человек в совокупности сложен симметрично, но если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Человек как пример симметричного существа
Абсолютно симметричного человека, скорее всего, не существует. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае, у большинства людей. Всем известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Именно вопросам симметрии и зеркального отражения здесь и уделяется внимание. Симметричность человеческого лица допустима и тела, но приме её обнаружить весьма сложно.
Однажды в Америке, обмерили 72 студента-добровольца. Данные подтвердили интуитивно предполагаемый факт: юноши с правильными лицами - те, у кого отклонения от симметрии не превышали 1 - 2 %, были найдены более привлекательными в целом, тогда как менее симметричные студенты - с отклонениями в 5 – 7% - были признаны менее привлекательными, "некрасивыми" в обычном смысле. Интересный факт
Примеры других видов симметрии СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ Точки А и А1 называются симметричными относительно прямой «а», если данная прямая проходит через середину отрезка АА1 и перпендикулярна к нему а А А1 Точки прямой «а» симметричны сами себе «а» - ось симметрии В биологии – двусторонняя симметрия
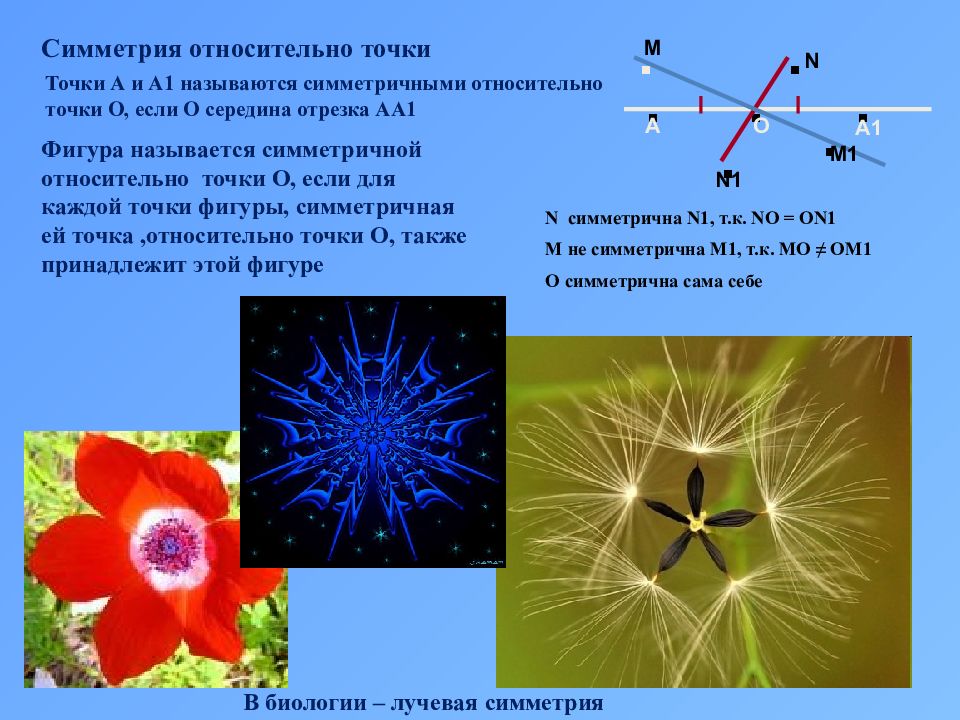
Симметрия относительно точки Точки А и А1 называются симметричными относительно точки О, если О середина отрезка АА1 . . . А О А1 . . М М1 . . N N1 N симметрична N1, т.к. N О = О N1 М не симметрична М1, т.к. МО ≠ ОМ1 О симметрична сама себе Фигура называется симметричной относительно точки О, если для каждой точки фигуры, симметричная ей точка,относительно точки О, также принадлежит этой фигуре В биологии – лучевая симметрия
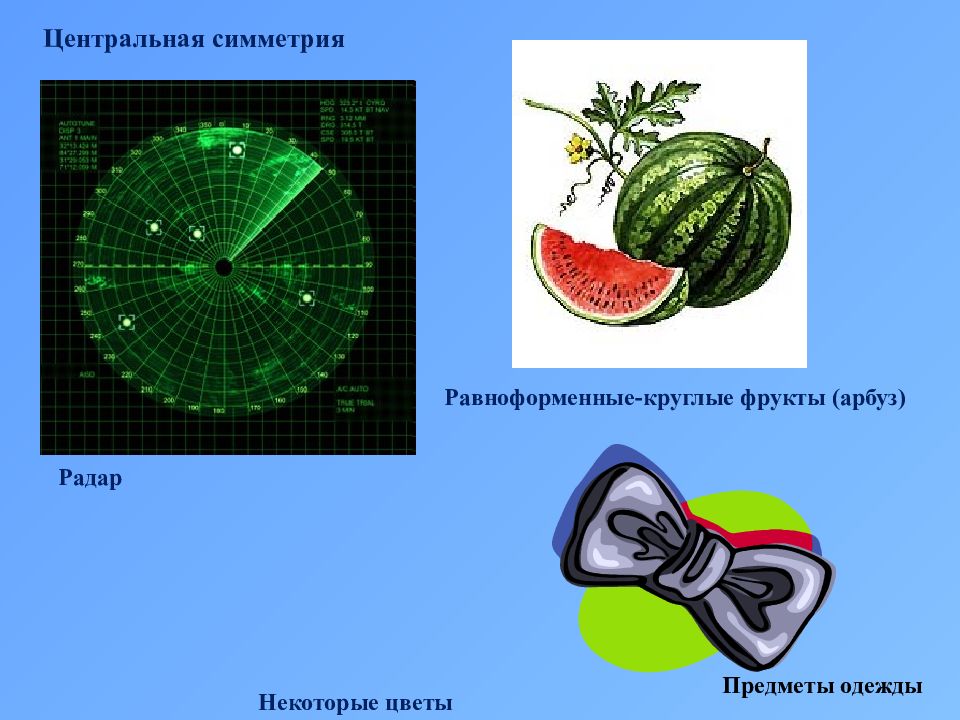
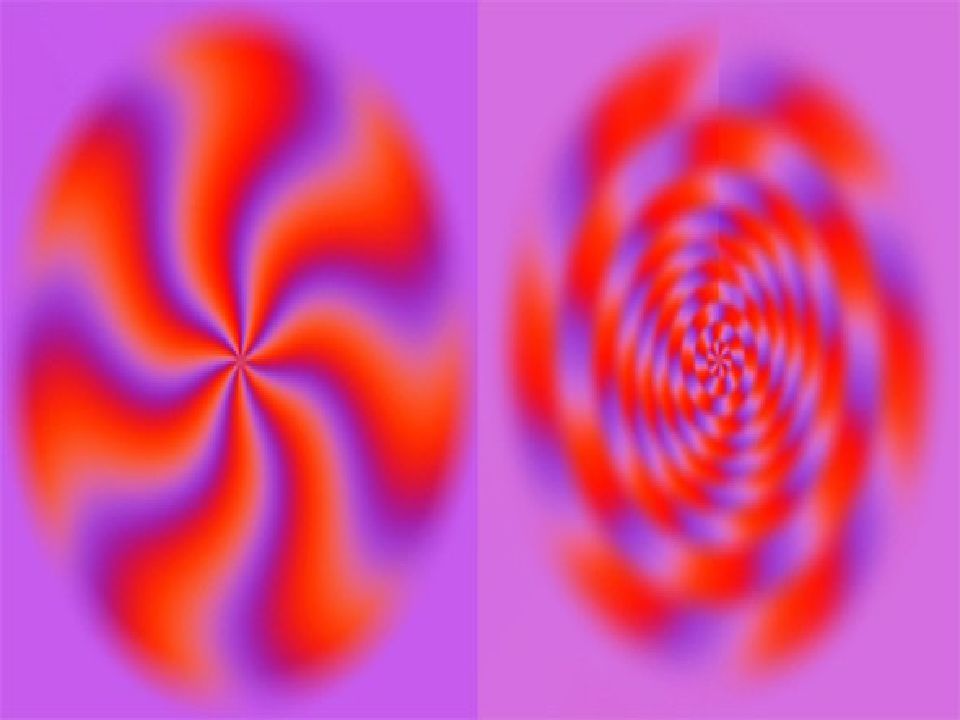
Центральная симметрия Радар Равноформенные-круглые фрукты (арбуз) Некоторые цветы Предметы одежды
Осевая симметрия (самая распространённая и легко определяемая) Мебель, предметы быта Положение в пространстве
Симметрия у животных
Симметрия у растений
Все фракталы симметричны
Симметрия в архитектуре
В одежде
Асимметрия в одежде
Симметрия подобия Связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки.
Подобие в технике, электронике Стереосистемы, колонки
Симметрия в поэзии-кольцевая рифма В гранит оделася Не ва, Мос ты повисли над вод ами ;_______________ Тёмно-зелёными сад ами Её покрылись остро ва … А. С. Пушкин «Медный всадник »
На первый взгляд, формулировка симметрии пространства довольно проста, однако, в сочетании с современными теориями физики, химии и других естественных наук, а также новыми открытиями (например, нейтрино) в этих областях становится всё более запутанной. Но несомненно одно: мир симметричен. В нём найдены, в принципе, зеркальное соответствие каждому изображению. ЗАКЛЮЧЕНИЕ
«Симметрия-устанавливает забавное и удивительное родство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой физикой, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности...". Дж. Ньюмен,
Обманчивая симметрия… Мона Лиза
Д/З: Найдите самостоятельно и запишите в тетради понятие «асимметрия» Творческая работа: создать симметричную композицию
