Первый слайд презентации: Относительные величины и их графическое изображение
1 Относительные величины и их графическое изображение
Слайд 2
2 В повседневной практической деятельности врач, как правило, получает любую информацию в абсолютных числах. Абсолютные величины несут важную информацию о размере того или иного явления и могут быть использованы в анализе, в том числе в сравнительном. Однако они часто не отвечают на все поставленные вопросы. Так, например, врачу интересны сведения о здоровье обслуживаемого населения (показатели заболеваемости и др.), а у него есть информация только о числе зарегистрированных заболеваний (абсолютные числа), которые «заболеваемость» не характеризуют.
Слайд 3
3 Для более углубленного анализа общественного здоровья и деятельности учреждений здравоохранения, а также деятельности медицинского работника используются обобщающие показатели, называемые относительными величинами. Они применяются для изучения совокупности, которая характеризуется, главным образом, альтернативным распределением качественных признаков
Слайд 4
4 Относительные величины (статистические коэффициенты) широко используются в официальной статистике для оценки медико-демографической и санитарно-эпидемиологической ситуации, оценки деятельности медицинских организаций и т.д. Вычисление и анализ этих коэффициентов является основой медицинских исследований, проводимых на уровне больших групп населения, населенных пунктов, городских и сельских районов, областей.
Слайд 5
5 Относительной статистической величиной в наиболее общем виде называется отношение двух чисел, выражающих меру каких-либо явлений. Смысл получения относительных величин – нахождение общей меры, приведение к общему знаменателю.
Слайд 6
6 Среди относительных величин наибольшее значение имеют: экстенсивные, интенсивные показатели, показатели соотношения и наглядности.
Слайд 8
8 Экстенсивные показатели отражают структуру, распределение. Они характеризуют отношение части статистической совокупности к целой совокупности (долю, удельный вес, часть от целого), т.е. отношение отдельного элемента к итогу. Выражаются только в процентах к итогу.
Слайд 9
9 Для расчета его необходимо иметь данные о численности всей совокупности и составляющих ее частях (или отдельной части этой совокупности). Рассчитывается обычно в процентах, где совокупность в целом принимается за 100%, а отдельные части – за «х». Способ получения экстенсивной величины выглядит сл. образом:
Слайд 10
10 Таким образом, для получения экстенсивного показателя нужна одна совокупность и ее составные части или отдельная часть. Экстенсивный показатель отвечает на вопрос, сколько процентов приходится на каждую конкретную часть совокупности.
11 В зависимости от того, что характеризуют экстенсивные показатели, их называют: Показатели удельного веса части в целом, например, удельный вес гриппа среди всех заболеваний; Показатели распределения или структуры (распределение всей совокупности зарегистрированных врачом заболеваний за год на отдельные заболевания).
Слайд 12
12 Экстенсивный показатель - показатель статики, т.е. с его помощью можно анализировать конкретную совокупность в конкретный момент. По экстенсивным показателям нельзя сравнивать различные совокупности – это приводит к неправильным, ошибочным выводам
Слайд 13: Пример расчета экстенсивного показателя
13 Пример расчета экстенсивного показателя В районе А в текущем году было зарегистрировано 500 случаев инфекционных заболеваний, из них: Эпидемического гепатита – 60 случаев; Кори – 100 случаев; Прочих инф-х заболеваний – 340 случаев. Задание: определить структуру инфекционных заболеваний, проанализировать и представить графически.
Слайд 14
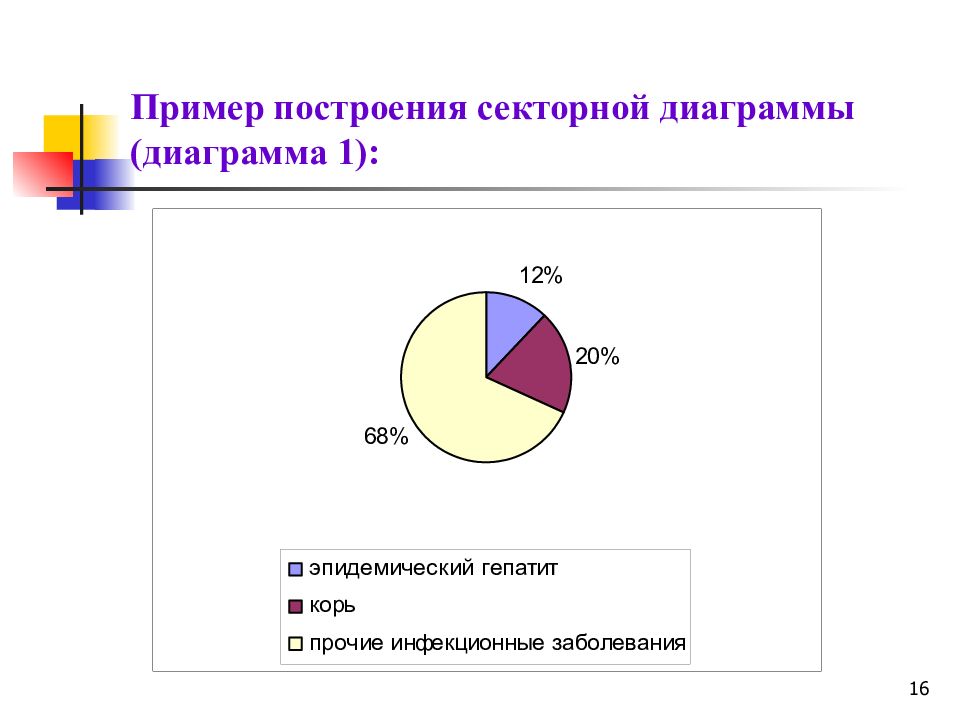
14 Решение: Вся совокупность – 500 случаев инф. заболеваний принимается за 100 %, составные части определяются как искомые. Удельный вес случаев эпидемического гепатита составит: Аналогично рассчитывается удельный вес других заболеваний. Вывод: в структуре инфекционных заболеваний доля эпидемического гепатита составила 12%, кори – 20%, прочих инфекционных заболеваний – 68%.
Слайд 15: Способы графического изображения экстенсивного показателя
15 Способы графического изображения экстенсивного показателя Поскольку экстенсивный показатель – показатель статики, то графически он изображается в виде столбиковой диаграммы или секторной (круговой) диаграмм, которые являются разновидностями плоскостных диаграмм.
Слайд 16: Пример построения секторной диаграммы (диаграмма 1):
16 Пример построения секторной диаграммы (диаграмма 1):
Слайд 17: Пример построения столбиковой диаграммы (диаграмма 2)
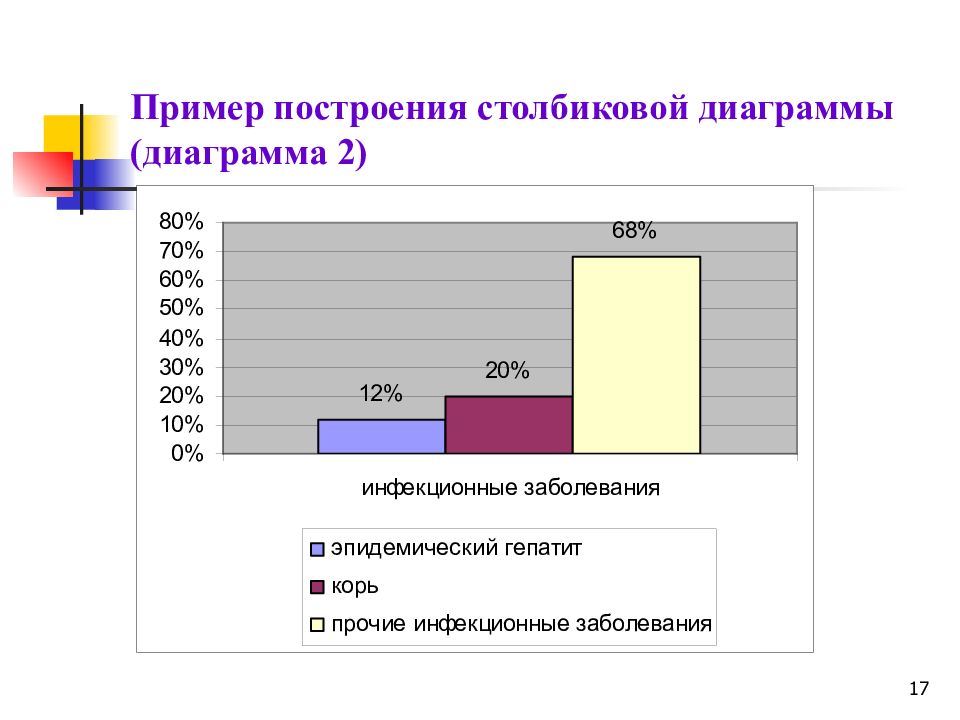
17 Пример построения столбиковой диаграммы (диаграмма 2)
Слайд 18: Удельный вес (доля) случаев эпидемического гепатита среди всех инфекционных заболеваний (в % к итогу) (диаграмма 3)
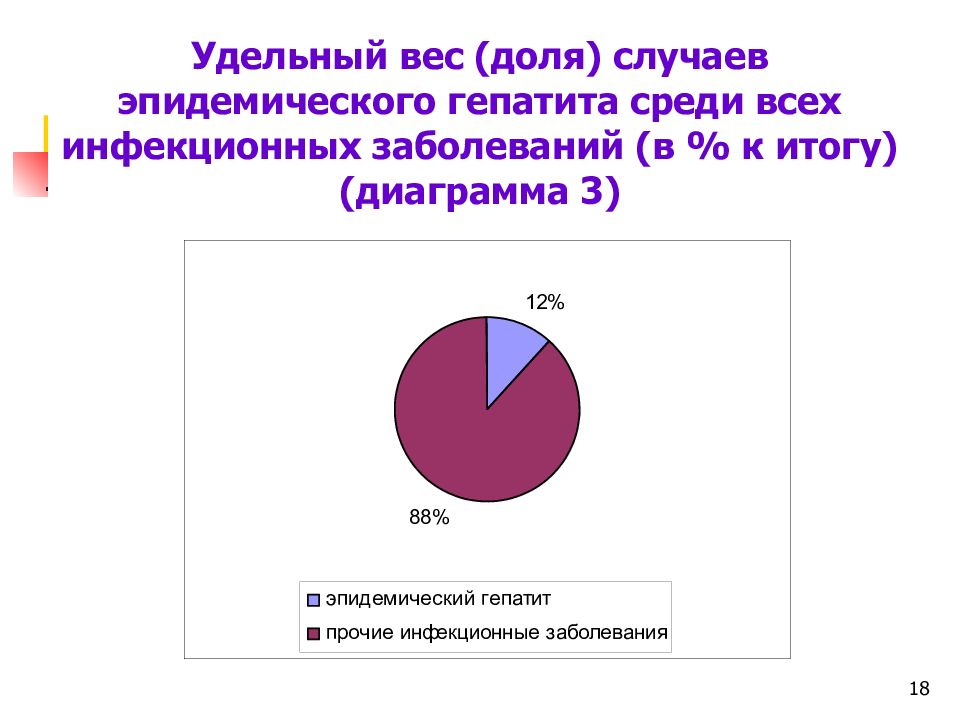
18 Удельный вес (доля) случаев эпидемического гепатита среди всех инфекционных заболеваний (в % к итогу) (диаграмма 3)
Слайд 20
20 Интенсивный показатель – показатель частоты, уровня, распространенности процессов, явлений, совершающихся в определенной среде, которая его продуцирует (заболеваемость, смертность, рождаемость и т.д.).
Слайд 21
21 Интенсивные показатели используются как для сравнения, сопоставления динамики частоты изучаемого явления во времени, так и для сравнения, сопоставления частоты этого же явления в один и тот же промежуток времени, но в различных учреждениях, на различных территориях и т.д.
Слайд 22
22 Для расчета интенсивного показателя необходимо иметь данные об абсолютном размере явления и среды. Абсолютное число, характеризующее размер явления, делится на абсолютное число, показывающее размер среды, внутри которой произошло данное явление, и умножается на 100, 1000 и т.д.
Слайд 23
23 Таким образом, способ получения интенсивного показателя выглядит следующим образом:
Слайд 24
24 Таким образом, для расчета интенсивного показателя всегда нужны две статистические совокупности (совокупность №1 – явление, совокупность №2 - среда ), причем изменение размера среды может повлечь за собой изменение размера явления.
Слайд 25
25 Множитель (основание) зависит от распространенности явления в среде – чем реже оно встречается, тем больше множитель. В практике для вычисления некоторых интенсивных показателей множители (основания) являются общепринятыми (так, например, показатели заболеваемости с временной утратой трудоспособности рассчитываются на 100 работающих или учащихся, показатели летальности, частоты осложнений и рецидивов заболеваний – на 100 больных, демографические показатели и многие показатели заболеваемости – на 1000 населения).
Слайд 26: Пример расчета интенсивного показателя
26 Пример расчета интенсивного показателя В городе проживает 120 000 человек (среда). В предыдущем году родилось 1080 детей (явление). Определить показатель рождаемости (рассчитывается на 1000 нас.)
Слайд 27
27 Таким образом, рождаемость в городе составила 9%. Графически интенсивные показатели могут быть представлены в виде любых из названных ниже диаграмм при наличии необходимой информации: а) линейной диаграммы (график); б) столбиковой или ленточной диаграммы; в) радиальной диаграммы; г) картограммы; д) картодиаграммы.
Слайд 28
28 Интенсивный показатель может быть также представлен в виде картограммы и картодиаграммы. Картограмма – изображение статистических данных на контурной карте. При этом частота изучаемого явления может быть обозначена разной интенсивностью окраски или разной штриховкой. Картодиаграмма – изображение на контурной карте статистических данных в виде столбиков или других символов различного размера.
Слайд 30
30 Показатель соотношения : характеризует соотношение между двумя не связанными между собой совокупностями (обеспеченность населения койками, врачами, дошкольными учреждениями, соотношение родов и абортов, соотношение врачей и медицинских сестер и др.).
Слайд 31
31 Для получения этого показателя нужны две совокупности (№1 и №2). Абсолютная величина, характеризующая одну совокупность ( совокупность №1 ), делится на абсолютную величину, характеризующую другую, с ней не связанную совокупность ( совокупность №2 ) и умножается на множитель (100, 1000, 10 000 и т.д.)
Слайд 32: Пример расчета показателя соотношения
32 Пример расчета показателя соотношения В городе 120 000 населения, общее число терапевтических коек – 300. Число коек – совокупность №1, численность населения – совокупность №2. Требуется рассчитать обеспеченность населения терапевтическими койками.
Слайд 33: Вывод:
33 Вывод: На 10 000 населения в городе приходится 25 терапевтических коек, или обеспеченность населения города терапевтическими койками равна 25 коек на 10 000 населения.
Слайд 35
35 Показатель наглядности применяется для анализа однородных чисел и используется, когда необходимо «уйти» от показа истинных величин (абсолютных чисел, относительных и средних величин). Как правило, эти величины представлены в динамике.
Слайд 36
36 Для вычисления показателей наглядности одна из сравниваемых величин принимается за 100 % (обычно это исходная величина), а остальные рассчитываются в процентном отношении к ней. Особенно их целесообразно использовать, когда исследователь проводит сравнительный анализ одних и тех же показателей, но в разное время или на разных территориях.
Слайд 37: Пример расчета показателя наглядности
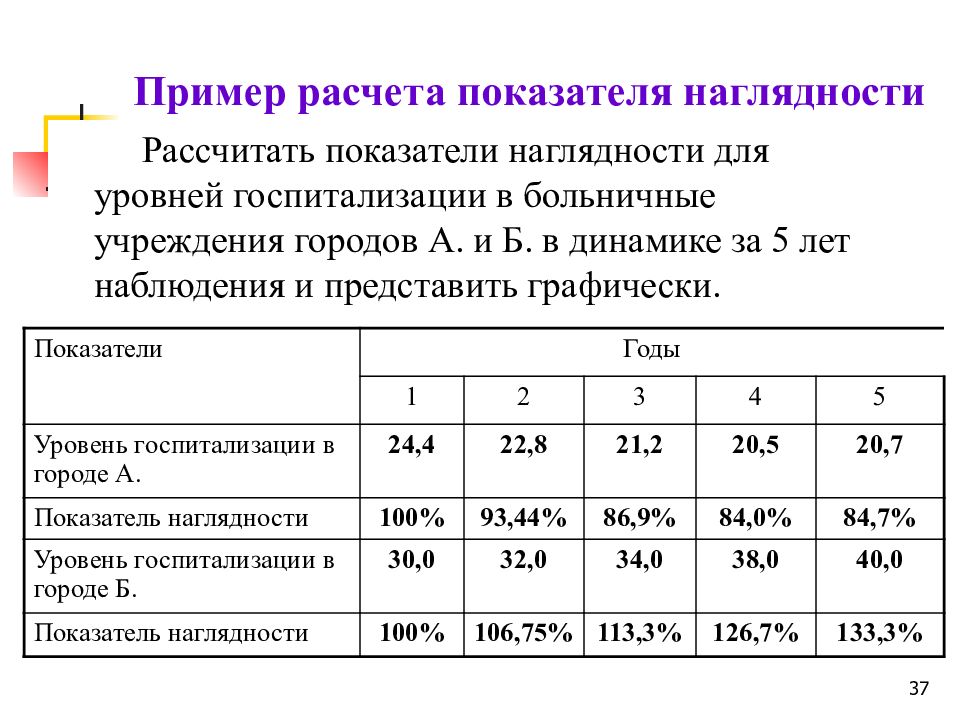
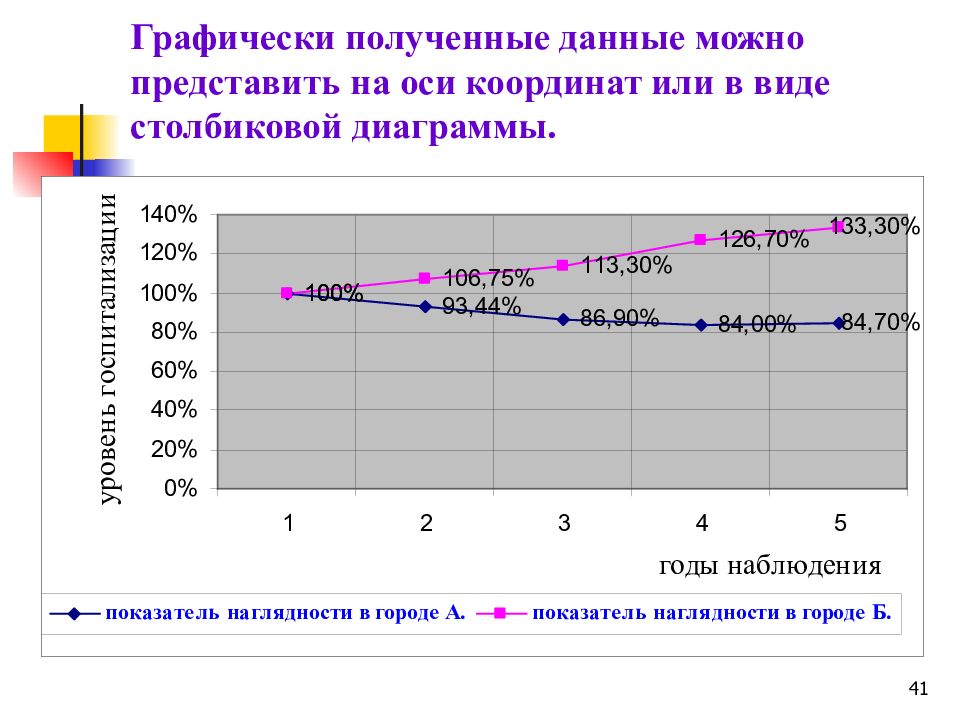
37 Пример расчета показателя наглядности Рассчитать показатели наглядности для уровней госпитализации в больничные учреждения городов А. и Б. в динамике за 5 лет наблюдения и представить графически. Показатели Годы 1 2 3 4 5 Уровень госпитализации в городе А. 24,4 22,8 21,2 20,5 20,7 Показатель наглядности 100% 93,44% 86,9% 84,0% 84,7% Уровень госпитализации в городе Б. 30,0 32,0 34,0 38,0 40,0 Показатель наглядности 100% 106,75% 113,3% 126,7% 133,3%
Слайд 38: Решение:
38 Решение: Снижение больны, поступивших в стационары, будет нагляднее, если приравнять показатель исходного уровня госпитализации в городе А. (1 год – 24,4) к 100%, а остальные показатели пересчитать в процентах по отношению к нему. 24,4 – 100% 22,8 – Х Х=(22,8х100)/24,4=93,44% (показатель наглядности для 2-го года)
Слайд 39
39 24,4 – 100% 21,2 – Х Х=(21,2х100)/24,4=86,9% (показатель 3-го года) 34,4 – 100% 20,5 – Х Х=(20,5х100)/24,4=84% (показатель наглядности для 4-го года) 24,4 – 100% 20,7 – Х Х=(20,7х100)/24,4=84,8% (показатель наглядности для 5-го года)
Слайд 40
40 Аналогично рассчитываются показатели наглядности, характеризующие уровень госпитализации в больничные учреждения города В. Вывод: в динамике за 5 лет наблюдения уровень госпитализации больных в городе А. снижается, а в городе В повышается.