Слайд 2
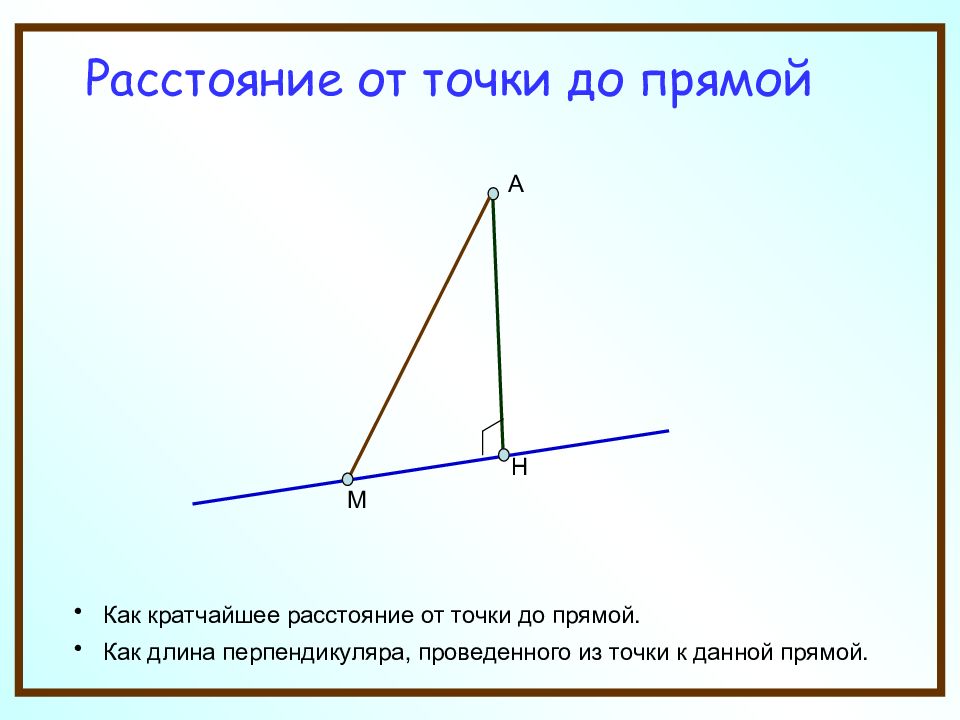
Расстояние от точки до прямой Как кратчайшее расстояние от точки до прямой. Как длина перпендикуляра, проведенного из точки к данной прямой. А М Н
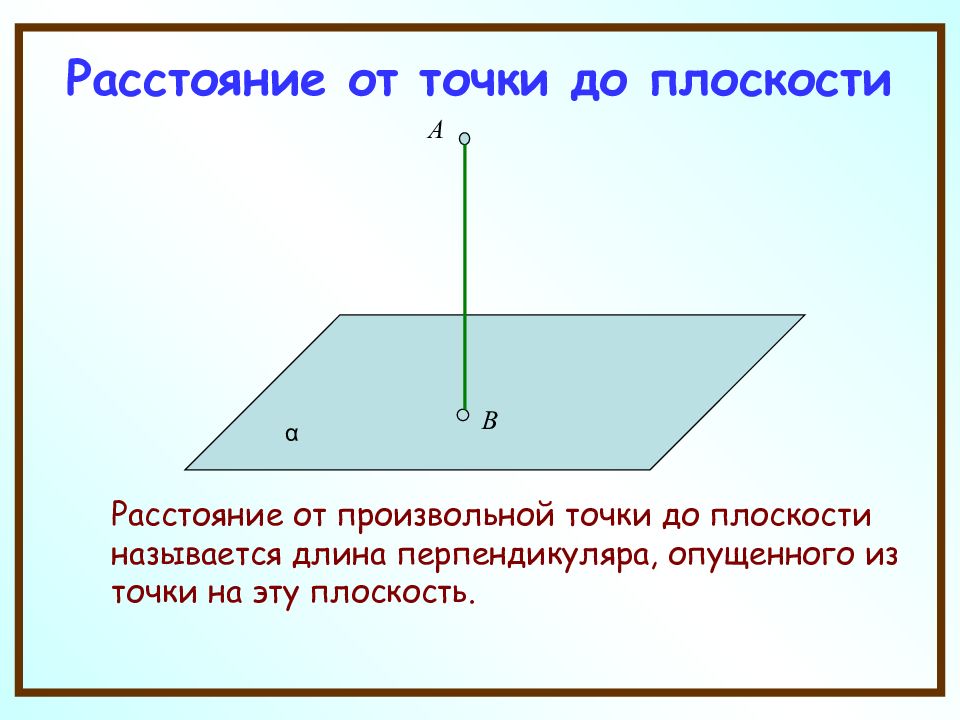
Слайд 3: Расстояние от точки до плоскости
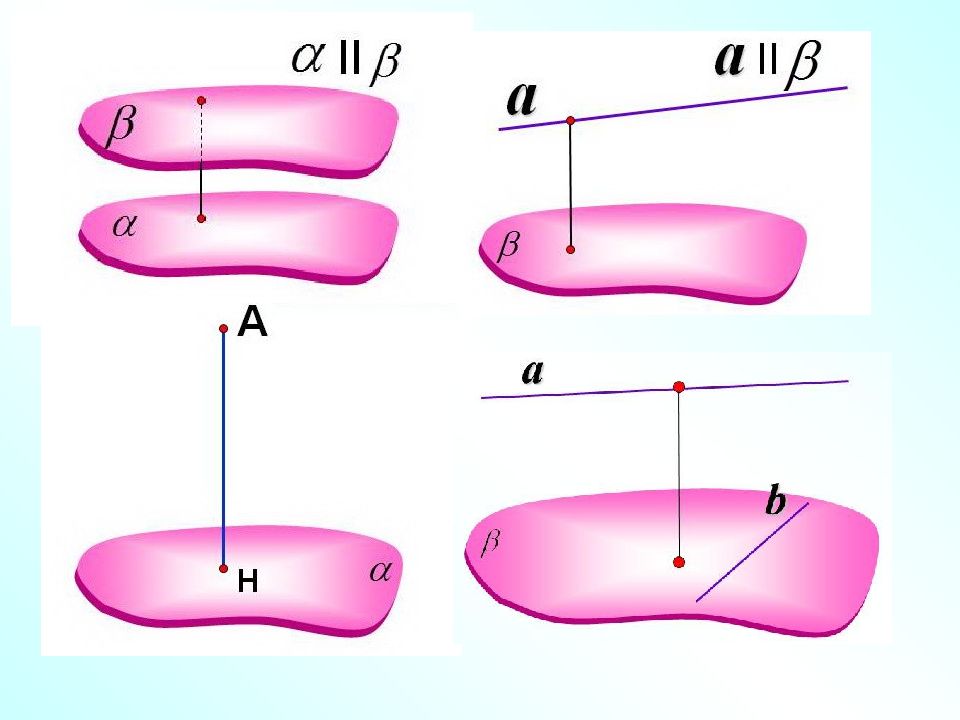
Расстояние от произвольной точки до плоскости называется длина перпендикуляра, опущенного из точки на эту плоскость. В А α
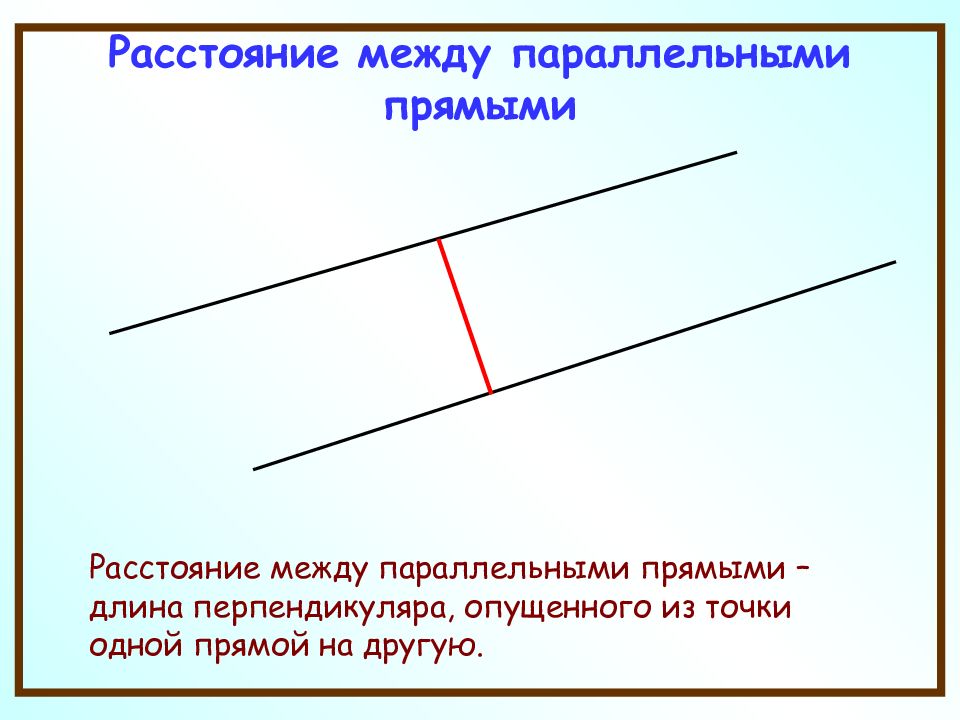
Расстояние между параллельными прямыми – длина перпендикуляра, опущенного из точки одной прямой на другую.
Слайд 5
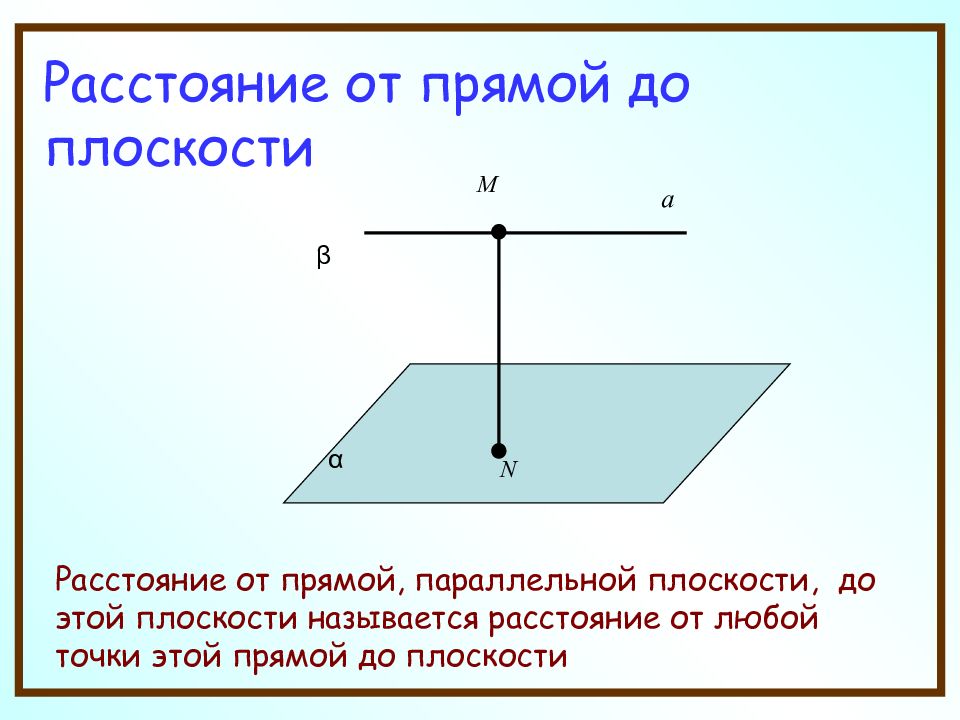
Расстояние от прямой до плоскости Расстояние от прямой, параллельной плоскости, до этой плоскости называется расстояние от любой точки этой прямой до плоскости а М β α N
Слайд 6
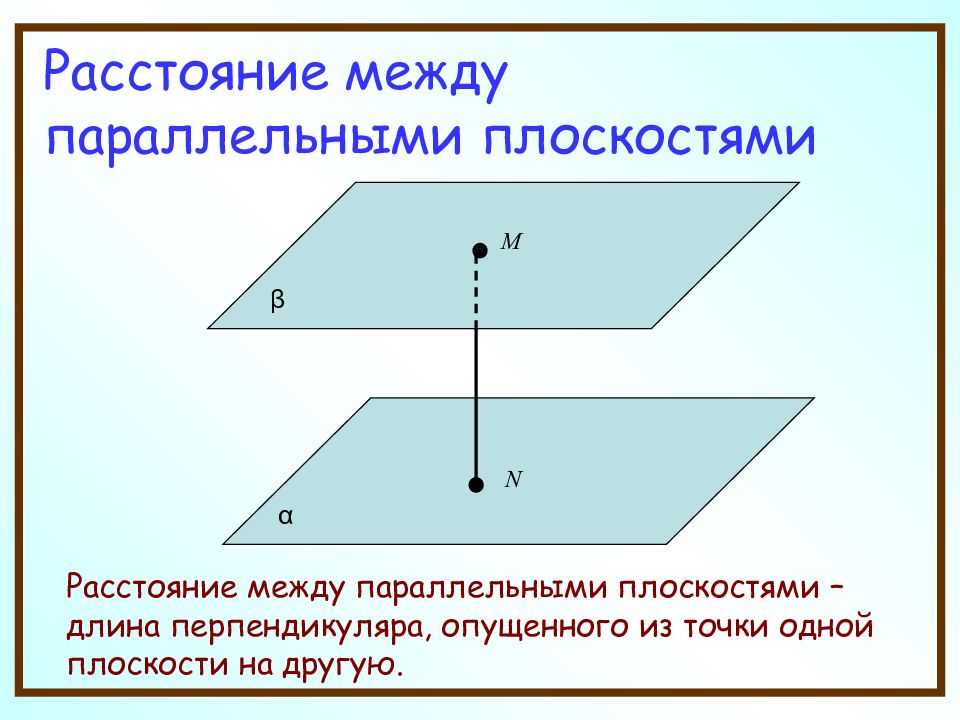
Расстояние между параллельными плоскостями Расстояние между параллельными плоскостями – длина перпендикуляра, опущенного из точки одной плоскости на другую. М β α N
Слайд 7
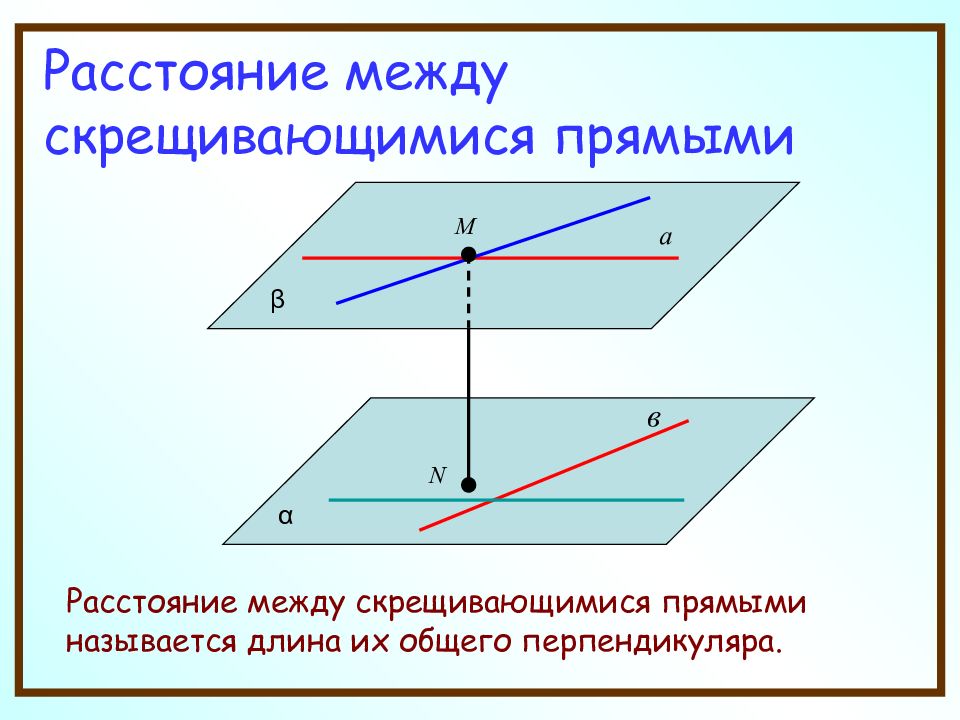
Расстояние между скрещивающимися прямыми Расстояние между скрещивающимися прямыми называется длина их общего перпендикуляра. а М β α N в
Слайд 8
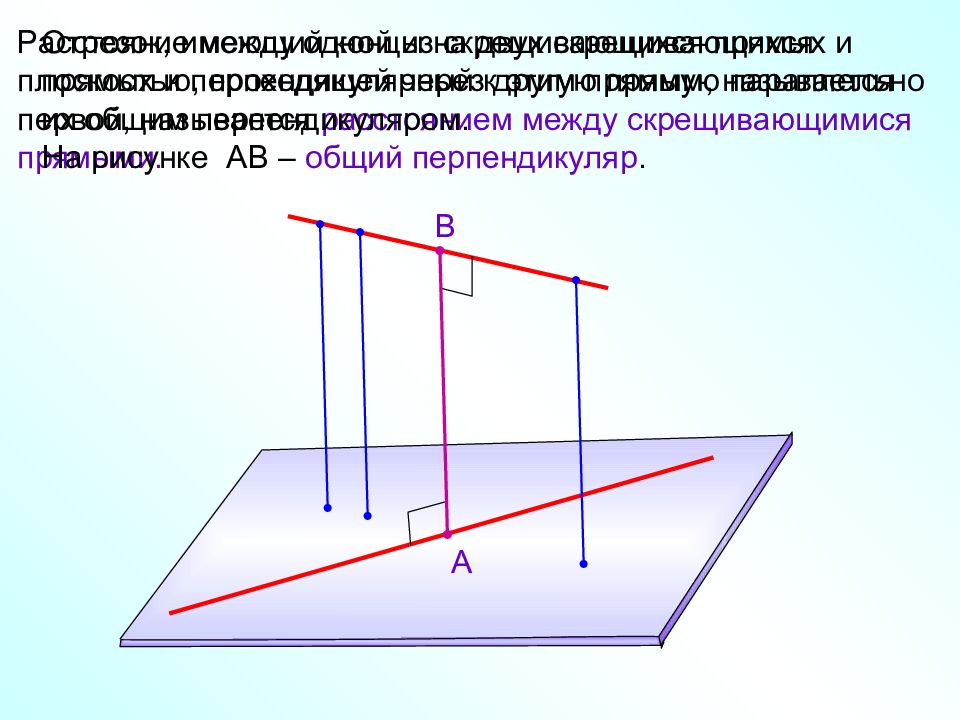
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим прямым, называется их общим перпендикуляром. На рисунке АВ – общий перпендикуляр. А В
Слайд 10
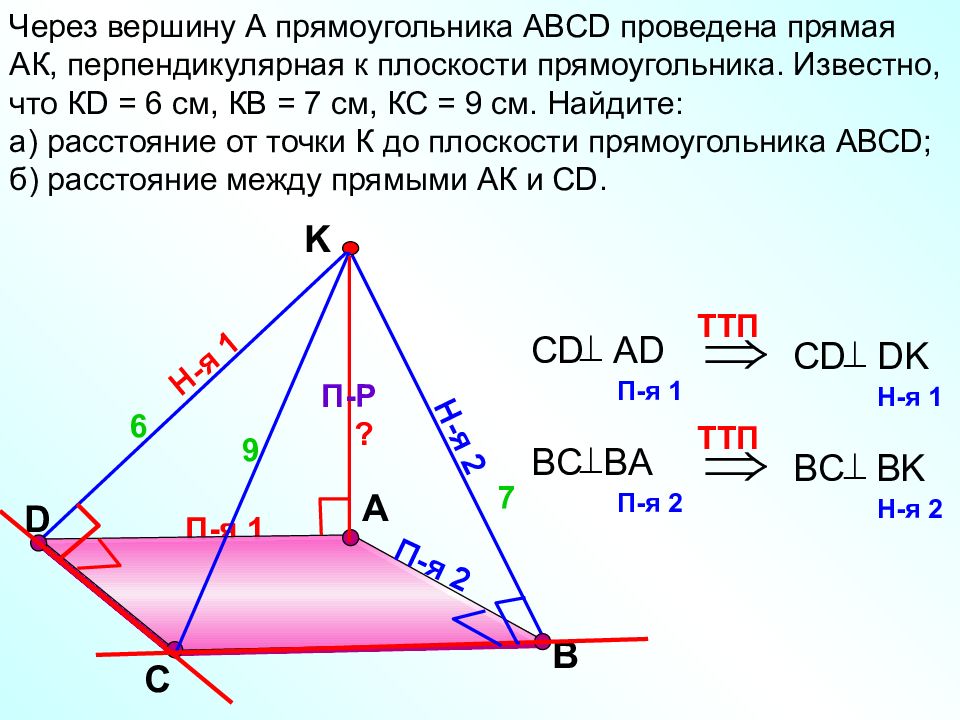
П-я 1 D А Через вершину А прямоугольника АВС D проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что К D = 6 см, КВ = 7 см, КС = 9 см. Найдите: а) расстояние от точки К до плоскости прямоугольника АВС D; б) расстояние между прямыми АК и С D. С В K П-Р Н-я 1 Н-я 2 П-я 2 TT П С D AD П-я 1 CD DK Н-я 1 TT П BC BA П-я 2 BC BK Н-я 2 6 7 9 ?
Слайд 12
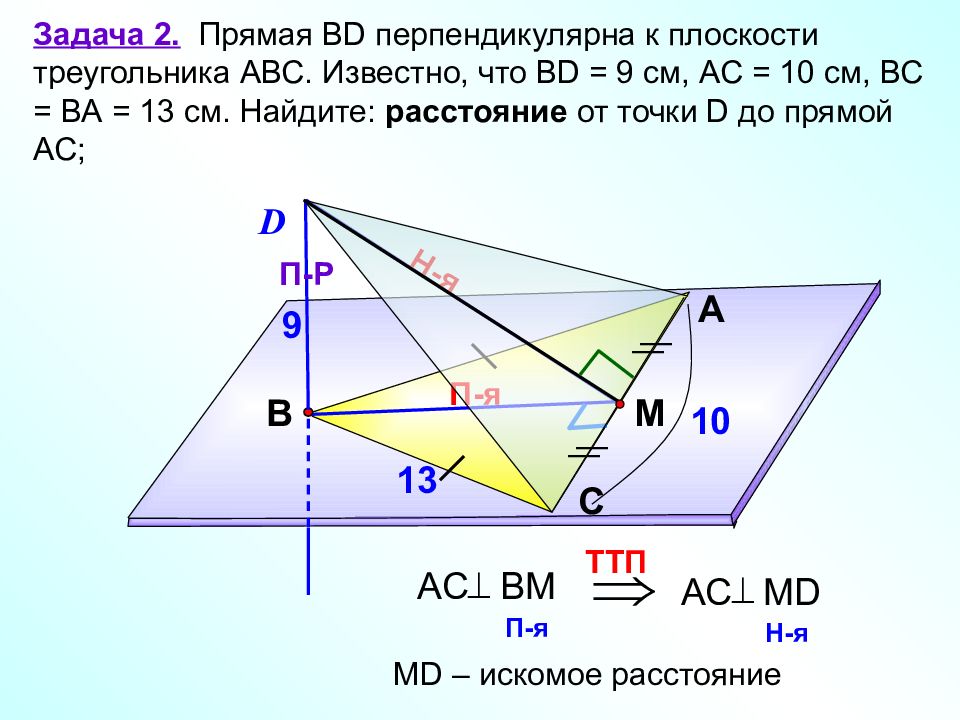
П-я Задача 2. Прямая В D перпендикулярна к плоскости треугольника АВС. Известно, что В D = 9 см, АС = 10 см, ВС = ВА = 13 см. Найдите: расстояние от точки D до прямой АС; А С В D П-Р Н-я TT П AC B М П-я AC MD Н-я М D – искомое расстояние М 9 10 13
Слайд 14
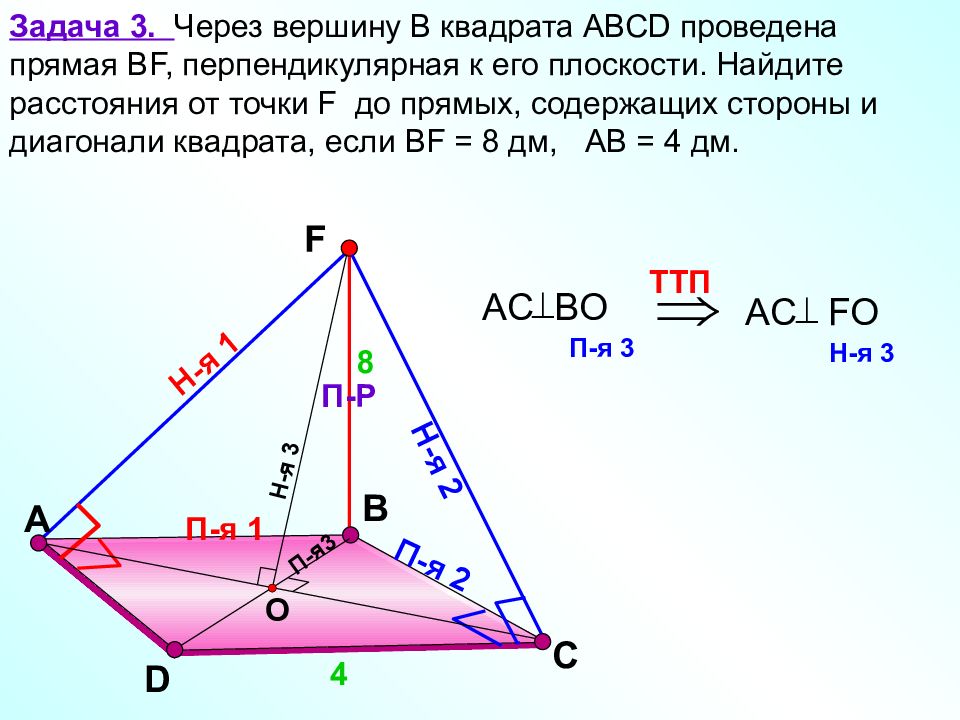
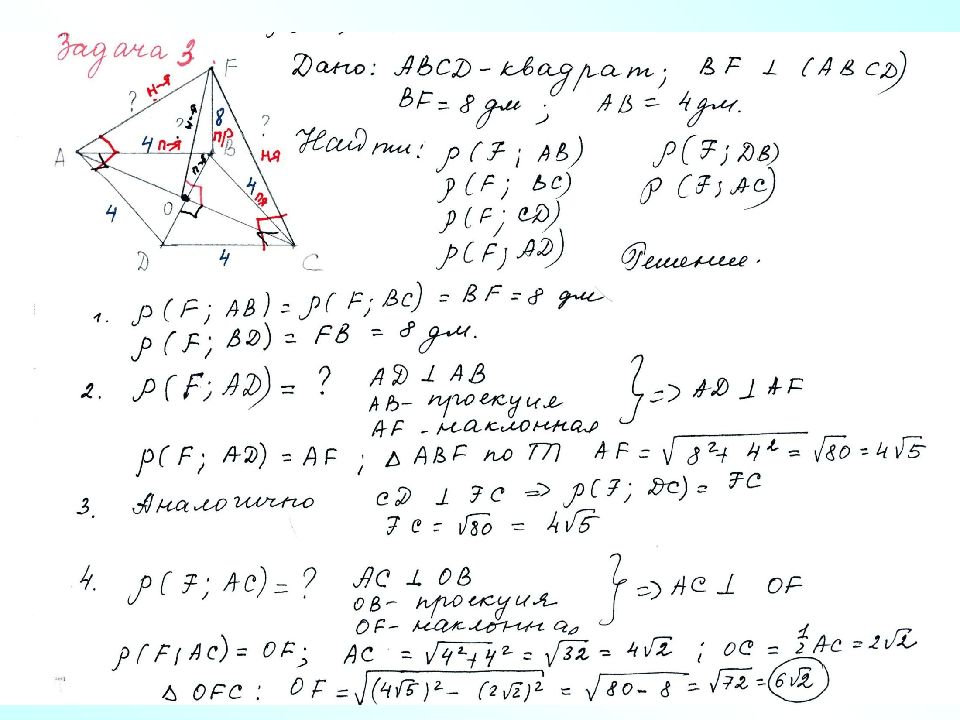
В Задача 3. Через вершину B квадрата АВС D проведена прямая В F, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если В F = 8 дм, АВ = 4 дм. D С 4 F П-Р 8 П-я 1 Н-я 1 Н-я 2 П-я 2 Н-я 3 П-я3 О TT П AC BO П-я 3 AC FO Н-я 3 А