РАЗДЕЛ 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПЕРСПЕКТИВНЫХ ИЗОБРАЖЕНИЙ ОБЩИЕ ПОЛОЖЕНИЯ ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ ПЕРСПЕКТИВА ТЕНЕЙ ПЕРСПЕКТИВА ОТРАЖЕНИЙ РАЗДЕЛ 2. ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВНЫХ ИЗОБРАЖЕНИЙ ПЕРСПЕКТИВА ПЛОСКИХ ФИГУР И ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЕРСПЕКТИВА ИНТЕРЬЕРА ПЕРСПЕКТИВА ЭКСТЕРЬЕРА АРХИТЕКТУРНЫХ ОБЪЕКТОВ
Метод центрального проецирования Перспектива – это наука о построении изображений предметов на какой-либо поверхности такими, какими их воспринимает глаз человека. В зависимости от вида поверхности, на которой выполнено перспективное изображение, перспектива делятся на виды: линейная (изображение на плоскости), панорамная (изображение на внутренней вертикальной цилиндрической поверхности), купольная (изображение, выполненное на внутренней поверхности сферы или эллипсоида), театральная (изображения, выполненные на нескольких вертикальных плоскостях, расположенных в различной глубине).
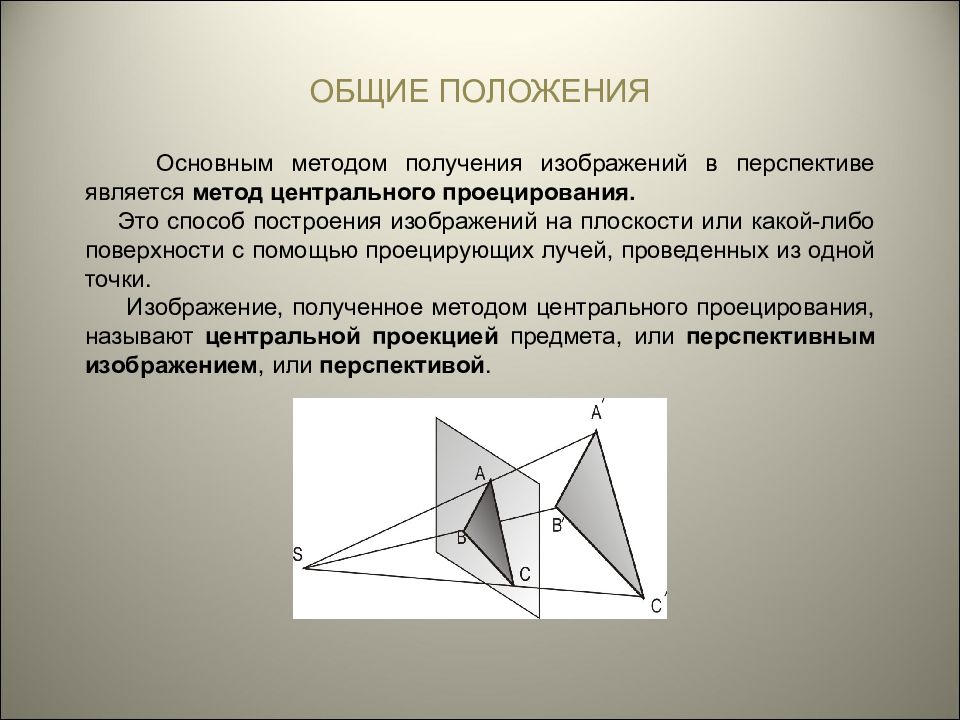
Основным методом получения изображений в перспективе является метод центрального проецирования. Это способ построения изображений на плоскости или какой-либо поверхности с помощью проецирующих лучей, проведенных из одной точки. Изображение, полученное методом центрального проецирования, называют центральной проекцией предмета, или перспективным изображением, или перспективой.
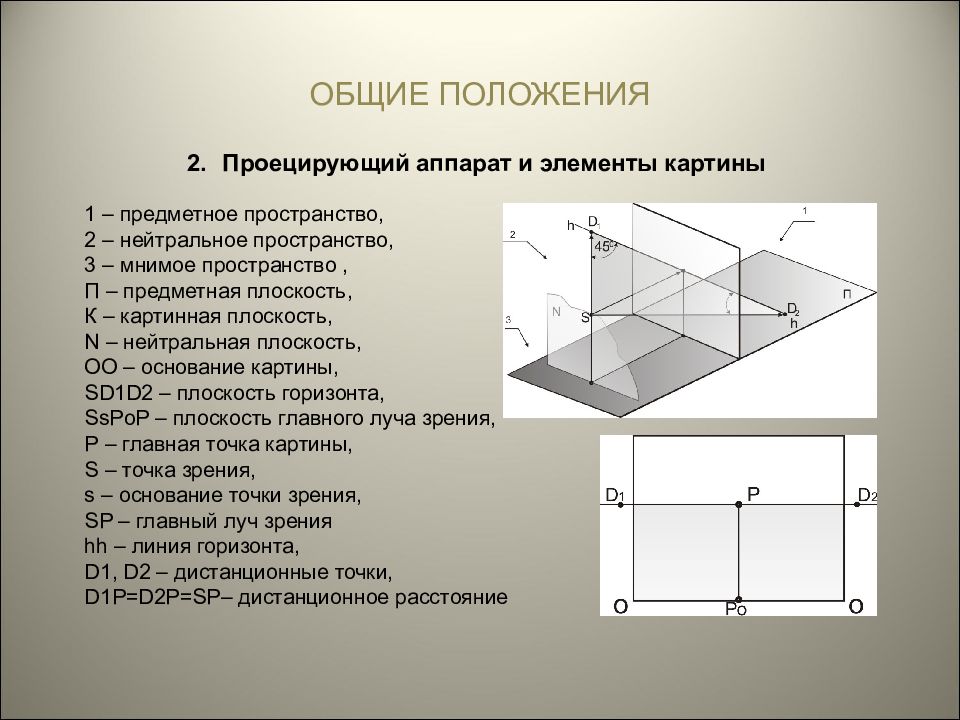
Проецирующий аппарат и элементы картины 1 – предметное пространство, 2 – нейтральное пространство, 3 – мнимое пространство, П – предметная плоскость, К – картинная плоскость, N – нейтральная плоскость, ОО – основание картины, SD 1 D 2 – плоскость горизонта, SsP о P – плоскость главного луча зрения, Р – главная точка картины, S – точка зрения, s – основание точки зрения, SP – главный луч зрения hh – линия горизонта, D 1, D 2 – дистанционные точки, D 1 P = D 2 P = SP – дистанционное расстояние
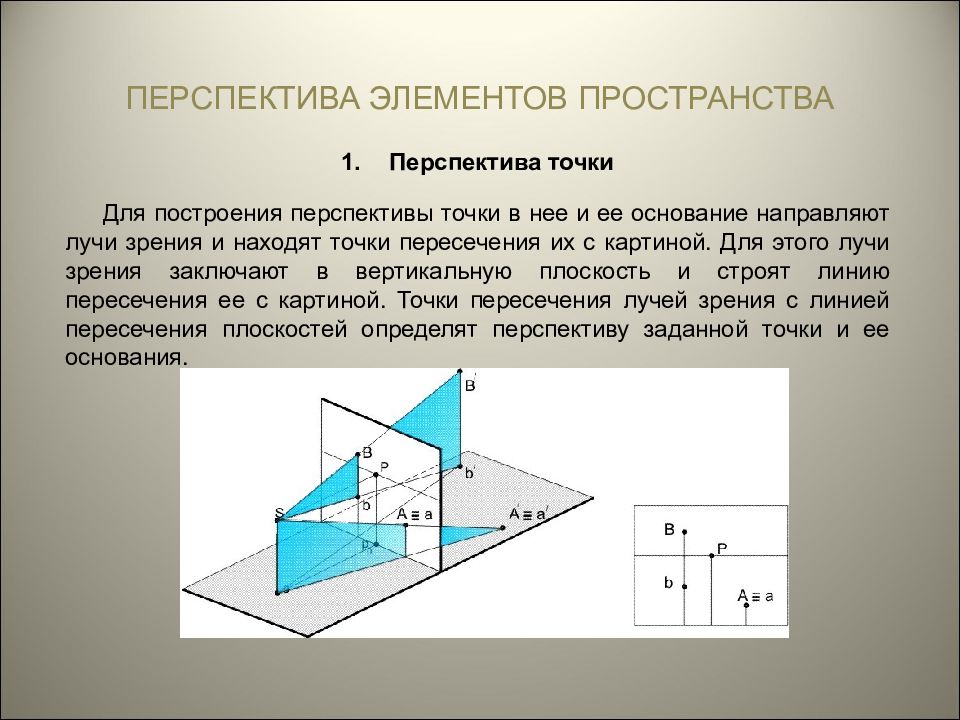
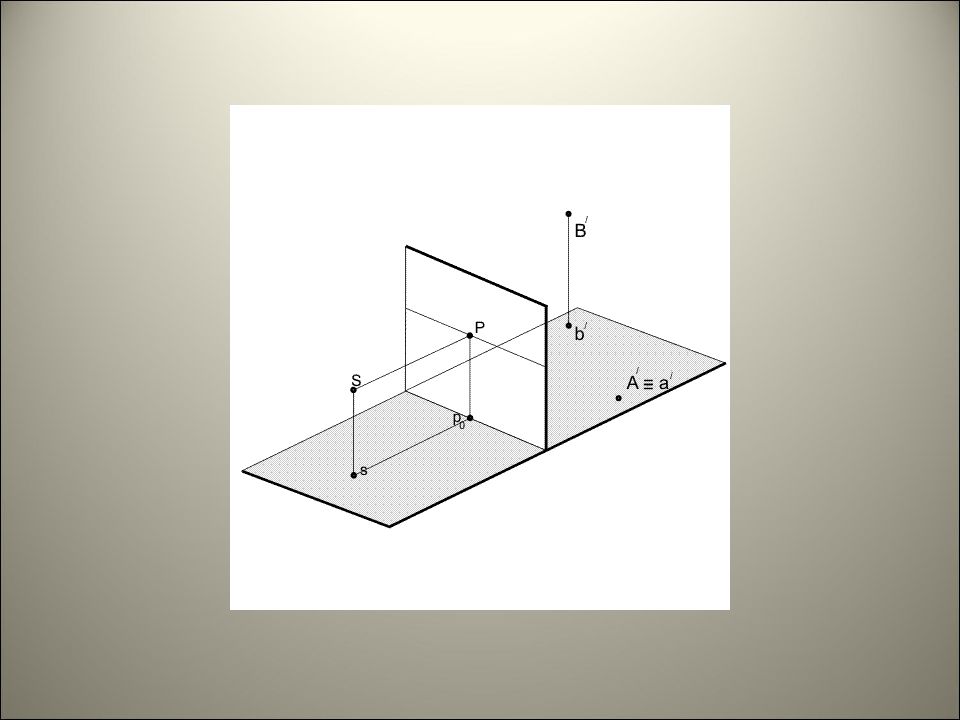
Перспектива точки Для построения перспективы точки в нее и ее основание направляют лучи зрения и находят точки пересечения их с картиной. Для этого лучи зрения заключают в вертикальную плоскость и строят линию пересечения ее с картиной. Точки пересечения лучей зрения с линией пересечения плоскостей определят перспективу заданной точки и ее основания.
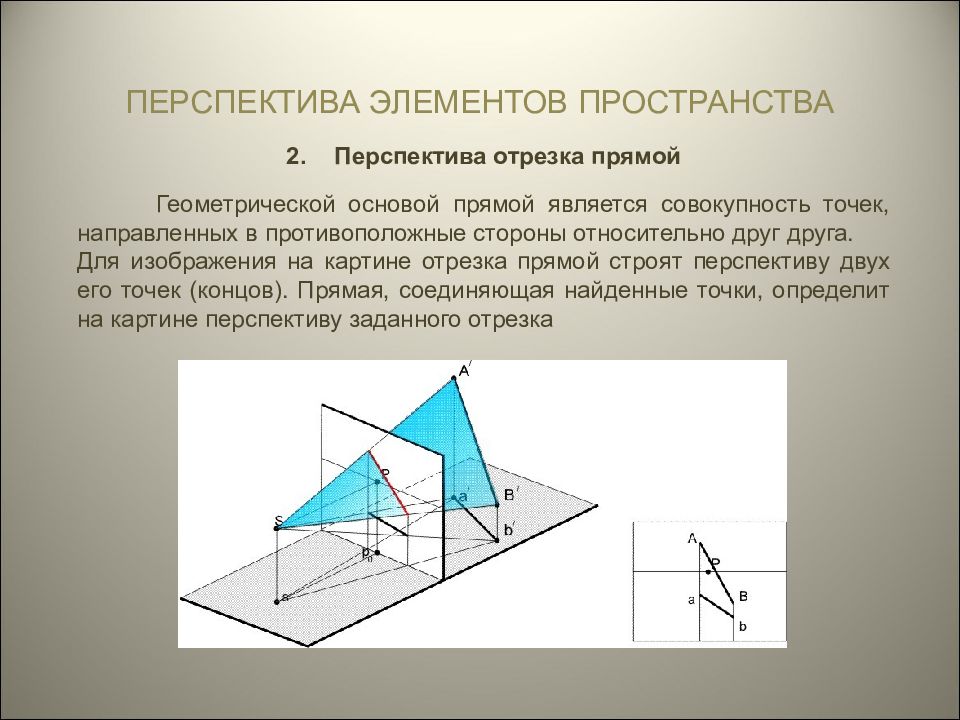
Перспектива отрезка прямой Геометрической основой прямой является совокупность точек, направленных в противоположные стороны относительно друг друга. Для изображения на картине отрезка прямой строят перспективу двух его точек (концов). Прямая, соединяющая найденные точки, определит на картине перспективу заданного отрезка
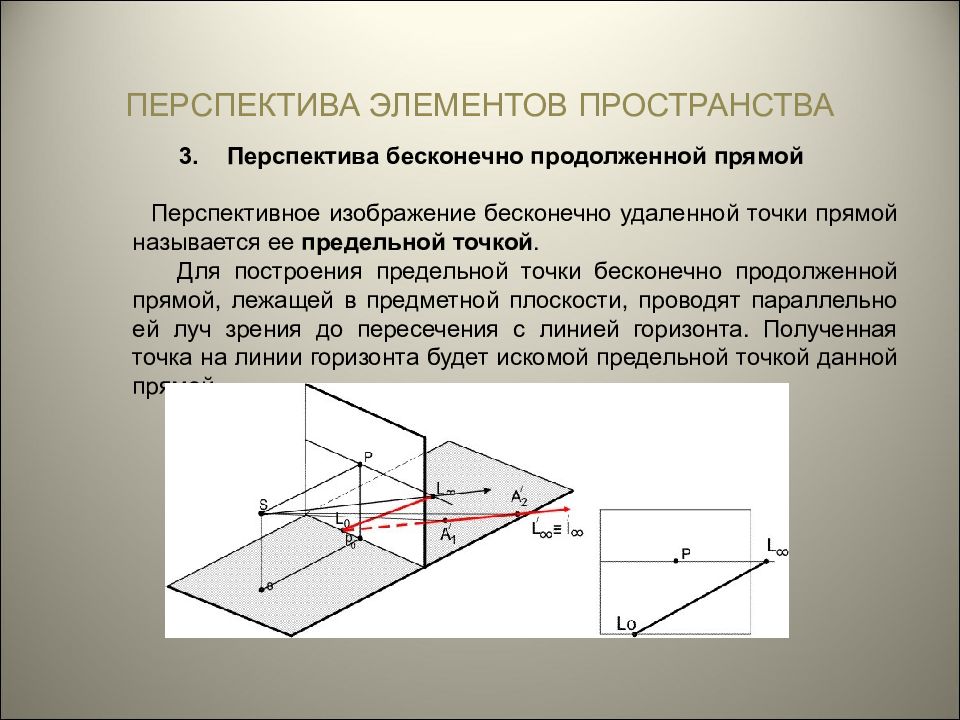
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Перспектива бесконечно продолженной прямой Перспективное изображение бесконечно удаленной точки прямой называется ее предельной точкой. Для построения предельной точки бесконечно продолженной прямой, лежащей в предметной плоскости, проводят параллельно ей луч зрения до пересечения с линией горизонта. Полученная точка на линии горизонта будет искомой предельной точкой данной прямой.
Прямые общего положения Прямые, расположенные под произвольным углом к предметной и картинной плоскостям, называются прямыми общего положения. Прямая общего положения в зависимости от ее направления может быть восходящей и нисходящей. Если точки прямой по мере удаления от картинной плоскости повышаются, то такая прямая называется восходящей. Восходящая прямая направлена снизу вверх от картинной плоскости. Если точки прямой по мере удаления от картинной плоскости понижаются, то такая прямая называется нисходящей. Нисходящая прямая направлена сверху вниз от картинной плоскости. ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА
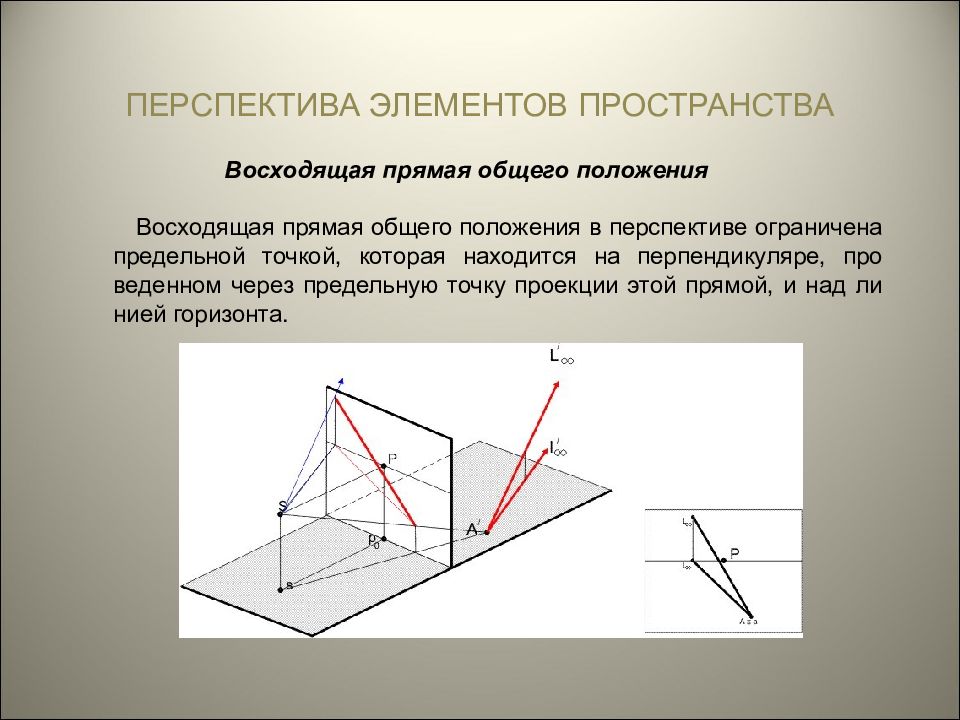
Восходящая прямая общего положения Восходящая прямая общего положения в перспективе ограничена предельной точкой, которая находится на перпендикуляре, проведенном через предельную точку проекции этой прямой, и над линией горизонта. ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА
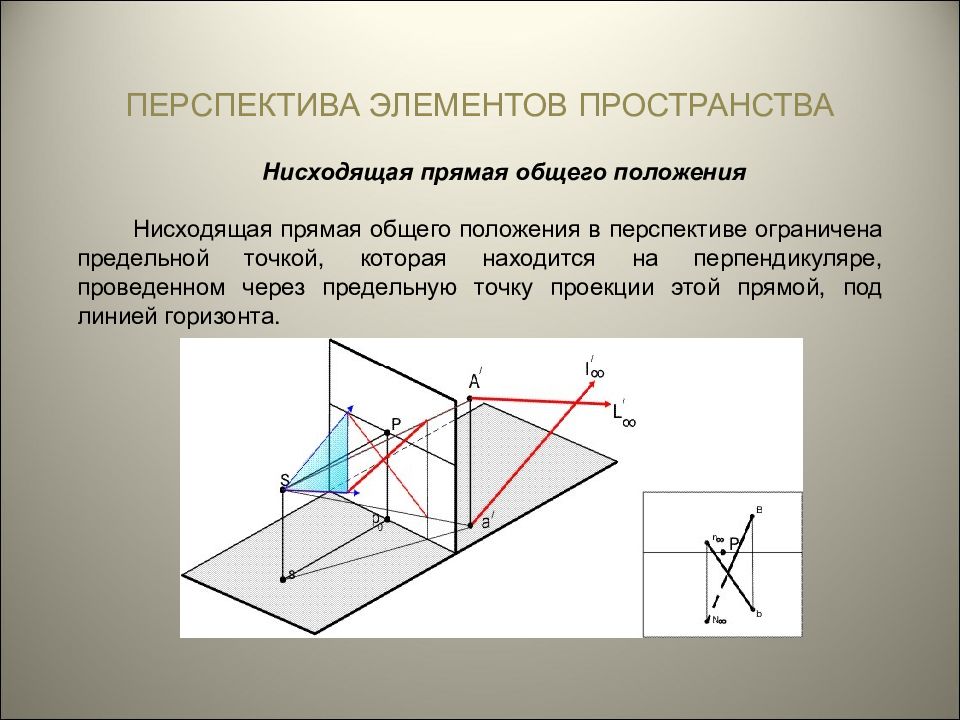
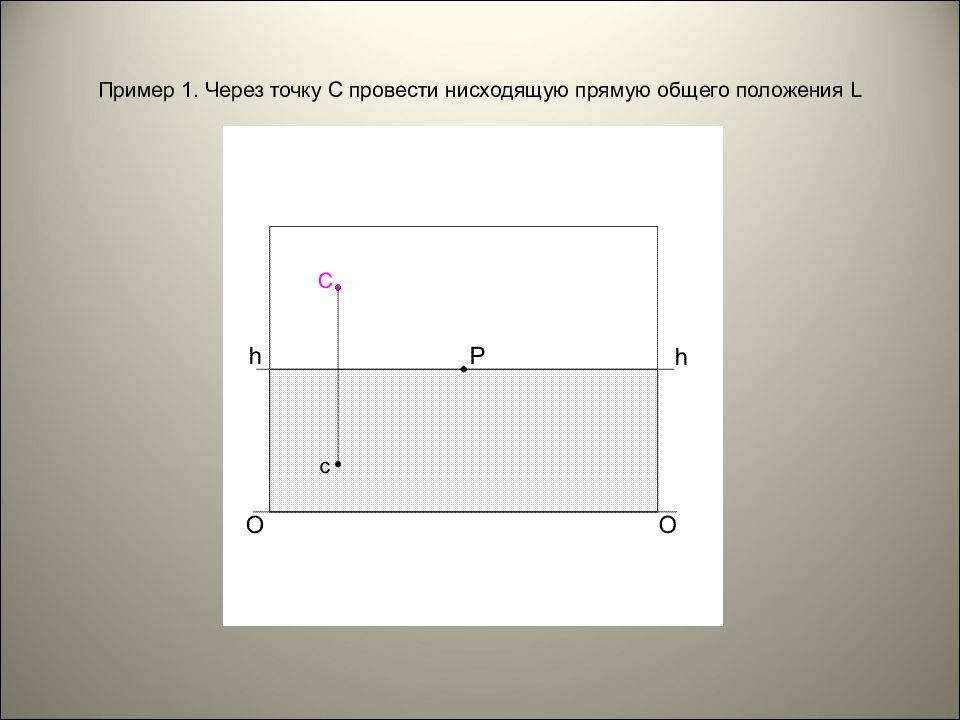
Нисходящая прямая общего положения Нисходящая прямая общего положения в перспективе ограничена предельной точкой, которая находится на перпендикуляре, проведенном через предельную точку проекции этой прямой, под линией горизонта. ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Прямые частного положения Прямые, параллельные предметной или картинной плоскости, называются прямыми частного положения. К ним относятся: Прямая широт – горизонтальная прямая, параллельная предметной и картинной плоскостям. Глубинная – г оризонтальная прямая, которая перпендикулярна к картине. Горизонтальная прямая произвольного направления – г оризонтальная прямая, не параллельная и не перпендикулярная к картине. Вертикальная – прямая, перпендикулярная к предметной плоскости. Фронтальная – прямая, параллельная картине и под произвольным углом наклонная к предметной плоскости.
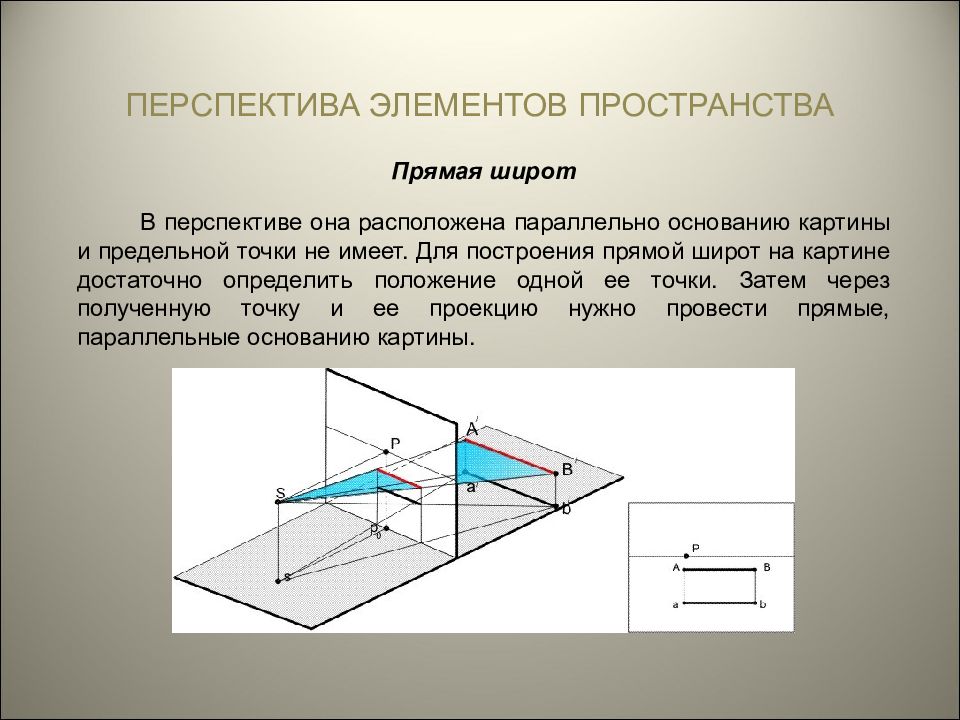
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Прямая широт В перспективе она расположена параллельно основанию картины и предельной точки не имеет. Для построения прямой широт на картине достаточно определить положение одной ее точки. Затем через полученную точку и ее проекцию нужно провести прямые, параллельные основанию картины.
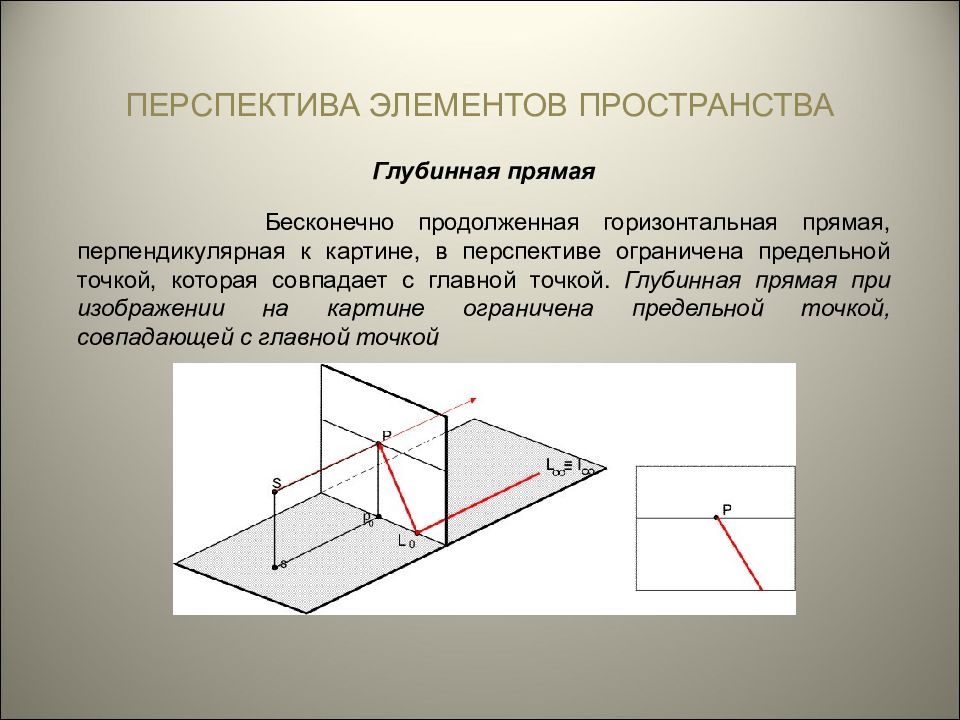
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Глубинная прямая Бесконечно продолженная горизонтальная прямая, перпендикулярная к картине, в перспективе ограничена предельной точкой, которая совпадает с главной точкой. Глубинная прямая при изображении на картине ограничена предельной точкой, совпадающей с главной точкой
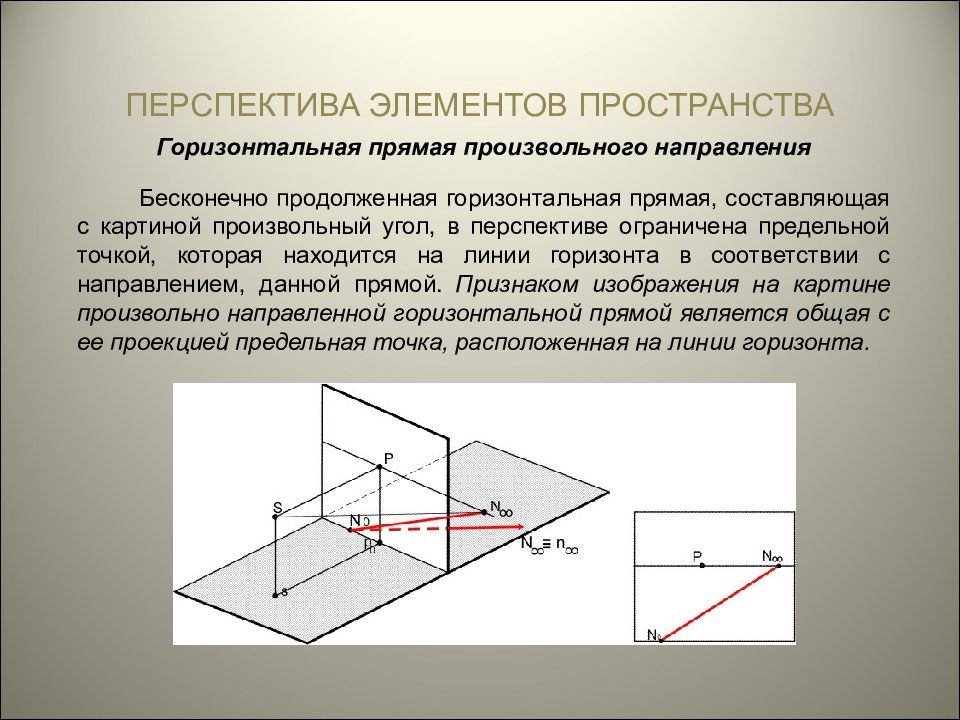
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Горизонтальная прямая произвольного направления Бесконечно продолженная горизонтальная прямая, составляющая с картиной произвольный угол, в перспективе ограничена предельной точкой, которая находится на линии горизонта в соответствии с направлением, данной прямой. Признаком изображения на картине произвольно направленной горизонтальной прямой является общая с ее проекцией предельная точка, расположенная на линии горизонта.
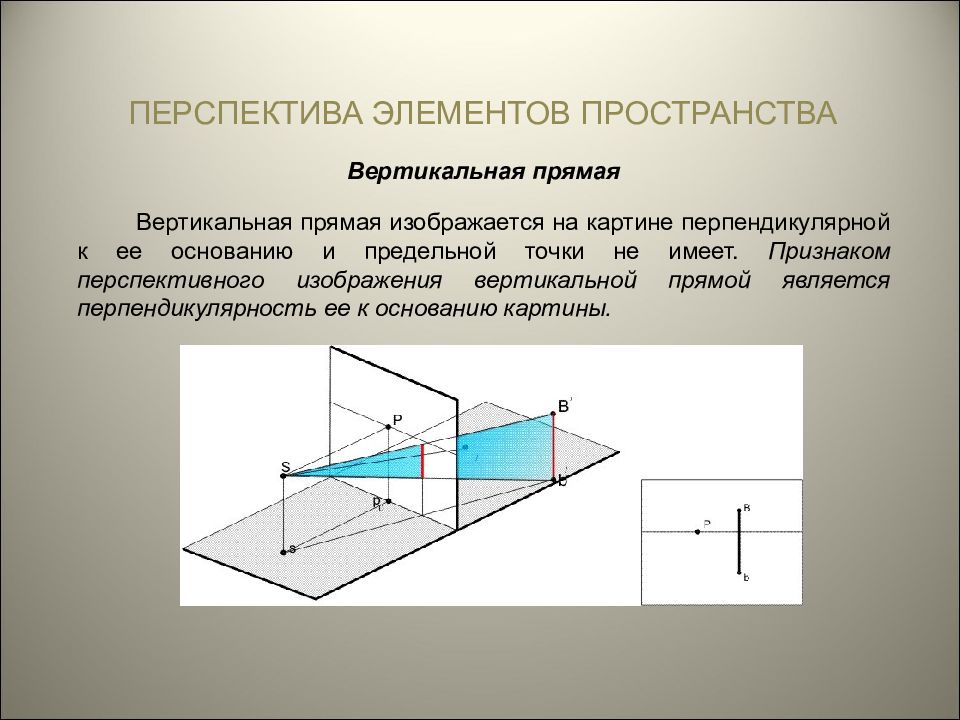
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Вертикальная прямая Вертикальная прямая изображается на картине перпендикулярной к ее основанию и предельной точки не имеет. Признаком перспективного изображения вертикальной прямой является перпендикулярность ее к основанию картины.
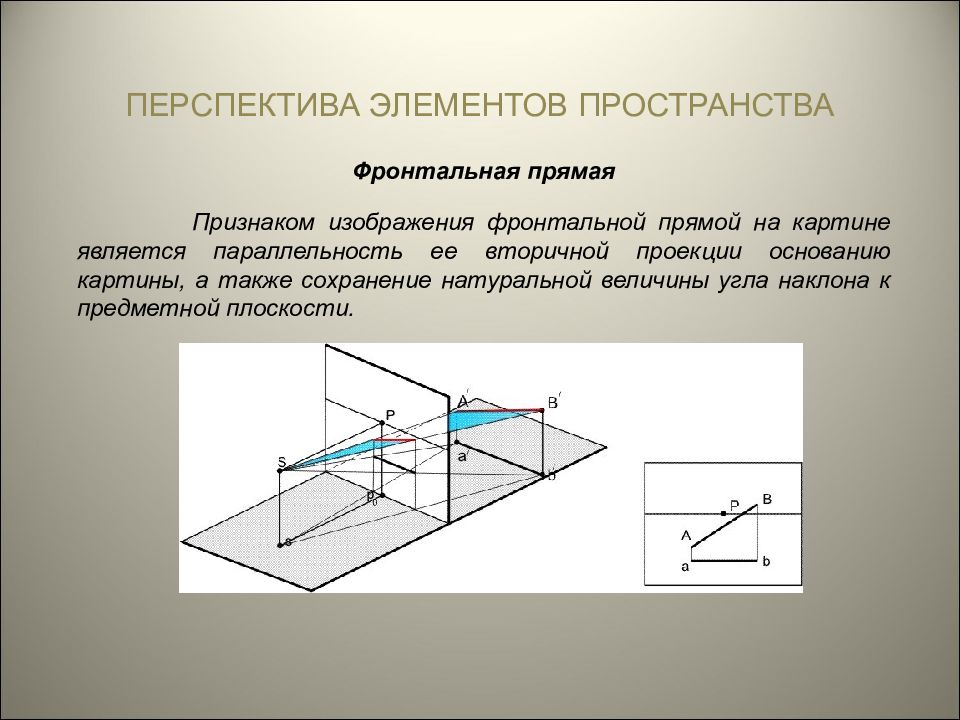
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Фронтальная прямая Признаком изображения фронтальной прямой на картине является параллельность ее вторичной проекции основанию картины, а также сохранение натуральной величины угла наклона к предметной плоскости.
Прямые особого положения Прямые, расположенные под произвольным углом к предметной и картинной плоскостям и параллельные плоскости главного луча зрения, называются прямыми особого положения. Прямая особого положения в зависимости от ее направления может быть восходящей и нисходящей. Если точки прямой по мере удаления от картинной плоскости повышаются, то такая прямая называется восходящей. Восходящая прямая направлена снизу вверх от картинной плоскости. Если точки прямой по мере удаления от картинной плоскости понижаются, то такая прямая называется нисходящей. Нисходящая прямая направлена сверху вниз от картинной плоскости. ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА
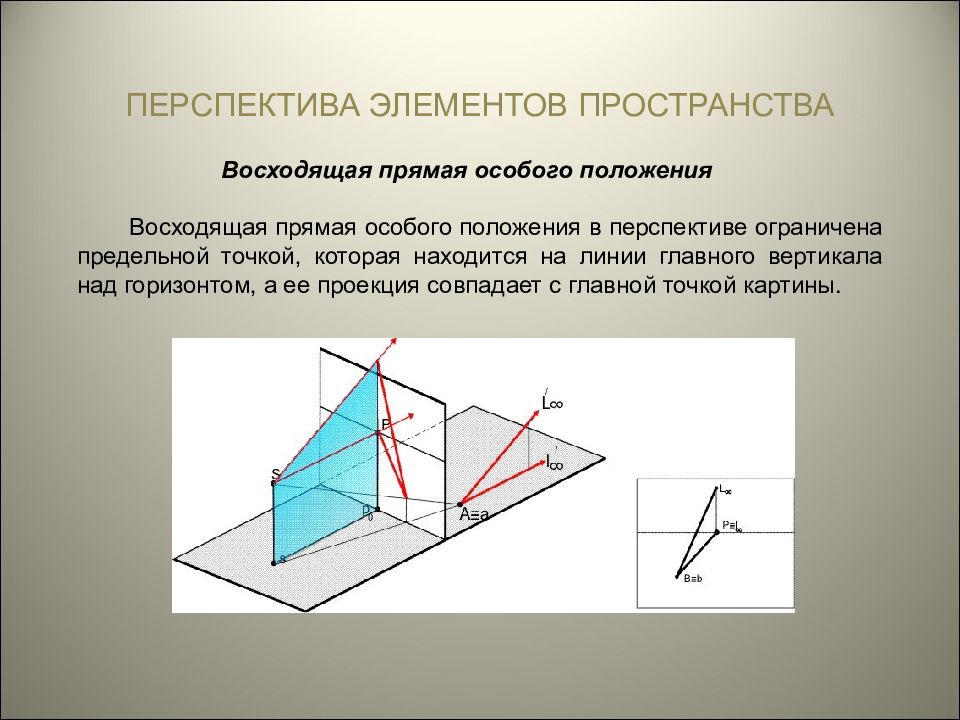
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Восходящая прямая особого положения Восходящая прямая особого положения в перспективе ограничена предельной точкой, которая находится на линии главного вертикала над горизонтом, а ее проекция совпадает с главной точкой картины.
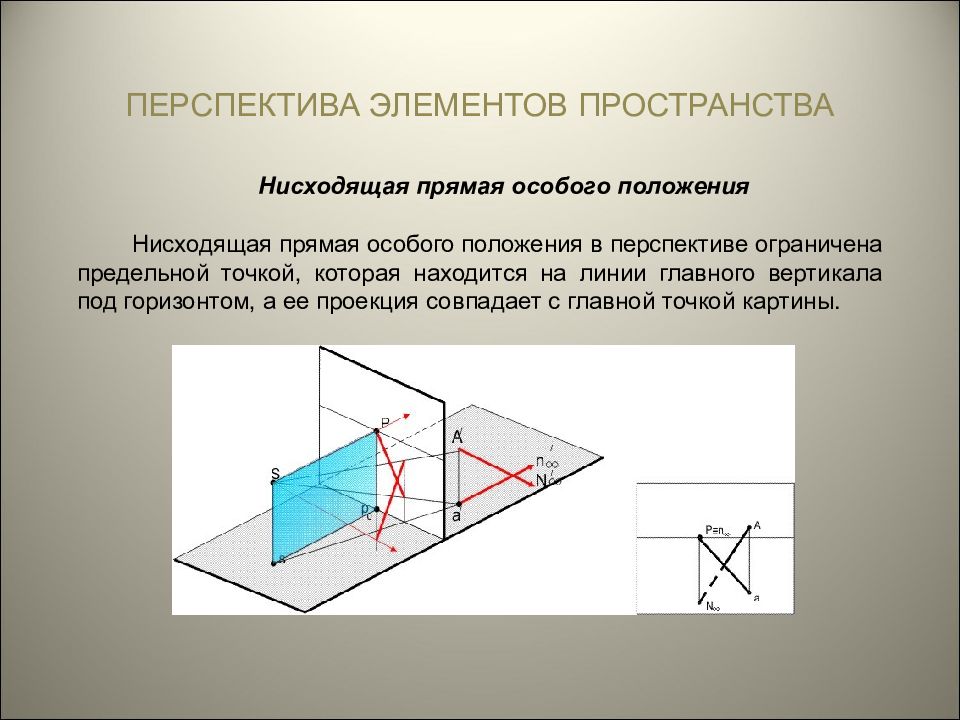
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Нисходящая прямая особого положения Нисходящая прямая особого положения в перспективе ограничена предельной точкой, которая находится на линии главного вертикала под горизонтом, а ее проекция совпадает с главной точкой картины.
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Следы прямых Точка пересечения прямой с плоскостью проекций называется следом этой прямой. Точки пересечения прямой с картинной ( картинный след ) и предметной ( предметный след ) плоскостями находятся на линиях пересечения вспомогательной предметно-проецирующей плоскости с плоскостями проекций и самой прямой.
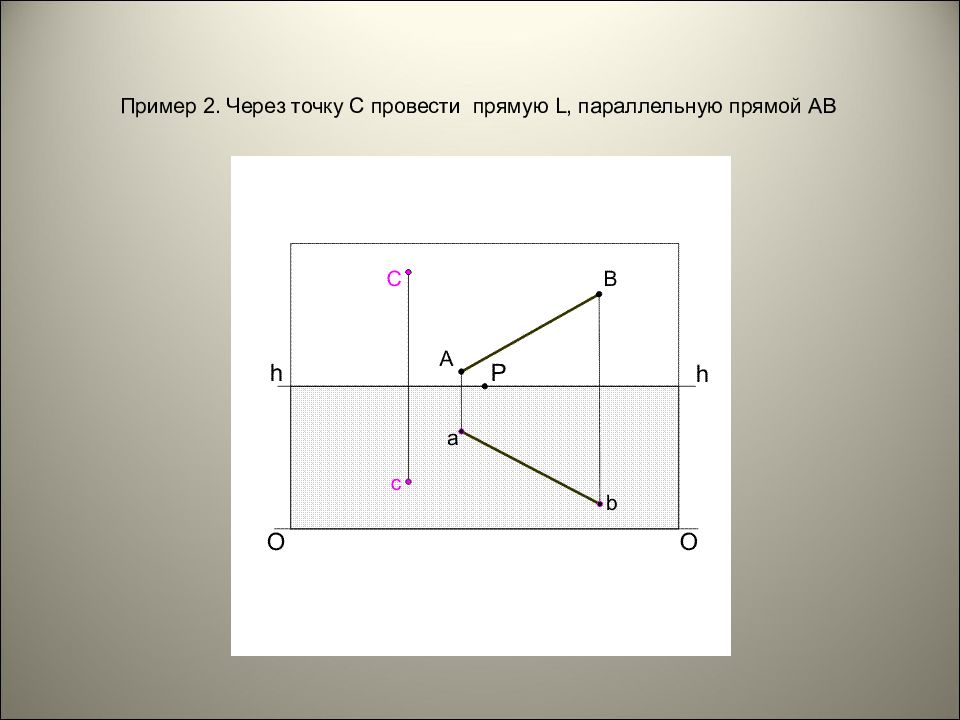
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Взаимное положение прямых Относительно друг друга прямые могут быть параллельными, пересекающимися или скрещивающимися. Произвольно направленные параллельные прямые на картине изображаются пучком прямых, сходящихся в одной предельной точке. Общая предельная точка произвольно расположенных горизонтальных прямых находится на линии горизонта и называется точкой схода.
Пример 2. Через точку С провести прямую L, параллельную прямой АВ
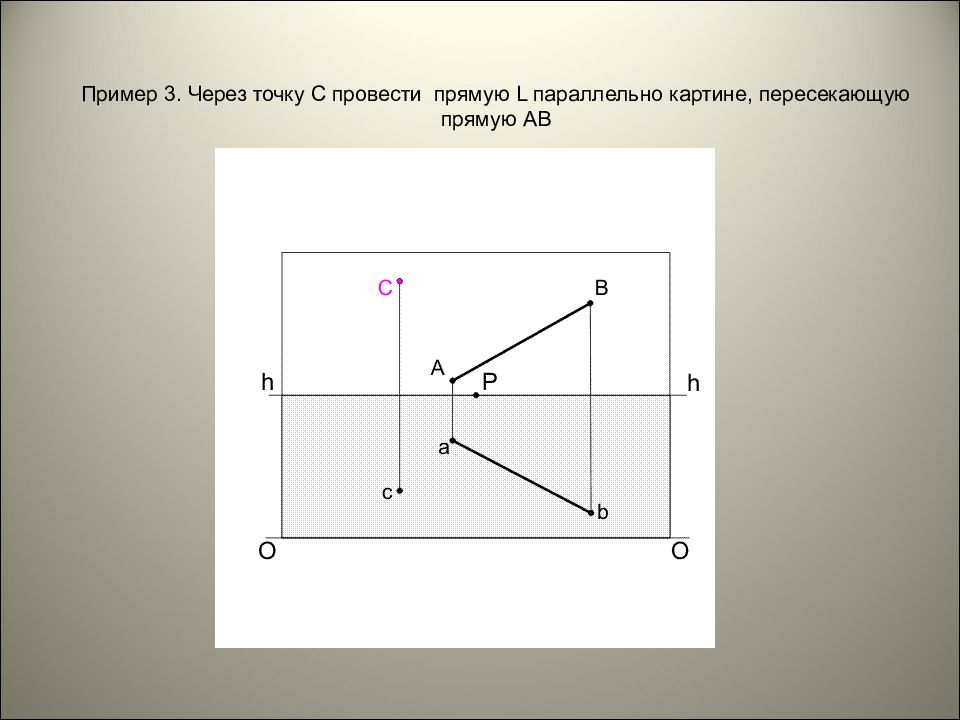
Пример 3. Через точку С провести прямую L параллельно картине, пересекающую прямую АВ
Пример 4. Построить следы прямой АВ
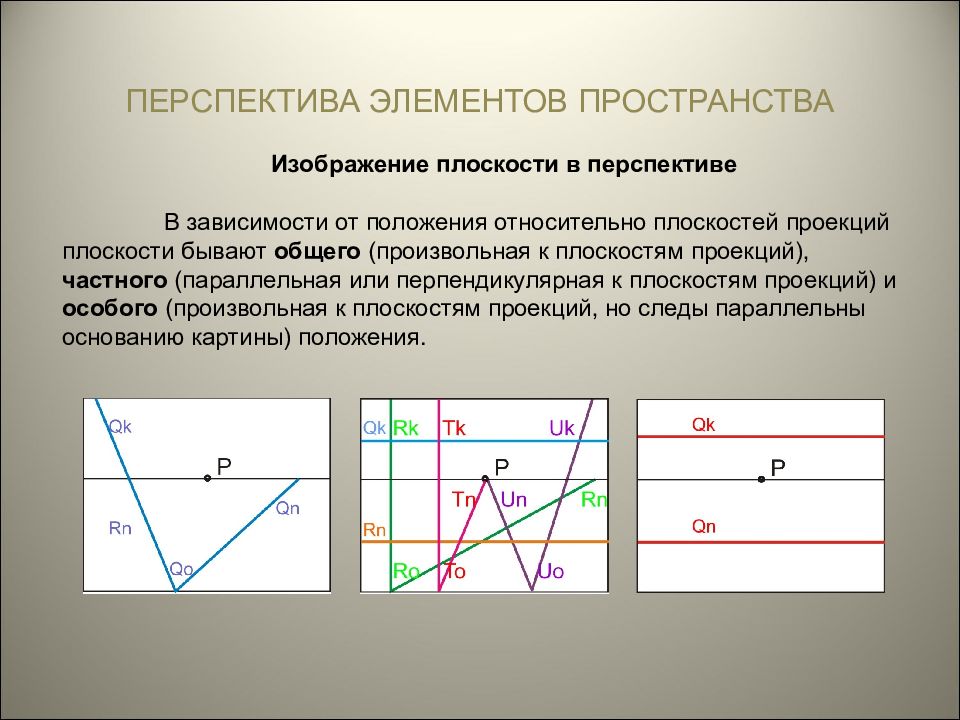
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Изображение плоскости в перспективе В перспективе плоскость может быть задана различными способами: тремя точками, не лежащими на одной прямой; прямой и точкой, не лежащей на этой прямой; двумя пересекающимися прямыми; двумя параллельными прямыми; плоской фигурой. Но для более наглядного изображения плоскости на картине ее задают следами. Следом плоскости в перспективе называют линию пересечения ее с предметной ( предметный след ) или картинной ( картинный след ) плоскостью. Предельной прямой плоскости называют совокупность множества предельных точек прямых, образующих эту плоскость. Предельная прямая плоскости параллельна ее картинному следу, и проходит через предельную точку предметного следа этой плоскости.
ПЕРСПЕКТИВА ЭЛЕМЕНТОВ ПРОСТРАНСТВА Изображение плоскости в перспективе В зависимости от положения относительно плоскостей проекций плоскости бывают общего (произвольная к плоскостям проекций), частного (параллельная или перпендикулярная к плоскостям проекций) и особого (произвольная к плоскостям проекций, но следы параллельны основанию картины) положения.
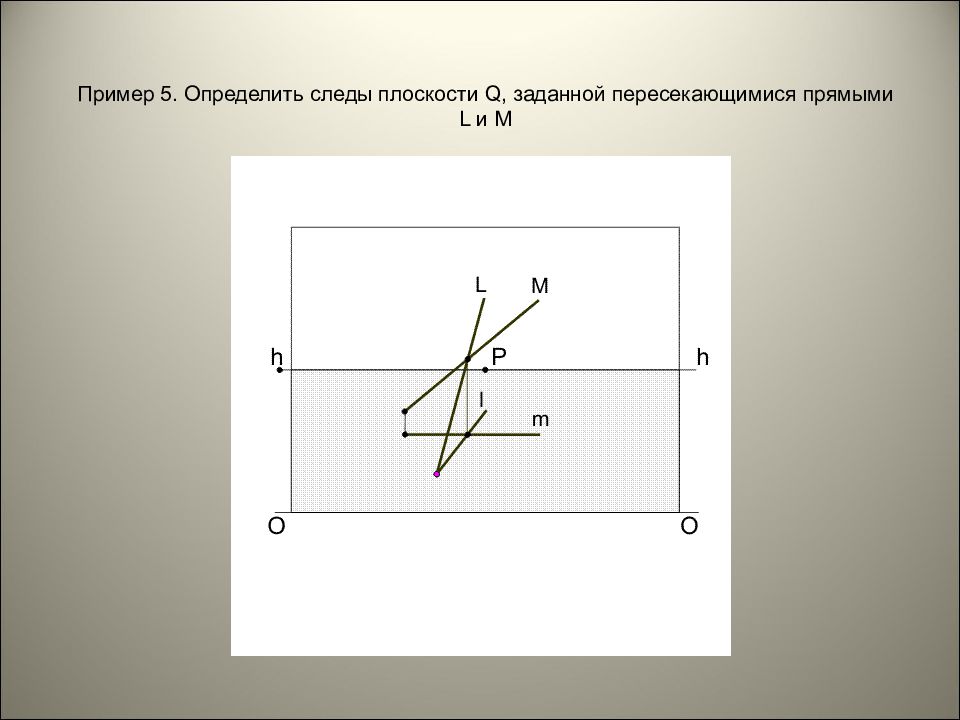
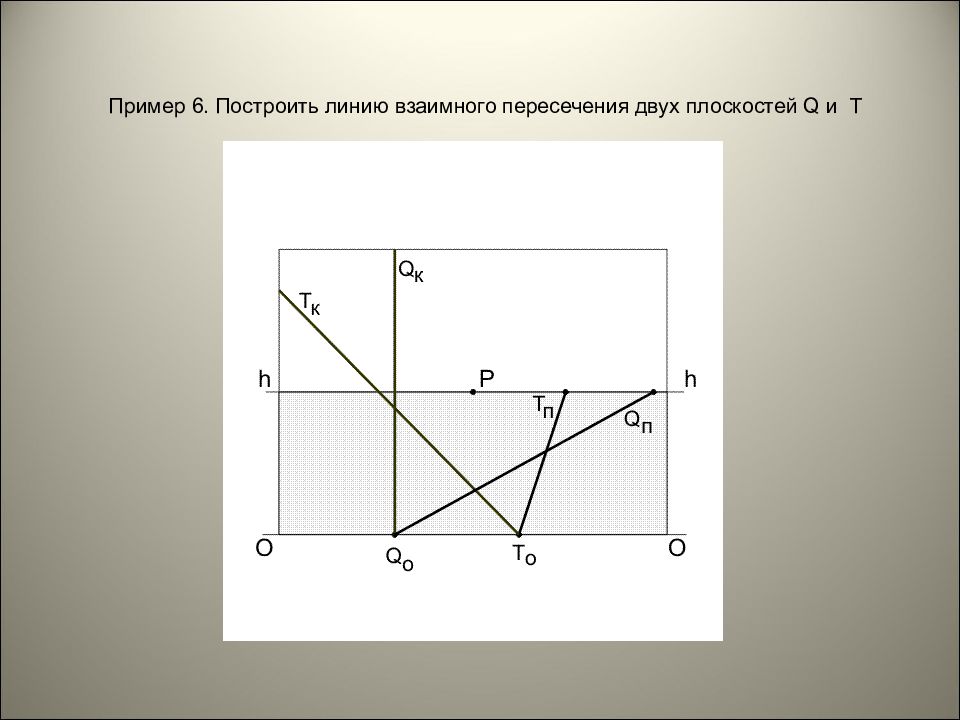
Пример 5. Определить следы плоскости Q, заданной пересекающимися прямыми L и M
Пример 6. Построить линию взаимного пересечения двух плоскостей Q и T
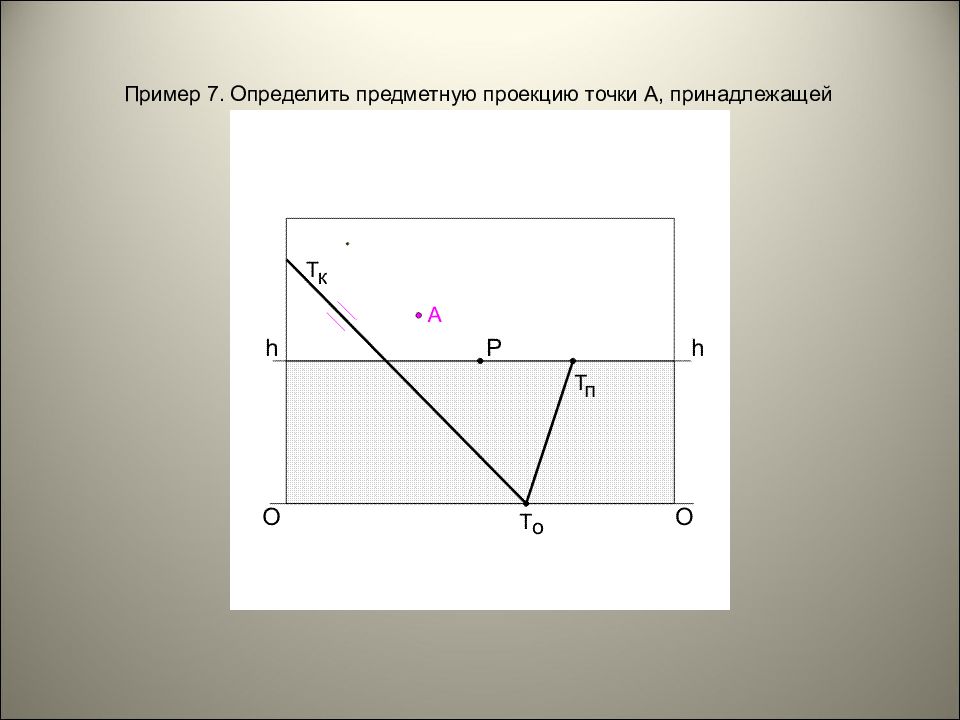
Пример 7. Определить предметную проекцию точки А, принадлежащей плоскости T
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Перспективные масштабы Для построения на картине объектов по их заданным размерам, применяют перспективный масштаб. Он позволяет установить соотношения между натуральными и перспективными линейными размерами предметов. Для этого задается масштаб картины с натуральной единицей длины линейного масштаба. Его строят в соответствии с положением в предметном пространстве измеряемых отрезков в трех главных направлениях: ширины, на прямых, расположенных параллельно основанию картины; глубины, на прямых, расположенных перпендикулярно к плоскости картины; высоты, на прямых, расположенных перпендикулярно к предметной плоскости. В соответствии с главными направлениями прямых строят перспективные масштабы: широт, глубин и высот.
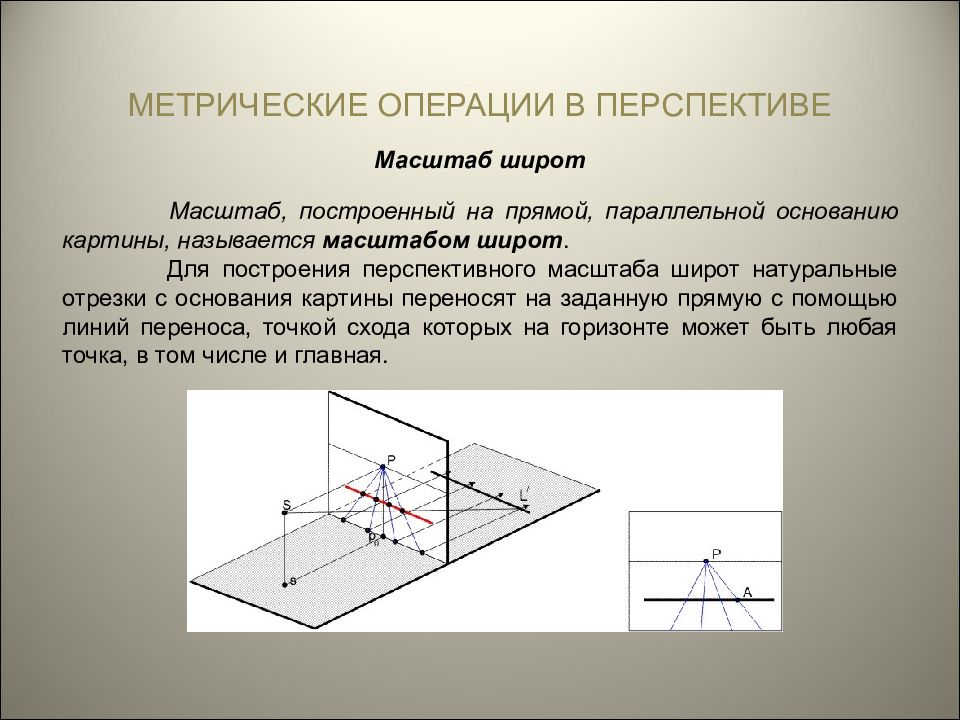
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Масштаб широт Масштаб, построенный на прямой, параллельной основанию картины, называется масштабом широт. Для построения перспективного масштаба широт натуральные отрезки с основания картины переносят на заданную прямую с помощью линий переноса, точкой схода которых на горизонте может быть любая точка, в том числе и главная.
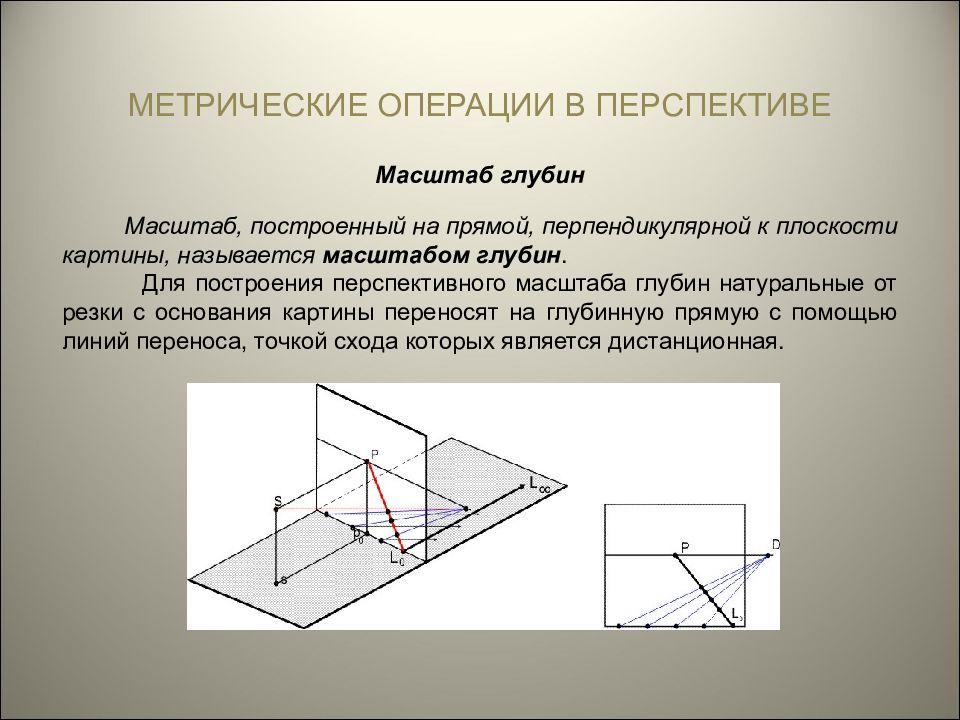
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Масштаб глубин Масштаб, построенный на прямой, перпендикулярной к плоскости картины, называется масштабом глубин. Для построения перспективного масштаба глубин натуральные отрезки с основания картины переносят на глубинную прямую с помощью линий переноса, точкой схода которых является дистанционная.
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Масштаб высот Масштаб, построенный на прямой, перпендикулярной к предметной плоскости, называется масштабом высот. Для построения перспективного масштабе высот натуральные отрезки откладывают но картинном следе вертикальной плоскости, в которую заключают заданную прямую, и переносят их с помощью горизонтальных линий, точкой схода которых является предельная точка предметного следа этой плоскости.
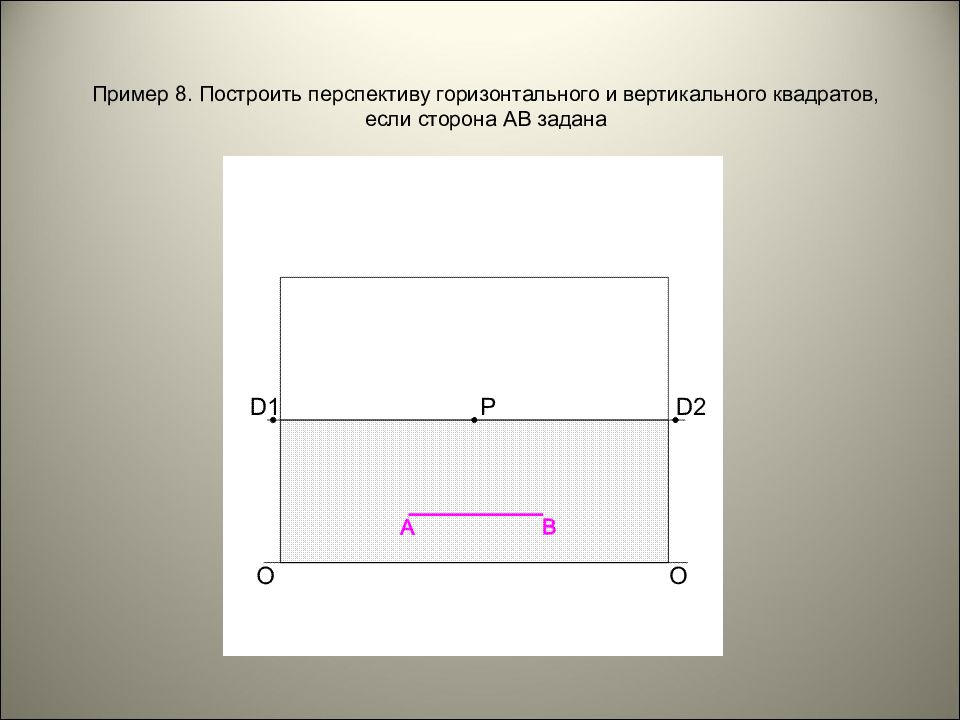
Пример 8. Построить перспективу горизонтального и вертикального квадратов, если сторона АВ задана
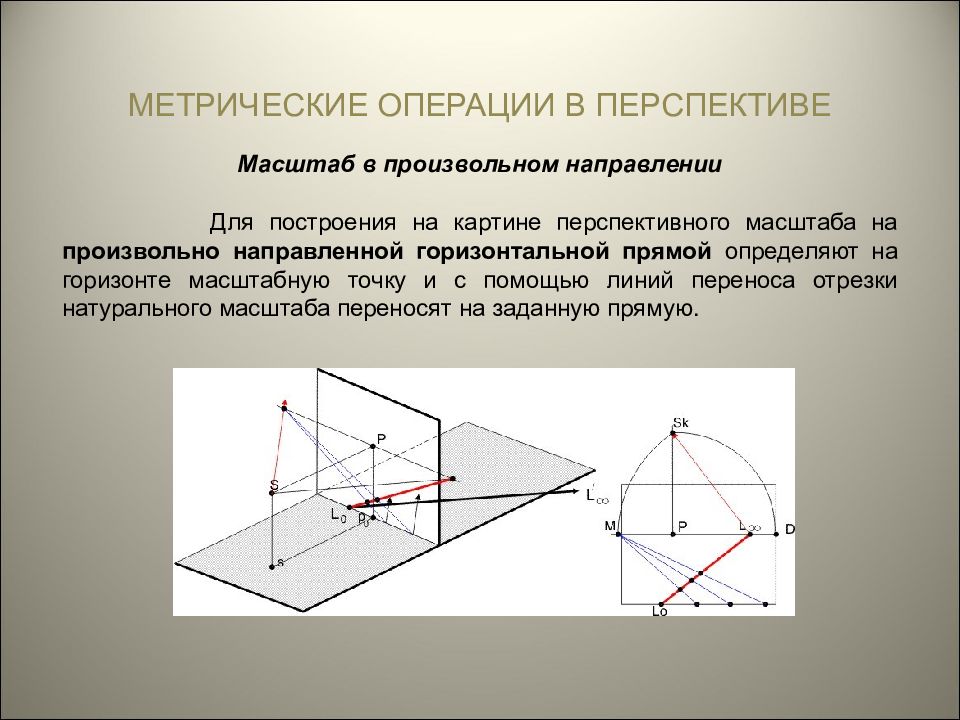
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Масштаб в произвольном направлении Для построения на картине перспективного масштаба на произвольно направленной горизонтальной прямой определяют на горизонте масштабную точку и с помощью линий переноса отрезки натурального масштаба переносят на заданную прямую.
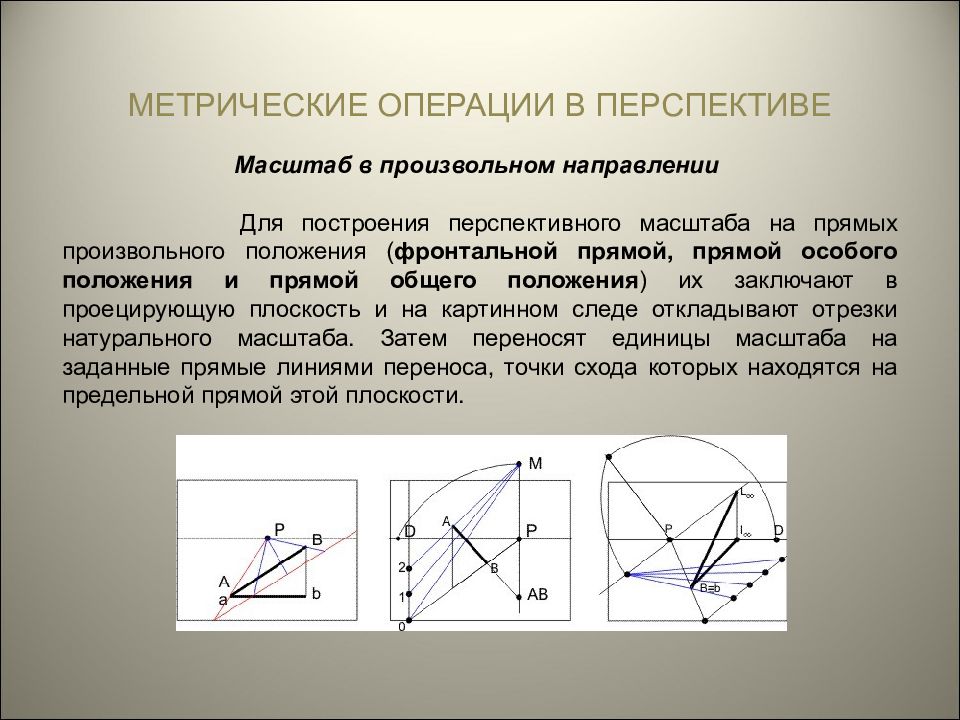
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Масштаб в произвольном направлении Для построения перспективного масштаба на прямых произвольного положения ( фронтальной прямой, прямой особого положения и прямой общего положения ) их заключают в проецирующую плоскость и на картинном следе откладывают отрезки натурального масштаба. Затем переносят единицы масштаба на заданные прямые линиями переноса, точки схода которых находятся на предельной прямой этой плоскости.
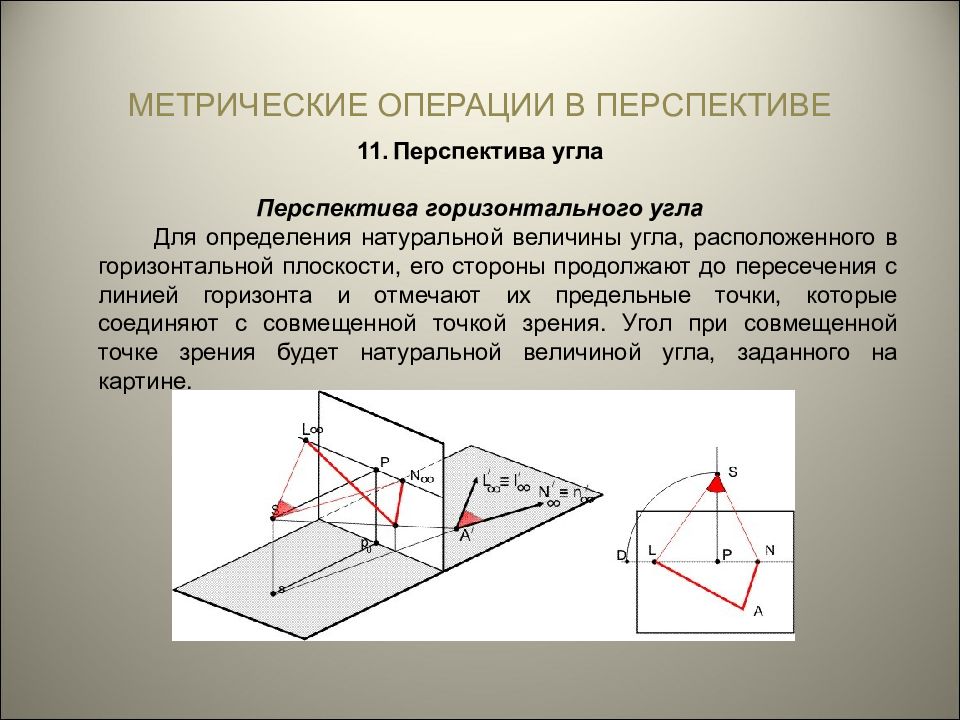
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Перспектива угла Перспектива горизонтального угла Для определения натуральной величины угла, расположенного в горизонтальной плоскости, его стороны продолжают до пересечения с линией горизонта и отмечают их предельные точки, которые соединяют с совмещенной точкой зрения. Угол при совмещенной точке зрения будет натуральной величиной угла, заданного на картине.
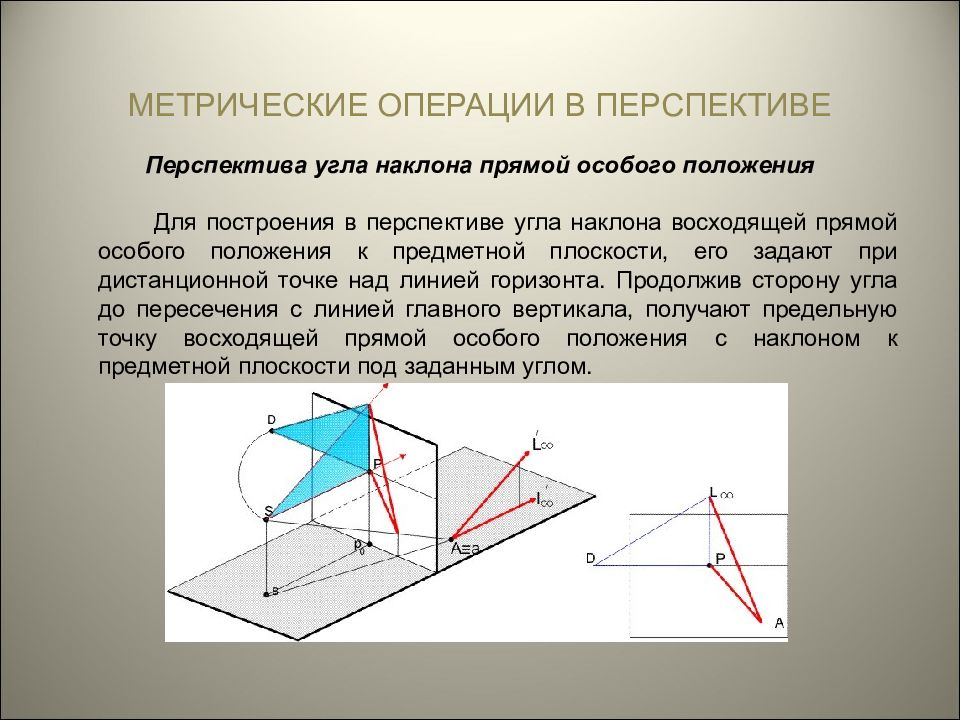
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Перспектива угла наклона прямой особого положения Для построения в перспективе угла наклона восходящей прямой особого положения к предметной плоскости, его задают при дистанционной точке над линией горизонта. Продолжив сторону угла до пересечения с линией главного вертикала, получают предельную точку восходящей прямой особого положения с наклоном к предметной плоскости под заданным углом.
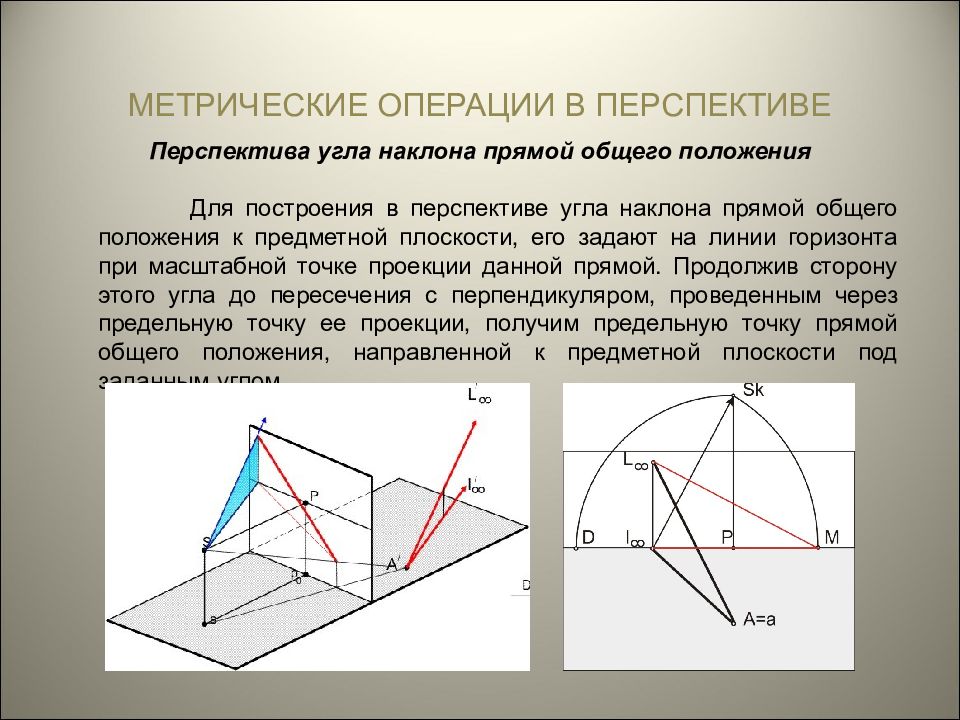
МЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ Перспектива угла наклона прямой общего положения Для построения в перспективе угла наклона прямой общего положения к предметной плоскости, его задают на линии горизонта при масштабной точке проекции данной прямой. Продолжив сторону этого угла до пересечения с перпендикуляром, проведенным через предельную точку ее проекции, получим предельную точку прямой общего положения, направленной к предметной плоскости под заданным углом.
Пример 9. Построить перспективу горизонтального квадрата, если сторона АВ задана
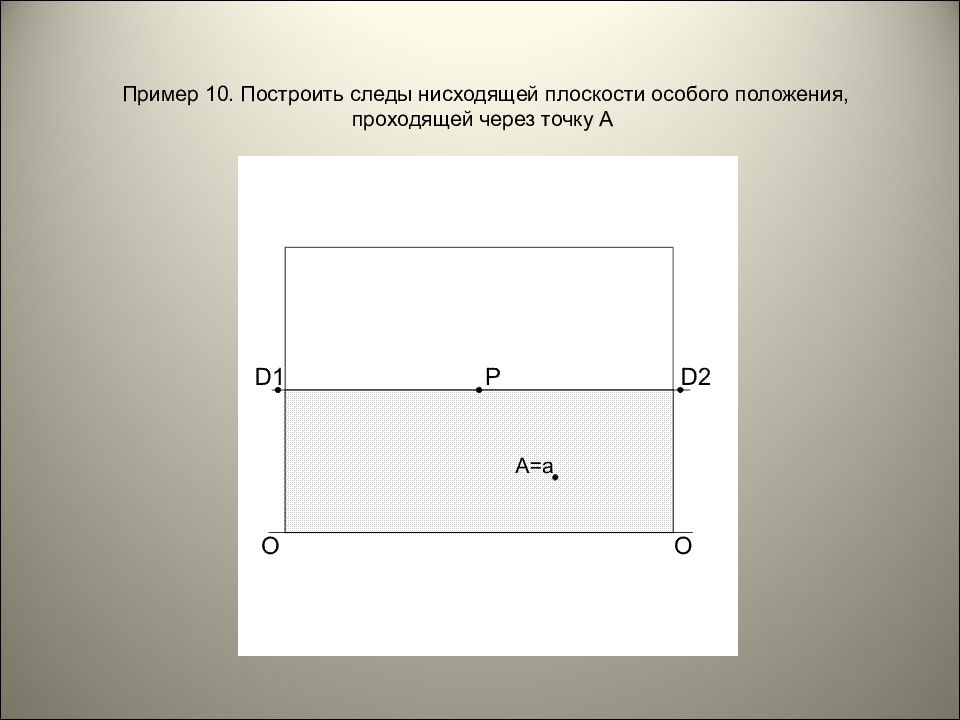
Пример 10. Построить следы нисходящей плоскости особого положения, проходящей через точку А
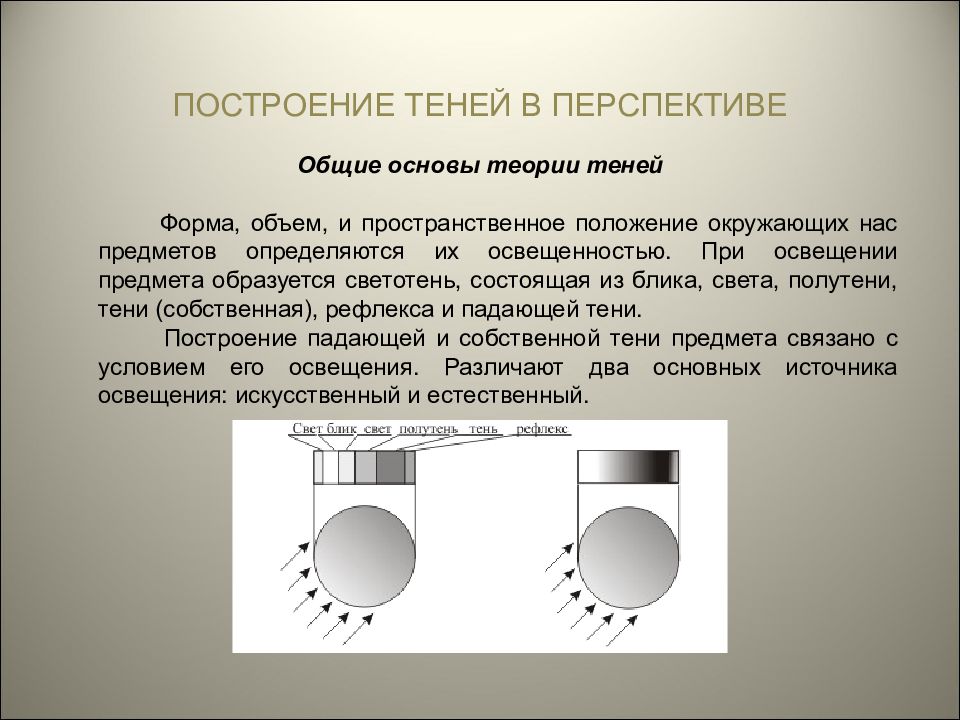
ПОСТРОЕНИЕ ТЕНЕЙ В ПЕРСПЕКТИВЕ Общие основы теории теней Форма, объем, и пространственное положение окружающих нас предметов определяются их освещенностью. При освещении предмета образуется светотень, состоящая из блика, света, полутени, тени (собственная), рефлекса и падающей тени. Построение падающей и собственной тени предмета связано с условием его освещения. Различают два основных источника освещения: искусственный и естественный.
ПОСТРОЕНИЕ ТЕНЕЙ В ПЕРСПЕКТИВЕ Построение теней при искусственном освещении Для построения падающих теней от предмета необходимо, чтобы на картине или недалеко за ее пределами были заданы проекции источника освещения и всех точек предмета, определяющих контур падающей тени на предметной плоскости. Для определения контура падающей тени от предмета строят тень от всех характерных его точек. Для этого проводят световые лучи и их проекции через светящуюся точку и точки предмета. Точка пересечения луча и его проекции определит падающую тень от каждой вершины предмета, а линия, соединяющая их, очертание контура всей тени
ПОСТРОЕНИЕ ТЕНЕЙ В ПЕРСПЕКТИВЕ Построение теней при солнечном освещении Солнечное освещение – это частный случай точечного освещения, когда источник света удален на бесконечно большое расстояние. Поэтому принцип построения теней один и тот же. Лучи света при солнечном освещении принимают за параллельные. На картине точку схода лучей задают выше или ниже линии горизонта, а ее проекцию - на линии горизонта. Если источник освещения необходимо задать спереди, на картине его задают выше линии горизонта, если сзади – ниже линии горизонта, если сбоку – лучи задают параллельно картине, а их проекции – параллельно основанию картины.
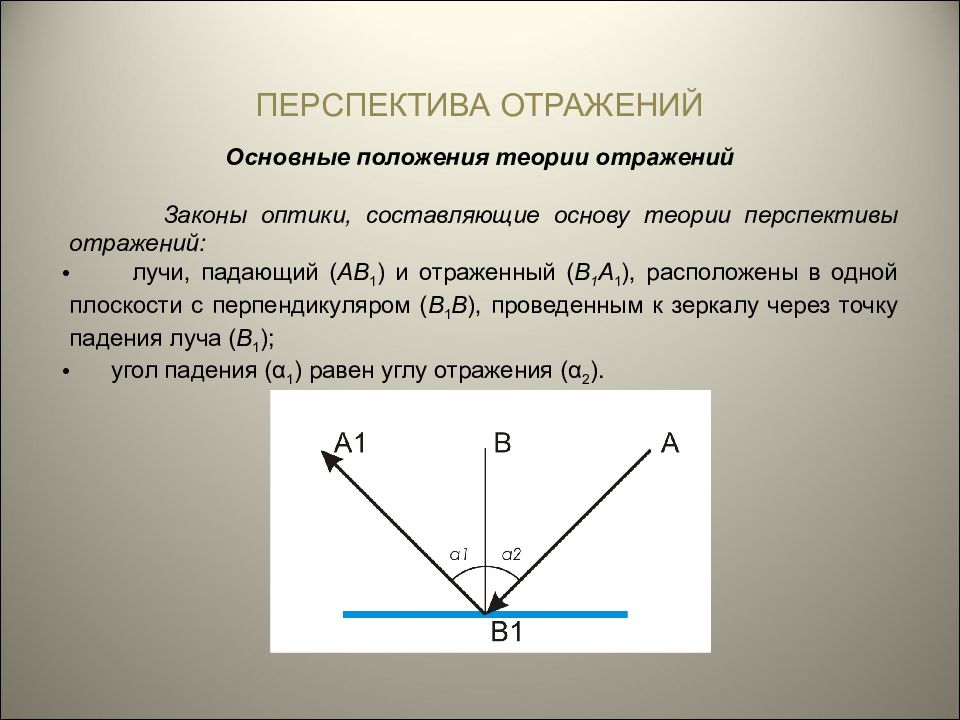
ПЕРСПЕКТИВА ОТРАЖЕНИЙ Основные положения теории отражений Законы оптики, составляющие основу теории перспективы отражений: лучи, падающий ( АВ 1 ) и отраженный ( В 1 А 1 ), расположены в одной плоскости с перпендикуляром ( В 1 В ), проведенным к зеркалу через точку падения луча ( В 1 ); угол падения (α 1 ) равен углу отражения (α 2 ).
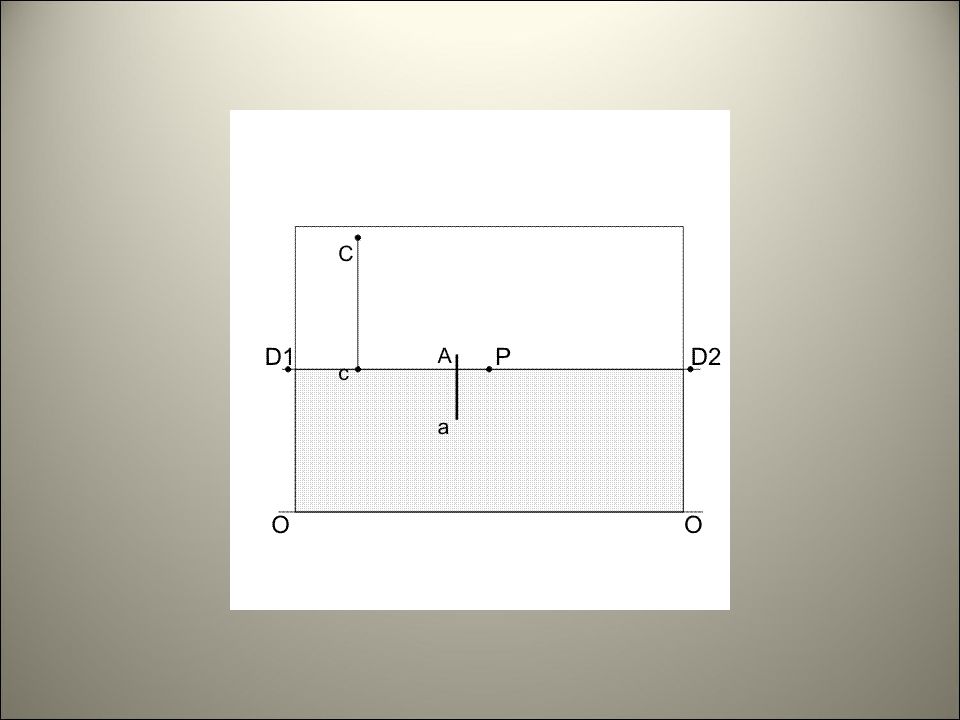
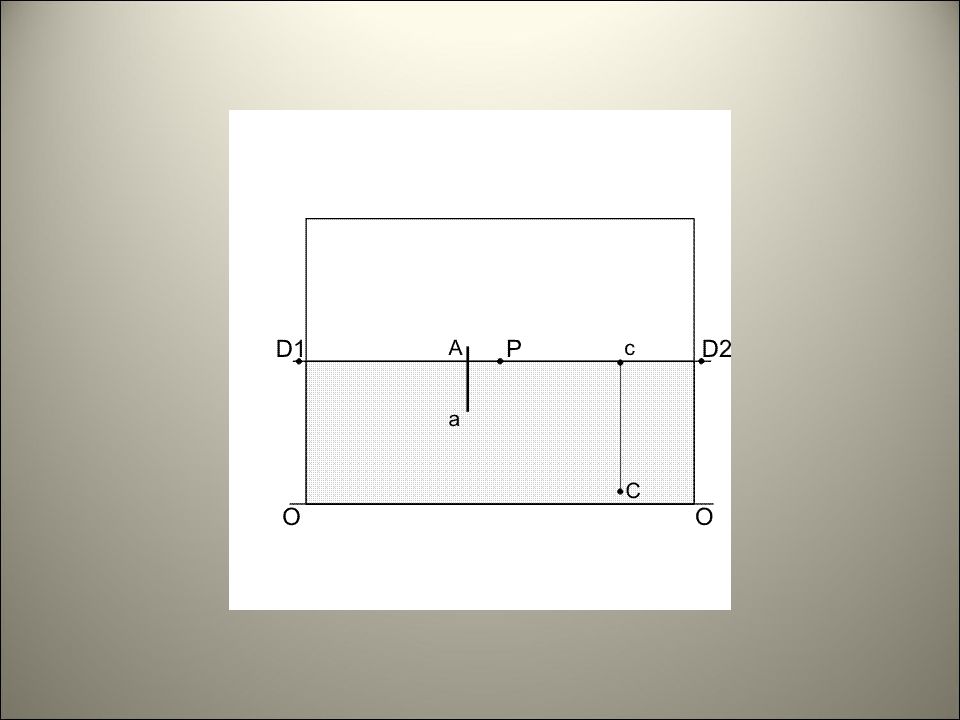
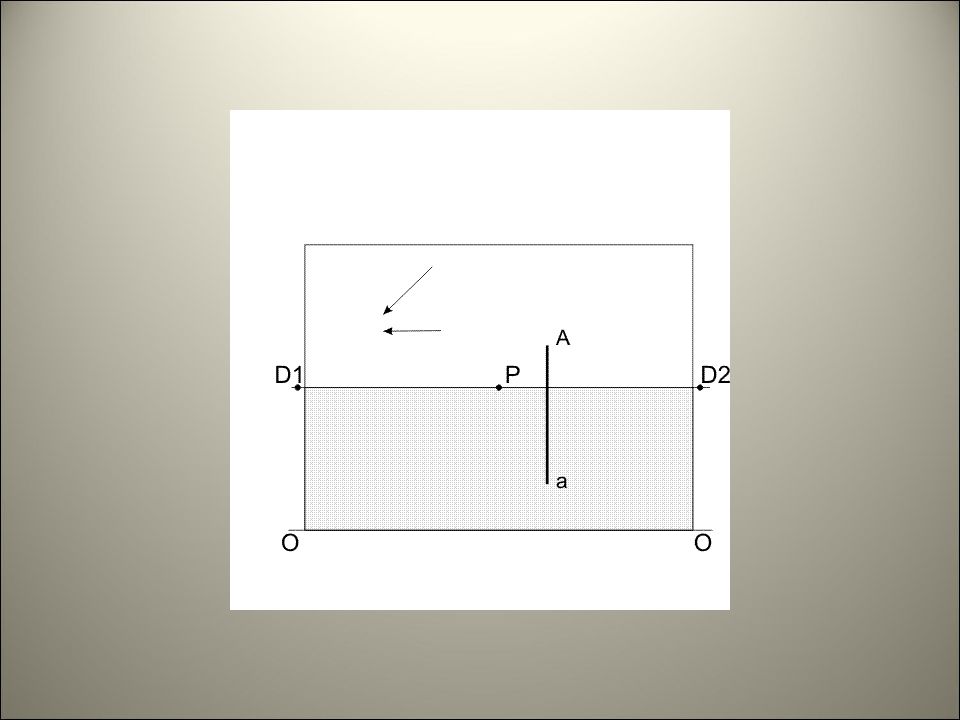
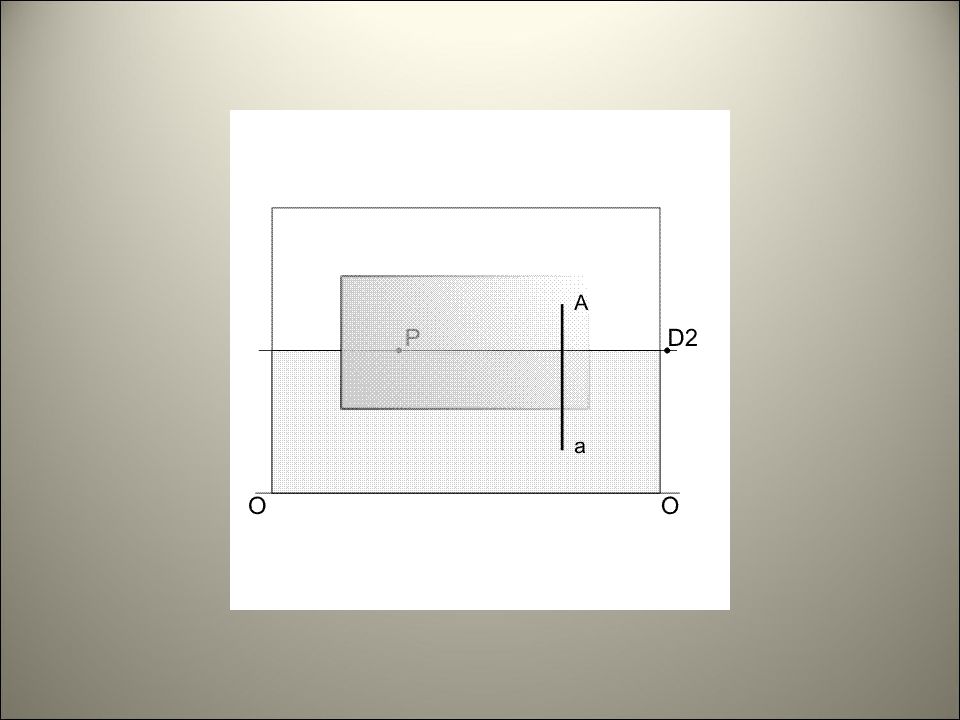
ПЕРСПЕКТИВА ОТРАЖЕНИЙ Построение перспективы отражений в плоских зеркалах Плоскость зеркала может располагаться относительно плоскостей зеркала по-разному: - параллельно картине; - параллельно предметной плоскости; - перпендикулярно картине, произвольно предметной плоскости; - перпендикулярно предметной, произвольно картинной плоскости; - перпендикулярно одновременно двум плоскостям проекций, - занимать особое или общее положение.
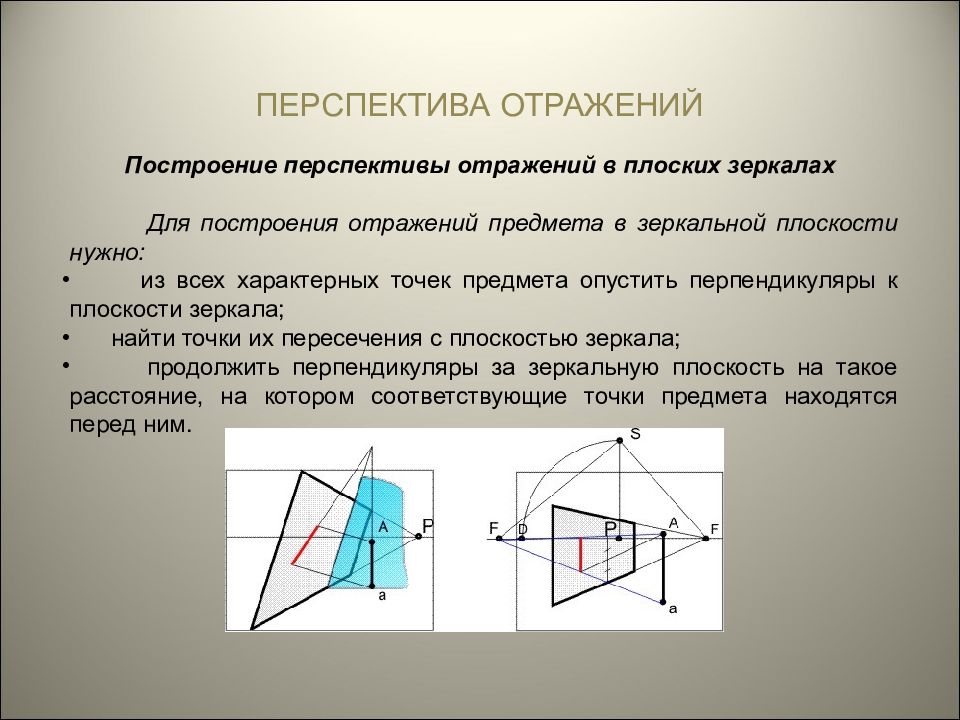
ПЕРСПЕКТИВА ОТРАЖЕНИЙ Построение перспективы отражений в плоских зеркалах Для построения отражений предмета в зеркальной плоскости нужно: из всех характерных точек предмета опустить перпендикуляры к плоскости зеркала; найти точки их пересечения с плоскостью зеркала; продолжить перпендикуляры за зеркальную плоскость на такое расстояние, на котором соответствующие точки предмета находятся перед ним.
