Первый слайд презентации
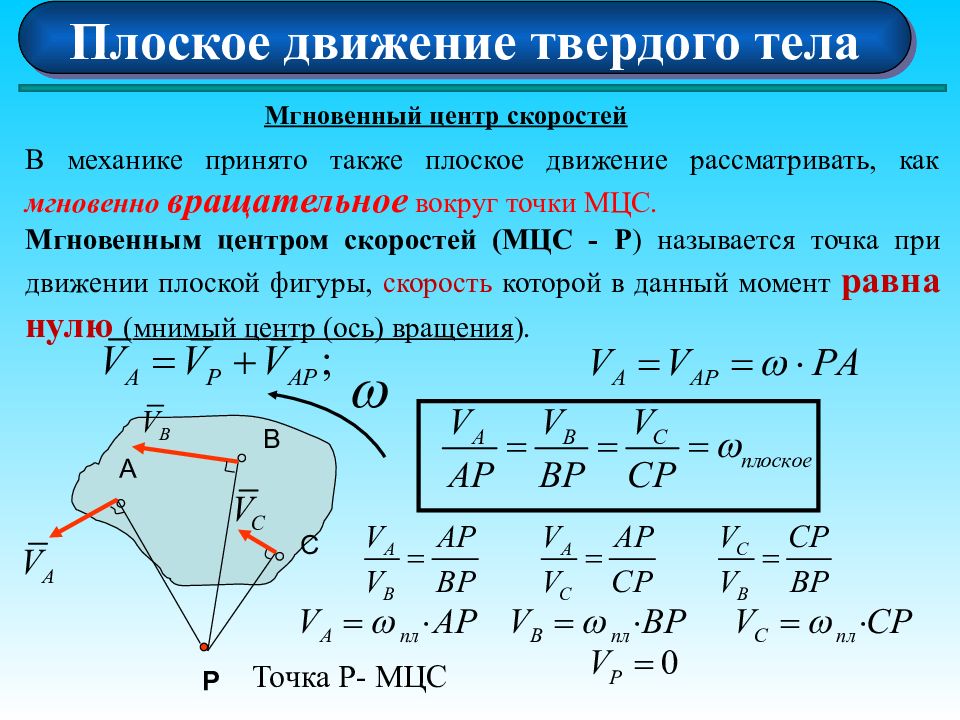
Плоское движение твердого тела Мгновенный центр скоростей В механике принято также плоское движение рассматривать, как мгновенно вращательное вокруг точки МЦС. Мгновенным центром скоростей (МЦС - Р ) называется точка при движении плоской фигуры, скорость которой в данный момент равна нулю ( мнимый центр (ось) вращения ). P A B C Точка Р- МЦС
Слайд 2
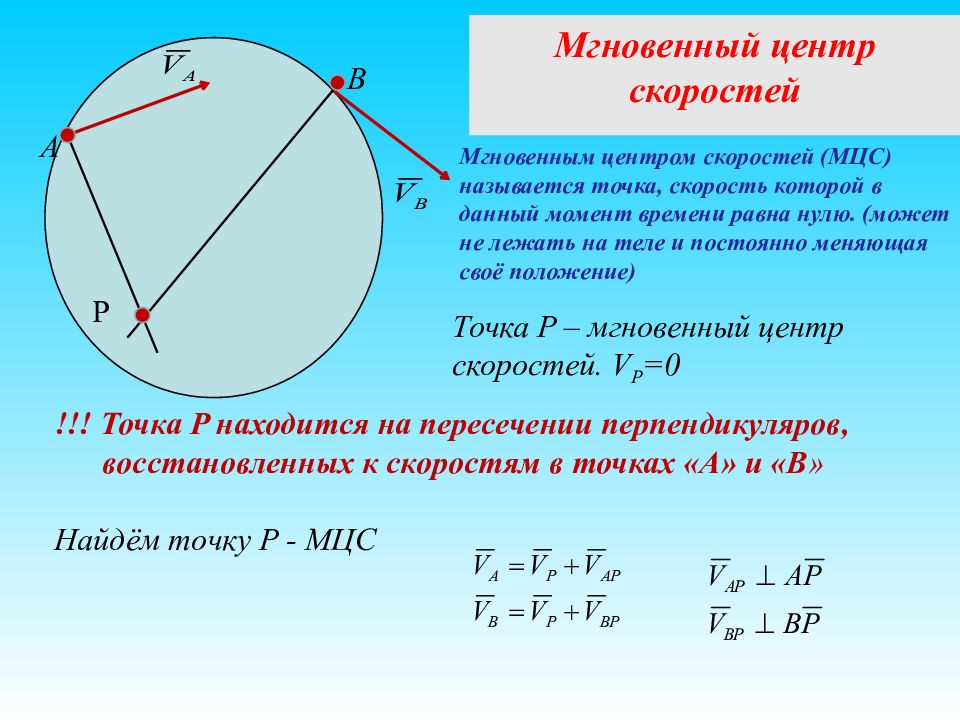
A P B Точка P – мгновенный центр скоростей. V P =0 !!! Точка P находится на пересечении перпендикуляров, восстановленных к скоростям в точках «А» и «В » Мгновенный центр скоростей Мгновенным центром скоростей (МЦС) называется точка, скорость которой в данный момент времени равна нулю. (может не лежать на теле и постоянно меняющая своё положение) Найдём точку P - МЦС
Слайд 3
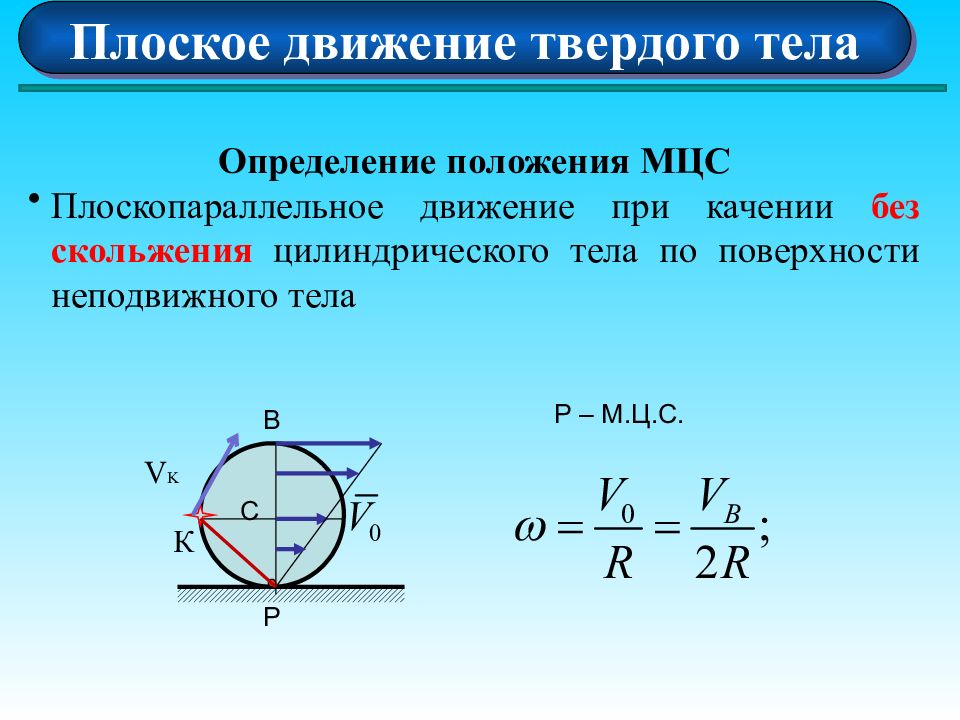
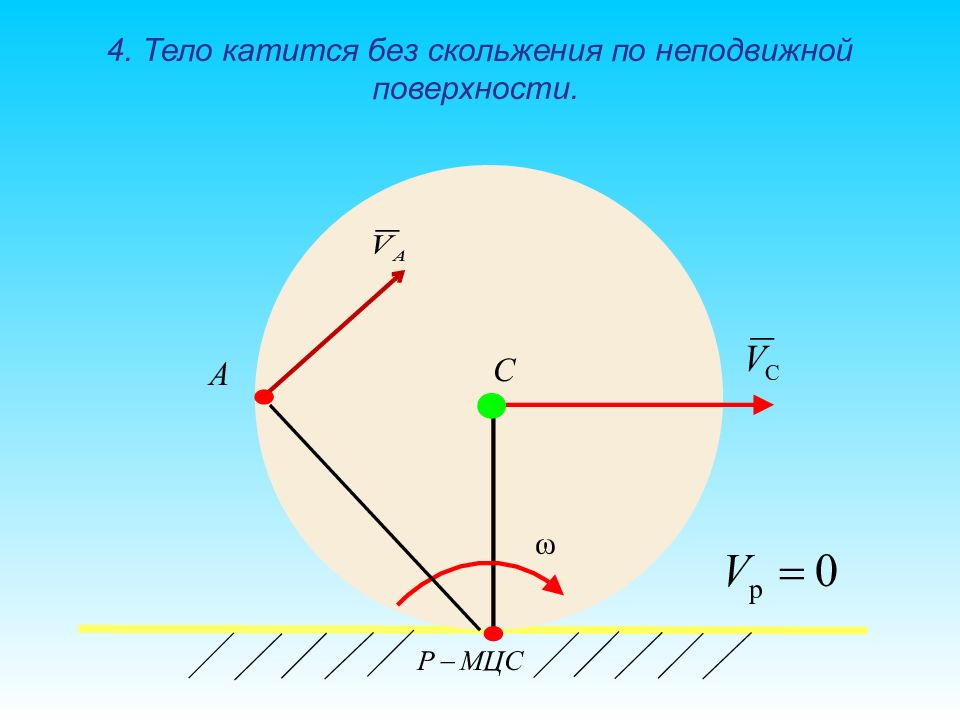
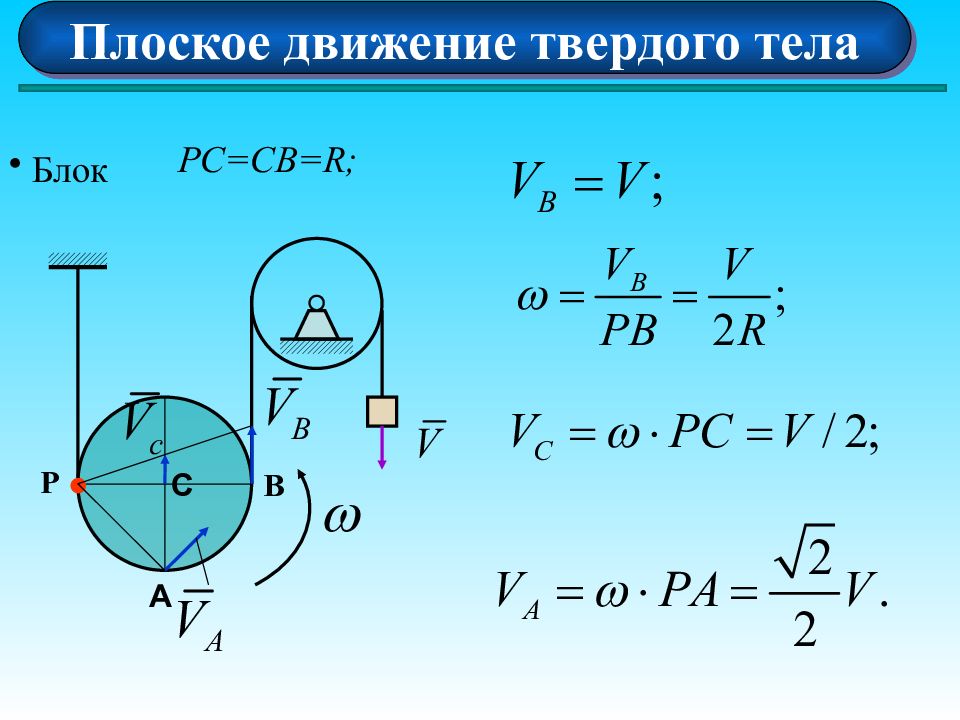
Плоское движение твердого тела Определение положения МЦС Плоскопараллельное движение при качении без скольжения цилиндрического тела по поверхности неподвижного тела C P B P – M.Ц.С. К V K
Слайд 4
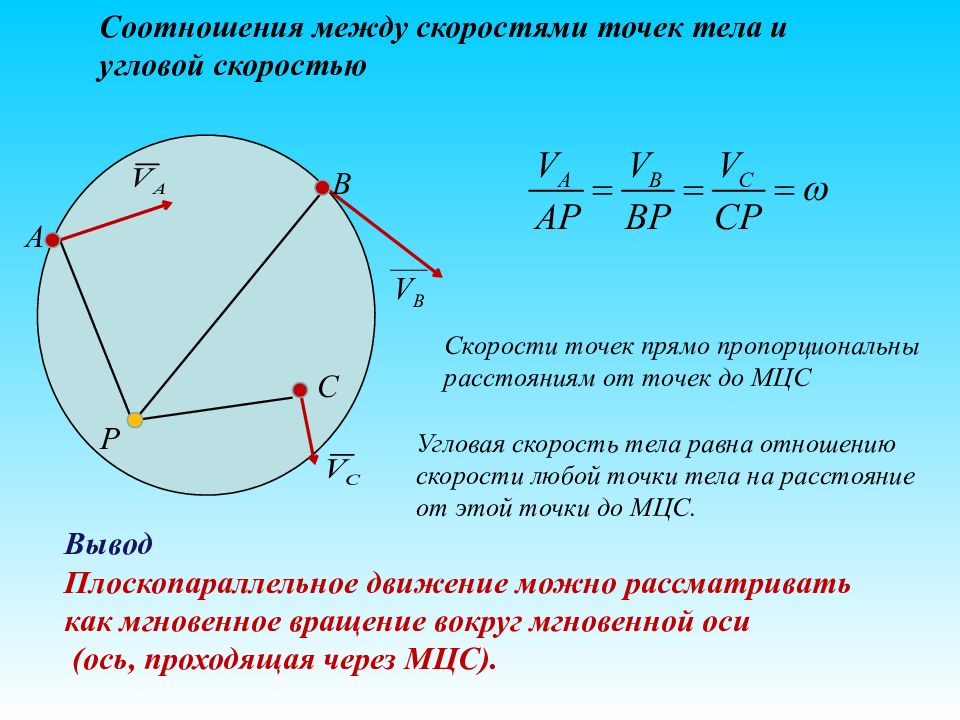
Соотношения между скоростями точек тела и угловой скоростью Вывод Плоскопараллельное движение можно рассматривать как мгновенное вращение вокруг мгновенной оси (ось, проходящая через МЦС). P A B V B С Скорости точек прямо пропорциональны расстояниям от точек до МЦС Угловая скорость тела равна отношению скорости любой точки тела на расстояние от этой точки до МЦС.
Слайд 6
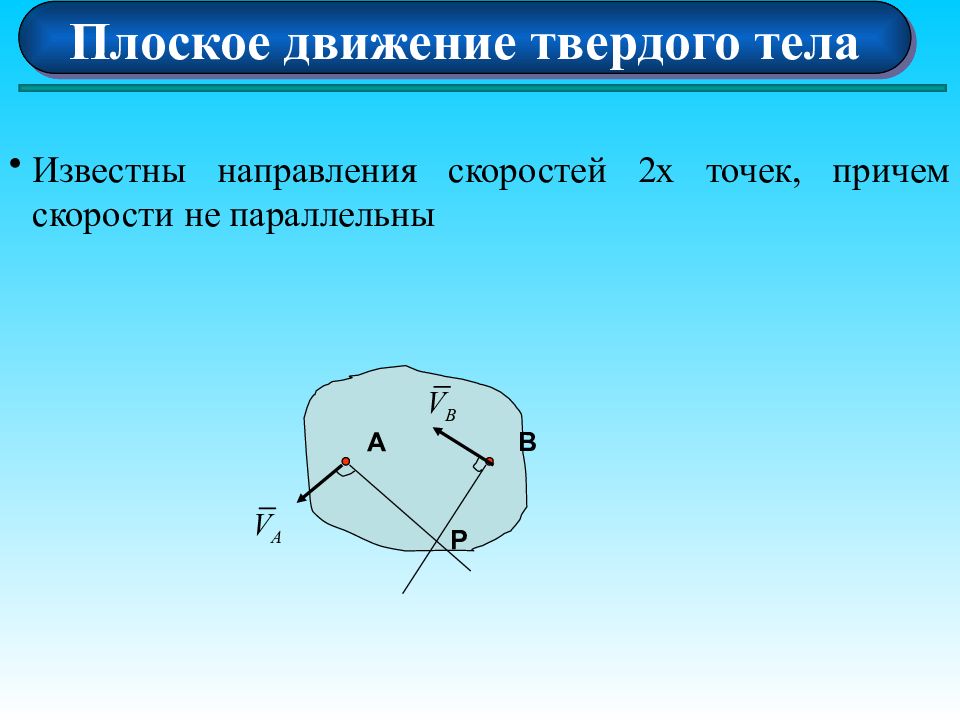
Плоское движение твердого тела Известны направления скоростей 2х точек, причем скорости не параллельны А В Р
Слайд 7
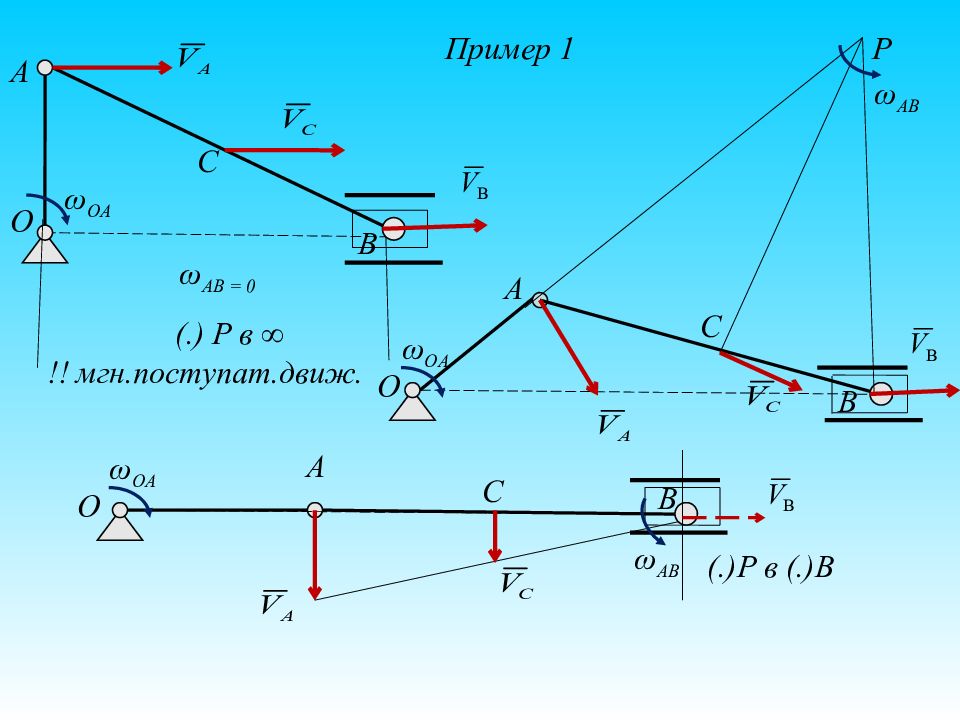
O O O A A A B B B C C C ω OA ω OA ω OA ω AB = 0 ω AB ω AB (.) P в ∞ !! мгн.поступат.движ. (.) P в (.)В P Пример 1
Слайд 8
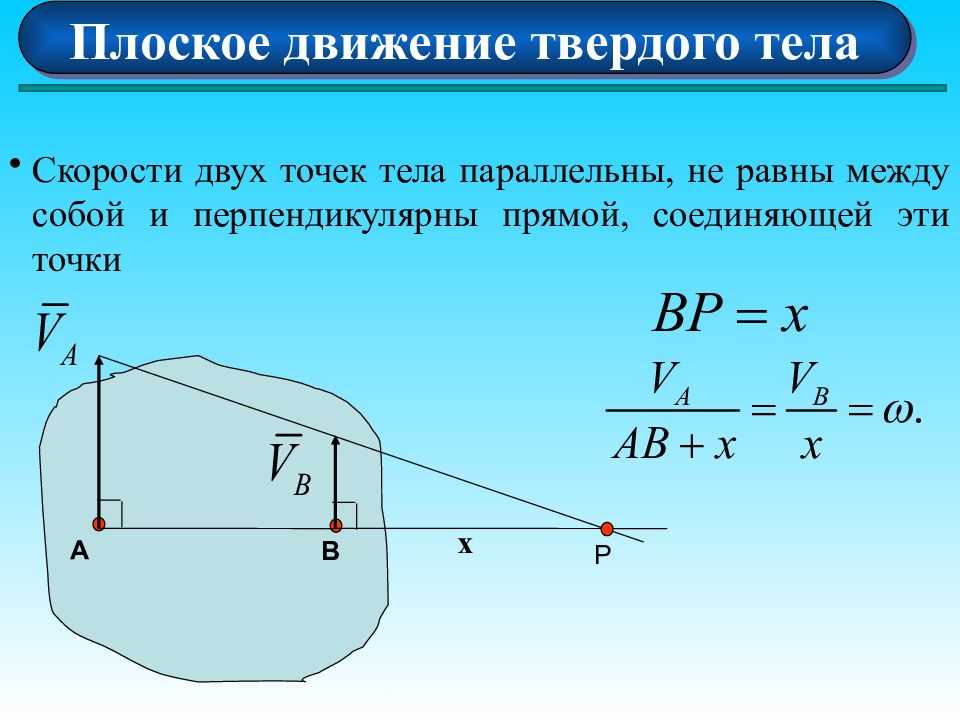
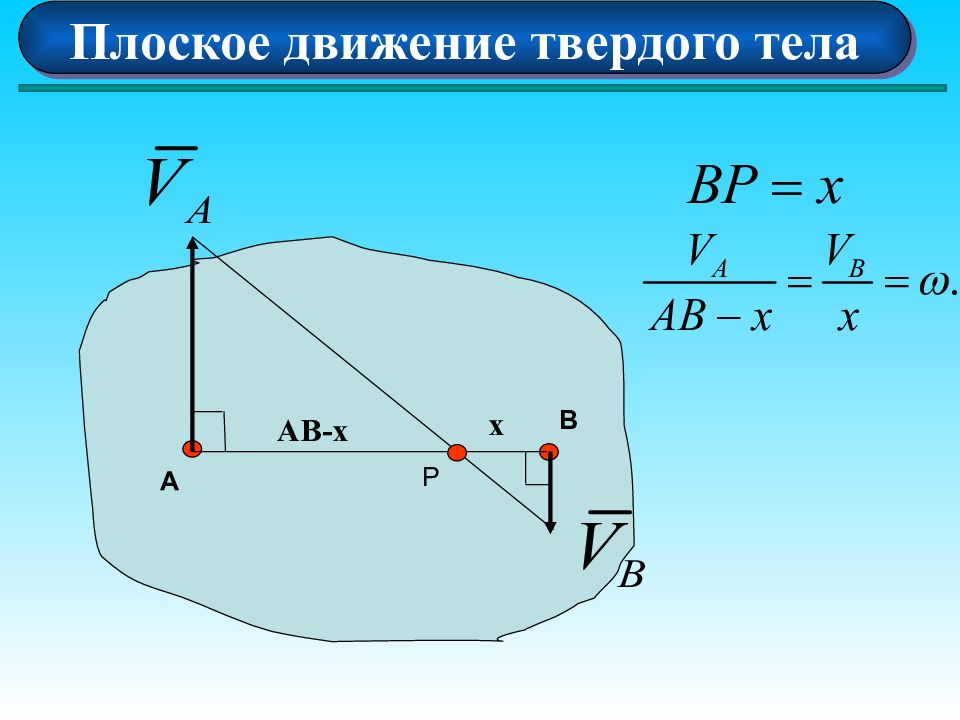
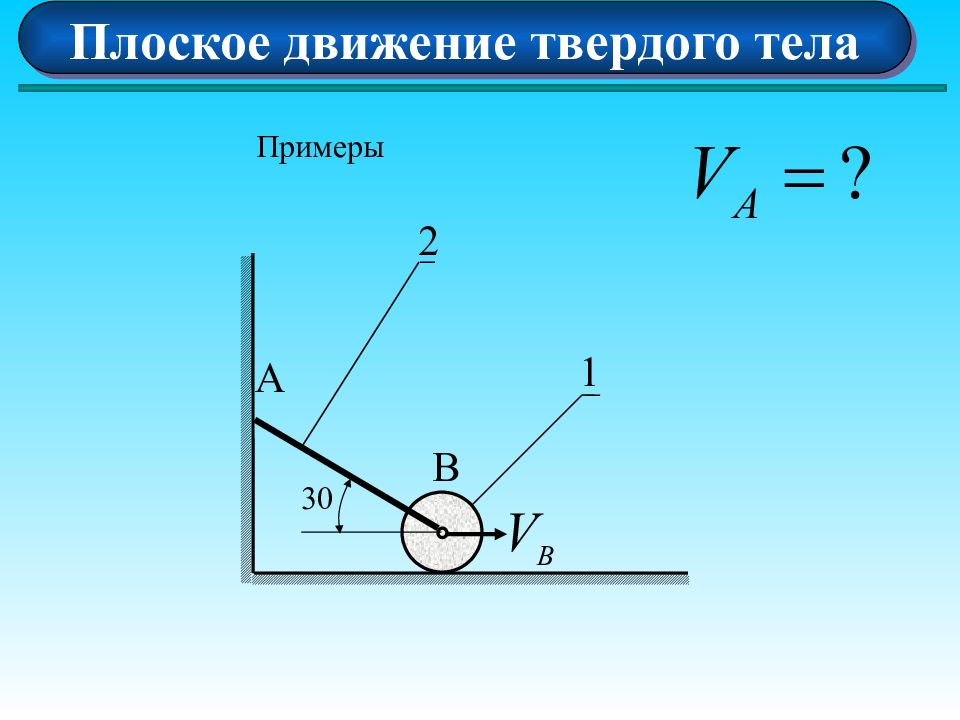
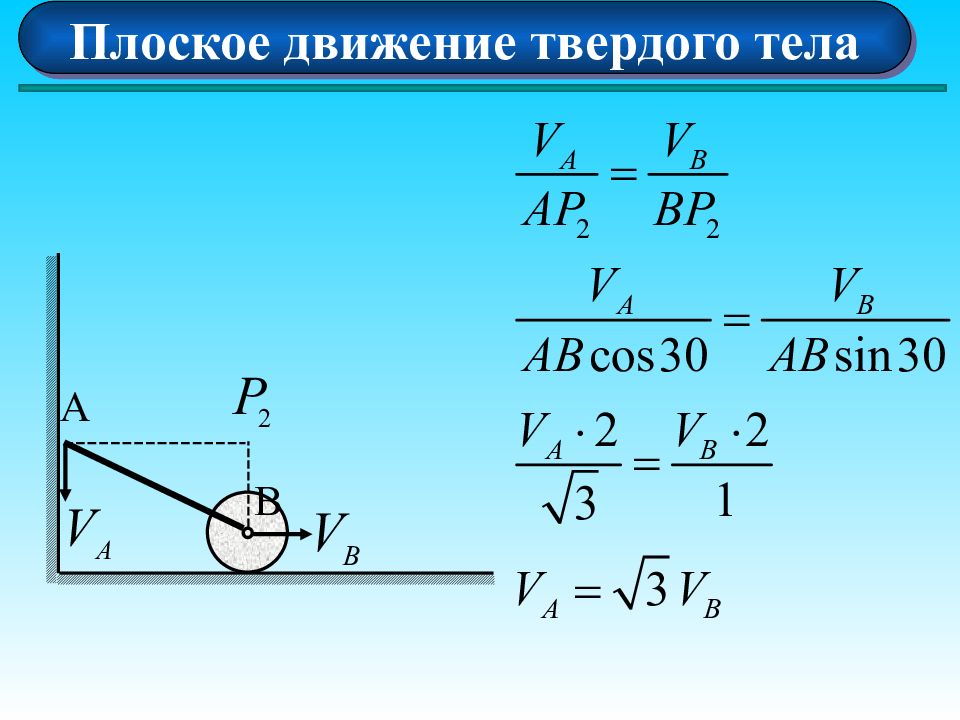
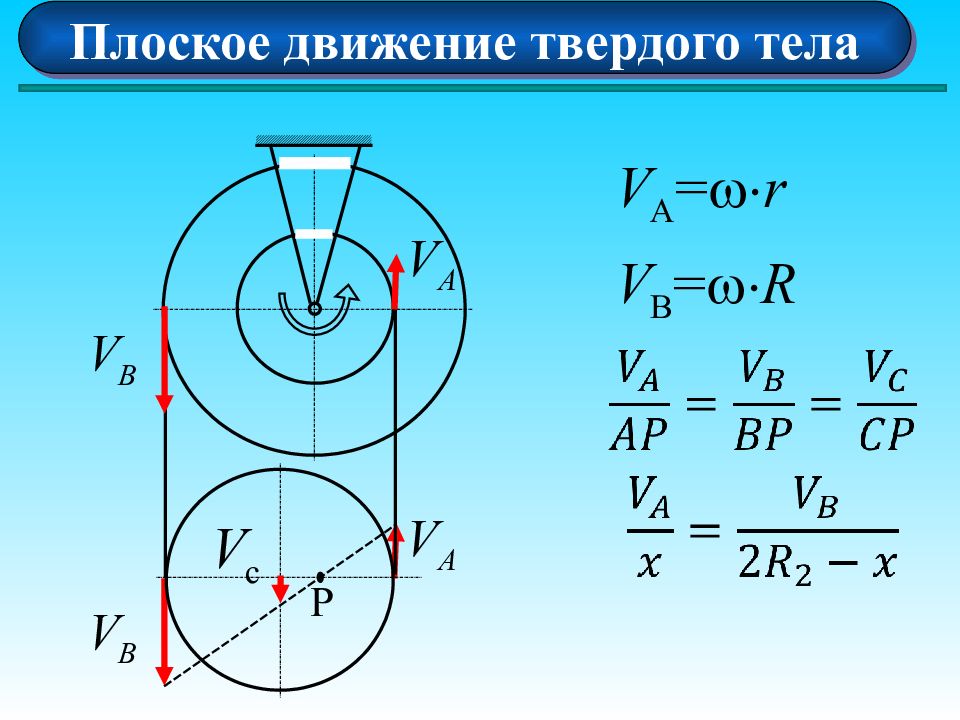
Плоское движение твердого тела Скорости двух точек тела параллельны, не равны между собой и перпендикулярны прямой, соединяющей эти точки А В Р х
Слайд 10
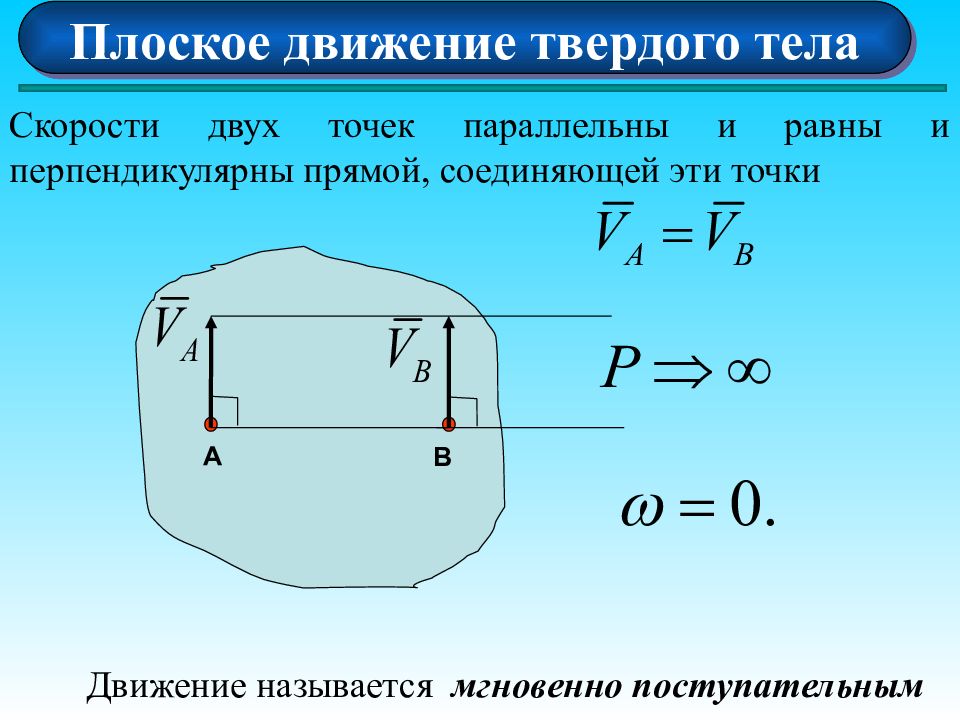
Плоское движение твердого тела Скорости двух точек параллельны и равны и перпендикулярны прямой, соединяющей эти точки Движение называется мгновенно поступательным А В
Слайд 11
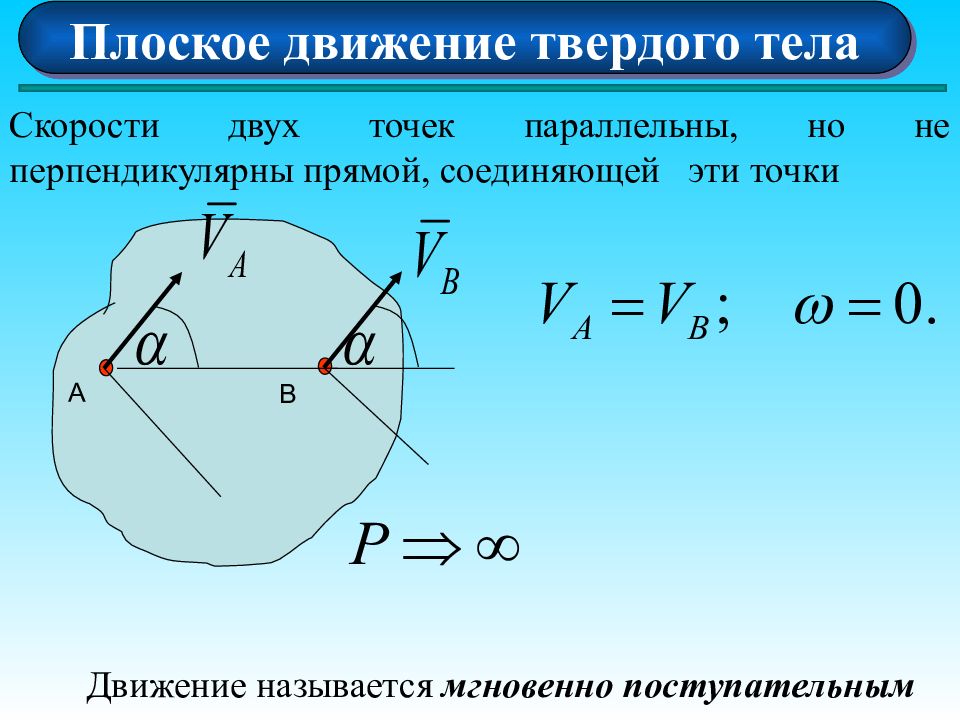
Плоское движение твердого тела Скорости двух точек параллельны, но не перпендикулярны прямой, соединяющей эти точки А В Движение называется мгновенно поступательным
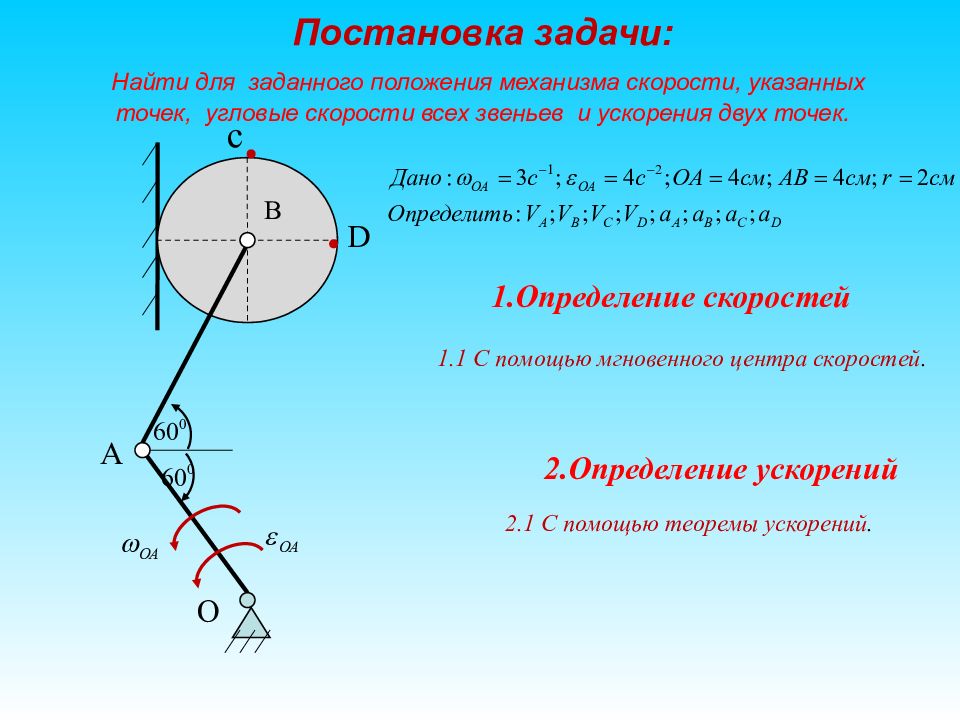
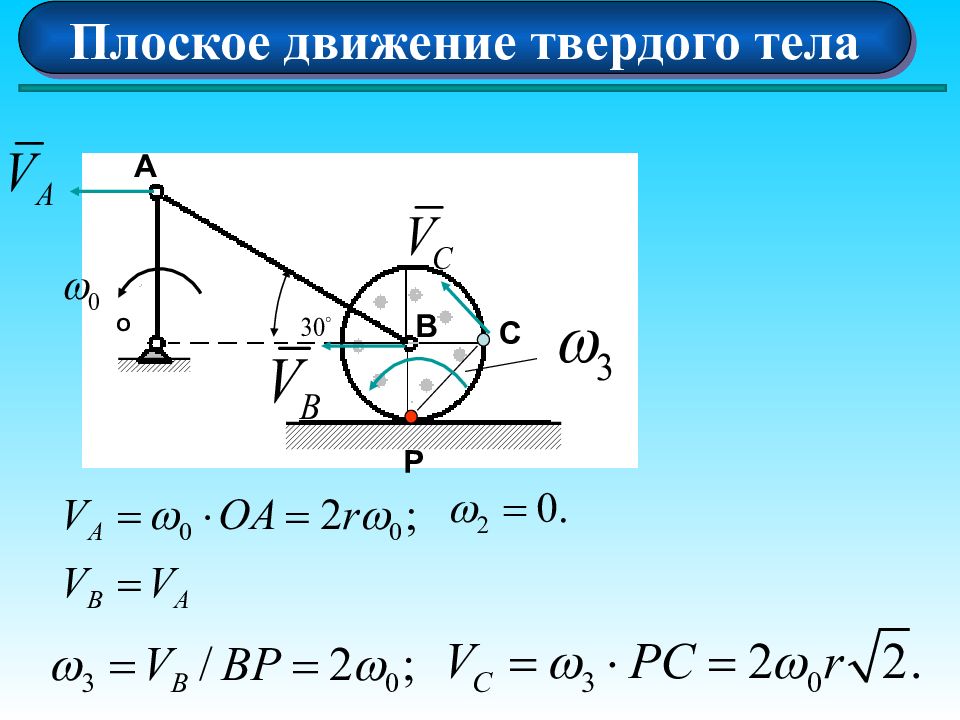
A D O В с 1.1 С помощью мгновенного центра скоростей. 1.Определение скоростей 2.Определение ускорений 2.1 С помощью теоремы ускорений. В
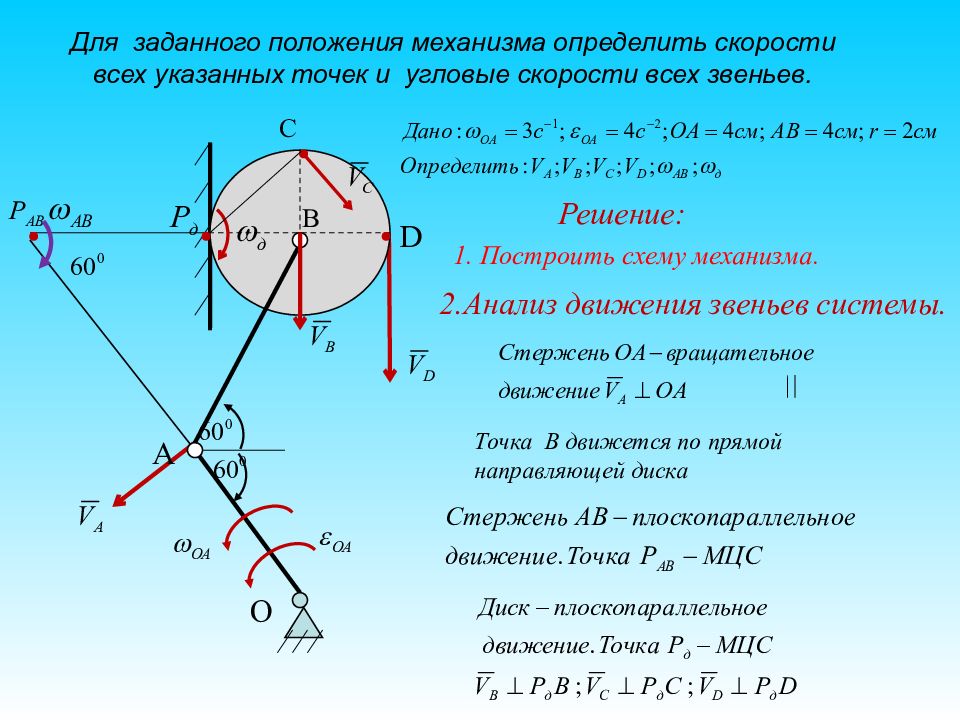
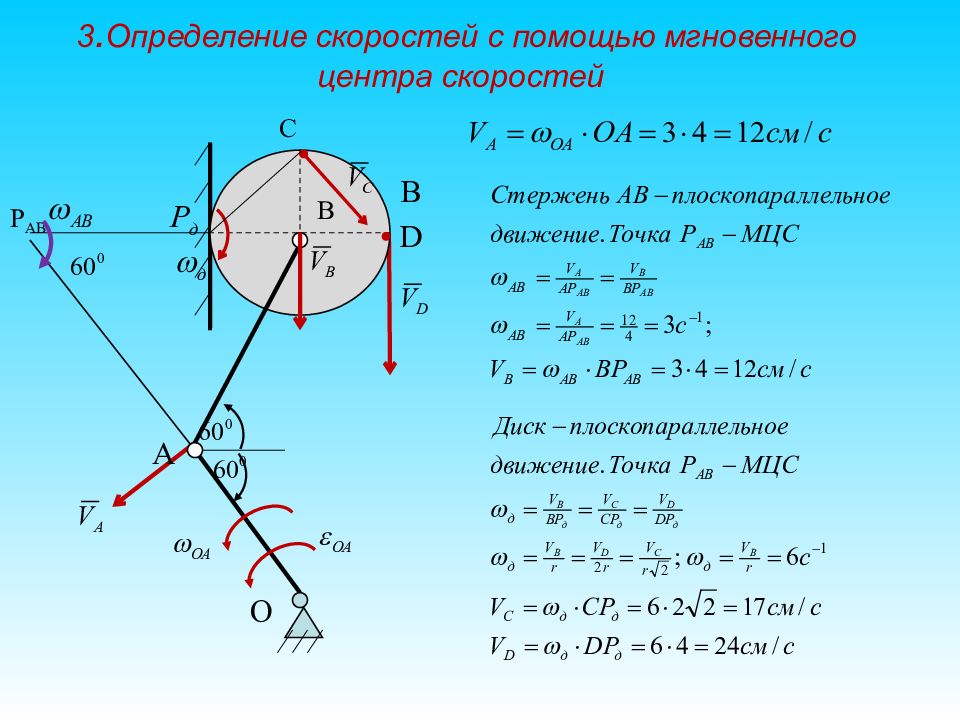
Слайд 13: Для заданного положения механизма определить скорости всех указанных точек и угловые скорости всех звеньев
С P AB Решение: 2.Анализ движения звеньев системы. A D O В В Точка В движется по прямой направляющей диска 1. Построить схему механизма.
В A D O В В P AB С
Слайд 19
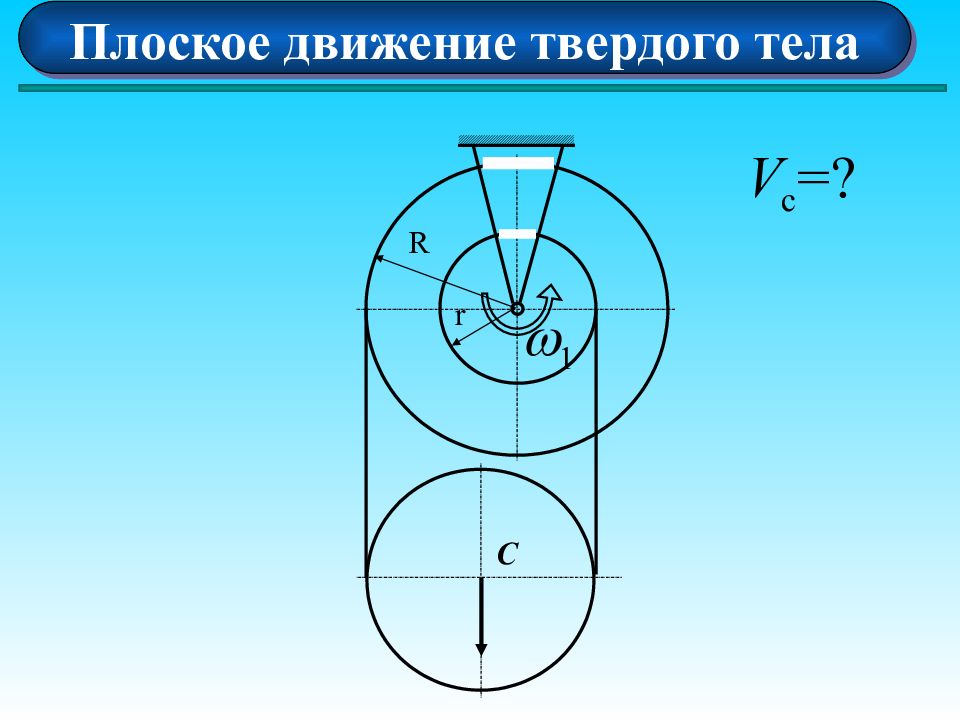
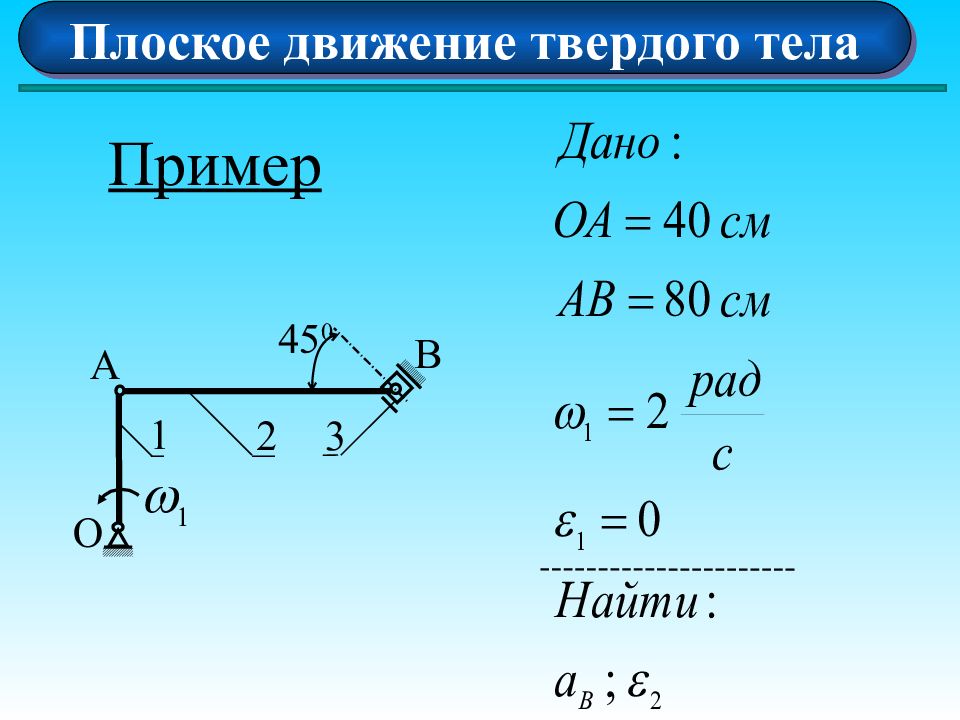
Плоское движение твердого тела O A B C 1 2 3 Дано: Качение без скольжения
Слайд 22
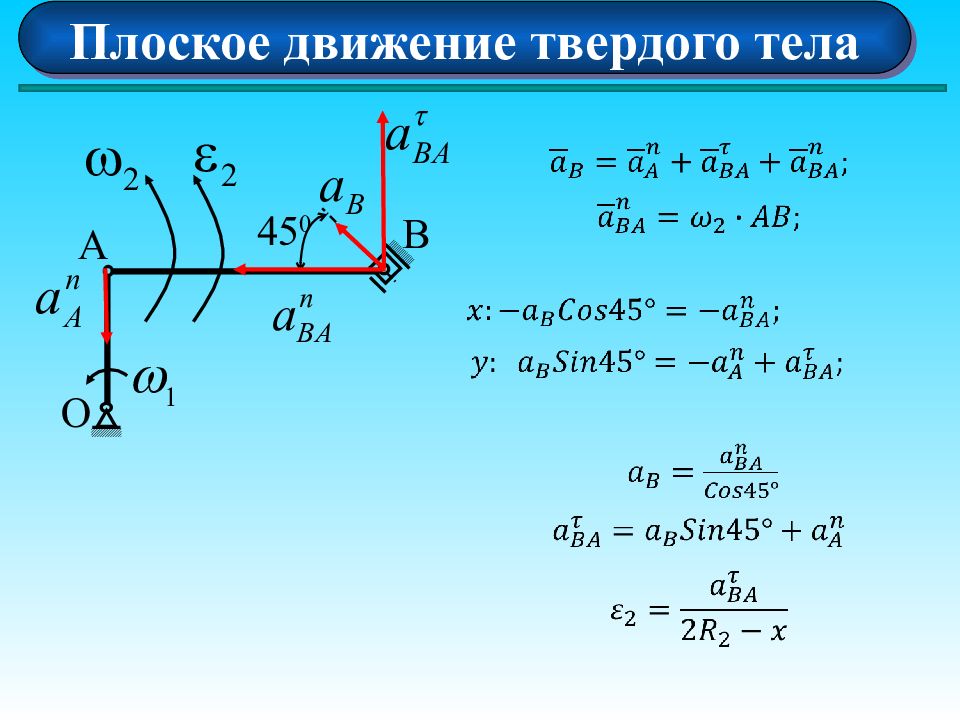
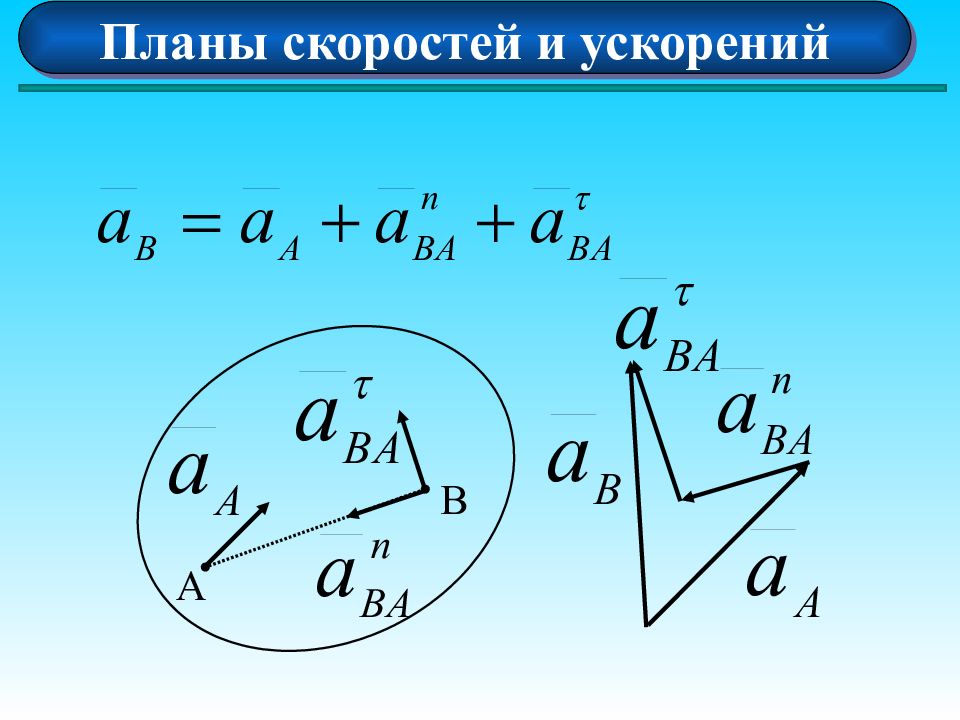
Плоское движение твердого тела Ускорения точек плоской фигуры Ускорение любой точки А геометрически складывается из ускорения полюса О и осестремительного и вращательного ускорений во вращении тела вокруг полюса O A
Слайд 24
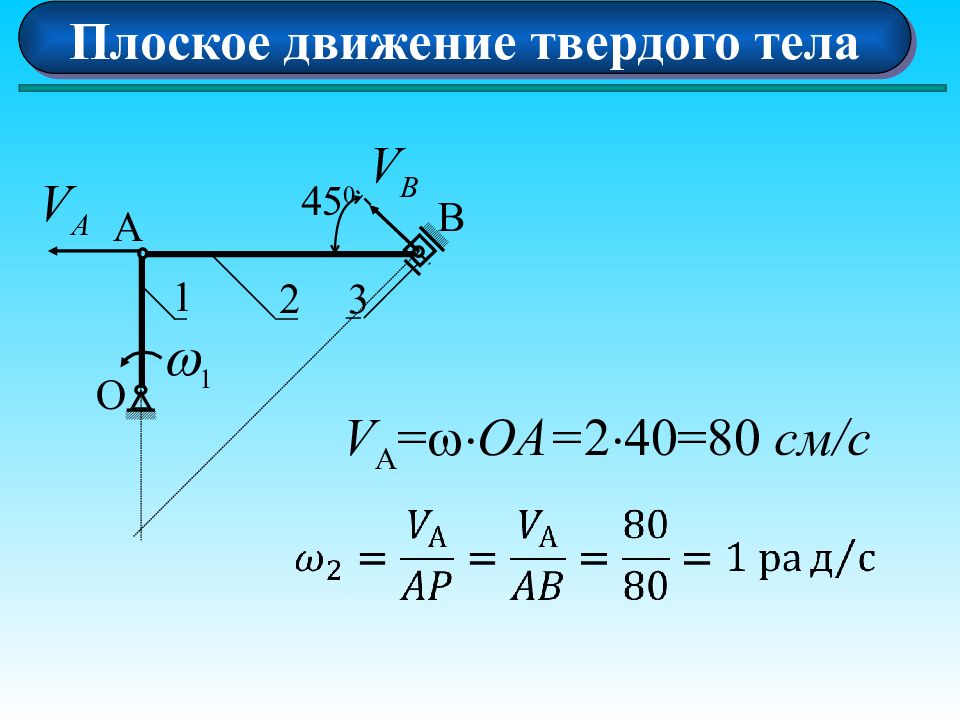
Плоское движение твердого тела О А В 1 2 3 45 0 V A = OA= 2 40=80 см/ c
Слайд 26
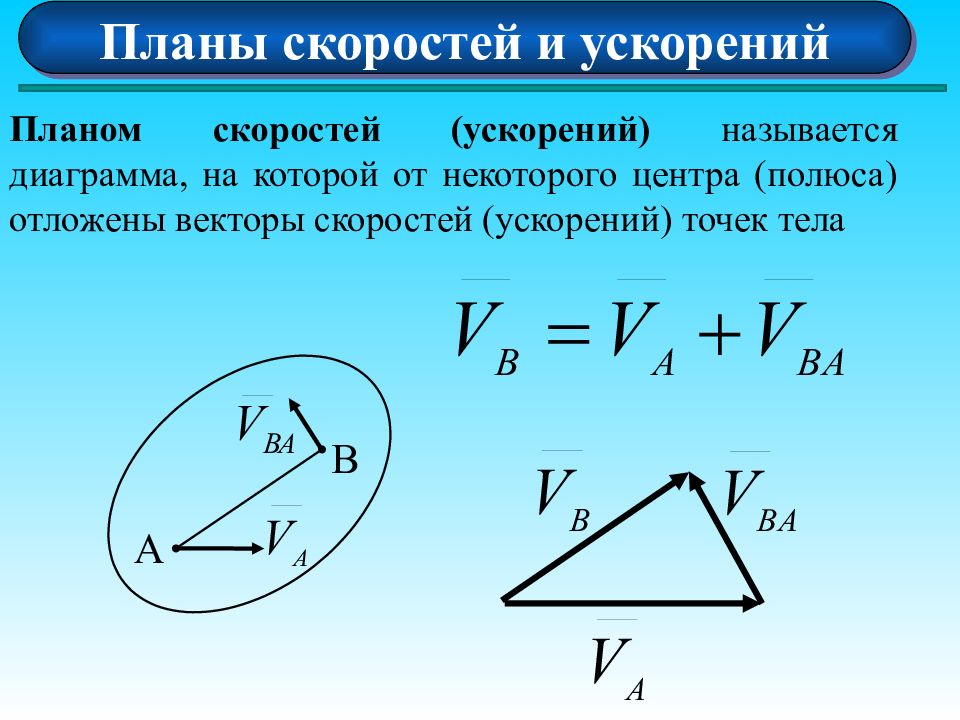
Планы скоростей и ускорений Планом скоростей (ускорений) называется диаграмма, на которой от некоторого центра (полюса) отложены векторы скоростей (ускорений) точек тела А В
Слайд 28
Планы скоростей и ускорений Свойства планов скоростей и ускорений Векторы выходящие из полюса плана скоростей (ускорений) изображают в масштабе векторы абсолютных скоростей (ускорений) соответствующих точек Отрезки, соединяющие концы векторов, выходящих из полюса, изображают в масштабе векторы относительных скоростей (ускорений) соответствующих точек Сходственные фигуры звеньев на плане механизма и плане скоростей (ускорений) – подобны Примечание (правило обхода букв) : направление обхода букв сходственных фигур на плане механизма и плане скоростей (ускорений)- одинаково
Слайд 29
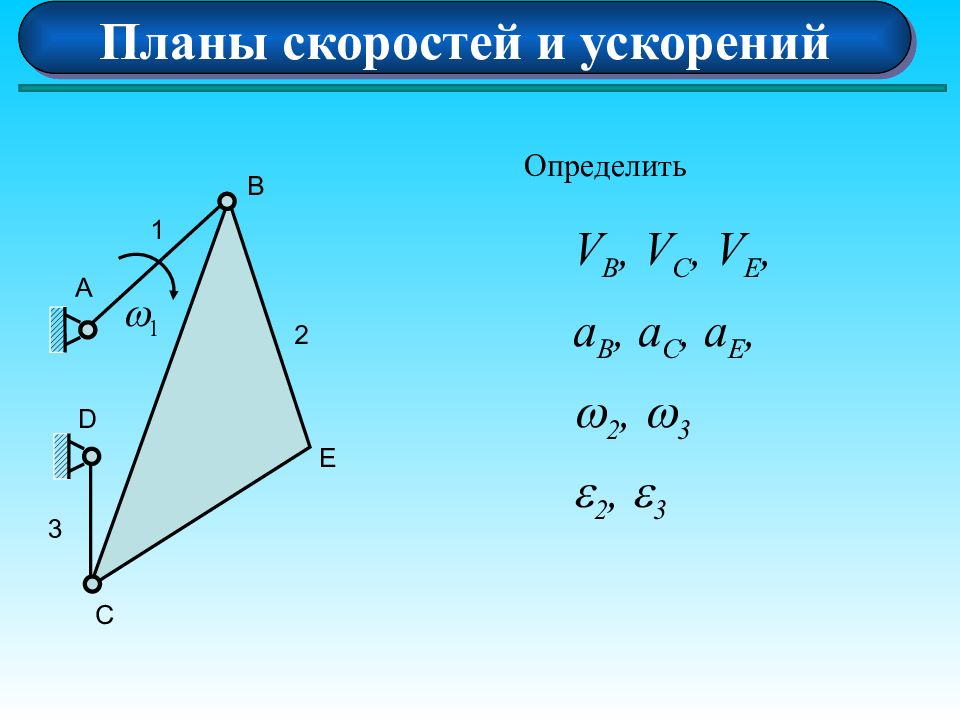
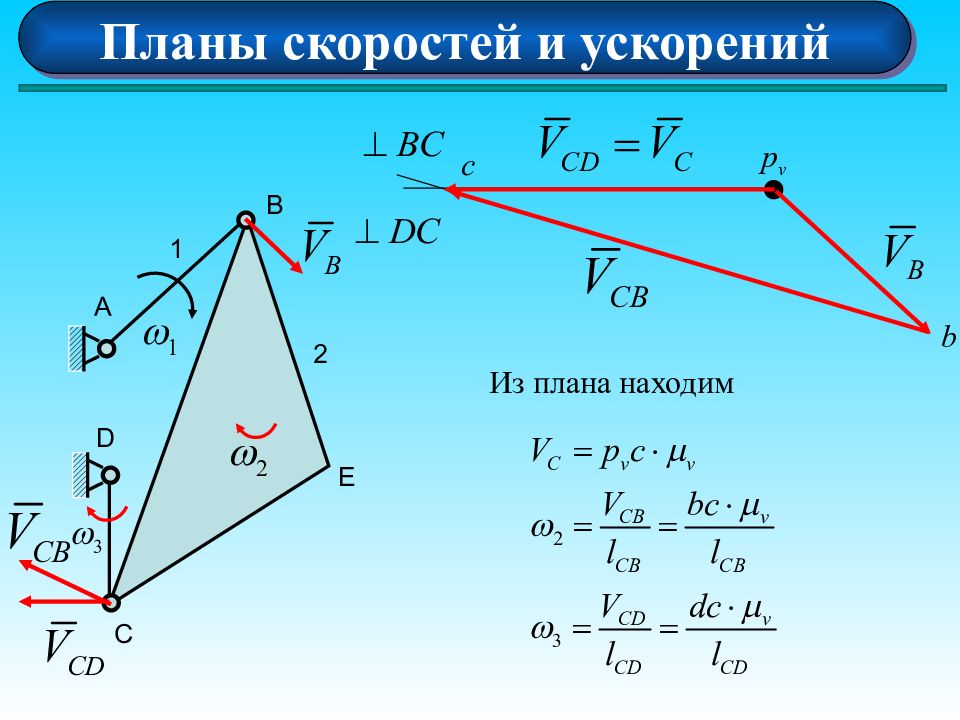
Планы скоростей и ускорений А 1 D B E C 2 3 Определить V B, V C, V E, a B, a C, a E, 2, 3 2, 3
Слайд 30
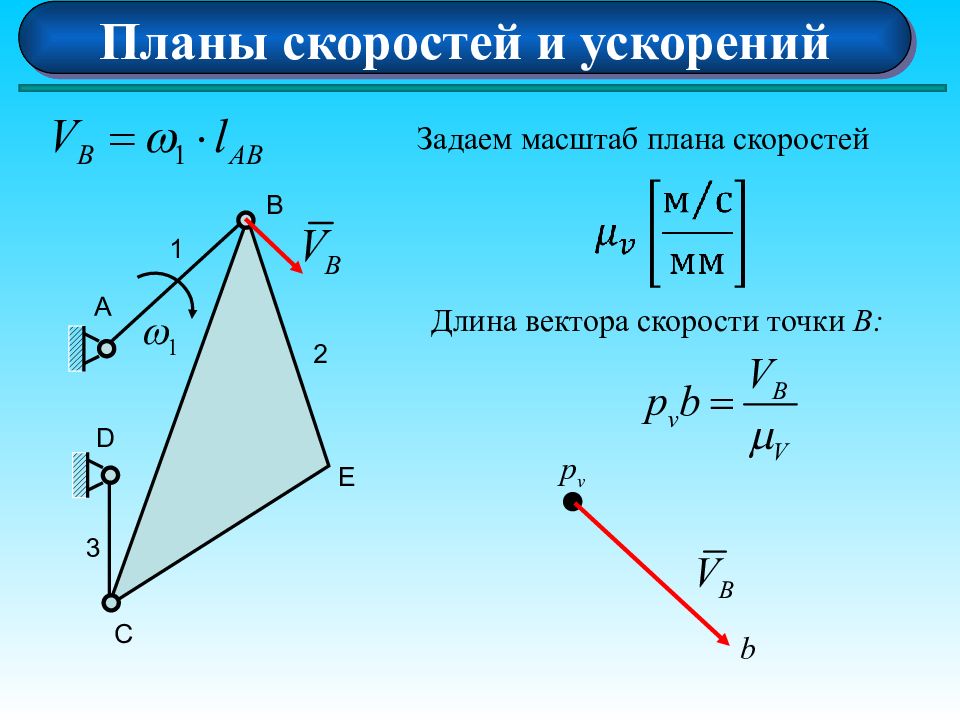
Планы скоростей и ускорений А 1 D B E C 2 3 Задаем масштаб плана скоростей Длина вектора скорости точки В : p v b
Слайд 33
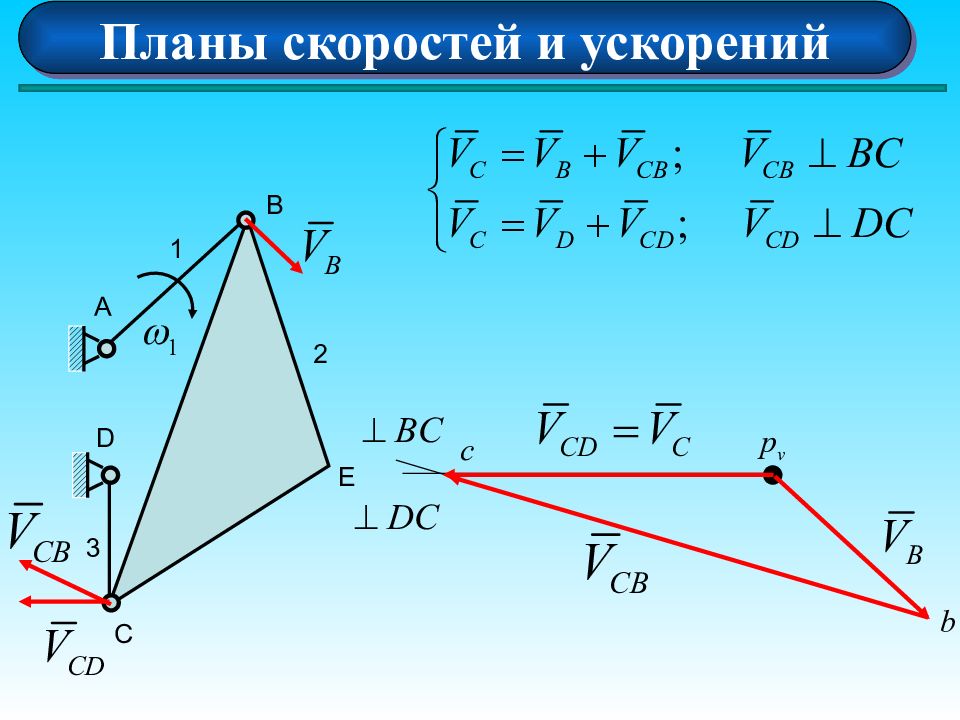
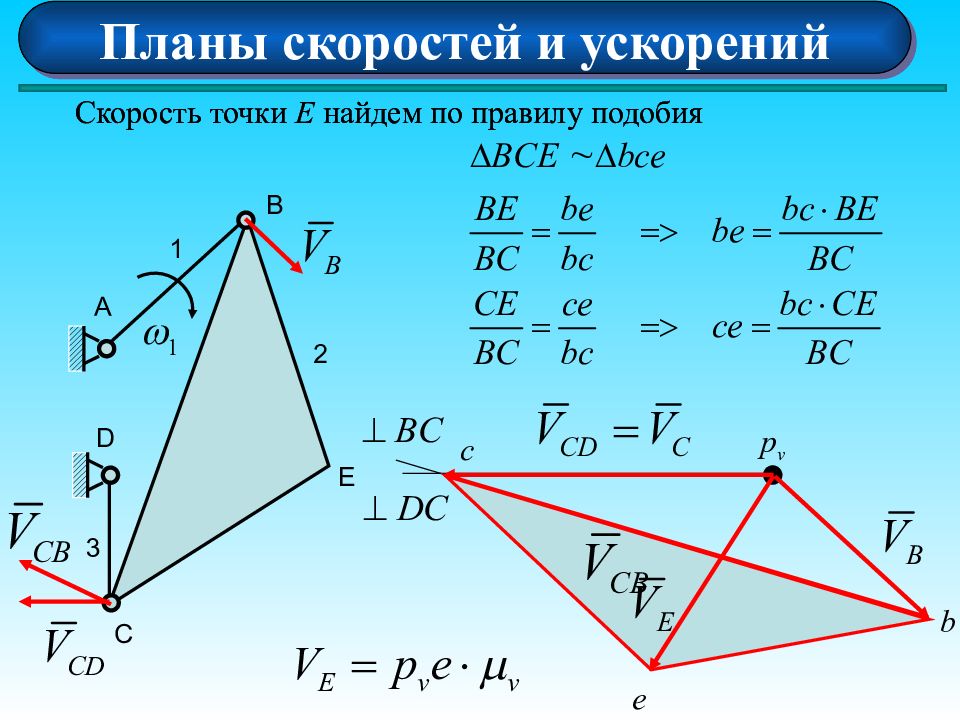
Планы скоростей и ускорений А 1 D B E C 2 3 p v b c Скорость точки Е найдем по правилу подобия e Скорость точки Е найдем по правилу подобия
Слайд 34
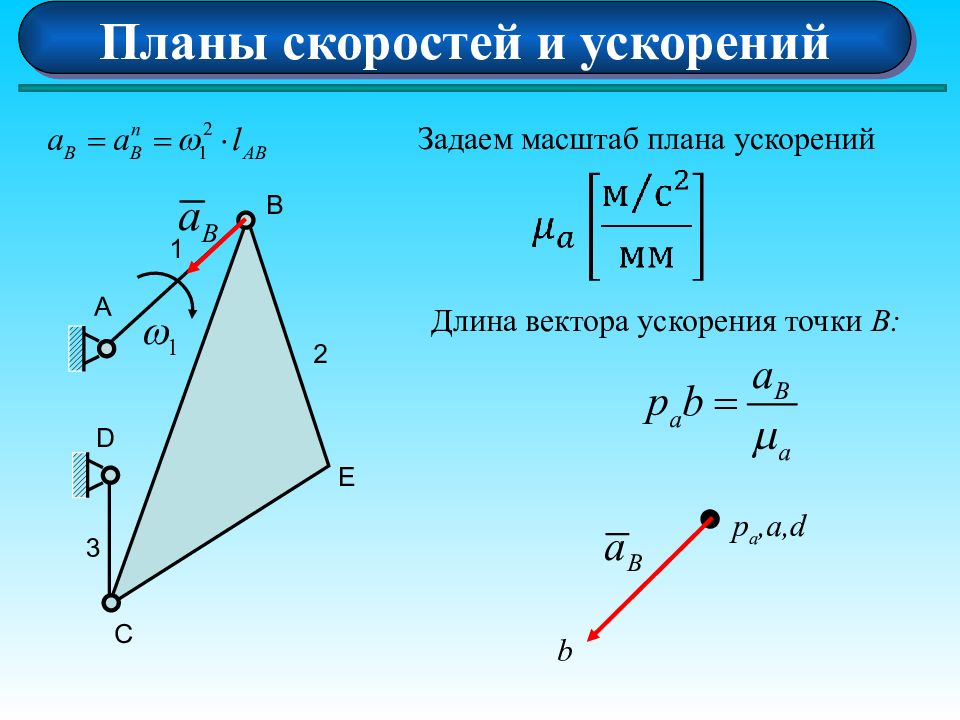
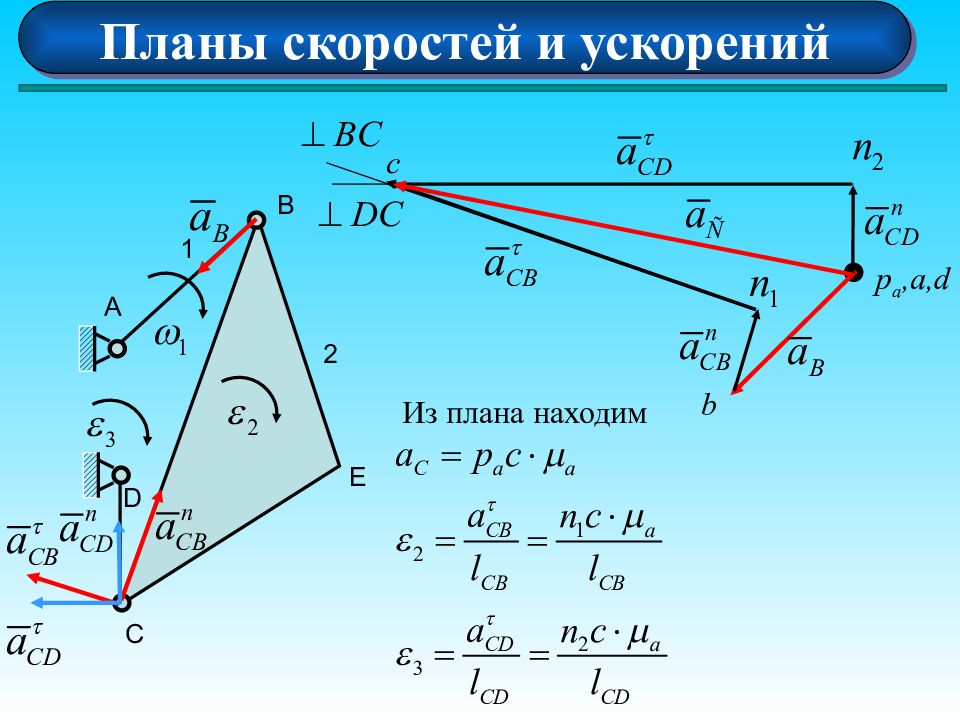
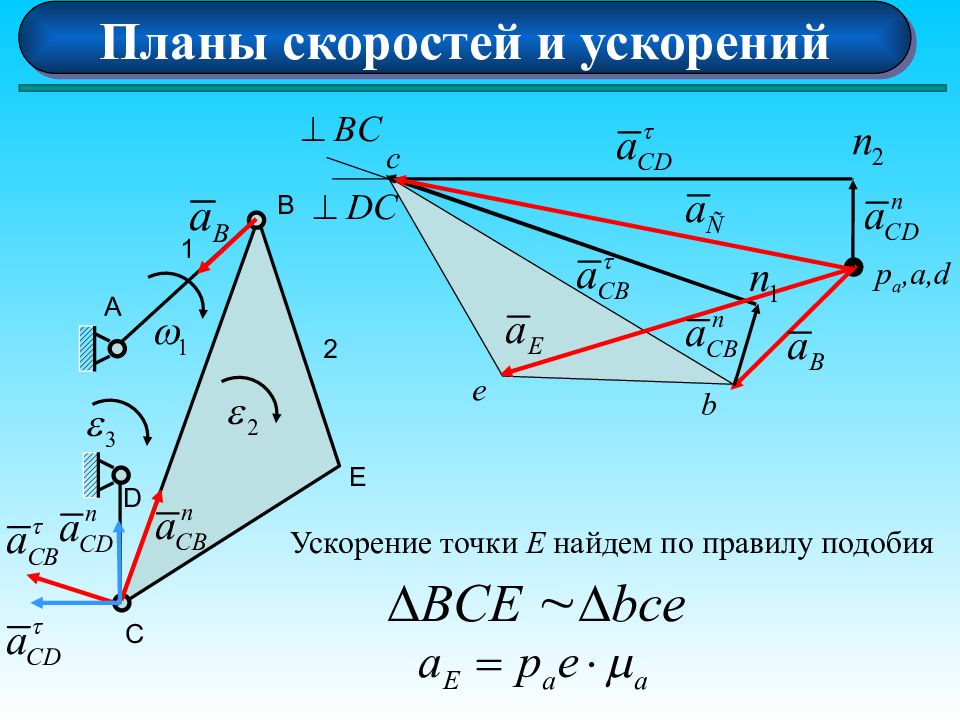
Планы скоростей и ускорений А 1 D B E C 2 3 Задаем масштаб плана ускорений Длина вектора ускорения точки В : p a,a,d b