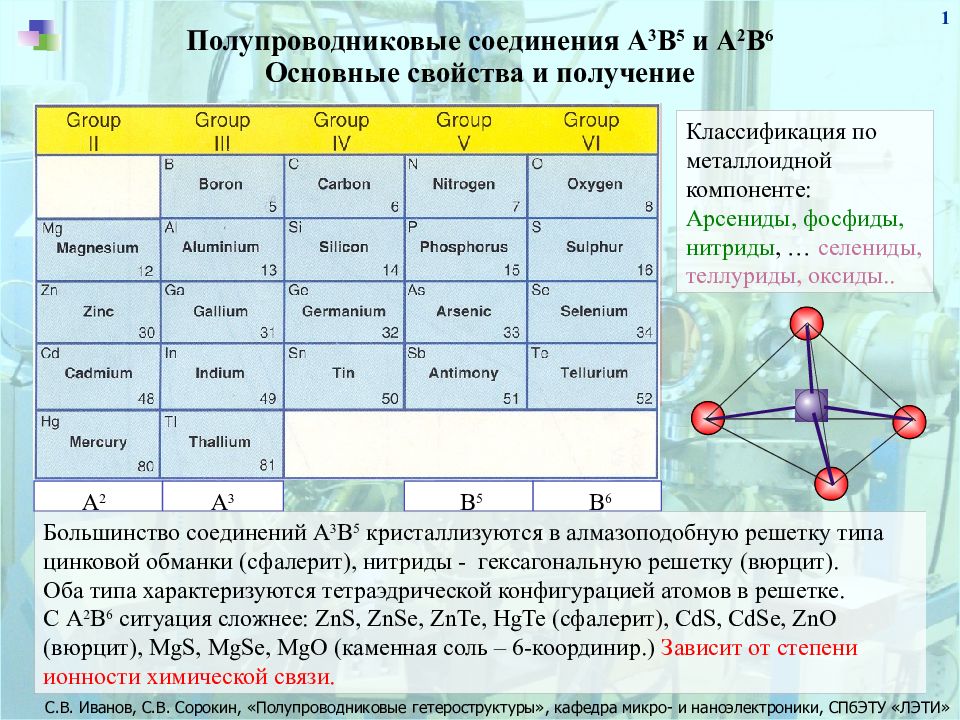
1 А 2 А 3 В 5 В 6 Berillium 4 Be Полупроводниковые соединения А 3 В 5 и А 2 В 6 Основные свойства и получение 20 соединений А 3 В 5 20 соединений А 2 В 6 Большинство соединений А 3 В 5 кристаллизуются в алмазоподобную решетку типа цинковой обманки (сфалерит), нитриды - гексагональную решетку (вюрцит). Оба типа характеризуются тетраэдрической конфигурацией атомов в решетке. С А 2 В 6 ситуация сложнее : ZnS, ZnSe, ZnTe, HgTe ( сфалерит), С dS, CdSe, ZnO (вюрцит), MgS, MgSe, MgO ( каменная соль – 6-координир.) Зависит от степени ионности химической связи. Классификация по металлоидной компоненте : Арсениды, фосфиды, нитриды, … селениды, теллуриды, оксиды..
2 В полупроводниках с 4 валентными электронами на атом ( Si – 3 s 2 3 p 2, Ge – 4 s 2 4 p 2 ) каждый атом находится в тетраэдрическом окружении себе подобных, что позволяет распределить 8 электронов (по 2 е - на связь), соответствующих заполненной оболочке. Такая связь является чисто ковалентной. B B B B A Химическая связь в А 3 В 5 – смешанная ионно-ковалентная, поскольку у металла 3 валентных электрона, а у металлоида – 5. Ее принято описывать как донорно-акцепторную. Атом металла А должен принять электрон от атома металлоида В на одну из гибридизованных орбиталей. Т.о., атом А приобретает избыточный заряд q=e -, величина которого зависит от расположения электронной плотности между атомами. А последнее определяется разностью электроотрицательностей и энергий ионизации атомов. Электроотрицательность - это способность атома притягивать электронную плотность от других атомов. Самый электроотрицательный элемент - фтор, самый электроположительный – франций. Электроотрицательность выше у В, а энергия ионизации ниже у А. Т.о. максимум электронной плотности находится у B, и чем больше эта разность, тем более сильно поляризованы ковалентные связи. Величина остаточного заряда на А определяет степень ионности связи f. Очевидно, что полупроводники А 2 В 6 должны обладать более ионной связью, чем полупроводники А 3 В 5. -q +q Химическая связь
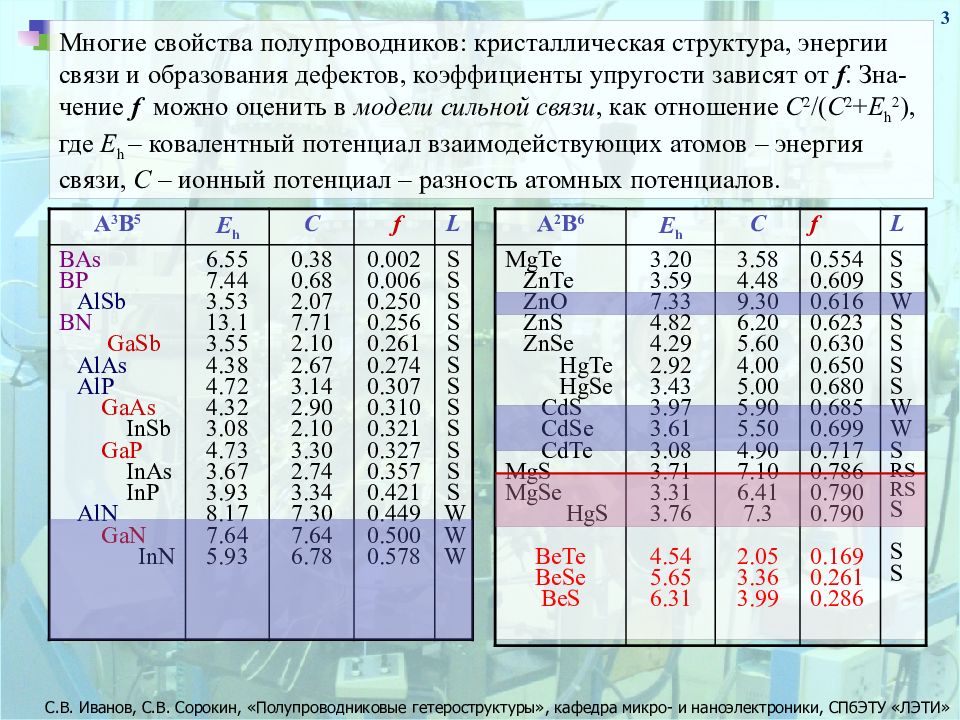
3 Многие свойства полупроводников : кристаллическая структура, энергии связи и образования дефектов, коэффициенты упругости зависят от f. Зна - чение f можно оценить в модели сильной связи, как отношение C 2 /( C 2 + E h 2 ), где Е h – ковалентный потенциал взаимодействующих атомов – энергия связи, С – ионный потенциал – разность атомных потенциалов. А 3 В 5 Е h С f L BAs BP AlSb BN GaSb AlAs AlP GaAs InSb GaP InAs InP AlN GaN InN 6.55 7.44 3.53 13.1 3.55 4.38 4.72 4.32 3.08 4.73 3.67 3.93 8.17 7.64 5.93 0.38 0.68 2.07 7.71 2.10 2.67 3.14 2.90 2.10 3.30 2.74 3.34 7.30 7.64 6.78 0.002 0.006 0.250 0.256 0.261 0.274 0.307 0.310 0.321 0.327 0.357 0.421 0.449 0.500 0.578 S S S S S S S S S S S S W W W А 2 В 6 Е h С f L MgTe ZnTe ZnO ZnS ZnSe HgTe HgSe CdS CdSe CdTe MgS MgSe HgS BeTe BeSe BeS 3.20 3.59 7.33 4.82 4.29 2.92 3.43 3.97 3.61 3.08 3.71 3.31 3.76 4.54 5.65 6.31 3.58 4.48 9.30 6.20 5.60 4.00 5.00 5.90 5.50 4.90 7.10 6.41 7.3 2.05 3.36 3.99 0.554 0.609 0.616 0.623 0.630 0.650 0.680 0.685 0.699 0.717 0.786 0.790 0.790 0.169 0.261 0.286 S S W S S S S W W S RSRS S S S
4 Большинство соединений А 3 В 5 и многие А 2 В 6 кристаллизуются со структурой цинковой обманки. Она представляет собой взаимопроникающие гранецентрирован-ные кубические (FCC) решетки атомов А и В, сдвинутые друг относительно друга на ¼ главной диагонали. В примитивной ячейке c о стороной a – по 4 атома каждого типа : 8 1 /8 А + 6 1 /2 А + 4 B = 8 атомов Плотность атомов в единице объема: r = 4/ a 3 ~ 2 10 22 атомов/см 3 (для GaAs). Плотность соединения r GaP = 4 M GaP /( a 3 N A )~4.13 г / см 3, M GaP = M Ga + M P =100.71 г Кристаллическая структура Пространственной группой структуры цинковой обманки является Td. Эта группа симметрии имеет 3 оси 2-порядка (180 ° ), 4 оси 3-порядка (120 ° ) и 6 плоскостей симметрии. В ней нет центра инверсии. a Примитивная ячейка А B Направления вдоль базовых векторов элементарной ячейки задают систему координат. Произвольное направление в кристалле обозначают с помощью индекса направления [ hkl ] – проекции вектора на оси элементарной ячейки, выраженные в единицах a и приведенные к целым числам. Если проекция отрицательна, над числом ставят знак “ – “. Группы эквивалентных с точки зрения симметрии направлений обозначают < hkl >. <100> <110> <111>
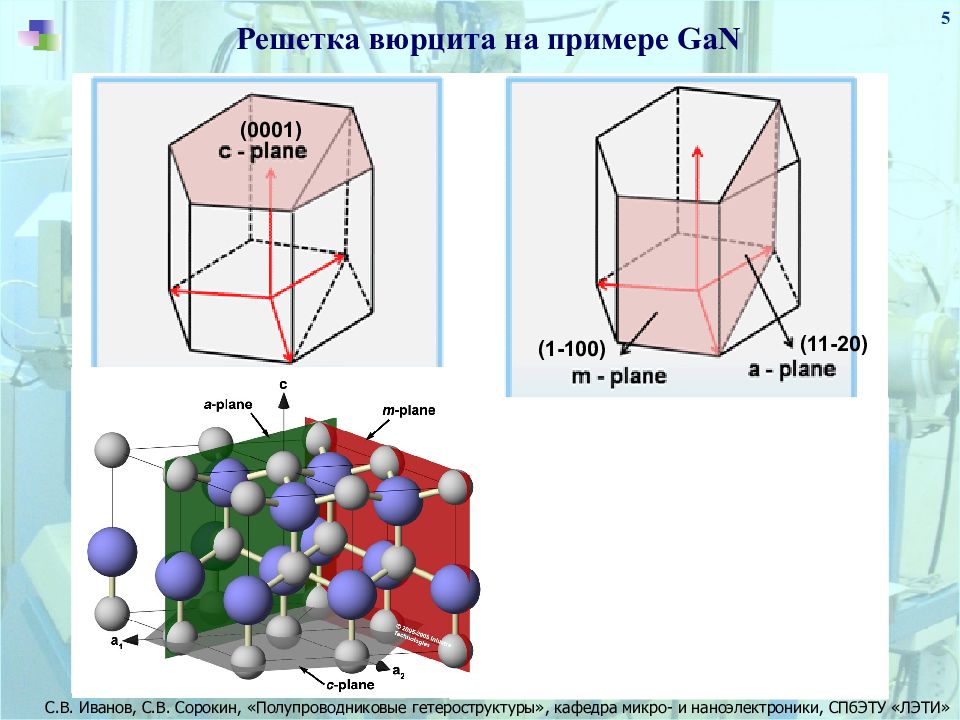
5 Решетка вюрцита на примере GaN (0001) (1-100) (11-20)
6 Кристаллические плоскости (или группы плоскостей) также обозначают с помощью трех чисел – индексов Миллера ( hkl ). Индексы Миллера h, k, l – связаны с длинами отрезков : x, y, z, отсекаемых плоскостью на осях координат: h = M / x ; k = M / y ; l = M / z, где M – число, которое при умножении на обратные значения отрезков образует ряд наименьших целых чисел. Для индексов направлений и индексов Миллера справедливы следующие правила: Плоскость, параллельная одной из осей координат, имеет индекс 0 для данного направления. Нормаль к плоскости ( hkl ) лежит в напра-влении [ hkl ] Расстояние между соседними плоскостями Расстояние между ближайшими соседними атомами ( вдоль <111>) – длина связи – равно сумме кова-лентных радиусов атомов A и В. Для GaAs: r As – 1. 18 Å, r Ga – 1.26 Å Тогда a = 4( r As + r Ga ) / 3 = 5.65 Å x y z
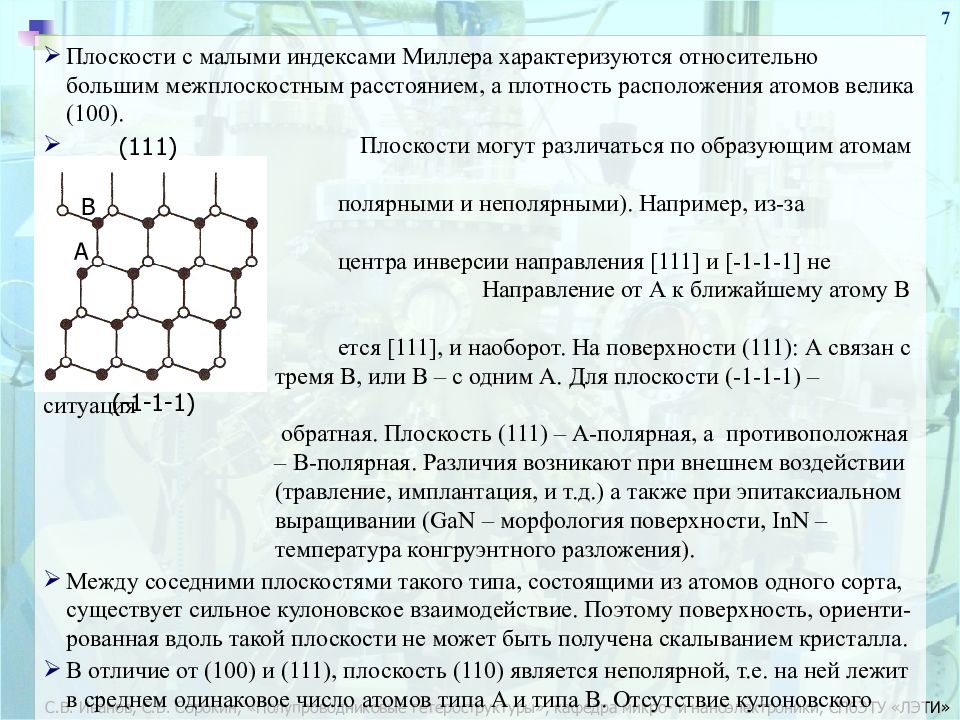
7 Плоскости с малыми индексами Миллера характеризуются относительно большим межплоскостным расстоянием, а плотность расположения атомов велика (100). Плоскости могут различаться по образующим атомам (быть полярными и неполярными). Например, из-за отсутствия центра инверсии направления [111] и [-1-1-1] не эквивлентны. Направление от А к ближайшему атому В обычно обознача- ется [111], и наоборот. На поверхности (111) : А связан с тремя В, или B – c одним А. Для плоскости (-1-1-1) – ситуация обратная. Плоскость (111) – А-полярная, а противоположная – В-полярная. Различия возникают при внешнем воздействии (травление, имплантация, и т.д.) а также при эпитаксиальном выращивании ( GaN – морфология поверхности, InN – температура конгруэнтного разложения). Между соседними плоскостями такого типа, состоящими из атомов одного сорта, существует сильное кулоновское взаимодействие. Поэтому поверхность, ориенти-рованная вдоль такой плоскости не может быть получена скалыванием кристалла. В отличие от (100) и (111), плоскость (110) является неполярной, т.е. на ней лежит в среднем одинаковое число атомов типа A и типа B. Отсутствие кулоновского взаимодействия между плоскостями позволяет получать такие поверхности скалыванием кристалла. Плоскость спайности. Для кристаллической пластины, ориентированной в плоскости (100) плоскостями спайности (скалывания) являются плоскости типа (011) и (0-11). А В (111) (-1-1-1)
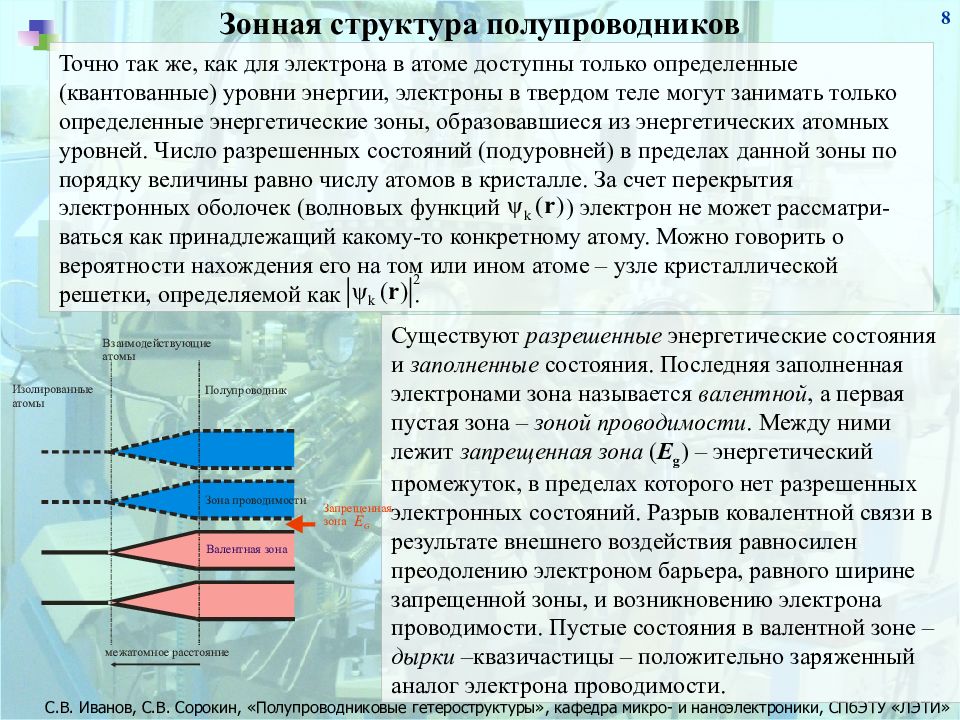
8 Зонная структура полупроводников Точно так же, как для электрона в атоме доступны только определенные (квантованные) уровни энергии, электроны в твердом теле могут занимать только определенные энергетические зоны, образовавшиеся из энергетических атомных уровней. Число разрешенных состояний (подуровней) в пределах данной зоны по порядку величины равно числу атомов в кристалле. За счет перекрытия электронных оболочек (волновых функций ) электрон не может рассматри-ваться как принадлежащий какому-то конкретному атому. Можно говорить о вероятности нахождения его на том или ином атоме – узле кристаллической решетки, определяемой как. Существуют разрешенные энергетические состояния и заполненные состояния. Последняя заполненная электронами зона называется валентной, а первая пустая зона – зоной проводимости. Между ними лежит запрещенная зона ( Е g ) – энергетический промежуток, в пределах которого нет разрешенных электронных состояний. Разрыв ковалентной связи в результате внешнего воздействия равносилен преодолению электроном барьера, равного ширине запрещенной зоны, и возникновению электрона проводимости. Пустые состояния в валентной зоне – дырки –квазичастицы – положительно заряженный аналог электрона проводимости.
9 Вследствие неэквивалентности различных направлений в кристаллической структуре полупроводников, реальная структура зон выглядит гораздо сложнее и представляет собой зависимость энергии электрона от его волнового вектора k, аналога импульса в обратном пространстве. Согласно теореме Блоха, электрон в кристалле – волна с периодом кристаллической решетки а Волновые функции находят из уравнения Шредингера Физически различимые решения соответствуют изменению волнового вектора k в пределах 1-й зоны Бриллюэна, определяемой на обратной решетке в k - пространстве как область, в пределах которой две точки отстоят друг от друга не дальше, чем на вектор обратной решетки 2 p / a. Зона Бриллюэна симметрична, относительно основных кристаллических направлений и имеет специфические точки симметрии – соответствующие энергетическим минимумам зоны проводимости – долинам. Существует несколько методов расчета зонной структуры : метод линейной комбинации атомных орбиталей в теории возмущений, метод пустой решетки, метод псевдопотенциала (наиболее точный).
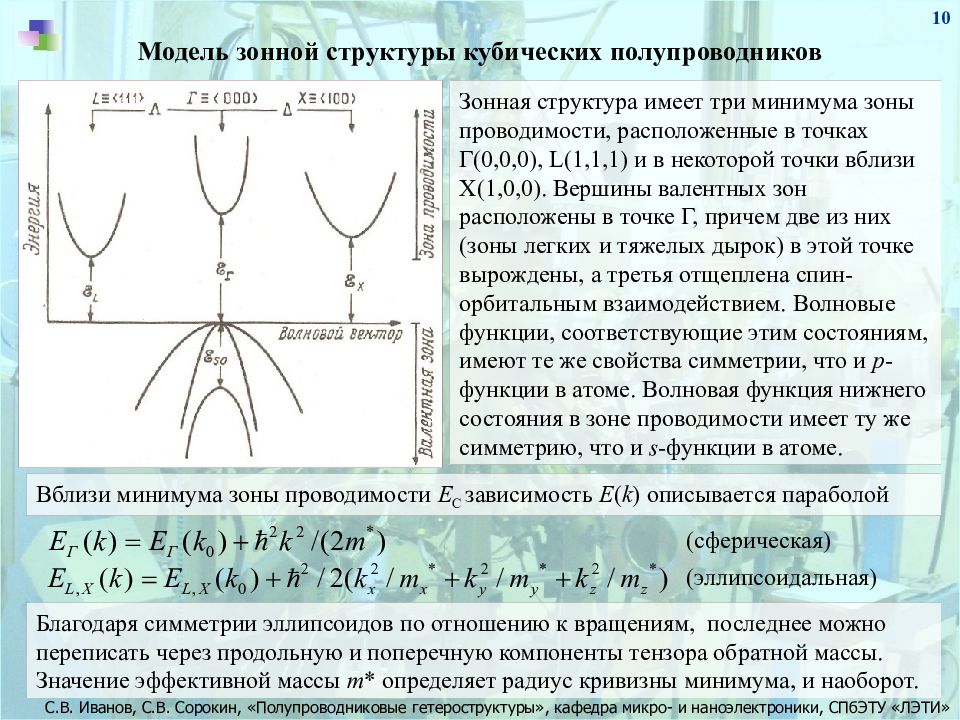
10 Модель зонной структуры кубических полупроводников Зонная структура имеет три минимума зоны проводимости, расположенные в точках Г(0,0,0), L (1,1,1) и в некоторой точки вблизи Х(1,0,0). Вершины валентных зон расположены в точке Г, причем две из них (зоны легких и тяжелых дырок) в этой точке вырождены, а третья отщеплена спин-орбитальным взаимодействием. Волновые функции, соответствующие этим состояниям, имеют те же свойства симметрии, что и p - функции в атоме. Волновая функция нижнего состояния в зоне проводимости имеет ту же симметрию, что и s - функции в атоме. Вблизи минимума зоны проводимости E C зависимость Е ( k ) описывается параболой (сферическая) (эллипсоидальная) Благодаря симметрии эллипсоидов по отношению к вращениям, последнее можно переписать через продольную и поперечную компоненты тензора обратной массы. Значение эффективной массы m * определяет радиус кривизны минимума, и наоборот.
11 Реальный спектр E ( k ) отклоняется от параболического. Непараболичность становится существенной при энергиях электронов, превышающих ~ 0.1эВ. Это особенно важно в сильно легированных полупроводниках или при высоких уровнях возбуждения, когда электроны высоко заливают зону проводимости. Спин-орбитально отщепленная валентная зона приобретает важное значение для узко-зонных полупроводников, когда E g, убывая с (М А +М В ) /2, становится сравнима с D 0 ( E gInAs =0.36 эВ (300K), D 0 =0.38эВ ). Внутризонное поглощение света и Оже-процессы с участием этой зоны существенно подавляют эффективность межзонного излучения. Все параметры, характеризующие зонную структуру, и прежде всего E g зависят от температуры. В интервале 0< Т <1000K для А 3 В 5 справедливо , где a и b – параметры Варшни. Если Г – нижний минимум в зоне проводимости, то полупроводник – прямозонный и переход электрона происходит без изменения k. Если нижний минимум L или X, то полупроводник – непрямозонный. С уменьшением (М А +М В ) /2 больше непрямозонных. GaAs D 0
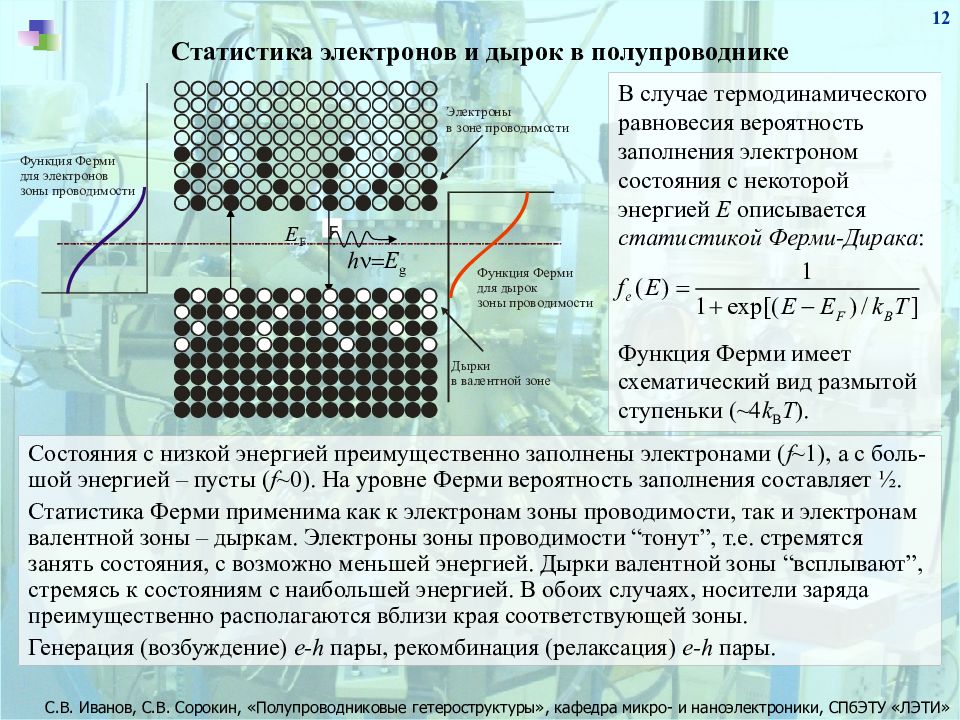
12 В случае термодинамического равновесия вероятность заполнения электроном состояния с некоторой энергией E описывается статистикой Ферми-Дирака : Функция Ферми имеет схематический вид размытой ступеньки (~4 k B T ). Статистика электронов и дырок в полупроводнике Состояния с низкой энергией преимущественно заполнены электронами ( f ~1), а с боль - шой энергией – пусты ( f ~0). На уровне Ферми вероятность заполнения составляет ½. Статистика Ферми применима как к электронам зоны проводимости, так и электронам валентной зоны – дыркам. Электроны зоны проводимости “тонут”, т.е. стремятся занять состояния, с возможно меньшей энергией. Дырки валентной зоны “всплывают”, стремясь к состояниям с наибольшей энергией. В обоих случаях, носители заряда преимущественно располагаются вблизи края соответствующей зоны. Генерация (возбуждение) e-h пары, рекомбинация (релаксация) e-h пары. E F h n= E g
13 Концентрации электронов и дырок в состоянии термодинамического (теплового) равновесия можно выразить с помощью энергии Ферми Уровень Ферми расположен ближе к той зоне, концентрация носителей какого типа преобладает. Можно говорить обратно – чем ближе уровень Ферми к данной зоне, тем выше в ней концентрация носителей. N c и N v – плотности состояний зоны проводимости и валентной зоны, которые в случае многодолинного полупроводника и с учетом сложной валентной зоны записываются как При тепловом равновесии концентрации электронов, n, и дырок, p, связаны соотношением При тепловом равновесии концентрации электронов и дырок связаны соотношением, где n i – собственная концентрация носителей заряда
14 Способы определения ширины запрещенной зоны 1 / T ln n E g /2 Измерение температурной зависимости концентрации носителей Оптическое измерения края фундаментального поглощения Поскольку E g есть функция температуры , то таким образом определяется экстраполяция E g 0 при низкой температуре (вблизи 0К) Данный метод работает в приближении параболической зоны и пренебрежении экситонным эффектом. Этот способ позволяет определить E g при любой температуре. E g
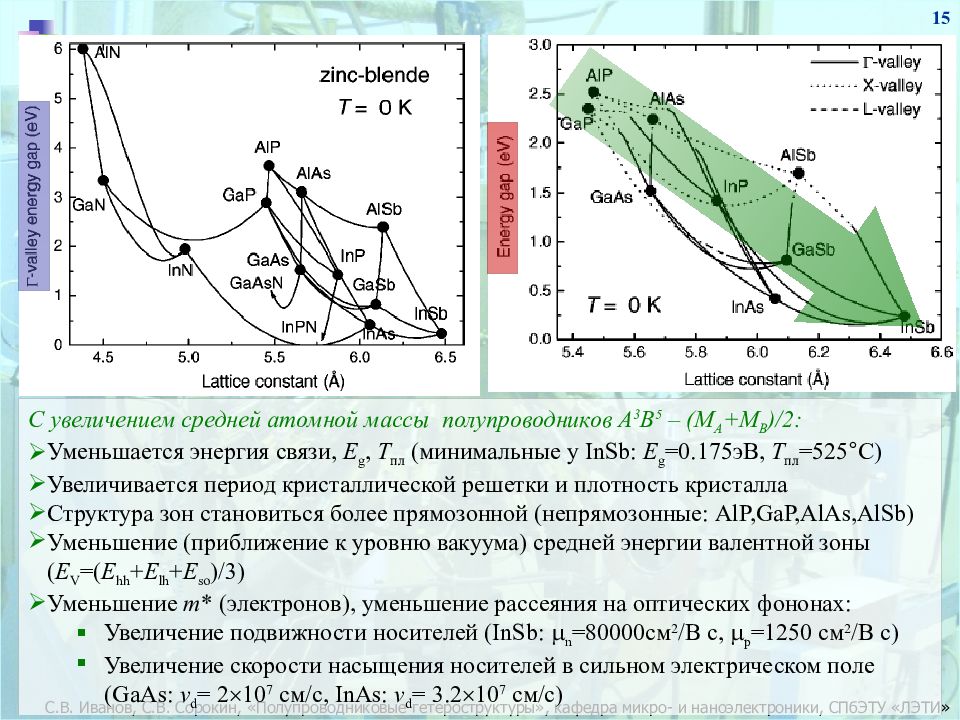
15 С увеличением средней атомной массы полупроводников А 3 В 5 – (М А +М В ) /2: Уменьшается энергия связи, E g, Т пл (минимальные у InSb: E g =0.175 эВ, Т пл =525 ° С) Увеличивается период кристаллической решетки и плотность кристалла Структура зон становиться более прямозонной (непрямозонные : AlP,GaP,AlAs,AlSb) Уменьшение (приближение к уровню вакуума) средней энергии валентной зоны ( E V =( E hh + E lh + E so )/3) Уменьшение m * (электронов), уменьшение рассеяния на оптических фононах : Увеличение подвижности носителей (InSb: m n = 80 000см 2 / В с, m р = 12 50 см 2 / В с ) Увеличение скорости насыщения носителей в сильном электрическом поле ( GaAs: v d = 2 10 7 см/с, InAs: v d = 3.2 10 7 см/с )
16 Краткая характеристика полупроводниковых соединений А 3 В 5 GaAs – наиболее технологически важный (лазеры, транзисторы, фотоприемники) и наиболее хорошо изученный материал ; AlAs – вследствие того, что он наиболее часто входит в структуры на основе GaAs, это также один из наиболее важных материалов для опто- и микроэлектроники ; InAs – КТ ; кроме того, важность этого материала возрастает в последнее время в связи с использованием в приборах оптоэлектроники среднего ИК диапазона (2-5 мкм) и в качестве квантовой ямы в транзисторах на основе InAs/GaSb/AlSb; GaP – легированный азотом, долгое время использовался, как активный элемент светодиодов видимого диапазона ; AlP – материал с самой большой E g ( Г ) среди А 3 В 5, наименее изучен ; InP – прямозонный полупроводник огромной технологической важности, поскольку используется много лет в качестве подложки для большинства оптоэлектронных приборов, работающих на длине волны 1.55мкм для (ВОЛС) ; GaSb – материал с промежуточной E g между GaAs, InP и InAs, InSb, чрезвычайно важный компонент для оптоэлектроники среднего ИК диапазона ; AlSb – непрямозонный, в последнее время очень перспективный в качестве барьерного материала для микроэлектронники и длинноволновой оптоэлектроники ; InSb – самый узкозонный, первый из открытых и наиболее хорошо изучен ; GaN – используется в решетке вюрцита, хит сезона с точки зрения применений в оптоэлектронике видимого и УФ диапазона, а также в силовой микроэлектронике ; AlN – необходимое дополнение к GaN, особенно в оптоэлектронике глубокого УФ ; InN – используется в виде твердых растворов с GaN, но по-прежнему загадка…
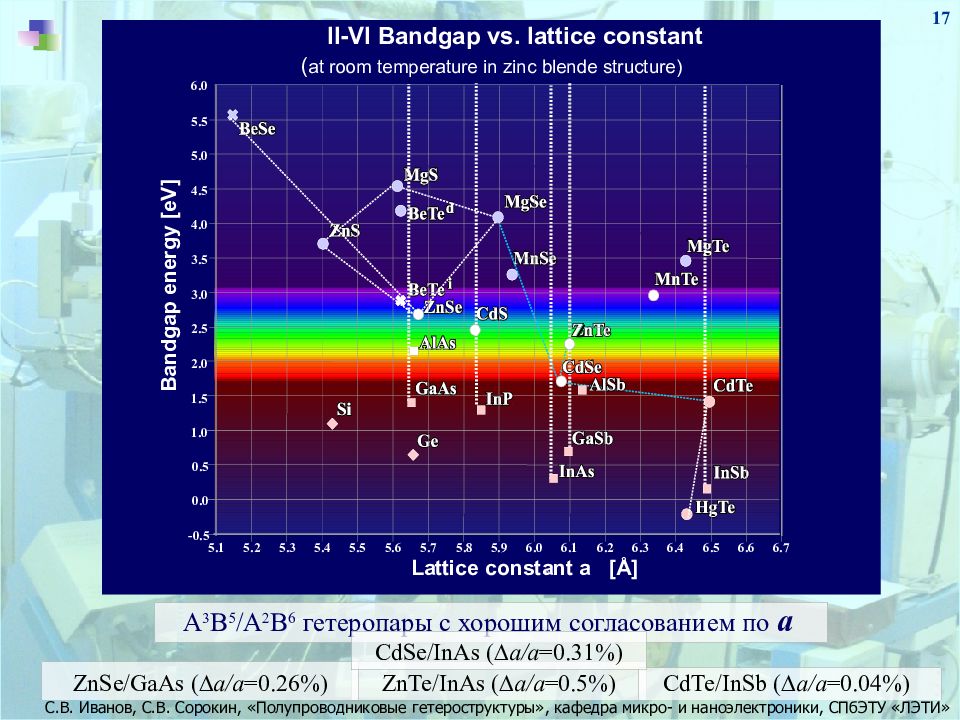
17 А 3 В 5 /A 2 B 6 гетеропары с хорошим согласованием по a ZnTe/InAs ( D a/a =0.5%) ZnSe/GaAs ( D a/a =0.26%) CdTe/InSb ( D a/a =0.04%) CdSe/InAs ( D a/a =0.31%) 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6.0 6.1 6.2 6.3 6.4 6.5 6.7 6.6 1.0 1.5 0.5 0.0 -0.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 6.0 5.5 II-VI Bandgap vs. lattice constant ( at room temperature in zinc blende structure) L attice constant a [Å] 0 Bandgap energy [eV]
18 Основные характеристики полупроводниковых соединений А 2 В 6 Большая степень ионности связи по сравнению с А 3 В 5 : сильное электростатическое взаимодействие, слабее колебания решетки – большие температуры плавления, ширины запрещенных зон соединений в структуре цинковой обманке – Сине-зеленые полупроводниковые лазеры. большая энергия активации акцепторных центров, даже водородоподобных (110-140мэВ в ZnSe по сравнению с 20мэВ в GaAs) – Сложность р-легирования. более низкая энергия образования точечных дефектов – низкое время жизни сине-зеленых лазеров на основе ZnSe ( открытие халькогенидов Ве – BeTe, BeSe ) большая энергия экситона, способность его доживать до комнатной температуры – открытие на Cu 2 O, но исследование в основном на А 2 В 6, выход на поляритонные эффекты при 300К. Больше разновидностей типов решеток вплоть до каменной соли Практически все – прямозонные полупроводники HgTe – бесщелевой полупроводник – полуметалл, поскольку валентная зона смыкается с зоной проводимости – с С dTe полный ряд твердых растворов с Е g от 0 до 1.5эВ – фотоприемники среднего и дальнего ИК диапазона. Много большие эффективные массы носителей по сравнению с А 3 В 5 – m e (CdTe)=0.11 m 0 – кроме HgTe, непригодность к использованию в транзисторах. Возможность изоэлектронного встраивания переходных металлов с незавершенными d -облочками, т.е. с нескомпенсированным магнитным моментом атома – Открытие полумагнитных полупроводников, эффекта гигантского Зеемановского расщепления – рождение спинтроники.
19 Контрольные вопросы 1. Параметры, определяющие свойства и качество гетероперехода ? 2. Специфические эффекты, открытые в гетероструктурах ? - Суперинжекция и односторонняя инжекция - Электронное и оптическое ограничение - Широкозонное окно 3. В какой решетке кристаллизуются соединения А3В5 и А2В6 и какая при этом конфигурация атомов ? 4. Тип химической связи А3В5 и А2В6 5. У каких соединений больше ионность 6. Как оценить параметр решетки, зная ковалентные радиусы ? 7. Нарисовать кристаллические плоскости с индексами Миллера (010), (101), (221) 8. Полярные плоскости в кристалле и плоскости спайности 9. Что такое прямозонный полупроводник, непрямозонный ? Примеры в А3В5. 10. Что и как меняется при увеличении средней массы соединения А3В5 (А2В6) ? 1 1. Две основные проблемы широкозонных соединений А2В6, мешающих созданию сине-зеленого лазера.
20
21 Движение электрона в кристалле (теория Лоренца-Друде) Подвижность, механизмы рассеяния Механизмы рассеяния носителей заряда В условиях равновесия v e =const Доминирующие : на полярных оптических фононах ; на ионизированных примесях. Другие : на акустических фононах – деформаци-онный потенциал ; пьезоэлектрическое ; междолинное (в сильном электр. поле).
22 Питер Ю, Мануэль Кардона, Основы физики полупроводников, М., Физматлит, 2002 (2 тома) М. Шур, Современные приборы на основе арсенида галлия, М., Мир, 1991
