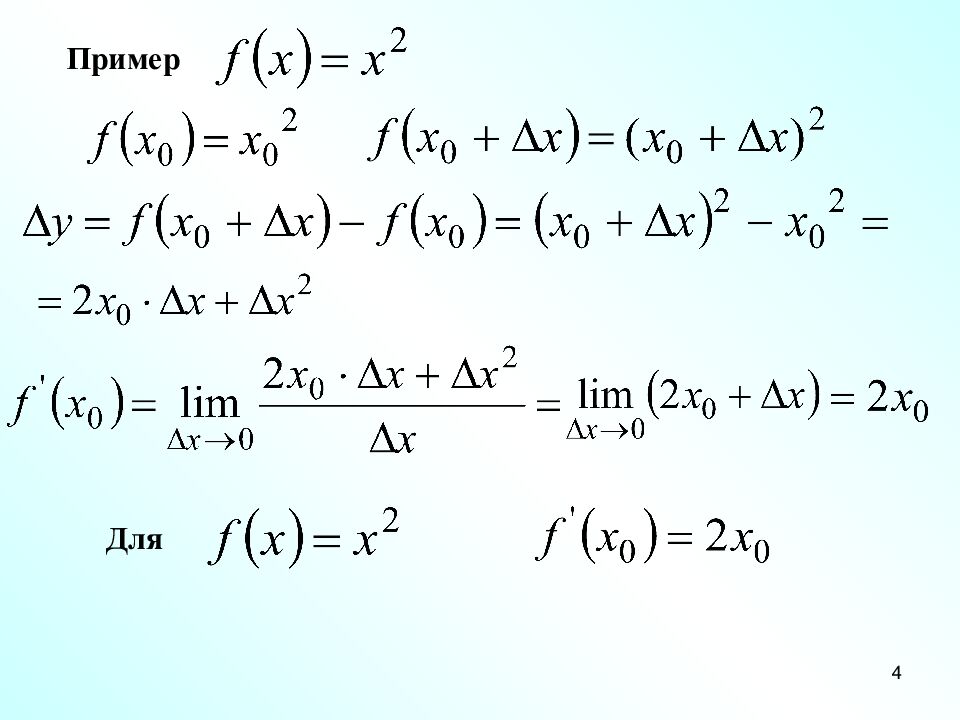‹#› Понятие ПРОИЗВОДНОЙ Преподаватель математики ФГКОУ СПб СВУ МО РФ Корнилова И.Ф.
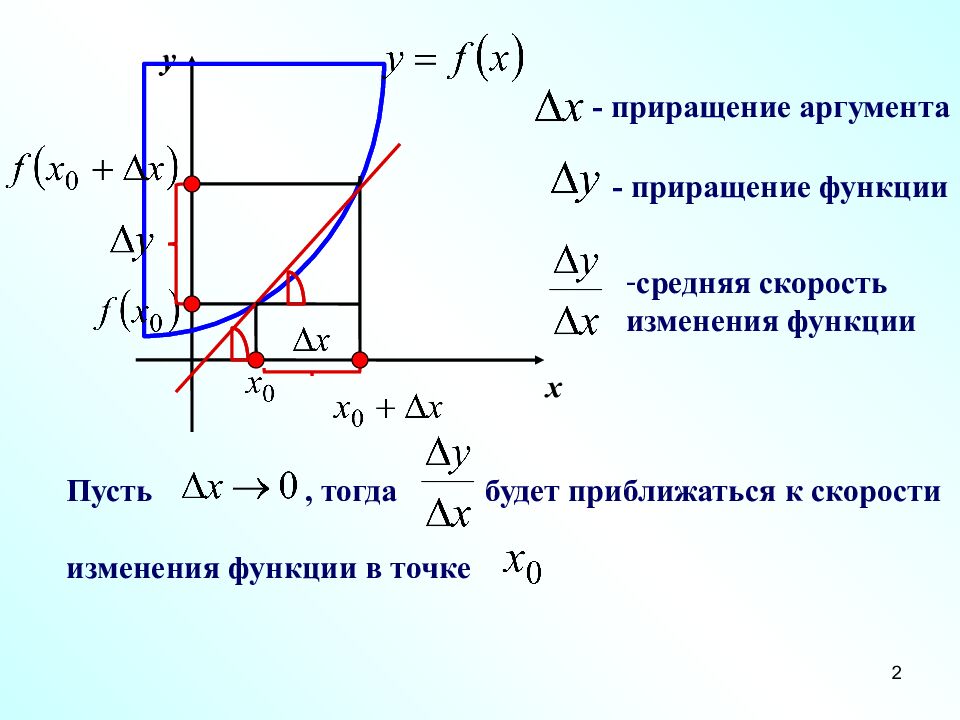
‹#› x y - приращение аргумента - приращение функции средняя скорость изменения функции Пусть, тогда будет приближаться к скорости изменения функции в точке
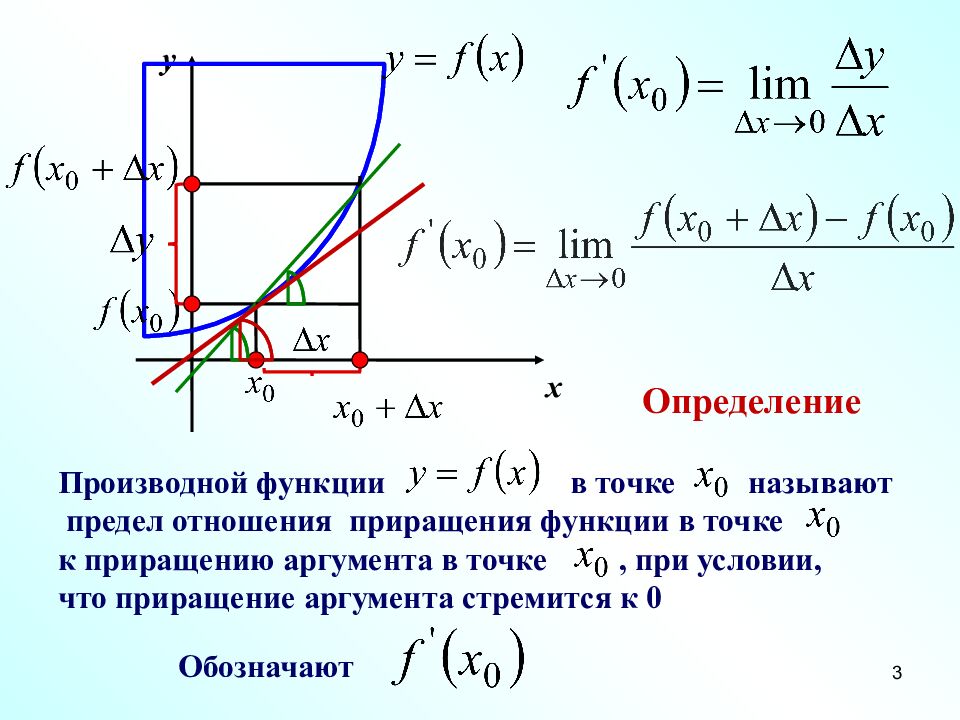
‹#› x y Определение Производной функции в точке называют предел отношения приращения функции в точке к приращению аргумента в точке, при условии, что приращение аргумента стремится к 0 Обозначают
‹#› Пример Для
‹#› Пример Для и т. д. Итак получаем новую функцию, производную данной Для функции производная функция Операция нахождения производной функции называется дифференцированием.
‹#› Таблица производных Функция Производная Производная константы Производная линейной функции Производная степенной функции
‹#› Таблица производных Функция Производная Производная степенной функции
‹#› Таблица производных Функция Производная Производная степенной функции
‹#› Таблица производных Функция Производная Производная показательной функции Производная логарифмической функции
‹#› Таблица производных Функция Производная
‹#› Правила дифференцирования Производная суммы функций Производная произведения функции на число
‹#› Правила дифференцирования Производная произведения функций Производная частного функций
‹#› Правила дифференцирования Производная сложной функции Частный случай
‹#› Найти производную Пример 1
‹#› Найти производную Пример 2 Пример 3
‹#› Найти производную Пример 4
‹#› Найти производную Пример 5
‹#› Найти производную Пример 5 Пример 6
