Статически неопределимой фермой называется ферма, для определения усилий в элементах которой кроме уравнений статического равновесия необходимы дополнительные уравнения – уравнения деформаций. Распределение усилий в статически неопределимых фермах зависит не только от внешних сил, но и от соотношений между поперечными размерами отдельных элементов. Если элементы фермы изготовлены из различных материалов, то распределение усилий зависит также от модулей упругости этих материалов. Поэтому для определения усилий в элементах таких ферм необходимо задавать их жесткости. Смещение опор, температурные воздействия и неточность сборки конструкции обычно вызывают в таких фермах дополнительные усилия. Расчет статически неопределимой фермы начинается с анализа ее схемы. Анализ, прежде всего, необходим для того, чтобы установить степень статической неопределимости.
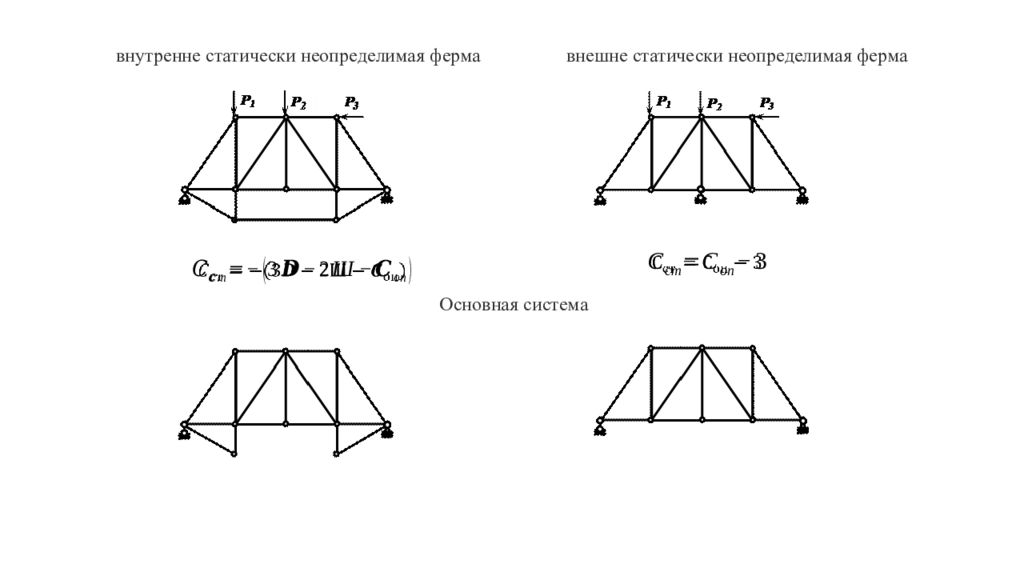
Степень статической неопределимости равна числу так называемых лишних связей, удаление которых превращает статически неопределимую ферму в определимую и геометрически неизменяемую систему. Геометрически неизменяемой называется такая система, изменение формы которой возможно лишь в связи с деформациями ее элементов. Различают внешне статически неопределимые фермы и внутренне статически неопределимые фермы. Внутренне статически неопределимые фермы - фермы с тремя опорными стержнями, имеющие лишние внутренние связи. Внешне статически неопределимые фермы имеют лишние внешние связи.
Статически неопределимую ферму, имеющую более трех опорных стержней, можно рассматривать как внешне, как внутренне, и как одновременно внешне и внутренне статически неопределимую систему – в зависимости от того, какие связи считать лишними. Для внешне статически неопределимых ферм степень статической неопределимости определяется по формуле: Где С оп – количество опорных связей (стержней) системы. Для внутренне статически неопределимых ферм степень статической неопределимости определяется по формуле: Где D – количество дисков (стержней), Ш – количество одиночных (простых) шарниров, С оп – количество опорных связей (стержней) системы.
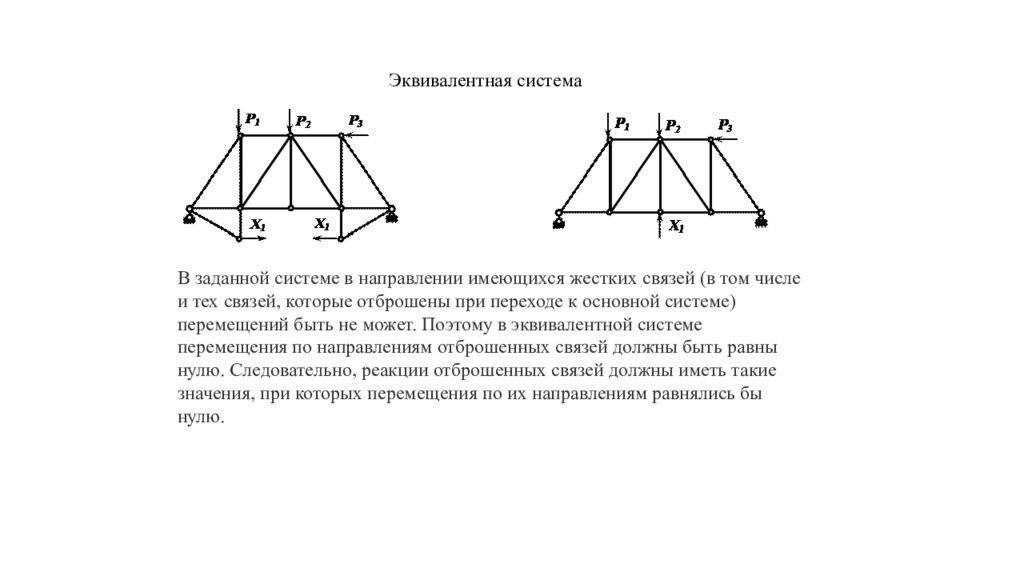
Канонические уравнения метода сил. Основной системой называется статически определимая и геометрически неизменяемая система, полученная из заданной системы путем отбрасывания всех лишних связей (за исключением абсолютно необходимых). Построение основной системы может быть произведено различными способами. Выбор основной системы является важным этапом расчета, т.к. от него зависит простота и точность расчета фермы. Устранение каких-либо связей не изменяет внутренних усилий, возникающих в системе, и ее деформаций, если к ней прикладываются дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Поэтому, если к основной системе, кроме заданной нагрузки, приложить реакции устраненных связей, то полученная система и заданная система будут эквивалентны. Полученная таким образом система называется эквивалентной системой.
внутренне статически неопределимая ферма внешне статически неопределимая ферма Основная система
Эквивалентная система В заданной системе в направлении имеющихся жестких связей (в том числе и тех связей, которые отброшены при переходе к основной системе) перемещений быть не может. Поэтому в эквивалентной системе перемещения по направлениям отброшенных связей должны быть равны нулю. Следовательно, реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям равнялись бы нулю.
Таким образом, условие равенства эквивалентной и заданной систем математически сводится к удовлетворению системы n линейных уравнений: Эти уравнения называются каноническими уравнениями метода сил. Первое из этих уравнений выражает равенство нулю перемещения в эквивалентной системе по направлению первой отброшенной связи Χ 1, второе – по направлению второй отброшенной связи и т.д. Число уравнений равно степени статической неопределимости заданной системы.
В системе канонических уравнений в качестве коэффициентов при неизвестных стоят перемещения основной системы, вызываемые единичными силами, действующими по направлениям отброшенных связей. Коэффициент δ ij представляет перемещение по направлению связи i, вызванное силой, равной единице, действующей по направлению связи j. Коэффициенты δ ij носят название единичных коэффициентов канонических уравнений. Коэффициент Δ iр представляет перемещение по направлению связи i, вызванное действием заданной внешней нагрузки. Коэффициенты Δ iр называются грузовыми коэффициентами или свободными членами канонических уравнений. Коэффициенты δ ii называются главными коэффициентами, а δ ij – побочными. На основании теоремы о взаимности перемещений δ ij = δ ji.
Определяются коэффициенты канонических уравнений с помощью интегралов Мора по формулам: т.к. фермы это конструкции, работающие преимущественно на сжатие (растяжение), то в выражении интегралов Мора остаются только слагаемые, зависящие от продольных усилий. А остальные усилия (М,Q) настолько малы, что ими можно пренебречь. Для подсчета коэффициентов используются способы определения продольных усилий в стержнях ферм.
В первую очередь определяются опорные реакции. Для определения опорных реакций ферм используются уравнения статики. Составляются три уравнения равновесия для всей фермы в целом: Для определения внутренних усилий следует выделять сечениями узлы или отдельные части ферм и рассматривать условия их равновесия под действием внешних нагрузок и усилий в рассеченных стержнях (метод сечений). Выделение частей или узлов фермы необходимо производить так, чтобы усилия в элементах определялись наиболее просто.
Различают следующие способы определения внутренних усилий в стержнях ферм: 1) способ моментной точки; 2) способ вырезания узлов; 3) способ проекций; 4)по признакам нулевых и ненулевых стержней.
Окончательные усилия в стержнях фермы определяются по формуле: Определив лишние неизвестные усилия Х 1, Х 2,…, Х n, находим усилие в любом стержне фермы, суммируя влияние нагрузки Р и лишних неизвестных усилий.
Проверки найденных усилий в стержнях фермы. а) Статическая проверка – основана на условии статического равновесия любого вырезанного узла фермы б) Деформационная проверка –нулевые перемещения в заданной системе должны получиться равными нулю и при расчете эквивалентной системы.
Порядок расчета 1. Вычертить в масштабе заданную схему фермы и загрузить ферму в узлах от заданной нагрузки. Пронумеровать узлы. 2. Определить степень статической неопределимости. 3. Выбрать основную и эквивалентную системы, назначив лишние неизвестные усилия (рационально). 4. Записать канонические уравнения. 5. Определить продольные усилия во всех стержнях фермы в единичном состоянии. 6. Определить продольные усилия во всех стержнях фермы в грузовом состоянии. 7. Занести данные в таблицу и определить коэффициенты канонических уравнений. 8. Решить канонические уравнения, найти неизвестные усилия. 9. Определить окончательные продольные усилия во всех стержнях фермы. 10. Выполнить деформационную и статическую проверки.
