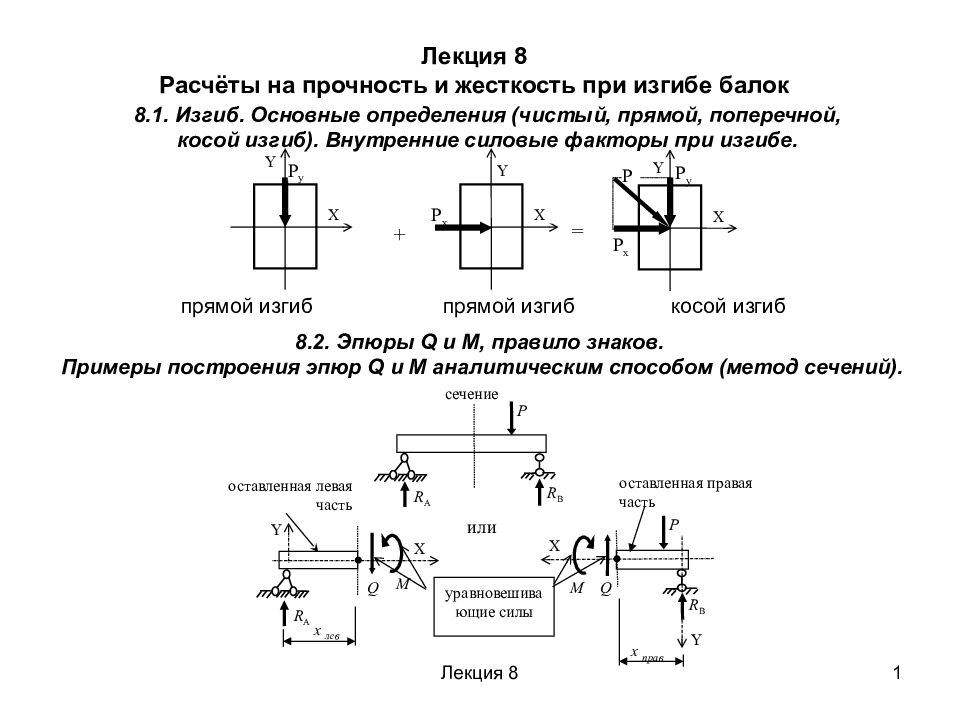
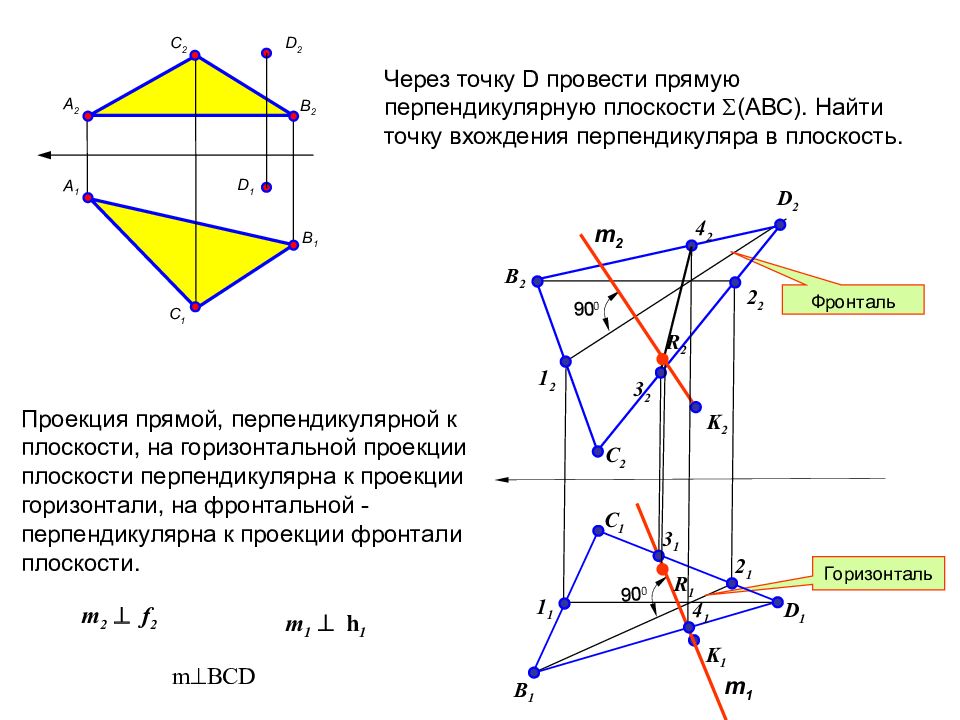
Первый слайд презентации
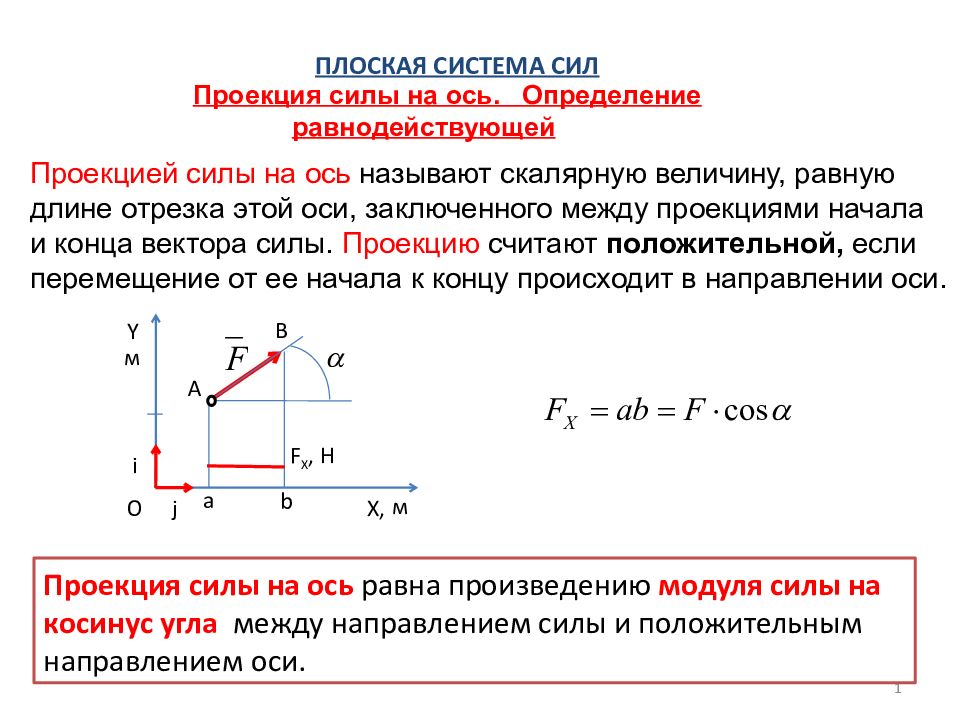
1 Проекция силы на ось. Определение равнодействующей Проекцией силы на ось называют скалярную величину, равную длине отрезка этой оси, заключенного между проекциями начала и конца вектора силы. Проекцию считают положительной, если перемещение от ее начала к концу происходит в направлении оси. Проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси. Y X, a b A B i j O м м F X, Н ПЛОСКАЯ СИСТЕМА СИЛ
Слайд 2
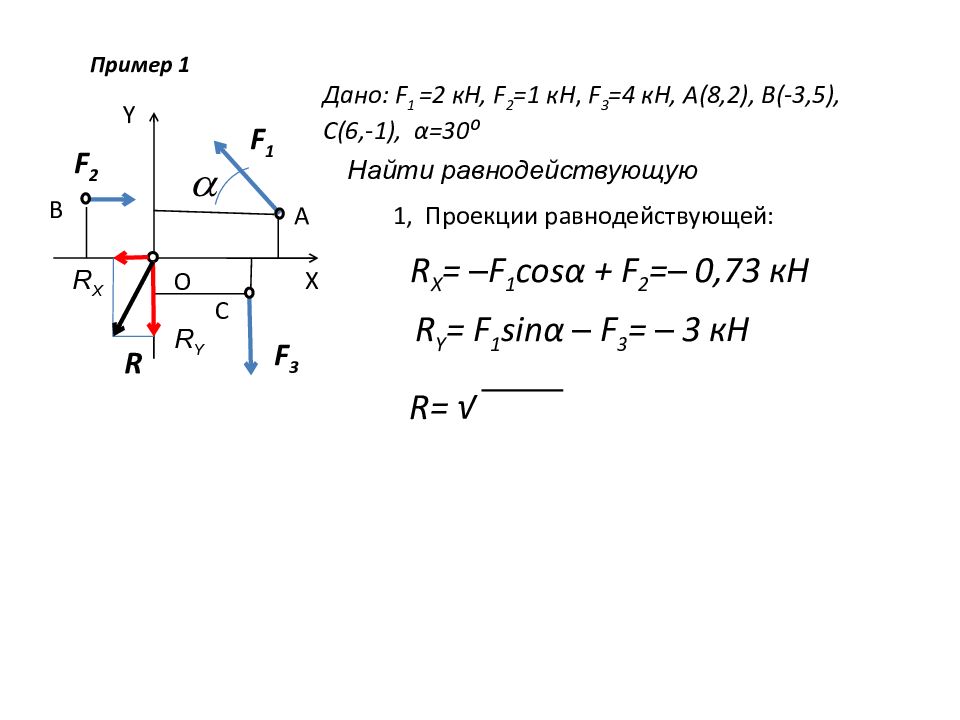
Y X F 1 F 2 F 3 A B C O Пример 1 Дано: F 1 =2 кН, F 2 =1 кН, F 3 = 4 кН, А(8,2), В(-3,5), С(6,-1), α =30⁰ Найти равнодействующую R = √ 1, Проекции равнодействующей: R X = ─F 1 cos α + F 2 =─ 0,73 кН R Y = F 1 sin α ─ F 3 = ─ 3 кН R Y R R X
Слайд 3
3 Разложение силы на составляющие Во многих случаях целесообразно представить силу в виде трех, а для плоской системы – двух составляющих : Y, X, A O м м X А Y А X A = F∙cos α Y A = F∙sln α x A y A
Слайд 4
A 4 M О = ─ X A ∙y A +Y A ∙x A Момент равнодействующей относительно центра равен алгебраической сумме моментов её составляющих относительно того же центра. здесь X A, Y A ─ координаты точки, приложения силы. алгебраическая величина, равная произведению модуля силы на плечо, взятая со знаком +, если вращение плоскости под действием силы происходит против часовой стрелки, и со знаком – в противном случае. Плечо силы – длина перпендикуляра, опущенного из точки на линию действия силы. Момент силы относительно точки на плоскости - Y, X, A O м м X А Y А x A y A
Слайд 5
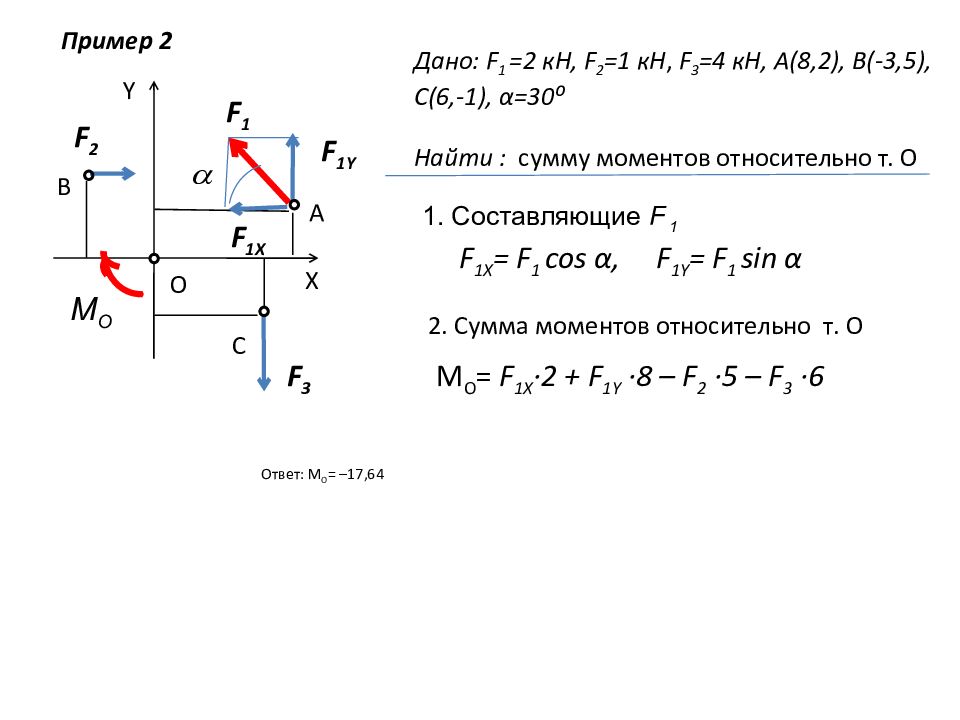
Y X F 1 F 2 F 3 A B C O Пример 2 Дано: F 1 =2 кН, F 2 =1 кН, F 3 = 4 кН, А(8,2), В(-3,5), С(6,-1), α =30⁰ Найти : сумму моментов относительно т. О 1. Составляющие F 1 F 1 X = F 1 cos α, F 1 Y = F 1 sin α 2. Сумма моментов относительно т. О M O = F 1 X ∙2 + F 1 Y ∙8 – F 2 ∙ 5 – F 3 ∙6 Ответ: M O = ─17,64 F 1Y F 1X M O
Слайд 6
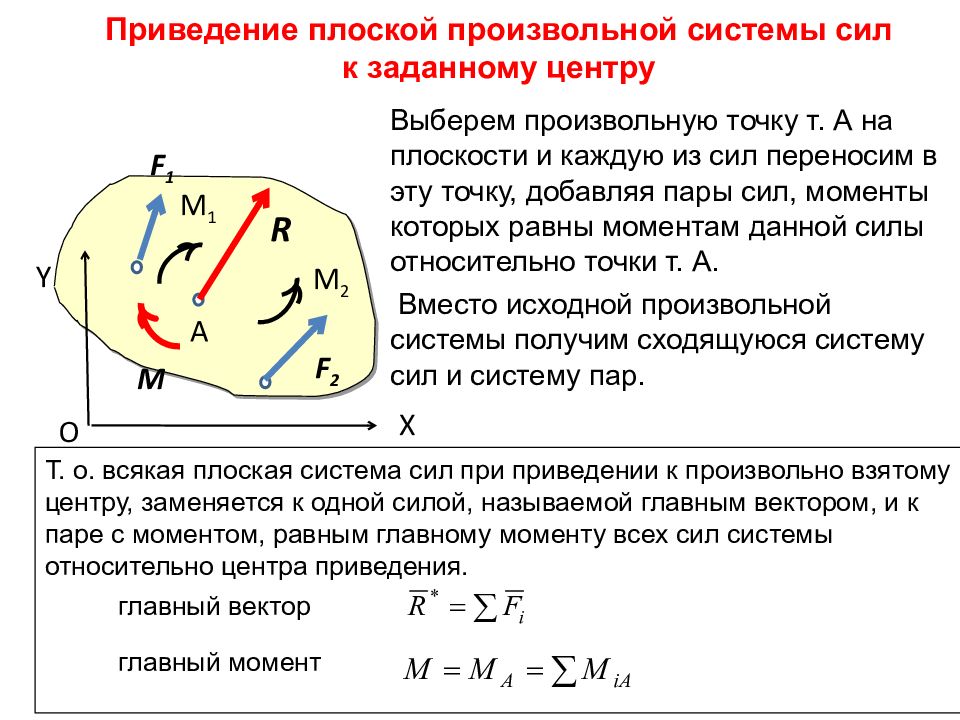
X Y O A R F 2 F 1 М 1 М 2 М Приведение плоской произвольной системы сил к заданному центру Т. о. всякая плоская система сил при приведении к произвольно взятому центру, заменяется к одной силой, называемой главным вектором, и к паре с моментом, равным главному моменту всех сил системы относительно центра приведения. главный вектор главный момент Выберем произвольную точку т. А на плоскости и каждую из сил переносим в эту точку, добавляя пары сил, моменты которых равны моментам данной силы относительно точки т. А. Вместо исходной произвольной системы получим сходящуюся систему сил и систему пар.
Слайд 7
7 А В С F R A R C В F N 1 N 2 1. Мысленно освобождаемся от связей в т. А, С и заменяем их реакциями R A, R B, которые направлены вдоль стержней 1, 2 (рис. 1) X Y X Y 3. Решая уравнения, определяем реакции связей : 2. Записываем уравнения равновесия для сходящейся системы сил. Согласно (1) для плоской системы: Рис. 1 Рис. 2 4. Методом вырезания узлов определим внутренние усилия в стержнях (рис. 2): N 1 =R A, N 2 =R C 1 2 Пример 3. Груз весом 1 кН подвешен на кронштейне АВС Определить опорные реакции и усилия в стержнях Ответ: N 1 = R A = 2 к Н, N 2 =R С = -1,73 кН. Стержень 1 растянут ( N 1 > 0 ), ст. 2 – сжат ( N 2 < 0).
Слайд 8
Расчет фермы методом вырезания узлов 8 2. Нумеруем или обозначаем буквами узлы и стержни. 3. Выбираем последовательность вырезания узлов таким образом, чтобы число неизвестных усилий было не более двух. Вырезаем первый узел. Действие отброшенных частей заменим осевыми силами N i, направленными от узлов, считая стержни растянутыми 4.Составляем уравнения равновесия для первого узла и определяем внутренние усилия. Положительное значение означает что данный стержень растянут, а отрицательное – сжат. Порядок расчета : 1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции : . 5. Последовательно вырезаем узлы фермы и определяем внутренние силовые факторы
Слайд 9
9 Рассмотрим ферму, (рис. 1). АВ= BC= DB=AD= 1 , силы Р= 1 кН, F= 0,5 кН. Пример решения. 1. Обозначим узлы и стержни. Мысленно освобождаемся от связей в т. А и В, а их воздействие заменяем реакциями X A, Y A, R В.
Слайд 10
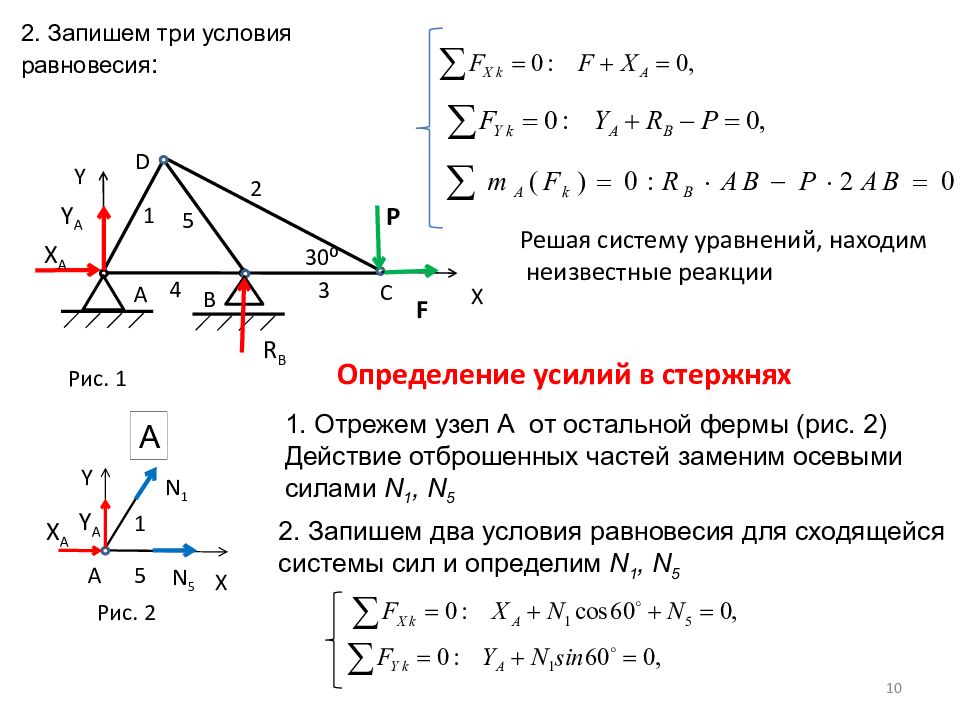
А F B X A Y A 1 2 3 4 5 C D P X Y R B А X A Y A 5 Y X А 1 N 5 N 1 2. Запишем три условия равновесия : Определение усилий в стержнях 1. Отрежем узел А от остальной фермы (рис. 2) Действие отброшенных частей заменим осевыми силами N 1, N 5 Рис. 1 Рис. 2 2. Запишем два условия равновесия для сходящейся системы сил и определим N 1, N 5 Решая систему уравнений, находим неизвестные реакции 10 30 ⁰
Слайд 11
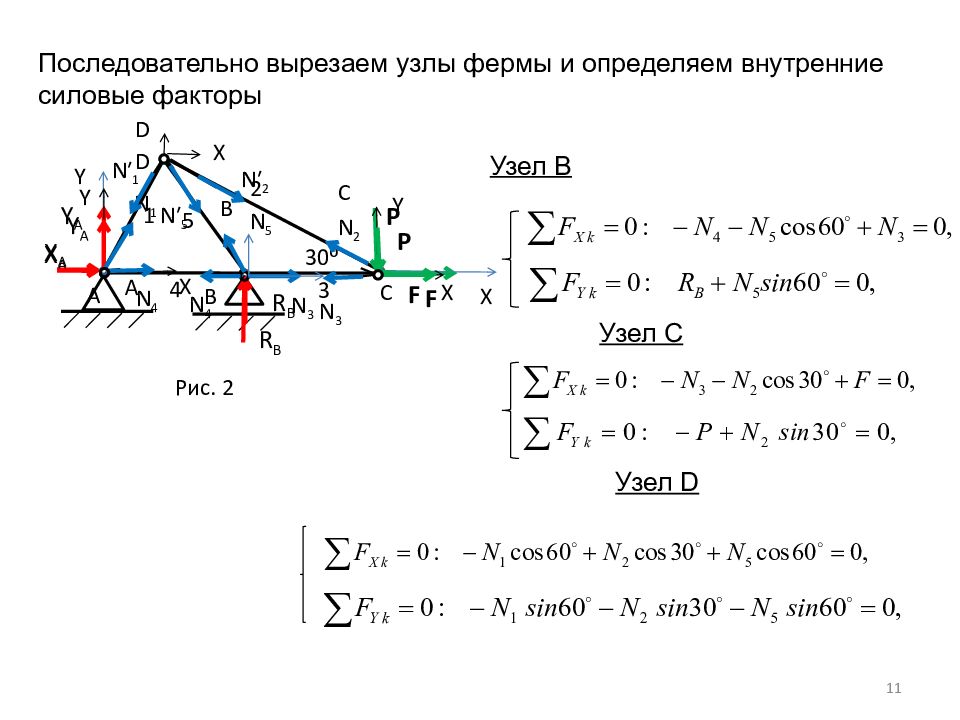
А F B X A Y A 1 2 3 4 5 C D P X Y R B Рис. 2 11 30 ⁰ А X A Y A Y X N 4 N 1 X N′ 1 N′ 5 N′ 2 D R B N 3 N 5 N 4 B X Y N 3 C N 2 P F Узел В Узел С Узел D Последовательно вырезаем узлы фермы и определяем внутренние силовые факторы
Слайд 12
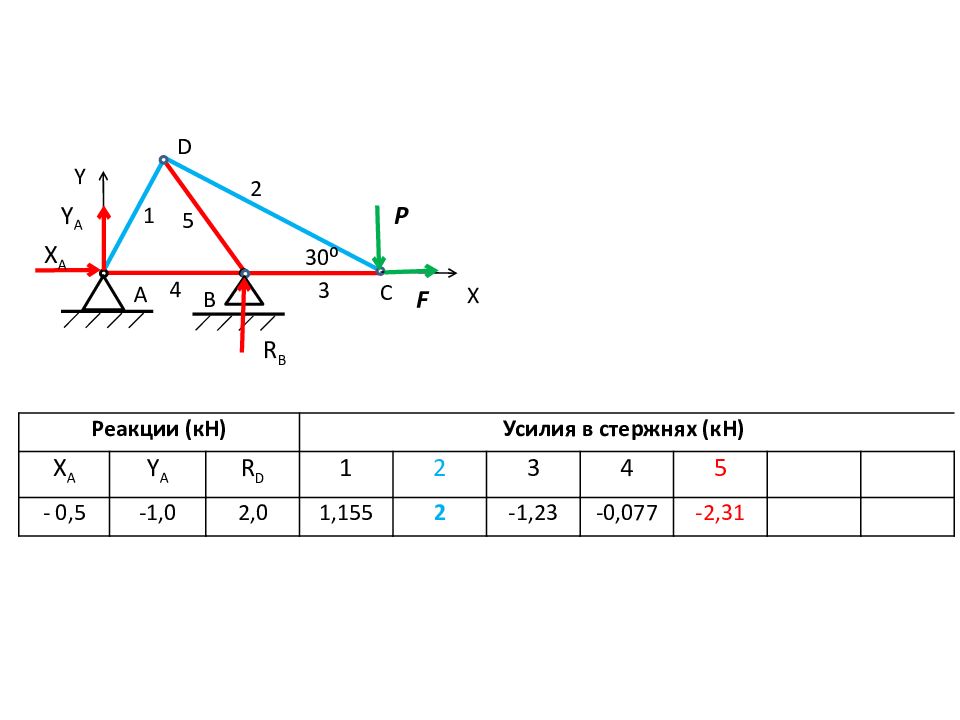
А F B X A Y A 1 2 3 4 5 C P Y R B 30 ⁰ Реакции (кН) Усилия в стержнях (кН) X A Y A R D 1 2 3 4 5 - 0,5 -1,0 2,0 1,155 2 -1,23 -0,077 -2,31 X D
Слайд 13
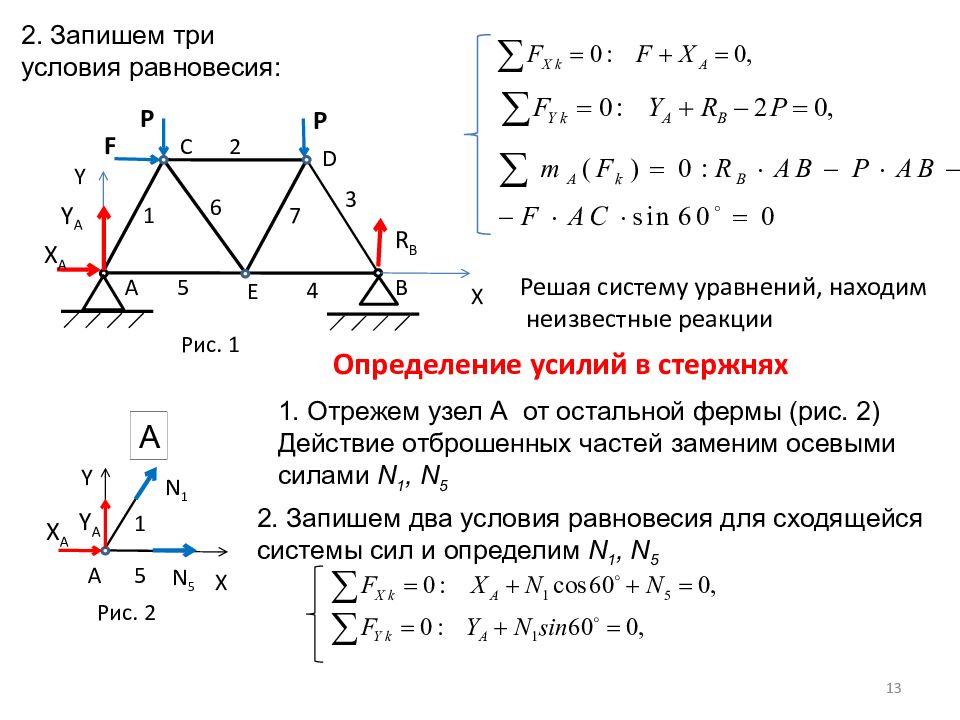
А F B X A Y A 1 2 3 4 5 6 7 C D E P X Y P R B А X A Y A 5 Y X А 1 N 5 N 1 2. Запишем три условия равновесия: Определение усилий в стержнях 1. Отрежем узел А от остальной фермы (рис. 2) Действие отброшенных частей заменим осевыми силами N 1, N 5 Рис. 1 Рис. 2 2. Запишем два условия равновесия для сходящейся системы сил и определим N 1, N 5 Решая систему уравнений, находим неизвестные реакции 13
Слайд 14
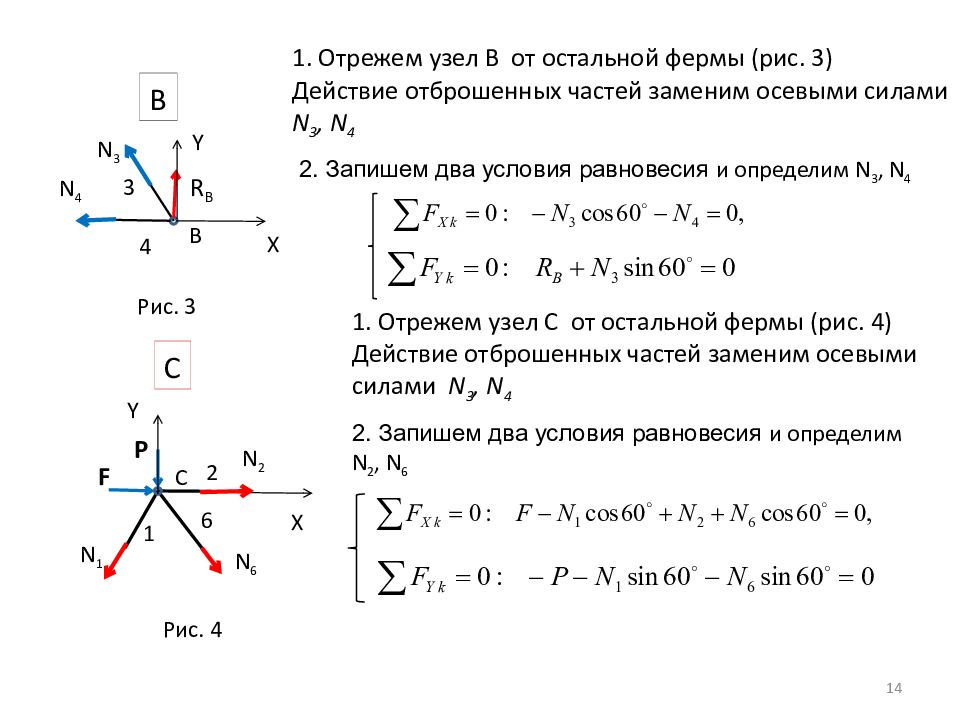
F 1 2 6 C X Y P N 1 N 6 N 2 C B 3 4 X R B Y B N 3 N 4 1. Отрежем узел В от остальной фермы (рис. 3) Действие отброшенных частей заменим осевыми силами N 3, N 4 Рис. 3 14 2. Запишем два условия равновесия и определим N 3, N 4 Рис. 4 1. Отрежем узел С от остальной фермы (рис. 4) Действие отброшенных частей заменим осевыми силами N 3, N 4 2. Запишем два условия равновесия и определим N 2, N 6
Слайд 15
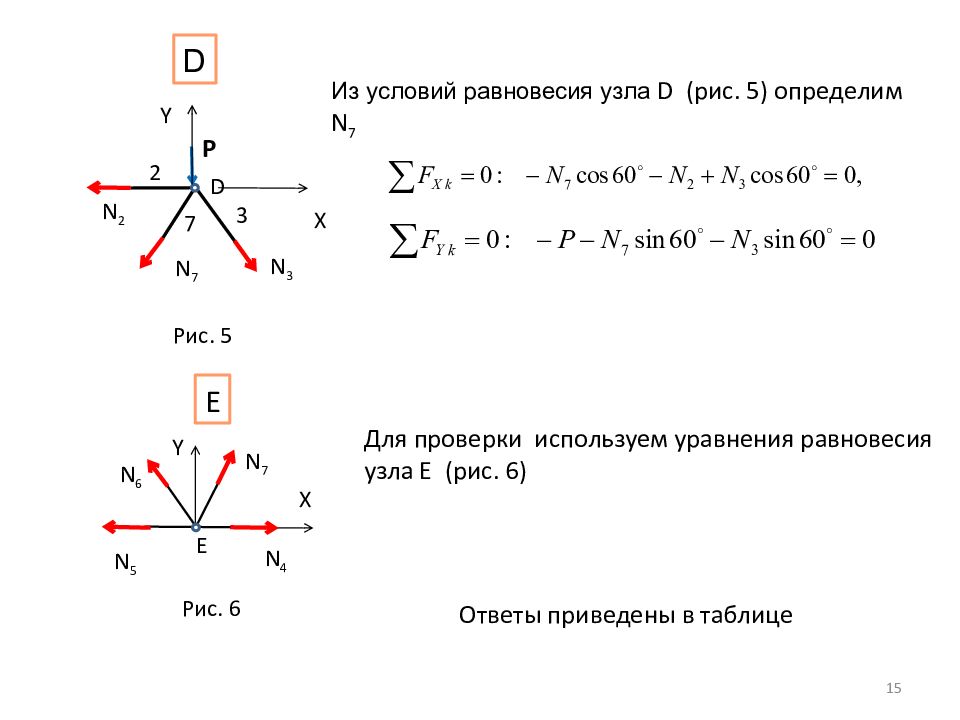
X Y N 4 N 6 N 7 N 5 E E 2 3 7 D P X Y N 2 N 7 N 3 D 15 Рис. 5 Рис. 6 Из условий равновесия узла D (рис. 5) определим N 7 Для проверки используем уравнения равновесия узла Е (рис. 6) Ответы приведены в таблице
Слайд 16
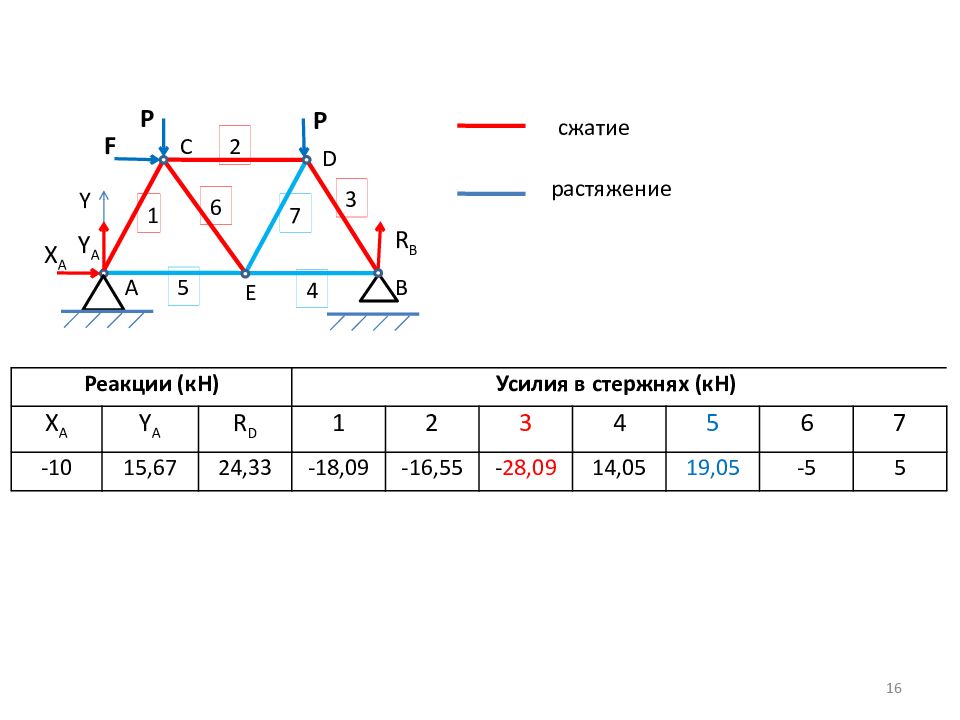
16 А F B X A Y A 1 2 3 4 5 6 7 C D E P Y P R B сжатие растяжение Реакции (кН) Усилия в стержнях (кН) X A Y A R D 1 2 3 4 5 6 7 -10 15,67 24,33 -18,09 -16,55 - 28,09 14,05 19,05 -5 5
Слайд 17
Статика С1У Пример 2.1 Определить опорные реакции Y A M A X A А В С Е F Р Решение : 1. Мысленно освобождаемся от связей в т. А и их воздействие заменяем реакциями X A, Y A, M A 3. Запишем три условия равновесия: 4. Проверка: Ответ: X A = -1 кН, Y A = 8,(6) кН, M A = ─ 24 кН м. Дано: АВ= 3 м; ВС=1м; СЕ= 0,5 м; Р=10 кН; F= 4 кН; =60 о 2. Сосредоточенную силу Р разложим на две составляющие P X, P Y : X Y Р Y Р X Р′
Слайд 18
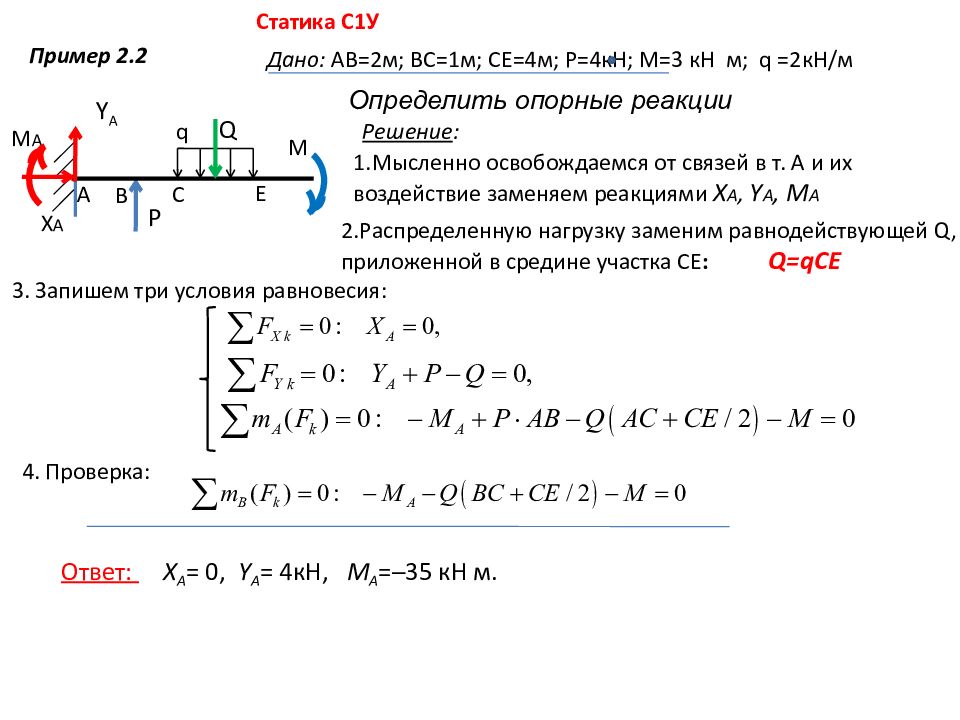
Статика С1У Пример 2.2 Дано: АВ=2м; ВС=1м; СЕ=4м; Р=4кН; М=3 кН м; q =2кН/м Определить опорные реакции Y A M A X A А В С Е q М Р Q Решение : 1. Мысленно освобождаемся от связей в т. А и их воздействие заменяем реакциями X A, Y A, M A 2. Распределенную нагрузку заменим равнодействующей Q, приложенной в средине участка СЕ : Q= qCE 3. Запишем три условия равновесия: 4. Проверка: Ответ: X A = 0, Y A = 4кН, M A =─35 кН м.
Последний слайд презентации: 1 Проекция силы на ось. Определение равнодействующей Проекцией силы на ось
Статика С1У Пример 2.3 Дано: АВ=2м; ВС=1м; С D = 3 м; DE= 2 м ; Р=4кН; F=1 кН; q = 1 кН/м Определить опорные реакции Y A X A А В С Е q F Р Q Решение : 1. Мысленно освобождаемся от связей в т. А и D, а их воздействие заменяем реакциями X A, Y A, RD 2. Распределенную нагрузку заменим равнодействующей Q, приложенной в средине участка BD : Q= qBD 3. Запишем три условия равновесия: 4. Проверка: Ответ: X A =0, Y A = -1 кН, R D = 2 кН. R D D X Y