1 Раздел 1. Множества, отношения и алгебраические структуры 1.1. Множества, элементы множеств Множество – определённая совокупность объектов. Объекты - элементы множества. Примеры множеств а) N – мн-во натуральных чисел 1, 2, 3,…; б) P – мн-во всех простых чисел 2, 3, 5, 7…; с) Z – мн-во всех целых чисел …-2, -1, 0, 1, 2,…; d ) R – мн-во всех действительных чисел. - x принадлежит М. - x не принадлежит М. Мн-во, элементы которого мн-ва, называются классом или семейством. Мн-во, не содержащее элементов, называется пустым – ø. Универсум ( U) – достаточно широкое мн-во, из которого берутся элементы в каждом конкретном случае. Способы задания мн-в : 1) перечисление элементов: ; 2) порождающей процедурой, например 3) характеристическим предикатом, например.
2 Литература Кузнецов О.П., Адельсон – Вельский Г.М. Дискретная математика для инженера / М., Энергоиздат, 1988.– 480с. Новиков Ф. А. Дискретная математика для программистов : Учебник/ СПб.: Питер, 2000. – 304с. Липский В. Комбинаторика для программистов. - М.: Мир, 1988. Пестунова Т.М. Введение в комбинаторику: Учебное пособие / Красноярск: КГТУ, 2001.– 96c. Богульская Н.А., Пестунова Т.М. Дискретная математика. Основы теории графов: Учебное пособие/ Красноярск: КГТУ, 2004. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов / М.: Наука, 1984. – 224с. Оре, О. Теория графов. – М., Наука, 1980. – 336c.
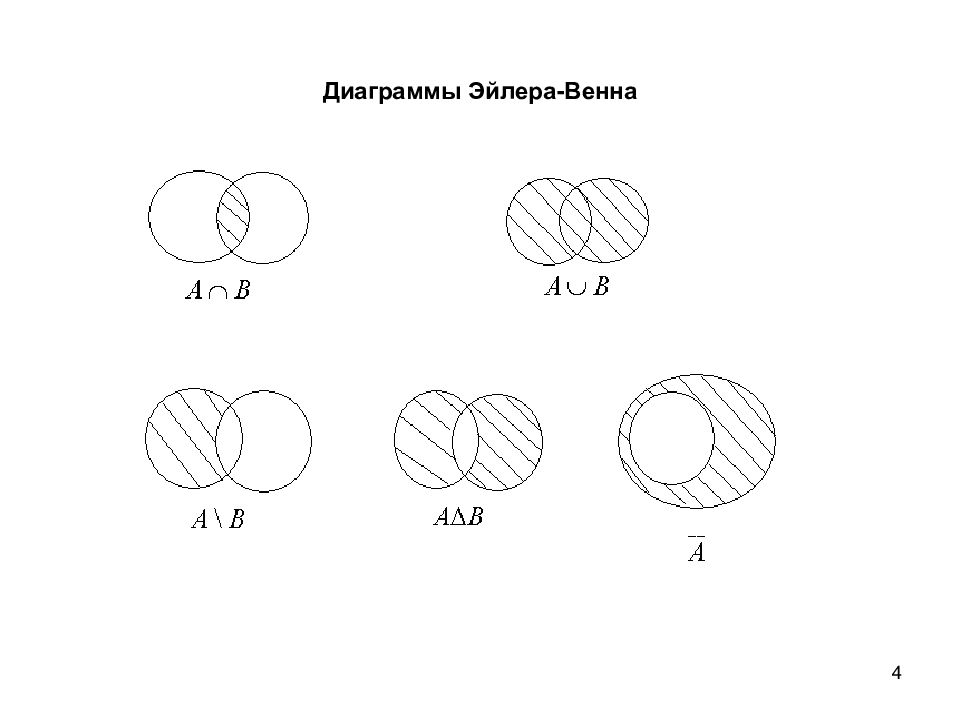
3 1.2. Операции над множествами Сравнение множеств: A=B ( эл-ты совпадают); (каждый эл-т А есть эл-т В); А - подмножество В. Если и, А – собственное или строгое подмножество В. По определению ø ; M. Два мн-ва равны, если они являются подмн-вами друг друга: Мощность конечного мн-ва – число его эл-тов - | ø|=0. Мн-ва равномощны - |A|=|B|. Операции над мн-вами: объединение пересечение разность симметрическая разность дополнение
4 Диаграммы Эйлера-Венна
5 Свойства операций над множествами 1. Идемпотентность 2. Коммутативность 3. Ассоциативность 4. Дистрибутивность 5. Поглощение 6. Св-ва нуля ø = ø = ø. 7.Св-ва единицы 8. Инволютивность 9. Законы де Моргана 10. Свойства дополнения 11. Свойства разности ø.
6 Прямое произведение множеств Прямое произведение множеств А и В -. . Пример. - множество координат точек плоскости. Прямое произведение называют декартовым.
7 1.3. Мощности множеств Мн-во всех подмн-в мн-ва М называют булеаном и обозначают. Теорема. Для конечного мн-ва Док-во: (по индукции) 1. ø. 2. Предположим верно Рассмотрим Обозначим ø. Мн-ва, равномощные N называются счётными
8 Теорема Кантора Т. Мн-во всех действительных чисел отрезка [0,1] не является счётным. Док-во. (от противного) Предположим, что существует нумерация. Расположим все числа, представленные десятичными дробями в порядке нумерации. … Рассмотрим дробь такую, что и т.д. Эта дробь не равна ни одному из чисел последовательности. Это противоречит предположению. Ч.т.д. Мощность мн-ва чисел отрезка [0,1] называется континуум. Равномощные ему множества – континуальные. Множество всех подмножеств счётного множества континуально.
9 1.4 Отношения Отношения - один из способов задания взаимосвязей между элементами множества. Определение. Подмножество R множества А Х А… х А называется n-местным отношением на множестве А. При этом говорят, что элементы a 1, a 2,..., a n находятся в отношении R, если ( a 1, a 2,..., a n ) элемент множества А Х А… х А. R. Для n = 1 - одноместное отношение, для n = 2 - двухместное, для n = 3 – трехместное и т.д. Одноместные (унарные) отношения – подмн-ва мн-ва А. Они отражают наличие какого-то признака R у элементов мн-ва A. Пример унарного отношения Подмн-во четных чисел N четн на мн-ве N. Двухместные (бинарные) отношения используются для определения взаимосвязей пар элементов в множестве А. Пример бинарного отношения: ( a > b ) на мн-ве N.
10 Примеры отношений на конечном множестве А = {1, 2, 3, 4, 5} 1. Одноместное отношение : R - нечетные элементы А. R = {1, 3, 5} 2. Двухместное отношение : R - отношение равенства. R ={( a, b ): a = b, a, b A }. R = = {(1, 1); (2, 2); (3, 3); (4, 4); (5, 5)}. 3. Трехместное отношение : R - отношение суммы R = {( a, b, c ): a + b = c, a, b, c A }. R + = {(1, 1, 2); (1, 2, 3); (1, 3, 4); (1, 4, 5); (2, 1, 3); (2, 2, 4); (2, 3, 5); (3, 1, 4); (3, 2, 5); (4, 1, 5)}. Отношения могут быть заданы и на множествах разной природы : R Mn. M 1 M 2 ... При этом элементы ( a 1, a 2,..., a n ), находящиеся в отношении R, принадлежат соответственно a 1 M 1, a 2 M 2,..., a n M n ).
11 Бинарные отношения Для R рассмотрим: а) область определения : б) область значений: в) обратное отношение: г) композицию (для отношений R 1 и R 2 ):
12 Способы задания бинарных отношений 1.Списком (перечислением) пар, для которых это отношение выполняется. 2. Матрицей - бинарному отношению, где А ={ a 1, a 2,..., an }, соответствует квадратная матрица S порядка n, в которой элементы sij принимают два возможных значения: Пример. Пусть А = {1, 2, 3}. Задать матрицей отношение :
13 Свойства бинарных отношений
14
15
16
17
18
19
20
21
22
23
24 РАЗДЕЛ 2 Комбинаторика
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
